假设检验案例集
t检验经典案例集
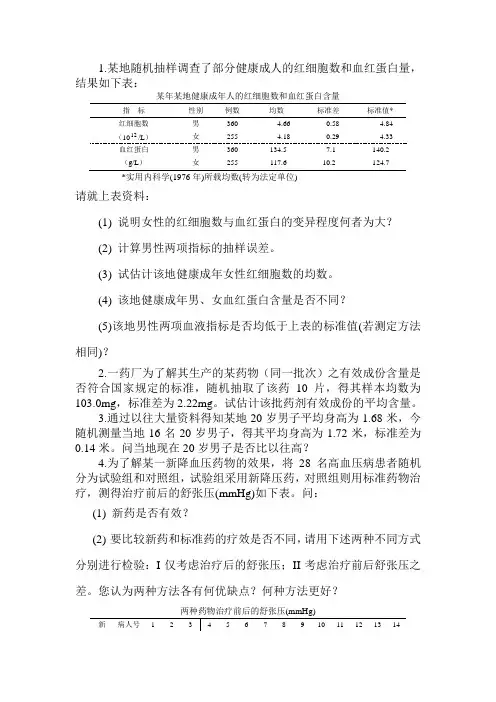
1.某地随机抽样调查了部分健康成人的红细胞数和血红蛋白量,结果如下表:某年某地健康成年人的红细胞数和血红蛋白含量指标性别例数均数标准差标准值*红细胞数男360 4.66 0.58 4.84(1012/L)女255 4.18 0.29 4.33血红蛋白男360 134.5 7.1 140.2(g/L)女255 117.6 10.2 124.7*实用内科学(1976年)所载均数(转为法定单位)请就上表资料:(1)说明女性的红细胞数与血红蛋白的变异程度何者为大?(2)计算男性两项指标的抽样误差。
(3)试估计该地健康成年女性红细胞数的均数。
(4)该地健康成年男、女血红蛋白含量是否不同?(5)该地男性两项血液指标是否均低于上表的标准值(若测定方法相同)?2.一药厂为了解其生产的某药物(同一批次)之有效成份含量是否符合国家规定的标准,随机抽取了该药10片,得其样本均数为103.0mg,标准差为2.22mg。
试估计该批药剂有效成份的平均含量。
3.通过以往大量资料得知某地20岁男子平均身高为1.68米,今随机测量当地16名20岁男子,得其平均身高为1.72米,标准差为0.14米。
问当地现在20岁男子是否比以往高?4.为了解某一新降血压药物的效果,将28名高血压病患者随机分为试验组和对照组,试验组采用新降压药,对照组则用标准药物治疗,测得治疗前后的舒张压(mmHg)如下表。
问:(1)新药是否有效?(2)要比较新药和标准药的疗效是否不同,请用下述两种不同方式分别进行检验:I仅考虑治疗后的舒张压;II考虑治疗前后舒张压之差。
您认为两种方法各有何优缺点?何种方法更好?两种药物治疗前后的舒张压(mmHg)药治疗前102 100 92 98 118 100 102 116 109 116 92 108 102 100 治疗后90 90 85 90 114 95 86 84 98 103 88 100 88 86标准药病人号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 治疗前98 103 110 110 110 94 104 92 108 110 112 92 104 90 治疗后100 94 100 105 110 96 94 100 104 109 100 95 100 855.某医师观察某新药治疗肺炎的疗效,将肺炎病人随机分为新药组和旧药组,得两组的退热天数如下表。
《数理统计》课程思政教学的最新探索和实践

Creative Education Studies 创新教育研究, 2023, 11(10), 2986-2990Published Online October 2023 in Hans. https:///journal/ceshttps:///10.12677/ces.2023.1110440《数理统计》课程思政教学的最新探索和实践李龙,朱笑雨*苏州科技大学数学科学学院,江苏苏州收稿日期:2023年8月23日;录用日期:2023年9月21日;发布日期:2023年10月9日摘要《数理统计》是统计专业基础课程,是研究随机现象客观规律性的数学学科,旨在从海量的实际数据中,挖掘具有实用价值的信息。
当前世界处于百年未有之变局,统计学作为第四次工业革命的最重要理论基础之一,正在影响着社会的方方面面。
传统的统计学课程思政内容侧重统计学理论本身,缺乏与当代最前沿的经济、社会、科技的联系,因此需要在传统思政内容的基础上,建设更加符合当代要求的思政课程。
文章从统计学在生命科学、大数据、人工智能、新能源、数字经济等国家发展重要领域的应用为切入点,可以很好地结合社会热点进行思政教育。
关键词《数理统计》,课程思政,第四次工业革命The New Exploration and Practice ofIdeological and Political Teaching in theCourse “Mathematical Statistics”Long Li, Xiaoyu Zhu*School of Mathematical Sciences, Suzhou University of Science and Technology, Suzhou JiangsuReceived: Aug. 23rd, 2023; accepted: Sep. 21st, 2023; published: Oct. 9th, 2023Abstract“Mathematical Statistics” is a basic course of statistics, which is a mathematical discipline that stu-dies the objective law of random phenomena, aiming to mine information with practical value from massive actual data. At present, the world is in a century of unprecedented changes, statistics, *通讯作者。
假设检验的案例与应用

假设检验的案例与应用摘要假设检验又称显著性检验,是统计推断的重要组成部分,其目的是在一定假设的基础上,用样本推断总体,检验实验组与对照组之间是否存在差异,差异是否显著。
在工程实践中,为了保证系统和部件的可靠性,需要建立相应的数学模型,采用概率分布和假设检验的方法进行必要的计算。
本文总结了假设检验处理检验数据的过程,并举例说明了该过程的应用。
本文首先分析了假设检验的基本思想、步骤、检验原理以及假设检验的方法等,重点讨论了假设检验在生产实践中的使用状况,丰富了假设检验在生活中的应用方面的结果。
关键词:假设检验;参数分析;实例验证1引言目前,在日常生活中,假设检验对生活和工作有着至关重要的作用,人们面对问题经常会使用假设检验进行思考,这样就可以降低人们自身因素带来的偏差,从而最大程度避免结果的不确定性给人们生活带来的影响。
通过实例的调查,可以进而拓展对假设检验的理论研究。
在现实生活中,建立的模型和解法被讨论,模型被完全讨论。
这些原则为将来假设检验在多个行业的应用提供了思路。
通常假设检验多是用在有针对性的解决问题,对问题进入深入的探讨,方案的制定等等方面。
所以,科学技术的发展,以及当前社会生活的进步都离不开假设检验。
从当前学术界关于假设检验的相关研究来看,研究成果十分丰富。
潘素娟等人[1]分别介绍了参数假设检验和非参数假设检验两种方法,并通过案例分析了假设检验理论的应用,对抽样的数据进行推断分析,为以后的实际应用提供理论依据。
缪海斌和周炳海[2]在对具体案例进行研究时发现,制造产品过程中的问题,可以引用假设检验来进行测试,从而以最短的时间找到解决的办法。
从产品在生产过程中的众多输入因素中,选出问题存在的深层次原因。
对于原因的查找需要采用假设检验的方法展开统计,从而可以探知真正的问题所在,并使用实验设计等工业工程和六西格玛改善工具对根本原因进行改进,最终显著改善了产品的质量。
张淑贵[3]指出假设检验亦称显著性检验,是统计推断的重要内容。
8.4列联表独立性检验

患心脏病 214 451 665
患其他病 597
不患心脏病 175 597 772
总计 389 1048 1437
患其他病
秃头 不秃头
患心脏病
相应的三维柱形图如图所 示, 比较来说 ,底面副对 角线上两个 柱体高度的乘 积要大一些 ,因此可以在 某种程度上认为“秃顶与 患心脏病有关”。
课题:选修2-3 8.4独立性检验
解:设H0:感冒与是否使用该血清没有关系。
1000258 284 242 216 2 K 7.075 474 526 500 500 因当H0成立时,K2≥6.635的概率约为0.01,故有99%的把握认 为该血清能起到预防感冒的作用。
2
课题:选修2-3 8.4独立性检验
第四步:查对临界值表,作出判断。
P(k≥k0) 0.50 0.40 0.25 0.15 0.10 0.05 0.025 0.010 0.005 0.001 k0 0.455 0.708 1.323 2.072 2.706 3.841 5.024 6.635 7.879 10.828
课题:选修2-3 8.4独立性检验
思考
如果K 2 6.635,就断定H0不成立,这种判断出错的可能性有多大 ?
答:判断出错的概率为0.01。
9965(7775 49 42 2099)2 现在观测值k 56.632太大了, 7817 2148 9874 91 在H 0成立的情况下能够出现这样的观测值的概率不超过0.01, 因此我们有99%的把握认为H 0不成立,即有99%的把握认为“吸烟 与患肺癌有关系”。
再冷的石头,坐上三年也会暖 !
独立性检验
2 n ( ad bc ) 随机变量-----卡方统计量 K 2 , (a b)(c d )(a c)(b d )
假设检验创新课程设计

假设检验创新课程设计一、课程目标知识目标:1. 学生能理解假设检验的基本概念,掌握其原理和步骤。
2. 学生能运用假设检验方法分析实际问题,解释检验结果。
3. 学生了解假设检验在不同领域的应用,如生物、医学、经济等。
技能目标:1. 学生能独立设计假设检验实验,包括选择检验方法、确定显著性水平等。
2. 学生能运用统计软件或计算器进行假设检验计算,处理数据并得出结论。
3. 学生具备一定的批判性思维,能对假设检验结果进行合理分析和评价。
情感态度价值观目标:1. 学生培养对统计学的好奇心和兴趣,认识到其在科学研究和现实生活中的重要性。
2. 学生在团队合作中进行假设检验实验,学会尊重他人观点,培养合作精神。
3. 学生通过解决实际问题,增强自信心,培养勇于探索、严谨治学的态度。
课程性质:本课程为高中数学选修课,旨在帮助学生掌握假设检验的基本知识和技能,提高数据分析能力。
学生特点:高中生具有较强的逻辑思维能力和抽象思维能力,对统计方法有一定了解,但实际应用能力有待提高。
教学要求:结合学生特点和课程性质,采用案例教学、小组讨论、实际操作等多种教学方法,注重培养学生的实际应用能力和批判性思维。
在教学过程中,关注学生的学习反馈,及时调整教学策略,确保课程目标的实现。
通过本课程的学习,使学生能够将假设检验应用于实际问题,提高数据分析素养。
二、教学内容本课程以人教版高中数学选修《概率与统计》教材为基础,围绕假设检验主题,组织以下教学内容:1. 假设检验的基本概念与原理- 假设检验的定义与分类- 假设检验的基本步骤- 假设检验中的两类错误2. 常见假设检验方法及其应用- 单样本t检验- 双样本t检验- 卡方检验- F检验3. 假设检验在实际问题中的应用案例分析- 生物领域的假设检验案例- 医学领域的假设检验案例- 经济领域的假设检验案例4. 假设检验中的统计软件应用- 使用Excel进行假设检验计算- 使用R语言进行假设检验分析教学内容安排与进度:第一课时:假设检验基本概念与原理第二课时:单样本t检验及其应用第三课时:双样本t检验及其应用第四课时:卡方检验及其应用第五课时:F检验及其应用第六课时:实际问题中的应用案例分析第七课时:统计软件在假设检验中的应用三、教学方法本课程采用多样化的教学方法,结合讲授法、讨论法、案例分析法、实验法等,充分激发学生的学习兴趣和主动性。
假设检验-单样本检验
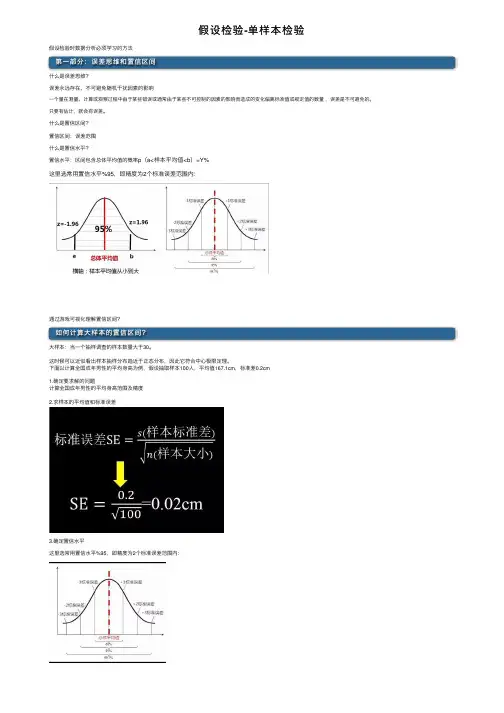
假设检验-单样本检验假设检验时数据分析必须学习的⽅法第⼀部分:误差思维和置信区间什么是误差思维?误差永远存在、不可避免随机⼲扰因素的影响⼀个量在测量、计算或观察过程中由于某些错误或通常由于某些不可控制的因素的影响⽽造成的变化偏离标准值或规定值的数量,误差是不可避免的。
只要有估计,就会有误差。
什么是置信区间?置信区间:误差范围什么是置信⽔平?置信⽔平:区间包含总体平均值的概率p(a<样本平均值<b)=Y%这⾥选常⽤置信⽔平%95,即精度为2个标准误差范围内:通过游戏可视化理解置信区间?如何计算⼤样本的置信区间?⼤样本:当⼀个抽样调查的样本数量⼤于30。
这时候可以近似看出样本抽样分布趋近于正态分布,因此它符合中⼼极限定理。
下⾯以计算全国成年男性的平均⾝⾼为例,假设抽取样本100⼈,平均值167.1cm,标准差0.2cm 1.确定要求解的问题计算全国成年男性的平均⾝⾼范围及精度2.求样本的平均值和标准误差3.确定置信⽔平这⾥选常⽤置信⽔平%95,即精度为2个标准误差范围内:4.求出置信区间上下限的值(1)由于选⽤的样本⼤⼩为100⼤于30符合正态分布,先求出如下图中两块红⾊区域⾯积(概率):(2)通过查z表格查出标准分Z=-1.96(3)求出a和b的值的⽅法:(4)根据中⼼极限定理,样本平均值约等于总体平均值,最终求出a和b的值:结论:当我们选⽤置信⽔平为%95时,求得置信区间为[167.0608,167.1392],即在两个标准误差范围内,全国成年男性的平均⾝⾼为167.0608cm到167.1392cm之间。
5.常⽤置信⽔平及其对应Z值(标准分)如何计算⼩样本的置信区间?⼩样本:当⼀个抽样调查的样本数量⼩于30。
这时候抽样分布符合t分布:在概率论和统计学中,t-分布(t-distribution)⽤于根据⼩样本来估计呈正态分布且⽅差未知的总体的均值。
如果总体⽅差已知(例如在样本数量⾜够多时),则应该⽤正态分布来估计总体均值。
第8章假设检验
24
6.假设检验的统计结论是根据原假设进行阐述的,
要么拒绝原假设,要么不拒绝原假设 • 当我们不能拒绝原假设时,我们不能说“接受 原假设”,因为我们没有证明原假设是真(如 果用“接受”则意味证明了原假设是正确的), 只不过我们没有足够的证据拒绝原假设,因此 不能拒绝原假设。当我们拒绝原假设时,得出 结论是清楚的。
拒绝原假设
小概率原理:小概率事件在一次试验中几乎不会发生 小概率的标准:与一个显著性水平a 有关, 0<a <1
13
四、假设检验的过程
提出假设 确定适当的检验统计量 规定显著性水平 计算检验统计量的值 作出统计决策
14
五、 原假设和备则假设
15
五、 原假设和备择假设
(一)原假设(null hypothesis)
我认为这种新药比原有 的药物更有效!
总体参数包括总体均 值、比例、方差等 分析之前必需陈述
如 产品合格率在80%以 上等。
9
二、什么是假设检验?
1.
2.
3.
一个假设的提出总是以一定的理由为基础,但 这些理由是不是完全充分的,要进行检验,即 进行判断。如在某种新药的研发中,研究者要 判断新药是否比原有药物更有效;海关人员对 进口货物进行检验,判断该批货物的属性是否 与申报的相一致。 假设检验就是先对总体的参数提出某种假设(原 假设和备择假设),然后利用样本信息判断假设 是否成立的过程 逻辑上运用反证法,统计上依据小概率原理
绝的却是一个真实的假设,采取的是错误行为。
31
二、显著性水平a
(significant level)
1.
2.
3.
4.
python蒙特卡洛假设检验-概述说明以及解释
python蒙特卡洛假设检验-概述说明以及解释1.引言1.1 概述蒙特卡洛方法是一种基于随机抽样的数值计算方法,在统计学中具有广泛应用。
其基本思想是通过模拟随机事件的重复实验来估计目标数量或分布的特征。
它以原型玩家蒙特卡洛赌场而得名,该赌场因为提供的随机性而难以预测结果。
在统计假设检验中,我们常常需要评估一组数据对于某个假设的支持程度。
传统的假设检验方法往往基于一些理论假设,这些假设可能在实际数据中并不成立。
而蒙特卡洛方法则提供了一种基于随机模拟的新思路,用于评估假设的可信度。
本文将首先介绍蒙特卡洛方法的基本概念和原理,包括如何使用随机抽样和重复实验来近似估计目标数量或分布的特征。
然后将对假设检验的基本概念进行详细说明,包括如何构建原假设和备择假设,以及如何计算样本统计量和p值等。
随后,本文将重点讨论蒙特卡洛方法在假设检验中的应用。
通过一系列实例和案例分析,我们将展示蒙特卡洛方法在不同类型的假设检验中的有效性和灵活性。
具体包括基于蒙特卡洛模拟的参数估计、贝叶斯假设检验和非参数检验等方面。
最后,我们将对本文进行总结,回顾蒙特卡洛方法在假设检验中的应用优势和潜在局限性,并展望其未来的发展方向。
希望本文能为读者提供一个全面了解和掌握蒙特卡洛方法在假设检验中的应用的基础,并激发更多的研究和应用探索。
1.2 文章结构本文主要分为三个主要部分,即引言、正文和结论。
每个部分都有其具体的内容和目的。
下面将对每个部分进行详细介绍:引言部分(Introduction):在引言部分,首先会对整篇文章的主题进行概述,介绍文章所要涉及的主要内容。
接着,会介绍文章结构,即对各个部分的安排进行说明,并指出各部分之间的联系和衔接。
最后,明确阐述文章的目的,即通过本文希望达到的目标或解决的问题。
正文部分(Main Body):正文部分是本文的核心内容,主要围绕Python蒙特卡洛假设检验展开。
首先,会简要介绍蒙特卡洛方法的基本概念和原理,包括其核心思想、应用领域和优势。
12and13假设检验与t检验
第12章分布类型的检验本章将涉及统计学分析中最为主要的理论之一:假设检验,它是分析统计数据、构建统计模型进行决策支持的基石。
12.1假设检验的基本思想12.1.1问题的提出12.1.2假设检验的基本步骤1.小概率事件在讨论假设检验的基本思想之前,首先需要明确小概率事件这一概念。
衡量一个事件发生与否可能性的标准是概率大小,通常概率大的事件容易发生,概率小的事件不容易发生。
习惯上将发生概率很小,如P<=0.05的事件称为小概率事件,表示在一次实验或观察中该事件发生的可能性很小,因此,如果只进行一次试验,可以视为不会发生。
这里需要澄清一个事实:注意上面的表述是“一次试验中小概率事件不应当发生”,这并不表示小概率事件不可能发生,也就是说,这里有一个前提:只进行一次试验,结果应当不会是小概率事件。
如果进行多次(可能无穷多)试验,那么小概率事件就肯定会发生,或者说,小概率事件在一次试验中不大可能发生,然而在大量试验中几乎是必然发生的。
2.小概率反证法假设检验的基本思想是统计学的“小概率反证法”原理:对于一个小概率事件而言,其对立面发生的可能性显然要大大高于这一小概率事件,可以认为,小概率事件在一次试验中不应当发生。
因此可以首先假定需要考察的假设是成立的,然后基于此进行推导,来计算一下在该假设所代表的总体中进行抽样研究得到当前样本(及更极端样本)的概率是多少。
如果结果显示这是一个小概率事件,则意味着如果假设是成立的,则在一次抽样研究中竟然就发生了小概率事件!这显然违反了小概率原理,因此可以按照反证法的思路推翻所给出的假设,认为它们实际上是不成立的,这就是小概率反证法原理。
假设检验的基本逻辑:先成立一个与H1相对立的H0。
各种假设检验方法都是根据H0来成立抽样分布,然后求出H0是正确的可能性。
如果我们能证明H0是对的可能性很小,那么就可以据此排除抽样误差的说法,认为H1可能是对的。
简言之,假设检验的基本原则是直接检验H0因而间接地检验H1,目的是排除抽样误差的可能性。
概率论与数理统计教案假设检验
概率论与数理统计教案-假设检验一、教学目标1. 理解假设检验的基本概念和原理;2. 学会使用假设检验方法对样本数据进行推断;3. 掌握假设检验的类型、步骤和判断准则;4. 能够运用假设检验解决实际问题。
二、教学内容1. 假设检验的基本概念和原理假设检验的定义假设检验的目的是什么假设检验的基本原理2. 假设检验的类型单样本检验双样本检验配对样本检验3. 假设检验的步骤建立假设选择检验统计量确定显著性水平计算检验统计量的值做出判断4. 假设检验的判断准则拒绝域和接受域检验的拒绝准则检验的接受准则5. 假设检验的应用实例应用假设检验解决实际问题实例分析与解答三、教学方法1. 讲授法:讲解假设检验的基本概念、原理、类型、步骤和判断准则;2. 案例分析法:分析实际问题,引导学生运用假设检验方法解决问题;3. 互动教学法:提问、讨论、解答学生提出的问题,促进学生理解和掌握知识;4. 练习法:布置课后作业,让学生巩固所学知识,提高运用能力。
四、教学准备1. 教案、教材、课件等教学资源;2. 投影仪、电脑等教学设备;3. 课后作业及答案。
五、教学过程1. 导入新课:回顾上一节课的内容,引入假设检验的基本概念和原理;2. 讲解假设检验的基本概念和原理,阐述其目的是什么;3. 讲解假设检验的类型,引导学生了解各种类型的假设检验;4. 讲解假设检验的步骤,让学生掌握进行假设检验的方法;5. 讲解假设检验的判断准则,使学生明白如何做出判断;6. 分析实际问题,引导学生运用假设检验方法解决问题;7. 布置课后作业,让学生巩固所学知识;8. 课堂小结,总结本节课的主要内容和知识点。
教学反思:在教学过程中,要注意引导学生理解和掌握假设检验的基本概念、原理和步骤,并通过实际问题让学生学会运用假设检验方法。
要关注学生的学习反馈,及时解答他们提出的问题,提高他们的学习兴趣和积极性。
六、教学评估1. 评估方式:课后作业、课堂练习、小组讨论、个人报告2. 评估内容:学生对假设检验基本概念的理解学生对假设检验类型和步骤的掌握学生对假设检验判断准则的应用学生解决实际问题的能力七、课后作业1. 完成教材后的练习题2. 选择一个实际问题,运用假设检验方法进行分析和解答3. 总结本节课的主要内容和知识点,写下自己的学习心得八、课堂练习1. 例题解析:分析教材中的例题,理解假设检验的步骤和判断准则2. 小组讨论:分组讨论课后作业中的问题,共同解决问题,交流学习心得3. 个人报告:选取一个实际问题,进行假设检验的分析和解题过程报告九、教学拓展1. 假设检验的扩展知识:学习其他类型的假设检验方法,如非参数检验、方差分析等2. 实际应用案例:搜集更多的实际问题,进行假设检验的分析和解答3. 软件操作实践:学习使用统计软件进行假设检验,提高数据分析能力十、教学计划1. 下一节课内容预告:介绍假设检验的扩展知识和实际应用案例2. 学习任务布置:预习下一节课的内容,准备相关问题和建议3. 课后自学计划:鼓励学生自主学习,深入了解假设检验的方法和应用教学反思:在完成本节课的教学后,要关注学生的学习情况,及时解答他们提出的问题,并提供必要的辅导。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
案例一:假设检验设备判断中的应用[1]
例如:某公司想从国外引进一种自动加工装置。
这种装置的工作温度X服从正态分布(μ,52),厂方说它的平均工作温度是80度。
从该装置试运转中随机测试16次,得到的平均工作温度是83度。
该公司考虑,样本结果与厂方所说的是否有显著差异?厂方的说法是否可以接受?
类似这种根据样本观测值来判断一个有关总体的假设是否成立的问题,就是假设检验的问题。
我们把任一关于单体分布的假设,统称为统计假设,简称假设。
上例中,可以提出两个假设:一个称为原假设或零假设,记为H0:μ=80(度);另一个称为备择假设或对立假设,记为H1 :μ≠80(度)这样,上述假设检验问题可以表示为:
H0:μ=80H1:μ≠80
原假设与备择假设相互对立,两者有且只有一个正确,备择假设的含义是,一旦否定原假设H0,备择假设H1备你选择。
所谓假设检验问题就是要判断原假设H0是否正确,决定接受还是拒绝原假设,若拒绝原假设,就接受备择假设。
应该如何作出判断呢?如果样本测定的结果是100度甚至更高(或很低),我们从直观上能感到原假设可疑而否定它,因为原假设是真实时,在一次试验中出现了与80度相距甚远的小概率事件几乎是不可能的,而现在竟然出现了,当然要拒绝原假设H0。
现在的问题是样本平均工作温度为83度,结果虽然与厂方说的80度有差异,但样本具有随机性,80度与83度之间的差异很可能是样本的随机性造成的。
在这种情况下,要对原假设作出接受还是拒绝的抉择,就必须根据研究的问题和决策条件,对样本值与原假设的差异进行分析。
若有充分理由认为这种差异并非是由偶然的随机因素造成的,也即认为差异是显著的,才能拒绝原假设,否则就不能拒绝原假设。
假设检验实质上是对原假设是否正确进行检验,因此,检验过程中要使原假设得到维护,使之不轻易被否定,否定原假设必须有充分的理由;同时,当原假设被接受时,也只能认为否定它的根据不充分,而不是认为它绝对正确。
[编辑]
案例二:假设检验在卷烟质量判断中的应用[2]
在卷烟生产企业经常会遇到如下的问题:卷烟检验标准中要求烟支的某项缺陷的不合格品率P不能超过3%,现从一批产品中随机抽取50支卷烟进行检验,发现有2支不合格品,问此批产品能否放行?按照一般的习惯性思维:50支中有2支不合格品,不合格品率就是4%,超过了原来设置的3%的不合格品率,因此不能放行。
但如果根据假设检验的理论,在α=0.05的显著性水平下,该批产品应该可以放行。
这是为什么呢?
最关键的是由于我们是在一批产品中进行抽样检验,用抽样样本的质量水平来判别整批的质量水平,这里就有一个抽样风险的问题。
举例来说,我们的这批产品共有10000支卷烟,里面有4支不合格品,不合格品率是0.04%,远低于3%的合格放行不合格品率。
但我们的检验要求是随机抽样50支,用这50支的质量水平来判别整批 10000支的质量水平。
如果在50支中恰好抽到了2支甚至更多的不合格品,简单地用抽到的不合格品数除以50来作为不合格品率来判断,那我们就会对这批质量水平合格的产品进行误判。
如何科学地进行判断呢?这就要用到假设检验的理论。
步骤1:建立假设
要检验的假设是不合格品率P是否不超过3%,因此立假设
H0:P≤0.03
这是原假设,其意是:与检验标准一致。
H1:P>0.03
步骤2:选择检验统计量,给出拒绝域的形式
若把比例P看作n=1的二项分别b(1,p)中成功的概率,则可在大样本场合(一般n≥25)获得参数p的近似μ的检验,可得样本统计量:近似服从N(0,1)
其中=2/50=0.04,p=0.03,n=50
步骤3:给出显著性水平α,常取α=0.05。
步骤4:定出临界值,写出拒绝域W。
根据α=0.05及备择假设知道拒绝域W为
步骤5:由样本观测值,求得样本统计量,并判断。
结论:在α=0.05时,样本观测值未落在拒绝域,所以不能拒绝原假设,应允许这批产品出厂。
假设检验中的两类错误。
进一步研究一下这个例子,在50个样品中抽到多少个不合格品,就要拒绝入库呢?我们仍取α=0.05,根据上述公式,得出,解得x>3.48,也就是在50个样品中抽到4个不合格品才能判整批为不合格。
而如果我们改变α的取值,也就是我们定义的小概率的取值,比如说取α=0.01,认为概率不超过0.01的事件发生了就是不合理的了,那又会怎样呢?
还是用上面的公式计算,则得出,解得x>4.30,也就是在50个样品中抽到5个不合格品才能判整批为不合格。
检验要求是不合格品率 P不能超过3%,而现在根据α=0.01,算出来50个样品中抽到5个不合格品才能判整批为不合格,会不会犯错误啊!假设检验是根据样本的情况作的统计推断,是推断就会犯错误,我们的任务是控制犯错误的概率。
在假设检验中,错误有两类:
第一类错误(拒真错误):原假设H0为真(批产品质量是合格的),但由于抽样的随机性(抽到过多的不合格品),样本落在拒绝域W内,从而导致拒绝H0(根据样本的情况把批质量判断为不合格)。
其发生的概率记为α,也就是显著性水平。
α控制的其实是生产方的风险,控制的是生产方所承担的批质量合格而不被接受的风险。
第二类错误(取伪错误):原假设H0不真(批产品质量是不合格的),但由于抽样的随机性(抽到过少的不合格品),样本落在W外,从而导致接受H0(根据样本的情况把批质量判断为合格)。
其发生的概率记为β。
β控制的其实是使用方的风险,控制的是使用方所承担的接受质量不合格批的风险。
再回到刚刚计算的上例的情况,α由0.05变化为0.01,我们对批质量不合格的判断由50 个样本中出现4个不合格变化为5个,批质量是合格的而不被接受的风险就小了,犯第一类错误的风险小了,也就是生产方的风险小了;但同时随着α的减小对批质量不合格的判断条件其实放宽了——50个样本中出现4个不合格变化为5个,批质量是不合格的而被接受的风险大了;犯第二类错误的风险大了,也就是使用方的风险大了。
在相同样本量下,要使α小,必导致β大;要使β小,必导致α大,要同时兼顾生产方和使用方的风险是不可能的。
要使α、β皆小,只有增大样本量,这又增加了质量成本。
因此综上所述,假设检验可以告诉我们如何科学地进行质量合格判定,又告诉我们要兼顾生产方和使用方的质量风险,同时考虑质量和成本的问题。
