假设检验案例
参数估计和假设检验案例
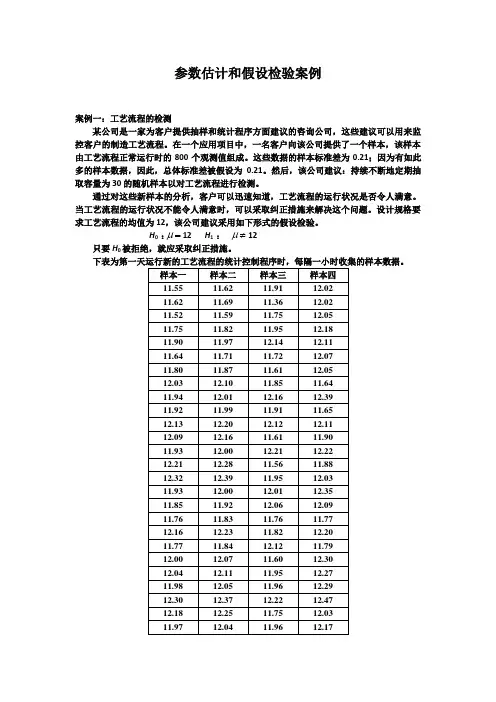
参数估计和假设检验案例案例一：工艺流程的检测某公司是一家为客户提供抽样和统计程序方面建议的咨询公司，这些建议可以用来监控客户的制造工艺流程。
在一个应用项目中，一名客户向该公司提供了一个样本，该样本由工艺流程正常运行时的800个观测值组成。
这些数据的样本标准差为0.21；因为有如此多的样本数据，因此，总体标准差被假设为0.21。
然后，该公司建议：持续不断地定期抽取容量为30的随机样本以对工艺流程进行检测。
通过对这些新样本的分析，客户可以迅速知道，工艺流程的运行状况是否令人满意。
当工艺流程的运行状况不能令人满意时，可以采取纠正措施来解决这个问题。
设计规格要求工艺流程的均值为12，该公司建议采用如下形式的假设检验。
μ=μ≠H0 ：12 H1 ：12只要H0被拒绝，就应采取纠正措施。
下表为第一天运行新的工艺流程的统计控制程序时，每隔一小时收集的样本数据。
问题：1、对每个样本在0.01的显著性水平下进行假设检验，并且确定，如果需要Z0.005=2.582、4、讨论将显著性水平改变为一个更大的值时的影响？如果增加显著性水平，哪种错误或误差将增加？显著性水平增加，置信区间减小，误差减小。
案例二：计算机辅助教学会使完成课程的时间差异缩小吗？某课程引导性教程采用一种个性化教学系统，每位学生观看教学录像，然后给以程式化的教材。
每位学生独立学习直至完成训练并通过考试。
人们关心的问题是学生完成训练计划的进度不同。
有些学生能够相当快地完成程式化教材，而另一些学生在教材上需要花费较长的时间，甚至需要加班加点才能完成课程。
学的较快的学生必须等待学得较慢的学生完成引导性课程才能一起进行其他方面的训练。
建议的替代系统是使用计算机辅助教学。
在这种方法中，所有的学生观看同样的讲座录像，然后每位学生被指派到一个计算机终端来接受进一步的训练。
在整个教程的自我训练过程中，由计算机指导学生独立操作。
为了比较建议的和当前的教学方法，刚入学的122名学生被随机地安排到这两种教学系统中。
bootstrap假设检验 案例
一、概述在统计学中，假设检验是一种常用的推断性统计方法，用于判断样本数据的特征是否符合某种假设条件。
bootstrap假设检验是一种基于重复抽样的非参数检验方法，相较于传统假设检验方法，其具有更广泛的适用范围和更强的鲁棒性。
本文将通过一个具体的案例来介绍bootstrap假设检验的应用和实现方法，并探讨其在实际数据分析中的价值和意义。
二、案例背景假设有一个电商评台A和一个电商评台B，它们分别在同一时间段内进行了一次促销活动，目的是比较两个评台的促销效果是否存在显著差异。
对于这个问题，我们可以使用bootstrap假设检验来进行分析，以确定两个评台的促销效果是否存在统计学上的显著差异。
三、数据收集为了进行bootstrap假设检验，我们首先需要收集来自两个电商评台的促销活动数据，包括参与活动的用户数量、用户下单金额等相关信息。
这些数据可以从两个评台的后台数据库中获取，或者通过统计分析工具来进行数据采集和整理。
四、假设设定在进行假设检验前，我们需要明确研究问题的假设设定。
针对本案例，我们可以进行如下假设设定：- 零假设H0：电商评台A和电商评台B的促销效果没有显著差异。
- 备择假设H1：电商评台A和电商评台B的促销效果存在显著差异。
五、bootstrap抽样在进行bootstrap假设检验时，我们首先需要进行重复抽样。
具体来说，我们可以从两个电商评台的促销活动数据中随机抽取一定数量的样本，然后利用这些样本数据来构建抽样分布。
重复这个过程多次，得到多个抽样分布。
六、统计量计算在得到多个抽样分布之后，我们需要计算统计量以进行假设检验。
对于本案例，可以选择比较两个评台的用户下单金额的平均值作为统计量，计算两个抽样分布的差异。
七、bootstrap假设检验我们可以进行bootstrap假设检验，以判断零假设H0的拒绝与否。
具体来说，可以计算出抽样分布中比真实观测值更特殊的概率，若该概率小于显著性水平（通常设定为0.05），则可以拒绝零假设，认为两个评台的促销效果存在显著差异；反之，则接受零假设。
参数估计和假设检验案例
参数估计和假设检验案例假设我们是一家制造公司的数据分析师，公司最近收到用户对产品的投诉，称产品的平均使用寿命低于承诺的使用寿命。
为了验证这一断言，我们希望利用采样数据对产品的平均使用寿命进行估计，并进行假设检验来验证用户的主张。
1.参数估计：为了对产品的平均使用寿命进行估计，我们需要收集一定数量的样本数据。
假设我们从该公司生产的100个产品中随机选择了20个，然后记录了它们的使用寿命（以年为单位）。
收集到的数据如下：15,12,18,20,14,16,19,17,13,11,14,16,21,15,17,14,13,12,19,18首先，我们需要计算这些数据的样本均值来进行参数估计。
样本均值的计算公式为：样本均值=(15+12+18+20+14+16+19+17+13+11+14+16+21+15+17+14+13+12+19+18)/2 0=16.5因此，用收集到的样本数据估计该公司生产的产品的平均使用寿命为16.5年。
2.假设检验：接下来，我们需要进行假设检验来验证用户的主张。
在本案例中，我们的原假设（H0）为产品的平均使用寿命等于承诺的使用寿命，备择假设（H1）为产品的平均使用寿命小于承诺的使用寿命。
我们设定显著性水平为0.05，即我们希望在5%的置信水平下进行判断。
在通过参数估计得到产品的平均使用寿命估计值后，我们可以利用假设检验来验证该估计值是否与承诺的使用寿命相符。
假设检验的步骤如下：1）设定原假设（H0）和备择假设（H1）；2）选择一个合适的统计检验方法；3）计算检验统计量（test statistic）；4）计算p值；5）根据p值判断是否拒绝原假设。
在本案例中，由于样本数量较小（n<30），符合正态分布的假设也未被验证，我们可以选择使用t检验来进行假设检验。
根据我们的备择假设，我们希望验证产品的平均使用寿命小于承诺的使用寿命。
因此，我们将进行单样本t检验，计算检验统计量和p值。
假设检验案例
案例在单个总体参数的检验中，用到的检验统计量主要有3个：Z统计量、t统计量和x2统计量。
Z统计量、t统计量常用于均值的检验。
x2统计量常用于方差的检验。
例1某地区20户家庭年收入数据为例进行均值的检验，20户家庭的年收入的原始数据见excel（第八章案例）。
（1）提出原假设和备择假设H 0：μ=15（2）计算样本个数count 。
单元格D2=“COUNT(A2:A21)”（3）计算样本均值average 。
单元格D3=“AVERAGE(A2:A21)”D4单元格输入公式“=（D3-15)/SQRT(16)/SQRT(D2)”，相当于z 值的计算公式nx /_σµ−Z＜-1.96或Z＞1.96rs,P值来判断是否接受原假设P=2*(1-D5）总体方差未知的情况下，对均值进行检验计算样本方差。
在D4单元格中输入函数“=VAR(A2:A21)例2一家百货公司的管理者打算为公司的信用卡客户安装一套新的账单系统。
在进行了全面的财务分析后，她发现只有当平均每人每月的账单上的消费超过170元时，安装这个新系统才可以收回成本。
抽取了400个人的每月账单构成随机样本，它们的平均数是178元。
这个管理者知道账单大致服从标准差为65元的正态分布。
H0：μ≤170（不安装新系统）H1：μ＞170（安装新系统）α1 1 --αμ=170 拒绝域α1 1 --α的值：=175.62L x −μ=170 拒绝域α1 1 --αμ=0 拒绝域α1 1 --α因为2.46>1.645，所以拒绝原假设，我们有足够的证据可推断每月账单均值大于170元。
近年来，很多公司在长途电话业务上和A公司竞争。
这些公司在广告上的费率明显低于A公司，从而有人认为客户账单上的花费也要少。
然后他抽取了100个客户的随机样本，用竞争对手在广告中所引用的费率重新计算了这些客户的话费账单。
假定总体的标准差和A公司的一样，在5%的置信水平下，我们能否认为A公司与其他竞争者的账单有区别。
【解决】用假设检验方法解决实际问题
【关键字】解决案例名：对饮酒对工作能力是否有显著的影响的假设检验分析姓名：范晓维班级：人力031学号：07提交时间：用假设检验方法解决实际问题一：假设检验实际案例：任选19个工人分成两组，让他们每人做一件同样的工作，测得他们的完工时间（单位：分钟）如下：饮酒者 30 46 51 34 48 45 39 61 58 67 未饮酒者 28 22 55 45 39 35 42 38 20 问：饮酒对工作能力是否有显著的影响？（显著水平α＝0.05）二：就案例中所面临的问题进行分析随是社会科学的快速发展，各种设施越发齐全，饮酒给大家带来快乐的同时也经常给大家带来不少的困扰和麻烦，甚至危急生命！本案例就饮酒是否对工作能力有影响做了一个假设检验的案例。
这个案例的特点是先提出了一个假设，然后要求从样本出发检验它是否成立，这就是假设检验问题。
假设检验的基本步骤：1：根据问题的性质和要求，提出零假设H0和备择假设H12:构造一个合适的统计量Q,它必须与假设有关，并且在H0成立的情况下，统计量Q的分布是已知的3：给定显著性水平α，确定H0的拒绝域W4：由样本观测值计算出统计量Q的值Q05:对假设H0做出判断：若统计量的值Q0落如拒绝域W内，则拒绝H0，否则接受H0对上题求解：解设两组工人的完工时间分别为总体ε～N（μ1，σ12）和η～N （μ2 ,σ22）,其中σ1，σ2 未知，但假设以知有σ1＝σ2，问题相当于要检验H0: μ1 = μ2是否成立。
m=10, =47.9,Sx2=125.29,n=9, =36.0, Sy2=112.00,Sω===11.5323T=(- )=2.2458对α＝0.05，m+n-2=17，查t分布表，可得由于=2.2458>2.1098,因此拒绝H0: μ1 = μ2,从检验得出的结论是：饮酒对工作能力有显著的影响。
用SPSS的方法：Independent-Samples T Test 过程Analyze-Compare means-Indepant Samples T test附页：数理统计学及其应用领域数理统计学是“数学的一个分支学科。
t检验-假设检验-案例
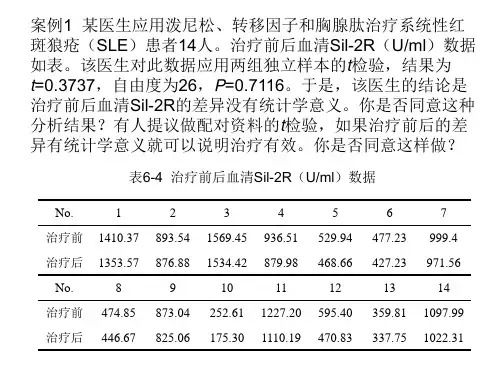
（1）本例结论是否正确？为什么？
（2）该结论可能犯第几型错误？
案例3 为确定老年人围手术期头孢唑林钠的合理用法和用 量，某研究小组对60岁及以上的老年患者与60岁以下的患 者，服用头孢唑林钠的药物动力学特征分别进行测量，并 进行了统计分析，结果见下表，研究者据此认为a和K10两 项指标在两组间无差别。该研究结论是否可靠？为什么？
病历号 1 2 3 4 5 6 7 8
8例恶性滋养细胞肿瘤患者灌注治疗前后hCG值
治疗前（x1） 1280000 75500 12450 1500000 10000 97000 15588 4223
治疗后（x2） 210000 3300 2210 9.3 2500 1203 4825 914
lg(x1) 6.1072 4.8779 4.0952 6.1761 4.0000 3.9868 4.1928 3.6256
lg(x2) 5.322 3.5185 3.3444 0.9685 3.3979 3.0803 3.6835 2.9609
两组患者头孢唑林钠药物动力学参数比较
组别
a
K10
60岁及以上老年组 （n=7）
60岁以下组(n=5）
0.6213±0.1177 3.5505±3.5553
假设检验女士品茶 教学案例
假设检验女士品茶教学案例假设检验在统计学中是一种常用的分析方法，用于判断样本数据是否支持某种假设。
假设检验可以帮助我们进行科学的实验设计和数据分析，从而得出可靠的结论。
在教学实践中，假设检验通常需要通过案例来进行深入的理解和应用。
本文将以“女士品茶”的教学案例为例，详细解释假设检验的理论和应用，并结合实际操作，帮助学生更好地掌握这一统计分析方法。
一、案例背景在一家茶叶公司中，经理想测试一种新的女士品茶的口感是否符合女性顾客的口味。
他假设该新品茶的口感更柔和、更香甜，适合女性消费者。
为了验证这一假设，经理决定通过假设检验来进行数据分析，以判断新品茶是否真的更受女性顾客喜爱。
二、实验设计为了进行这项实验，经理决定邀请100名女性顾客参与品尝两种茶的实验。
50名女性顾客品尝传统茶叶，另外50名女性顾客品尝新品茶。
经理要求参与者在品尝后填写调查表，评价茶叶的口感，并且记录每位参与者的年龄、喜好等信息。
三、数据收集经理在实验结束后收集了所有调查表并整理数据。
他得到了传统茶叶和新品茶的口感评分数据，以及参与者的个人信息。
他还得到了相应的样本均值和标准差。
四、假设检验过程1. 建立假设在进行假设检验前，我们需要先建立原假设（H0）和备择假设（H1）。
在这个案例中，经理的原假设可以是：“新品茶的口感更柔和、更香甜”，备择假设可以是：“新品茶的口感不一定更柔和、更香甜”。
经理希望通过假设检验得出的结论能够支持原假设，从而认可新品茶更适合女性消费者的口味。
2. 选择检验方法根据实际情况，经理可以选择合适的检验方法。
在这个案例中，如果口感评分数据符合正态分布且满足方差齐性的要求，可以选择t检验来进行假设检验。
如果数据不符合正态分布或者不满足方差齐性要求，可以选择非参数检验方法。
3. 计算统计量并进行假设检验经理可以利用样本数据计算出相应的t值或者z值，并结合显著性水平α（通常取0.05）来进行假设检验。
根据计算结果，经理可以判断是否拒绝原假设。
假设检验流程案例分析
假设检验流程案例分析一、假设检验的基本概念。
1.1 什么是假设检验呢？简单来说，这就像是一场法庭审判。
我们有一个“被告”，也就是我们要检验的假设。
比如说，我们想知道一种新的减肥方法是不是真的有效，那“这种减肥方法有效”就是我们的假设。
我们不能轻易就相信这个说法，得拿出证据来。
1.2 这里面有个很重要的东西叫“显著性水平”。
这就好比是我们判断事情的一个标准。
如果把生活中的事情比作考试，那显著性水平就是及格线。
一般我们会设定一个值，像0.05或者0.01。
如果计算出来的结果小于这个值，那就像考试不及格一样，我们就有理由怀疑我们的假设是错的。
2.1 案例背景。
咱就说有个工厂，他们生产的灯泡，以前一直说平均使用寿命是1000小时。
但是最近呢，工人换了新的生产工艺，老板就想知道，这新的工艺下，灯泡的平均使用寿命是不是还是1000小时。
这时候我们的假设就出来了。
原假设就是“新工艺下灯泡平均使用寿命还是1000小时”，那备择假设就是“新工艺下灯泡平均使用寿命不是1000小时”。
2.2 收集数据。
这就好比破案要找线索一样。
我们得去收集灯泡使用寿命的数据。
从新生产的灯泡里随机抽取一些，比如抽取了50个灯泡，然后测试它们各自的使用寿命。
这一步可得认真，要是数据不准确，那就好比地基没打好，后面全是白搭。
2.3 选择检验统计量并计算。
这里就有点技术含量了。
根据我们的问题和数据类型，选择合适的检验统计量。
就像我们要开锁，得选对钥匙一样。
对于这个灯泡的例子，可能会用到t检验或者z 检验。
计算出这个统计量的值之后，就像是我们算出了一个“关键指标”。
2.4 做出决策。
计算出统计量的值后，我们就可以根据显著性水平来做决定了。
如果这个值落在了我们事先设定的“拒绝域”里，那就像证据确凿一样，我们就拒绝原假设。
就好比我们发现这个新生产工艺下灯泡的平均使用寿命和1000小时相差太多，那我们就有理由相信原假设不成立了。
要是不在拒绝域里，那我们就没有足够的证据拒绝原假设，只能暂时认为原假设是对的。
假设检验案例
假设检验案例Quality Associates 是一家咨询公司，为委托人监控其制造过程提供抽样和统计程序方面的建议。
在某一应用中，一名委托人向Quality Associates 提供了其生产过程正常运行时的800个观察值组成的一个样本。
这些数据的样本标准差为0.21，因而我们假定总体的标准差为0.21。
Quality Associates 建议该委托人连续地定期选取样本容量为30的随机样本来对该生产过程进行监控。
通过对这些样本的分析，委托人可以迅速了解该生产过程的运行状况是否令人满意。
当生产过程运行不正常时，应采取纠正措施以避免出现问题。
设计规格要求该生产过程的均值为12，Quality Associates 建议采用如下形式的假设检验：12:12 :10≠=μμH H只要0H 被拒绝，就应采取纠正措施。
以下的样本为新的统计监控程序运行的第一天，每间隔1小时所收集到的。
管理报告:1.对每个样本在0.01的显著水平下进行假设检验，如果需要采取措施的话，确定应该采取何种措施？给出每个检验的检验统计量和p－值。
2.计算每一样本的标准差。
假设总体标准差为0.21是否合理？3. 当样本均值x 在12=μ附近的多大范围内，我们可以认为该生产过程的运行令人满意？如果x 超过上限或低于下限，则应对其采取纠正措施。
在质量控制中，这类上限或下限被称作上侧或下侧控制限。
4. 当显著水平变大时，暗示着什么？这时，哪种错误或误差将增大？管 理 报 告1. 对每个样本在0.01的显著水平下进行假设检验，如果需要采取措施的话，确定应该采取何种措施？给出每个检验的检验统计量和p －值。
(1) 假设检验 a) 提出假设：12:12:10≠=μμH Hb) 统计量及分布： ()()1,0~N X n Z σμ-=c) 给出显著水平 01.0=α576.22=−→−αZ置信区间为：⎥⎦⎤⎢⎣⎡+-=n Z x n Z x I σσααα22 , 样本1： 1αI ⎥⎦⎤⎢⎣⎡+-=3021.0576.296.11,3021.0576.296.11 [][]06.12 ,86.1110.096.11,10.096.11=+-= 样本2：2αI ⎥⎦⎤⎢⎣⎡+-=3021.0576.203.12,3021.0576.203.12 [][]13.12 ,93.1110.003.12,10.003.12=+-=样本3：3αI ⎥⎦⎤⎢⎣⎡+-=3021.0576.289.11,3021.0576.289.11 [][]99.11 ,79.1110.089.11,10.089.11=+-=样本4：4αI ⎥⎦⎤⎢⎣⎡+-=3021.0576.203.12,3021.0576.203.12 [][]18.12 ,98.1110.008.12,10.008.12=+-=d) 统计决策：因为432112,12,12,12ααααI I I I ∉∈∉∉，所以对于样本1、样本2、样本4来讲可做出拒绝原假设12:0=μH 的统计决策，而对于样本3来讲则不拒绝原假设12:0=μH 。
假设检验的案例与应用
假设检验的案例与应用
案例1：一家电商网站新上线了一个广告推广功能，想要测试该功能是否能够有效提升用户成交率。
他们将5000个随机选取的用户分成两组，其中一组只看到常规的广告，另外一组则看到常规广告和新推出的广告。
在一个月的时间内，两组用户的成交率分别为5.7%和6.2%。
经过计算和分析，得到的假设检验结果为t值为2.56，p值为0.011，意味着该网站可以拒绝0.05的显著性水平，即可以认为新广告推广功能确实可以有效提升用户成交率。
应用：电商网站可以通过假设检验来验证其新产品或功能是否有助于提升或改善客户的体验。
案例2：一位医生想要测试药物对于一种病毒的治疗效果，他们将100名患者随机分成两组，其中一组接受药物治疗，另外一组则接受安慰剂治疗。
在4周后，两组患者的病情好转率分别为65%和40%。
经过计算和分析，得到的假设检验结果为t值为3.12，p值为0.002，说明该医生可以拒绝0.05的显著性水平，即认为药物确实具有能够提高患者病情好转率的治疗效果。
应用：医生和药物制造商可以通过假设检验来验证药物是否有效，以及在何种程度上有效治疗疾病。
案例3：一家公司想要测试早上和下午两个时间段对于员工工作效率的影响。
他们选择了同一组员工，在早上和下午分别工作了8小时，工作时长和任务的性质
是相同的。
经过计算和分析，得到的假设检验结果为t值为1.27，p值为0.21，无法拒绝0.05的显著性水平，说明该公司无法判断早上和下午对员工工作效率的影响是否显著不同。
应用：公司可以通过假设检验来验证员工是否对特定因素有敏感性，以得出更好的工作时间和任务分配方案。
利用Excel假设检验解决实际问题的案例分析
利用Excel假设检验解决实际问题的案例分析在当今的数据驱动时代，数据分析和决策制定变得日益重要。
Excel 作为一款广泛使用的电子表格软件，不仅在数据整理和计算方面表现出色，还提供了强大的统计分析功能，其中假设检验就是解决实际问题的有力工具之一。
假设检验是一种基于样本数据来判断关于总体的某个假设是否成立的统计方法。
它在商业、金融、医疗、科研等众多领域都有着广泛的应用。
接下来，我们将通过几个具体的案例来展示如何利用 Excel 中的假设检验功能解决实际问题。
案例一：产品质量改进假设某工厂生产一种电子元件，其平均使用寿命的目标值为 5000 小时。
为了提高产品质量，工厂采取了一项新的生产工艺。
从改进后的生产线上随机抽取了 50 个电子元件进行测试，得到样本的平均使用寿命为 5100 小时，样本标准差为 200 小时。
那么，能否认为新的生产工艺显著提高了产品的平均使用寿命呢？在 Excel 中，我们可以使用 t 检验来解决这个问题。
首先，我们提出假设：原假设（H0）：新生产工艺下产品的平均使用寿命没有提高，即μ ≤ 5000 小时。
备择假设（H1）：新生产工艺下产品的平均使用寿命有所提高，即μ ＞ 5000 小时。
然后，在 Excel 中选择“数据分析”工具，找到“t 检验：平均值的成对二样本分析”。
输入相关数据，得到 t 统计量和 p 值。
假设显著水平（α）为 005，如果 p 值小于 005，我们就拒绝原假设，认为新的生产工艺显著提高了产品的平均使用寿命；如果 p 值大于 005，则不能拒绝原假设。
案例二：营销活动效果评估一家电商企业开展了一次促销活动，想知道这次活动是否显著提高了产品的平均销售额。
活动前，产品的平均日销售额为 10000 元。
活动期间，随机抽取了 30 天的销售额数据，样本平均日销售额为 12000 元，样本标准差为 3000 元。
同样，我们先提出假设：原假设（H0）：促销活动没有显著提高产品的平均销售额，即μ ≤ 10000 元。
假设检验案例范文
假设检验案例范文假设检验是统计分析中最常用的方法之一，用于判断统计样本与其中一种已知条件是否相符。
在假设检验中，我们通常会提出一个假设（称为原假设）和另外一个相反的假设（称为备择假设），然后利用样本数据来判断两个假设的成立情况。
下面我们以一个实例来进行假设检验的分析。
假设我们想要研究医院住院患者的平均住院天数。
我们假设该医院的平均住院天数为7天，并使用样本数据对这个假设进行检验。
我们从该医院中随机抽取了100个患者，并记录了他们的住院天数。
假设这100个患者的住院天数的均值为8天，标准差为2天。
首先，我们需要明确原假设和备择假设。
在这个例子中，原假设可以表示为“该医院的平均住院天数为7天”，备择假设可以表示为“该医院的平均住院天数不等于7天”。
接下来，我们需要选择适当的统计检验方法。
由于我们关注的是一个总体均值，并且样本的大小大于30，所以我们可以使用z检验。
z检验的计算公式如下：z=(x-μ)/(σ/√n)其中，x是样本均值，μ是假设的总体均值，σ是总体标准差，n是样本大小。
根据我们的例子，代入具体数值进行计算。
x=8，μ=7，σ=2，n=100z=(8-7)/(2/√100)=5得到z的值为5接下来，我们需要根据选择的显著性水平来确定拒绝域。
显著性水平是一个预先设定的阈值，用于判断原假设是否应该被拒绝。
通常使用的显著性水平有0.05和0.01、在这个例子中，我们选择显著性水平为0.05根据显著性水平，我们可以查找标准正态分布表，找到对应的临界值。
在这个例子中，显著性水平为0.05，双侧测试，所以我们需要查找临界值的两侧各0.025的z值。
查表可知，对应的两个临界值分别为-1.96和1.96最后，我们将计算得到的z值与临界值进行对比。
如果z值在临界值范围内，那么我们接受原假设；如果z值超出了临界值范围，那么我们拒绝原假设。
在这个例子中，计算得到的z值为5，远远超过了临界值范围。
因此，我们可以拒绝原假设，即认为该医院的平均住院天数不等于7天。
t检验 经典案例
t检验经典案例经典案例：t检验1. 研究背景t检验是统计学中常用的假设检验方法之一，用于比较两个样本均值是否有显著差异。
下面将介绍一些经典案例，以帮助读者更好地理解t检验的应用。
2. 独立样本t检验案例案例1：某医院想比较两种降压药物的疗效，随机选取了两组高血压患者，一组服用药物A，另一组服用药物B，通过测量患者的收缩压，使用独立样本t检验来判断两种药物的疗效是否有显著差异。
案例2：某公司想评估两种不同培训方法对员工销售业绩的影响，随机选取了两组员工，一组接受传统培训，另一组接受新的培训方法，通过比较两组员工的销售额，使用独立样本t检验来判断两种培训方法是否有显著差异。
3. 配对样本t检验案例案例3：某学校想研究一种新的学习方法对学生的成绩是否有帮助，随机选取了一组学生，在某次考试前和考试后分别进行测试，使用配对样本t检验来比较学生在考试前后的成绩是否有显著差异。
案例4：某厂商想评估一种新的生产工艺对产品质量的影响，随机选取了一批产品，在使用新工艺前和使用新工艺后进行质量检测，使用配对样本t检验来判断产品在两种工艺下的质量是否有显著差异。
4. 单样本t检验案例案例5：某公司想评估员工的满意度水平，随机选取了一组员工，使用单样本t检验来判断员工的满意度是否显著高于平均水平。
案例6：某城市想研究居民的平均月收入水平，随机选取了一批居民，使用单样本t检验来判断居民的平均月收入是否显著高于全国平均水平。
5. 非参数t检验案例案例7：某医院想比较两组癌症患者的存活率，由于数据不符合正态分布，使用非参数t检验（如Wilcoxon秩和检验）来判断两组患者的存活率是否有显著差异。
案例8：某公司想比较两种广告宣传方式对销售额的影响，由于数据不符合正态分布，使用非参数t检验（如Mann-Whitney U检验）来判断两种宣传方式是否有显著差异。
6. 多样本t检验案例案例9：某学校想评估不同年级学生的平均成绩是否有显著差异，随机选取了三个年级的学生，使用多样本t检验（如单因素方差分析）来判断不同年级学生的平均成绩是否有显著差异。
假设检验案例集
案例一：假设检验设备判断中的应用1例如：某公司想从国外引进一种自动加工装置..这种装置的工作温度X服从正态分布μ;52;厂方说它的平均工作温度是80度..从该装置试运转中随机测试16次;得到的平均工作温度是83度..该公司考虑;样本结果与厂方所说的是否有显著差异厂方的说法是否可以接受类似这种根据样本观测值来判断一个有关总体的假设是否成立的问题;就是假设检验的问题..我们把任一关于单体分布的假设;统称为统计假设;简称假设..上例中;可以提出两个假设：一个称为原假设或零假设;记为H0：μ=80度；另一个称为备择假设或对立假设;记为H1 ：μ≠80度这样;上述假设检验问题可以表示为：H0：μ=80H1：μ≠80原假设与备择假设相互对立;两者有且只有一个正确;备择假设的含义是;一旦否定原假设H0;备择假设H1备你选择..所谓假设检验问题就是要判断原假设H0是否正确;决定接受还是拒绝原假设;若拒绝原假设;就接受备择假设..应该如何作出判断呢如果样本测定的结果是100度甚至更高或很低;我们从直观上能感到原假设可疑而否定它;因为原假设是真实时; 在一次试验中出现了与80度相距甚远的小概率事件几乎是不可能的;而现在竟然出现了;当然要拒绝原假设H0..现在的问题是样本平均工作温度为83度;结果虽然与厂方说的80度有差异;但样本具有随机性;80度与83度之间的差异很可能是样本的随机性造成的..在这种情况下;要对原假设作出接受还是拒绝的抉择;就必须根据研究的问题和决策条件;对样本值与原假设的差异进行分析..若有充分理由认为这种差异并非是由偶然的随机因素造成的;也即认为差异是显著的; 才能拒绝原假设;否则就不能拒绝原假设..假设检验实质上是对原假设是否正确进行检验;因此;检验过程中要使原假设得到维护;使之不轻易被否定;否定原假设必须有充分的理由；同时;当原假设被接受时;也只能认为否定它的根据不充分;而不是认为它绝对正确..编辑案例二：假设检验在卷烟质量判断中的应用2在卷烟生产企业经常会遇到如下的问题：卷烟检验标准中要求烟支的某项缺陷的不合格品率P不能超过3%;现从一批产品中随机抽取50支卷烟进行检验;发现有2支不合格品;问此批产品能否放行按照一般的习惯性思维：50支中有2支不合格品;不合格品率就是4%;超过了原来设置的3%的不合格品率;因此不能放行..但如果根据假设检验的理论;在α＝0.05的显著性水平下;该批产品应该可以放行..这是为什么呢最关键的是由于我们是在一批产品中进行抽样检验;用抽样样本的质量水平来判别整批的质量水平;这里就有一个抽样风险的问题..举例来说;我们的这批产品共有10000支卷烟;里面有4支不合格品;不合格品率是0.04%;远低于3%的合格放行不合格品率..但我们的检验要求是随机抽样50支;用这50支的质量水平来判别整批 10000支的质量水平..如果在50支中恰好抽到了2支甚至更多的不合格品;简单地用抽到的不合格品数除以50来作为不合格品率来判断;那我们就会对这批质量水平合格的产品进行误判..如何科学地进行判断呢这就要用到假设检验的理论..步骤1：建立假设要检验的假设是不合格品率P是否不超过3%;因此立假设H0：P≤0.03这是原假设;其意是：与检验标准一致..H1：P＞0.03步骤2：选择检验统计量;给出拒绝域的形式若把比例P看作n=1的二项分别b1;p中成功的概率;则可在大样本场合一般n≥25获得参数p的近似μ的检验;可得样本统计量：近似服从N0;1其中＝2/50＝0.04;p=0.03;n＝50步骤3：给出显著性水平α;常取α＝0.05..步骤4：定出临界值;写出拒绝域W..根据α＝0.05及备择假设知道拒绝域W为步骤5：由样本观测值;求得样本统计量;并判断..结论：在α＝0.05时;样本观测值未落在拒绝域;所以不能拒绝原假设;应允许这批产品出厂..假设检验中的两类错误..进一步研究一下这个例子;在50个样品中抽到多少个不合格品;就要拒绝入库呢我们仍取α＝0.05;根据上述公式;得出;解得x>3.48;也就是在50个样品中抽到4个不合格品才能判整批为不合格..而如果我们改变α的取值;也就是我们定义的小概率的取值;比如说取α＝0.01;认为概率不超过0.01的事件发生了就是不合理的了; 那又会怎样呢还是用上面的公式计算;则得出;解得x>4.30;也就是在50个样品中抽到5个不合格品才能判整批为不合格..检验要求是不合格品率 P不能超过3%;而现在根据α＝0.01;算出来50个样品中抽到5个不合格品才能判整批为不合格;会不会犯错误啊假设检验是根据样本的情况作的统计推断;是推断就会犯错误;我们的任务是控制犯错误的概率..在假设检验中;错误有两类：第一类错误拒真错误：原假设H0为真批产品质量是合格的;但由于抽样的随机性抽到过多的不合格品;样本落在拒绝域W内;从而导致拒绝H0根据样本的情况把批质量判断为不合格..其发生的概率记为α;也就是显著性水平..α控制的其实是生产方的风险;控制的是生产方所承担的批质量合格而不被接受的风险..第二类错误取伪错误：原假设H0不真批产品质量是不合格的;但由于抽样的随机性抽到过少的不合格品;样本落在W外;从而导致接受H0根据样本的情况把批质量判断为合格..其发生的概率记为β..β控制的其实是使用方的风险;控制的是使用方所承担的接受质量不合格批的风险..再回到刚刚计算的上例的情况;α由0.05变化为0.01;我们对批质量不合格的判断由50 个样本中出现4个不合格变化为5个;批质量是合格的而不被接受的风险就小了;犯第一类错误的风险小了;也就是生产方的风险小了；但同时随着α的减小对批质量不合格的判断条件其实放宽了——50个样本中出现4个不合格变化为5个;批质量是不合格的而被接受的风险大了；犯第二类错误的风险大了;也就是使用方的风险大了.. 在相同样本量下;要使α小;必导致β大；要使β小;必导致α大;要同时兼顾生产方和使用方的风险是不可能的..要使α、β皆小;只有增大样本量;这又增加了质量成本..因此综上所述;假设检验可以告诉我们如何科学地进行质量合格判定;又告诉我们要兼顾生产方和使用方的质量风险;同时考虑质量和成本的问题..。
假设检验案例
假设检验案例【篇一：假设检验案例】在自己对数据进行分析后只觉得直方图有异常，但缺乏实际运用的经验，没有更深入的再作分析，李老师出于对数据的敏感度和多年实践经验的积累，以及认真、严谨、敬业的态度让人非常敬佩，受益匪浅。
我们有很好的条件，本身就在现场，稍微摸索下，就可以和我们的生产联系起来了。
在实际工作中注意挖掘数据背后的信息，充分利用有效信息指导生产，把所学的工具都用用，逐步积累实践经验，一定可以在实际工作中发挥作用！【篇二：假设检验案例】假设检验案例分析案例6-1 为研究直肠癌患者手术前后血清cea 含量有无差异，作者收集了资料：前（24例）：31.5 30.0 28.6 39.7 45.2 20.3 37.3 24.0 36.2 20.5 23.1 29.0 33.1 35.2 28.9 26.4 25.9 23.8 30.4 31.6 27.9 33.0 34.0 32.7 2.03.2 2.3 3.1 1.9 2.2 1.5 1.8 3.2 3.0 2.8 2.1 （1）有人采用了两独立样本的t 检验，结果t =15.92，自由度 =34，p【篇三：假设检验案例】双侧检验单侧检验h0： = 0单侧左尾检验单侧右尾检验h1: 0h0： = 0h1: 0h0： = 0h1: 0接受域1- 接受域1- 接受域1- 拒绝域：两侧 /2拒绝域：两侧拒绝域：两侧目的：观察在给定的显著用于检测样本统计量是否用于检测样本统计量是否假设检验的步骤1 设定原假设和备择假设2 设定显著水平 3 选择检验统计量(f/t/x2/z) ，计算统计量的观测值4 根据统计量和显著水平确定临界点，给出拒绝域5 判断样本统计量所在区域，在拒绝域内拒绝原假设，接受备择假设假设检验按照参数分为总体均值的检验、两总体均值之差的检验、总体比例的检验和总体方差的检验z检验t检验f检验卡方检验独立样本t检用于比较两个不同样本之间的均值是否相等配对样本t检指同一样本在两个不同时候的均值比较，比如比较某种减肥药的效果方差分析用于检验某因素的影响显著程度用于检验正态样本均值是否等于某个假设值，事先知道总体方差，得到的统计量服从正态分布，一般用于大样与z检验相似， t检验不需要知道总体方差，他用样本方差代替总体方差，得到的统计量服从t分布。
假设检验的案例
假设检验的案例想象一下你是一家披萨店的老板，你一直觉得自己店的招牌超大号披萨平均直径是30厘米。
这就是你的原假设（H₀）。
有一天，一个特别挑剔的顾客跑来跟你说：“你家这披萨根本没有30厘米，我感觉小多了。
”你心里就有点不服气，但也开始有点怀疑了，这时候就需要进行假设检验啦。
于是你随机抽取了最近做的20个超大号披萨，仔仔细细地量了它们的直径。
结果算出来这20个披萨的平均直径是28厘米，样本标准差呢假设是2厘米。
现在就开始分析啦。
从这个样本数据看，好像确实比你认为的30厘米小。
但是呢，这有可能只是偶然现象啊，毕竟你不可能每次做出来的披萨直径都丝毫不差。
那怎么判断这个差异是不是真的说明你的原假设不对呢？这就需要用到统计学的魔法啦。
我们可以计算一个统计量（就像给这个差异打个分数一样），然后看看这个分数在正常情况下是不是很容易出现。
假如我们用t 检验（因为总体标准差不知道嘛），根据公式算出t值。
然后再看看这个t值对应的概率（p 值）。
比如说这个p 值算出来是0.03。
这是什么意思呢？这就好比是在说，如果你的披萨真的平均直径是30厘米（原假设成立），那么得到像28厘米这么小（或者更小）的平均直径的可能性只有3%。
一般来说，如果这个p 值小于5%（这个5%就是一个大家常用的临界值，当然你也可以根据自己的情况定），那就像在说：“这么小的概率都发生了，那很可能原假设是错的。
”所以你可能就不得不承认，也许你家的招牌超大号披萨的平均直径确实不是30厘米，得想办法改进制作流程啦。
要是p 值大于5%呢，你就可以松口气，对那个挑剔的顾客说：“亲，这个数据显示我们的披萨还是符合30厘米这个标准的，你这次可能只是运气不好，拿到了几个稍微小一点的。
”。
假设检验的思政案例
假设检验的思政案例以假设检验的思政案例为题，列举以下10个案例：1. 假设检验在选举调查中的应用：假设调查表明某政党在选举前的支持率为50%，通过收集样本数据，可以利用假设检验来判断该政党的支持率是否真的为50%。
2. 假设检验在教育研究中的应用：假设研究表明某种教学方法可以提高学生的成绩，通过收集样本数据，可以利用假设检验来判断该教学方法是否真的有效。
3. 假设检验在社会调查中的应用：假设调查表明某种社会问题的比例为20%，通过收集样本数据，可以利用假设检验来判断该社会问题的比例是否真的为20%。
4. 假设检验在环境科学中的应用：假设研究表明某种污染物对环境的影响可以降低，通过收集样本数据，可以利用假设检验来判断该污染物对环境的影响是否真的降低。
5. 假设检验在经济学中的应用：假设研究表明某种政策可以提高国民经济的增长率，通过收集样本数据，可以利用假设检验来判断该政策是否真的能够提高国民经济的增长率。
6. 假设检验在医学研究中的应用：假设研究表明某种药物可以治疗某种疾病，通过收集样本数据，可以利用假设检验来判断该药物是否真的能够治疗该疾病。
7. 假设检验在农业科学中的应用：假设研究表明某种肥料可以提高农作物的产量，通过收集样本数据，可以利用假设检验来判断该肥料是否真的能够提高农作物的产量。
8. 假设检验在心理学研究中的应用：假设研究表明某种心理治疗方法可以减轻抑郁症状，通过收集样本数据，可以利用假设检验来判断该心理治疗方法是否真的能够减轻抑郁症状。
9. 假设检验在物理实验中的应用：假设研究表明某种材料具有特殊的导电性能，通过收集样本数据，可以利用假设检验来判断该材料是否真的具有特殊的导电性能。
10. 假设检验在法律案件中的应用：假设研究表明某种证据可以证明被告的罪行，通过收集样本数据，可以利用假设检验来判断该证据是否真的可以证明被告的罪行。
h0h1假设例题
h0h1假设例题
H0和H1是统计学假设检验中的两个基本概念，分别代表零假设（Null Hypothesis, H0）和备择假设（Alternative Hypothesis, H1）。
下面是一个简单的H0与H1的假设检验例题：
例题：
某公司声称其新产品的合格率为95%。
为验证这一说法是否准确，质检部门随机抽取了该新产品200件进行检测，并发现其中190件产品合格。
零假设（H0）：
- H0: 新产品的实际合格率为95%，即产品质量符合公司的声明。
-具体数学形式表示为：H0: p = 0.95，其中p代表新产品的实际合格率。
备择假设（H1）：
-H1: 新产品的实际合格率不等于95%，即产品质量可能不符合公司的声明。
-双侧备择假设：H1: p ≠0.95，意味着实际合格率可能高于或低于95%。
-单侧备择假设（假设我们只想知道是否合格率偏低）：H1: p < 0.95
或者H1: p > 0.95 （取决于问题的具体方向性）
接下来，我们会根据样本数据计算检验统计量，并基于显著性水平α确定拒绝域，通过比较样本结果与拒绝域来决定是否拒绝零假设，从而判断公司声称的产品合格率是否可信。
参数估计和假设检验案例
参数估计和假设检验案例下面将通过一个实际案例来说明参数估计和假设检验的应用。
假设我们想要研究一些国家的大学生平均每天在手机上花费的时间。
我们希望通过对一部分学生进行调查来估计总体的平均时间，并且判断是否存在大学生在手机上花费的平均时间超过全国平均水平的情况。
首先，我们需要制定一个合适的假设。
在这个案例中，我们可以设立如下假设：-零假设H0：国家大学生在手机上花费的平均时间不超过全国平均水平-备择假设H1：国家大学生在手机上花费的平均时间超过全国平均水平接下来，我们需要收集一定数量的样本数据。
根据我们的研究目标，我们可以随机抽取一部分大学生作为样本，并且记录他们每天在手机上花费的时间。
在这个案例中，我们假设抽取了100名大学生作为样本，然后每天记录他们在手机上花费的时间。
接着，我们计算出样本的平均时间，记为X̄。
接下来，我们需要进行参数估计。
参数估计是通过样本数据来推断总体参数的取值。
在这个案例中，我们希望估计的参数是国家大学生在手机上花费的平均时间。
假设样本平均时间为X̄，我们可以使用样本均值X̄来估计总体均值μ。
对于大样本情况，可以使用正态分布进行参数估计。
假设我们计算得到的样本均值为4小时，标准差为1小时。
然后，我们需要进行假设检验来判断总体参数是否符合一些特定的假设。
在这个案例中，我们希望判断国家大学生在手机上花费的平均时间是否超过全国平均水平。
我们可以使用t检验进行假设检验。
假设我们选择了显著性水平为0.05、如果计算出的t值落在拒绝域内，则拒绝原假设，否则接受原假设。
假设样本平均时间为X̄，总体均值为μ0（全国平均水平），样本标准差为S，样本容量为n。
我们可以计算出t值，然后查找查表得到相应的临界值。
假设计算所得t值为2.5，自由度为99、根据查表可以得到在显著性水平为0.05时，临界值为1.984、由于计算所得t值大于临界值，所以我们可以拒绝原假设。
通过参数估计和假设检验，我们得出结论：国家大学生在手机上花费的平均时间超过全国平均水平。
参数估计与假设检验案例
参数估计与假设检验案例在统计学中，参数估计是一种通过对样本数据做出合理的推测来估计总体参数的方法。
假设检验则是一种基于样本数据进行统计推断的方法，用于判断对于一个总体的一些假设是否可接受。
为了更好地理解参数估计和假设检验的应用，我们可以考虑以下案例：假设我们是一家电商公司的数据分析师，想要评估一项新推出的增值服务是否对用户购买力有正面影响。
具体而言，我们想知道购买了增值服务的用户相对于没有购买的用户，在订单总金额上是否存在显著差异。
首先，我们需要建立两个假设：1.零假设（H0）：购买增值服务与订单总金额之间不存在显著差异；2.备择假设（H1）：购买增值服务与订单总金额之间存在显著差异。
接下来，我们需要进行参数估计。
假设我们从公司的数据库中随机抽取了两组用户数据：一组是购买了增值服务的用户，另一组是没有购买增值服务的用户。
我们从这两组用户中分别计算出了订单总金额的均值和标准差。
然后，我们可以使用参数估计的方法来估计总体订单总金额的均值差异。
具体而言，我们可以使用两个样本的均值差（例如，购买了增值服务的用户订单总金额的均值减去没有购买增值服务的用户订单总金额的均值）作为总体均值差的估计。
此外，我们还可以使用标准差来估计总体均值差的标准误差。
然后，我们可以进行假设检验。
我们使用一个统计量来评估观察到的样本均值差是否足够大，以至于我们可以拒绝零假设并接受备择假设。
在这种情况下，我们可以使用一个双侧t检验来进行假设检验。
假设我们设置了一个显著性水平（α）为0.05，即我们愿意承担5%的错误接受备择假设的风险。
然后，我们计算出双侧t检验的p值（即观察到的样本均值差在零假设下出现的概率）。
如果p值小于0.05，我们可以拒绝零假设，并得出结论：购买了增值服务的用户与没有购买的用户在订单总金额上存在显著差异。
最后，我们可以汇报我们的研究结果和结论。
我们可以得出结论：购买了增值服务的用户相对于没有购买的用户，在订单总金额上存在显著差异。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
以下的样本为新的统计监控程序运行的第一天，每间隔 1 小时所收集到的。
假设检验案例
Quality
Associates 是一家咨询公司，为委托人监控其制造过程提供抽样
和统计程序方面的建议。
在某一应用中，一名委托人向 Quality
Associates 提
供了其生产过程正常运行时的 800 个观察值组成的一个样本。
这些数据的样本标
准差为 0.21，因而我们假定总体的标准差为 0.21。
Quality
Associates 建议该
委托人连续地定期选取样本容量为 30 的随机样本来对该生产过程进行监控。
通
过对这些样本的分析，委托人可以迅速了解该生产过程的运行状况是否令人满意。
当生产过程运行不正常时，应采取纠正措施以避免出现问题。
设计规格要求该生
产过程的均值为 12，Quality Associates 建议采用如下形式的假设检验：
H 0 : μ = 12 H 1 : μ ≠ 12
只要 H 0 被拒绝，就应采取纠正措施。
管理报告:
1.对每个样本在0.01的显著水平下进行假设检验，如果需要采取措施的话，
确定应该采取何种措施？给出每个检验的检验统计量和p－值。
2.计算每一样本的标准差。
假设总体标准差为0.21是否合理？
( )
~ N (0,1) I α = ⎢x - Z α 样本 1： I α 1 = ⎢11.96 - 2.576
[ [ 样本 2： I α 2 = ⎢12.03 - 2.576
[ [ 样本 3： I α 3 = ⎢11.89 - 2.576
[ [
3. 当样本均值 x 在 μ = 12 附近的多大范围内，我们可以认为该生产过程的运
行令人满意？如果 x 超过上限或低于下限，则应对其采取纠正措施。
在质量控制
中，这类上限或下限被称作上侧或下侧控制限。
4. 当显著水平变大时，暗示着什么？这时，哪种错误或误差将增大？
管 理 报 告
1. 对每个样本在 0.01 的显著水平下进行假设检验，如果需要采取措施的话，
确定应该采取何种措施？给出每个检验的检验统计量和 p －值。
(1) 假设检验
a) 提出假设： H 0 : μ = 12
H 1 : μ ≠ 12
b) 统计量及分布： Z =
n X
- μ σ
c) 给出显著水平 α = 0.01 −→ Z α = 2.576
2
置信区间为：
⎡ ⎣
2 σ n , x + Z α
2σ ⎤ n ⎥⎦
⎡ ⎣
0.21
, 11.96 + 2.576 0.21⎤ ⎥⎦
= 11.96 - 0.10, 11.96 + 0.10]
= 11.86, 12.06]
⎡ ⎣
0.21 30
, 12.03 + 2.576 0.21⎤ ⎥⎦
= 12.03 - 0.10, 12.03 + 0.10] = 11.93, 12.13]
⎡ ⎣
0.21 30
, 11.89 + 2.576 0.21⎤ ⎥⎦
= 11.89 - 0.10, 11.89 + 0.10] = 11.79, 11.99]
样本 4： I α 4 = ⎢12.03 -
2.576 [
[ 各个样本的检验统计量及 p －值为： ⎡ ⎣
0.21 30
, 12.03 + 2.576
0.21⎤ ⎥⎦
= 12.08 - 0.10, 12.08 + 0.10] = 11.98, 12.18]
d) 统计决策：因为12 ∉ I α1, 12 ∉ I α 2 , 12 ∈ I α 3 , 12 ∉ I α 4 ，所以对于样本 1、样
本 2、样本 4 来讲可做出拒绝原假设 H 0 : μ = 12 的统计决策，而对于样本 3 来
讲则不拒绝原假设 H 0 : μ = 12 。
可见，生产过程还不够稳定，有必要缩短监控时间，并收集更多的样
本进行检验，以进一步做出比较准确的决策。
(2) 每个检验的检验统计量和 p －值
利用检验统计量及 p －值可以得到相同的统计决策结论。
2．计算每一样本的标准差。
假设总体标准差为 0.21 是否合理？
从每一个样本的标准差来看，假设总体标准差为 0.21 基本合理。
n
3．当样本均值在 μ = 12 附近的多大范围内，我们可以认为该生产过程的
运行令人满意？如果超过上限或低于下限，则应对其采取纠正措施。
在质量
控制中，这类上限或下限被称作上侧或下侧控制限。
对于置信水平α = 0.01 ，当 Z 0 > Z α 时，则拒绝原假设 H 0 : μ = 12 。
即认为 2
生产过程是不正常的。
而当 Z 0 (X -)≤ Z α 时，被认为生产过程是正常运行
2
的，从而有：
上侧控制限：U α ＝ μ + Z α
2
σ n
＝12.10
下侧控制限： L α ＝ μ - Z α
2σ n
＝11.90
4. 当显著水平变大时，暗示着什么？这时，哪种错误或误差将增大？
当显著水平α 变大时，则增大了拒绝原假设 H 0 的可能性，即犯第一类错
误的概率增大。