假设检验案例教学研究
假设检验的启发式教学方法研究
假设检验的启发式教学方法研究摘要：假设检验是概率论与数理统计课程教学中的重点和难点。
针对以往教学中出现的弊端，本文通过启发式教学方法，使学生在掌握原理的同时树立主动思维与统计思想。
关键词：假设检验；启发式教学0引言参数估计与假设检验是统计推断中两大基本问题，特别是假设检验问题，是概率论与数理统计课程教学中的重点和难点[1-2]。
本文通过启发式教学方法，使学生在掌握原理的同时树立主动思维与统计思想。
1介绍预备在讲解假设检验问题之前，首先通过实例小概率事件原理，不仅可以激发起学生的学习兴趣，而且还避免因直接给出抽象复杂的理论给学生带来困惑。
乘坐火车时，我们可以放心大胆地乘坐，很少考虑安全问题，因为火车事故发生的概率非常小，而且在我们一次乘车中，这个小概率事件基本上不发生的。
这个实例体现了人们根据长期经验所坚信的一个原则，即小概率事件在一次试验中基本上是不发生的，我们把这一规律称为小概率原理。
2通过实例分析问题结合案例教学，引导学生积极思考，调动学习的积极性。
例：某工厂生产的一种螺钉，合格螺钉标准长度是32.5毫米，根据以往生产的螺钉实际情况，可以认为其长度某~（μ，σ2），σ=0.5现从该厂生产的一批产品中抽取６件，得尺寸数据如下：32.56,29.66,31.64,30.00,31.87,31.03向学生提出问题：如果现在我们是质检员，那么我们能否认为这批产品是合格的呢？引导学生分析案例，现在这批螺钉长度的全体组成了问题的总体，产品合格的标准是长度为32.5mm，也就是判断总体均值μ=3.25vμ≠3.25，显然，这是对参数μ的检验的问题，即参数的假设检验。
为了检验哪种说法正确，首先要提出两个相互对立的假设：原假设H0：μ=μ0=3.25，备择假设H1:μ≠μ0，问题转化为检验假设H0是否成立。
怎样来判断是否接受这一假设呢？由于要检验的假设涉及总体均值μ，所以首先想到的是能否借助样本均值这个统计量来进行判断？答案是肯定的。
假设检验教案
假设检验的基本思想从一个例子来说明假设检验的基本思想.例 某工厂用包装机包装奶粉，额定标准为每袋净重0.5kg .设包装机称的奶粉重量X 服从正态分布2(,)N μσ.根据长期经验知其标准差为0.015kg σ=.为检验某台包装机的工作是否正常，随机抽取包装的奶粉9袋，称得其平均质量为0.511x kg =，问该包装机的工作是否正常？为了回答该问题，先做出假设0010:0.5:0.5H vs H μμμμ==≠=，检验的目的就是在0H 与1H 之间选一个：若认为0H 正确，则接受0H ；若认为0H 不正确，则拒绝0H 而接受1H .自然，对0H 或1H 的取舍是以样本数据为依据的，即：若数据与0H 一致，就不应该拒绝0H ，若数据与0H 相去甚远，就应拒绝0H .那么如何确定样本数据与0H 是否一致呢？这样来考虑：样本均值X 是检验对象——总体均值μ的无偏估计，所以X 的观测值x 一定程度上反映了μ的大小.若0H 成立0μμ=，则x 与0μ的差异0x μ-不会太大，即检验0H 成立与否，可转为检验0x μ-是否太大.本例中，00.5kg μ=，0.511x kg =，00.011x kg μ-=，x 与0μ之间的差异可有两种不同的解释：1）0H 正确，差异由抽样的随机性造成；2）0H 不正确，差异由系统误差即包装机不正常工作造成.哪一种解释比较合理呢？这样考虑：若0H 为真，则x 与0μ之间的偏差0x μ-不会太大，或者说偏差0x μ-较大的可能性较小，即0x μ-的值较大（太大）是小概率事件，小概率事件在一次试验中不会发生，若0x μ-的值太大则小概率事件发生，就有理由怀疑0H 的正确性而拒绝0H .那么，现在偏差00.011x a -=算不算太大呢？或在0H 成立的条件下，00.011x a -=是否小概率事件呢？多小的概率是小概率事件？为此，首先确定一个我们认为足够小的概率α，若()P A α=，则事件A 为小概率事件.α称为检验（显著性）水平.通常取0.05α=或0.01.然后，对给定的α，确定c ，使事件0x c μ->为小概率事件，即0()P x c μα->=如何确定c ？由抽样分布定理知，当0H 成立时，~(0,1)X U N =.从而，0())P X c μα->=>= ∴u α=，则c u α=.此时，若0X c u αμ->=，则小概率事件发生，应拒绝0H .事实上，()P X u P u ααμα->=>=即事件X u αμ⎧->⎨⎩与事件u α⎫⎪>⎬⎪⎭等价.为了方便起见，不妨用统计量U 替代X μ-，用u α替代c u α=，于是当观测值0U u α>时，拒绝0H .取0.05α=，则1.96u α=，即(1.96)0.05P U >=，即1.96U >是小概率事件.本例中， 2.2 1.96U ==>，小概率事件发生了，表明抽样检查结果与0H 不符，x 与0μ之间的偏差较大，∴当检验水平0.05α=时，应拒绝0H ，认为包装机工作不正常. 本例中，是根据统计量X U=的值来作检验的，称其为检验统计量（检验函数），当0U u α>，即U 的观测值落在(,)(,]D u u αα=-∞-+∞ 内时，拒绝0H ，称区间D 为拒绝域.由上述内容，可确定假设检验的一般步骤为：1）根据实际问题，提出原假设0H 与备择假设1H ；2）选取适当的显著水平α及样本n ；3）选取适当的统计量U ，0H 成立时确定其分布，对给定的α，确定0H 的拒绝域D ；4）根据样本观测值计算统计量U 的观测值0U ；5）作出判断：将0U 与临界值u α比较，落入拒绝域D 内，则拒绝0H ；否则，则不能拒绝0H .听过何老师的讲座，有很多收获，在此仅对何老师讲座中提到的一些教学中的小技巧进行总结：1）本节课程常用的公式置黑板的某个小角落，方便使用；2）解题中常用到的数值给学生指出，记住，方便使用；3）每节课讲完内容后应进行梳理、总结，方便学生学习复习；4）例题不要太平淡，应尽可能给出各个学科的例子，在丰富学生知识的同时，提高学生的学习兴趣，给学生留下深刻印象；5）假设检验部分内容复杂，所有理论不要一次性给出。
假设检验教案（课时备课）
注：板书设计可在教学进程中直接用横线、浪线等标示出。
1
章、节、目
教学目的 和要求
假设检验教案（课时备课）
第 2 次课
第七章第一节[2]
学时 2
弄清两个正态总体均值或方差的假设检验，百分比假设检验．
重点 难点
重点：掌握各类假设检验的方法． 难点：假设检验的原理以及统计量的选择．
见讲稿
教学进程 （含课堂 教学内容、 教学方法、 辅助手段、 师生互动、 时间分配、 板书设计）
注：板书设计可在教学进程目的 和要求
假设检验教案（课时备课）
第 ４ 次课
第七章第二节[2]
学时 2
弄清独立性检验的原理与步骤
重点 难点
重点：结合实例讲解 2 检验法的具体计算步骤，掌握独立性的检验方法． 难点：弄清独立性检验的原理
见讲稿
教学进程 （含课堂 教学内容、 教学方法、 辅助手段、 师生互动、 时间分配、 板书设计）
重点 难点
重点：掌握总体分布的假设检验的方法。 难点：理解总体分布的假设检验的原理
学时 2
见讲稿
教学进程 （含课堂 教学内容、 教学方法、 辅助手段、 师生互动、 时间分配、 板书设计）
（基本定义要有英文标识）
P１９３－１９４, 习题７.２：１，２，３，４。 作业布置
课后自我总 结分析
注重对总体分布的假设检验的步骤与原理的掌握，对具体计算推倒可以不用过多讲解．
见讲稿
教学进程 （含课堂 教学内容、 教学方法、 辅助手段、 师生互动、 时间分配、 板书设计）
（基本定义要有英文标识）
P１８３－１８４, 习题７.１：１，３，４，６。 作业布置
课后自我总 结分析
假设检验的原理结合反证法的思想予以讲解，让学生理解假设检验的原理．同时结合具 体实例讲解一个正态总体假设检验统计量的选择与拒绝域的理解．
假设检验流程案例分析
假设检验流程案例分析一、假设检验的基本概念。
1.1 什么是假设检验呢？简单来说，这就像是一场法庭审判。
我们有一个“被告”，也就是我们要检验的假设。
比如说，我们想知道一种新的减肥方法是不是真的有效，那“这种减肥方法有效”就是我们的假设。
我们不能轻易就相信这个说法，得拿出证据来。
1.2 这里面有个很重要的东西叫“显著性水平”。
这就好比是我们判断事情的一个标准。
如果把生活中的事情比作考试，那显著性水平就是及格线。
一般我们会设定一个值，像0.05或者0.01。
如果计算出来的结果小于这个值，那就像考试不及格一样，我们就有理由怀疑我们的假设是错的。
2.1 案例背景。
咱就说有个工厂，他们生产的灯泡，以前一直说平均使用寿命是1000小时。
但是最近呢，工人换了新的生产工艺，老板就想知道，这新的工艺下，灯泡的平均使用寿命是不是还是1000小时。
这时候我们的假设就出来了。
原假设就是“新工艺下灯泡平均使用寿命还是1000小时”，那备择假设就是“新工艺下灯泡平均使用寿命不是1000小时”。
2.2 收集数据。
这就好比破案要找线索一样。
我们得去收集灯泡使用寿命的数据。
从新生产的灯泡里随机抽取一些，比如抽取了50个灯泡，然后测试它们各自的使用寿命。
这一步可得认真，要是数据不准确，那就好比地基没打好，后面全是白搭。
2.3 选择检验统计量并计算。
这里就有点技术含量了。
根据我们的问题和数据类型，选择合适的检验统计量。
就像我们要开锁，得选对钥匙一样。
对于这个灯泡的例子，可能会用到t检验或者z 检验。
计算出这个统计量的值之后，就像是我们算出了一个“关键指标”。
2.4 做出决策。
计算出统计量的值后，我们就可以根据显著性水平来做决定了。
如果这个值落在了我们事先设定的“拒绝域”里，那就像证据确凿一样，我们就拒绝原假设。
就好比我们发现这个新生产工艺下灯泡的平均使用寿命和1000小时相差太多，那我们就有理由相信原假设不成立了。
要是不在拒绝域里，那我们就没有足够的证据拒绝原假设，只能暂时认为原假设是对的。
假设检验案例分析
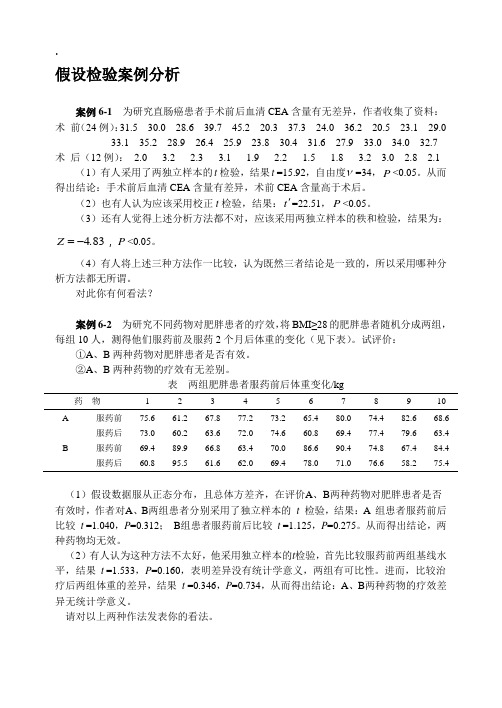
.假设检验案例分析案例6-1 为研究直肠癌患者手术前后血清CEA含量有无差异，作者收集了资料：术前（24例）：31.5 30.0 28.6 39.7 45.2 20.3 37.3 24.0 36.2 20.5 23.1 29.033.1 35.2 28.9 26.4 25.9 23.8 30.4 31.6 27.9 33.0 34.0 32.7 术后（12例）：2.0 3.2 2.3 3.1 1.9 2.2 1.5 1.8 3.2 3.0 2.8 2.1 （1）有人采用了两独立样本的t检验，结果t=15.92，自由度ν=34，P<0.05。
从而得出结论：手术前后血清CEA含量有差异，术前CEA含量高于术后。
（2）也有人认为应该采用校正t检验，结果：t'=22.51，P<0.05。
（3）还有人觉得上述分析方法都不对，应该采用两独立样本的秩和检验，结果为：=，P<0.05。
Z-834.（4）有人将上述三种方法作一比较，认为既然三者结论是一致的，所以采用哪种分析方法都无所谓。
对此你有何看法？案例6-2 为研究不同药物对肥胖患者的疗效，将BMI≥28的肥胖患者随机分成两组，每组10人，测得他们服药前及服药2个月后体重的变化（见下表）。
试评价：①A、B两种药物对肥胖患者是否有效。
②A、B两种药物的疗效有无差别。
表两组肥胖患者服药前后体重变化/kg药物 1 2 3 4 5 6 7 8 9 10 A 服药前75.6 61.2 67.8 77.2 73.2 65.4 80.0 74.4 82.6 68.6服药后73.0 60.2 63.6 72.0 74.6 60.8 69.4 77.4 79.6 63.4 B 服药前69.4 89.9 66.8 63.4 70.0 86.6 90.4 74.8 67.4 84.4服药后60.8 95.5 61.6 62.0 69.4 78.0 71.0 76.6 58.2 75.4（1）假设数据服从正态分布，且总体方差齐，在评价A、B两种药物对肥胖患者是否有效时，作者对A、B两组患者分别采用了独立样本的t 检验，结果：A 组患者服药前后比较t =1.040，P=0.312；B组患者服药前后比较t =1.125，P=0.275。
统计分析假设检验原理及案例分析PPT学习教案
2. 建立的原假设与备择假设应为 H0: 10 H1: 10
第30页/共122页
双侧检验
(显著性水平与拒绝域 )
抽样分布
拒绝域 /2
1-
置信水平 拒绝域 /2
临界值
H0值
临界值
样本统计量
第31页/共122页
双侧检验
(显著性水平与拒绝域)
3. 先确立备择假设H1 第35页/共122页
单侧检验
(原假设与备择假设的确定)
一项研究表明，采用新技术 生产后，将会使产品的使用 寿 命 明 显 延 长 到 1500 小 时 以 上。检验这一结论是否成立
研究者总是想证明自己的研 究结论(寿命延长)是正确的
备择假设的方向为“>”(寿命延长)
结论:
有证据表明新机床加工的零件 的椭圆度与以前有显著差异
第50页/共122页
2 已知均值的检验
(P 值的计算与应用)
第1步：进入Excel表格界面，选择“插入”下拉菜 单 第2步：选择“函数”点击 第3步：在函数分类中点击“统计”，在函数名的 菜
单下选择字符“NORMSDIST”然后确定 第4步：将Z的绝对值2.83录入，得到的函数值为
一. 假设问题的提出 二. 假设的表达式 三. 两类错误 四. 假设检验中的值 五. 假设检验的另一种方法 六. 单侧检验
第4页/共122页
假设检验的概念与思想
第5页/共122页
什么是假设?
(hypothesis)
对总体参数的的
数值所作的一种陈 述
我认为该地区新生婴儿 的平均体重为3190克!
积 右侧检验时，P-值为曲线下方
《解决问题的策略——假设》案例分析（优秀范文五篇）
《解决问题的策略——假设》案例分析（优秀范文五篇）第一篇：《解决问题的策略——假设》案例分析《解决问题的策略——假设法》案例分析今天教学了《解决问题的策略——假设法》，用了多媒体课件，整节课的教学效果显得比较好，其实在解决“鸡兔同笼”的问题时已经涉及到了假设法，对于六年级的学生，其实假设法并不是很难的。
对于这一知识点的教学，我主要通过以下三点进行的：第一，是要弄清与例1的区别，例1主要是用替换的策略，而例2是用假设的策略。
主要区别在于，如果继续用“替换”的方法但不像例1那样有两种船的只数，当然两个不同的量的关系可以从各船的人数中得到。
由此引到先假设都是大船或者假设都是小船。
第二，我主要按照下面的思路进行教学。
假设都是其中一个量——画图（或列表）发现多了或少了——进行调整——列出综合算式——算出结果。
第三，要弄清调整时要选择什么辅助策略。
例2时，学生既用了画图法，又用了列表法，而“练一练”的两题，教材主要让学生分别用画图法和列表法来解决。
特别是在练习第2题时，要让学生感觉到，数目太大了，画图法太麻烦了，选择用列表法解决方便些。
而且在学生用列表解决后，要让学生先估计大约各要几块，再假设，这一点可以从教材的表格中的数据来理解，发现用5块大展板时比176件少了，然后调整，同样用8块大展板比176多了，然后调整。
在假设与调整的过程中，要充分利用估计与算出的数据信息，灵活调整，得出结果。
第二篇：解决问题的策略假设教案《解决问题的策略—假设》教学预案教学内容六上教科书第68~69页例1和“练一练”，第72页第1~2题教学目标1、使学生经历解决问题的过程，体会通过假设把复杂问题转化成简单问题的过程，初步感悟假设的策略，并能用策略解答一些问题。
2、使学生在运用假设的策略解决实际问题的过程中，初步感受假设的策略对于解决问题的价值，进一步发展观察、比较、分析和推理的能力。
3、使学生进一步积累解决问题的经验，增强解决问题的策略意识，获得解决问题的成功体验，增强学好数学的信心。
假设检验方法在社会科学研究中的应用
假设检验方法在社会科学研究中的应用在社会科学研究中，假设检验方法是一种常用的统计分析工具，它能够帮助研究者评估样本数据与总体数据之间的差异，从而进行科学的结论推断。
本文将探讨假设检验方法在社会科学研究中的应用，并对其原理、步骤和局限性进行详细的阐述。
一、假设检验方法的原理假设检验方法是基于样本数据对总体参数进行推断的一种统计方法。
它通过比较样本数据与研究者提出的假设之间的差异来推断总体参数的真实情况。
在假设检验方法中，研究者需要提出一个原假设（H0）和一个备择假设（H1），并进行统计检验以确定哪个假设更为合理。
假设检验方法的核心思想是通过计算样本数据得到的统计量与理论分布之间的差异来进行决策。
二、假设检验方法的步骤假设检验方法通常包括以下步骤：1. 确定研究问题和建立假设：在开始假设检验之前，研究者需要明确研究问题，并建立合适的原假设（H0）和备择假设（H1）。
原假设通常是一种没有变化或效果的陈述，备择假设则是对原假设的补充或替代。
2. 选择合适的统计检验方法：根据研究设计和数据类型，研究者需要选择适当的统计检验方法。
常见的统计检验方法包括t检验、方差分析、回归分析等。
3. 收集和整理数据：研究者需要收集样本数据，并进行数据的整理和清洗，以确保数据的准确性和可靠性。
4. 计算统计量：根据所选择的统计检验方法，研究者需要计算出相应的统计量，如t值、F值等。
5. 确定显著性水平：显著性水平通常设定为0.05或0.01，表示进行检验时犯错误的概率上限。
根据研究需要和样本大小，选择合适的显著性水平。
6. 做出决策：通过计算得到的统计量与临界值进行比较，研究者可以判断原假设是否成立。
如果统计量落在拒绝域内，则拒绝原假设；反之，则接受原假设。
三、假设检验方法的应用案例在社会科学研究中，假设检验方法被广泛运用于各个领域。
以教育研究为例，研究者可能感兴趣于了解某种教学方法对学生学习成绩的影响。
他们可以通过将学生分为实验组和对照组，然后采集数据并运用假设检验方法来比较两组学生之间的学习成绩是否存在显著差异。
假设检验流程案例
假设检验流程案例一、假设检验是啥。
1.1 简单来说呢，假设检验就像是一场科学的审判。
咱们有个想法，这个想法就是咱们的假设。
比如说，你觉得某种新肥料能让庄稼长得更好，这就是你的假设。
然后呢，咱们不能光凭感觉，得找证据来证明这个假设是不是对的。
1.2 就好比你怀疑邻居家的猫偷吃了你家的鱼，你不能直接就定它的罪，得找些蛛丝马迹。
在假设检验里，我们要从数据里找这些“蛛丝马迹”。
二、假设检验的流程。
2.1 第一步是提出假设。
这里面有原假设和备择假设。
原假设呢，就像是默认的情况，通常是那种比较保守的说法。
还是拿肥料来说，原假设可能就是新肥料和旧肥料对庄稼生长没区别。
备择假设就是你心里希望证明的那个，就是新肥料能让庄稼长得更好。
这就像是在法庭上，有被告无罪（原假设）和被告有罪（备择假设）这两种情况。
2.2 第二步就是选个合适的检验统计量。
这就有点像选个合适的工具来衡量证据的力度。
不同的情况得用不同的工具，就像修东西，修电器和修水管用的工具肯定不一样。
要是比较两个平均数，可能就用t检验之类的统计量。
这一步可不能马虎，选错了工具，那得出的结论可能就不靠谱。
2.3 第三步就是确定显著性水平。
这就好比是定个标准，多大的证据力度才能判定假设成立。
这个显著性水平就像是门槛，一般常用的是0.05或者0.01。
这就像是在法庭上，法官心里有个标准，达到这个标准才能定罪。
如果证据的概率小于这个显著性水平，就像是证据确凿，咱们就可以拒绝原假设。
要是大于这个水平呢，咱们就只能说证据不足，不能拒绝原假设，就像没有足够证据给邻居家猫定罪一样。
三、假设检验的案例。
3.1 咱举个例子。
有个工厂生产灯泡，他们声称他们生产的灯泡平均使用寿命是1000小时。
这就是原假设。
咱们作为怀疑者，就觉得可能不是这样，咱们的备择假设就是平均使用寿命不等于1000小时。
然后咱们抽取了一批灯泡进行测试，得到了这些灯泡的使用寿命数据。
接着选个合适的检验统计量，这里可能用Z检验比较合适。
假设检验案例教学研究
假设检验案例教学研究作者：宋继革来源：《知识文库》2017年第21期一、引言推断统计中的一个重要内容，就是假设检验。
通过多年的教学实践，发现学生对这部分教学内容接受困难。
甚至在毕业多年之后，还坦言，自己当时没有搞清楚。
通过思考，引入了一个“中大奖”判断的例子，将假设检验的基本思想与方法串连起来，取得了非常好的教学效果。
二、案例的引入假设检验是统计学一个非常重要的内容，思想性强。
学生们往往把假设检验这部分内容当成数学来学，忽略了其中的部分主观性。
原假设与备择假设、小概率原理、两类错误、拒绝域与接受域、P值检验等概念本身的逻辑性与连贯性，需要一个背景简单的案例串连起来，以便取得良好的教学效果。
1、“中大奖”问题的提出如果，作为统计学教师的我，今天向大家宣布：我昨天买了一张彩票，中了500万。
你们信不信？信的同学有自己的理由：这是老师说的。
不信的同学也有理由：可能性太小了。
这就需要统计学意义上的假设检验。
2、原假设与备择假设概念的引入谁来做假设检验呢？是不信的同学，他们希望收集证据，以支持不信的观点。
这就是假设检验的主观性，它是有立场的。
假设检验不是纯粹的数学。
原假设：研究者想收集证据予以反对的假设称为原假设，记为；备择假设：研究者想收集证据予以支持的假设称为备择假设，记为。
这里，原假设应该是“老师说的是真话”，备择假设应该是“老师说的是假话”。
原假设与备择假设是“非此即彼”的关系。
3、小概率原理与显著性水平的引入一个事件如果发生概率很小，那么它在一次试验中是不可能发生的。
通常把5%作为一个界限，发生概率在5%以下的事件，被称为小概率事件。
如果老师说的话，连5%的可能性都没有，我们就有充分的理由拒绝相信。
假设检验的核心思想就是，在肯定原假设的基础上，是不是会引起小概率事件？如果发生了小概率事件，就拒绝原假设；如果没有发生小概率事件，就不能拒绝原假设。
这个5%，就是显著性水平。
我们可以设的更小，以增加说服力。
假设检验的案例式教学方法研究
假设检验的案例式教学方法研究作者：黄文蝶周江霖来源：《大东方》2016年第03期摘要：假设检验是统计教学中的一个重点和难点。
本文以案例式教学方法为主导，结合启发式教学，力图将这一问题的基本思想与步骤阐述清楚，引导学生在掌握原理的同时进一步深化统计思想的培养。
关键词：假设检验；案例式教学；启发式教学假设检验是统计推断中非常重要的一个问题，也是统计教学中的一个难点所在。
本文以案例式教学方法为主导，结合启发式教学，力图将这一问题的基本思想与步骤阐述清楚，引导学生在掌握原理的同时进一步深化统计思想的培养。
一、提出问题产品质量问题是当今社会的一个热门话题，这节课我们就用假设检验的方法来检验一种非处方药的质量是否合乎规定。
例：一种无需医生处方可得到的治疗咳嗽和鼻塞的药，按规定其酒精含量为5%.今从已出厂的一批药中，随机抽取10瓶，测试其酒精含量为：5.01，4.87，5.11，5.21，5.03，4.96，4.78，4.98，4.88，5.06。
已知酒精含量服从正态分布N（μ，0.00016）。
向学生提出问题：如果现在你是一名质检员，那么你认为这批药品是否合格？二、分析问题引导学生对这一问题进行逐步深入地分析：现在关注的是这一批药的酒精含量——这是我们的研究总体；手头掌握的资料有，10瓶药品的酒精含量数据以及总体所服从的分布。
判定这批药品是否合格，关键是看总体均值μ是否为5：若μ=5，则药品合格；若μ≠5，则药品不合格。
通过点估计的学习，我们知道总体均值可以用样本均值去估计，容易得到μ的估计值为4.989，显然4.989≠5，那么这个时候能否下结论：这批药品不合格？如果贸然下这样的结论，既不能让人信服，自己也会存在疑惑：一方面，样本均值只是总体均值的一个估计量，并不能完全代表总体均值；另一方面，样本均值受随机因素的影响比较大，而4.989与5相差这么小，这个误差似乎是可以接受的。
到底可以容忍的最大误差是多少呢？这成了我们最终关注的问题。
对假设检验的教学探讨
对假设检验的教学探讨摘要：本文旨在探讨假设检验的教学策略。
介绍了假设检验的概念、用途和方法，以及其在统计分析中的作用。
然后，介绍了一些让学生更容易理解假设检验的有效教学方法，并给出了一些有利的示例。
最后，本文总结了一些建议，希望这些建议能够有助于教师老师在课程中更好地引导学生使用假设检验，从而达到更加有效的统计学习结果。
关键词：假设检验、教学策略、教师引导、统计分析正文：假设检验是统计学中一种重要的方法，有助于测试研究假设的可信性和可行性，提高数据分析的准确性。
随着数据分析能力的提升，越来越多的学生都需要学习假设检验，以使其拥有更扎实的统计学知识和更深厚的数据分析能力。
有效的教学策略是让学生们更好地理解假设检验的关键。
因此，教师需要充分利用平时的教学时间，结合学生在课堂上所学，用多种方法指导学生。
首先，教师应该尝试使用形象化的解释方法，使学生能够更容易理解假设检验的过程及其作用。
其次，教师可以通过练习题的形式，指导学生如何实施假设检验，深入理解和掌握假设检验的知识。
接下来，也可以用真实案例来说明假设检验的运用，让学生更容易把假设检验与现实社会环境紧密联系起来。
综上所述，假设检验是一种非常重要的统计分析方法，其正确使用可以极大地提高数据分析的正确性。
因此，教师有责任在教学中引导学生正确学习并使用假设检验，以帮助他们更好地掌握统计学知识，并从中受益。
因此，将以上教学策略融入教学，会为学生提供更有效的假设检验学习体验。
要使学生充分学习和掌握假设检验，教师还可以采用评估的方式来检测学生是否有效地掌握了假设检验的知识。
教师可以设计多种不同形式的考核，比如让学生完成一些小型统计学习项目，看看他们在提出假设以及实施假设检验时都采用了哪些方法。
这些练习，也可以帮助学生熟悉假设检验的数据分析步骤，从而更好地应用假设检验去解决实际问题。
此外，为了提高学生对假设检验的理解能力，教师还可以利用实验教学方法来让学生体验假设检验的具体过程。
探索概率与统计的假设检验与置信区间的教学案例
探索概率与统计的假设检验与置信区间的教学案例概率与统计是一门重要的数学学科，在现代社会中具有广泛的应用。
其中，假设检验与置信区间是概率与统计中一项重要的内容，对于理解和应用统计学原理具有重要意义。
本文将探索概率与统计的假设检验与置信区间的教学案例，通过实际案例的介绍与分析，旨在帮助学生深入理解和掌握该内容。
一、引言概率与统计的假设检验与置信区间是许多实际问题中必不可少的方法。
它们可以用来验证或推断总体的特性，并且在决策制定、实验设计、品质管理等领域中发挥着重要作用。
下面将通过实际案例的讲解，具体介绍假设检验与置信区间的应用过程与原理。
二、案例一：医学实验假设我们正在进行一项新药的研发，在试验前我们对100名患者的病情进行了观察，并记录了他们的疾病指标。
现在，我们想要验证这种新药是否能够显著提高患者的治疗效果。
1. 假设检验我们首先提出两个假设：零假设(H0)和备择假设(H1)。
零假设是默认的假设，通常表示没有治疗效果或者两种药物无差异；备择假设则是我们希望验证的假设，即新药能够显著提高治疗效果。
在此案例中，我们可以假设H0：新药与原药物无显著差异；H1：新药与原药物有显著差异。
接下来，我们需要选择一个合适的统计检验方法。
由于我们的样本具有连续性变量，并且样本容量较大，可以使用t检验进行假设检验。
通过计算统计量t值和p值，我们可以得出结论是否拒绝或接受零假设。
2. 置信区间除了假设检验，我们还可以使用置信区间来对结果进行更加全面的描述。
置信区间是对总体参数的一个估计区间，可以用来表示我们的估计结果的不确定性程度。
一般而言，我们可以选择95%的置信水平，计算出置信区间来描述新药的治疗效果。
三、案例二：市场调查假设我们是一家食品公司，想要了解消费者对我们的产品评价的平均分数。
我们对1000名消费者进行了一项匿名调查，收集到了他们对产品的评分。
现在，我们希望通过统计方法来推断总体的平均评分。
1. 假设检验类似于案例一，我们需要提出零假设和备择假设。
苏教版科学二上用实验验证假设教学设计和教学反思
苏教版科学二上用实验验证假设教学设计和教学反思1. 引言本文旨在设计一个科学实验来验证假设，并对教学过程进行反思。
这个实验将使用苏教版科学二上教材中的相关知识和实验设计原则进行实施。
2. 实验目标- 验证一个特定假设的科学性- 培养学生的实验设计和实施能力- 加深学生对科学原理的理解和应用3. 实验设计3.1 材料准备- 一台电子计时器- 一段导线- 一节电池- 一块铜板和一块锌板- 盐水溶液3.2 实验步骤1. 搭建一个简单的电池电路，将一块铜板和一块锌板通过导线连接起来。
2. 将电池的正极与铜板相连，将电池的负极与锌板相连。
3. 准备一段盐水溶液，并把铜板和锌板分别插入溶液中。
4. 开始计时器，并记录下两块板子分别在溶液中的时间。
5. 结束实验后，关闭电池电路，并停止计时器。
4. 实验结果根据实验的设计，我们可以观察到以下现象：- 锌板在盐水溶液中会逐渐腐蚀，溶解反应会产生电子。
- 铜板在盐水溶液中会因为锌板的腐蚀而产生电子反应。
5. 实验分析根据我们所观察到的实验现象，我们可以得出以下结论：- 锌和铜具有不同的电位，当它们在盐水中相连时，锌会释放电子给铜，并产生电流。
- 这个实验验证了涉及电池中化学反应的假设，即化学反应会产生电能。
6. 教学反思这个实验设计有助于学生通过实践来验证假设，并培养他们的实验设计和实施能力。
在教学过程中，我们可以通过以下方式进一步提升学生的研究效果：- 提前向学生介绍实验的目标和背景知识，帮助他们理解实验的科学原理。
- 引导学生观察实验现象，鼓励他们记录实验结果并进行分析。
- 引导学生思考实验结果的意义，帮助他们建立科学推理和解释的能力。
7. 结论通过这个实验，学生可以通过实践来验证科学假设，并深入理解化学反应和电池的原理。
通过教学反思，我们可以不断改进教学方法，提高学生的科学素养和实践能力。
这样的教学设计有助于提升学生的研究兴趣和效果，使他们更好地掌握科学知识和方法。
假设检验教学中的案例设计
假设检验教学中的案例设计思想。
鉴于概率论与数理统计这门课程的实用性比较强，在金融、保险、投资、运筹、教育、心理学等领域的应用也比较广泛，在课堂上完全可以借助各应用领域中的具体实例让学生从直觉和理智两个方面来对实际问题进行决策分析。
关于假设检验这部分内容，就可以结合案例教学来提高学生学习的兴趣和增强学生参与竞争的意识。
选择的案例尽可能地贴近学生的实际，给予学生发挥的空间比较大，在案例分析的过程当中，学生能够阐述自己的意见并能给出当前合理的解释。
一、将心理学融入假设检验的教学案例下面将以心理暗示为例说明假设检验的各项要素。
心理学中有一个名词叫做心理暗示，心理暗示中的期望定律即是当怀着对某件事情非常强烈期望的时候，所期望的事物就会出现。
从某种意义上说当对某件事情的发生充满信心的时候，这件事情发生的可能性就越大。
现在就来对这一理论进行实践的验证。
在课堂之初，学生对做好测验的信心或者说先对自己的成果进行预测期许：用1～5分进行评定“这次课堂测验我一定可以达到及格水平”。
数值越大，表明学生的自信心越强，对自己积极的心理暗示性越强。
通过对教学班67名同学的答卷用SPSS进行1/ 4统计，得到如下结果。
从表2的描述统计结果，可以看到学生的平均自信心强度得分为3.5375，大多数学生对自己的学习还是很有信心的；样本方差仅为0.586，说明不同的学生对学习的信念差异不大。
通过频数分布可以知道，绝大部分学生给予自己的多是积极的心理暗示。
通过表1的频率分布，能够看出50.75%的学生的自信心强度为4，56.72%的学生自信心强度超过均值3.5373。
现在针对刚才的数据结果将学生样本分为2组，超过均值的归为自信心强的一组，低于均值的记为自售心弱的组。
根据分组可得到如下结果。
现在要研究的是按照自信心的强弱分组，各组的测验成绩是否显著不同。
假定通过测验，已经得到了一组测验成绩值，该怎么对成绩的组别成绩做推断？也许会发现这两组的平均成绩有所不同，但这些差异是否显著，究竟是由自信心强弱导致的还是随机的？现在通过测验已经实际得到一组成绩，对成绩按自信心的强弱分组统计有如表4所示的结果。
假设检验的思政案例
假设检验的思政案例以假设检验的思政案例为题，列举以下10个案例：1. 假设检验在选举调查中的应用：假设调查表明某政党在选举前的支持率为50%，通过收集样本数据，可以利用假设检验来判断该政党的支持率是否真的为50%。
2. 假设检验在教育研究中的应用：假设研究表明某种教学方法可以提高学生的成绩，通过收集样本数据，可以利用假设检验来判断该教学方法是否真的有效。
3. 假设检验在社会调查中的应用：假设调查表明某种社会问题的比例为20%，通过收集样本数据，可以利用假设检验来判断该社会问题的比例是否真的为20%。
4. 假设检验在环境科学中的应用：假设研究表明某种污染物对环境的影响可以降低，通过收集样本数据，可以利用假设检验来判断该污染物对环境的影响是否真的降低。
5. 假设检验在经济学中的应用：假设研究表明某种政策可以提高国民经济的增长率，通过收集样本数据，可以利用假设检验来判断该政策是否真的能够提高国民经济的增长率。
6. 假设检验在医学研究中的应用：假设研究表明某种药物可以治疗某种疾病，通过收集样本数据，可以利用假设检验来判断该药物是否真的能够治疗该疾病。
7. 假设检验在农业科学中的应用：假设研究表明某种肥料可以提高农作物的产量，通过收集样本数据，可以利用假设检验来判断该肥料是否真的能够提高农作物的产量。
8. 假设检验在心理学研究中的应用：假设研究表明某种心理治疗方法可以减轻抑郁症状，通过收集样本数据，可以利用假设检验来判断该心理治疗方法是否真的能够减轻抑郁症状。
9. 假设检验在物理实验中的应用：假设研究表明某种材料具有特殊的导电性能，通过收集样本数据，可以利用假设检验来判断该材料是否真的具有特殊的导电性能。
10. 假设检验在法律案件中的应用：假设研究表明某种证据可以证明被告的罪行，通过收集样本数据，可以利用假设检验来判断该证据是否真的可以证明被告的罪行。
对假设检验的教学探讨
对假设检验的教学探讨
假设检验是统计学常用的方法之一，用来检验样本数据是否代表总体特征。
在教学中，正确有效地传授假设检验的基本概念和步骤至关重要，下面将分步骤探讨教学方法。
第一步：介绍基本概念
首先要让学生掌握基本概念，如总体、样本、假设等，并解释假设检验的作用和意义。
通过实例讲解，引导学生了解何时需要进行假设检验。
第二步：阐述假设检验的步骤
在掌握基本概念后，需要帮助学生掌握假设检验的步骤。
步骤包括确定零假设和备择假设、选择合适的检验统计量、计算出检验统计量的数值，以及判断结果并做出结论。
第三步：教授常见假设检验方法
此步骤可以针对不同类型的假设检验进行讲解，如t检验、z检验、F 检验等，通过实例演示让学生掌握如何选择合适的假设检验方法。
第四步：提高学生应用能力
在上述基础上，引导学生通过实际数据进行假设检验，让他们掌握如何识别问题、确定假设、选择检验方法和作出结论。
尤其是要让学生了解假设检验的局限性和应该采取的更多方法。
第五步：强化实际应用
指导学生掌握如何在实际研究中利用假设检验。
通过提供一些实际问题，让学生自己确定假设、选择检验方法、设计检验并给出结论。
同
时提醒学生在进行实际应用时需注意假设检验的前提条件和条件限制，避免假设检验的错误使用。
总之，针对假设检验的教学，我们应该注重基本概念、步骤、方法及
实际应用的教学，并且谨记教学过程需要通过实例引导学生掌握方法，并提高学生的实践和创新能力。
教学实践研究假设(3篇)
第1篇摘要：本文针对当前我国教育现状，提出了一种基于教学实践的研究假设，旨在探索提高教育教学质量的有效途径。
通过分析教学实践中的问题，提出相应的假设，为教育教学改革提供理论依据。
一、引言随着我国教育事业的不断发展，教育教学质量逐渐成为人们关注的焦点。
然而，在实际教学过程中，教师和学生普遍面临着诸多问题，如教学方法单一、教学资源匮乏、学生参与度低等。
为了解决这些问题，提高教育教学质量，本文提出了一种基于教学实践的研究假设。
二、研究假设1. 教学方法多样化假设假设：采用多样化的教学方法可以提高学生的学习兴趣和参与度，从而提高教育教学质量。
论证：多样化的教学方法可以满足不同学生的学习需求，激发学生的学习兴趣，提高学生的学习积极性。
同时，多样化的教学方法有助于培养学生的创新能力和实践能力，为学生的全面发展奠定基础。
2. 教学资源整合假设假设：整合各类教学资源，构建优质教学资源库，可以提高教育教学质量。
论证：教学资源是教育教学活动的基础，整合各类教学资源有助于提高教学效率，丰富教学内容。
构建优质教学资源库可以为教师提供丰富的教学素材，有助于教师更好地开展教育教学活动。
3. 学生参与度提升假设假设：通过提高学生参与度，激发学生的学习动力，可以促进教育教学质量的提高。
论证：学生参与度是教育教学质量的重要体现。
提高学生参与度有助于激发学生的学习兴趣，培养学生的自主学习能力，使学生在学习过程中发挥主体作用。
同时，学生参与度高的课堂氛围有助于提高教师的教学效果。
4. 教师专业发展假设假设：加强教师专业发展，提高教师教育教学水平，有助于提高教育教学质量。
论证：教师是教育教学活动的主体，教师的专业水平直接影响着教育教学质量。
加强教师专业发展，提高教师教育教学水平，有助于教师更好地适应教育教学改革的需要，提高教育教学质量。
5. 家校合作共育假设假设：加强家校合作，形成教育合力，有助于提高教育教学质量。
论证：家庭是孩子成长的重要环境，家校合作有助于形成教育合力，共同促进孩子的全面发展。
大学科学实验假设验证教案
大学科学实验假设验证教案1. 引言•介绍实验的目的和意义：验证科学实验的重要性，培养学生的科学思维和实验技能。
2. 教学目标•知识目标：了解科学实验的概念和意义，掌握实验规范和步骤。
•技能目标：培养学生观察、推理、实验设计和结果分析的能力。
3. 教学内容3.1 科学实验的概念和意义•定义科学实验：科学实验是通过设计、观察和记录来验证或证伪科学假设的活动。
•说明科学实验的意义：科学实验是科学研究的重要手段，可以帮助学生理解和应用科学知识。
3.2 实验规范和步骤•强调实验规范的重要性：实验规范能确保实验的可重复性和结果的可比较性。
•介绍实验步骤：包括准备材料、制定实验方案、实施实验、记录观察数据、分析结果和总结等。
3.3 观察、推理和实验设计能力培养•观察能力培养：通过实例演示和实践训练，让学生学会仔细观察并记录实验现象。
•推理能力培养：引导学生根据观察数据进行推理，发现规律和解释实验现象。
•实验设计能力培养：通过给出实验前提和目标，让学生设计符合科学原理和规范的实验方案。
3.4 结果分析和总结•结果分析：学生根据实验数据和推理，分析实验结果的合理性和科学性。
•总结：学生总结实验过程中所学到的知识和经验，提出自己的想法和改进方法。
4. 教学过程•第一步：引入科学实验的概念和意义，激发学生对实验的兴趣和好奇心。
•第二步：详细介绍实验规范和步骤，并给出实例演示。
•第三步：培养学生的观察能力，通过实例让学生观察和记录实验现象。
•第四步：培养学生的推理能力，引导学生根据观察数据进行推理和解释。
•第五步：培养学生的实验设计能力，给出实验前提和目标，让学生设计实验方案。
•第六步：引导学生分析实验结果，检验实验假设的合理性。
•第七步：总结实验过程，让学生对实验中所学到的知识和经验进行归纳和总结。
5. 教学评价•通过学生的实际表现、实验报告和答辩等方式进行评价，评估其实验设计和结果分析的能力。
6. 教学资源•实验室设备和材料：根据实验内容准备相应的实验设备和材料。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
假设检验案例教学研究
一、引言
推断统计中的一个重要内容，就是假设检验。
通过多年的教学实践，发现学生对这部分教学内容接受困难。
甚至在毕业多年之后，还坦言，自己当时没有搞清楚。
通过思考，引入了一个“中大奖”判断的例子，将假设检验的基本思想与方法串连起来，取得了非常好的教学效果。
二、案例的引入
假设检验是统计学一个非常重要的内容，思想性强。
学生们往往把假设检验这部分内容当成数学来学，忽略了其中的部分主观性。
原假设与备择假设、小概率原理、两类错误、拒绝域与接受域、P值检验等概念本身的逻辑性与连贯性，需要一个背景简单的案例串连起来，以便取得良好的教学效果。
1、“中大奖”问题的提出
如果，作为统计学教师的我，今天向大家宣布：我昨天买了一张彩票，中了500万。
你们信不信？信的同学有自己的理由：这是老师说的。
不信的同学也有理由：可能性太小了。
这就需要统计学意义上的假设检验。
2、原假设与备择假设概念的引入
谁来做假设检验呢？是不信的同学，他们希望收集证据，以支持不信的观点。
这就是假设检验的主观性，它是有立场的。
假设检验不是纯粹的数学。
原假设：研究者想收集证据予以反对的假设称为原假设，记为；备择假设：研究者想收集证据予以支持的假设称为备择假设，记为。
这里，原假设应该是“老师说的是真话”，备择假设应该是“老师说的是假话”。
原假设与备择假设是“非此即彼”的关系。
3、小概率原理与显著性水平的引入
一个事件如果发生概率很小，那么它在一次试验中是不可能发生的。
通常把5%作为一个界限，发生概率在5%以下的事件，被称为小概率事件。
如果老师说的话，连5%的可能性都没有，我们就有充分的理由拒绝相信。
假设检验的核心思想就是，在肯定原假设的基础上，是不是会引起小概率事件？如果发生了小概率事件，就拒绝原假设；如果没有发生小概率事件，就不能拒绝原假设。
这个5%，就是显著性水平。
我们可以设的更小，以增加说服力。
4、两类错误
其实，我们无论是信，还是不信，都无法避免出错。
弃真错误：原假设为真，拒绝原假设。
取伪错误：原假设为假，接受原假设。
我们拒绝老师说的话，认为他不可能中大奖时，有可能犯弃真错误；我们接受老师说的话，认为他中了大奖，有可能犯取伪错误。
一般认为，需要控制弃真错误的概率，使之不超过5%、1%等。
5、拒绝域与接受域、P值检验
基本概念了解之后，拒绝域与接受域、P值检验不过是具体操作过程，来进行判断了。
我们可以到彩票站收集样本数据，发现中大奖的概率不足5%，甚至不足万分之一。
中大奖完全是一个小概率事件，拒绝原假设，理由是充分的，犯错误的概率很小，远低于显著性水平。
三、假设检验基本原理的实际应用
1、问题分析
由统计资料得知，去年某地区新生儿平均体重为3190克，标准差80克。
现从今年新生儿中随机抽取了100个，测得其平均体重为3210克，请问今年与上一年相比新生儿体重有无明显差异？
20克的差异究竟意味着什么呢？两种观点。
第一种观点：20克的差异不过是抽样的随机性引起的，也就是说抽取的100个新生儿中恰好有几个超重的，拉高了平均值。
不需要进一步调查分析。
第二种观点：20克的差异太大了，抽样的随机性不足以解释这么大的差异。
有必要进一步调查分析。
所以，假设检验工作是由持第二种观点的人做的。
2、原假设与备择假设的确定
原假设是研究者想收集证据予以反对的假设。
进行假设检验的人，是持第二种观点的人。
所以，原假设应该是：“今年与去年相比，新生儿体重没什么变化”，备择假设则与之相反，应该是：“今年与去年相比，新生儿体重有明显变化”。
我们把它用数学语言来描述，就是：（这是一个双侧检验，过大或是过小，都将导致推翻原假设）
3、檢验统计量的确定
假设检验从逻辑上说，是一种反证法，在肯定原假设的基础上，看看是不是能推导出一个小概率事件。
如果说，“今年与去年相比，新生儿体重没什么变化”是正确的话，那么根据中心极限定理，。
这就是我们构造的检验统计量。
样本均值是一个均值为总体均值，方差为总体方差的N分之一倍。
4、拒绝域和接受域的确定
令=0.05，即显著性水平为5%。
我们犯第一类错误的概率不超过5%，=±1.96。
这样，接受域和拒绝域就确定下来了。
如果原假设是正确的，检验统计量落入接受域的概率为0.95。
5、计算检验统计量的值，作出推断：，落入拒绝域，我们有充分的理由拒绝原假设，20克的差异无法用抽样随机性解释。
结论：去年与今年相比，新生儿的平均体重确实有明显差异（原因不属于统计学的研究范围）。
如果原假设是正确的，导致一件真实发性的事件成为不可能的小概率事件。
所以，我们拒绝原假设是有充分理由的。