载流圆线圈周围磁场分布
计算载流圆线圈空间磁场分布的方法
计算载流圆线圈空间磁场分布的方法载流圆线圈是一种常见的电磁设备，广泛应用于电子、电力等领域。
计算载流圆线圈的空间磁场分布是一个重要的问题，本文将介绍几种常见的计算方法。
一、Biot-Savart定律Biot-Savart定律是电磁学中的一条基本定律，描述了电流元产生的磁场。
对于一个载流圆线圈，可以将其看做由许多电流元组成的，因此可以利用Biot-Savart定律计算其空间磁场分布。
具体计算步骤为：1. 将圆线圈分成若干个电流元，每个电流元的磁场可以用Biot-Savart定律计算。
2.将所有电流元的磁场叠加起来，就得到了整个圆线圈的磁场分布。
二、安培环路定理安培环路定理是电磁学中的另一个重要定理，它描述了磁场沿闭合回路的环路积分等于穿过该回路的总电流。
对于一个载流圆线圈，可以利用安培环路定理计算其磁场分布。
具体计算步骤为：1.假设有一个闭合回路围绕圆线圈。
2.根据安培环路定理，计算沿该回路的环路积分，等于穿过该回路的总电流。
3.通过调整回路位置和形状，可以计算得到不同点的磁场分布。
三、矢势法矢势是描述磁场分布的重要工具，可以通过矢势来计算载流圆线圈的空间磁场分布。
具体计算步骤为：1.将载流圆线圈看作由无限多小电流回路组成的，分别计算每个小电流回路产生的矢势。
2.将所有小电流回路产生的矢势相加，得到整个载流圆线圈的矢势分布。
3.根据矢势和磁场的关系，可以得到磁场分布。
四、有限元法有限元法是一种常见的数值计算方法，可以用于计算载流圆线圈的空间磁场分布。
具体计算步骤为：1.将载流圆线圈的空间区域离散为许多小单元。
2.在每个小单元内，建立磁场分布的数学模型。
3.利用数值计算方法，求解得到每个小单元内磁场的近似解。
4.根据近似解，在整个空间区域内得到磁场的分布。
总结：以上介绍了几种常见的计算载流圆线圈空间磁场分布的方法，包括Biot-Savart定律、安培环路定理、矢势法和有限元法。
这些方法各有特点，可以根据具体情况选择合适的方法进行计算。
磁场的描绘实验.
实验3—9 磁场的描绘【实验目的】1．掌握感应法测量磁场的原理和方法。
2．研究载流圆线圈轴向磁场的分布。
3．描绘亥姆霍兹线圈的磁场均匀区。
【实验仪器】非均匀磁场测量仪，400H Z 交流电源，晶体管毫伏表，探测线圈等。
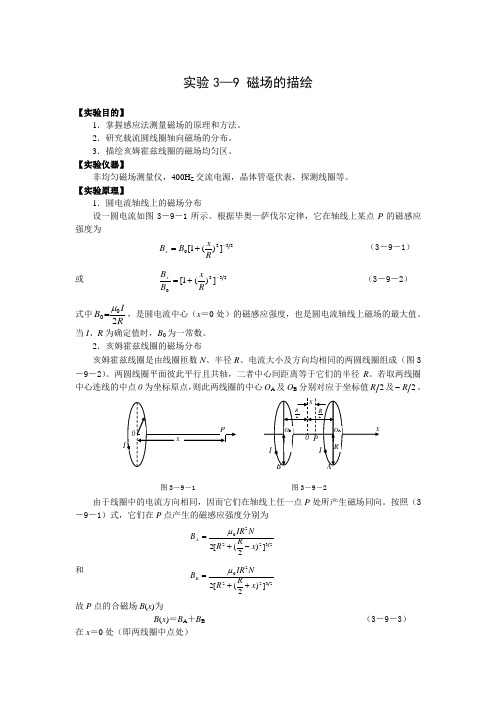
【实验原理】1．圆电流轴线上的磁场分布设一圆电流如图3－9－1所示。
根据毕奥—萨伐尔定律，它在轴线上某点P 的磁感应强度为320])(1[-+=R xB B x （3－9－1）或2320])(1[-+=RxB B x （3－9－2） 式中RIB 200μ=，是圆电流中心（x ＝0处）的磁感应强度，也是圆电流轴线上磁场的最大值。
当I 、R 为确定值时，B 0为一常数。
2．亥姆霍兹线圈的磁场分布亥姆霍兹线圈是由线圈匝数N 、半径R 、电流大小及方向均相同的两圆线圈组成（图3－9－2）。
两圆线圈平面彼此平行且共轴，二者中心间距离等于它们的半径R 。
若取两线圈中心连线的中点0为坐标原点，则此两线圈的中心O A 及O B 分别对应于坐标值2R 及2R -。
由于线圈中的电流方向相同，因而它们在轴线上任一点P 处所产生磁场同向。
按照（3－9－1）式，它们在P 点产生的磁感应强度分别为232220])2([2x RR N IR B A -+=μ和32220])2([2x RR N IR B B ++=μ故P 点的合磁场B (x )为B (x )＝B A ＋B B （3－9－3） 在x ＝0处（即两线圈中点处）523R计算表明，当)10(R x <时，B (x)和B (0)间相对差别约万分之一，因此亥姆霍兹线圈能产生比较均匀的磁场。
在生产和科研中，若所需磁场不太强时，常用这种方法来产生较均匀的磁场。
3．测量磁场的方法磁感应强度是一个矢量，因此磁场的测量不仅要测量磁场的大小且要测出它的方向。
测定磁场的方法很多，本实验采用感应法测量磁感应强度的大小和方向。
感应法是利用通过一个探测线圈（如图3－9－3）中磁通量变化所感应的电动势大小来测量磁场。
实验1 感应法测载流圆环的磁场分布
实验1 感应法测载流圆环的磁场分布本实验是通过感应法测量载流圆环的磁场分布。
该实验的目的是掌握感应法测量磁场的原理和方法，并通过实验结果验证安培环路定理。
实验仪器和材料：1. 载流圆环2. U型磁铁3. 磁场感应线圈4. 极限电流表5. 示波器6. 夹具实验原理：当电流通过载流圆环时，会在圆环周围产生磁场。
感应法测量磁场的原理是利用磁感应线圈感应磁场产生电动势，然后通过安培定理计算出磁场的强度和方向。
安培环路定理表明了磁场的形成和磁场的作用，即“磁场是由电流产生的，电流又可以受磁场的作用而产生力”。
实验步骤：1. 将U型磁铁放置在实验台上，并将载流圆环放置在磁铁中间。
2. 将极限电流表接在载流圆环的两端，记录圆环所通过的电流大小。
3. 调整载流圆环的位置，使其与磁铁中心对齐。
4. 将磁场感应线圈放置在载流圆环周围，并调整线圈的位置，使其与载流圆环保持一定距离，并且线圈面积垂直于载流圆环的平面。
5. 将磁场感应线圈连接到示波器上，并调整示波器的灵敏度。
6. 测量磁场感应线圈的输出信号，并根据安培环路定理计算磁场的强度和方向。
7. 记录不同电流下载流圆环的磁场分布情况，并进行数据处理和分析。
实验注意事项：1. 实验中要注意安全，避免电击和磁场对人体的影响。
2. 实验操作过程中要慢慢移动线圈，避免因移动过快导致误差。
3. 实验后要将仪器设备放置整齐，注意保养和维护，避免损坏。
实验结果：通过实验测量，我们可以得到不同电流下载流圆环的磁场分布情况并进行数据处理。
根据实验结果，我们可以绘制出载流圆环的磁场分布图像，进一步验证安培环路定理。
磁场的描绘实验33
实验33 磁场描绘二、载流圆线圈及亥姆霍兹线圈磁场的测定了解载流圆线圈的磁场是研究一般载流回路的基础。
本实验用感应法测定圆线圈的交流磁场，从而掌握低频交变磁场的测定方法。
以及了解如何用探测线圈确定磁场方向。
【实验目的】1．研究载流圆线圈轴线上磁场的分布，加深对毕奥—萨伐尔定律的理解；2．掌握感应法测磁场的原理和方法；3．考查亥姆霍兹线圈的磁场的均匀区；【实验仪器】亥姆霍兹线圈、低频信号发生器(或磁场描绘仪专用电源)、万用表（或交流毫伏表）、探测线圈和毫米方格纸等。
ZE-1型磁场描绘仪参数：圆线圈，N=640匝， R=10㎝；亥姆霍兹线圈距离，R=10㎝；探测线圈，N 0=1200匝，d=4㎜，D=12.8㎜，L=6㎜。
【实验原理】1．载流圆线圈轴线上的磁场分布设圆线圈的半径为R ，匝数为N ，在通以电流I 时，则线圈轴线上一点P 的磁感应强度2/32202/32220)1(2)(2R x R IN x R NIR B +=+=μμ (3-193)式中0μ为真空磁导率，x 为P 点坐标，原点在线圈中心．这就是线圈轴线上磁场B 与x 的定量关系式．2．亥姆霍兹线圈轴线上的磁场分布亥姆霍兹线圈是由一对半径R 、匝数N 均相同的四线圈组成，二线圈彼此平行而且共轴，线圈间距离正好等于半径R 如图3-118所示，坐标原点取在二线圈中心联线的中点O ． 给二线圈通以同方向、同大小的电流I ，它们对轴上任一点P 产生的磁场的方向将一致．P点处的磁感应强度等于在A 线圈和B 线圈在P 点产生的磁感应强度的和，应为：图3-118亥姆霍兹线圈 图3-119 亥姆霍兹线圈轴线上B x -Rx 曲线2/322202/32220])2([2])2([2x R R N IR x R R NIR B X -++++=μμ (3-194)从式(3-194)可以看出，B 是x 的函数．很容易算出在x=0处和x=R/10处两点B 值的相对差异约为0．012％，在理论上可以证明，当二线圈的距离等于半径时，在原点O 附近的磁场非常均匀，图3-119为B x -Rx 曲线． 3．磁场的测量磁感应强度是一个矢量，对它的测量既要测大小，又要测方向．测磁场的方法很多，在此实验中是用探测线圈去测交变磁场．法拉第电磁感应定律指出，处于磁场中的导体回路，磁感应电动势的大小与穿过它的磁通量的变化率成正比。
圆线圈和亥姆霍兹线圈的磁场
1.实验平台
两个线圈各500匝，圆线圈的内径19.00cm、外径21.00cm、平均半径 =10.00cm.。实验平台的台面应在两个对称圆线圈轴线上（台面中心横刻线与两个对称圆线圈轴线重合），台面上有相间1.00cm的均匀网格线。
2.高灵敏度毫特计
它采用两个参数相同的SS95A型集成霍尔传感器，配对组成探测器，经信号放大后，用三位半数字电压表测量探测器输出信号。该仪器量程0—2.000mT，分辨率为1
四、霍尔传感器
1.霍尔传感器
近年来，在科研和工业中，集成霍尔传感器被广泛应用于磁场测量，它测量灵敏度高，体积小，易于在磁场中移动和定位。本实验用SS95A型集成霍尔传感器测量载流圆线圈磁场分布，其工作原理也基于霍尔效应。
本实验采用的SS95A型集成霍尔传感器由霍尔元件、放大器和薄膜电阻剩余电压补偿器组成，测量时输出信号大，剩余电压的影响已被消除。一般的霍尔元件有四根引线，两根为输入霍尔元件电流的“电流输入端”；另两根为霍尔元件的“霍尔电压输出端”。本实验在设计安装时，传感器、圆线圈的工作回路相互独立，并且传感器的工作电流已设定为标准工作电流（定值）。即KHI＝K（常数）
3.两线圈采用串接或并接与电源相连时，必须注意磁场的方向。如果接错线有可能使双线圈中间轴线上的磁场为零或极小。
4.测每一点的B值之前，毫特计必须事先调零。
5.测双线圈磁场分布时，两线圈应串联。
[思考题]
1单线圈轴线上磁场的分布规律如何？亥姆霍兹线圈是怎样组成的？其基本条件有哪些？它的磁场分布特点又怎样？
〔实验原理〕
一、圆线圈
载流圆线圈在轴线（通过圆心并与线圈平面垂直的直线）上磁场情况如图3.14.1所示。
根据毕奥-萨伐尔定律，轴线上某点的磁感应强度 为
实验八212《亥姆霍兹线圈磁场》实验报告
三、 实验仪器
4501A 型亥姆霍兹线圈磁场实验仪
四、
实验步骤
1、测量载流圆线圈轴线上磁场的分布 （1）仪器使用前，请先开机预热 10min 接好电路，调零。 （2）调节磁场实验仪的输出功率，使励磁电流有效值为 I=200mA，以圆电
流线圈中心为坐标原点，每隔 10.00mm 测一个 Bmax 值，测量过程中注意保持励 磁电流值不变，记录数据并作出磁场分布曲线图。 2、测量亥姆霍兹线圈轴上磁场分布 （1）关掉电源，把磁场实验仪的两组线圈串联起来（注意极性不要接反）， 接到磁场测试仪的输出端钮，调零。 （2）调节磁场实验仪的输出功率，使励磁电流有效值为 I=200A，以圆电流 线圈中心为坐标原点，每隔 10.00mm 测一个 Bmax 值，测量过程中注意保持励磁 电流值不变，记录数据并作出磁场分布曲线图。
实验数据及处理1圆电流线圈轴线上磁场分布的测量数据记录注意坐标原点设在圆心处要求列表记录表格中包括测点位置并在表格中表示出各测点位置对应的理论值在坐标纸上画出实验曲线
班级：食品学院食品科学与工程 141 班
上课班级：生命科学学院生物科学类 165 班 姓名：黄素君
学号：5000414080
亥姆霍兹线圈磁场
一、
实验目的
1、掌握霍尔效应原理测量磁场； 2、测量单匝载流原线圈和亥姆霍兹线圈轴线上的磁场分布。
二、
实验原理
1、载流圆线圈磁场 一半径为 R，通以电流Ｉ的圆线圈，轴线上磁场的公式为：
B1 2 R2 X2
0 NR 2 I
3
2
（1）
式中， N 为圆线圈的匝数。 X 为轴上一点到圆心Ｏ的距离， 0 4 10 -7 H / m , 称为真空磁导率，因此它的轴线上磁场分布图如图。
关于电磁感应法测量载流圆线圈轴线上磁场分布的研究
第３３卷第１期大学物理实验Ｖｏｌ.３３Ｎｏ.１２０２０年２月ＰＨＹＳＩＣＡＬＥＸＰＥＲＩＭＥＮＴＯＦＣＯＬＬＥＧＥＦｅｂ.２０２０收稿日期:２０１９￣１０￣１５基金项目:西京学院校级教改项目(ＪＧＹＢ１９２５)ꎻ西京学院重点课程(ＺＤＫＣ２０１９１８)文章编号:１００７￣２９３４(２０２０)０１￣００４３￣０４关于电磁感应法测量载流圆线圈轴线上磁场分布的研究王㊀倩ꎬ张建祥ꎬ辛督强ꎬ黄海清ꎬ罗积军(西京学院理学院ꎬ陕西西安㊀７１０１２３)摘要:利用毕奥￣萨伐尔定律求解载流导线所产生的磁场分布是电磁学中一个非常重要的问题ꎮ由于载流圆线圈上的所取的电流元ｄｌ⇀在轴线上某点处所产生的磁感应强度ｄＢ⇀方向的取向是三维空间的取向ꎬ导致学生对此普遍认为比较抽象ꎬ对计算结果难以理解ꎮ本文以载流圆线圈轴线上磁场分布为例ꎬ通过电磁感应法测量磁场的实验方法测量载流圆线圈轴线上的磁场ꎬ实验测量所得的数据图表能够将载流圆线圈轴线上磁分布特点形象的描绘出来ꎬ并且实验结果很好的验证了由毕奥￣萨伐尔定律求解得到的载流圆线圈轴线上磁感应强度公式ꎬ此应用在实践教学中将新的实验技术与电磁学理论相结合的教学模式ꎬ使抽象的物理概念和公式变得更加具体化㊁形象化ꎬ也收到了良好的教学效果ꎮ关键词:磁感应强度ꎻ圆线圈ꎻ磁场分布ꎻ轴向磁场ꎻ毕奥￣萨伐尔定律中图分类号:Ｏ４￣３４文献标志码:ＡＤＯＩ:１０.１４１３９/ｊ.ｃｎｋｉ.ｃｎ２２￣１２２８.２０２０.０１.０１１㊀㊀随着科学技术的飞速发展和在高等院校的普及应用ꎬ对大学物理课程的教学方法进行改革势在必行ꎮ因此ꎬ越来越多的实验方法和实验技术应用于大学物理的理论课程教学之中ꎮ例如在学习磁场概念和毕奥￣萨伐尔定律求解磁感强度的过程中ꎬ以载流圆线圈轴线上磁场分布为例ꎬ应用电磁感应法测量磁场的实验技术ꎬ将实验和理论教学相结合ꎬ取得了较好的教学效果ꎮ载流圆线圈磁场分布一直是电磁理论的典型问题[１￣３]ꎮ笔者在从事大学物理和大学物实验教学过程中ꎬ发现基础知识薄弱的学生学习载流圆线圈轴线上磁场分布和利用毕￣萨定律求解轴线上某点磁感应强度时往往理解比较困难ꎬ学生认为概念抽象难理解㊁数学求解过程复杂等等ꎮ因此ꎬ从这一角度来看ꎬ实验方法与理论相结合的教学方式对解决实际问题将会有很大的帮助ꎮ为了便于学生理解这些知识ꎬ笔者在教学过程中利用电磁感应法测磁场的实验知识ꎬ帮助学生们理解载流圆线圈轴线上磁场分布的特点ꎬ并将实验测量所得数据进行数值分析ꎬ最后将实验值与理论计算值作对比ꎬ对比结果表明两者结论非常吻合ꎮ该教学方法使得学生对毕￣萨定律的理解进一步加深ꎬ激发了浓厚的学习兴趣ꎬ受到学生的一致好评ꎮ因此ꎬ将实验技术应用在载流圆线圈磁场分布特点的理论教学中取得了较好的教学效果ꎮ１㊀载流圆线圈轴线上磁场的理论分析㊀㊀设在真空中ꎬ有一半径为Ｒꎬ通电流为Ｉ的细导线圆环ꎬ在其轴线上距圆心Ｏ为ｘ处有一点Ｐꎬ如图１所示ꎬ任取电流元ꎬ由毕￣萨定律可知ꎬ该电流元在Ｐ点所激发的磁感应强度[４]ｄＢ的大小为:ｄＢ＝μ０４πＩｄｌｓｉｎθｒ２＝μ０４πＩｄｌｓｉｎ９０ʎｒ２由于:ｄＢ⇀ʅ(ｒ⇀ꎬＩｄｌ⇀)ꎬ所有ｄＢ⇀形成锥面ꎬ如图２所示ꎮ将ｄＢ⇀进行正交分解:ｄＢ⇀＝ｄＢ⇀ʊ＋ｄＢ⇀ʅ则由对称性分析得:Ｂʅ＝ʏｄＢʅ＝０Ｂʊ＝ʏｄＢʊ＝ʏｄＢｓｉｎθìîíïïïï则可得:Ｂ＝μ０ＩＲ４πｒ３ʏ２πＲ０ｄｌ＝μ０ＩＲ２４ｒ３＝μ０ＩＲ２２(Ｒ２＋ｘ２)３/２(１)图１㊀载流圆线圈轴线上磁场图２㊀载流圆线圈轴线上磁场对称分布由公式(１)可知ꎬ载流圆线圈轴线上的磁感应强度随着ｘ的增大而逐渐减小ꎬ当缠绕有Ｎ０匝圆导线ꎬ那么此时载流圆线圈轴线上磁场的大小分布为:Ｂ＝μ０Ｎ０ＩＲ２２(Ｒ２＋ｘ２)(２)则通过(２)式可得出载流圆线圈轴线上磁场的分布如图３所示ꎮ图３㊀载流圆线圈轴线上磁场分布２㊀载流圆线圈轴线上磁场的测量２.１㊀实验仪器介绍ＦＢ５２６型非均匀磁场测量实验仪和ＦＢ２０１型交变磁场测试仪ꎬ如图４所示ꎮ图４㊀ＦＢ５２６型实验仪和ＦＢ２０１型测试仪其中ＦＢ５２６型非均匀磁场测量实验仪中的两个线圈半径和匝数都相同ꎬ即Ｒ＝０.１０７ｍꎬＮ０＝４００匝ꎮ２.２㊀电磁感应法测量磁场(１)测量原理设均匀交变磁场为(由通交变电流的线圈产生)Ｂ＝Ｂｍｓｉｎωｔ磁场中一探测线圈的磁通量为Φ＝ＮＳＢｍｃｏｓθｓｉｎωｔ式中:Ｎ为探测线圈的匝数ꎬＳ为该线圈的截面积ꎬθ为Ｂ⇀与线圈法线夹角ꎬ如图５所示ꎮ图５㊀探测线圈在磁场中的示意图４４关于电磁感应法测量载流圆线圈轴线上磁场分布的研究根据法拉第电磁感应定律得线圈产生的感应电动势为:ε＝－ｄΦｄｔ＝ＮＳωＢｍｃｏｓθｃｏｓωｔ＝－εｍｃｏｓωｔ式中εｍ＝ＮＳωＢｍｃｏｓθ是线圈法线和磁场成θ角时ꎬ感应电动势的幅值ꎮ当θ＝０ꎬεｍａｘ＝ＮＳωＢｍꎬ这时的感应电动势的幅值最大ꎮ如果用数字式毫伏表测量此时线圈的电动势ꎬ则毫伏表的示值(有效值)Ｕｍ应为εｍａｘ２ꎬ则εｍａｘ＝２Ｕｍ＝ＮＳωＢｍꎮＢｍ＝εｍａｘＮＳω＝２ＵｍＮＳω(３)因此ꎬ由(３)式可计算出Ｂｍꎮ(２)探测线圈的设计:实验中由于磁场的不均匀性ꎬ探测线圈又不可能做得很小ꎬ否则会影响测量灵敏度ꎮ如图６所示ꎮ一般设计的线圈长度Ｌ和外径Ｄ有Ｌ＝２３Ｄ的关系ꎬ线圈的内径ｄ与外径Ｄ有ｄ⩽Ｄ３的关系(本实验选Ｄ＝０.０１２ｍꎬＮ＝８００匝的线圈)ꎮ线圈在磁场中的等效面积ꎬ经过理论计算ꎬ可用下式表示:Ｓ＝１３１０８πＤ２(４)这样的线圈测得的平均磁感强度可以近似看成是线圈中心点的磁感应强度ꎮ图６㊀探测线圈设计图本实验励磁电流由专用的ＦＢ２０１型交变磁场测试仪提供ꎬ该仪器输出的交变电流的频率ｆ可以从２０~２００Ｈｚ之间连续调节ꎬ本实验中选择ｆ＝５０Ｈｚꎬ则:ω＝２πｆ＝１００πＳ－１将Ｄ㊁Ｎ及ω值代人(３)(４)式得Ｂｍ＝０.１０３Ｕｍˑ１０－３(Ｔ)(５)或Ｂｍ＝０.１０３Ｕｍ(ｍＴ)(６)２.３ 单个载流圆线圈轴线上磁场测量调节交变磁场测试仪的输出频率㊁励磁电流有效值为ｆ＝５０ＨｚꎬＩ＝４００ｍＡꎮ建立坐标系ꎬ以圆电流线圈中心为坐标原点ꎬ轴向为Ｘ方向ꎬ径向为Ｙ方向ꎮ本例中采用每隔１０.０ｍｍ测量一个Ｕｍ值(注意:测量过程中保持励磁电流和频率值不变及径向方向使终在坐标原点)ꎬ并保证探测线圈法线方向与圆电流线圈轴线Ｄ的夹角为０ʎ(从理论上可知ꎬ如果转动探测线圈ꎬ当θ＝０ʎ和θ＝１８０ʎ时应该得到两个相同的Ｕｍ值ꎬ但实际测量时ꎬ需分别测出这两个值ꎮ本实验测得相应点的正㊁反两值的所有数据中ꎬ正㊁反方向测量值的测量误差小于１％ꎬ因此只记录θ＝０ʎ的Ｕｍ值)ꎮＵｍ的测量数据及磁场强度数据如表１所示ꎬ实测值与理论值所对应的曲线如图７所示ꎮ由此可见ꎬ实验值与理论值吻合的非常好ꎮ表１㊀实验数据Ｘ轴向距离ｘ/ｍｍＵｍ/ｍＶＢ(实验值)(ｍＴ)Ｂ(理论值)(ｍＴ)－１１０３.８００.２７７０.３１９－１００４.５００.３２８０.３７１－９０５.２００.３７９０.４１８－８０６.０００.４３７０.４８６－７０６.９００.５０３０.５４８－６０８.０００.５８３０.６２２－５０９.０００.６５６０.７０２－４０１０.０００.７２８０.７７７－３０１１.７００.８５２０.８５２－２０１２.０００.８７４０.８９４－１０１２.６００.９１８０.９２００１２.８００.９３２０.９４０１０１２.６００.９１８０.９２０２０１２.１００.８８１０.８９４３０１１.３００.８２３０.８５２４０１０.３００.７５００.７７７５０９.４００.６８５０.７０２６０８.２００.５９７０.６２２７０７.１００.５１７０.５４８８０６.２００.４５２０.４８６９０５.４００.３９３０.４１８１００４.５００.３２８０.３７１１１０４.１００.２９９０.３１９５４关于电磁感应法测量载流圆线圈轴线上磁场分布的研究图７㊀载流圆线圈轴线上磁场分布对比３㊀结㊀论通过理论推导和实验测量的数据分析[５]得到了相同的结论ꎬ即两种数据结果同样说明了单个载流圆线圈轴线上磁场分布的特点ꎮ磁感应强度在圆心处最大ꎬ并且沿着轴线两端逐渐减小ꎬ与轴线两端呈对称分布[６]ꎮ因此ꎬ该实验能够形象的描述载流圆线圈磁场的分布特点ꎬ实验数值结果也能给出用毕￣萨定律求解载流圆线圈轴线上磁感应强度[７]分布的结论ꎮ根据笔者多年的教学实践经验表明ꎬ对于物理基础知识薄弱的学生学习载流圆流线圈轴线上磁场分布和应用毕￣萨定律求解时利用该实验方法帮助学生理解㊁掌握相应的知识ꎮ学生们通过新的实验方法能够很好的避开繁琐的理论分析和数学求解过程ꎬ加深了对抽象概念的理解ꎬ并顺利的掌握毕￣萨定律应用ꎮ这种教学方式一方面可以提高学生学习抽象的磁场理论知识的兴趣ꎬ另一方面可以提高学生处理实际问题和实际应用的能力ꎮ因此ꎬ将新的实验技术和理论教学的相结合对大学物理理论的教学起到较好的辅助作用ꎮ参考文献:[１]㊀侯宏涛ꎬ侯双霞.载流圆线圈轴线上磁场理论分布与实测对比分析[Ｊ].皖西学院学报ꎬ２０１７ꎬ３３(２):５９￣６２.[２]㊀高静ꎬ孙鑫ꎬ刘俊伟.亥姆霍兹线圈磁场空间分布的研究[Ｊ].科技通报ꎬ２０１８ꎬ３４(７):３５￣３７.[３]㊀刘雅洁ꎬ朱宁.圆线圈及亥姆霍兹线圈的磁场分布[Ｊ].嘉兴学院学报ꎬ２００４ꎬ１６(３):４７￣５０.[４]㊀渊小春.大学物理[Ｍ].上海:同济大学出版社ꎬ２０１４.[５]㊀范程颖.基于亥姆霍兹线圈的旋转磁场设计方法和ＣＯＭＳＯＬ有限元仿真[ｔ].科技与创新ꎬ２０１９ꎬ４６(６):４６￣４８.[６]㊀杜珊珊ꎬ王琼辉ꎬ王婧ꎬ等.载流圆线圈的磁场分布研究[Ｊ].昆明学院学报ꎬ２０１７ꎬ３９(６):９４￣９７.[７]㊀程军.载流圆线圈的磁场的ＭＡＴＬＡＢ数值计算[Ｊ].物理通报ꎬ２０１５(５):１９￣２０.ＳｔｕｄｙｏｎＭｅａｓｕｒｅｍｅｎｔｏｆＭａｇｎｅｔｉｃＦｉｅｌｄＤｉｓｔｒｉｂｕｔｉｏｎａｂｏｕｔｔｈｅＡｘｉｓｏｆＣｕｒｒｅｎｔ￣ＣａｒｒｙｉｎｇＣｏｉｌｂｙＥｌｅｃｔｒｏｍａｇｎｅｔｉｃＩｎｄｕｃｔｉｏｎＷＡＮＧＱｉａｎꎬＺＨＡＮＧＪｉａｎｘｉａｎｇꎬＸＩＮＤｕｑｉａｎｇꎬＨＵＡＮＧＨａｉｑｉｎｇꎬＬＵＯＪｉｊｕｎ(ＤｅｐａｒｔｍｅｎｔｏｆＰｈｙｓｉｃｓꎬＸｉｊｉｎｇＵｎｉｖｅｒｓｉｔｙꎬＸｉ ａｎ７１０１２３ꎬＣｈｉｎａ)Ａｂｓｔｒａｃｔ:Ｉｔｉｓａｖｅｒｙｅｓｓｅｎｔｉａｌｐｒｏｂｌｅｍｉｎｅｌｅｃｔｒｏｍａｇｎｅｔｉｓｍｔｏｓｏｌｖｅｔｈｅｄｉｓｔｒｉｂｕｔｉｏｎｏｆｍａｇｎｅｔｉｃｆｉｅｌｄｇｅｎｅｒａｔｅｄｂｙｃｕｒｒｅｎｔ￣ｃａｒｒｙｉｎｇｗｉｔｈｔｈｅｍｅｔｈｏｄｏｆＢｉｏ￣Ｓａｖａｒｔ ｓｌａｗ.ＡｓｔｈｅｍａｇｎｅｔｉｃｉｎｄｕｃｔｉｏｎｉｎｔｅｎｓｉｔｙｄＢｇｅｎｅｒａｔｅｄｂｙｔｈｅｃｕｒｒｅｎｔｅｌｅｍｅｎｔｄｌｏｎｔｈｅｃｕｒｒｅｎｔ￣ｃａｒｒｙｉｎｇｃｉｒｃｕｌａｒｃｏｉｌａｔａｃｅｒｔａｉｎｐｏｉｎｔｏｎｔｈｅａｘｉｓｉｓｏｒｉｅｎｔｅｄｉｎａｔｈｒｅｅ￣ｄｉｍｅｎｓｉｏｎａｌｓｐａｃｅꎬｗｈｉｃｈｌｅａｄｓｔｏｔｈｅｒｅｓｕｌｔｔｈａｔｓｔｕｄｅｎｔｓｇｅｎｅｒａｌｌｙｔｈｉｎｋｉｔａｂｓｔｒａｃｔａｎｄｄｉｆｆｉｃｕｌｔｔｏｕｎｄｅｒｓｔａｎｄ.Ｔｈｅａｒｔｉｃｌｅｔａｋｅｓｔｈｅｍａｇｎｅｔｉｃｆｉｅｌｄｄｉｓｔｒｉｂｕｔｉｏｎｏｎｔｈｅａｘｉｓｏｆｔｈｅｃｕｒｒｅｎｔ￣ｃａｒｒｙｉｎｇｃｏｉｌａｓａｎｅｘａｍｐｌｅꎬｃｏｎｃｅｒｎｉｎｇａｂｏｕｔｔｈｅｍａｇｎｅｔｉｃｆｉｅｌｄｏｎｔｈｅａｘｉｓｏｆｔｈｅｃｕｒｒｅｎｔ￣ｃａｒｒｙｉｎｇｃｏｉｌｉｓｍｅａｓｕｒｅｄｂｙｔｈｅｅｘｐｅｒｉｍｅｎｔａｌｍｅｔｈｏｄｏｆｅｌｅｃｔｒｏｍａｇｎｅｔｉｃｉｎｄｕｃｔｉｏｎ.Ｔｈｅｏｂｔａｉｎｅｄｄａｔａｃｈａｒｔｓｃａｎｖｉｓｕａｌｌｙｄｅｓｃｒｉｂｅｔｈｅｍａｇｎｅｔｉｃｄｉｓｔｒｉｂｕｔｉｏｎｃｈａｒａｃｔｅｒｉｓｔｉｃｓｏｎｔｈｅａｘｉｓｏｆｔｈｅｃｕｒｒｅｎｔ￣ｃａｒｒｙｉｎｇｃｉｒｃｕｌａｒｃｏｉｌꎬａｎｄｔｈｅｅｘｐｅｒｉｍｅｎｔａｌｒｅｓｕｌｔｓａｒｅｖｅｒｙｐｒｏｖｅｄｏｆＢｉｏｔ￣Ｓａｖａｒｔｌａｗ.Ｔｈｅｆｏｒｍｕｌａｏｆｍａｇｎｅｔｉｃｉｎｄｕｃｔｉｏｎｉｎｔｅｎｓｉｔｙｏｎｔｈｅａｘｉｓｏｆｃｕｒｒｅｎｔ￣ｃａｒｒｙｉｎｇｃｉｒｃｕｌａｒｃｏｉｌｉｓａｐｐｌｉｅｄｔｏｔｈｅｔｅａｃｈｉｎｇｍｏｄｅｏｆｃｏｍｂｉｎｉｎｇｎｅｗｅｘｐｅｒｉｍｅｎｔａｌｔｅｃｈｎｏｌｏｇｙｗｉｔｈｅｌｅｃｔｒｏｍａｇｎｅｔｉｃｓｔｈｅｏｒｙｉｎｐｒａｃｔｉｃａｌｔｅａｃｈｉｎｇꎬｓｏａｓｔｏｍａｋｅｉｔａｂｓｔｒａｃｔ.Ｐｈｙｓｉｃａｌｃｏｎｃｅｐｔｓａｎｄｆｏｒｍｕｌａｓｈａｖｅｂｅｃｏｍｅｍｏｒｅｓｐｅｃｉｆｉｃａｎｄｖｉｓｕａｌｉｚｅｄꎬａｎｄｈａｖｅａｌｓｏｒｅｃｅｉｖｅｄｇｏｏｄｔｅａｃｈｉｎｇｒｅｓｕｌｔｓ.Ｋｅｙｗｏｒｄｓ:ｍａｇｎｅｔｉｃｉｎｄｕｃｔｉｏｎｉｎｔｅｎｓｉｔｙꎻｃｉｒｃｕｌａｒｃｏｉｌꎻｍａｇｎｅｔｉｃｆｉｅｌｄｄｉｓｔｒｉｂｕｔｉｏｎꎻａｘｉａｌｍａｇｎｅｔｉｃｆｉｅｌｄꎻＢｉｏ￣Ｓａｖａｒｔ ｓｌａｗ６４关于电磁感应法测量载流圆线圈轴线上磁场分布的研究。
试验四十五用电磁感应法测磁场分布
实验四十五 用电磁感应法测磁场分布在工业、国防、科研中都需要对磁场进行测量，测量磁场的方法不少，如冲击电流计法、霍耳效应法、核磁共振法、天平法、电磁感应法等等。
本实验介绍电磁感应法测磁场的方法，它具有测量原理简单、测量方法简便及测试灵敏度较高等优点。
一 实 验 目 的（1）了解用电磁感应法测交变磁场的原理和一般方法，掌握FB-201型交变磁场实验仪及测试仪的使用方法。
（2）测量载流圆形线圈和亥姆霍兹线圈的轴向上的磁场分布。
（3）了解载流圆形线圈（或亥姆霍兹线圈）的径向磁场分布情况。
（4）研究探测线圈平面的法线与载流圆形线圈（或亥姆霍兹线圈）的轴线成不同夹角时所产生的感应电动势的值的变化规律。
二 实 验 原 理1. 载流圆线圈与亥姆霍兹线圈的磁场 （1）载流圆线圈磁场一半径Ｒ，通以电流I 的圆线圈，轴线上磁场分布的公式为： 2/322200)(2X R IR N B +=μ （1）式中N 0为圆线圈的匝数，为轴上某一点到圆心X O ′的距离。
,H/m 10470−×=πμ它的分布图如图1所示。
图1 载流圆线圈磁场分布图2 亥姆霍兹线圈的磁场分布本实验取:圆心处, m 100.0 ,A 400.0 ,4000===R I N 匝 'O 0=X ，图 3探测线圈在磁场可算得圆心O'处磁感应强度为： (T)1001.13−×=B （2）亥姆霍兹线圈(图23-2)两个相同圆线圈彼此平行且共轴，通以同方向电流I ，理论计算证明：线圈间距等于线圈半径时，两线圈合磁场在轴上（两线圈圆心连线）附近较大范围内是均匀的，这样的一对线圈称为亥姆霍兹线圈。
这种均匀磁场在科学实验中应用十分广泛，例如，显像管中的行、场偏转线圈就是根据实际情况经过适当变形的亥姆霍兹线圈。
a R2. 用电磁感应法测磁场的原理 设均匀交变磁场为（由通交变电流的线圈产生）:t B B m sin ω= 磁场中一探测线圈的磁通量为: Φ=NSB m cosθsinωt ，式中：Ｎ为探测线圈的匝数，S 为该线圈的截面积，θ为B v与线圈法线夹角，如图23-3所示。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
对 的进一步求解过程如下：
②
③
以上两式相减，考虑到
则
由此得到
故
对比①式中出现的积分，引入参量 并令
则由
其中：
得到结果
④
令 ，则对①式整理，得到以下结果
⑤
以上②结果便是求解得到的载流圆线圈周围任意处空间磁感应强度分布，当然上式还不算是最终结果，因为式中所涉及的不完全椭圆积分的具体形式 还没有确定，以下便是对其具体形式的求解。
本文与已发文章《闭合载流导线周围磁感应强度的空间分布》 （物理学刊27期）、《一个重要公式在电磁学中的应用》 （物理学刊29期）同属姊妹篇。第一篇文章提出了解决该问题的一般方法，并推广到任意形状的闭合载流线圈，同时作为例子计算了过垂直载流圆线圈环面中心直线上的磁感应强度。第二篇文章是对第一篇文章的进一步探索，运用椭圆积分精确求解了载流圆线圈在其所在整个平面的强度分布情况。本文是前两篇文章的更深一步探索，最终精确求解了载流圆线圈在空间任意处的分布情况。通过这三篇文章，希望给大家带来的不仅仅是问题的答案，更为重要的是将作者一步步探索问题的过程呈献给大家，希望能给大家未来的学习和研究带来帮助。
1.载流圆线圈磁感应强度
这里直接引用文章 中的结果：
①
其中
2.积分公式求解
分析式①中的积分不难发现，积分的困难就在于分母的复杂性。而分母可以表示为下面的形式：
因此本文就先从最基本的积分形式入手。令 ，引入新的参量 ，并满足 ，则
作第二次变量替换，引入角度变量 、数值变量 ，并作替换 ，则可得
写成一般形式，即
载流圆线圈周围
孟雨
孟雨物理工程学院11级物理学类三班
Email:1240123245@
摘要：本文第一次在直角坐标系中直接从磁感应强度的计算公式毕奥-萨伐尔定律出发，精确求解了圆电流空间任一点磁场分布。并通过数值模拟，给出了圆电流周围磁场的空间分布情况。
关键词：载流圆线圈、椭圆积分、磁感应强度、数值模拟
对⑤式中的 进行数值模拟，当 分别取0,4,10,20时，磁场 分布如下列图所示：
同理，磁场 分布如下列图所示：
参考文献：
【1】赵凯华 陈熙谋电磁学（第三版）[M].高等教育出版社2012:法[J]大学物理 2007.26（7）
【3】王竹溪郭敬仁.特殊函数概论[M].北京:北京大学出版社.2000:549
Key words:electric round string ; ellipse integral ; magnetic field strength;numerical simulation
指导老师：陈长青
王明星
【4】张之翔 电磁学中几个简单问题里的椭圆积分[J].大学物理2002.21（4）
【5】孟雨闭合载流导线周围磁感应强度的空间分布[J].物理学刊2012.27
【6】孟雨一个重要公式在电磁学中的应用[J].物理学刊2012.29
D
Abstract:The article firstly precisely solves the question of distribution of magnetic field strength of electric round string in everywhere of three-dimensionality directly by Biot-Savart’s law in rectangular coordinate system.By numerical simulation, the article visually gives the distribution of magnetic field.
又由式⑧得
又
故
⑨
5.数值模拟
综合上式④、⑤、⑨，用软件 进行数值模拟，相关取值如下：
首先对⑤式中的 进行数值模拟，由于目标函数 是关于空间变量 的三元函数，实际模拟时本文采用降维方法：固定其中一个空间变量 ，对目标函数进行三维模拟。并通过令变量 取不同的数值进行多次模拟，比较结果的差异，从而得到 的空间分布。当 分别取0,4,10,20时，磁场分量 的分布如下列图所示。
首先确定参数的取值范围
由
得
且
3. 的计算
⑥
又由于
从而得到
故
将上式带入到式③中，得到
⑦
由于
从而可以确定出
⑧
综上所述，④已是严格意义上的精确解。至此，载流圆线圈周围任意处空间磁感应强度分布已由④严格给出。
4.结果分析
虽然结果已由上文给出，但④式结果依然比较复杂，先对其进一步简化。考虑到
则由⑥、⑦式并取幂级数首项，得
0.引言
圆电流的磁场分布是电磁学中一个重要而典型的问题，不少学者进行求解此方面问题时一般采用矢势方法，而即使采用最为基本的毕奥-萨伐尔定律求解时，求解的也是简化后的磁场在固定平面内的分布，而非整个三维空间内的分布。究其原因，在于积分的复杂性。即使求解磁场在平面内的分布，也涉及复杂的椭圆积分，因此对于磁场在三维空间任意处的分布，很多学者避而不答。本文仅采用最为基本的毕奥-萨伐尔定律，通过一系列变量替换直接在直角系给出了磁场分布的级数形式解。