23不等式的解集与区间
二元二次不等式解法步骤_概述及解释说明

二元二次不等式解法步骤概述及解释说明1. 引言1.1 概述二元二次不等式是数学中常见的一类不等式,其形式为ax^2 + bxy + cy^2 + dx + ey + f > 0 或者ax^2 + bxy + cy^2 + dx + ey + f < 0。
解决这类不等式需要运用特定的解法步骤,以得出满足条件的变量取值范围。
本文将介绍二元二次不等式解法步骤,并详细解释其基本原理和概念。
1.2 文章结构本文分为五个部分,每个部分内容各有侧重。
首先在引言部分进行概述,介绍文章的结构和目标。
接下来,在第2部分探讨二元二次不等式的定义、解法步骤的概述以及基本原理说明。
第3部分会详细介绍方法一:因式分解与区间判断法,并提供相关示例演示与实例分析。
在第4部分中,我们将介绍方法二:图像法与辅助函数法,并对比两种方法的优缺点以及适用情况进行讨论。
最后,在第5部分进行总结回顾并展望可能的拓展方向。
1.3 目的本文旨在帮助读者更好地理解和掌握二元二次不等式的解法步骤。
通过对问题背景和基本原理的介绍,读者将能够学会使用因式分解与区间判断法以及图像法与辅助函数法来解决这类不等式问题。
文章也将探讨两种方法的优缺点及其适用情况,以帮助读者选择最合适的解题方法。
通过阅读本文,读者将能够提升对二元二次不等式解法步骤的理解和运用能力,并在实际问题中更加灵活地应用所学知识。
2. 二元二次不等式解法步骤的基本原理和概念2.1 二元二次不等式的定义二元二次不等式是具有一般形式Ax^2 + Bxy + Cy^2 + Dx + Ey + F > 0(或< 0)的不等式,其中A、B、C、D、E 和F 是实数系数,而x 和y 是变量。
2.2 解法步骤概述解决二元二次不等式的一般步骤可以总结如下:(a) 将不等式表达式整理为标准形式,即将项排列顺序调整,并保持主项为正(负)。
(b) 将一元项进行配方,使问题转化为一元二次不等式。
不等式的解集与区间教学设计人教版

此外,还需要准备一些教学工具,如黑板、粉笔、投影仪等,以便进行课堂教学的演示和讲解。同时,确保每位学生都有足够的学习空间,可以准备一些桌椅,以适应不同的教学活动需求。
二、新课讲授(用时10分钟)
1.理论介绍:首先,我们要了解不等式的解集和区间的基本概念。不等式的解集是……(详细解释概念),它能够表示所有满足不等式的实数构成的集合。区间是……(解释其概念和表示方法),它用于表示不等式解集的一种图形化表示方法。
2.案例分析:接下来,我们来看一个具体的案例。这个案例展示了不等式的解集和区间在实际中的应用,以及它们如何帮助我们解决问题。
5.请将不等式2x^2+x+1<0的解集用区间表示出来。
答案:
1.解集为{x | x>3或x<1}
2.解集为{x | x<1或x>2}
3.解集为{x | 1<x<3}
4.解集为{x | x>-1或x<-3}
5.解集为{x | -1<x<-3}
不等式的解集与区间教学设计人教版
授课内容
授课时数
授课班级
授课人数
授课地点
授课时间
教材分析
本节课的教学内容是“不等式的解集与区间教学设计”,所使用的是人教版教材。本节课的主要内容是让学生理解不等式的解集及其表示方法,掌握区间的概念及其表示方法,能够将实际问题转化为不等式,并求出其解集和区间。
本节课的教学对象是初中二年级的学生,他们已经掌握了不等式的基本性质,具备了一定的代数基础。在学习本节课的内容时,他们需要将已有的知识与新的知识进行整合,形成系统的不等式知识体系。
2020年高考数学(文)母题题源解密23 不等式选讲(全国Ⅱ专版原卷版)

专题23 不等式选讲【母题来源一】【2020年高考全国Ⅱ卷文数】已知函数2()|21|f x x a x a =-+-+. (1)当2a =时,求不等式()4f x 的解集; (2)若()4f x ≥,求a 的取值范围. 【答案】(1)32x x ⎧≤⎨⎩或112x ⎫≥⎬⎭;(2)(][),13,-∞-+∞.【分析】(1)分别在3x ≤、34x <<和4x ≥三种情况下解不等式求得结果; (2)利用绝对值三角不等式可得到()()21f x a ≥-,由此构造不等式求得结果. 【解析】(1)当2a =时,()43f x x x =-+-.当3x ≤时,()43724f x x x x =-+-=-≥,解得:32x ≤;当34x <<时,()4314f x x x =-+-=≥,无解;当4x ≥时,()43274f x x x x =-+-=-≥,解得:112x ≥; 综上所述:()4f x ≥的解集为32x x ⎧≤⎨⎩或112x ⎫≥⎬⎭.(2)()()()()22222121211f x x a x a x ax a aa a =-+-+≥---+=-+-=-,当且仅当221a x a -≤≤时取等号,()214a ∴-≥,解得:1a ≤-或3a ≥,a ∴的取值范围为(][),13,-∞-+∞.【点睛】本题考查绝对值不等式的求解、利用绝对值三角不等式求解最值的问题,属于常考题型. 【母题来源二】【2019年高考全国Ⅱ卷文数】已知()|||2|().f x x a x x x a =-+-- (1)当1a =时,求不等式()0f x <的解集; (2)若(,1)x ∈-∞时,()0f x <,求a 的取值范围. 【答案】(1)(,1)-∞;(2)[1,)+∞【解析】(1)当a =1时,()=|1| +|2|(1)f x x x x x ---.当1x <时,2()2(1)0f x x =--<;当1x ≥时,()0f x ≥.所以,不等式()0f x <的解集为(,1)-∞. (2)因为()=0f a ,所以1a ≥.当1a ≥,(,1)x ∈-∞时,()=() +(2)()=2()(1)<0f x a x x x x a a x x -----. 所以,a 的取值范围是[1,)+∞.【名师点睛】本题主要考查含绝对值的不等式,熟记分类讨论的方法求解即可,属于常考题型. 【母题来源三】【2018年高考全国Ⅱ卷文数】设函数()5|||2|f x x a x =-+--. (1)当1a =时,求不等式()0f x ≥的解集; (2)若()1f x ≤,求a 的取值范围.【答案】(1){|23}x x -≤≤;(2)(,6][2,)-∞-+∞.【解析】(1)当1a =时,24,1,()2,12,26, 2.x x f x x x x +≤-⎧⎪=-<≤⎨⎪-+>⎩可得()0f x ≥的解集为{|23}x x -≤≤. (2)()1f x ≤等价于|||2|4x a x ++-≥.而|||2||2|x a x a ++-≥+,且当2x =时等号成立. 故()1f x ≤等价于|2|4a +≥. 由|2|4a +≥可得6a ≤-或2a ≥, 所以a 的取值范围是(,6][2,)-∞-+∞.【命题意图】1.理解绝对值的几何意义,并能利用含绝对值不等式的几何意义证明以下不等式: (1)a b a b +≤+. (2) a b a c c b -≤-+-.(3)会利用绝对值的几何意义求解以下类型的不等式:; ; ax b c ax b c x a x b c +≤+≥-+-≥.2.了解证明不等式的基本方法:比较法、综合法、分析法、反证法、放缩法.3.主要考查逻辑推理能力、运算求解能力,考查分类讨论、数形结合思想方法,考查逻辑推理、数学运算等核心素养. 【命题规律】从近三年高考情况来看,此类知识点以解答题的形式出现,主要考查绝对值不等式的解法、不等式的证明、求最值问题等. 【方法总结】(一)解绝对值不等式的常用方法有:(1)公式法:对于形如|f (x )|>g (x )或|f (x )|<g (x ),利用公式|x|<a ⇔−a<x<a (a>0)和|x|>a ⇔x>a 或x<−a (a>0)直接求解不等式;(2)平方法:对于形如|f (x )|≥|g (x )|,利用不等式两边平方的技巧,去掉绝对值,需保证不等式两边同正或同负,即|f (x )|≥|g (x )|⇔f (x )2≥g 2(x );(3)零点分段法:对于形如|f (x )|±|g (x )|≥a ,|f (x )|±|g (x )|≤a ,利用零点分区间法脱去绝对值符号,将其转化为与之等价的不含绝对值符号的不等式(组)求解;(4)几何法:对于形如|x±a|±|x±b|≤c ,|x±a|±|x±b|≥c ,利用绝对值三角不等式的性质求解,即 ①定理1:如果a ,b 是实数,则|a+b|≤|a|+|b|,当且仅当ab ≥0时,等号成立.②定理2:如果a ,b ,c 是实数,那么|a−c|≤|a−b|+|b−c|,当且仅当(a−b )(b−c )≥0时,等号成立. ③推论1:||a|−|b||≤|a+b|. ④推论2:||a|−|b||≤|a−b|.(5)图象法:对于形如|f (x )|+|g (x )|≥a 可构造y=|f (x )|+|g (x )|−a 或y=|f (x )|+|g (x )|与y=a ,在直角坐标系中作出不等式两边所对应的两个函数的图象,利用函数图象求解或通过移项构造一个函数. (二)含绝对值不等式的恒成立问题的常见类型及其解法:(1)分享参数法运用“max min ()(),()()f x a f x a f x a f x a ≤⇔≤≥⇔≥”可解决恒成立中的参数范围问题.求最值的思路:利用基本不等式和不等式的相关性质解决;将函数解析式用分段函数形式表示,作出函数图象,求得最值;利用性质“||||||||||||a b a b a b -≤±≤+”求最值.(2)更换主元法不少含参不等式恒成立问题,若直接从主元入手非常困难或不可能解决时,可转换思维角度,将主元与参数互换,常可得到简捷的解法.(3)数形结合法在研究曲线交点的恒成立问题时,若能数形结合,揭示问题所蕴含的几何背景,发挥形象思维和抽象思维各自的优势,可直接解决问题. (三)不等式的证明(1)比较法证明不等式最常用的是差值比较法,其基本步骤是:作差—变形—判断差的符号—下结论.其中“变形”是证明的关键,一般通过因式分解或配方将差式变形为几个因式的积或配成几个代数式平方和的形式,当差式是二次三项式时,有时也可用判别式来判断差值的符号.个别题目也可用柯西不等式来证明.(2)基本不等式:如果a ,b>0,那么2a b+≥,当且仅当a=b 时,等号成立.用语言可以表述为:两个正数的算术平均数不小于(即大于或等于)它们的几何平均数.(3)算术平均—几何平均定理(基本不等式的推广):对于n 个正数a 1,a 2,…,a n ,它们的算术平均数不小于它们的几何平均数,即12nn a a a n+++≥当且仅当a 1=a 2=…=a n 时,等号成立.1.(2020·山西省高三)已知函数()|1||2|f x x x a =++-. (1)若1a =,解不等式()4f x <;(2)对任意的实数m ,若总存在实数x ,使得224()m m f x -+=,求实数a 的取值范围.2.(2020·四川省泸县第二中学高三二模)已知函数()211f x x x =-++. (1)求不等式()2f x x ≤+的解集;(2)若函数()y f x =的最小值记为m ,设0a >,0b >,且有a b m +=.求1212a b +++的最小值. 3.(2020·深圳市宝安中学(集团)高三月考)已知定义在R 上的函数()|1||2|f x x x =++-的最小值为a .(1)求a 的值.(2)若p ,q ,r 为正实数,且p q r a ++=,求证:2223p q r ++≥.4.(2020·江西省高三)已知函数()221f x x x =-+-. (1)求不等式()6f x <的解集;(2)若函数()f x 的最小值为m ,且实数a ,b 满足222a b m +=,求34a b +的最大值. 5.(2020·山西省高三月考)已知函数()|1|2|2|)(R f x x x x =-+-∈,记()f x 得最小值为m . (1)解不等式()5f x ≤;(2)若2a b m +=,求22a b +的最小值.6.(2020·吉林省高三)已知函数()12f x x x =-+(1)在平面直角坐标系中作出函数()f x 的图象,并解不等式()2f x ≥; (2)若不等式()15f x x k +-≥-对任意的x ∈R 恒成立,求证:65k k+≥.7.(2020·山西省高三)已知函数()12f x x x a =++-. (1)若1a =,解不等式()4f x <;(2)对任意的实数m ,若总存在实数x ,使得()224m m f x -+=,求实数a 的取值范围.8.(2020·山西省太原五中高三月考)已知函数()1211f x x x =-+++ (1)求不等式()8f x <的解集;(2)若x R ∀∈,函数()2log f x a ≥恒成立,求实数a 的取值范围.9.(2020·全国高三)设函数()|2|f x x x =+-+,集合M 为不等式()0f x <的解集. (1)求集合M ;(2)当m ,n M ∈时,证明:3mn n ++.10.(2020·山西省高三)已知不等式23x x -<与不等式()20,x mx n m n R -+<∈的解集相同.(1)求m n -;(2)若(),,0,1a b c ∈,且ab bc ac m n ++=-,求222a b c ++的最小值. 11.(2020·重庆高三)已知函数f (x )=|2x ﹣1|﹣3|x +1|,设f (x )的最大值为M . (1)求M ;(2)若正数a ,b 满足3311a b +=Mab ,证明:a 4b +ab 443≥. 12.(2020·福建省高三)已知函数()1f x x a x =-+-. (1)当0a =时,求不等式()1f x ≤的解集A . (2)设()32f x x ≤-的解集为B ,若A B ⊆,求这数a 的值. 13.(2020·福建省高三)已知函数()12f x x x =-+-. (1)求不等式()3f x <的解集I ;(2)当a ,b ,c I ∈时,求证:11191111114333abb cc a++≤+++---.14.(2020·山西省高三)已知函数()2f x x =.(1)求不等式()1f x >的解集; (2)若正数,,a b c 满足24923a b c f ⎛⎫++=+⎪⎝⎭,求149a b c ++的最小值. 15.(2020·山西省太原五中高三月考)已知函数()()0, 0f x x a x b a b =-++>>. (1)当1a b ==时,解不等式()2f x x <+;(2)若()f x 的值域为[)3,+∞,证明:()224281a b b a b +++≥+.16.(2020·山西省高三)已知函数()()220f x x a x a a =-++>. (1)求不等式()3f x a ≥的解集;(2)若()f x 的最小值为()20b b ->17.(2020·陕西省西安中学高三)已知,,a b c R +∈,x R ∀∈,不等式|1||2|x x a b c ---≤++恒成立.(1)求证:22213a b c ++≥(2)求证 18.(2020·江苏省高三)已知x ,y ,z 均为正数,且11131112x y z ++≤+++,求证:4910x y z ++≥. 19.(2019·四川省高三月考)已知函数f (x )=|2x ﹣1|﹣|x +1|. (1)求不等式f (x )≤﹣1的解集M ;(2)结合(1),若m 是集合M 中最大的元素,且a +b =m (a >0,b >0),求+ 20.(2020·广东省高三月考) 已知函数()()20,0f x x a x b a b =-++>>. (1)当1a b ==时,解不等式()2f x x ≥-;(2)若函数()f x 的值域为[)2,+∞,求2242a b b a+的最小值. 21.(2020·宁夏回族自治区银川一中高三)已知()12f x x x =-+-. (1)求使得()2f x >的x 的取值集合M ;(2)求证:对任意实数a ,()0b a ≠,当R x C M ∈时,()a b a b a f x ++-≥恒成立. 22.(2020·河南省高三三模)已知是a ,b ,c 正实数,且21a b c ++=.()1求111abc++的最小值;()2求证:22216a b c ++≥. 23.(2020·江西省高三三模)已知()|||1|.f x k x x =+- (Ⅰ)若2k =,解不等式()5f x ≤.(Ⅱ)若关于x 的不等式()|1||22|f x x x ≤++-的充分条件是1,22x ⎡∈⎤⎢⎥⎣⎦,求k 的取值范围.24.(2020·河北省高三)已知a ,b ,c 为正实数,且a+b+c=1. (Ⅰ)证明:1111118a b c ⎛⎫⎛⎫⎛⎫---≥ ⎪⎪⎪⎝⎭⎝⎭⎝⎭; (Ⅱ)证明:32a b c b c a c a b ++≥+++. 25.(2020·南昌市新建一中高三)已知函数()21f x x x =---,函数()421g x x x m =---+-. (1)当()0f x >时,求实数x 的取值范围;(2)当()g x 与()f x 的图象有公共点时,求实数m 的取值范围. 26.(2020·四川省高三三模)已知函数()||f x x a =-.(1)当1a =时,求不等式11()x f x +>的解集; (2)设不等式|21|()x f x x -+的解集为M ,若1,12M ⎡⎤⊆⎢⎥⎣⎦,求实数a 的取值范围. 27.(2020·福建省高三)已知函数()212f x x x =--+,()221g x x m x =-++. (1)求不等式()2f x <的解集;(2)若存在1x ,2x ∈R ,使得()()120f x g x +=,求m 的取值范围. 28.(2020·青海省高三)设函数()21|1|f x x x =---. (1)求不等式()3f x <的解集;(2)若方程2()f x x ax =+有两个不等实数根,求a 的取值范围. 29.(2020·贵州省高三)设函数()16f x x x a =++--. (1)当2a =时,求不等式()0f x ≤的解集; (2)若()23f x a ≥-,求a 的取值范围.30.(2020·重庆高三)已知函数()22f x x x =+-的最小值为m . (1)求m 的值;(2)若实数a ,b 满足22a b m +=,求221112a b+++的最小值. 31.(2020·广州市天河外国语学校高三月考)已知函数()123f x x x =--+. (1)求不等式()1f x <的解集;(2)若存在实数x ,使得不等式()230m m f x --<成立,求实数m 的取值范围. 32.(2020·广东省高三)已知函数()1=-f x x . (1)解不等式()(1)4f x f x ++≥;(2)当0x ≠,x ∈R 时,证明:1()()2f x f x-+≥.33.(2020·福建省高三)已知函数2()1,()|||21|,f x x g x x a x a R =+=---∈.(1)当12a =时,解不等式27()2g x <-;(2)对任意12,x x R ∈,若不等式12()()f x g x ≥恒成立,求实数a 的取值范围. 34.(2020·湖北省高三)已知函数()|4||24|f x x x =--+. (1)解不等式()3f x ;(2)若()f x 的最大值为m ,且2a b c m ++=,其中0a ,0b ,3c >,求(1)(1)(3)a b c ++-的最大值.35.(2020·辽宁省高三三模)已知a ,b ,c 均为正数,设函数f (x )=|x ﹣b |﹣|x +c |+a ,x ∈R . (1)若a =2b =2c =2,求不等式f (x )<3的解集; (2)若函数f (x )的最大值为1,证明:14936a b c++≥. 36.(2020·广西柳城县中学高三)设函数()133f x x x a a =-+-+,x ∈R . (1)当1a =时,求不等式()7f x >的解集; (2)对任意m R +∈,x ∈R 恒有()49f x m m≥--,求实数a 的取值范围. 37.(2020·安徽相山淮北一中高三月考)已知函数()|2|f x ax =-. (Ⅰ)当4a =时,求不等式()|42|8f x x ++≥的解集;(Ⅱ)若[2,4]x ∈时,不等式()|3|3f x x x +-≤+成立,求a 的取值范围. 38.(2020·河南高三月考)已知函数()21f x x x =--+.(1)解不等式()2f x <;(2)若正实数m ,n 满足3m n +=,试比较122m n +与()32f x -的大小,并说明理由. 39.(2020·湖南衡阳市八中高三)已知实数正数x ,y 满足1x y +=.(1)解关于x 的不等式522x y x y ++-≤; (2)证明:2211119x y ⎛⎫⎛⎫--≥ ⎪⎪⎝⎭⎝⎭. 40.(2020·湖南雨花雅礼中学高三)已知函数()33f x x a x =-++. (1)若3a =,解不等式()6f x ≤;(2)若不存在实数x ,使得()162f x a x ≤--+,求实数a 的取值范围. 41.(2020·湖北黄州黄冈中学高三)已知()3f x x x =+-. (1)求不等式()5xf x x>的解集; (2)若()f x 的最小值为M ,且22a b c M ++=(a ,b ,c ∈R ),求证:2221a b c ++≥. 42.(2020·湖北黄州黄冈中学高三)已知1()||f x x a x a=++-. (1)当1a =时,求不等式()6f x 的解集M ; (2)若a M ∈,求证:10()3f x . 43.(2020·河北桃城衡水中学高三三模)已知函数()11f x x a x =+--. (1)当2a =-时,解不等式()5f x >; (2)若()3f x a x ≤+,求a 的最小值.44.(2020·宁夏原州固原一中高三)已知函数()|3|2f x x =+-. (1)解不等式|()|4f x <;(2)若x R ∀∈,2()|1|41f x x t t ≤--+-恒成立,求实数t 的取值范围. 45.(2020·河南郑州一中高三)已知a ,b ,c 为正实数,且满足a +b +c =1.证明:(1)|a 12-|+|b +c ﹣1|12≥; (2)(a 3+b 3+c 3)(222111a b c ++)≥3. 46.(2020·贵州贵阳一中高三)已知函数()3f x x x a =--.(1)当0a =时,求解关于x 的不等式2()10f x x +->的解集;(2)当[]2,3x ∈时,该不等式()1f x ≥-恒成立,求a 的取值范围.47.(2020·云南红河高三)已知函数()|1||1|f x x x =++-.(Ⅰ)求不等式()8f x ≤的解集M ;(Ⅱ)若m 为M 中的最大元素,正数a ,b 满足.12m a b +=,证明2142a b ab ++≥.48.(2020·重庆九龙坡高三)已知函数()f x =(1)求()f x 的最大值;(2)若关于x 的不等式()|1|f x a -有解,求实数a 的取值范围.49(2019·河北辛集中学高三月考)已知函数()43f x x x =-++.(1)解不等式()9f x <;(2)若不等式()21f x a <-+在实数R 上的解集不是空集,求正数a 的取值范围.50.(2020·河南南阳高三二模)已知a ,b ,c 均为正实数,函数222111()4f x x x a b c =+-++的最小值为1.证明:(1)22249a b c ++≥;(2)111122ab bc ac++≤. 51.(2020·河南高三)已知函数()221f x x x =-++.(1)求不等式()4f x ≤的解集;(2)若函数()1y f x x =++的最小值为k ,求()220km m m+>的最小值. 52.(2020·安徽六安一中高三)已知()()2f x x m m m R =-+∈.(1)若不等式()2f x ≤的解集为13,22⎡⎤⎢⎥⎣⎦,求m 的值; (2)在(1)的条件下,若a ,b ,c +∈R ,且4a b c m ++=,求证:4436ac bc ab abc ++≥. 53.(2020·辽宁实验中学高三)设函数()|21|f x x =-.(1)设()(1)5f x f x ++<的解集为A ,求集合A ;(2)已知m 为(1)中集合A 中的最大整数,且a b c m ++=(其中a ,b ,c 为正实数),求证:1118a b c a b c---⋅⋅≥. 54.(2020·安徽芜湖高三一模)设,,x y z ∈R ,且1x y z ++=.(1)证明:22213x y z ++≥; (2)求()()()222111x y z -++++的最小值.55.(2020·河南高三)已知函数()2f x x a x =-++.(1)当1a =时,求不等式()7f x ≤的解集;(2)若0x R ∃∈,()03f x a ≤-,求实数a 的取值范围.56.(2020·河南开封高三二模)已知函数()2231f x x x =+--.(1)求函数()f x 的最大值M ;(2)已知0a >,0b >,4a b M +=,求2221a b a b +++的最大值. 57.(2020·福建高三)已知函数()12f x x x =-+-.(1)求不等式()3f x <的解集I ;(2)当a ,b ,c I ∈时,求证:11191111114333a b b c c a ++≤+++---.58.(2020·湖南雅礼中学高三月考)已知不等式15|2|22x x -++≤的解集为M . (1)求集合M ; (2)设集合M 中元素的最大值为t .若0a >,0b >,0c >,满足111223t a b c ++=,求2993a b c ++的最小值.59.(2020·甘肃省静宁县第一中学高三)已知函数()211f x x x =++-. (1)解不等式()3f x ≥;(2)记函数()f x 的最小值为m ,若,,a b c 均为正实数,且122a b c m ++=,求222a b c ++的最小值. 60.(2020·广东东莞高三)已知函数1()|||3|2()2f x x k x k R =-++-∈. (1)当1k =时,解不等式()1f x ≤;(2)若()f x x 对于任意的实数x 恒成立,求实数k 的取值范围.。
数学(第一册)不等式22.2 区间

§2.2 区 间【教学目的】理解区间的概念,掌握用区间表示不等式解集的方法,并能在数轴上表示出来.【教学重点】各类区间的符号表示.【教学难点】对“∞”符号的理解.【教学过程】不等式(组)的解集也可以用区间来表示.介于两个实数之间的所有实数的集合叫做区间.这两个实数叫做区间的端点. 设a ,为任意两个实数,且,规定: 注:符号“”读作“无穷大”,它不是一个数,只是一个记号,“”表示可以无限制地增大,“-∞”表示可以无限制地减小.例1 用区间表示下列不等式的解:3113x x +≥-.解 移项得31103x x +-≥-,(问:能不能先去分母?) 整理得203x x +≥-.它可化为不等式组:(1) 2030x x +≥⎧⎨->⎩ 或 (2) 2030x x +≤⎧⎨-<⎩.解(1)得 3x >;解(2)得 2x ≤-. 所以,原不等式的解为 ()(,2]3,x ∈-∞-+∞.例2 求下列不等式的解集:⎩⎨⎧≤->+053062x x .解 解 ⎩⎨⎧≤->+053062x x 得353x x >-⎧⎪⎨≤⎪⎩,即533x -<≤. 则原不等式的解集为533x x ⎧⎫-<≤⎨⎬⎩⎭,用区间表示为53,3⎛⎤- ⎥⎝⎦. 课堂练习练习1:见书P35.练习2:1. 用区间表示下列数集:(1) 数集B 是大于等于1的实数; (2) 数集A 是大于0、不大于5的实数; 2.解不等式265x -<,并用区间表示不等式的解集.【小结与作业】课堂小结:本次课主要学习了用区间表示数集.理解区间概念,会用区间表示不等式(组)的数集.本课作业:习题2.2.。
不等式的基本性质与解法

不等式的基本性质与解法不等式是数学中常见的一种数学关系,它描述了两个数之间的大小关系。
在解决实际问题中,经常需要研究不等式的基本性质和解法。
本文将介绍不等式的基本性质以及解决不等式的方法,并且给出一些例子来说明。
一、不等式的基本性质1. 加减性性质:对于两个不等式,如果它们的左右两边分别相加或相减,那么它们的不等关系不变。
例如:对于不等式 2x < 6 和 3x > 9,我们可以将两个不等式的左右两边分别相加得到 2x + 3x < 6 + 9,即 5x < 15。
不等式的不等关系保持不变。
2. 乘除性性质:对于不等式,如果两边都乘以一个正数,则不等关系保持不变;如果两边都乘以一个负数,则不等关系发生改变。
例如:对于不等式 2x < 6,如果两边同时乘以一个正数 3,我们得到 3 * 2x < 3 * 6,即 6x < 18,不等关系保持不变。
但如果两边同时乘以一个负数 -3,我们得到 -3 * 2x > -3 * 6,即 -6x > -18,不等关系发生改变。
3. 反号性质:对于不等式,如果两边同时取负号,不等关系发生改变。
例如:对于不等式 2x < 6,如果两边同时取负号,我们得到 -2x > -6,不等关系发生改变。
4. 绝对值性质:对于不等式,如果绝对值符号"|" 出现在不等式中,我们需要分别讨论绝对值大于零和绝对值小于零的情况。
例如:对于不等式|2x - 4| < 6,我们可以将其分为两个部分来讨论。
当 2x - 4 > 0 时,不等式简化为 2x - 4 < 6,解得 x < 5;当 2x - 4 < 0 时,不等式简化为 -(2x - 4) < 6,解得 x > -1。
二、不等式的解法1. 图像法:对于一些简单的一元不等式,我们可以使用图像法来解决。
将不等式转化为图像表示,通过观察图像来确定不等式的解集。
不等式知识点大全

不等式知识点大全一、不等式的基本概念:1.不等式的定义:不等式是一个包含不等号(>,<,≥,≤)的数学语句。
2.不等式的解集:解集是满足不等式的所有实数的集合。
3.不等式的求解方法:解不等式的方法主要有代入法、分析法、图像法和区间法等。
二、一元一次不等式:1.一元一次不等式的定义:一元一次不等式是指只含有一个未知数的一次函数与一个实数的大小关系。
2.一元一次不等式的解集:一元一次不等式的解集可以用一个开区间或闭区间表示。
三、二次不等式:1.二次不等式的定义:二次不等式是指含有一个未知数的二次函数与一个实数的大小关系。
2.二次不等式的解集:二次不等式的解集可以用一个开区间、闭区间、半开半闭区间或不等式组表示。
四、绝对值不等式:1.绝对值不等式的定义:绝对值不等式是指含有绝对值符号的不等式。
2.绝对值不等式的解集:绝对值不等式的解集可以用一个开区间、闭区间、半开半闭区间或不等式组表示。
五、分式不等式:1.分式不等式的定义:分式不等式是指含有一个未知数的分式与一个实数的大小关系。
2.分式不等式的解集:分式不等式的解集可以用一个开区间、闭区间、半开半闭区间或不等式组表示。
六、三角不等式:1.三角不等式的定义:三角不等式是指三角函数与一个实数之间的大小关系。
2.三角不等式的解集:三角不等式的解集可以用一个开区间、闭区间、半开半闭区间或不等式组表示。
七、复合不等式:1.复合不等式的定义:复合不等式是由两个或多个不等式通过与或或连接构成的不等式。
2.复合不等式的解集:复合不等式的解集是满足所有不等式的实数的交集或并集。
八、常用的不等式:1.平均不等式:包括算术平均不等式、几何平均不等式、加权平均不等式等。
2.布尔不等式:包括与或非不等式和限制条件不等式等。
3.等价不等式:等式两边取绝对值后变为不等式。
4.单调性不等式:利用函数单调性性质证明不等式。
5.导数不等式:利用函数的导数性质证明不等式。
6.积分不等式:利用积分性质及定积分的性质来推导不等式。
2.2(2)一元二次不等式的解法
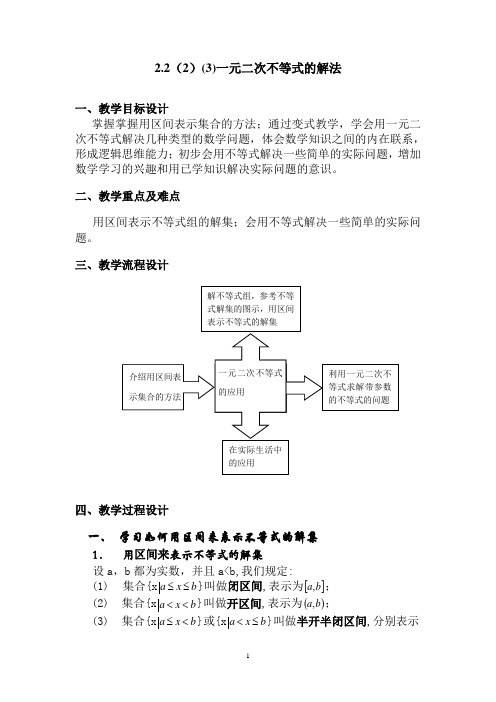
2.2(2)(3)一元二次不等式的解法一、教学目标设计掌握掌握用区间表示集合的方法;通过变式教学,学会用一元二次不等式解决几种类型的数学问题,体会数学知识之间的内在联系,形成逻辑思维能力;初步会用不等式解决一些简单的实际问题,增加数学学习的兴趣和用已学知识解决实际问题的意识。
二、教学重点及难点用区间表示不等式组的解集;会用不等式解决一些简单的实际问题。
三、教学流程设计四、教学过程设计一、 学习如何用区间来表示不等式的解集1. 用区间来表示不等式的解集设a ,b 都为实数,并且a<b,我们规定:(1) 集合{x b x a ≤≤}叫做闭区间,表示为[]b a ,;(2) 集合{x b x a <<}叫做开区间,表示为()b a ,;(3) 集合{x b x a <≤}或{x b x a ≤<}叫做半开半闭区间,分别表示为[)b a ,或(]b a ,。
(4) 把实数集R 表示为(-∞,+∞);把集合{x a x ≥}表示为[a ,+∞);把集合{x a x >}表示为(a,+∞);把集合{x b x ≤}表示为(-∞,b];把集合{x b x <}表示为(-∞,b );在上述所有的区间中,a ,b 叫做区间的端点,以后我们可以用区 间表示不等式的解集。
2.区间在数轴上的表示[a ,b] (a ,b )[a ,b )(a ,b][a ,+∞)a,+∞)-∞,(-∞,b )3.练习将上节课中不等式的解集用区间表示。
二、典型例题例1.解不等式组:3x 2-7x-10≤0, ①2x 2-5x+2>0 ②解:由不等式①的解集为⎥⎦⎤⎢⎣⎡-310,1,不等式②的解集为⎪⎭⎫ ⎝⎛∞-21,⋃()+∞,2,可知原不等式组的解集为⎥⎦⎤⎝⎛⋃⎪⎭⎫⎢⎣⎡-310,221,1,它在数轴上的表示如图:以将解集表示在同一条数轴上,这样更直观和清晰。
能否在数轴上准确的找到几个解集的公共部分,对一部分学生解决这个问题有一定的困难。
不等式的性质和解法

不等式的性质和解法一、不等式的性质1.不等式的定义:表示两个数之间的大小关系,用“>”、“<”、“≥”、“≤”等符号表示。
2.不等式的基本性质:(1)传递性:如果a>b且b>c,那么a>c。
(2)同向相加:如果a>b且c>d,那么a+c>b+d。
(3)同向相减:如果a>b,那么a-c>b-c。
(4)乘除性质:如果a>b且c>0,那么ac>bc;如果a>b且c<0,那么ac<bc。
二、不等式的解法1.解不等式的基本步骤:(1)去分母:将不等式两边同乘以分母的最小正整数,使分母消失。
(2)去括号:将不等式两边同乘以括号内的正数,或者将不等式两边同除以括号内的负数,使括号内的符号改变。
(3)移项:将不等式中的常数项移到一边,将含有未知数的项移到另一边。
(4)合并同类项:将不等式两边同类项合并。
(5)化简:将不等式化简到最简形式。
2.解一元一次不等式:(1)ax+b>c(a≠0):移项得ax>c-b,再除以a得x>(c-b)/a。
(2)ax+b≤c(a≠0):移项得ax≤c-b,再除以a得x≤(c-b)/a。
3.解一元二次不等式:(1)ax2+bx+c>0(a>0):先求出方程ax2+bx+c=0的解,然后根据a的符号确定不等式的解集。
(2)ax2+bx+c≤0(a>0):先求出方程ax2+bx+c=0的解,然后根据a的符号确定不等式的解集。
4.不等式的组:(1)解不等式组的步骤:先解每个不等式,再根据不等式的解集确定不等式组的解集。
(2)不等式组解集的表示方法:用区间表示,例如:[x1, x2]。
三、不等式的应用1.实际问题中的不等式:例如,距离、温度、速度等问题。
2.不等式在生活中的应用:例如,购物、制定计划、比较大小等问题。
3.不等式在其他学科中的应用:例如,在物理学中描述物体的运动状态,在经济学中描述市场的供求关系等。
