结构力学_第七章_作业参考答案
南京航空航天大学 结构力学 课后习题答案 第7章
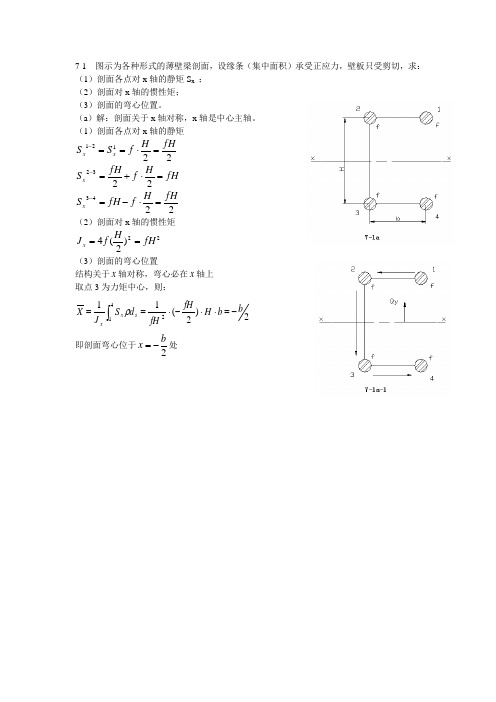
7-1 图示为各种形式的薄壁梁剖面，设缘条（集中面积）承受正应力，壁板只受剪切，求： （1）剖面各点对x 轴的静矩S x ； （2）剖面对x 轴的惯性矩； （3）剖面的弯心位置。
（a ）解：剖面关于x 轴对称，x 轴是中心主轴。
（1）剖面各点对x 轴的静矩22121fHH f S S x x =⋅==- fH H f fH S x =⋅+=-2232 2243fHH f fH S x=⋅-=- （2）剖面对x 轴的惯性矩22)2(4fH H f J x == （3）剖面的弯心位置结构关于x 轴对称，弯心必在x 轴上 取点3为力矩中心，则：2)2(11241b b H fH fHd S J X s x x-=⋅⋅-⋅==⎰ρ 即剖面弯心位于2b x -=处（1）剖面各点对x 轴的静矩12233445563()28837828711828117()82873()828x x x x x H H S f fH H S fH f fH H S fH f fHH S fH f fH H S fH f fH -----=⋅-==+⋅==+⋅==+⋅-==+⋅-= 剪流沿1-2-3-4-5-6方向为正（2）剖面对x 轴的惯性矩2222412[()2()]28232x i i H H H J f y f f fH ==⋅-+⋅=∑ （3）剖面的弯心结构关于x 轴对称，弯心必在x 轴上设弯心在3-4杆左侧，距3-4杆的距离为X ，由弯心的定义可知当弯心处作用有y Q 时，结构上的剪流和y Q 在结构上任意一点的合力矩为零 现对x 轴和3-4杆交点处取矩，则1223455608228y H H H HQ X q b q b q b q b ----⋅-⋅⋅-⋅⋅-⋅⋅-⋅⋅= （1） 又知y x y xQ q S J =则（1）式可化为12234556131()822841x x x x x bH bH bH bH X S S S S b J ----=⋅+⋅+⋅+⋅=即结构弯心在x 轴上3-4杆左侧3141b 处题7-1b 图（1）剖面各点对x 轴的静矩12322545651221221122221()221()22x x x x x H S f fH H S f fH H S fH fH f H S f fHH S f fH-----=⋅==⋅==++⋅=⋅-=-=⋅-=- 剪流方向如图（2）剖面对x 轴的惯性矩22224()22()222x i i H HJ f y f f fH ==⋅+⋅⋅=∑（3）剖面的弯心结构关于x 轴对称，弯心必在x 轴上设弯心在2-5杆左侧，距2-5杆的距离为X ，由弯心的定义可知当弯心处作用有y Q 时，结构上的剪流和y Q 在结构上任意一点 的合力矩为零现对x 轴和2-5杆交点处取矩，则12234556022222222y b H b H b H b HQ X q q q q ----⋅+⋅⋅-⋅⋅+⋅⋅-⋅⋅= （1）又知y x y xQ q S J =则（1）式可化为122345561()04444x x x xx bH bH bH bH X S S S S J ----=-⋅+⋅-⋅+⋅= 即结构弯心在x 轴上与2-5杆相交处题7-1c 图（1）剖面各点对x 轴的静矩x S fR =（2）剖面对x 轴的惯性矩222x i i J f y fR ==∑（3）剖面的弯心结构关于x 轴对称，弯心必在x 轴上11Rx x xs X S ds fR ds J J πρρ=⋅=⋅⎰⎰（1）其中ρ为承受剪流的面积到x 轴的距离，取极坐标θ，记上缘条处0θ=，逆时针方向为正，则cos R ρθ=，代入（1）式得11cos cos 0RxxX fR R ds fR R Rd J J ππθθθ=⋅=⋅⋅=⎰⎰即剖面弯心在两缘条中心连线与x 轴的交点处题7-1d 图（1）剖面各点对x 轴的静矩122343355667871099714452424144515244225722227522221()441()44152()424x x x x x x x x x H S f fH fH H S f fHH S f fHH S fH fH f fHH S fH f fHH S fH f fHH S f fHH S f fHH S fH f fH---------=⋅==+⋅==⋅==++⋅==+⋅==-⋅==⋅-=-=⋅-=-=-+⋅-=- 剪流方向如图（2）剖面对x 轴的惯性矩2222134()62()224x i i H H J f y f f fH ==⋅+⋅⋅=∑ （3）剖面的弯心结构关于x 轴对称，弯心必在x 轴上设弯心在5-6杆右侧，距5-6杆的距离为X ，由弯心的定义可知当弯心处作用有y Q 时，结构上的剪流和y Q 在结构上任意一点的合力矩为零 现对x 轴和5-6杆交点处取矩，则1223433567()42422y H H H H HQ X q a b q a q b q b q b -----⋅-⋅⋅+-⋅⋅-⋅⋅-⋅⋅-⋅⋅ 7879910()0424H H Hq b q a q a b ----⋅⋅-⋅⋅-⋅⋅+= （1） 又知y x y xQ q S J =代入（1）式可得11(2)26X a b =+ 即结构弯心在x 轴上5-6杆右侧11(2)26a b +处 题7-1e 图7-2 题7－2图所示薄壁梁剖面，缘条承受正应力，其截面积为22cm f =。
南京航空航天大学 结构力学 课后习题答案 第7章
7-1 图示为各种形式的薄壁梁剖面，设缘条（集中面积）承受正应力，壁板只受剪切，求： （1）剖面各点对x 轴的静矩S x ； （2）剖面对x 轴的惯性矩； （3）剖面的弯心位置。
（a ）解：剖面关于x 轴对称，x 轴是中心主轴。
（1）剖面各点对x 轴的静矩22121fHH f S S x x =⋅==- fH H f fH S x =⋅+=-2232 2243fHH f fH S x=⋅-=- （2）剖面对x 轴的惯性矩22)2(4fH H f J x == （3）剖面的弯心位置结构关于x 轴对称，弯心必在x 轴上 取点3为力矩中心，则：2)2(11241b b H fH fHd S J X s x x-=⋅⋅-⋅==⎰ρ 即剖面弯心位于2b x -=处（1）剖面各点对x 轴的静矩12233445563()28837828711828117()82873()828x x x x x H H S f fH H S fH f fH H S fH f fHH S fH f fH H S fH f fH -----=⋅-==+⋅==+⋅==+⋅-==+⋅-= 剪流沿1-2-3-4-5-6方向为正（2）剖面对x 轴的惯性矩2222412[()2()]28232x i i H H H J f y f f fH ==⋅-+⋅=∑ （3）剖面的弯心结构关于x 轴对称，弯心必在x 轴上设弯心在3-4杆左侧，距3-4杆的距离为X ，由弯心的定义可知当弯心处作用有y Q 时，结构上的剪流和y Q 在结构上任意一点的合力矩为零 现对x 轴和3-4杆交点处取矩，则1223455608228y H H H HQ X q b q b q b q b ----⋅-⋅⋅-⋅⋅-⋅⋅-⋅⋅= （1） 又知y x y xQ q S J =则（1）式可化为12234556131()822841x x x x x bH bH bH bH X S S S S b J ----=⋅+⋅+⋅+⋅=即结构弯心在x 轴上3-4杆左侧3141b 处题7-1b 图（1）剖面各点对x 轴的静矩12322545651221221122221()221()22x x x x x H S f fH H S f fH H S fH fH f H S f fHH S f fH-----=⋅==⋅==++⋅=⋅-=-=⋅-=- 剪流方向如图（2）剖面对x 轴的惯性矩22224()22()222x i i H HJ f y f f fH ==⋅+⋅⋅=∑（3）剖面的弯心结构关于x 轴对称，弯心必在x 轴上设弯心在2-5杆左侧，距2-5杆的距离为X ，由弯心的定义可知当弯心处作用有y Q 时，结构上的剪流和y Q 在结构上任意一点 的合力矩为零现对x 轴和2-5杆交点处取矩，则12234556022222222y b H b H b H b HQ X q q q q ----⋅+⋅⋅-⋅⋅+⋅⋅-⋅⋅= （1）又知y x y xQ q S J =则（1）式可化为122345561()04444x x x xx bH bH bH bH X S S S S J ----=-⋅+⋅-⋅+⋅= 即结构弯心在x 轴上与2-5杆相交处题7-1c 图（1）剖面各点对x 轴的静矩x S fR =（2）剖面对x 轴的惯性矩222x i i J f y fR ==∑（3）剖面的弯心结构关于x 轴对称，弯心必在x 轴上11Rx x xs X S ds fR ds J J πρρ=⋅=⋅⎰⎰（1）其中ρ为承受剪流的面积到x 轴的距离，取极坐标θ，记上缘条处0θ=，逆时针方向为正，则cos R ρθ=，代入（1）式得11cos cos 0RxxX fR R ds fR R Rd J J ππθθθ=⋅=⋅⋅=⎰⎰即剖面弯心在两缘条中心连线与x 轴的交点处题7-1d 图（1）剖面各点对x 轴的静矩122343355667871099714452424144515244225722227522221()441()44152()424x x x x x x x x x H S f fH fH H S f fHH S f fHH S fH fH f fHH S fH f fHH S fH f fHH S f fHH S f fHH S fH f fH---------=⋅==+⋅==⋅==++⋅==+⋅==-⋅==⋅-=-=⋅-=-=-+⋅-=- 剪流方向如图（2）剖面对x 轴的惯性矩2222134()62()224x i i H H J f y f f fH ==⋅+⋅⋅=∑ （3）剖面的弯心结构关于x 轴对称，弯心必在x 轴上设弯心在5-6杆右侧，距5-6杆的距离为X ，由弯心的定义可知当弯心处作用有y Q 时，结构上的剪流和y Q 在结构上任意一点的合力矩为零 现对x 轴和5-6杆交点处取矩，则1223433567()42422y H H H H HQ X q a b q a q b q b q b -----⋅-⋅⋅+-⋅⋅-⋅⋅-⋅⋅-⋅⋅ 7879910()0424H H Hq b q a q a b ----⋅⋅-⋅⋅-⋅⋅+= （1） 又知y x y xQ q S J =代入（1）式可得11(2)26X a b =+ 即结构弯心在x 轴上5-6杆右侧11(2)26a b +处 题7-1e 图7-2 题7－2图所示薄壁梁剖面，缘条承受正应力，其截面积为22cm f =。
结构力学习题及答案
构造力学习题第2章平面体系的几何组成分析2-1～2-6 试确定图示体系的计算自由度。
题2-1图题2-2图题2-3图题2-4图题2-5图题2-6图2-7～2-15 试对图示体系进展几何组成分析。
假设是具有多余约束的几何不变体系，那么需指明多余约束的数目。
题2-7图题2-8图题2-9图题2-10图题2-11图题2-12图题2-13图题2-14图题2-15图题2-16图题2-17图题2-18图题2-19图题2-20图题2-21图2-11=W2-1 9-W=2-3 3-W=2-4 2-W=2-5 1-W=2-6 4-W=2-7、2-8、2-12、2-16、2-17无多余约束的几何不变体系2-9、2-10、2-15具有一个多余约束的几何不变体系2-11具有六个多余约束的几何不变体系2-13、2-14几何可变体系为2-18、2-19 瞬变体系2-20、2-21具有三个多余约束的几何不变体系第3章静定梁和静定平面刚架的内力分析3-1 试作图示静定梁的内力图。
〔a〕〔b〕(c) (d)习题3-1图3-2 试作图示多跨静定梁的内力图。
〔a〕〔b〕(c)习题3-2图3-3～3-9 试作图示静定刚架的内力图。
习题3-3图习题3-4图习题3-5图习题3-6图习题3-7图习题3-8图习题3-9图3-10 试判断图示静定构造的弯矩图是否正确。
(a)(b)(c)(d)局部习题答案3-1〔a 〕m kN M B ⋅=80〔上侧受拉〕，kN F RQB 60=，kN F L QB 60-=〔b 〕m kN M A ⋅=20〔上侧受拉〕，m kN M B ⋅=40〔上侧受拉〕，kN F RQA 5.32=，kN F L QA 20-=，kN F LQB 5.47-=，kN F R QB 20=(c)4Fl M C =〔下侧受拉〕，θcos 2F F L QC =3-2 (a)0=E M ，m kN M F ⋅-=40〔上侧受拉〕，m kN M B ⋅-=120〔上侧受拉〕〔b 〕m kN M RH ⋅-=15(上侧受拉)，m kN M E ⋅=25.11〔下侧受拉〕〔c 〕m kN M G ⋅=29(下侧受拉)，m kN M D ⋅-=5.8(上侧受拉)，m kN M H ⋅=15(下侧受拉) 3-3 m kN M CB ⋅=10〔左侧受拉〕，m kN M DF ⋅=8〔上侧受拉〕，m kN M DE ⋅=20〔右侧受拉〕 3-4 m kN M BA ⋅=120〔左侧受拉〕3-5 m kN M F ⋅=40〔左侧受拉〕，m kN M DC ⋅=160〔上侧受拉〕，m kN M EB ⋅=80(右侧受拉) 3-6 m kN M BA ⋅=60〔右侧受拉〕，m kN M BD ⋅=45〔上侧受拉〕，kN F QBD 46.28=3-7 m kN M C ⋅=70下〔左侧受拉〕，m kN M DE ⋅=150〔上侧受拉〕，m kN M EB ⋅=70(右侧受拉) 3-8 m kN M CB ⋅=36.0〔上侧受拉〕，m kN M BA ⋅=36.0〔右侧受拉〕 3-9 m kN M AB ⋅=10〔左侧受拉〕，m kN M BC ⋅=10〔上侧受拉〕 3-10 〔a 〕错误 〔b 〕错误 〔c 〕错误 〔d 〕正确第4章 静定平面桁架和组合构造的内力分析4-1 试判别习题4-1图所示桁架中的零杆。
结构力学习题集-矩阵位移法习题及答案
第七章 矩阵位移法一、是非题1、单元刚度矩阵反映了该单元杆端位移与杆端力之间的关系。
2、单元刚度矩阵均具有对称性和奇异性。
3、局部坐标系与整体坐标系之间的坐标变换矩阵T 是正交矩阵。
4、结构刚度矩阵反映了结构结点位移与荷载之间的关系。
5、用 矩 阵 位 移 法 计 算 连 续 梁 时 无 需 对 单 元 刚 度 矩 阵 作 坐 标 变 换。
6、结 构 刚 度 矩 阵 是 对 称 矩 阵 ，即 有K i j = K j i ，这 可 由 位 移 互 等 定 理 得 到 证 明 。
7、结构刚度方程矩阵形式为：[]{}{}K P ∆=，它是整个结构所应满足的变形条件。
8、在直接刚度法的先处理法中，定位向量的物理意义是变形连续条件和位移边界条件。
9、等效结点荷载数值等于汇交于该结点所有固端力的代数和。
10、矩阵位移法中，等效结点荷载的“等效原则”是指与非结点荷载的结点位移相等。
11、矩阵位移法既能计算超静定结构，也能计算静定结构。
二、选择题1、已知图示刚架各杆EI = 常数，当只考虑弯曲变形，且各杆单元类型相同时，采用先处理法进行结点位移编号，其正确编号是：(0,1,2)(0,0,0)(0,0,0)(0,1,3)(0,0,0)(1,2,0)(0,0,0)(0,0,3)(1,0,2)(0,0,0)(0,0,0)(1,0,3)(0,0,0)(0,1,2)(0,0,0)(0,3,4)A.B.C.D.21341234123412342、平面杆件结构一般情况下的单元刚度矩阵[]k 66⨯，就其性质而言，是： A ．非对称、奇异矩阵； B ．对称、奇异矩阵； C ．对称、非奇异矩阵； D ．非对称、非奇异矩阵。
3、单元i j 在图示两种坐标系中的刚度矩阵相比：A ．完全相同；B ．第2、3、5、6行(列)等值异号；C ．第2、5行(列)等值异号；D ．第3、6行(列)等值异号。
xi4、矩阵位移法中，结构的原始刚度方程是表示下列两组量值之间的相互关系： A ．杆端力与结点位移； B ．杆端力与结点力； C ．结点力与结点位移； D ．结点位移与杆端力 。
结构力学选择原题带答案
问题反馈【教师释疑】正确答案：【去除基础，再去除二元体后，小三角形、大三角形用三根链杆相连，故体系为无多余约束的几何不变体系。
】2、试对图示体系进行几何构造分析。
答题说明：简单给出分析过程。
最后给出结论。
问题反馈【教师释疑】正确答案：【先去掉基础在分析上部体系，上部体系为两刚片用一个铰一根杆3、对图示体系进行几何组成分析。
答题说明：简单给出分析过程。
最后给出结论。
问题反馈【教师释疑】正确答案：【依次去除二元体A、B、C、D、E、F、G后剩下大地，故该体系为无多余约束的几何不变体系。
】4、试对图示体系进行几何构造分析。
问题反馈【教师释疑】正确答案：【依次去除二元体DGF,FHE,DFE,ADC,CEB后，B点少一个约束。
该体系为有一个自由度的几何常变体系】1、找出图示桁架中的零杆。
答题说明：按你的分析结果，给出零杆总数和零杆编号（以两端结点编号表示）。
问题反馈【教师释疑】正确答案：【 23、34、49、89、59、96、65、57共8根零杆。
】2、找出图示桁架中的零杆。
答题说明：按你的分析结果，给出零杆总数和零杆编号（以两端结点编号表示）。
问题反馈【教师释疑】正确答案：【 13、12、27、25、56、64、67杆为零杆。
共7根零杆。
】答题说明：按你的分析结果，给出零杆总数和零杆编号（以两端结点编号表示）。
问题反馈【教师释疑】正确答案：【 EA、EB、AF、AC、BG、GD共有6根零杆。
】1、图乘法的应用条件是什么？问题反馈【教师释疑】正确答案：【图乘法的应用条件：1）杆轴线为直线，2）杆端的EI为常数3）MP和M图中至少有一个为直线图形。
】弯矩影响线与弯矩土有什么区别？问题反馈【教师释疑】正确答案：【①弯矩影响线的每一个竖标均表示同一个截面上弯矩的大小，不同的竖标只是反映单位荷载位置的不同而已。
②弯矩图的竖标则表示对应截面弯矩的大小，不同的竖标表示不同的截面上弯矩的大小。
③影响线对应的是单位行动荷载，而弯矩图对应的是某一固定荷载。
李廉锟《结构力学》笔记和课后习题(含考研真题)详解-第7章 力 法【圣才出品】
第7章 力 法
7.1 复习笔记【知识框架】
【重点难点归纳】
一、概述（见表7-1-1） ★★
表7-1-1 概述
二、超静定次数的确定（见表7-1-2） ★★★★
表7-1-2 超静定次数的确定
三、力法的基本概念（见表7-1-3） ★★★
力法的基本概念，包括基本未知量、基本体系、基本结构以及基本方程见表7-1-3，此外，表中还归纳了超静定结构的力法分析步骤。
表7-1-3 力法的基本未知量、基本体系和基本方程
四、力法的典型方程（见表7-1-4） ★★★
表7-1-4 力法的典型方程
五、对称性的利用 ★★★★
1．对称结构及作用荷载的对称性（表7-1-5）
表7-1-5 对称结构及作用荷载的对称性
2．非对称荷载的处理（表7-1-6）
表7-1-6 非对称荷载的处理。
西北工业大学航空学院结构力学课后答案第七章
(c)
(d)
(e)
(f)
分析：平面四边形板f=1，三角板f=0；一个“内十字”结点增加一次静不 定。结构分析有：增加元件法，去掉约束法。 解：(a)几何不变系统，有多余约束f=8.
增加元件法：将开洞处的一块板补全，则系统有9个“内十字”结 点。因而f=9-1=8. (b)几何不变系统，有多余f=5.
(e)静定结构。 零力杆端： 取4-5杆得,即4-3-6-5板上无剪流分布。从而，则
取总体平衡，得， 取结点2 得， 取杆3-2，有 取杆6-3，有 校核总体平衡，满足。 内力图：
0.5P
0.5P P 0.5P
(f)静定结构。 零力杆端:
杆3-4 杆2-3 杆5-4 杆7-6 ， 杆5-6 杆8-7 节点5 有 ， 杆2-5 ，得 杆1-2 杆1-8 ，得 校核总体平衡，满足。
P P
(c)静定结构。 零力杆端： 取1-2杆得
，并令； 取1-3杆得; 取2-6杆得; 取1-4杆得; 取2-5杆得; 校核总体平衡，满足。
内力图：
P P (d)静定结构，受自平衡力系。
零力杆端:
取杆1-2 有 ；取杆1-4 有 ；取杆2-3 有 ；取杆4-3 有
记
同理
取杆2-6 有 得 ；取杆5-6 有 则
(b)几何不变系统，多余约束数f=3. 增加元件法：将开洞处的板1-2-5-6、2-3-4-5补全，依次为一个三缘 条盒段以四边形面与基础连接有1次静不定和四个四缘条盒段单边连接 有1次静不定。因而f=1+4-2=3. (c) 几何不变系统，多余约束数f=4. 一个单边连接四缘条盒段，一个双边连接四缘条盒段。因而f=1+3=4. (d) 几何不变系统，多余约束数f=3. 一个单边连接三缘条盒段，一个双边连接四缘条盒段。因而f=3. (e) 几何不变系统，多余约束数f=8. 一个单边连接三缘条盒段，两个双边连接四缘条盒段，一个双边连 接三缘条盒段。因而f=2×3+2=8. (f) 几何不变系统，多余约束数f=2. 进行结构分析，短的四缘条盒段与基础为单边连接静不定次数为1， 在此基础上增加了4个结点，5个板，8根杆。因而f=1+5+8-4×3=2. (g) 几何不变系统，多余约束数f=2. 以自由短四缘条盒段为基础，静定结构；以四边形形式单边连接三 缘条盒段，静不定次数为1；单边连接四缘条盒段，静不定次数为1。因 而f=1+1=2. (h) 几何不变系统，多余约束数f=10. 以四边形形式单边连接三缘条盒段，静不定次数为1；连个双边连接 的四缘条盒段，静不定次数为2×3；双边四边形形式连接三缘条盒段，
（完整版）哈工大结构力学题库七章
（完整版）哈⼯⼤结构⼒学题库七章176第七章影响线⼀判断题1. 图⽰梁AB 与A 0B 0，其截⾯C 与C 0弯矩影响线和剪⼒影响线完全相同。
（X ）题1图题2图 2.图⽰结构Q E 影响线的AC 段纵标不为零。
（X ）3. 图⽰梁K 截⾯的M K 影响线、Q K 影响线形状如图a 、b 所⽰。
4. 图⽰梁的M C 影响线、Q C 影响线形状如图a 、b 所⽰。
5. 图⽰梁的M C 影响线、M B 影响线形状如图a 、b 所⽰。
1776. 图⽰结构M B 影响线的AB 段纵标为零。
7. 图⽰梁跨中C 截⾯弯矩影响线的物理意义是荷载P=1作⽤在截⾯C 的弯矩图形。
（X ） 8. ⽤静⼒法作静定结构某量值的影响线与⽤机动法作该结构同⼀量值的影响线是不等价的。
（X ）9. 求某量值影响线⽅程的⽅法，与恒载作⽤下计算该量值的⽅法在原理上是相同的。
（√） 10. 影响线是⽤于解决活载作⽤下结构的计算问题，它不能⽤于恒载作⽤下的计算。
（X ） 11. 移动荷载是指⼤⼩，指向不变，作⽤位置不断变化的荷载，所以不是静⼒荷载。
（X ） 12. ⽤静⼒法作影响线，影响线⽅程中的变量x 代表截⾯位置的横坐标。
（X ）13. 表⽰单位移动荷载作⽤下某指定截⾯的内⼒变化规律的图形称为内⼒影响线。
（√） 14. 简⽀梁跨中截⾯弯矩的影响线与跨中有集中⼒P 时的M 图相同。
（X ） 15. 简⽀梁跨中C 截⾯剪⼒影响线在C 截⾯处有突变。
（√） 16. 绝对最⼤弯矩是移动荷载下梁的各截⾯上最⼤的弯矩。
（√） 17. 静定结构及超静定结构的内⼒影响线都是由直线组成。
（X） 18. 图⽰结构Q C 影响线的CD 段为斜直线。
19. 图⽰结构K 断⾯的剪⼒影响线如图b 所⽰。
（√）178题19图20. ⽤机动法作得图a 所⽰Q B 左结构影响线如图b 。
题20图题21图 21. 图⽰结构a 杆的内⼒影响线如图b 所⽰22. 荷载处于某⼀最不利位置时，按梁内各截⾯得弯矩值竖标画出得图形，称为简⽀梁的弯矩包络图。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
7－7 作刚架的 M 图。 D C E
3m
56kN EI=常数
C
56kN
X2 X2
3m
56kN
EI=常数
EI=常数
3m
3m
A
3m 3m
B
A
3m
基本体系
B
168
A
3m
M P 图(kN m)
B
3m
3m
解： （1）该结构为二次超静定结构，拆除 B 点多余联系，得到基本体系。 （2）根据位移条件，得：
⎧δ11 X 1 + δ12 X 2 + Δ1P = 0 ⎨ ⎩δ 21 X 1 + δ 22 X 2 + Δ 2 P = 0
梁。
6 I2 =nI1 I1 A M1 图(kN m) I1 B
6
I2 =nI1 I1 187.5 M P 图(kN m)
3
62.5
62.5
I1 B
A
187.5 M图(kN m) B
X1 =1
A
华南农业大学 水利与土木工程学院（College of water conservancy and Civil Engineering, SCAU）
（4）求解出多余未知力。
5
3m
EI=常数
7.2
4.8 12
3m
华南农业大学 水利与土木工程学院（College of water conservancy and Civil Engineering, SCAU）
⇒ X1 =
8 kN 5
（5）按照叠加法做出最后弯矩图如下。
M = M1 X1 + M P
（4）求解出多余未知力。
⇒ X1 =
（5）按照叠加法做出最后弯矩图如下。
M = M1 X1 + M P
F 12 C
EI=常数
G D E
4kN
3m
F C 3 A D
G
3m
F
7.2 12 4.8
3m
G D
EI=常数
3 E B
12
3m
M P 图(kN m)
C A
3m
M图(kN m)
A
B
3m
M 1 图(kN m)
δ11 X 1 + Δ1P = 0
1
华南农业大学 水利与土木工程学院（College of water conservancy and Civil Engineering, SCAU）
（3）做出基本结构的各单位内力图和荷载内力图。
δ11 =
2 1 2 2l i( i1il )i = 3 3 EI EI 2 1 1 Fl 1 Fl 2 Δ1P = i( i il )i = EI 2 4 2 16 EI 3Fl 32
（4）求解出多余未知力。
⇒ X1 = −
（5）按照叠加法做出最后弯矩图和剪力图（如下图） 。
M = M1 X1 + M P
F A FL/4 B C
A 1 B 1 1 C
MP
3FL/32 A B FL/4 C
M
13F/32 A B 3F/32 C
19F/32
M图
FS 图
7－4 试作图示超静定梁的 M 、 FS 图。
δ11 X 1 + Δ1P = 0
（3）做出基本结构的各单位内力图和荷载内力图。
δ11 =
2 1 2 1 2 30 [( i3i3)i i3 + ( i3i 2)i i 2] = 3 2 3 EI 2 EI 2 1 2 48 ( i2i3)i i12 = − Δ1P = − 3 EI 2 EI 8 kN 5
X1 =1
B
3m
3m
3m
3m
3m
7－9 试求图示桁架各杆的内力，各杆 EI 相同。
解： （1）该结构为一次超静定结构，拆除 B 点多余联系，得到基本体系。 （2）根据位移条件，得：
δ11 X 1 + Δ1P = 0
（3）做出基本结构的各单位内力图和荷载内力图。
δ11 =
2 1 2 1 2 30 [( i3i3)i i3 + ( i3i 2)i i 2] = 3 2 3 EI 2 EI 2 1 2 48 ( i2i3)i i12 = − Δ1P = − 3 EI 2 EI
（3）做出基本结构的各单位内力图和荷载内力图。
2 1 2 126 [( i3i3)i i3 + (3i6)i3] = 3 EI 2 EI δ12 = δ 21 = 0 2 1 2 144 δ 22 = i( 6i6)i i6 = 3 EI 2 EI 1 1 756 ( i168i3)i3 = − Δ1P = − EI 2 EI 1 3 1260 [2i6i168 + 3i168] = − Δ2P = − EI 6 EI
M = M1 X1 + M P
FL/2
F
EI
A MP
3FL/16 FL/4
B A L
11F/16
B M
A M图
7－3 试作图示超静定梁的 M 、 FS 图。
B
A FS 图
F A
EI
B
5F/16
F A
EI
X1 B X1
EI
C L
B
EI
C
L/2
L/2
基本体系
L/2
L/2
L
解： （1）该结构为一次超静定结构，刚结点 B 变成铰结点，得到基本体系。 （2）根据位移条件，得：
A 6
M 2 图(kN m)
B 6
97.5
A
M图(kN m)
B
3m
3m
X1 X1
E
C
E
18
7－8 作刚架的 M 图。
4
结构力学 第七章 习题 参考答案
F C A D
EI=常数 基本体系
G
4kN
3m
F C D
EI=常数
G
4kN E
3m
E
3m
B
3m
A
基本体系
B
3m
X1
3m
3m
解： （1）该结构为一次超静定结构，拆除 B 点多余联系，得到基本体系。 （2）根据位移条件，得：
δ11 X 1 + Δ1P = 0
（3）做出基本结构的各单位内力图和荷载内力图。
δ11 =
Δ1P
2 1 2 1 1 360 (144 + ) i( i6i6)i i6 + i(6i10)i6 = 3 EI1 2 nEI1 EI1 n 1 2 7500 ( i10i187.5)i6 = − =− nEI1 3 nEI1
（3）做出基本结构的各单位内力图和荷载内力图。
δ11 =
1 1 2l l3 i( il il )i = EI 2 3 3EI 1 1 Fl l 5l 5 Fl 3 Δ1P = − i( i i )i = − EI 2 2 2 6 48 EI
5F 16
（4）求解出多余未知力。
⇒ X1 =
（5）按照叠加法做出最后弯矩图和剪力图（如下图） 。
q=2kN/m A
5I I
q=2kN/m
B
6m 3m
A
5I I
B
6m
基本体系
3m
X1
解： （1）该结构为一次超静定结构，拆除 B 点多余联系，得到基本体系。 （2）根据位移条件，得：
δ11 X 1 + Δ1P = 0
（3）做出基本结构的各单位内力图和荷载内力图。
δ11 =
1 6 1 1 2 279 i (2i9i9 + 2i3i3 + 9i3 + 3i9) + i( i3i3)i i3 = 5 EI 6 3 5 EI EI 2 1 6 2 9+3 1 1 2 2 9 1 Δ1P = − [ i(2i9i81 + 2i3i9 + 3i81 + 9i9) − ( i6i9)i ] − [( i9i3)i i3 − ( i i3)i i3] 5 EI 6 3 2 3 3 4 2 EI 2 1377 =− 4 EI
7－6 图示刚架 E = 常数， n =
5 ，试作其 M 图，并讨论 n 增大和减少时， M 图如何变化。 2
q=15kN/m C I1 A
10m
q
D I1 B6mຫໍສະໝຸດ I2 =nI1C I1
I2 =nI1 I1
基本体系
D
6m
A
10m
B
X1
解： （1）该结构为一次超静定结构，拆除 B 点多余联系，得到基本体系。 （2）根据位移条件，得：
δ11 =
（4）求解出多余未知力。
⎧X = 6 ⇒⎨ 1 ⎩ X 2 = 8.75
（5）按照叠加法做出最后弯矩图（如下图） 。
M = M1 X1 + M 2 X 2 + M P
C
3 3 X1 =1
EI=常数
C
E
X2 =1 E X2 =1
C
18
D E
18
EI=常数
84
A 3
M 1 图(kN m)
B 3
（4）求解出多余未知力。
7500 5 n ⇒ X1 = kN 当 n = 时， X 1 = 10.42 kN 360 2 144 + n 5 （5）按照叠加法做出最后弯矩图和剪力图（当 n = 时，弯矩如下图） 。 2 M = M1 X1 + M P 当 n 增大时，AC 和 BD 杆件弯矩减少，CD 跨中弯矩增大，当 n = ∞ 时，BD 杆相当于简支
结构力学 第七章 习题 参考答案