人教版数学高一教学设计第1课时顺序结构与条件分支结构
顺序结构与条件分支结构
数学必修 3 1.1.3算法的三种逻辑结构和框图表示——顺序结构与条件分支结构编号06学习目标:目标:1.掌握程序框图的概念;2.了解顺序结构和条件分支结构的概念;3.会用顺序结构和条件分支结构表示算法。
重点:用顺序结构和条件分支结构表示算法难点:用条件分支结构表示算法预习案一.学法指导1.仔细阅读课本,探究课本的内容,熟记基础知识,体会每一段文字的意义。
说明了什么?应该注意些什么?哪些词语要特别注意?2.完成教材助读提出的问题,然后结合课本的基础知识和例题,完成预习自测题。
3.将预习中不能解决的问题标出来,并写在后面的“我的疑惑”处。
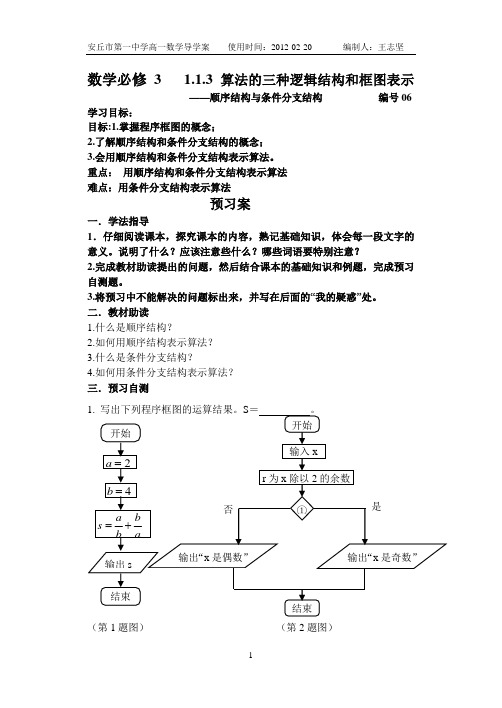
二.教材助读1.什么是顺序结构?2.如何用顺序结构表示算法?3.什么是条件分支结构?4.如何用条件分支结构表示算法?三.预习自测(第1题图)(第2题图)2. 判断正整数x 的奇偶性的程序框图如下,则①处应为 。
我的收获:我的疑惑探究案探究点一:用顺序结构表示算法例1. 已知三角形边长分别为a,b,c ,设)(21c b a P ++=,则三角形的面积))()((c p b p a p p s ---=,这个公式称为海伦公式,写出用这个公式求三边长分别是2,3,4的三角形面积的算法,并画出程序框图。
规律方法总结:探究点二:用条件分支结构表示算法例2. 画出计算函数|1|y x =-的函数值的程序框图。
规律方法总结:拓展提升1:设计算法,求一元二次方程ax2+bx+c=0(a≠0)的根,画出相应的流程图。
例3. 已知分段函数21(0)0(0)21(0)x xy xx x-+<⎧⎪==⎨⎪->⎩,对于输入任意一个x值,都得到相应的函数值,试画出这种算法的程序框图。
规律方法总结:探究点三:在实际生活中的应用例4.为了节约用水,保护水资源,北京市拟出台新的用水收费规定:每个市民如果每月用水不超过8吨,则每吨收费2元;如果超过8吨,则超过的部分每吨收费2.5元.试设计一个计算每个市民收取水费的算法,要求写出算法,画出程序框图.规律方法总结:当堂检测(带★为选作题):1、阅读下边的流程图,若输入的a、b、c分别为21、32、75,则输出的a、b、c分别是()A.75、21、32B.21、32、75C.32、21、75D.75、32、21(第1题图)(第2题图)2、运行下面的算法流程,当任意输入实数x时,输出的y值不可能是( )A.0B.1C.2D.33、已知函数y=|x+3|,下边程序框图表示的是给出x值,求所对应的y值的算法.请将该程序框图补充完整,①处应填;②处应填.(第3题图)(第4题图)4、★如图是某种算法的流程图,回答下面的问题:当输出的y值的范围大于2时,则输入的x的取值范围为.。
教学设计2:1.1.3 第1课时 顺序结构与条件分支结构

1.1.3 第1课时顺序结构与条件分支结构教学目标:1.掌握程序框图的概念;会用通用的图形符号表示算法,掌握算法的三个基本逻辑结构;掌握画程序框图的基本规则,能正确画出程序框图.2.通过模仿、操作、探索,经历通过设计程序框图表达解决问题的过程;学会灵活、正确地画程序框图.3.通过本节的学习,使我们对程序框图有一个基本的了解;掌握算法语言的两种基本逻辑结构,明确程序框图的基本要求;认识到学习程序框图是我们学习计算机的一个基本步骤,也是我们学习计算机语言的必经之路.教学重难点:教学重点:程序框图的基本概念、基本图形符号和两种基本逻辑结构.教学难点:能综合运用这些知识正确地画出程序框图.教学过程:一、创设情境:如果你向全班同学介绍一下你心中偶像的形象,你认为用语言描述好还是拿出偶像的照片给同学们看好?说明一下你的理由算法除了用自然语言表示外,还可用程序框图表示.二、基本概念:(1)起止框图:起止框是任何流程图都不可缺少的,它表明程序的开始和结束,所以一个完整的流程图的首末两端必须是起止框.(2)输入、输出框:表示数据的输入或结果的输出,它可用在算法中的任何需要输入、输出的位置.(3)处理框:它是采用来赋值、执行计算语句、传送运算结果的图形符号.(4)判断框:判断框一般有一个入口和两个出口,有时也有多个出口,它是惟一的具有两个或两个以上出口的符号,在只有两个出口的情形中,通常都分成“是”与“否”(也可用“Y”与“N”)两个分支.三、算法的基本逻辑结构(1)顺序结构:顺序结构描述的是是最简单的算法结构,语句与语句之间,框与框之间是按从上到下的顺序进行的.例1.已知一个三角形的三边分别为2、3、4,利用海伦公式设计一个算法,求出它的面积,并画出算法的程序框图.算法分析:这是一个简单的问题,只需先算出p的值,再将它代入公式,最后输出结果,只用顺序结构就能够表达出算法.解:程序框图:点评:顺序结构是由若干个依次执行的步骤组成的,是任何一个算法都离不开的基本结构. 变式训练1.输入矩形的边长求它的面积,画出程序框图.(2)条件结构:根据条件选择执行不同指令的控制结构.例2.任意给定3个正实数,设计一个算法,判断分别以这3个数为三边边长的三角形是否存在,画出这个算法的程序框图.算法分析:判断分别以这3个数为三边边长的三角形是否存在,只需要验收这3个数当中任意两个数的和是否大于第3个数,这就需要用到条件结构.程序框图:点评:条件结构的显著特点是根据不同的选择有不同的流向.变式训练2.求x的绝对值,画出程序框图.四、当堂检测1.条件分支结构不同于顺序结构的特征是含有()A.处理框B.判断框C.输入、输出框D.起、止框【解析】条件分支结构必须有判断框.【答案】B2.程序框图中条件分支结构的判断框有________个入口和________个出口.() A.1,2B.2,3C.1,3 D.都不确定【答案】A3.阅读下面的程序框图,若输入a,b,c分别是21、32、75,则输出的值是()A.96 B.53C.107 D.128【解析】∵21<32,∴m=21+75=96,即输出96.【答案】A4.根据如图程序框图,若输入m的值是3,则输出的y的值是________.【解析】若输入m的值是3.则p=8,y=8+5=13,故输出y的值为13.【答案】135.下面程序框图表示的算法功能是________.【解析】其功能是比较a 、b 、c 的大小,输出最大值. 【答案】输出a ,b ,c 中最大者6.以下给出了一个程序框图,其作用是输入x 的值,输出相应的y 的值.若要使输入的x 的值与输出的y 的值相等,求x 的值.解:该程序框图描述的算法是求分段函数y =⎩⎪⎨⎪⎧x 2,x ≤2,2x -3,2<x ≤5,1x ,x >5.因为输入的x 值与输出的y 值相等,所以y =x .(1)∵⎩⎪⎨⎪⎧x 2=x ,x ≤2,∴x =0或x =1.(2)∵⎩⎪⎨⎪⎧2x -3=x ,2<x ≤5,∴x =3.(3)∵⎩⎪⎨⎪⎧1x =x ,x >5,∴x 无解.综上所述,x 的值为0,1,3. 五、课堂小结:本节课主要讲述了程序框图的基本知识,包括常用的图形符号、算法的基本逻辑结构,算法的基本逻辑结有三种,本节讲了顺序结构、条件结构.其中顺序结构是最简单的结构,也是最基本的结构,循环结构必然包含条件结构,所以这三种基本逻辑结构是相互支撑的,它们共同构成了算法的基本结构,无论怎样复杂的逻辑结构,都可以通过这三种结构来表达 六、布置作业:1.输入3个实数按从大到小的次序排序. 解:程序框图:2.给出50个数,1,2,4,7,11,…,其规律是:第1个数是1,第2个数比第1个数大1,第3个数比第2个数大2,第4个数比第3个数大3,…,以此类推. 要求计算这50个数的和. 将上面给出的程序框图补充完整. (1)i < = 50 (2) p = p + i。
【成才之路】高中数学 第1课时顺序结构与条件分支结构学案课件 新人教A版必修3

重点:(1)程序框图符号的含义和画程序框图的规则.
(2)条件分支结构的特点. 难点:(1)理解程序框图符号的含义和画程序框图的规 则. (2)条件分支结构的运用.
1.学习本节要注意每一种框图都有特定的含义,应用
框图时,一是要弄清每一种框图的含义,注意其区别,如 起止框与处理框及判断框的区别,熟练掌握它们;二是要 遵循画程序框图的规则;三是要注重模仿、操作、探索, 于画框图过程中,进一步体会算法思想、提高逻辑思维能
体积.写出该问题的一个算法,并画出流程图. (4)求底面边长为4,侧棱长为5的正四棱锥的侧面积及 体积.为该问题设计不同的算法并分别画出流程图.
[解析]
1 (1)根据梯形的面积公式 S= (a+b)h.其中 a 2
是上底,b 是下底,h 是高,只要令 a=2,b=4,h=5, 代入公式即可.算法如下: 第一步:输入梯形的两底 a,b 与高 h 的值; 1 第二步:计算 S= (a+b)h; 2 第三步:输出 S. 该算法的流程图如图所示.
力.
2.算法中间任何需要输入、输出的位置都可以用输入
和输出,需要输入的字母、符号、数据都填在输入框内; 算法中间处理数据所需要的算式、公式等可分别写在不同 的用以处理数据的处理框内;同时还可以对变量进行赋 值.它们可以使用输入框输入的数据进行运算;算法中需
对两个不同结果进行判断时,需将实现判 Nhomakorabea所需条件写在
判断框内;任何算法都要有起止框 ( 终端框 ) 表明一个算法 程序的开始和结束. 3.一般计算S+i的值,并把结果赋给S,用S=S+i表 示,这是后面要学的赋值语句.
4.一些简单的算法中不包含判断和重复操作过程,只
须用顺序结构描述即可.对于只有几次重复操作的也可以 只用顺序结构来描述.如一些套用公式求值、函数求值 等.在一个问题中含有条件判断,而根据条件是否成立有 不同的处理过程时,需采用条件结构来处理.利用条件结
高中数学 1.1.3 逻辑结构 第1课时 顺序结构与条件分支结构课件 新人教A版必修3

S5 输出d.
(2)用框图来描述算法:
开始 输入x0,y0,A,B,C
z1=Ax0+By0+C
z2=A2+B2
d= |z1| z2
输出d 结束
例2、请用数学语言和程序框图描述求一元二次方程
ax2 bx c 0 根的过程。 解:(1)用数学语言来描述算法:
S1 计算Δ= b2 4ac;
1.1.3 算法的三种基本 逻辑结构和框图表示
第1课时 顺序结构与条件分支结构
1.算法框图的理解; 2.顺序结构的理解; 3.条件结构的理解。
首先用一个浅显的例子总结算法结构;新课讲 授部分,讲解顺序和条件结构;例题部分,通过 典例讲解让学生熟悉两种结构。复习巩固部分通 过练习对知识巩固,让学生更系统掌握本节课的 所学知识,最后总结作业。
例1. 已知点P0(x0,y0)和直线l:Ax+By+C=0,求点P0(x0, y0)到直线l的距离d. 解:(1)用数学语言来描述算法:
S1 输入点的坐标x0,y0,输入直线方程的系数A,B,C; S2 计算z1=Ax0+By0+C; S3 计算z2=A2+B2; S4 计算 d | z1 |;
用框图来描述算法:
开始 输入P、D 是
P>30
Y=0.3×30+0.5(P-30)
否 Y=0.3P
M=D×Y 输出M 结束
1.对顺序结构,下列说法:①是最基本、最简单的算法
结构;②框与框之间是依次进行处理;③除输入、输出
框之外,中间过程都是处理框;④可以从一个框图跳到
另一个框图执行;其中正确的有( B )
S2 如果Δ<0,则原方程无实数解;
人教版数学高一课时作业第1课时顺序结构与条件分支结构

1.1.3第1课时顺序结构与条件分支结构1.下列算法中,含有条件分支结构的是()A.求两个数的积B.求点到直线的距离C.解一元二次方程D.已知梯形两底和高求面积2.给出下列程序框图若输出的结果为2,则①处的执行框内应填的是()A.x=2 B.b=2C.x=1 D.a=53.下列关于条件分支结构的描述,不正确的是()A.条件分支结构的出口有两个,但在执行时,只有一个出口是有效的B.条件分支结构的判断条件要写在判断框内C.双选择条件分支结构有两个出口,单选择条件结构只有一个出口D.条件分支结构根据条件是否成立,选择不同的分支执行4.中山市的士收费办法如下:不超过2公里收7元(即起步价7元),超过2公里的里程每公里收2.6元,另每车次超过2公里收燃油附加费1元(不考虑其他因素).相应收费系统的程序框图如图所示,则①处应填()A.y=7+2.6xB.y=8+2.6xC.y=7+2.6(x-2)D.y=8+2.6(x-2)5.输入-5,按图中所示程序框图运行后,输出的结果是()A.-5 B.0 C.-1 D.16.给出一个程序框图,如图所示,其作用是输入x的值,输出相应的y的值.若要使输入的x的值与输出的y的值相等,则输入的这样的x的值有()A.1个B.2个C.3个D.4个7.如图是求实数x的绝对值的算法程序框图,则判断框①中可填________.8.根据下边的程序框图所表示的算法,输出的结果是______.9.已知函数y =⎩⎪⎨⎪⎧log 2x , x ≥22-x , x <2.如图表示的是给定x 的值,求其对应的函数值y 的程序框图.①处应填写________;②处应填写________.10.画出计算函数y =|2x -3|的函数值的程序框图.(x 由键盘输入)11.已知函数y =2x +3,设计一个算法,若给出函数图象上任一点的横坐标x (由键盘输入),求该点到坐标原点的距离,并画出程序框图.12.画出解一元一次不等式ax >b 的程序框图.13.到银行办理个人异地汇款(不超过100万)时,银行要收取一定的手续费.汇款额不超过100元,收取1元手续费;超过100元但不超过5 000元,按汇款额的1%收取;超过5 000元但不超过100万时,一律收取50元手续费,其他情况不予办理.试设计一个算法描述汇款额为x元时,银行收取手续费为y元的过程,并画出程序框图.参考答案1.【解析】【答案】C2.【解析】【答案】C3.【答案】C4.【解析】【答案】D5.【解析】【答案】D6.【解析】【答案】C7.【答案】x≥08.【解析】该算法的第1步分别将X,Y,Z赋于1,2,3三个数,第2步使X取Y的值,即X 取值变成2,第3步使Y取X的值,即Y的值也是2,第4步让Z取Y的值,即Z取值也是2,从而第5步输出时,Z的值是2.【答案】29.【解析】∵满足判断框中的条件执行y=2-x,∴①处应填x<2.不满足x<2即x≥2时,y=log2x,故②处应填y=log2x.【答案】x<2y=log2x10.解:11.解:算法如下:第一步,输入横坐标的值x.第二步,计算y=2x+3.第三步,计算d=x2+y2.第四步,输出d.程序框图如图:12.解:13.解:由题意知本题是一个分段函数问题,分段函数解析式为y =⎩⎪⎨⎪⎧ 1 0<x ≤1000.01x 100<x ≤5 00050 5 000<x ≤1 000 000.其算法如下:S1,输入汇款额x ; S2,判断x ≤100是否成立;若成立,则y =1,转执行S5,若不成立,则执行S3; S3,判断x ≤5 000是否成立;若成立,则y =x ×1%,转执行S5,若不成立,则执行S4; S4,判断x ≤1 000 000是否成立;若成立,则y =50,转执行S5,若不成立,则输出“不予办理”;S5,输出y .程序框图如图:。
人教版高中数学全套教案导学案2.顺序结构与条件分支结构

教师课时教案备课人授课时间课题1.1.2程序框图与算法的基本逻辑结构(一)课标要求1.掌握程序框图的概念;2.会用通用的图形符表示算法;3.掌握画程序框图的基本规则,能正确画出程序框图;教学目标知识目标掌握程序框图的概念;会用通用的图形符表示算法,掌握算法的三个基本逻辑结构;掌握画程序框图的基本规则,能正确画出程序框图。
技能目标通过模仿、操作、探索,经历通过设计程序框图表达解决问题的过程;学会灵活、正确地画程序框图。
情感态度价值观通过本节的学习,使我们对程序框图有一个基本的了解;掌握算法语言的三种基本逻辑结构,明确程序框图的基本要求;认识到学习程序框图是我们学习计算机的一个基本步骤,也是我们学习计算机语言的必经之路。
重点程序框图的基本概念、基本图形符和3种基本逻辑结构难点综合运用这些知识正确地画出程序框图。
教学过程及方法问题与情境及教师活动学生活动一.导入新课用自然语言表示的算法步骤有明确的顺序性,但是对于在一定条件下才会被执行的步骤,以及在一定条件下会被重复执行的步骤,自然语言的表示就显得困难,而且不直观、不准确.因此,本节有必要探究使算法表达得更加直观、准确的方法.今天开始学习程序框图.二.研探新知探究(一):程序框图自学P6,总结以下问题:(1)什么是程序框图?(2)说出终端框(起止框)的图形符与功能.(3)说出输入、输出框的图形符与功能.(4)说出处理框(执行框)的图形符与功能.(5)说出判断框的图形符与功能.(6)说出流程线的图形符与功能.(7)说出连接点的图形符与功能.(8)总结几个基本的程序框、流程线和它们表示的功能.思考1:“判断整数n(n>2)是否为质数”的算法步骤如何?第一步,给定一个大于2的整数n;第二步,第三步,,1否是 是 输入ni=2求n 除以i 的余数 i 的值增加1,仍用i 表开始 i>n-1或r=0? r=0?输出“n 不是质数”结束 输出“n 是质数” 否问题与情境及教师活动学生活动第四步 第五步,思考2:我们将上述算法用下面的图形表示:思考3:在上述程序框图中,有4种程序框,2种流程线,它们分别有何特定的名称和功能? 试分别说明。
最新人教版高一数学必修1第一章《课程安排》教案

最新人教版高一数学必修1第一章《课程
安排》教案
一、教学目标
1.了解数学必修1的教学内容和研究要求。
2.掌握第一章的重点知识和技能。
3.培养学生的数学思维和解决问题的能力。
二、教学重点和难点
1.掌握数学必修1第一章的基本概念。
2.理解并运用代数记号和符号进行数学运算。
3.解决与线性方程组相关的实际问题。
三、教学内容和研究活动安排
1.课堂导入:通过引入实际问题,激发学生的研究兴趣。
2.知识讲解:结合教材内容,讲解数学必修1第一章的基本概念和相关理论知识。
3.教学实践:组织学生进行线性方程组的解题练和实际问题的解决。
4.研究巩固:布置相关作业,检验学生对本章内容的理解和掌握程度。
四、教学评价
1.通过课堂听讲和课堂练,对学生的研究情况进行实时评价。
2.组织小组合作研究和交流,促进学生之间的互动和合作。
3.针对学生的研究情况进行个性化辅导和指导,提高学生的研究成绩。
五、教学资源准备
1.教材:最新人教版高一数学必修1。
2.教具:黑板、彩色粉笔、教学PPT等。
3.其他辅助材料:相关的练题和实际问题。
六、教学反思
本教案主要围绕数学必修1第一章的教学内容展开,通过灵活多样的教学方法和活动,激发学生的学习兴趣和解决问题的能力。
同时,针对学生不同的学习情况,采取个性化的辅导和指导手段,全面提高学生的数学水平。
通过教学评价和反思,不断总结经验,进一步完善教学过程,提高教学效果。
高中数学第一章1.1.3第一课时顺序结构与条件分支结构教学案新人教B版必修20

第一课时 顺序结构与条件分支结构
预习课本 P10~ 12,思考并完成以下问题
(1)顺序结构是怎样定义的?
(2)什么是条件分支结构?
[新知初探 ]
顺序结构
条件分支结构
定义
描述的是最简单的算法结构, 语句和语句 之间,框和框之间按从上到下的顺序进行
n 否则,计算 ω= 的值.
2 S3 输出 ω. 程序框图如图所示.
[层级二 应试能力达标 ]
1.如图是程序框图的一部分,其算法的逻辑结构是
()
马鸣风萧萧整理
》》》》》》》》》积一时之跬步 臻千里之遥程《 《《《《《《《《《《《
A.顺序结构
B.条件分支结构
C.判断结构
D .以上都不对
解析:选 B 此逻辑结构是条件分支结构.
积数,输出应付的房租.
[解 ] 算法如下:
S1 输入住房面积 S.
S2 根据面积选择计费方式:若 S≤90,则租金为 M= 3S;若 S>90 ,则租金为 M= 5S
-180.
S3 输出房租 M 的值.
程序框图如下:
利用条件分支结构求解实际应用题的策略
与现实生活有关的题目经常需用到条件分支结构.
解答时, 首先根据题意写出函数解析
4.给出一个如图所示的程序框图,若要使输入 的值的个数是 ( )
x 的值与输出 y 的值相等,则这样的 x
A. 1
B. 2
C. 3
D.4
解析:选 C 当 x≤ 2 时, y=x2= x,解得 x1= 0, x2= 1;当 2< x≤ 5 时, y= 2x- 3= x,
1 解得 x3= 3;当 x>5 时, y=x= x,解得 x=± 1(舍去 ),故 x 的值可以为 0,1,3.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.1.3 第1课时顺序结构与条件分支结构
教学目标:
1.掌握程序框图的概念;会用通用的图形符号表示算法,掌握算法的三个基本逻辑结构;掌握画程序框图的基本规则,能正确画出程序框图.
2.通过模仿、操作、探索,经历通过设计程序框图表达解决问题的过程;学会灵活、正确地画程序框图.
3.通过本节的学习,使我们对程序框图有一个基本的了解;掌握算法语言的两种基本逻辑结构,明确程序框图的基本要求;认识到学习程序框图是我们学习计算机的一个基本步骤,也是我们学习计算机语言的必经之路.
教学重难点:
教学重点:程序框图的基本概念、基本图形符号和两种基本逻辑结构.
教学难点:能综合运用这些知识正确地画出程序框图.
教学过程:
一、创设情境:如果你向全班同学介绍一下你心中偶像的形象,你认为用语言描述好还是拿出偶像的照片给同学们看好?说明一下你的理由算法除了用自然语言表示外,还可用程序框图表示.
二、基本概念:
(1)起止框图:起止框是任何流程图都不可缺少的,它表明程序的开始和结束,所以一个完整的流程图的首末两端必须是起止框.
(2)输入、输出框:表示数据的输入或结果的输出,它可用在算法中的任何需要输入、输出的位置.
(3)处理框:它是采用来赋值、执行计算语句、传送运算结果的图形符号.
(4)判断框:判断框一般有一个入口和两个出口,有时也有多个出口,它是惟一的具有两个或两个以上出口的符号,在只有两个出口的情形中,通常都分成“是”与“否”(也可用“Y”与“N”)两个分支.
三、算法的基本逻辑结构
(1)顺序结构:顺序结构描述的是是最简单的算法结构,语句与语句之间,框与框之间是按从上到下的顺序进行的.
例1.已知一个三角形的三边分别为2、3、4,利用海伦公式设计一个算法,求出它的面积,并画出算法的程序框图.
算法分析:这是一个简单的问题,只需先算出p的值,再将它代入公式,最后输出结果,只用顺序结构就能够表达出算法.
解:程序框图:
点评:顺序结构是由若干个依次执行的步骤组成的,是任何一个算法都离不开的基本结构. 变式训练1.输入矩形的边长求它的面积,画出程序框图.
(2)条件结构:根据条件选择执行不同指令的控制结构.
例2.任意给定3个正实数,设计一个算法,判断分别以这3个数为三边边长的三角形是否存在,画出这个算法的程序框图.
算法分析:判断分别以这3个数为三边边长的三角形是否存在,只需要验收这3个数当中任意两个数的和是否大于第3个数,这就需要用到条件结构.
程序框图:
点评:条件结构的显著特点是根据不同的选择有不同的流向.
变式训练2.求x的绝对值,画出程序框图.
四、当堂检测
1.条件分支结构不同于顺序结构的特征是含有()
A.处理框B.判断框
C.输入、输出框D.起、止框
【解析】条件分支结构必须有判断框.
【答案】B
2.程序框图中条件分支结构的判断框有________个入口和________个出口.() A.1,2B.2,3
C.1,3 D.都不确定
【答案】A
3.阅读下面的程序框图,若输入a,b,c分别是21、32、75,则输出的值是()
A.96 B.53
C.107 D.128
【解析】∵21<32,∴m=21+75=96,即输出96.
【答案】A
4.根据如图程序框图,若输入m的值是3,则输出的y的值是________.
【解析】若输入m的值是3.
则p=8,y=8+5=13,
故输出y的值为13.
【答案】13
5.下面程序框图表示的算法功能是________.
【解析】其功能是比较a 、b 、c 的大小,输出最大值. 【答案】输出a ,b ,c 中最大者
6.以下给出了一个程序框图,其作用是输入x 的值,输出相应的y 的值.若要使输入的x 的值与输出的y 的值相等,求x 的值.
解:该程序框图描述的算法是求分段函数
y =⎩⎪⎨⎪⎧
x 2,x ≤2,
2x -3,2<x ≤5,1x ,x >5.
因为输入的x 值与输出的y 值相等,所以y =x .
(1)∵⎩
⎪⎨⎪⎧
x 2=x ,x ≤2,∴x =0或x =1.
(2)∵⎩
⎪⎨⎪⎧
2x -3=x ,2<x ≤5,∴x =3.
(3)∵⎩⎪⎨⎪⎧
1x =x ,x >5,∴x 无解.
综上所述,x 的值为0,1,3. 五、课堂小结:
本节课主要讲述了程序框图的基本知识,包括常用的图形符号、算法的基本逻辑结构,算法的基本逻辑结有三种,本节讲了顺序结构、条件结构.其中顺序结构是最简单的结构,也是最基本的结构,循环结构必然包含条件结构,所以这三种基本逻辑结构是相互支撑的,它们共同构成了算法的基本结构,无论怎样复杂的逻辑结构,都可以通过这三种结构来表达 六、布置作业:
1.输入3个实数按从大到小的次序排序. 解:程序框图:
2.给出50个数,1,2,4,7,11,…,其规律是:第1个数是1,第2个数比第1个数大1,第3个数比第2个数大2,第4个数比第3个数大3,…,以此类推. 要求计算这50个数的和. 将上面给出的程序框图补充完整. (1)i < = 50 (2) p = p + i。
