线性定常离散控制系统
自动控制原理例题详解线性离散控制系统的分析与设计考习题及答案

精心整理----------2007--------------------一、(22分)求解下列问题: 1. (3分)简述采样定理。
解:当采样频率s ω大于信号最高有效频率h ω的2倍时,能够从采样信号)(*t e 中 完满地恢复原信号)(t e 。
(要点:h s ωω2>)。
2.(3分)简述什么是最少拍系统。
解:在典型输入作用下,能以有限拍结束瞬态响应过程,拍数最少,且在采样时刻上无稳态误差的随动系统。
3.(34.(x()∞5.(5解:(G 6.(5试用Z 解:二、((i X s )z 图11.(5分)试求系统的闭环脉冲传递函数()()o i X z X z ; 2.(5分)试判断系统稳定的K 值范围。
解:1.101111111()(1)(1)11(1)1(1)()1e11e 1e G G z z Z s s z Z s s z z z z z z z e z -------⎡⎤=-⎢⎥+⎣⎦⎡⎤=--⎢⎥+⎣⎦=-----=---=-11010*******1e ()()e 1e ()1()1e (1e )(e )(1e )(1e )e e o i K X z KG G z z X z KG G z K z K z K K z K K ------------==-++--=-+--=-+- 2.(5三、(8已知(z)1Φ=1.(3分)简述离散系统与连续系统的主要区别。
解:连续系统中,所有信号均为时间的连续函数;离散系统含有时间离散信号。
2.(3分)简述线性定常离散系统的脉冲传递函数的定义。
解:在系统输入端具有采样开关,初始条件为零时,系统输出信号的Z 变换与输入信号的Z 变换之比。
3.(3分)简述判断线性定常离散系统稳定性的充要条件。
解:稳定的充要条件是:所有特征值均分布在Z 平面的单位圆内。
4.(5分)设开环离散系统如图所示,试求开环脉冲传递函数)(z G 。
解:22522510252510()[[25e e (e e )eT T T T Tz z z G z Z Z s s z z z z -----=⨯==++---++ 5.(5分)已知系统差分方程、初始状态如下:0)(2)1(3)2(=++++k c k c k c ,c(0)=0,c(1)=1。
1.4 自动控制系统的分类

输入 + A/D
--
计算 机
输出
D/A
放大器
执行器
被控对象
反馈装置
采样数字控制系统结构图
广东交通职业技术学院机电工程系
18:18
4. 按输入量变化的规律分类
1) 恒值控制系统(Fixed Set-Point Control System) 特点是:系统的输入量是恒量,并且要求系统 的输出量相应地保持恒定。例如电机速度控制、水 位控制等。
且要求输出量随之变化。例如数控伺服系统以及一些 自动化生产线等。
广东交通职业技术学院机电工程系
18:18
广东交通职业技术学院机电工程系
18:18
2) 非线性系统(Non Liner System)
特点是:系统中含有非线性元件,如具有死区、 出现饱和等非线性特性的元件,它的输出量与输入 量间的关系要用非线性微分方程来描述。
广东交通职业技术学院机电工程系
18:18
2. 按系统中的参数对时间的变化情况 1) 定常系统(Time-Invariant System) (又称时
1.4 自动控制系统的分类
自动控制系统可以从不同的角度来进行分类, 常见的有以下几种。
1. 按系统的输出量和输入量间的关系分类 1) 线性系统(Liner System) 特点是:系统全部由线性元件组成,它的输出
量与输入量间的关系用线性微分方程来描述。
线性系统的主要特点是具有叠加性和齐次性,即 当c1(系t)和统c的2(t输),入则分当别输为入r1为(t)r和(t)r=2a(t1)r时1(t,)+对a2r应2(t的)时输,出输分出别量为 为c(t)=a1c1(t)+a2c2(t),其中为a1、a2为常系数。
自动控制理论重点考点归纳

判断1、反馈控制系统具有任何抑制内外扰动对被控量产生影响的能力,能较好的控制精度。
对2、原函数经过拉氏变换后得到象函数。
对3、线性系统的(闭环)极点均位于左半s平面,系统稳定. 错4、根轨迹可用于分析系统稳态性能和动态性能。
对5、对数幅相曲线是以角频率w(lgw)为横坐标对数幅值与相角(φw)为纵坐标的.错6、最小相位惯性环节和非最小相位惯性环节,其幅频特性相同,相频特性符号相反。
对7、一反馈控制系统,有五个开环正实部极点,半闭合曲线顺时针(逆时针)包围(—1,j0)点五圈,则系统稳定。
错8、相角裕度和截止频率属于开环频域性能指标.对9、与连续控制系统一样,在离散控制系统中,变化前向通路中不同环节的相对位置,不会影响系统的开环脉冲传递函数。
错10、不同连续信号得到的采样信号一定不同。
错11、采用(负)反馈并利用偏差进行控制的过程称为反馈控制。
错12、通过拉普拉斯反变换可根据象函数得到原函数。
对13、线性系统在初始条件为零时,受到单位阶跃信号(脉冲信号)作用时,系统输出在t趋近于正无穷条件下趋于0,即说该系统稳定。
错14、根轨迹是指根轨迹增益(开环系统某一参数)从零变到无穷大时,系统闭环特征根大复平面上变化的轨迹. 错15、幅相曲线是绘制在以角频率w为横坐标幅值为纵坐标的复平面上的曲线错16、传递函数互为倒数的典型环节,其幅相曲线关于实轴(对数幅频曲线关于0db,相频关于0°线)对称。
错17、一反馈控制系统,有4个开环正实部极点,半闭合曲线从上向下穿越(—1,j0)点左侧实轴两次,则该系统稳定。
对18、截止频率和带宽频率(闭环)是两个常用的开怀频域性能指标。
错19、在离散控制系统中,采样开关位置的变化不影响系统的开环脉冲传递函数,但会影响系统的闭环脉冲传递函数. 错20。
同一采样信号有可能对应不同的连续信号.对简答题1,对控制系统的基本要求1.稳定性稳定性是系统正常工作的必要条件。
2.准确性要求过渡过程结束后,系统的稳态精度比较高,稳态误差比较小.或者对某种典型输入信号的稳态误差为零。
自动控制原理概念最全整理要点

自动控制原理概念最全整理要点1.在零初始条件下,线性定常系统输出量的拉普拉斯变换与输入量的拉普拉斯变换值比,定义为线性定常系统的传递函数。
传递函数表达了系统内在特性,只与系统的结构、参数有关,而与输入量或输入函数的形式无关。
2.一个一般控制系统由若干个典型环节构成,常用的典型环节有比例环节、惯性环节、积分环节、微分环节、振荡环节和延迟环节等。
3.构成方框图的基本符号有四种,即信号线、比较点、方框和引出点。
4.环节串联后总的传递函数等于各个环节传递函数的乘积。
环节并联后总的传递函数是所有并联环节传递函数的代数和。
5.在使用梅森增益公式时,注意增益公式只能用在输入节点和输出节点之间。
6.上升时间tr、峰值时间tp和调整时间t反应系统的快速性;而最大超调量Mp和振荡次数则反应系统的平稳性。
7.稳定性是控制系统的重要性能,使系统正常工作的首要条件。
控制理论用于判别一个线性定常系统是否稳定提供了多种稳定判据有:代数判据(Routh与Hurwitz判据)和Nyquit稳定判据。
8.系统稳定的充分必要条件是系统特征根的实部均小于零,或系统的特征根均在跟平面的左半平面。
9.稳态误差与系统输入信号r(t)的形式有关,与系统的结构及参数有关。
10.系统只有在稳定的条件下计算稳态误差才有意义,所以应先判别系统的稳定性。
11.Kp的大小反映了系统在阶跃输入下消除误差的能力,Kp越大,稳态误差越小;Kv的大小反映了系统跟踪斜坡输入信号的能力,Kv越大,系统稳态误差越小;Ka的大小反映了系统跟踪加速度输入信号的能力,Ka越大,系统跟踪精度越高12.扰动信号作用下产生的稳态误差en除了与扰动信号的形式有关外,还与扰动作用点之前(扰动点与误差点之间)的传递函数的结构及参数有关,但与扰动作用点之后的传递函数无关。
13.超调量仅与阻尼比ξ有关,ξ越大,Mp则越小,相应的平稳性越好。
反之,阻尼比ξ越小,振荡越强,平稳性越差。
当ξ=0,系统为具有频率为Wn的等幅震荡。
第3章-线性离散系统数学描述

根据线性系统叠加原理 ,已知 h * ( t )后,任意输入脉冲序列 u * ( t ), 可得系统输出为 y * ( t ) = u( 0 ) h * ( t ) + u (1) h * ( t − T ) + L + u( n ) h * ( t − nT ) + L y ( k ) = ∑ u ( j ) h( k − j ) =
z →1
i =0 i =1 m n
已知,用递推法求解。 例3 − 2 − 2 y ( k + 1) = ay ( k ) + bu( k ), 设 y ( 0 )、 u( k )已知,用递推法求解。 解: k = 0 k =1 M
k
y (1) = ay ( 0 ) + bu( 0 ) y ( 2 ) = ay (1) + bu(1) = a 2 y ( 0 ) + abu ( 0 ) + bu(1)
它的齐次方程为 y( k + n) + a1 y( k + n − 1) + L + a n y( k ) = 0
它的特征方程为 r n + a1 r n −1 + a 2 r n − 2 + L + a n = 0
个特征根: 有 n个特征根: 则方程通解为: (1)若解为 n个单根 r1 , r2 , L , rn , 则方程通解为: y ( k ) = c 1 r1k + c 2 r2k + L + c n rnk; 重根, (2)若解有 m 重根,则 m 重根的解的形式为 r k , kr k , k 2 r k, , k m -1 r k的线性组合, 的线性组合, L 通解中的系数 c n由系统的初始条件确定 。
第7章 线性离散控制系统分析

f * (t )
7. 3 Z 变换
7.3.1 Z变换的定义
连续信号 f (t ) 经过采样后的离散信号 f * (t ) 为
f * (t ) f (nT ) (t nT )
其拉普拉斯变换为 令
z e Ts
F (s) L[ f (t )] f (nT )e nTs
* * n 0
的根都位于[W] 的左半部。
7. 5 线性离散系统的稳定性与稳态误差
7.5.1 线性定常离散系统稳定的充要条件
7. 5 线性离散系统的稳定性与稳态误差
7.5.2开环增益和采样周期对离散系统稳定性的影响
开环增益与采样周期对离散系统稳定性的影响: (1)采样周期一定时,增大开环增益会使离散系统的稳 定性变差,甚至使系统不稳定; (2)开环增益一定时,采样周期越长,丢失的信息越 多,离散系统的稳定性及动态性能变差,甚至使系
7. 6 线性离散系统的动态性能分析
7.6.1 线性离散系统的单位阶跃响应
离散系统的闭环脉冲传递函数为 式中,
R( z ) z /( z 1)
。系统输出的变换式为
将上式按幂级数展开,进行Z反变换,可求出输出信号的 脉冲序列 c* (t ) ,绘制单位阶跃响应曲线 c* (t ) ,从而分析 离散系统的动态性能。若不能求出离散系统的闭环脉冲传 递函数 ( z ) ,而R( z) 是已知的,可直接写出 C ( z ) 的表达式。
在线性采样系统理论中,把初始条件为零情况下,系统的离 散输出信号的变换与离散输入信号的变换之比,定义为脉冲 C ( z) 传递函数,记为 G(z)
R( z)
系统输出采样的脉冲序列为 c* (t ) z 1[C ( z)] z 1[G( z) R( z)]
6_离散控制系统(2)

Z变换
解: E * ( s ) = ∑ e( kT )e − kTs = 1 + e −Ts + e − 2Ts +
k =0 ∞
E * ( s ) = ∑ e( kT )e − kTs
k =0
∞
例1:设e(t)=1(t),试求e*(t)的拉氏变换。
= 1 , − Ts 1− e e −Ts < 1
给定值 + 反 馈 信 号
扰动
-
A/D
数字 计算机 控制器
D/A
执行 元件
对象
测量元件
2
线性定常连续控制系统:微分方程、传递函数; r(t) e(t)
控制器
u(t)
执行元件 被控对象
c(t)
b(t)
检测元件
采样控制系统:差分方程、脉冲传递函数; 连续 信号
r(t) b(t) 测量元件
3
离散 信号
采样开关 e*(t)
k =0
∞ k =0
20
∞
x*(t)的z变换记为Z[x*(t)], Z (x* ( t )) = X ( z ) = ∑ x( kT ) z − k
Z变换
1、定义法(级数求和法)
知道连续函数x(t)在各采样时刻的离散值x*(t),按定义求。 例2:求 x1 ( t ) = u( t ) 和 x 2 ( t ) = ∑ δ ( t − kT ) 的z变换表达式。 解: X ( z ) = x ( kT ) z − k = 1 + z −1 + z − 2 + ∑ 1
零阶保持器的频率特征
eh ( s ) 1 − e − Ts = = Gh ( s ) * e ( s) s
(整理)控制系统的能控性和能观测性
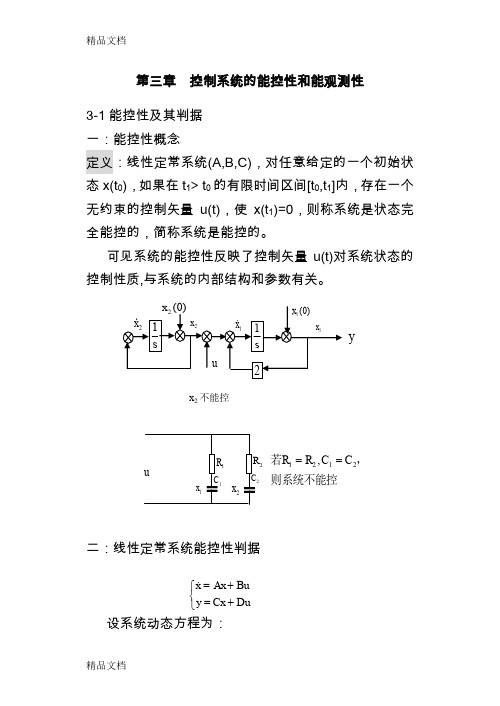
第三章 控制系统的能控性和能观测性3-1能控性及其判据 一:能控性概念定义:线性定常系统(A,B,C),对任意给定的一个初始状态x(t 0),如果在t 1> t 0的有限时间区间[t 0,t 1]内,存在一个无约束的控制矢量u(t),使x(t 1)=0,则称系统是状态完全能控的,简称系统是能控的。
可见系统的能控性反映了控制矢量u(t)对系统状态的控制性质,与系统的内部结构和参数有关。
二:线性定常系统能控性判据设系统动态方程为:x 2不能控y2则系统不能控,若2121,C C R R ==⎩⎨⎧+=+=DuCx y Bu Ax x设初始时刻为t 0=0,对于任意的初始状态x(t 0),有: 根据系统能控性定义,令x(t f )=0,得:即:由凯莱-哈密尔顿定理:令 上式变为:对于任意x(0),上式有解的充分必要条件是Q C 满秩。
判据1:线性定常系统状态完全能控的充分必要条件是:⎰-+=ft f f f d Bu t x t t x 0)()()0()()(τττφφ⎰⎰---=--=-ff t f f t f f d Bu t t d Bu t t x 01)()()()()()()0(τττφφτττφφ⎰--=f t d Bu x 0)()()0(τττφ∑-=-==-1)()(n k kk A A eτατφτ∑⎰⎰∑-=-=-=-=101)()()()()0(n k t k k t n k k k ff d u B A d Bu A x ττταττταkt k u d u f=⎰)()(ττταUQ u u u u B A B A AB B Bu A x c k n n k kk -=⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡-=-=--=∑ 321121],,,[)0(能控性矩阵Q C =[B ,AB ,A 2B ,…A n-1B]满秩。
对于单输入系统,Q C =[b ,Ab ,A 2b ,…A n-1b] 如果系统是完全能控的,称(A 、B )或(A 、b )为能控对。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
自动控制理论发展概况;古典控制
理论的基本内容;自动控制与自动控制
系统的基本概念及对控制系统的基本要
求。
重点内容
自动控制与自动控制系统的基本概念
对控制系统的基本要求
第一节
引言
一、自动控制在国民经济中的作用:
1、生活中,
洗衣机、 电冰箱、
电饭煲。
2、铁路上
高速列车、
磁悬浮列车
日本新干线100系(1985)
大
n
器
人工闭环控制系统 电动机转速开环控制系统
2、开环系统的优、缺点:
优点:组成简单、易实现;工作稳定。 缺点:抗干扰能力差,无法消除输出量产生的偏差。
3、电机转速开环速度控制系统结构图:
输入量
电压和功率 放大器
扰 动 量
直流电动机
输出量
电机转速开环速度控制系统结构图
二、闭环控制系统:
在控制器和被控对象之间不仅存在着正向作用,而且 存在着负反馈的作用来减小系统的误差,因此又称为 负反馈控制。
汽阀
Wate飞轮调节器
1945年,美国Bode在《网络分析和反馈放大 器设计》中提出频率响应分析法-Bode图。
1948年,Evans提出了根轨迹法,这时美国 Wiener在《控制论-关于在动物和机器中控 制和通信的科学》中系统地论述了控制理论 的一般原理和方法。 ---标志控制学科的诞生 控制论:研究动物(包括人类)和机器内部 控制和通信的一般规律的学科。
(4)自动化投资少
iB
电
ui
压
u
功 率
ua
SM
放
大
n
器
u 2 TG
ic
电机转速闭环控制系统
输入量 u1
W1 +
ui
_
u 电压、功
率放大器
u2
W2
扰动量
M fz f t
输出量
ua
n ct
直流电动机
测速发电机
直流电动机闭环控制系统结构框图
3、特点: (1)有前向及反馈支路 (2)有检测环节 (3)靠偏差信号进行工作,闭环系统是有源的
2、控制系统:
控制器和被控对象的总和,称为 控制系统
3、输入量(参考输入、控制输入、给定输入):
是作用于系统的激发信号,其中使系统具有预定性能或
预定输出的,称为控制输入、指令输入或参考输入。
4、扰动量:
干扰或破坏系统具有预定性或预定输出的,称为扰动输 入。
5、被控制量(输出量)
系统的输出就是被控制的量,它表征对象或过程的 状态和性能。
日本新干线300系(1992)
日本新干线700系(1999)
国产“中华之星”
法国TGV高速列车
普通轮轨列车最大时速为350-400公里
中科院院士严陆光—高速磁悬浮技术倡导者。中国铁道科学研 究院、西南交大、国防科大、中科院电工所等单位对常导低速 磁悬浮列车的悬浮、导向、推进等关键技术做了基础性研究。
扰动量
输入量 +
_
控制环节
输出量 被控对象
反馈量
反馈环节
1、举例:电枢控制的直流电动机闭环控制系统
假设ui不变,n希 1500r / min
n实 u2 u u ui u2 ua n
2、优点: (1)可有效地抑制扰动对系统的影响 (2)可提高系统的稳态精度 (3)加快系统的过渡过程
4、缺点:
可能引起超调,造成系统振荡,甚至使得系统不稳定。
三、复合控制系统
开环控制和闭环控制相结合的控制方式。分为按输 入信号补偿和按扰动信号补偿两种方式。
流出量
流入量
输入量
+
控制器
水箱
_
H希
H实
反馈量
浮子
图 4 水箱水位自动控制系统示意图
自动控制系统的基本方式 一、开环控制:
即系统的输出量对控制量没有影响。其结构示意图如 图所示:
控制量 控制器
被控制量 对象或过程
图 5 开环控制系统 1、举例:电动机转速控制系统
ui
iB
电
压
功
uc 率
SM
放 ua
引例:水箱水位自动控制系统
流入量
气动阀门
控制器 浮子
H希
H实
流出量
图 1 水箱水位自动控制系统示意图
第二节 自动控制与自动控制系统的基本概念
1、自动控制:
应用控制装置自动地、有目的地控制或操纵机器设 备或过程,使之具有一定的状态和性能。 被控制的机器设备或物体、生产过程,称为被控制对象; 所用的控制装置,常称为控制器
6、反馈量:
与输出成正比或某种函数关系,但量纲与参考输入相
同的信号。
7、偏差量:
等于参考输入与主反馈量之差的信号。
8、比较元件:
相当于一个偏差器,其输出信号等于各输入信号 的代数和。
9、负反馈控制系统的示意图
扰动量
输入量 + 偏差量
_
控制环节
输出量 被控对象
反馈量
反馈环节
图 2 控制系统结构示意图
1954年,钱学森的《工程控制论》在美国出 版。 ---奠定了工程控制论的基础
现代控制理论
1960——1970 现代控制理论 机组自动化
1958年,R.E.Kalman采用状态空间法分析系统,提 出能控性、能观性、Kalman滤波概念
1961年,庞特里亚金证明了最优控制中的极大值原理。 1970——1980 大系统理论 控制管理综合 1980——1990 智能控制理论 智能自动化 1990——21c 集成控制理论 网络控制自动化
上海磁浮列车
全长30公里,将上海市区与东海之滨的浦东国际机场连接起来, 单向运行时间约8分钟,平均运行速度达到每秒60-70米。列车 大部分时间时速为300多公里,达到最高设计时速430公里的时间 有20多秒。
日本磁悬浮列车
超导线圈与U型列车行驶导槽中设置的推力、上浮、导向线圈一 起使列车获得上浮、推进、导向力。日本使用的超导物质是将 超细铌钛合金多芯线埋入铜母线内制成的超导电线,当此种超 导电线浸入液氦(-269℃)中时进入超导状态产生强大磁场。
古典控制论
1788年,英国Wate利用反馈原理发明蒸汽机 用的离心调速机。→
1875年,1895年,英国Routh和德国Hurwitz 先后提出判别系统稳定性的代数方法。
1892年,俄国李雅普诺夫在《论运动稳定性 的一般问题》中建立了动力学系统的一般稳 定性理论。
1932年,Nyquist提出了根据频率响应判断系 统稳定性的准则。
3、军事上
航空:(F-15)战斗机
航天:APOLLO宇宙飞船
海上:核潜艇
“库尔斯克”号核潜艇
4、工业上 二、自动控制理论发展概要
1、古典控制论: 研究SISO线性定常时不变系统,其数学基础为传 递函数。
2、现代控制论:
以状态空间法为基础研究多输入-多输出、变参 数、非线性系统。其数学基础是线性代数。
