第十章 动荷载
合集下载
第10章动载荷与交变载荷

3、交变应力:应力随时间作周期性变化,属疲劳问题。疲 劳破坏是指在反复载荷作用下,结构中裂纹形成、扩展乃至 断裂的过程。
4、振动问题: 求解方法很多。
4
工 程 力 学§10-2 构件作等加速直线运动
时的动应力计算
钢索起吊重物,W、a, 求:钢索 d
钢索具有a,不为平衡状态,不能用平
衡方程求内力。
kd
动荷因数
kd
FNd Fst
d st
d st
结论:只要将静载下的应力,变形,乘以动荷系数Kd即得 动载下的应力与变形。
6
工 程 力 学§10-3 构件受冲击载荷作用时
的动应力计算
冲击荷载问题的动响应
方法原理:能量法 ( 机械能守恒 )
在冲击物与受冲构件的接触区域内,应力状态异常复杂, 且冲击持续时间非常短促,接触力随时间的变化难以准确分析, 放弃动静法。工程中通常采用能量法来解决冲击问题,即在若 干假设的基础上,根据能量守恒定律对受冲击构件的应力与变 形进行偏于安全的简化计算。
7
工 程 力 学§10-3 构件受冲击载荷作用件受冲击载荷作用时
的动应力计算
9
工 程 力 学§10-3 构件受冲击载荷作用时
的动应力计算
10
工 程 力 学§10-3 构件受冲击载荷作用时
的动应力计算
在冲击过程中,运动中的物体称为冲击物。 阻止冲击物运动的构件,称为被冲击物。
(3)、构件在交变应力作用下发生破坏需要经历一定数量的应 力循环,其循环次数与应力的大小有关。应力愈大,循环次数 愈少。
实验表明在静载荷下服从胡克定律的材料,只要应力不超 过比例极限 ,在动载荷下虎克定律仍成立且E静=E动.
动荷因数:
动响应 Kd 静响应
4、振动问题: 求解方法很多。
4
工 程 力 学§10-2 构件作等加速直线运动
时的动应力计算
钢索起吊重物,W、a, 求:钢索 d
钢索具有a,不为平衡状态,不能用平
衡方程求内力。
kd
动荷因数
kd
FNd Fst
d st
d st
结论:只要将静载下的应力,变形,乘以动荷系数Kd即得 动载下的应力与变形。
6
工 程 力 学§10-3 构件受冲击载荷作用时
的动应力计算
冲击荷载问题的动响应
方法原理:能量法 ( 机械能守恒 )
在冲击物与受冲构件的接触区域内,应力状态异常复杂, 且冲击持续时间非常短促,接触力随时间的变化难以准确分析, 放弃动静法。工程中通常采用能量法来解决冲击问题,即在若 干假设的基础上,根据能量守恒定律对受冲击构件的应力与变 形进行偏于安全的简化计算。
7
工 程 力 学§10-3 构件受冲击载荷作用件受冲击载荷作用时
的动应力计算
9
工 程 力 学§10-3 构件受冲击载荷作用时
的动应力计算
10
工 程 力 学§10-3 构件受冲击载荷作用时
的动应力计算
在冲击过程中,运动中的物体称为冲击物。 阻止冲击物运动的构件,称为被冲击物。
(3)、构件在交变应力作用下发生破坏需要经历一定数量的应 力循环,其循环次数与应力的大小有关。应力愈大,循环次数 愈少。
实验表明在静载荷下服从胡克定律的材料,只要应力不超 过比例极限 ,在动载荷下虎克定律仍成立且E静=E动.
动荷因数:
动响应 Kd 静响应
10 动荷载

F 牵引力: Nd = G + F ′ = ρ Axg + ρ Axa
a = ρ Axg (1 + ) g
② x位置处截面的动应力
l
n x
n
F′ G
FNd a = ρ xg (1 + ) σd = g A
x 数: 动荷因数:
a = ρ lg (1 + ) = K d σ st max g
相应的应力(一般称为动应力 动应力)为 动应力
M Aρ g a l σd = = (1 + )( − b )l W 2W g 4
当加速度 a 为零时,上式求得静载下的静应力 静应力为 静应力
Aρ g l σ st = ( − b )l 2W 4
F F
比较动应力与静应力两式 a σ d = σ st (1 + ) g
§10.4
杆件受冲击时的应力和变形
a
冲击物
冲击问题的特点: 冲击问题的特点
构件受到外力作用的时间很短,冲击物 的速度在很短的时间(瞬间)内发生很 大的变化,甚至降为零,冲击物得到一 个很大的负加速度 a
v
被冲击物
解决冲击问题的方法: 解决冲击问题的方法
精确计算十分困难, 近似但偏安全的方法——能量法
荷载由零缓慢增长至最终值,然后保持不变。 静载荷: 静载荷:
Static load
加载过程构件各点加速度很小,可略去不计。 荷载作用过程中随时间快速变化,或其本身 动载荷: 动载荷:
Dynamic load
不稳定(包括大小、方向),构件内各质点 加速度较大。
演示小车与弹簧的撞击
§10.2
动静法的应用
FNd
D 2 FNd = ∫0 qd dϕ ⋅ sin ϕ = qd D 2 2 2 强度校核准则 σ d = ρ v ≤ [σ ] qd D Aρ D 2 FNd = = ω 2 4 与横截面积 A 无关。因此要 FNd ρ D 2 2 减小应力,应减小圆环的线 2 σd = = ω = ρv 速度(或转速)。 A 4
材料力学课件-动载荷

材料力学课件-动载荷
材料力学课件-动载荷是一门关于结构承受动态荷载的力学课程。本课程包括 动载荷的定义、分类以及动力学分析的方法与应用等内容。
引言
动载荷是指作用在结构上的具有变化的力、加速度或位移。了解动载荷的特 点对于结构设计与分析至关重要。
单自由度系统动力学
1
自由振动
当结构受到激励时,会出现自由振动,即结构围绕着自身固有频率振动。
2
非自由振动
在存在阻尼的情况下,结构会出现非自由振动,时间的影响让振动不再是简单的周期 性。
3
减振措施
为了减少结构的振动响应,可以采取各种减振措施,例如引入阻尼器或减振器。
多自由度系统动力学
简化模型
多自由度系统可以用简化模型 进行分析,将结构转化为一系 列简谐振动的叠加。
模态分析
通过模态分析可以确定结构的 固有频率和振型,对于地震分 析和结构设计至关重要。
结构地震响应
地震动的特点
地震动具有复杂的时程特征, 包括频率、幅值、相位和持 续时间等方面的变化。
结构地震响应分析
通过结构地震响应分析可以 评估结构在地震作用下的振 动性能和安全性,以指导工 程设计与抗震设计。
结构抗震设计原则
结构抗震设计的原则包括提 高结构的刚度和强度、控制 位移和引入阻尼等方面的考 虑。
1 冲击响应定义
冲击响应是指结构在突然受到冲击载荷时的振动响应,常见于爆炸、碰撞或地震等情况。
2 冲击响应的计算
通过冲击响应计算可以预测结构在冲击载荷下的应力、变形和破坏情况,以评估结构的 安全性。
3 冲击响应的控制措施
为了减少冲击响应的影响,可以采取一些控制措施,如增加结构的刚度和引入冲击吸收 器。
地震反应分析
材料力学课件-动载荷是一门关于结构承受动态荷载的力学课程。本课程包括 动载荷的定义、分类以及动力学分析的方法与应用等内容。
引言
动载荷是指作用在结构上的具有变化的力、加速度或位移。了解动载荷的特 点对于结构设计与分析至关重要。
单自由度系统动力学
1
自由振动
当结构受到激励时,会出现自由振动,即结构围绕着自身固有频率振动。
2
非自由振动
在存在阻尼的情况下,结构会出现非自由振动,时间的影响让振动不再是简单的周期 性。
3
减振措施
为了减少结构的振动响应,可以采取各种减振措施,例如引入阻尼器或减振器。
多自由度系统动力学
简化模型
多自由度系统可以用简化模型 进行分析,将结构转化为一系 列简谐振动的叠加。
模态分析
通过模态分析可以确定结构的 固有频率和振型,对于地震分 析和结构设计至关重要。
结构地震响应
地震动的特点
地震动具有复杂的时程特征, 包括频率、幅值、相位和持 续时间等方面的变化。
结构地震响应分析
通过结构地震响应分析可以 评估结构在地震作用下的振 动性能和安全性,以指导工 程设计与抗震设计。
结构抗震设计原则
结构抗震设计的原则包括提 高结构的刚度和强度、控制 位移和引入阻尼等方面的考 虑。
1 冲击响应定义
冲击响应是指结构在突然受到冲击载荷时的振动响应,常见于爆炸、碰撞或地震等情况。
2 冲击响应的计算
通过冲击响应计算可以预测结构在冲击载荷下的应力、变形和破坏情况,以评估结构的 安全性。
3 冲击响应的控制措施
为了减少冲击响应的影响,可以采取一些控制措施,如增加结构的刚度和引入冲击吸收 器。
地震反应分析
动载荷

H L L a
2.88 Fd K d Fst 6.05 8.71kN 2
(2)柱的稳定性校核
i1 I1 a 25 mm, 40, A1 i1
s P
σcr=373-2.15λ=373-2.15*40=289MPa
Fcr 289 10 10
Pa Δst 3EI
A (b)
st max
max
W
Fa W
于是,杆在危险点处的冲击应力 d 为
d max K d st max
v 2 Fa gΔst W
§14—5 提高构件抵抗冲击能力的措施
工程上常利用冲击进行锻造、冲压、打桩以及粉 碎等,这时就需要尽量降低冲击应力,以提高构件抗冲 击的能力。
2QL(h d ) 2 st (h d ); 2 d 2 st d 2 st h 0 EA
2 d
d
( 2 st ) (2 st ) 2 4( 2 st h) 2
2h st (1 1 ) st
d 2h 1 1 动荷系数—— K d st st
§14—6 材料的动力强度和冲击韧度
由于冲击时材料变脆变硬, s和 b随冲击速度而变化, 因此工程上不用 s和 b,而用冲击韧度(ductility)来衡量材 料的抗冲击能力。
W G ( H 0 H1 ) K A A
冲击韧度是在冲击试验机上测定的,通常做的Fra bibliotek冲击弯曲试验。
冲击韧度 K 的单位为焦耳/毫米2,是材料的性能指标之一
(4)动应力、动变形 Q Fd h Δd Q Δj
Q d K d j K d ; A QL (Ld K d Lst K d ) EA
2.88 Fd K d Fst 6.05 8.71kN 2
(2)柱的稳定性校核
i1 I1 a 25 mm, 40, A1 i1
s P
σcr=373-2.15λ=373-2.15*40=289MPa
Fcr 289 10 10
Pa Δst 3EI
A (b)
st max
max
W
Fa W
于是,杆在危险点处的冲击应力 d 为
d max K d st max
v 2 Fa gΔst W
§14—5 提高构件抵抗冲击能力的措施
工程上常利用冲击进行锻造、冲压、打桩以及粉 碎等,这时就需要尽量降低冲击应力,以提高构件抗冲 击的能力。
2QL(h d ) 2 st (h d ); 2 d 2 st d 2 st h 0 EA
2 d
d
( 2 st ) (2 st ) 2 4( 2 st h) 2
2h st (1 1 ) st
d 2h 1 1 动荷系数—— K d st st
§14—6 材料的动力强度和冲击韧度
由于冲击时材料变脆变硬, s和 b随冲击速度而变化, 因此工程上不用 s和 b,而用冲击韧度(ductility)来衡量材 料的抗冲击能力。
W G ( H 0 H1 ) K A A
冲击韧度是在冲击试验机上测定的,通常做的Fra bibliotek冲击弯曲试验。
冲击韧度 K 的单位为焦耳/毫米2,是材料的性能指标之一
(4)动应力、动变形 Q Fd h Δd Q Δj
Q d K d j K d ; A QL (Ld K d Lst K d ) EA
动荷载的概念

工程实际中的动荷载很多,通常遇到的动荷载有如下几类: 1)作加速运动或匀速转动的系统中构件的惯性力。例如,起 重机加速起吊重物时吊索受到的惯性力,飞轮作等速转动时其轮缘 受到的惯性力等。目录动Fra bibliotek载\动荷载的概念
2)冲击荷载或突加荷载。这种荷载的特点是能在某一瞬时内 就把荷载加在被冲击物上。例如,锤对桩的冲击力,波浪对堤岸的 冲击力,炸药对物体的爆破力,地震对建筑物的作用力等。
目录
力学
3)周期性荷载。这种荷载的特点是其大小和方向都随时间作 周期性的变化。例如,厂房内的机器在运转时对厂房建筑的周期性 作用力等。
在大部分的情况下,构件受动荷载作用所产生的动应力要比受 数值相同的静荷载作用所产生的静应力大得多,因而动荷载对构件 的破坏性要大得多,必须认真对待。
本章仅讨论两类简单的动荷载问题:构件作匀加速直线运动或 匀速转动,以及受冲击时的动应力计算,对求解动荷载问题的基本 原理和动应力的计算方法作简单介绍。
力学
动荷载\动荷载的概念
动荷载的概念
前面各章研究了构件在静荷载作用下的强度、刚度和稳定性计 算问题。所谓静荷载是指从零缓慢地增加到某一固定值,不再随时 间变化(或变化很小)的荷载。构件受静荷载作用所产生的应力和 变形称为静应力和静变形。若构件处于加速运动状态或静止的构件 受到处于运动状态的物体的作用时,即构件受到随时间变化的荷载, 构件在变形过程中,各质点的加速度相当显著,以致对变形和应力 的影响不能忽略,象这样的荷载称为动荷载。构件受动荷载作用所 产生的应力和变形称为动应力和动变形。
2)冲击荷载或突加荷载。这种荷载的特点是能在某一瞬时内 就把荷载加在被冲击物上。例如,锤对桩的冲击力,波浪对堤岸的 冲击力,炸药对物体的爆破力,地震对建筑物的作用力等。
目录
力学
3)周期性荷载。这种荷载的特点是其大小和方向都随时间作 周期性的变化。例如,厂房内的机器在运转时对厂房建筑的周期性 作用力等。
在大部分的情况下,构件受动荷载作用所产生的动应力要比受 数值相同的静荷载作用所产生的静应力大得多,因而动荷载对构件 的破坏性要大得多,必须认真对待。
本章仅讨论两类简单的动荷载问题:构件作匀加速直线运动或 匀速转动,以及受冲击时的动应力计算,对求解动荷载问题的基本 原理和动应力的计算方法作简单介绍。
力学
动荷载\动荷载的概念
动荷载的概念
前面各章研究了构件在静荷载作用下的强度、刚度和稳定性计 算问题。所谓静荷载是指从零缓慢地增加到某一固定值,不再随时 间变化(或变化很小)的荷载。构件受静荷载作用所产生的应力和 变形称为静应力和静变形。若构件处于加速运动状态或静止的构件 受到处于运动状态的物体的作用时,即构件受到随时间变化的荷载, 构件在变形过程中,各质点的加速度相当显著,以致对变形和应力 的影响不能忽略,象这样的荷载称为动荷载。构件受动荷载作用所 产生的应力和变形称为动应力和动变形。
动荷载

13/63
动载荷
10-4 构件受冲击时的应力和变形
动载荷
动载荷
动能改变:T=T 势能改变:V=Q d 弹簧应变能: Vεd 机械能守恒定律
动能 T
Q
Q
d
动能 0
T V Vεd
1 Vεd Fd d 2
Fd
d
动载荷
若Q以静载的方式作用在构件上,构件有静变形和静应力为st 、△ st 在动载Fd作用在构件上,构件有动变形和动应力为d、△ d 在线弹性范围内:
Fd d d Q st st P d d Q d Fd P st , st st
1 Vεd Fd d 2
1 Q Vεd P 2 st
2 d
动载荷
T=T V=Q d
1 Vεd P Q 2 st
2 d
T V Vεd
2T st d 2 st d 0 d st (1 Q P
2
1
2T ) P st Q
冲击动荷因素
动载荷
Q
自由落体冲击问题
h
=Qh
v
or
19/63
动载荷
动载荷
动载荷
若无弹簧,许可高度 为多少?
9.56mm
动载荷 例题10 图示分别为不同支承的钢梁,承受相同的重物冲
动载荷
Fd 2 D 2 d A 4g
y
qd ( D d ) 2
D v 2
圆环轴线上点的 线速度
FNd Rd
qd d
d
2
g
o
FNd
强度条件 d
v
g
2
[ ]
动载荷
10-4 构件受冲击时的应力和变形
动载荷
动载荷
动能改变:T=T 势能改变:V=Q d 弹簧应变能: Vεd 机械能守恒定律
动能 T
Q
Q
d
动能 0
T V Vεd
1 Vεd Fd d 2
Fd
d
动载荷
若Q以静载的方式作用在构件上,构件有静变形和静应力为st 、△ st 在动载Fd作用在构件上,构件有动变形和动应力为d、△ d 在线弹性范围内:
Fd d d Q st st P d d Q d Fd P st , st st
1 Vεd Fd d 2
1 Q Vεd P 2 st
2 d
动载荷
T=T V=Q d
1 Vεd P Q 2 st
2 d
T V Vεd
2T st d 2 st d 0 d st (1 Q P
2
1
2T ) P st Q
冲击动荷因素
动载荷
Q
自由落体冲击问题
h
=Qh
v
or
19/63
动载荷
动载荷
动载荷
若无弹簧,许可高度 为多少?
9.56mm
动载荷 例题10 图示分别为不同支承的钢梁,承受相同的重物冲
动载荷
Fd 2 D 2 d A 4g
y
qd ( D d ) 2
D v 2
圆环轴线上点的 线速度
FNd Rd
qd d
d
2
g
o
FNd
强度条件 d
v
g
2
[ ]
第十章土在动荷载作用下的力学性质
பைடு நூலகம்
土在动荷载作用下的力学性质
2)土的压实特性 (1) 压实曲线性状
击实曲线是研究土的压实特性的基本关系图。从图中可见, 击实曲线上有一峰值,此处的干容重为最大,称为最大干容 重。与之对应的制备土样含水量则称为最佳含水量。
(2) 土类对压实特性的影响
土在动荷载作用下的力学性质
土在动荷载作用下的力学性质
➢(3) 可以查出液化时大体积饱和土中实际孔隙水压力的分布。
➢(4) 在振动时能用肉眼观察试样。
土在动荷载作用下的力学性质
6)离心模型试验 离心机模型试验首先需要根据试验研究的目的和要求,选
择适合的用于单向或双向振动试验的模型箱,然后与静力离心 模型试验一样需要综合考虑离心机的容量、原型的尺寸、模型 箱尺寸和观测仪器的布置等,合理确定模型比尺。理想的模型 箱应该具备的条件 :
土在动荷载作用下的力学性质
10.1 概述
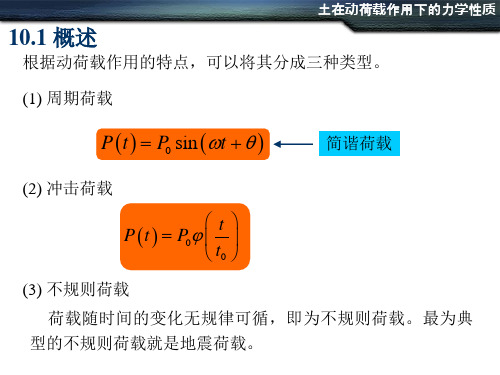
根据动荷载作用的特点,可以将其分成三种类型。
(1) 周期荷载
Pt P0 sin t
简谐荷载
(2) 冲击荷载
P
t
P0
t t0
(3) 不规则荷载 荷载随时间的变化无规律可循,即为不规则荷载。最为典
型的不规则荷载就是地震荷载。
10.2 土的动强度和变形特性
2)《公路工程抗震设计规范》判别方法 在《公路工程抗震设计规范》(JTJ004-89)中,砂性土液化 判别公式是以Seed H B的液化判别图 / v ~ N1 曲线族中震级 M=7.5的分界线为基础换算得到的,对地面以下20m 深度范 围内的砂土和亚砂土,其液化判别公式如下:
N1 Cn N63.5
Nc
11.8
1
13.06
土在动荷载作用下的力学性质
2)土的压实特性 (1) 压实曲线性状
击实曲线是研究土的压实特性的基本关系图。从图中可见, 击实曲线上有一峰值,此处的干容重为最大,称为最大干容 重。与之对应的制备土样含水量则称为最佳含水量。
(2) 土类对压实特性的影响
土在动荷载作用下的力学性质
土在动荷载作用下的力学性质
➢(3) 可以查出液化时大体积饱和土中实际孔隙水压力的分布。
➢(4) 在振动时能用肉眼观察试样。
土在动荷载作用下的力学性质
6)离心模型试验 离心机模型试验首先需要根据试验研究的目的和要求,选
择适合的用于单向或双向振动试验的模型箱,然后与静力离心 模型试验一样需要综合考虑离心机的容量、原型的尺寸、模型 箱尺寸和观测仪器的布置等,合理确定模型比尺。理想的模型 箱应该具备的条件 :
土在动荷载作用下的力学性质
10.1 概述
根据动荷载作用的特点,可以将其分成三种类型。
(1) 周期荷载
Pt P0 sin t
简谐荷载
(2) 冲击荷载
P
t
P0
t t0
(3) 不规则荷载 荷载随时间的变化无规律可循,即为不规则荷载。最为典
型的不规则荷载就是地震荷载。
10.2 土的动强度和变形特性
2)《公路工程抗震设计规范》判别方法 在《公路工程抗震设计规范》(JTJ004-89)中,砂性土液化 判别公式是以Seed H B的液化判别图 / v ~ N1 曲线族中震级 M=7.5的分界线为基础换算得到的,对地面以下20m 深度范 围内的砂土和亚砂土,其液化判别公式如下:
N1 Cn N63.5
Nc
11.8
1
13.06
10 动荷载

例: 汽轮机叶片在工作时通常 顶 要发生拉伸、扭转和弯曲的组 部 合变形。本题计算在匀速转动 时叶片的拉伸应力和轴向变形。 设叶片可近似地简化为变截面 叶 直杆, 且横截面面积沿轴线按 根 线性规律变化。叶根的横截面 面积A0为叶顶的横截面面积A1 的两倍, 即A0=2A1。令叶根和 叶顶的半径分别为R0和R1。转 速为 w, 材料单位体积的质量 为 r 。试求叶片根部的应力和 总伸长。
动能无变化: T=0
AB增加的应变能:
B
Δd
h
B
1 Vεd Pd d 2
根据能量守恒定理:
1 V P(h d ) Vεd Pd d 2
1 P h d Pd d 2 Pd l d EA EA Pd d l 1 1 EA 2 Vεd Pd d ( ) d 2 2 l P l 令st EA EA P st l 2 d 2st d 2st h 0
v h 2g
2h v2 Kd 1 1 1 1 st g st
3.若已知冲击物自高度h处以初速度v下落,则
2
v 2 v0 2 2 gh
2 v2 v0 2 gh Kd 1 1 1 1 g st g st
例: 图示分别为不同支承的钢梁, 承受相同的重物冲击, 已知弹簧刚度k=100 kN/m, h=50 mm, G=1 kN, l=3 m, 钢梁的I=3.04×107 mm4, W=3.09×105 mm3, E= 200 GPa。试比较两者的冲击应力。
3) 过程中只有势能, 动能与应变能的转化, 略去 其它能量的损失。
例: 一重量为P的重物由高度为h的位置自由下落,与一 块和直杆AB相连的平板发生冲击。杆的横截面面积为 A。求: 杆的冲击应力。 解: 重物是冲击物, 杆AB(包 括圆盘)是被冲击物。 冲击物减少的势能:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
m
r Ag
m
FNd K d FNst
x
r Ag r Aa
x
绳索中的动应力为
d
FNd A
Kd
FNst A
K d st
P
P
P g
a
st为静荷载下绳索中的静应力
强度条件为 d K d st [ ]
(Dynamic Loading)
△d表示动变形 △st表示静变形
T,V 是 冲击物 在冲击过程中所 减少的 动能和势能. Vεd是被冲击物所增加的应变能.
(Dynamic Loading)
一、自由落体冲击问题(Impact problem about the free falling body) 假设 (Assumption)
1.冲击物视为刚体,不考虑其变形 (The impacting body is rigid); 2.被冲击物的质量远小于冲击物的质量,可忽略不计 (The mass of the impacted deformable body is negligible in comparison with the impacting mass); 3.冲击后冲击物与被冲击物附着在一起运动 (The impact body do not rebound); 4.不考虑冲击时热能的损失,即认为只有系统动能与势能的转化 (The loss of energy of sound light heat ect. in the process of impact is lost in the impact).
当材料中的应力不超过比 例极限时荷载与变形成正比
m
r Ag
F Nst
m
F Nd
x
r Ag r Aa
d K d st
P
P
P g
a
结论:只要将静载下的应力,变形,乘以动荷系数Kd即得动载 下的应力与变形.
(Dynamic Loading)
例题2 起重机丝绳的有效横截面面积为A, [] =300MPa, 物体单
(Dynamic stress of the rotating member) 例题4 一平均直径为D的薄圆环,绕通过其圆心且垂于环平面的 轴作等速转动.已知环的角速度为 ,环的横截面面积为A,材料的 单位体积质量为r.求圆环横截面上的正应力.
O r
(Dynamic Loading)
解:
O r
可近似地简化为变截面直杆,且横截面面积沿轴线按线性规律变
化.叶根的横截面面积A0为叶顶的横截面面积A1的两倍, 即A0= 2 A1.令叶根和叶顶的半径分别为R0 和R1 .转速为 , 材料单位体积 的质量为r.试求叶片根部的应力和总伸长.
(Dynamic Loading)
解:设距叶根为 x 的横截面
T 0
V P ( h d ) Vεd
1 2 Fd d 1 2 Fd d
(Dynamic Loading)
重物P从高度为h处自由落下, P
冲击到弹簧顶面上,然后随弹簧一 起向下运动.当重物P的速度逐渐 降低到零时,弹簧的变形达到最大 值Δd,与之相应的冲击载荷即为Fd.
h v
P
h
(Dynamic Loading)
根据能量守恒定律可知,冲击物 所减少的动能T和势能V,应全部转换 为弹簧的变形能 Vεd ,即 T V Vεd 其中 所以
FNd
FNd (G ql )(1
a g
)
(2)动应力
lq(1+a/g)
d
FNd A
1
4
1 A
(G ql )(1
3
a g
)
2 9.8 )
2.9 10
( 50 10 25.5 60)(1
G(1+a/g)
214MPa [ ] 300MPa
(Dynamic Loading) 二、转动构件的动应力
(Dynamic Loading)
二、动响应 (Dynamic response)
构件在动载荷作用下产生的各种响应(如应力、应变、位
移等),称为动响应(dynamic response). 实验表明 在静载荷下服从胡克定律的材料,只要应力不超过
比例极限,在动载荷下胡克定律仍成立且E静=E动.
三、动荷因数 (Dynamic factor)
面上绕O点旋转,已知许用应力[],求转臂的截面面积(不计转
臂自重) 解:
(1)受力分析如图
FG
惯性力为
O
FG man Rm lG/g
2 2
(2)强度条件
l
FG / A
A FG [ ]
Gl
2
(g[ ])
(Dynamic Loading)
例题6 轮机叶片在工作时通常要发生拉伸,扭转和弯曲的组合变 形.本题只计算在匀速转动时叶片的拉伸应力和轴向变形. 设叶片
(Dynamic Loading)
机械能守恒定律
冲击时,冲击物在极短的时间间隔内速度发生很大的变化,其 加速度a很难测出,无法计算惯性力, 故无法使用动静法.在实用计 算中,一般采用能量法. 即在若干假设的基础上,根据能量守恒定律 对受冲击构件的应力与变形进行偏于安全的简化计算.
T V Vεd
强度条件 dmax K d stmax [ ]
(Dynamic Loading)
例题3 起重机钢丝绳长60m,名义直径28cm,有效横截面面积A=2. 9cm2 ,单位长重量q=25. 5N/m , [] =300MPa, 以a=2m/s2的加速度 提起重50kN 的物体,试校核钢丝绳的强度. 解:(1)受力分析如图
x r
l 2
( R 0 )A( )d
叶 根
m-m截面上的轴力FNx等于 F
FNx
R0
x
l
r 2 ( R0 ) A( )d
转 轴
(Dynamic Loading)
最大的惯性力发生在叶根截面上
FNmax r A0 [
2
l
2
3 4
顶 部
x d m m x dF
惯性力(Inertia force): 大小等于质点的质量m与加速度a
的乘积,方向与 a 的方向相反,即 F= -ma
(Dynamic Loading) 一、直线运动构件的动应力(Dynamic stress of the body in the straight-line motion)
例题1 一起重机绳索以加速度 a 提升 一重为 P 的物体,设绳索的横截面面积为 A,绳索单位体积的质量r,求距绳索下端为 x 处的 m-m 截面上的应力.
m-m 的面积为A(x)
1 x A( x ) A0 (1 ) 2 l
顶 部 d m 叶 根 m x l
在距叶根为 处取长为d 的微元,其质量应
dm r A( )d
R1 R0
转 轴
(Dynamic Loading)
在距叶根为 处的向心加速度为
2 an ( R0 )
d
D 2
Fd A
v
r D
2
2
y
qd ( D 2 d )
4
圆环轴线上点的 线速度
2
qd Fd d
d rv
强度条件
o
FNd FNd
d
rv
g
2
[ ]
环内应力与横截面面积无关.要保证强度,应限制圆环的转速.
(Dynamic Loading)
例题5 重为G的球装在长L的转臂端部,以等角速度在光滑水平
2012-6-4
(Dynamic Loading)
§10-1 概述(Instruction)
一、基本概念 (Basic concepts)
1、静荷载(Static load) 荷载由零缓慢增长至最终值,然后保持不变.构件内各质点加 速度很小,可略去不计. 2、动荷载 (Dynamic load) 荷载作用过程中随时间快速变化,或其本身不稳定(包括大 小、方向),构件内各质点加速度较大.
顶 部
d m m x l
dm 的惯性力应为
dF 2( R0 ) dm
叶 根
R1 R0
r ( R 0 ) A( )d
2
转 轴
(Dynamic Loading)
m-m以上部分的惯性力为
F
顶 部 x d m m x l m R1 m FNx dF
dF
π
D 2
)
2
Ar D
2
y
qd ( D 2 d )
2
d
Fd
0 qd ( 2 d ) sin
Ar D
2 2
D
qd
Fd
4 Ar D
2 2
0 sin d
π
O
FNd FNd
2
FNd
Fd 2
Ar D
2
2
4
d
FNd A
r D
2
2
4
(Dynamic Loading)
位体积的质量r, 以加速度a上升,试校核钢丝绳的强度. 解:(1)受力分析如图 惯性力 qG rAa
a l
x
a FNd qst qG
FNd ( qst qG ) x rAgx (1
rx (1 ) A g a 动荷因数 K d 1 g
§10-2 动静法的应用 (The application for method of dynamic equilibrium)
