第9章+组合变形
工程力学 (杨庆生 崔芸 龙连春 著) 科学出版社 课后答案 第9章

m ( F ) 0 P 1 Q 0.5 0 Q 2 P
mA ( F ) 0 1.5Q 3.5P 5 FB 0 FB 1.3P mB ( F ) 0 1.5P 3.5Q 5FA 0 FA 1.7 P
课
P 2. 4 4 2. 4 9.6(kN m) 2 8 2 P =2.561(kN ) FN cos 2 2 22 2.42
w.
9.6
A
25
-
2.561
+
FN (kN
25
z
co
)
FQ D2
M
M 图( kN .m )
m
P/2
补充 2: 水塔盛满水时连同基础总重量为 G, 在离地面 H 处, 受一水平风力合力为 P 作用, 圆形基础直径为 d,基础埋深为 h,若基础土壤的许用应力[σ]=300kN/m ,试校核基础的承载
梁上各横截面上轴力弯矩均为常2510253应力分析判危险点如右所示图整个横截面上均有n引起的均布的拉应力my引起后拉前压的弯曲应力mz引起上拉下压的弯曲应力点于d100025pa1010101010206060mpa140mpa四点的应力值
课后答案网,用心为你服务!
大学答案 --- 中学答案 --- 考研答案 --- 考试答案 最全最多的课后习题参考答案,尽在课后答案网()! Khdaw团队一直秉承用心为大家服务的宗旨,以关注学生的学习生活为出发点, 旨在为广大学生朋友的自主学习提供一个分享和交流的平台。 爱校园() 课后答案网() 淘答案()
ww
w.
max
(4)强度计算选择槽钢的型号:
1)忽略轴力项的正应力,仅由弯曲项选槽钢的型号:
建筑力学 第9章 组合变形杆件的应力分析与强度计算

§9-1 组合变形的概念
一、组合变形的概念
前面几章研究了构件的基本变形: 轴向拉(压)、扭转、平面弯曲。
由两种或两种以上基本变形组合的情况称为组合变形
组合变形
斜弯曲 拉(压)弯组合变形 偏心拉伸(压缩)变形 弯扭组合变形
§9-1 组合变形的概念
斜弯曲:
压弯组合变形:
F
Fy
z
Fz
x
y
§9-1 组合变形的概念
M z max Wz
z
Fx x
Fy
y
F
设图示简易吊车在当小车运行到梁端D时,吊车横梁处于最 不利位置。已知小车和重物的总重量F=20kN, 钢材的许用应力[]=160MPa,暂不考虑梁的自重。 按强度条件选择横梁工字钢的型号。
C
2m
A
A
FAx FAy
30 3.46m
FBC
30 3.46m
解:1、横梁AD受力分析
z
F2
b
(最大拉应力)
l y
解:
h
z
l
F1
(最大压应力)y
§9-3 拉伸(压缩)与弯曲的组合变形
横向力与轴向力共同作用的组合变形 一、荷载分解
Fx F cos
z
Fx x
Fy
y
F
Fy F sin
§9-3 拉伸(压缩)与弯曲的组合变形
二、内力计算 a
z
Fx F cos
Fx Fy F sin
解:1、荷载分解
q
qy q cos 800 0.894 714 N / m A
B
L
qz q sin 800 0.447 358 N / m
材料力学-单祖辉-第三版课后答案-(第九章—第十九章)

3Fx 4a 2
[
]
x2 0.1277x6.39104 0
由此得切口的允许深度为
x5.20 mm
10-3 图示矩形截面钢杆,用应变片测得上、下表面的纵向正应变分别为 εa =1.0×10-3
2Sz(a)
S z,max
[2.23104
1 0.0085(0.140 0.0137)2 ]m3 2
2.90104 m3
式中:足标 b 系指翼缘与腹板的交界点;足标 a 系指上翼缘顶边中点。 3.应力计算及强度校核
三个可能的危险点( a , b 和 c )示如图 9-5。
a 点处的正应力和切应力分别为
x1
4F πD 2
x2 0
设圆柱体与外管间的相互作用力的压强为 p,在其作用下,外管纵截面上的周向正应力为
t2
pD 2
(a)
在外压 p 作用下(图 b,尺寸已放大),圆柱体内任一点处的径向与周向正应力均为
r1 t1 p
根据广义胡克定律,圆柱体外表面的周向正应变为
t1
1 E1
t1
1
x1
松比 均为已知。试求内压 p 与扭力偶矩 M 之值。
题 9-14 图 解:圆筒壁内任意一点的应力状态如图 9-14 所示。
图中所示各应力分量分别为
图 9-14
由此可得
x
pD 4
,
t p2D,
2M πD2
σ0 σ x , σ90 σt ,
σ 4 5
τ
3pD, 8δ
根据广义胡克定律,贴片方向的正应变为
σ1
σ2
σt
pD,σ 4δ
3
0
9-13 图示组合圆环,内、外环分别用铜与钢制成,已知铜环与钢环的壁厚分别为
中国民航大学 2024 年研究生招生考试大纲 804材料力学

材料力学 804一、参考教材:《材料力学I、II》,第四版,高等教育出版社,单辉祖编著。
二、课程内容的基本要求:第一章:绪论第二章:轴向拉压应力第三章:轴向拉压变形第四章:扭转第五章:弯曲内力第六章:弯曲应力第七章:弯曲变形第八章:应力分析和强度理论第九章:组合变形第十章:压杆稳定第十一章:能量方法第十二章:动载荷第十三章:应力分析的实验方法三、应该掌握的内容和重点内容第一章绪论材料力学的任务、基本概念,变形体的基本假设,杆件变形的基本形式。
第二章轴向拉压应力1、轴向拉(压)的概念、内力、截面法、轴力的计算和轴力图的画法。
2、轴向拉(压)杆件横截面及斜截面上的应力计算;许用应力;强度条件及应用。
3、材料在拉伸、压缩时的机械性能。
4、剪切面、挤压面的概念及其判定;剪应力和挤压的公式及其计算。
重点:1、轴力及轴力图的画法。
2、拉(压)应力及强度计算。
3、材料的主要性能。
第三章轴向拉压变形1、轴向拉(压)杆件的变形,纵向变形、弹性模量、抗拉刚度、横向变形、泊松比等概念;虎克定律及其应用。
2、桁架节点位移计算。
3、简单静不定问题的计算。
重点:1、轴向拉(压)变形计算。
2、静不定问题的分析和计算。
第四章扭转1、外力扭矩的计算,扭矩、扭矩图。
2、圆轴扭转时横截面上的应力分布和计算;强度条件及其应用。
3、圆轴扭转时变形和刚度计算;材料的扭转破坏实验。
4、扭转静不定问题的计算。
重点:1、圆轴扭转应力和强度计算。
2、圆轴扭转变形和刚度计算。
3、简单扭转静不定的计算。
第五章弯曲内力1、平面弯曲、剪力、弯矩的概念。
2、剪力方程、弯矩方程的列法;剪力图与弯矩图的画法。
3、利用微分关系画剪力图和弯矩图。
重点:剪力图与弯矩图的画法。
第六章弯曲应力1、纯弯曲的概念和平面假设;平面图形的几何性质。
2、弯曲正应力公式及应用;弯曲剪应力计算。
3、弯曲强度计算;提高梁的强度的主要措施。
重点:弯曲正应力分析与强度计算。
第七章弯曲变形1、挠度、转角及其关系;挠曲线微分方程式;积分法、叠加法求梁的变形。
材料力学_陈振中_习题第九章组合变形
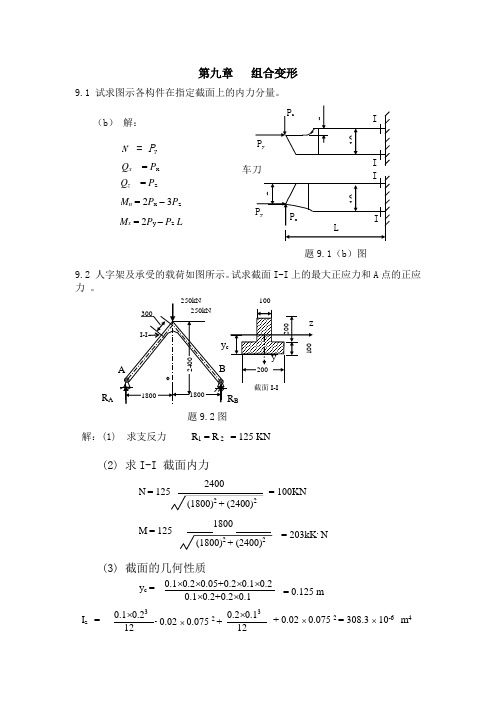
第九章组合变形9.1 试求图示各构件在指定截面上的内力分量。
9.2 人字架及承受的载荷如图所示。
试求截面I-I上的最大正应力和A点的正应力9.3 图示起重架的最大起吊重量(包括行走小车等)为P = 40kN ,横梁AC 由两根No.18槽钢组成,材料为A3钢,许用应力[σ] = 120 MPa 。
试校核横梁的强度。
9.7 图示短柱受载荷P 和H 的作用,试求固定端截面上角点A 、B 、C 及D 的正应力,并确定其中性轴的位置。
9.14 图为操纵装置水平杆,截面为空心圆形,内径d = 24 mm,外径D = 30 mm。
材料为A3钢,[σ] = 100 MPa。
控制片受力P1= 600 N。
试用第三强度理论校核杆的强度。
9.17图示皮带轮传动轴,传递功率N = 7kW,转速n =200r/min。
皮带轮重量Q = 1.8kN。
左端齿轮上啮合力Pn与齿轮节圆切线的夹角(压力角)为200。
轴的材料为A5钢,其许用应力[σ] = 80 MPa。
试分别在忽略和考虑皮带轮重量的两种情况下,按第三强度理论估算轴的直径。
9.19 飞机起落架的折轴为管状截面,内径d =70 mm ,外径D = 80 mm 。
材料的许用应力[σ] = 100 MPa ,试按第三强度理论校核折轴的强度。
若P = 1 kN ,Q = 4 kN 。
9.24 端截面密封的曲管的外径为100mm ,壁厚t = 5mm ,内压p = 8MPa 。
集中力P = 3kN 。
A 、B 两点在管的外表面上,一为截面垂直直径的端点,一为水平直径的端点。
试确定两点的应力状态。
解:在内压p 作用下,B 点应力状态分别如图9.24a ,b 所示。
σp1 = pD/(2t) = 8⨯100/(2⨯5) = 80 MPa, σp2 = pD/(4t) = 40 MPa 在集中力P 作用下,曲管受弯扭组合变形,A 点和B 点应力状态分别如图9.24c ,d 所示。
第9章组合变形

— 43 —第9章组合变形[本章重点]明确叠加原理的应用条件,杆件在拉(压)弯组合、弯扭组合变形下的强度计算。
[本章难点](1)将组合变形分解为若干基本变形。
所涉及方法有:载荷分解法、截面法和内力分解法。
(2)确定危险面、危险点。
因组合变形的构件各内力分量不一定在同一截面上达到最大值,所以对内力较大、截面较小的截面都应该列为可能的危险面并进行试算。
可能的危险点应是可能的危险截面上产生最大应力的点。
注意在较复杂的组合变形下杆件的危险截面、危险点常常不止一个。
并注意在组合变形中,一般情况下不计由剪力引起的剪应力,但要计由扭矩引起的剪应力。
[本章考点]组合变形下杆件的强度分析常常是必考内容。
主要涉及杆件拉(压)弯组合变形(含偏心拉压)的强度分析、弯扭组合变形的强度分析;也可能是其他基本变形组合情况下的强度分析。
[本章的习题分类与解题要点]本章计算题大致可分为4类:(1)拉(压)弯的组合变形。
应先画出杆件的轴力图和弯矩图,确定其危险截面,然后分别计算轴力和弯矩对应的正应力,并分别画出两类内力所对应的正应力分布图,再将其正应力叠加即可确定出危险点的位置。
而此类组合变形的危险点均为单向应力状态,故可直接利用强度条件进行强度计算。
(2)偏心拉压组合变形。
其本质为拉(压)弯的组合,常要求确定截面核心(在土木工程中)。
(3)圆截面轴的弯扭组合。
先画出轴的受力简图,并根据受力图画出轴的扭矩、弯矩图(对两个平面弯曲要计算合成弯矩),确定出危险截面。
这类轴常用塑性材料,可直接用扭矩和弯矩(合成弯矩)所表示的第三或第四强度理论进行强度计算。
(4)斜弯曲及其他形式的组合变形。
矩形截面杆弯弯组合变形的,可先分析横截面上的内力,判断杆件受到哪几种基本变形。
叠加危险面上各基本变形对应的应力。
若危险点处于单向应力状态或纯剪应力状态,则可分别直接用正应力和切应力表示强度条件进行强度计算;若危险点处于平面或空间的复杂应力状态,则还需计算三个主应力,并以此选择合适的强度条件或理论进行计算。
第九章 组合变形
一、是非题9.1 斜弯曲时,危险截面上的危险点是距形心主轴最远的点。
()9.2 工字形截面梁发生偏心拉伸变形时,其最大拉应力一定在截面的角点处。
()9.3 对于偏心拉伸或偏心压缩杆件,都可以采用限制偏心矩的方法,以达到使全部截面上都不出现拉应力的目的。
()9.4 直径为d 的圆轴,其危险截面上同时承受弯矩M 、扭矩T 及轴力N 的作用。
若按第三强度理论计算,则危险点处的9.5 图示矩形截面梁,其最大拉应力发生在固定端截面的a 点处。
()二、选择题9.6 图( a )杆件承受轴向拉力F ,若在杆上分别开一侧、两侧切口如图( b )、图( c )所示。
令杆( a )、( b )、( c )中的最大拉应力分别为和,则下列结论中()是错误的。
A. B.C. D.9.7 对于偏心压缩的杆件,下述结论中()是错误的。
A. 截面核心是指保证中性轴不穿过横截面的、位于截面形心附近的一个区域B. 中性轴是一条不通过截面形心的直线C. 外力作用点与中性轴始终处于截面形心的相对两边D. 截面核心与截面的形状、尺寸及载荷大小有关三. 计算题9.8材料为灰铸铁HT 15-33的压力机框架如图所示。
许用拉应力为,许用压应力为,试校核该框架立柱的强度。
9.9图示皮带轮传动轴,传递功率N =7kW ,转速n =200 r/min 。
皮带轮重量Q =1.8 kN 。
左端齿轮上啮合力与齿轮节圆切线的夹角(压力角)为。
轴的材料为A5钢,其许用应力。
试分别在忽略和考虑皮带轮重量的两种情况下,按第三强度理论估算轴的直径。
答案9.1 × 9.2 √ 9.3 × 9.4 √ 9.5 √ 9.6 C 9.7 D9.8解:9.9解:。
组合变形
第10章组合变形§10-1 组合变形的概念1.组合变形的概念组合变形:构件往往会发生两种或两种以上的基本变形的这类变形。
在前面各章分别讨论了杆件在拉(压)、剪切、扭转和弯曲基本变形时的应力和强度计算。
工程实际中,杆件在荷载作用下所发生的变形,经常是两种或两种以上基本变形的组合,这种变形称为组合变形。
例如图10.1(a)所示屋架檩条的变形,是由y/z两个方向的平面弯曲变形组成的斜弯曲;如图10.1(b)所示厂房柱,在偏心力F作用下,会发生压缩和弯曲的组合变形;如图10.1(c)所示的卷扬机轴在力F作用下,则发生弯曲和扭转的组合变行。
2.组合变形的分析方法及计算原理处理组合变形问题的方法:1.将构件的组合变形分解为基本变形;2.计算构件在每一种基本变形情况下的应力;3.将同一点的应力叠加起来,便可得到构件在组合变形情况下的应力。
叠加原理是解决组合变形计算的基本原理叠加原理应用条件:即在材料服从胡克定律,构件产生小变形,所求力学量定荷载的一次函数的情况下,计算组合变形时可以将几种变形分别单独计算,然后再叠加,即得组合变形杆件的内力、应力和变形。
计算原理:(1)圣维南原理以静力等效力系代替构件原有的荷载,为此,要求构件为细长杆,且所求应力的截面远离外力作用点;(2)叠加原理 按各基本变形计算后进行叠加,为此,要求构件处于线弹性范围内,且变形很小,可按构件的原始形状的尺寸进行计算。
在小变形和线弹性条件下,杆件上各种力的作用彼此独立,互不影响,即杆上同时有几种力作用时,一种力对杆的作用效果(变形或应力),不影响另一种力对杆的作用效果(或影响很小可以忽略)。
因此组合变形下杆件内的应力,可视为几种基本变形下杆件内应力的叠加。
本章中组合变形下杆件的应力计算,将以各基本变形的应力及叠加法为基础。
叠加法的主要步骤:a 、将组合变形按照各基本变形的条件,分解为几种基本变形,简称分解。
b 、利用基本变形的应力计算公式,分别计算各点处的正应力和切应力。
材料力学试卷及答案
材料⼒学试卷及答案⼀、低碳钢试件得拉伸图分为、、、四个阶段。
(10分)⼆、三⾓架受⼒如图所⽰。
已知F=20kN,拉杆BC采⽤Q235圆钢,[σ钢]=140MPa,压杆AB采⽤横截⾯为正⽅形得松⽊,[σ⽊]=10MPa,试⽤强度条件选择拉杆BC得直径d与压杆AB得横截⾯边长a。
(1n=180r/min,材料得许⽤切分)2六、单元体应⼒如图所⽰,试计算主应⼒,并求第四强度理论得相当应⼒。
(10分)e =200m⼋、图⽰圆杆直径d =100mm,材料为Q235钢,E =200GP a,λp =100,试求压杆得临界⼒F cr 。
(10《材料⼒学》试卷(1)答案及评分标准⼀、弹性阶段、屈服阶段、强化阶段、颈缩断裂阶段。
评分标准:各2、5分。
⼆、d=15mm ; a =34mm.评分标准:轴⼒5分, d 结果5分,a 结果5分。
三、τ=87、5MPa, 强度⾜够. 评分标准:T3分,公式4分,结果3分。
四、评分标准:受⼒图、⽀座反⼒5分,剪⼒图55分。
五、σmax =155、8M Pa]=100 M P,但没超过许⽤应⼒得5%,安全. 评分标准:弯矩5分, 3分,正应⼒公式5分结果2分。
六、(1)σ1=141、42 M Pa,σ=0,σ3=141、42 MP a;(2)σr 4=245 M Pa。
评分标准:主应⼒5分,相当应⼒5分。
七、σmax =0、64 MPa,σmin =-6、04 MPa 。
评分标准:内⼒5分,公式6分,结果4分。
⼋、F c r =53、39kN评分标准:柔度3分,公式5分,结果2分。
⼀、什么就是强度失效、刚度失效与稳定性失效?⼆、如图中实线所⽰构件内正⽅形微元,受⼒后变形为图中虚线得菱形,则微元得剪应变为?A 、B 、C、 D 、答案:D三、材料⼒学中得内⼒就是指( )。
A 、物体内部得⼒。
B 、物体内部各质点间得相互作⽤⼒。
C 、由外⼒作⽤引起得各质点间相互作⽤⼒得改变量。
D、由外⼒作⽤引起得某⼀截⾯两侧各质点间相互作⽤⼒得合⼒得改变量。
工程力学课第9章 拉伸与压缩
1.轴向拉伸或压缩 在一对方向相反、作用线与杆轴线重合的外 力作用下,杆件的主要变形是长度的改变,这种变形形式称为轴向 拉伸或轴向压缩。 2.剪切 在一对相距很近、大小相等、方向相反的横向外力作用 下,杆件的横截面 将沿外力作用方向发生错动,这种变形形式称为剪切。 3.扭转 在一对转向相反、作用面垂直于杆轴线的外力偶作用下, 杆的任意二横截面将发生相对转动,而轴线仍维持直线,这种变形 形式称为扭转。 4.弯曲 在一对转向相反、作用面在杆件的纵向平面(即包含杆 轴线在内的平面)内的外力偶作用下,杆件将在纵向平面内发生弯 曲,这种变形形式称为弯曲。 工程实际中的杆件可能同时承受不同形式的外力,常常同时发生两 种或两种以上的基本变形,这种变形情况称为组合变形。
(b)
图9.3 拉(压)杆计算简图
本章主要研究拉(压)杆的内力、应力及变形的计算。同时还将通过 拉伸和压缩试验,来研究材料在拉伸与压缩时的力学性能。
9.2 内力、轴力及轴力图 9.2.1 内力
如前所述,材料力学的研究对象是构件,对于所研究的构件而言, 其他物体作用于该构件上的力均为外力。 构件在受到外力作用而变形时,其内部各部分之间将产生相互作用 力,这种由外力的作用而引起的物体内部的相互作用力,称为材料 力学中所研究的内力。内力随着外力的变化而变化,外力增加,内 力也增加,外力去掉后,内力也将随之消失。显然,作用在构件上 的外力使其产生变形,而内力的作用则力图使受力构件恢复原状, 内力对变形起抵抗和阻止作用。由于假设了物体是连续均匀的,因 此在物体内部相邻部分之间相互作用的内力,实际上是一个连续分 布的内力系,而将分布内力系的合成结果(力或力偶),简称为内力。 在研究构件的强度、刚度、稳定性等问题时,经常需要知道构件在 已知外力作用下某一截面上的内力值。与理论力学中计算物系内力 的方法相仿,为了显示和计算某一截面上的内力,可在该截面处用 一假想的平面将构件截为两部分,取其中任一部分为研究对象,弃 去另一部分,将弃去部分对研究对象的作用以力的形式来表示,此 力就是该截面上的内力。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
FAx A yFAy
FC
FCy
FCx C
B xFAx A
F
yFAy
FC
FCy
FCx C
Bx
F
=
FAx A
A
FAy
FCx C
+ FCy
C
B
FN
B
FM
F
40 kN
12kN m
§9.2 拉伸(压缩)与弯曲的组合
例1最大吊重 F 8 kN 的起重机如图所示。若AB杆为工字钢,材
800
(2)考虑轴力的影响,进行强度校核 A
C
B
max
F A
Mmax W
40 103
12 103 FAx A
26.1104 141106
yFAy
100.5 MPa [ ]
FN
2500
1500
FC
FCy
FCx C
F
Bx
F
F
40 kN
取16号工字钢
M
12kN m
§9.2 拉伸(压缩)与弯曲的组合
料为A3钢,[ ] 100 MPa ,试选择工字钢型号。
解:2.确定危险截面
D
C截面为危险截面
800 A
C
B
3.选择截面
(1)W先mzm不aaxx考M[虑MmFA轴W]axm力zaxM的1W2影m0[a响cxm],3[选 ]择截F面AFx NAyFAy
2500
1500
FC
82.8MPa [ ]
500
500
6kN
1.6kN m
M -
1.5kN m
1.6kN m
+
T
二、双向弯曲与扭转强度计算
§9.4 扭转与弯曲的组合
例4 图示皮带轮传动轴,传递功率P=7kW,转速n=200r/min。皮
带轮G=1.8kN。左端齿轮上啮合力Fn与齿轮节圆切线的夹角为20o。 轴材料许用应力[ ]=80MPa,试按Tresca准则设计轴的直径。
二、双向弯曲与扭转强度计算 讨论: 1)对于圆轴,由于对称性,同一横截面上两个方向的弯矩 可以矢量合成,按单一弯矩计算:
MW
M
2 y
M
2 z
2)可以证明两平面弯矩图所有尖点间的合成弯矩图为凹曲 线,因此危险截面可能在两个平面弯矩图的所有尖点处
§9.4 扭转与弯曲的组合
T
T
2)作内力图(My、Mz 、T):
脆性材料: tmax [ t ]
cmax [ c ]
§9.2 拉伸(压缩)与弯曲的组合
例1最大吊重 F 8 kN 的起重机如图所示。若AB杆为工字钢,材
料为A3钢,[ ] 100 MPa ,试选择工字钢型号。
D
解:1. AB杆受力分析
800 A
C
B
lCD 2.52 0.82 2.62 m
2500
1500
MA 0
FC 42 kN
2.5 FCx FC 2.62 40 kN
0.8 FCy FC 2.62 12.8 kN
FAx A yFAy
FAx A
A
FAy
FC
FCy
FCx C
=
FCx C
+ FCy
C
F
Bx
F
B
B
F
§9.2 拉伸(压缩)与弯曲的组合 例1最大吊重 F 8 kN 的起重机如图所示。若AB杆为工字钢,材 料为A3钢,[ ] 100 MPa ,试选择工字钢型号。
FCy
FCx C
F
Bx
F
F
40 kN
取16号工字钢
M
Wz 141cm3 A 26.1cm2
12kN m
§9.2 拉伸(压缩)与弯曲的组合
例1最大吊重 F 8 kN 的起重机如图所示。若AB杆为工字钢,材
料为A3钢,[ ] 100 MPa ,试选择工字钢型号。
D
解: 3.选择截面
第四强度理论
1
Wz
M
2 A
TA2
[ ]
r4
2 3t 2 1
Wz
M
2 A
0.75TA2
[ ]
(四)选择强度条件
第三强度理论
r3
1 Wz
M 2 T 2 [ ]
第四强度理论
r4
1 Wz
M 2 0.75T 2 [ ]
M ——危险截面的弯矩
第九章 组合变形时的强度计算
第一节 组合变形与叠加原理 第二节 拉伸(压缩)与弯曲的组合 第三节 偏心压缩与截面核心* 第四节 扭转与弯曲的组合
第九章 组合变形时的强度计算
第一节 组合变形与叠加原理
一、工程实例 二、计算方法
一、工程实例 1.齿轮传动轴
F 啮合力
F m
2.烟囱
二、计算方法 1.叠加原理
ቤተ መጻሕፍቲ ባይዱ
z m Fa F
x
B
截面A为危险截面
Fa
§9.4 扭转与弯曲的组合
(二)应力
1t
(1)M对应的应力
MAy
Iz
z (2) T 对应的应力
x
t TA
IP
t2
y
(3) 叠加后,1点和2点为危险点
A z m Fa F 截面A为危险截面
x
B
y
M
Fl T
Fa
(三)危险点的应力状态
Fy
B
F
j x Fx
危险截面: 固定端A
FN A Fx M A Fyl
二、应力
z
§9.2 拉伸(压缩)与弯曲的组合
Fy F
cmax
y
FN
Fyl
x l
Fx
+
+
3M.z FNA和MA同时作用时
j x Fx
t max
1.FNA对应的应力分布
FN A Fx
小变形情况
由几个外力(变形)同时作用时所引起的构件内的某一参数 (内力、应力或位移等)
== 由各个外力(变形)单独作用时所引起的构件内的该一 参数的 矢量和或代数和
二、计算方法 2.强度计算的基本步骤:
分析组合变形是由那几种基本变形组合而成的
内力情况
危险截面 应力分析
危险点
应力状态(取单元体)
单向应力状态、纯剪切、复杂应力状态
第九章 组合变形时的强度计算
第二节 拉伸(压缩)与弯曲的组合
一、内力 二、应力 三、强度计算
z
l y
z
l y
+
z
l y
=
§9.2 拉伸(压缩)与弯曲的组合 Fy F
j x Fx
j xFx
Fy
x
j
简单拉压 平面弯曲
一、内力
A
z
l y
Fx单独作用时Fx
+
FFy单N 独作用时
Fyl
+ Mz
§9.2 拉伸(压缩)与弯曲的组合
B
解:4.强度条件
14
3
t max
F A
M z y1max Iz
8
63.6 MPa [t ]
cmax
M z y2max Iz
F A
63.0 MPa [c ]
Mz
F
FN
M
1 26 FF
Mz
F
F
+
F e
+
第九章 组合变形时的强度计算
第四节 扭转与弯曲的组合
一、单向弯曲与扭转强度计算
M 2 T 2 Wz
(3)
—圆轴的弯扭组合变形
§9.4 扭转与弯曲的组合
例3如图所示,悬臂梁直径d=30mm,材料为3号钢[]=85MPa,试
按第三强度理论较核梁的强度
解: 危险截面:C截面
A
3kN
C
B
r3
M
2 C
TC2
W
1.52 1.62 103
303 109 32
Iz 1078 mm4
A 57 mm2
y2max 7.55 mm
y2max
z
y1max
e 1 26 FF
Mz
F
Mz
F
F
+ FN
F e
M
+
3.内力分析
§9.2 拉伸(压缩)与弯曲的组合
例2 铸铁制作的螺旋夹具如图,已知材料的 [t ] 30 MPa ,
[c ] 60 MPa , F 300 N ,试3校核AB段的强度 A 1
§9.4 扭转与弯曲的组合
MW
M
2 y
M
2 z
r3
M
2 W
T
W
2
,
r4
M
2 W
0.75T
2
W
W是抗弯截面系数
FS1=2FS2 y
f300 D2 f500 D1
A
200 y T Fz Fy
C
D
B
z
400
200
G
FS2
Fy
G
Fz Fn 20o
T
x 解:1)作计算简图:
3FS2 G
T Fz D2 /2 (FS1 FS2 )D1 /2
