2020年秋季高二数学第一学期期初考试(生)
2020学年第一学期高二第一次月考数学试题

2020学年第一学期高二级月考数学试题注意事项:1.本试题共4页,四大题,18小题,满分130分(含附加题10分),考试时间90分钟,答案必须填写在答题卡上,在试题上作答无效,考试结束后,只交答题卡。
2.作答前,认真浏览试卷,请务必规范、完整填写答题卡的卷头。
3.考生作答时,请使用0.5mm黑色签字笔在答题卡对应题号的答题区域内作答。
第Ⅰ卷选择题(共50分)一、选择题(本大题共10小题,共50分)1.在△ABC中,已知A=75°,B=45°,b=4,则c=()A. √6B. 2C. 4√3D. 2√62.若a>b,c>d,则下列不等关系中不一定成立的是()A. a−b>c−dB. a+c>b+dC. a−c>b−cD. a−c<a−d3.已知△ABC中,AB=2,BC=3,AC=√10,则cosB=()A. √108B. √104C. 14D. 124.正项等比数列{a n}的前n项和为S n,若a1=3,S3=21,则公比q=()A.1B. 2C. 3D. 45.已知x>0,y>0,且1x+4y=1,则x+y的最小值为()A.6B. 8C. 9D. 126.已知数列{a n}是首项a1=4,公比q≠1的等比数列,且4a1,a5,−2a3成等差数列,则公比q等于()A. 12B. −1C. 2D. −27.任取实数x∈[−2,8],则所取x满足不等式x2−5x+6≤0的概率为()A. 18B. 19C. 110D. 1118.我国古代数学名著《九章算术》里有一道关于玉石的问题:“今有玉方一寸,重七两;石方一寸,重六两.今有石方三寸,中有玉,并重十一斤(176两).问玉、石重各几何?”如图所示的程序框图反映了对此题的一个求解算法,运行该程序框图,则输出的x,y分别为()A. 98,78B. 96,80C. 94,74D. 92,729.设等差数列{a n}前n项和为S n,等差数列{b n}前n项和为T n,若S nT n=20n−12n−1,则a3b3=()A. 595B. 11C. 12D. 1310.在△ABC中,若AB=√37,BC=4,C=2π3,则△ABC的面积S=()A.3√3B. 3√2C. 6D. 4第Ⅱ卷非选择题(共80分)二、填空题(本大题共2小题,共10分)11.若变量x,y满足约束条件{x+y⩾−12x−y≤1y⩽1,则z=3x−y的最小值为__________.12.已知数列{a n}满足a1=1,log2a n+1=log2a n+1,若a m=32,则m=________.三、解答题(本大题共5小题,共60分)13.(10分)解下列不等式:>1(1)3x2−7x+2>0 (2)2x+4x−314.(12分)设S n为等差数列{a n}的前n项和.已知a3=5,S7=49.(1)求数列{a n}的通项公式;(2)设b n=1,求数列{b n}的前n项和T n.a n a n+115.(12分)△ABC的内角A,B,C的对边分别为a,b,c,sin2B+sin2C−sin2A=sinBsinC.(1)求A;(2)若a=4,△ABC的面积为4√3,求b,c.16.(12分)在一次海上联合作战演习中,红方一艘侦察艇发现在北偏东45°方向,相距12nmile的水面上,有蓝方一艘小艇正以每小时10nmile的速度沿南偏东75°方向前进,若红方侦察艇以每小时14nmile的速度沿北偏东45°+α方向拦截蓝方的小艇,若要在最短的时间内拦截住,求红方侦察艇所需的时间和角α的正弦值.17.(14分)已知正项数列{a n}的前n项和为S n,对任意n∈N∗,点(a n,S n)都在函数f(x)=2x−2的图象上.(1)求数列{a n}的通项公式;(2)若数列b n=(2n−1)a n,求数列{b n}的前n项和T n.四、附加题(本大题共1小题,共10分)18.“我将来要当一名麦田里的守望者,有那么一群孩子在一块麦田里玩,几千万的小孩子,附近没有一个大人,我是说……除了我”《麦田里的守望者》中的主人公霍尔顿将自己的精神生活寄托于那广阔无垠的麦田.假设霍尔顿在一块成凸四边形ABCD的麦田里成为守望者,如图所示,为了分割麦田,他将BD连接,设ΔABD中边BD所对的角为A,ΔBCD中边BD所对的角为C,经测量已知AB=BC=CD=2,AD=2√3.霍尔顿发现无论BD多长,√3cosA−cosC为一个定值,请你验证霍尔顿的结论,并求出这个定值.。
2020-2021学年高二数学上学期学期初考试试题

2020-2021 学年高二数学上学 期学期初考试试题一、选择题(每小题 5 分,共 12 小题 60 分)1、已知实数 满足,则的大小关系是( )A.B.C.D.2、三点在同一条直线上,则 的值为( )A.B.C.D.3、若向量,分别表示两个力,则为( )A.B.C.D.4、若,,且,则 有( )A.最大值B.最小值C.最小值D.最小值5、已知,则 ( )A.B.C.D.6、数列 的通项,则数列的前 项和等于( )A.B.C.D.7、已知一个几何体的三视图如图所示,其中正视图、侧视图都是由半圆和矩形组成,根据图 中标出的尺寸,可得这个几何体的表面积是( )A. 8、过定点A.B.的直线与过定点的最大值为( )B.C. 的直线C.9、函数的一个单调增区间是()-1- / 9D. 交于点 ,则D.A.B.C.D.10、光线从点射出,经轴反射与圆则光线从 点到 点所经过的路程为( )A.B.C.11、如果一个等差数列前 项的和为 ,最后 项的和为列有( )A. 项B. 项C.相切,设切点为 ,D. ,且所有项的和为 ,则这个数项D. 项12、已知函数(,且)是上的减函数,则的取值范围是( )C.A.B.D.二、填空题(每小题 5 分,共 4 小题 20 分)13、一个三角形在其直观图中对应一个边长为 的正三角形,原三角形的面积为__________.14、已知两条直线 :,:,若 ∥ ,则=__________.15、若, 满足约束条件则 的最大值为__________.16、正四棱锥的所有棱长均相等, 是 的中点,那么异面直线 与 所成的角的余弦值等于__________.三、解答题(第 17 题 10 分,第 18 题 12 分,第 19 题 12 分,第 20 题 12 分,第 21 题 12 分,第 22 题 12 分,共 6 小题 70 分)17、已知 (1)求线段 (2)求、、.的中点坐标;的边 上的中线所在的直线方程.18、已知,,,设.(1)求的解析式及单调递增区间;(2)在中,角 , , 所对的边分别为 , , ,且,,,求的面积.-2- / 919、如图,已知 AB 是圆 O 的直径,C 为圆上一点,AB=2,AC= 1,P 为⊙O 所在平面外一点,且 PA 垂直于圆 O 所在平面,PB 与 平面所成的角为 . (1)求证:BC⊥平面 PAC; (2)求点 A 到平面 PBC 的距离.20、在等差数列 中,,.(1)求数列 的通项公式;(2)设,求21、如图,在三棱柱是、的中点.求证:(1)平面(2)平面⊥平面; .的值. 中,侧棱垂直于底面,且,M、N 分别22、已知圆,直线. (1)求证:直线 恒过定点. (2)判断直线 被圆 截得的弦何时最长、何时最短?并求截得的弦长最短时 度.的值以及最短长-3- / 9逊克一中 xx----xx 上学期高二上学期初考试数学科试卷答案解析第 1 题答案A第 1 题解析根据不等式两边同时乘以一个数,不等号的方向的改变来得到,也可以借助于数轴法来得到,由于,且,那么借助于数轴法可知结论为,选 A.第 2 题答案 C 第 2 题解析因为三点在同一条直线上,所以有.,即,解得第 3 题答案 D 第 3 题解析,故选 D...第 4 题答案 D 第 4 题解析,∴,即 有最小值 ,等号成立的条件是,第 5 题答案 B 第 5 题解析 由题可得:第 6 题答案 C 第 6 题解析,所以前 项和.. .-4- / 9第 7 题答案 B 第 7 题解析由三视图可知这个几何体上部是一个半球,下部是一个圆柱,所以它的表面积为第 8 题答案 D 第 8 题解析 动直线点 的直线 ∴经过定点,动直线,即,经过点定点,∵过定点 的直线始终垂直, 又是两条直线的交点,∴有与定 ,,故(当且仅当时取“”),故选 D.第 9 题答案 C 第 9 题解析由图象易得函数单调递增区间为,当 时,得为的一个单调递增区间.故选 C.第 10 题答案 D 第 10 题解析 解:点关于轴的对称点为路程为切线长第 11 题答案 A 第 11 题解析,∴点 到点 .的距离为 ,∴所求-5- / 9∵前 项的和为 ,最后 项的和为 ,∴前 项 最后三项,从而可知,第 12 题答案 A 第 12 题解析由是上的减函数,可得第 13 题答案,.,化简得.第 13 题解析 如图,由底边长,那么原来的高线为,则原三角形的面积.第 14 题答案 .第 14 题解析两条直线,故.,若,则,第 15 题答案3第 15 题解析不等式组表示的平面区域是一个三角形区域(包含边界),其三个点坐标分别为、、.而,可表示为两点与连线的斜率,其中在平面区域内,知 运动到 时,此时 斜率最大,为 3.第 16 题答案-6- / 9第 16 题解析 连接 AC、BD 交于 O,异面直线则,,与 所成的角即为 EO 与 BE 所成的角,设棱长为 1,,,所以,第 17 题答案 (1) (2) 第 17 题解析(1)设 的中点为,由中点坐标公式得:,即.(2)因为,,所以,由点斜式方程可得:第 18 题答案 (1)见解析;(2) .第 18 题解析(1)∵,令,解得∴的单调递增区间为(2)由,可得又,∴由余弦定理可知∴,故,,∴. ,,解得,. ,∴.-7- / 9第 19 题答案 (1)证明略(2) .第 19 题解析 (1)证明:∵PA⊥平面 ABC,∴PA⊥BC. ∵AB 是圆 O 的直径,C 为圆上一点,∴BC⊥AC. 又∵PA∩AC=A,∴BC⊥平面 PAC. (2)如图,过点 A 作 AD⊥PC 于点 D,∵BC⊥平面 PAC,AD 平面 PAC,∴BC⊥AD,∴AD⊥平面 PBC.∴AD 即为点 A 到平面 PBC 的距离.依题意知∠PBA 为 PB 与平面 ABC 所成角,即∠PBA=45°,∴PA=AB=2,AC=1,可得.∵AD·PC=PA·AC.∴,即点 A 到平面 PBC 的距离为.第 20 题答案(1);(2).第 20 题解析(1)设等差数列 的公差为 .由已知,得解得所以 (2)由(1)可得 所以. .-8- / 9.第 21 题答案(1)略;(2)略.第 21 题解析⑴证明:(1)因为,即 BC∥ ,BC 平面,平面,所以平面.(2),即 BC⊥AC,又 ⊥平面 ABC,BC 平面 ABC,所以 ⊥BC,又 ∩AC=C,故 BC⊥平面.又 BC 平面,所以平面⊥平面.第 22 题答案 解:(1)证明略;(2)直线 被圆 截得的弦最短时 的值是 ,最短长度是 .第 22 题解析 解:(1)直线 的方程经整理得.由于 的任意性,于是有,解此方程组,得.即直线 恒过定点.(2)因为直线 恒经过圆 内一点 ,所以(用《几何画板》软件,探究容易发现)当直线经过圆心 时被截得的弦最长,它是圆的直径;当直线 垂直于 时被截得的弦长最短.由,,可知直线 的斜率为,所以当直线 被圆 截得弦最短时,直线 的斜率为 ,于是有 ,即,解得.此时直线 l 的方程为.又.所以,最短弦长为.直线被圆 截得的弦最短时 的值是 ,最短长度是 .【感谢您的阅览,下载后可自由编辑和修改,关注我 每天更新】-9- / 9。
2020-2021学年高二数学上学期期初检测试题

2020-2021学年高二数学上学期期初检测试题一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知椭圆上的点到椭圆一个焦点的距离为7,则到另一焦点的距离为()A.2 B.3 C.5 D.72.过点P(2,4)作圆(x-1)2+(y-1)2=1的切线,则切线方程为( )A.3x+4y-4=0 B.4x-3y+4=0C.x=2或4x-3y+4=0 D.y=4或3x+4y-4=03.设为双曲线的两个焦点,点在双曲线上且满足,则的面积是()A.1 B.C.2 D.4.已知抛物线的焦点在直线上,则此抛物线的标准方程是()A.B.C.或 D.或5.已知抛物线与双曲线有共同的焦点,为坐标原点,在轴上方且在双曲线上,则的最小值为()A. B. C. D.6.若双曲线的渐近线与圆无交点,则的离心率的取值范围为()A. B. C. D.7.在中,角所对应的边分别为,已知,则( )A. B.2 C.D.18.如图,椭圆的右顶点为A,上顶点为B,动直线l 交椭圆C于两点,且始终满足,作交MN于点H,则的取值范围是( )A.B.C. D.二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求,全部选对的得5分,有选错的得0分,部分选对的得3分.9.如图,在四棱锥中,底面是正方形,底面,,截面与直线平行,与交于点E,则下列判断正确的是()A.E为的中点 B.平面C.与所成的角为D.三棱锥与四棱锥的体积之比等于.10.三角形有一个角是,这个角的两边长分别为8和5,则().A.三角形另一边长为7 B.三角形的周长为20C.三角形内切圆周长为 D.三角形外接圆面积为11.在平面直角坐标系中,动点到两个定点和的距离之积等于8,记点的轨迹为曲线,则()A.曲线经过坐标原点B.曲线关于轴对称C.曲线关于轴对称 D.若点在曲线上,则12.已知椭圆的左、右焦点分别为、,直线与椭圆相交于点、,则()A.当时,的面积为B.不存在使为直角三角形C.存在使四边形面积最大 D.存在,使的周长最大三、填空题:本题共4小题,每小题5分,共20分.13.在中,若三边的比是,则此三角形的最大角为_________.14.椭圆的左、右焦点分别为,,直线经过交椭圆于,两点,则的周长为__________.15.已知直线与椭圆交于、两点,若,则的取值范围是_____.16.已知抛物线的准线方程为,在抛物线上存在两点关于直线对称,且为坐标原点,则的值为__________.四、解答题:本题共6小题,共70分。
2020 学年高二数学上学期开学考试题(含解析)
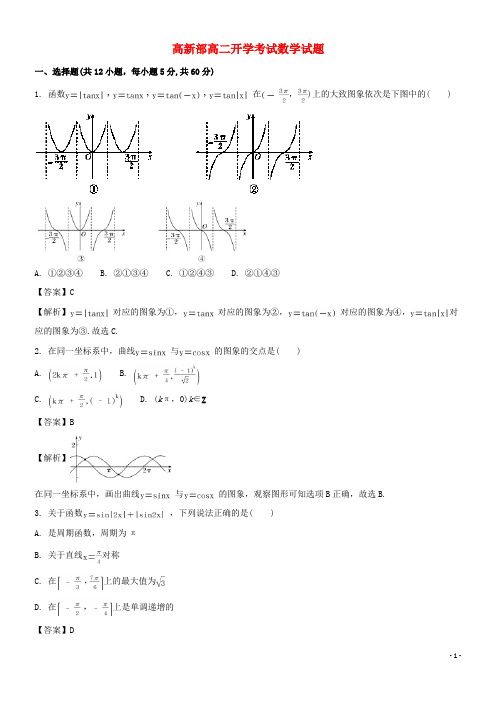
高新部高二开学考试数学试题一、选择题(共12小题,每小题5分,共60分)1. 函数在,)上的大致图象依次是下图中的( )A. ①②③④B. ②①③④C. ①②④③D. ②①④③【答案】C【解析】对应的图象为①,对应的图象为②,对应的图象为④,对应的图象为③.故选C.2. 在同一坐标系中,曲线与的图象的交点是( )A. B.C. D. (kπ,0)k∈Z【答案】B【解析】在同一坐标系中,画出曲线与的图象,观察图形可知选项B正确,故选B.3. 关于函数,下列说法正确的是( )A. 是周期函数,周期为πB. 关于直线对称C. 在上的最大值为D. 在上是单调递增的【答案】D【解析】.4. 函数x的最小值、最大值分别是( )A. B. C. D.【答案】A【解析】由于,故函数的最小值为,最大值为 .故选A.5. 函数的最小值和最大值分别为( )A. B. C. D.【答案】C【解析】2. ∴当时,,当时,,故选C.6. 的值为( )A. B. C. D.【答案】B【解析】 .故选B.7. 使函数为奇函数,且在区间上为减函数的的一个值为( )A. B. C. D.【答案】C【解析】为奇函数,所以=,所以,排除A和D;因为在区间]上为减函数,又,所以为奇数,故选C.【点睛】本题的关键步骤有:利用辅助角公式化简表达式;根据奇函数的特征求得=.8. 若α是锐角,且)=,则的值等于( )A. B. C. D.【答案】A【解析】是锐角,∴,又),∴sin(x+),∴sinα=sin[(α+)-])).故选A.9. 的大小关系是( )A. cos 1>cos 2>cos 3B. cos 1>cos 3>cos 2C. cos 3>cos 2>cos 1D. cos 2>cos 1>cos 3【答案】A【解析】∵余弦函数在上单调递减,又,故选A.10. 已知角的终边上一点),则等于( )A. B. C. D.【答案】A【解析】角的终边上一点),则,则.故选A.11. 化简式子++的结果为( )A. 2(1+cos 1-sin 1)B. 2(1+sin 1-cos 1)C. 2D. 2(sin 1+cos 1-1)【答案】C【解析】++=++.【点睛】解决此类问题的要领有:被开方式化简成完全平方;熟练运用公式;结合三角函数值判定的符号,再去绝对值.12. 如图是函数)的图象,那么( )A. ,B. ,C. ,D. ,【答案】C【解析】由点在图象上,,,此时.又点在的图象上,且该点是“五点”中的第五个点,,∴2π,∴,综上,有,故选C.【点睛】解决此类题型的常用方法有:1、采用直接法(即按顺序求解).2、排除法(抓住部分特征进行排除).分卷II二、填空题(共4小题,每小题5.0分,共20分)13. ________.【答案】-【解析】∵,∴原式.故答案为14. ________.【答案】1-【解析】原式··.故答案为1-15. ________.【答案】【解析】∵,∴,∴原式.故答案为16. 化简: ________.【答案】-1【解析】原式)(.故答案为【点睛】本题的关键点有:先切化弦,再通分;利用辅助角公式化简;同角互化.三、解答题(共6小题,17.10分。
湖北省部分中学2020年秋高二数学上学期期中联考试卷附答案解析

D.
0,1 2
二、选择题:本题共 4 小题,每小题 5 分,共 20 分,在每小题给出的选项中有多项符合题目要求,全部选 对的得 5 分,有选错的得 0 分,部分选对的得 3 分
9.下列说法正确的是( )
A.命题“ x R , x2 1 ”的否定是“ x0 R , x02 1”
B.命题“ x0 (3, ) , x02 9 ”的否定是“ x (3, ) , x2 9 ” C.“ m 0 ”是“关于 x 的方程 x2 2x m 0 有一正一负根”的充分不必要条件 D.“ a 5 ”是命题“ x R, x2 ax a 0 ”为假命题的充分不必要条件
湖北省部分中学 2020 年秋高二数学上学期期中联考试卷
第 I 卷(选择题)
一、选择题:本题共 8 小题,每小题 5 分,共 40 分,在每小题给出的四个选项中只有一项是符合题目要 求的
1.已知点 A(-3, 2) , B(0, 1) ,则直线 AB 的倾斜角为( )
A. 300
B. 450
C.1350
10.抛掷一枚骰子 1 次,记“向上的点数是 4,5,6”为事件 A,“向上的点数是 1,2”为事件 B,“向上的点 数是 1,2,3”为事件 C,“向上的点数是 1,2,3,4”为事件 D,则下列关于事件 A,B,C,D 判断正确的是 ()
A.A 与 B 是互斥事件但不是对立事件
B.A 与 C 是互斥事件也是对立事件
所以“ m ”是“ m l ”的充要条件 故选 C
5.【答案】B
【解析】由圆的几何性质两圆在点 A 处的切线互相垂直,且过对方圆心 O2O1.则
在 Rt△O2AO1 中,|O1A|= 5 |O2A|= 20 ,斜边上的高为半弦,用等积法易 得: AB 5 5 20 ⇒|AB|=4.故答案为:B
高二第一学期期中考试数学试卷含答案

高二数学第一学期期中考试试卷一、选择题(本大题共10小题,每小题4分,共40分)(每小题给出的四个选项中,只有一项是符合题目要求的把答案写在题号前) 1. 已知数列{a n }的通项公式为n n a n -=2,则下列各数中不是数列中的项的是( ) A.2 B.40 C.56 D.90 2. 等差数列{a n }的前n 项和为S n ,若12231a ==S ,,则a 6等于( ) A.8 B.10 C.12 D.14 3. 若0<<b a ,则下列不等式一定成立的是( ) A.b a22> B.a 2ab > C.ab b 2> D.b <a4. 等差数列{a n }中,a 1,a 2,a 4这三项构成等比数列,则公比q=( ) A.1 B.2 C.1或2 D.1或21 5. 已知数列{a n }的前n 项和为S n ,且3a 1=,a n n 2a 1=+,则S 5=( ) A.32 B.48 C.62 D.93 6. 若椭圆122=+kyx 的离心率是21,则实数k 的值为( ) A.3或31 B.34或43 C.2或21 D.32或237. 已知双曲线C :12222=-bya x ()0,0a >>b 的一条渐近线方程为x 3y =,一个焦点坐标为(2,0),则双曲线方程为( )A.16222=-y x B.12622=-y x C.1322x=-y D.13yx 22=-8. 若关于x 的不等式a xx ≥+4对于一切∈x (0,+∞)恒成立,则实数x 的取值范围是( )A.(-∞,5]B.(-∞,4]C.(-∞,2]D.(-∞,1] 9. 已知椭圆12222=+bya x ()0a >>b 的两个焦点分别为F F 21,,若椭圆上存在点P 使得∠PFF 21是钝角,则椭圆离心率的取值范围是( )A.(0,22) B.(22,1) C.(0,21) D.(21,1)10. 设O 为坐标原点,P 是以F 为焦点的抛物线()02y 2>=p px 上任意一点,M 是线段PF 的中点,则直线OM 的斜率的最大值为( ) A.22B.1C.2D.2 二、填空题(本大题共8小题,每小题5分,共40分)11. 在数列0,41,83,…,2n 1-n ,…中,94是它的第______项.12. 在等差数列{a n }中,542a =+a ,则=a 3______.13. 请写出一个与1322=-yx 有相同焦点的抛物线方程:____________.14. 椭圆14222=+ayx 与双曲线12222=-y a x 有相同的焦点,则实数a=______. 15. 函数()()111>-+=x x x x f 的最小值是______;此时x=______. 16. 要使代数式01a 2<-+ax x 对于一切实数x 都成立,则a 的取值范围是______.17. 已知椭圆的两个焦点1222=+yxFF 21,,点P 在椭圆上,且PF PF21⊥,则PF2=______.18. 在数列{a n }中,5,12113-==a a ,且任意连续三项的和均为11,则a 2019=______;设S n 是数列{a n }的前n 项和,则使得100≤S n 成立的最大整数n=______.三、解答题(本大题共5小题,共70分)19. 设{a n }是等差数列,-101=a ,且a a a a a a 6483102,,+++成等比数列. (Ⅰ)求数列{a n }的通项公式;(Ⅱ)记{a n }的前n 项和为S n ,求S n 的最小值.20. 已知数列{a n }的前n 项和n n S n +=2,其中N n +∈. (Ⅰ)求数列{a n }的通项公式;(Ⅱ)设12+=nn b ,求数列{b n }的前n 项和T n .21. 已知函数()R a ax x f x ∈-=,22.(Ⅰ)当a=1时,求满足()0<x f 的x 的取值范围; (Ⅱ)解关于x 的不等式()a x f 32<.22. 已知抛物线C :()022>=p px y ,经过点(2,-2). (Ⅰ)求抛物线C 的方程及准线方程;(Ⅱ)设O 为原点,直线02=--y x 与抛物线相交于B A ,两点,求证:OA ⊥OB .23. 已知椭圆C :的右焦点为12222=+by a x (),且经过点,01F ().10,B (Ⅰ)求椭圆C 的方程;(Ⅱ)直线()2:+=x k y l 与椭圆C 交于两个不同的点N M ,,若线段MN 中点的横坐标为32-,求直线l的方程及ΔFMN的面积.。
学2020-2021学年高二数学上学期期初考试试题

学2020-2021学年高二数学上学期期初考试试题一、选择题(本大题共12小题,共60.0分)若a,b,,,则下列不等式成立的是A. B. C. D.若是的内角,且,则A与B的关系正确的是A. B. C. D. 无法确定已知、a、x、b、依次成等比数列,则实数x的值为A. 3 B. C. 3或 D. 不确定过点且与直线垂直的直线方程是A. B.C. D.一圆锥形物体的母线长为4,其侧面积为,则这个圆锥的体积为A. B. C. D.已知m,n是两条不同的直线,,是两个不同的平面,若,,则下列命题正确的是A. 若,,则B. 若,且,则C. 若,,则D. 若,且,则已知a,b,c分别为内角A,B,C的对边,若,,,则A. B. C. D.点为圆的弦AB的中点,则直线AB的方程为A. B. C.D.已知正数满足,则的最小值为A. 5B.C.D. 2如图,长方体中,,,那么异面直线与所成角的余弦值是A. B. C. D.已知数列的通项公式,前n项和为,若,则的最大值是A. 5B. 10C. 15D. 20在三棱锥中,平面ABC,,,则三棱锥的外接球的表面积为A. B. C. D.二、填空题(本大题共4小题,共20.0分)直线恒过定点______.中,角A,B,C的对边分别为a,b,c,已知,,则的最大值为______设数列的前n项和为,若,且,则______.设圆:圆:点A,B分别是圆,上的动点,P为直线上的动点,则的最小值为______.三、解答题(本大题共4小题,共48.0分)在长方体中,底面ABCD是边长为2的正方形,E是AB的中点,F是的中点.求证:平面;若,求二面角的正弦值.在中,内角A,B,C的对边分别是a,b,c,且满足:.Ⅰ求角A的大小;Ⅱ若,求的最大值.设为正项数列的前n项和,且满足.求的通项公式;令,若恒成立,求m的取值范围.20.已知两个定点,,动点P满足设动点P的轨迹为曲线E,直线l:.求曲线E的轨迹方程;若l与曲线E交于不同的C,D两点,且为坐标原点,求直线l的斜率;若,Q是直线l上的动点,过Q作曲线E的两条切线QM,QN,切点为M,N,探究:直线MN是否过定点.数学试卷答案和解析1.【答案】D【解析】解:由,A.取,时不成立;B.取,时不成立;C.取时不成立;D.,可得:恒成立.故选:D.通过赋值法及利用不等式的基本性质即可判断出结论.本题考查了赋值法、不等式的基本性质,考查了推理能力与计算能力,属于基础题.2.【答案】B【解析】解:由正弦定理得,即.故选:B.根据正弦定理转化为,利用大角对大边的性质进行判断即可.本题主要考查三角函数角的大小比较,结合正弦定理以及大边对大角是解决本题的关键.3.【答案】B【解析】【分析】本题考查了等比数列的通项公式及其性质,考查了推理能力与计算能力,属于中档题.由、a、x、b、依次成等比数列,奇数项的符合相同,即可得出.【解答】解:、a、x、b、依次成等比数列,奇数项的符合相同,则.故选:B.4.【答案】C【解析】解:由于直线的斜率为,故所求直线的斜率等于,故所求直线的方程为,即,故选:C.由两直线垂直的性质求出所求直线的斜率,再用点斜式求直线的方程,化为一般式.本题主要考查两直线垂直的性质,用点斜式求直线的方程,属于基础题.5.【答案】C【解析】解:圆锥的展开图为扇形,半径,侧面积为为扇形的面积,所以扇形的面积,解得,所以弧长,所以底面周长为,由此可知底面半径,所以底面面积为,圆锥体的高为,故圆锥的体积,故选:C.利用圆锥的侧面展开图,扇形的面积,然后转化求解圆锥的体积.本题考查圆锥的体积的求法,考查转化思想以及计算能力.6.【答案】D【解析】解:对于A,若,,则或与相交,故错;对于B,若,且,则m与不一定垂直,故错;对于C,若,,则与位置关系不定,故错;对于D,,,,则,故正确.故选:D.利用面面、线面位置关系的判定和性质,直接判定.本题考查命题真假的判断,是中档题,解题时要认真审题,注意空间中线线、线面、面面间相互关系的合理运用.7.【答案】D【解析】解:,,,由正弦定理,可得:,由余弦定理,可得:,解得:,负值舍去.故选:D.由已知利用正弦定理可求c的值,根据余弦定理可得,解方程可得a的值.本题主要考查了正弦定理,余弦定理在解三角形中的应用,考查了方程思想,属于基础题.8.【答案】C【解析】解:是圆的弦,圆心为设AB的中点是满足因此,AB的斜率可得直线AB的方程是,化简得故选:C.由垂径定理,得AB中点与圆心C的连线与AB互相垂直,由此算出AB的斜率,结合直线方程的点斜式列式,即可得到直线AB的方程.本题给出圆的方程,求圆以某点为中点的弦所在直线方程,着重考查了直线与圆的方程、直线与圆的位置关系等知识,属于基础题.9.【答案】C【解析】解:,所以,,则,所以,,当且仅当,即当时,等号成立,因此,的最小值为,故选:C.由得,再将代数式与相乘,利用基本不等式可求出的最小值.本题考查利用基本不等式求最值,对代数式进行合理配凑,是解决本题的关键,属于中等题.10.【答案】A【解析】【分析】本题主要考查异面直线所成的角,考查空间想象能力、运算能力和推理论证能力,属于基础题.先将平移到,得到的锐角就是异面直线所成的角,在三角形中再利用余弦定理求出此角即可.【解答】解:如图,设,则,,,.将平移到,则是异面直线与所成角,,,.故选:A.11.【答案】B【解析】解:根据题意,数列的通项公式是,其前n项和是,有,即当最大时,取得最大值;若,且,解可得:,即当时,的值为正.即当,时,,此时取得最大值10.故选:B.根据题意,由数列的性质可得,结合数列的通项公式以及二次函数的性质分析可得当时,的值为正,进而可得当,时,取得最大值,利用通项公式计算的值,即可得答案.本题考查等差数列的前n项和与前m项和的最大值的求法,考查等差数列的性质等基础知识,考查运算求解能力,是基础题.12.【答案】C【解析】解:如图,由题意,的外接圆的半径.平面ABC,且,三棱锥的外接球的半径R满足.三棱锥的外接球的表面积为.故选:C.由题意画出图形,求出底面三角形ABC的外接圆的半径,进一步求得三棱锥的外接球的半径,再由球的表面积公式求解.本题考查多面体外接球表面积的求法,考查数形结合的解题思想方法,是中档题.13.【答案】【解析】解:直线,由题得,,解得,,直线过定点故答案为:直线,化为,由此能求出直线经过的定点.本题考查直线经过的定点坐标的求法,考查直线方程的性质等基础知识,考查运算求解能力,是基础题.14.【答案】【解析】解:由,,由余弦定理得,即,故,即的最大值为,故答案为:.结合余弦定理以及基本不等式,利用三角形的面积公式进行求解即可.本题主要考查三角形面积最值的计算,结合余弦定理,以及基本不等式进行转化是解决本题的关键.15.【答案】【解析】解:由于数列的前n项和为,若,所以常数,所以数列是以为首项,1为公差的等差数列,故,整理得,故答案为:.直接利用递推关系式的变换求出数列的通项公式,进一步求出结果.本题考查的知识要点:数列的通项公式的求法及应用,主要考查学生的运算能力和转换能力及思维能力,属于基础题型.16.【答案】【解析】解:可知圆的圆心,,圆的圆心,,如图所示对于直线上的任一点P,由图象可知,要使的得最小值,则问题可转化为求的最小值,即可看作直线上一点到两定点距离之和的最小值减去7,又关于直线对称的点为,由平面几何的知识易知当与P、共线时,取得最小值,即直线上一点到两定点距离之和取得最小值为的最小值为.故答案为:求出圆心坐标和半径,结合圆的地产进行转化求解即可.本题主要考查圆与圆位置关系的应用,利用数形结合结合对称性进行转化是解决本题的关键.综合性较强,有一定的难度.17.【答案】证明:连接,,F分别为AB,的中点,长方体中,,,四边形是平行四边形,,平面,平面,平面解:在长方体中,分别以DA,DC,为x,y,z轴建立如图所示空间直角坐标系,则0,,0,,2,,1,,,,,,,设平面的一个法向量,则,取,则同样可求出平面的一个法向量二面角的正弦值为.【解析】连接,推导出,则四边形是平行四边形,从而,,由此能证明平面.在长方体中,分别以DA,DC,为x,y,z轴建立空间直角坐标系,利用向量法能求出二面角的正弦值.本题考查线面平行的证明,考查三面角的正弦值的求法,考查面面垂直的证明,考查空间中线线、线面、面面间的位置关系等基础知识,考查运算求解能力,是中档题.18.【答案】解:Ⅰ,,,,由余弦定理可得:,又在中,,.Ⅱ由Ⅰ及,可得:,即,,当且仅当时等号成立,,则,当且仅当时等号成立,故的最大值为2.【解析】本题主要考查了正弦定理,余弦定理,基本不等式在解三角形中的综合应用,考查了计算能力和转化思想,属于基础题.Ⅰ由正弦定理化简已知等式可得,由余弦定理可得,结合范围,可求A的值.Ⅱ由Ⅰ及,可得,由,即可求得的最大值.19.【答案】解:由题,令,得,解得,当时,,得:,,,即是以3为首项,2为公差的等差数列,;,,若恒成立,则,的取值范围为.【解析】由已知和数列的性质,可推出此数列为等差数列,利用定义写出通项即可;首先将变形成差的形式,利用这一特点可以消项化简,解不等式的m范围.本题属于一般题型,考察了数列的定义和基本性质,对式子的变形有所考察,总体上属于中档题.20.【答案】解:设点P的坐标为,,即,整理可得,所以曲线E的轨迹方程为.依题意,,且,则点O到CD边的距离为1,即点到直线l:的距离,解得,所以直线l的斜率为.依题意,,,则M,N都在以OQ 为直径的圆F上,Q是直线l:上的动点,设,则圆F的圆心为,且经过坐标原点,即圆的方程为.又因为M,N在曲线E:上,由,可得,即直线MN的方程为.由且可得,,解得,所以直线MN是过定点.【解析】本题考查轨迹方程,涉及点到直线的距离公式,两点间的距离公式等,属于综合题,难度较大.设点P的坐标为,根据列方程化简可得轨迹方程;,且,则点O到CD边的距离为1,列方程求解即可;依题意,,,则M,N都在以OQ 为直径的圆F上,Q是直线l:上的动点,设,联立两个圆的方程求解即可.学2020-2021学年高二数学上学期期初考试试题一、选择题(本大题共12小题,共60.0分)若a,b,,,则下列不等式成立的是A. B. C. D.若是的内角,且,则A与B的关系正确的是A. B. C. D. 无法确定已知、a、x、b、依次成等比数列,则实数x的值为A. 3B.C. 3或D. 不确定过点且与直线垂直的直线方程是A. B. C.D.一圆锥形物体的母线长为4,其侧面积为,则这个圆锥的体积为A. B. C. D.已知m,n是两条不同的直线,,是两个不同的平面,若,,则下列命题正确的是A. 若,,则B. 若,且,则C. 若,,则D. 若,且,则已知a,b,c分别为内角A,B,C的对边,若,,,则A. B. C. D.点为圆的弦AB的中点,则直线AB的方程为A. B. C.D.已知正数满足,则的最小值为A. 5B.C.D. 2如图,长方体中,,,那么异面直线与所成角的余弦值是A. B. C. D.已知数列的通项公式,前n项和为,若,则的最大值是A. 5B. 10C. 15D. 20在三棱锥中,平面ABC,,,则三棱锥的外接球的表面积为A. B. C. D.二、填空题(本大题共4小题,共20.0分)直线恒过定点______.中,角A,B,C的对边分别为a,b,c,已知,,则的最大值为______设数列的前n项和为,若,且,则______.设圆:圆:点A,B分别是圆,上的动点,P为直线上的动点,则的最小值为______.三、解答题(本大题共4小题,共48.0分)在长方体中,底面ABCD是边长为2的正方形,E是AB的中点,F是的中点.求证:平面;若,求二面角的正弦值.在中,内角A,B,C的对边分别是a,b,c,且满足:.Ⅰ求角A的大小;Ⅱ若,求的最大值.设为正项数列的前n项和,且满足.求的通项公式;令,若恒成立,求m的取值范围.20.已知两个定点,,动点P满足设动点P的轨迹为曲线E,直线l:.求曲线E的轨迹方程;若l与曲线E交于不同的C,D两点,且为坐标原点,求直线l的斜率;若,Q是直线l上的动点,过Q作曲线E的两条切线QM,QN,切点为M,N,探究:直线MN是否过定点.数学试卷答案和解析1.【答案】D【解析】解:由,A.取,时不成立;B.取,时不成立;C.取时不成立;D.,可得:恒成立.故选:D.通过赋值法及利用不等式的基本性质即可判断出结论.本题考查了赋值法、不等式的基本性质,考查了推理能力与计算能力,属于基础题.2.【答案】B【解析】解:由正弦定理得,即.故选:B.根据正弦定理转化为,利用大角对大边的性质进行判断即可.本题主要考查三角函数角的大小比较,结合正弦定理以及大边对大角是解决本题的关键.3.【答案】B【解析】【分析】本题考查了等比数列的通项公式及其性质,考查了推理能力与计算能力,属于中档题.由、a、x、b、依次成等比数列,奇数项的符合相同,即可得出.【解答】解:、a、x、b、依次成等比数列,奇数项的符合相同,则.故选:B.4.【答案】C【解析】解:由于直线的斜率为,故所求直线的斜率等于,故所求直线的方程为,即,故选:C.由两直线垂直的性质求出所求直线的斜率,再用点斜式求直线的方程,化为一般式.本题主要考查两直线垂直的性质,用点斜式求直线的方程,属于基础题.5.【答案】C【解析】解:圆锥的展开图为扇形,半径,侧面积为为扇形的面积,所以扇形的面积,解得,所以弧长,所以底面周长为,由此可知底面半径,所以底面面积为,圆锥体的高为,故圆锥的体积,故选:C.利用圆锥的侧面展开图,扇形的面积,然后转化求解圆锥的体积.本题考查圆锥的体积的求法,考查转化思想以及计算能力.6.【答案】D【解析】解:对于A,若,,则或与相交,故错;对于B,若,且,则m与不一定垂直,故错;对于C,若,,则与位置关系不定,故错;对于D,,,,则,故正确.故选:D.利用面面、线面位置关系的判定和性质,直接判定.本题考查命题真假的判断,是中档题,解题时要认真审题,注意空间中线线、线面、面面间相互关系的合理运用.7.【答案】D【解析】解:,,,由正弦定理,可得:,由余弦定理,可得:,解得:,负值舍去.故选:D.由已知利用正弦定理可求c的值,根据余弦定理可得,解方程可得a的值.本题主要考查了正弦定理,余弦定理在解三角形中的应用,考查了方程思想,属于基础题.8.【答案】C【解析】解:是圆的弦,圆心为设AB的中点是满足因此,AB的斜率可得直线AB的方程是,化简得故选:C.由垂径定理,得AB中点与圆心C的连线与AB互相垂直,由此算出AB的斜率,结合直线方程的点斜式列式,即可得到直线AB的方程.本题给出圆的方程,求圆以某点为中点的弦所在直线方程,着重考查了直线与圆的方程、直线与圆的位置关系等知识,属于基础题.9.【答案】C【解析】解:,所以,,则,所以,,当且仅当,即当时,等号成立,因此,的最小值为,故选:C.由得,再将代数式与相乘,利用基本不等式可求出的最小值.本题考查利用基本不等式求最值,对代数式进行合理配凑,是解决本题的关键,属于中等题.10.【答案】A【解析】【分析】本题主要考查异面直线所成的角,考查空间想象能力、运算能力和推理论证能力,属于基础题.先将平移到,得到的锐角就是异面直线所成的角,在三角形中再利用余弦定理求出此角即可.【解答】解:如图,设,则,,,.将平移到,则是异面直线与所成角,,,.故选:A.11.【答案】B【解析】解:根据题意,数列的通项公式是,其前n项和是,有,即当最大时,取得最大值;若,且,解可得:,即当时,的值为正.即当,时,,此时取得最大值10.故选:B.根据题意,由数列的性质可得,结合数列的通项公式以及二次函数的性质分析可得当时,的值为正,进而可得当,时,取得最大值,利用通项公式计算的值,即可得答案.本题考查等差数列的前n项和与前m项和的最大值的求法,考查等差数列的性质等基础知识,考查运算求解能力,是基础题.12.【答案】C【解析】解:如图,由题意,的外接圆的半径.平面ABC,且,三棱锥的外接球的半径R满足.三棱锥的外接球的表面积为.故选:C.由题意画出图形,求出底面三角形ABC的外接圆的半径,进一步求得三棱锥的外接球的半径,再由球的表面积公式求解.本题考查多面体外接球表面积的求法,考查数形结合的解题思想方法,是中档题.13.【答案】【解析】解:直线,由题得,,解得,,直线过定点故答案为:直线,化为,由此能求出直线经过的定点.本题考查直线经过的定点坐标的求法,考查直线方程的性质等基础知识,考查运算求解能力,是基础题.14.【答案】【解析】解:由,,由余弦定理得,即,故,即的最大值为,故答案为:.结合余弦定理以及基本不等式,利用三角形的面积公式进行求解即可.本题主要考查三角形面积最值的计算,结合余弦定理,以及基本不等式进行转化是解决本题的关键.15.【答案】【解析】解:由于数列的前n项和为,若,所以常数,所以数列是以为首项,1为公差的等差数列,故,整理得,故答案为:.直接利用递推关系式的变换求出数列的通项公式,进一步求出结果.本题考查的知识要点:数列的通项公式的求法及应用,主要考查学生的运算能力和转换能力及思维能力,属于基础题型.16.【答案】【解析】解:可知圆的圆心,,圆的圆心,,如图所示对于直线上的任一点P,由图象可知,要使的得最小值,则问题可转化为求的最小值,即可看作直线上一点到两定点距离之和的最小值减去7,又关于直线对称的点为,由平面几何的知识易知当与P、共线时,取得最小值,即直线上一点到两定点距离之和取得最小值为的最小值为.故答案为:求出圆心坐标和半径,结合圆的地产进行转化求解即可.本题主要考查圆与圆位置关系的应用,利用数形结合结合对称性进行转化是解决本题的关键.综合性较强,有一定的难度.17.【答案】证明:连接,,F分别为AB,的中点,长方体中,,,四边形是平行四边形,,平面,平面,平面解:在长方体中,分别以DA,DC,为x,y,z轴建立如图所示空间直角坐标系,则0,,0,,2,,1,,,,,,,设平面的一个法向量,则,取,则同样可求出平面的一个法向量二面角的正弦值为.【解析】连接,推导出,则四边形是平行四边形,从而,,由此能证明平面.在长方体中,分别以DA,DC,为x,y,z轴建立空间直角坐标系,利用向量法能求出二面角的正弦值.本题考查线面平行的证明,考查三面角的正弦值的求法,考查面面垂直的证明,考查空间中线线、线面、面面间的位置关系等基础知识,考查运算求解能力,是中档题.18.【答案】解:Ⅰ,,,,由余弦定理可得:,又在中,,.Ⅱ由Ⅰ及,可得:,即,,当且仅当时等号成立,,则,当且仅当时等号成立,故的最大值为2.【解析】本题主要考查了正弦定理,余弦定理,基本不等式在解三角形中的综合应用,考查了计算能力和转化思想,属于基础题.Ⅰ由正弦定理化简已知等式可得,由余弦定理可得,结合范围,可求A的值.Ⅱ由Ⅰ及,可得,由,即可求得的最大值.19.【答案】解:由题,令,得,解得,当时,,得:,,,即是以3为首项,2为公差的等差数列,;,,若恒成立,则,的取值范围为.【解析】由已知和数列的性质,可推出此数列为等差数列,利用定义写出通项即可;首先将变形成差的形式,利用这一特点可以消项化简,解不等式的m范围.本题属于一般题型,考察了数列的定义和基本性质,对式子的变形有所考察,总体上属于中档题.20.【答案】解:设点P的坐标为,,即,整理可得,所以曲线E的轨迹方程为.依题意,,且,则点O到CD边的距离为1,即点到直线l:的距离,解得,所以直线l的斜率为.依题意,,,则M,N都在以OQ为直径的圆F上,Q是直线l:上的动点,设,则圆F的圆心为,且经过坐标原点,即圆的方程为.又因为M,N在曲线E:上,由,可得,即直线MN的方程为.由且可得,,解得,所以直线MN是过定点.【解析】本题考查轨迹方程,涉及点到直线的距离公式,两点间的距离公式等,属于综合题,难度较大.设点P的坐标为,根据列方程化简可得轨迹方程;,且,则点O到CD边的距离为1,列方程求解即可;依题意,,,则M,N都在以OQ为直径的圆F上,Q是直线l:上的动点,设,联立两个圆的方程求解即可.。
江苏省苏州中学2020-2021学年度第一学期期初考试高二数学试题

江苏省苏州中学2020-2021学年度一学期期初考试高二数学本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,满分100分,考试时间45分钟。
所有答案均写在答题纸上。
第Ⅰ卷(选择题,共40分)一、选择题:本题共6小题,每小题5分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的.1. 设集合A ={x | x 2-x -2<0},集合B ={y | y =3x },则A ∩B =( ) A. (0,+∞)B. (0, 2)C. (-1, 0)D. (-1, 2)2. 已知f (x +1)=x +2x ,则函数f (x )的解析式为( ) A. f (x )=x 2-1(x ≥0)B. f (x )=x 2-1(x ≥1)C. f (x )=x 2(x ≥0)D. f (x )=x 2(x ≥1)3. 在△ABC 中,M 是BC 的中点,AM =1,点P 在AM 上且满足AP →=2PM →,则PA →·(PB →+PC →)=( )A. -49B. -43C. 43D. 494. 直线y =ax -a 是圆C :x 2+y 2-4x -2y +1=0的一条对称轴,过点A (4a , 2a )作圆C 的一条切线,切点为B , 则|AB |=( )A.2B. 2 2C. 5D. 15. 已知锐角△ABC 中,角A , B , C 所对的边分别为a , b , c ,若b 2=a (a +c ),则sin(B -A )sin 2A 的取值范围是( ) A. (2,+∞)B. (3,+∞)C. (2, 2)D. (3, 2)6. 如右图,体积为V 的大球内有4个小球,每个小球的球面过大球球心且与大球球面有且只有一个交点,4个小球的球心是以大球球心为中心的正方形的4个顶点.V 1为小球相交部分(图中阴影部分)的体积,V 2为大球内、小球外的图中黑色部分的体积,则下列关系中正确的是( ) A. V 1=V2B. V 2=V2C. V 1>V 2D. V 1<V 2二、选择题:本题共2小题,每小题5分,共10分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,有选错的得0分,部分选对的得3分.7. 已知函数f (x )=(log 2 x )2-log 2 x 2-3,则下列说法正确的是( )A. 函数y =f (x )的图象与x 轴有两个交点B. 函数y =f (x )的最小值为-4C. 函数y =f (x )的最大值为4D. 函数y =f (x )的图象关于直线x =2对称8. 已知圆C 被x 轴分成两部分的弧长之比为1: 2,且被y 轴截得的弦长为4,当圆心C 到直线x +5y =0的距离最小时,圆C 的方程为( )第6题A. (x +4)2+(y -5)2=20B. (x -4)2+(y +5)2=20C. (x +4)2+(y +5)2=20D. (x -4)2+(y -5)2=20第Ⅱ卷(非选择题,共60分)三、填空题:本题共3小题,每小题5分,共15分.9. 已知函数f (x )=cos2x +a sin x +c 在区间(-π6, π2)内是减函数,则实数a 的取值范围是 . 10. 已知直线l 1:ax − by − 4 = 0和直线l 2:(a − 2)x + y − b = 0,若l 1∥l 2,且坐标原点到这两条直线距离相等,则ab 的值为 .11. 如图,已知线段AB = 4,四边形ABNM 的两顶点M 、N 在以AB 为直径的半圆弧上,且MN = 2,则AM →·BN →的取值范围是 .四、解答题:本题共3小题,共45分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2020年秋季高二见面会
一、单选题(共8小题,满分40分,每小题5分)
1、(2020·浙江省学军中学高一期末)设全集为R ,集合A ={x |0<x <2},B ={x |x ≥1},则A ∩B =( ) A .{x |1≤x <2}
B .{x |0<x <2}
C .{x |0<x ≤1}
D .{x |0<x <1}
2、(2020·洛阳市第一高级中学高一月考)学校为了调查学生在课外读物方面的支出情况,抽取了一个容量为n 的样本,其频率分布直方图如图所示,其中支出在[)50,60的同学有30人,则n 的值为( )
A .100
B .1000
C .90
D .900
3、(2020·山东省青岛二中高一期末)下列哪个函数的定义域与函数12x
y ⎛⎫= ⎪⎝⎭
的值域相同( )
A .2x
y =
B .1
y x x
=+
C .12
y x =
D .ln y x x =-
4、(2020·湖南省雅礼中学高三月考)如果()()2
21f x ax a x =--+在区间1,2
⎛⎤-∞ ⎥⎝
⎦
上为减函数,则a 的
取值( ) A .(]0,1
B .[)0,1
C .[] 0,1
D .()0,1
5、(2020·浙江省杭州第二中学高一期末)若5
sin 13
α=-
且a 为第三象限角,则tan α的值等于( ) A .125 B .125- C .5
12 D .512-
6、(2020·莆田第二十五中学高一期末)以下命题(其中a ,b 表示直线,α表示平面):
①若//a b ,b α⊂,则//a α;②若//a α,//b α,则//a b ; ③若//a b ,//b α,则//a α;④若//a α,b α⊂,则//a b .
其中正确命题的个数是( ) A .0个
B .1个
C .2个
D .3个
7、(2020·成都七中高一月考)某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2017年1月至2020年12月期间月接待游客量(单位:万人)的数据,绘制了下面的折线图.根据该折线图,下列结论错误的是( )
A .年接待游客量逐年增加
B .各年的月接待游客量高峰期大致在8月
C .2017年1月至12月月接待游客量的中位数为30万人
D .各年1月至6月的月接待游客量相对于7月至12月,波动性更小,变化比较平稳
8、(2020·河北省石家庄一中高一期末)在ABC 中,D 为线段AC 的中点,点E 在边BC 上,且1
2
BE EC =,AE 与BD 交于点O ,则=AO ( )
A .11
24AB AC + B .
11
44AB AC + C .11
42
AB AC +
D .11
22
AB AC +
二、多选题(共4小题,满分20分,每小题5分,少选的3分,多选不得分) 9、(2020·山东省济南一中高一月考)(多选题)下列关系中,正确的有() A .{}0∅
B .1
3
Q ∈
C .Q Z ⊆
D .{}0∅∈
10、(2020·山东省青岛二中高一期末)在ABC ∆中,下列关系恒成立的是( ) A .()tan tan A B C += B .()cos 22cos2A B C += C .sin sin 22A B C +⎛⎫
=
⎪
⎝⎭ D .sin cos 22A B C +⎛⎫
=
⎪
⎝⎭
11、(2020·山东省青岛二中高一期末)某市12月17日至21日期间空气质量呈现重度及以上污染水平,经市政府批准,该市启动了空气重污染红色预警,期间实行机动车“单双号”限行等措施.某报社会调查中心联合问卷网,对2400人进行问卷调查,并根据调查结果得到如下饼图则下列结论正确的是( )
A .“不支持”部分所占的比例大约是整体的1
12
; B .“一般”部分所占的人数估计是800人;
C .饼图中如果圆的半径为2,则“非常支持”部分扇形的面积是76
π; D .“支持”部分所占的人数估计是1100人
12、(2020·福建省永春第一中学高一期末)以下四个命题表述正确的是( ) A .直线()()34330m x y m m R ++-+=∈恒过定点()3,3--
B .圆224x y +=上有且仅有3个点到直线:0l x y -+=的距离都等于1
C .曲线22120C :x y x ++=与曲线22
2480C :x y x y m +--+=恰有三条公切线,则4m =
D .已知圆22:4C x y +=,点P 为直线142
x y
+=上一动点,过点P 向圆C 引两条切线PA 、PB ,A 、B 为切点,则直线AB 经过定点(1,2)
三、填空题(共4小题,满分20分,每小题5分,一题两空,第一空2分)
13、(2020·上海格致中学高一期末)函数 ()()lg 1f x x =
-的定义域为_____.
14、(2020·上海交大附中高一期末)已知函数()()1
1231
21x a x a x f x x -⎧-+<=⎨≥⎩
的值域为R ,则实数a 的取值范围是_____.
15、(2020·浙江省杭州第二中学高一期末)已知函数()sin (01)3f x x πωω⎛
⎫
=+
<< ⎪⎝
⎭
.()f x 在x π=处取得最大值,则(7)(6)f f ππ-=________;若函数()f x 的周期是4π,函数|()|f x 的单调增区间是________. 16、(江苏省南通巿2019-2020学年第一次教学质量调研)在平面直角坐标系xOy 中,AB 是圆
()()2
2
:224C x y -+-=的弦,
且AB =若存在线段AB 的中点P ,使得点P 关于x 轴对称的点Q 在直线30kx y ++=上,则实数k 的取值范围是_______________________.
四、解答题(共6小题,满分70分,第17题10分,其它12分)
17、(2020·福建省福州第一中学高一期末)在平面直角坐标系中,已知()1,2a =-,()3,4b =. (Ⅰ)若()()
3//a b a kb -+,求实数k 的值; (Ⅰ)若()
a t
b b -⊥,求实数t 的值.
18、(2020·山西省长治市第二中学校高一期末)某校从参加某次知识竞赛的同学中,选取60名同学将其成
绩(百分制,均为整数)分成[4050),
,[5060),,[6070),,[7080),,[8090),,[90100],六组后,得到部分频率分布直方图(如图),观察图形中的信息,回答下列问题:
(1)求分数[7080),
内的频率,并补全这个频率分布直方图; (2)从频率分布直方图中,估计本次考试成绩的中位数;
(3)若从第1组和第6组两组学生中,随机抽取2人,求所抽取2人成绩之差的绝对值大于10的概率.
19、(2020·湖南省常德市一中高一期末)如图四棱锥P ABCD -中,底面ABCD 是边长为2的正方形,其
E 为AB 的中点,
F 为PC 的中点.
(1)证明://BF 平面PDE ; (2)求三棱锥E BDF -的体积
20、(2020·合肥一六八中学高二期末)在ABC ∆中,BC 边上的高所在直线的方程为210x y -+=,A ∠的平分线所在直线方程为0y =,若点B 的坐标为(1,2). (1)求点A 和点C 的坐标;
(2)求AC 边上的高所在的直线l 的方程.
21、(2018·天津一中高三月考)已知函数()πf x sinx sin x 6⎛
⎫=⋅+
⎪⎝
⎭
. ()1求()f x 的对称轴所在直线方程及其对称中心;
()2在
ABC 中,内角A 、B 、C 所对的边分别是a 、b 、c ,且A f 2⎛⎫
=
⎪⎝⎭,a 4=,求ABC 周长的取值范围.
22、(2020·重庆巴蜀中学高一期末)已知函数()f x ,()g x 分别是定义在R 上的偶函数和奇函数,且
()()12x f x g x ++=.
(1)求函数()f x ,()g x 的解析式;
(2)若对任意[)1,x ∈+∞,不等式()()22f x mg x ≥-恒成立,求实数m 的最大值;
(3)设()()224x
h x a a =-⋅+-,若函数()f x 与()h x 的图象有且只有一个公共点,求a 的取值范围.。
