概率论参考答案 刘金山 主编 第3章
概率论与数理统计(第三版)第三章课后答案
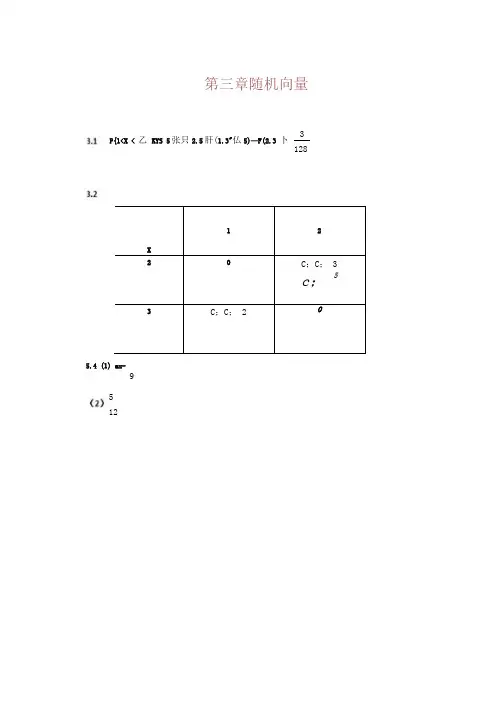
第三章随机向量X122C ;C ; 3c ; 53C ;C ; 25.4 (1) a=-95 12P{1<X < 乙 KYS 5张只2.5肝(1.3"仏5)—F(2.3 卜3 128<3)P{(X.r)eD}=f^『*6*必"制:[(6-〉”-討疗&T:(护-®+5討詁(护3+5”)|:=諾=善3.5 K: (1)y)工J: J:01 皿=f eP寸"血=(-<- UXr^ IS)=(1 -0X1 - 严)<2>P(rsx)= f:\f*如2严创;『dy =「2严(-八Qdx =J; 2宀(i十肚.j:(2宀》女肚=(・严3.6H: PC^ + JSa3.9B : x 術加HK 昨通»斤(0为:饴X>1 或xvOirL /(xj) = Op斤0) = [4.8>・(2-如=4 83[2*4门:*8川卜2》+黑计Zr(x) = O y > 或 <00<><1A(x) = f>.8y(2 “妙=2 妒(2-纠;=2*(2-x)©SOSxMl 时,/t (x) = | 4.8y(2-x>A =2 4y :(2-x)|r =2 4工(2・兀)3・7參见课本后面P227的答案3.8 f x (x) = J :/(x, >•>” J:訊如扌吟|:■专厶ox J :討法訐£ 'X0SXS2AW= 2* 0苴它/iO)h3>20<> <1 0其它Zr(x)h [(沖0<x<l=V2工+3°"幻3其它0 其它0<> <23 60< v<2其它 b 其它Y的血利K率密度跚齐3为:® 当或<0时尸/(x f>) = 0, /}(>) = 0②当0 Sg 时,力3 = f 4.8>(2-x>ft = 4 8>[2x-lr]|; = 4.8口1 卜2)+ £y2] =2.4>(3-4y+>:)MO (1〉券见课本石面P227的答案3 J2聲见课本后面P228的答案313 (1) 6x(17 0<x<l 0 其它0^x<l其它0<y<l其它311參见课本后面P228的答案【3+卸对TO<x<irt, A(x)>o2 5 X 她缘分布 1 0.15 0.250350.75 30.050.18 0.02 0.2S布0.2 0.430.371由表格可知 P{X-l;Y-2b0.29/:P{X.l}P{Y-2)-0.3225对于0<y<2时,/;(i)>0?0<x<l6x 2+ln0<x<lTT3 6 0 ■其它o+y其它-3-咖2卄犒h=2<+兰30 »JiX X故p^X=x)P{Y=y)所以X与Y不独立由鮭僚件P {X二工;丫二)[} "{工=卫尸{ Y=y)则P{X =2;K=2} = P{X = 2}P{Y = 2}P(X=2;r = 3) = P{X= 2}P{Y = 3}y;P{x=?}=iCO""30<x<2, 时,几(力齐(>)=4冷—/(兀“当x>2或x<OH,当)〉1 或y<o时,A(x)/iO) = o=/(x?j) 所以,x与Y之硼互独立・(訐(2〉衽3・9中,f x(x) =‘2.4三(2-力»0<x<l其它A(J)=2.4r(3-4v +y2)b 0^ v<l 其它3.16 B (J 在 3.8 中f x M= 2Io OSxS2其它AO) = <3y2 0<j ^16其它Xr(或40)二2・4疋(2-力2・4丿(3-4,+护)“・7&?(2-如3-令+小*/Uy),所以x与丫之冋不相5独NJ.17 解:二严=xe »)=匸心) f t(0=.匚fg 沁二 f* xe'(妇c以詁;芦希Z (x)/ o)=xe詁孑=fg >')故x与Y相歹檢立J・18聲见课本后面P228的答案。
概率与数理统计第3章答案

第3章习题答案祥解1.现有10件产品,其中6件正品,4件次品。
从中随机抽取2次,每次抽取1件,定义两个随机变量、如下:X Y ⎩⎨⎧=。
次抽到次品第次抽到正品第11,0;,1X ⎩⎨⎧=。
次抽到次品第次抽到正品第22,0;,1Y 试就下面两种情况求的联合概率分布和边缘概率分布。
),(Y X (1)第1次抽取后放回;(2)第1次抽取后不放回。
解(1)依题知所有可能的取值为.因为),(Y X )1,1(),0,1(),1,0(),0,0(; 254104104)0|0()0()0,0(1101411014=⨯=⋅===⋅====C C C C X Y P X P Y X P 256106104)0|1()0()1,0(1101611014=⨯=⋅===⋅====C C C C X Y P X P Y X P 256104106)1|0()1()0,1(1101411016=⨯=⋅===⋅====C C C C X Y P X P Y X P ; 259106106)1|1()1()1,1(1101611016=⨯=⋅===⋅====C CC C X Y P X P Y X P 所以的联合概率分布及关于、边缘概率分布如下表为:),(Y X X Y (2)类似于(1),可求得; 15293104)0|0()0()0,0(191311014=⨯=⋅===⋅====C C C C X Y P X P Y X P YX01⋅i p 0254256251012562592515jp ⋅251025151YX01⋅i p -111p 041021p 22p 21; 15496104)0|1()0()1,0(191611014=⨯=⋅===⋅====C C C C X Y P X P Y X P ; 15494106)1|0()1()0,1(191411016=⨯=⋅===⋅====C C C C X Y P X P Y X P 15595106)1|1()1()1,1(191511016=⨯=⋅===⋅====C C C C X Y P X P Y X P 所以的联合概率分布及关于、边缘概率分布如下表为:),(Y X X Y 2.已知随机变量、的概率分布分别为X Y 且,求1)0(==⋅Y X P (1)和的联合概率分布;(2).X Y )(Y X P =解(1)因为)1,0()0,0()0,1()0,1()0(=======-===⋅Y X Y X Y X Y X Y X 所以1)1,0()0,0()0,1()0,1()0(22213111=+++==+==+==+=-===⋅p p p p Y X P Y X P Y X P Y X P Y X P = 又根据得,从而.于是由表12131=∑∑==j i ijp03212=+p p 03212==p p YX01⋅i p 01521541561154155159jp ⋅1561591X P-11412141Y P12121YX01⋅i p -141041002121141021jp ⋅21211可得,,,.4111=p 4131=p 2122=p 0212221=-=p p 故的联合概率分布为),(Y X (2)由(1)知.0)1,1()0,0()(===+====Y X P Y X P Y X P 3.设二维随机向量服从矩形区域上的均匀分),(Y X {}10,20),(≤≤≤≤=y x y x D 布,且⎩⎨⎧>≤=.,1;,0Y X Y X U ⎩⎨⎧>≤=.2,1;2,0Y X Y X V 求与的联合概率分布。
概率论与数理统计第三章习题及答案

概率论与数理统计习题 第三章 多维随机变量及其分布习题3-1 盒子里装有3只黑球、2只红球、2只白球,在其中任取4只球.以X 表示取到黑球的只数,以Y 表示取到红球的只数,求X 和Y 的联合分布律.(X ,Y )的可能取值为(i , j ),i =0,1,2,3, j =0,12,i + j ≥2,联合分布律为 P {X=0, Y=2 }=351472222=C C C P {X=1, Y=1 }=35647221213=C C C C P {X=1, Y=2 }=35647122213=C C C C P {X=2, Y=0 }=353472223=C C C P {X=2, Y=1 }=351247121223=C C C C P {X=2, Y=2 }=353472223=C C C P {X=3, Y=0 }=352471233=C C C P {X=3, Y=1 }=352471233=C C C P {X=3, Y=2 }=0习题3-2 设随机变量),(Y X 的概率密度为⎩⎨⎧<<<<--=其它,0,42,20),6(),(y x y x k y x f(1) 确定常数k ; (2) 求{}3,1<<Y X P (3) 求{}5.1<X P ; (4) 求{}4≤+Y X P . 分析:利用P {(X , Y)∈G}=⎰⎰⎰⎰⋂=oD G Gdy dx y x f dy dx y x f ),(),(再化为累次积分,其中⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧<<<<=42,20),(y x y x D o解:(1)∵⎰⎰⎰⎰+∞∞-+∞∞---==2012)6(),(1dydx y x k dy dx y x f ,∴81=k (2)83)6(81)3,1(321⎰⎰=--=<<dy y x dxY X P (3)3227)6(81),5.1()5.1(425.10=--=∞<≤=≤⎰⎰dy y x dx Y X P X P (4)32)6(81)4(4020=--=≤+⎰⎰-dy y x dxY X P x习题3-3 将一枚硬币掷3次,以X 表示前2次出现H 的次数,以Y 表示3次中出现H 的次数,求Y X ,的联合分布律以及),(Y X 的边缘分布律。
《概率论与随机过程》第3章习题答案

《概率论与随机过程》第三章习题答案3.2 随机过程()t X 为()()ΦωX +=t cos A t 0式中,A 具有瑞利分布,其概率密度为()02222>=-a eaa P a A ,σσ,()πΦ20,在上均匀分布,A Φ与是两个相互独立的随机变量,0ω为常数,试问X(t)是否为平稳过程。
解:由题意可得:()[]()()002121020022222002222=⇒+=*+=⎰⎰⎰⎰∞--∞φφωπσφπσφωX E πσσπd t cos da e a a dad eat cos a t a a ()()()[]()()()()()()[]()()()()()12021202120202120202221202022021012022022202010022222200201021212122112210212212121221212222222222222t t cos t t cos t t cos det t cos da e e a t t cos dea d t t cos t t cos a d ea d t cos t cos da eaadad e at cos a t cos a t t t t R a a a a a a a -=-⨯=-⨯-=-⨯⎪⎩⎪⎨⎧⎪⎭⎪⎬⎫-∞+-=-⨯-=⎩⎨⎧⎭⎬⎫+++---=++=++==-∞∞---∞∞-∞--∞⎰⎰⎰⎰⎰⎰⎰⎰⎰ωσωσωσωωφφωωπσφπφωφωσφσπφωφωX X E σσσσπσπσσπXX )(,可见()[]t X E 与t 无关,()21t t R ,XX 与t 无关,只与()12t t -有关。
∴()t X 是平稳过程另解:()[][]0022000000[cos()][cos()][];(,)cos()cos(())cos()cos(())t E A t E A E t E A R t t E A t t E A E t t E X ωΦωΦτωΦωτΦωΦωτΦ⎡⎤=+=+=⨯=⎣⎦⎡⎤⎡⎤+=+++=+++⎣⎦⎣⎦[][][])cos()cos())cos((τωτωτωω0200022222A E t E A E =+Φ++= ∴()t X 是平稳过程3.3 设S(t) 是一个周期为T 的函数,随机变量Φ在(0,T )上均匀分布,称X(t)=S (t+Φ),为随相周期过程,试讨论其平稳性及各态遍历性。
最新概率论与数理统计第三章习题及答案

概率论与数理统计习题 第三章 多维随机变量及其分布习题3-1 盒子里装有3只黑球、2只红球、2只白球,在其中任取4只球.以X 表示取到黑球的只数,以Y 表示取到红球的只数,求X 和Y 的联合分布律.(X ,Y )的可能取值为(i , j ),i =0,1,2,3, j =0,12,i + j ≥2,联合分布律为 P {X=0, Y=2 }=351472222=C C C P {X=1, Y=1 }=35647221213=C C C C P {X=1, Y=2 }=35647122213=C C C C P {X=2, Y=0 }=353472223=C C C P {X=2, Y=1 }=351247121223=C C C C P {X=2, Y=2 }=353472223=C C C P {X=3, Y=0 }=352471233=C C C P {X=3, Y=1 }=352471233=C C C P {X=3, Y=2 }=0习题3-2 设随机变量),(Y X 的概率密度为⎩⎨⎧<<<<--=其它,0,42,20),6(),(y x y x k y x f(1) 确定常数k ; (2) 求{}3,1<<Y X P (3) 求{}5.1<X P ; (4) 求{}4≤+Y X P . 分析:利用P {(X , Y)∈G}=⎰⎰⎰⎰⋂=oD G Gdy dx y x f dy dx y x f ),(),(再化为累次积分,其中⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧<<<<=42,20),(y x y x D o解:(1)∵⎰⎰⎰⎰+∞∞-+∞∞---==2012)6(),(1dydx y x k dy dx y x f ,∴81=k (2)83)6(81)3,1(321⎰⎰=--=<<dy y x dxY X P (3)3227)6(81),5.1()5.1(425.10=--=∞<≤=≤⎰⎰dy y x dx Y X P X P (4)32)6(81)4(4020=--=≤+⎰⎰-dy y x dxY X P x习题3-3 将一枚硬币掷3次,以X 表示前2次出现H 的次数,以Y 表示3次中出现H 的次数,求Y X ,的联合分布律以及),(Y X 的边缘分布律。
概率论第三章部分习题解答PPT课件

(3 )E 3 Y E 3 2 X X 2 2 2 3 E 1 2 X E 2 X 2 3 1 .2 1 2 2 .1 0 6 .72 E 3 2 Y 1 4 E [X 2 (3 X )2 ] 1 4 ( 4 0 .4 3 4 0 .2) 8 0 .7 82
11的相关系数定义定理3定理5如果x不相关12十切比雪夫不等式与大数定律1切比雪夫不等式4伯努利大数定律3辛钦大数定律若方差一致有上界独立同分布在独立试验序列中事件a的频率按概率收敛于事件a一批零件有9个合格品与3个废品安装机器时从中任取一个
第三章 随机变量的数字特征
(一)基本内容 一、一维随机变量的数学期望
定义1:设X是一离散型随机变量,其分布列为:
X x 1 x 2 x i
P p(x1) p(x2 ) p(xi )
则随机变量X 的数学期望为: EXxipxi
i
定义2:设X是一连续型随机变量,其分布密度为 f x,
则随机变量X的数学期望为 EX xfxdx
.
1
二、二维随机变量的数学期望
(1)设二维离散随机变量(X,Y)的联合概率函数为p(xi , yj),则
0
.
17
5 设随机变量X 的概率密度为:
f x Ax2eax22 x0 (a0),求系数A及EX与D X.
0 x0
x2
解 f(x)d xA2e xa2d x1
0
令
x2 a2
t,即 xa
t,dx at1 2dt 2
x2
Ax2e a2
dx
0
A a2te tat 1 2d tA a3
概率论与数理统计教程(答案及课件)chapter3
,
则有
1 PZ x 2
e
x
du x
故
于是
Z
X
~ N 0 , 1 .
X ~ N , 2
X x FX x P X x P x
根据定理1,只要将标准正态分布的分布函数制 成表,就可以解决一般正态分布的概率计算问题.
2
设 X~ N ( , 2 ) ,
X 的分布函数是
2σ 2
F x
x 1 e 2πσ
( t μ )2
dt , x
正态分布由它的两个参数μ和σ唯一确定, 当μ和
σ不同时,是不同的正态分布。 下面我们介绍一种最重要的正态分布
标准正态分布
3
标准正态分布
7 (3)求P 1 X 2
解
kx , x f ( x ) 2 , 2 0,
0 x3 3 x4 其它
(1) 由
0
1 f ( x )dx 1得k 6
3
4
x
F x
x
f t dt , x
x2 x1
f ( x )dx
利用概率密度可确 定随机点落在某个 范围内的概率
4
若 f (x) 在点 x 处连续 , 则有
F ( x ) f ( x ).
5. 对连续型 r.v X , 有
P (a X b) P (a X b) P (a X b) P (a X b)
F(x) = P(X x) x<0 时,{ X x } = , 故 F(x) =0 0 x < 1 时, 1 F(x) = P{X x} = P(X=0) = 3
概率论习题解答
证明: 记
F1(x) = 1(0,∞)(x),
1 F (x) = F (x) − 3 F1(x).
令
F2(x)
=
3 2
F
(x),
则
F1
和
F2
分别是离散型和连续型分布函数,
且
1
2
F (x) = 3 F1(x) + 3 F2(x),
即 F 可以写成离散型和连续型分布函数的线性组合.
§3.2.4 练习题
练习3.2.1 向目标进行 20 次独立的射击, 假定每次命中率均为 0.2. 试求至少命中 19 次的概率.
∪
{ξ x} =
Ak
k:ak x
练习3.1.5 若 F 为 ξ 的分布函数, 试证明如下等式
P(ξ = x) = F (x) − F (x−), P(ξ > x) = 1 − F (x), P(a < ξ b) = F (b) − F (a).
证明: 由概率的上连续性得 (
F (x) − F (x−) = P(ξ x) − lim P ξ
练习3.2.8 广义 Bernoulli 实验中假定一实验有 r 个可能结果 A1, A2, · · · , Ar, 并且 P(Ai) = pi > 0, p1 + p2 + · · · + pr = 1. 现将此实验独立地重复 n 次.求 A1 恰出现入 k1 次, · · · , Ar 恰出现 kr 次(ki 0, k1 + k2 + · · · + kr = n)的概率.
设 D = {a1, a2, · · · }, 定义
{
p(x) =
dF (x) dx
,
《概率论》数学3章课后习题详解
概率论第三章习题参考解答1. 如果ξ服从0-1分布, 又知ξ取1的概率为它取0的概率的两倍, 求ξ的期望值 解:由习题二第2题算出ξ的分布率为ξ0 1 P1/32/3因此有E ξ=0×P (ξ=0)+1×P (ξ=1)=2/3+2η, ξ与η的分布律如下表所示:: 求周长的期望值, 用两种方法计算, 一种是利用矩形长与宽的期望计算, 另一种是利用周长的分布计算.解: 由长和宽的分布率可以算得E ξ=29×P (ξ=29)+30×P (ξ=30)+31×P (ξ=31) =29×0.3+30×0.5+31×0.2=29.9E η=19×P (η=19)+20×P (η=20)+21×P (η=21) =19×0.3+20×0.4+21×0.3=20 由期望的性质可得E ζ=2(E ξ+E η)=2×(29.9+20)=99.8而如果按ζ的分布律计算它的期望值, 也可以得E ζ=96×0.09+98×0.27+100×0.35+102×0.23+104×0.06=99.8 验证了期望的性质.4. 连续型随机变量ξ的概率密度为⎩⎨⎧><<=其它)0,(10)(a k x kx x aϕ又知Eξ=0.75, 求k 和a 的值。
解: 由性质⎰+∞∞-=1)(dx x ϕ得111)(|10110=+=+==++∞∞-⎰⎰a kx a k dx kx dx x a aϕ即k =a +1(1)又知75.022)(|10211=+=+===+++∞∞-⎰⎰a kx a k dx kx dx x x E a a ϕξ得k =0.75a +1.5(2)由(1)与(2)解得0.25a =0.5, 即a =2, k =36. 下表是某公共汽车公司的188辆汽车行驶到发生一次引擎故障的里程数的分布数列.若表中各以组中值为代表. 从188辆汽车中, 任意抽选15辆, 得出下列数字: 90, 50, 150, 110, 90, 90, 110, 90, 50, 110, 90, 70, 50, 70, 150. (1)求这15个数字的平均数; (2) 计算表3-9中的期望并与(1)相比较.解: (1) 15个数的平均数为(90+50+150+110+90+90+110+90+50+110+90+70+50+70+150)/15 = 91.33 (2) 按上表计算期望值为(10×5+30×11+50×16+70×25+90×34+110×46+130×33+150×16+170×2)/188 =96.177. 两种种子各播种300公顷地, 调查其收获量, 如下表所示, 分别求出它们产量的平均值解: 假设种子甲的每公顷产量数为, 种子乙的每公顷产量数为, 则 E ξ=(4500×12+4800×38+5100×40+5400×10)/100=4944 E η=(4500×23+4800×24+5100×30+5400×23)/100=49598. 一个螺丝钉的重量是随机变量, 期望值为10g , 标准差为1g . 100个一盒的同型号螺丝钉重量的期望值和标准差各为多少?(假设各个螺丝钉的重量相互之间独立) 解: 假设这100个螺丝钉的重量分别为ξ1, ξ2,…, ξ100, 因此有E ξi =10, Dξi =102=12=1, (i =1,2,…,100), 设ξ为这100个螺丝钉的总重量,因此∑==1001i i ξξ,则ξ的数学期望和标准差为gD D D kgg E E E i ii i i i i i 1011001)(1000101001001100110011001=⨯==⎪⎭⎫⎝⎛====⨯==⎪⎭⎫ ⎝⎛=∑∑∑∑====ξξξσξξξξ9. 已知100个产品中有10个次品,求任意取出的5个产品中次品数的期望值.解: 假设ξ为取出5个产品中的次品数, 又假设ξi 为第i 次取出的次品数, 即, 如果第i 次取到的是次品, 则ξi =1否则ξi =0, i =1,2,3,4,5, ξi 服从0-1分布,而且有 P {ξi =0}=90/100, P {ξi =1}=10/100, i =1,2,3,4,5因此, E ξi =10/100=1/10, 因为∑==51i iξξ因此有5.010155151=⨯==⎪⎭⎫ ⎝⎛=∑∑==i i i i E E E ξξξ10. 一批零件中有9个合格品和3个废品, 在安装机器时, 从这批零件中任取一个, 如果取出的是废品就不再放回去. 求取得第一个合格品之前, 已经取出的废品数的数学期望和方差. 解: 假设在取到第一个合格品之前已取出的废品数为ξ, 则可算出0045.02201101112123}3{041.02209109112123}2{2045.0119123}1{75.0129}0{==⋅⋅====⋅⋅===⋅=====ξξξξP P P P因此有319.009.0409.0)(409.090045.04041.02045.03.030045.02041.02045.0222===-==⨯+⨯+==⨯+⨯+=ξξξξξE E D E E11. 假定每人生日在各个月份的机会是同样的, 求3个人中生日在第一个季度的平均人数. 解: 设三个随机变量ξi ,(i =1,2,3), 如果3个人中的第i 个人在第一季度出生, 则ξi =1, 否则ξi =0, 则ξi 服从0-1分布, 且有 P (ξi =1)=1/4, 因此E ξi =1/4, (i =1,2,3)设ξ为3个人在第一季度出生的人数, 则ξ=ξ1+ξ2+ξ3, 因此Eξ=E (ξ1+ξ2+ξ3)=3Eξi =3/4=0.7512. ξ有分布函数⎩⎨⎧>-=-其它1)(x e x F xλ, 求E ξ及D ξ. 解: 因ξ的概率密度为⎩⎨⎧>='=-其它)()(x e x F x xλλϕ, 因此 ()λλλϕξλλλλλ11)(0=-=+-=-===∞+-∞+-∞+-+∞-+∞-+∞∞-⎰⎰⎰⎰xx xxxe dx e xe e xd dx ex dx x x E()2220222222)(|λξλλϕξλλλλ==+-=-===⎰⎰⎰⎰∞+-∞+-+∞-+∞-+∞∞-E dx xe ex e d x dx ex dx x x E x x x x22222112)(λλλξξξ=-=-=E E D13. ⎪⎩⎪⎨⎧<-=其它1||11)(~2x x x πϕξ, 求E ξ和D ξ.解: 因φ(x )是偶函数, 因此Eξ=0,则D ξ=Eξ2-(Eξ)2=Eξ2 因此有⎰⎰-===+∞∞-1222212)(dx xx dx x x E D πϕξξ令θθθd dx x cos ,sin ==则上式=2112sin 21212cos 2sin 12||20202022=+=+=⎰⎰ππππθπθπθθπθθπd d 即D ξ=1/2=0.516. 如果ξ与η独立, 不求出ξη的分布直接从ξ的分布和η的分布能否计算出D (ξη), 怎样计算?解: 因ξ与η独立, 因此ξ2与η2也独立, 则有[]()()222222)()()(ηξηξξηξηξηE E E E E E D -=-=17. 随机变量η是另一个随机变量ξ的函数, 并且η=e λξ(λ>0), 若E η存在, 求证对于任何实数a 都有λξλξEe ea P a⋅≤≥-}{.证: 分别就离散型和连续型两种情况证. 在ξ为离散型的情况: 假设P (ξ=x i )=p i , 则λξλξλλλξEe e e E p e p ep a P a a i i a x ax i a x ax i i i i i --∞=-≥-≥==≤≤=≥∑∑∑][){)(1)()(在ξ为连续型的情况假设ξ的概率密度为φ(x ), 则λξλξλλλϕϕϕξEe e Ee dx x e dx x edx x a P a a a x aa x a--+∞∞--+∞-+∞==≤≤=≥⎰⎰⎰)()()()()()(}{证毕.18. 证明事件在一次试验中发生次数的方差不超过1/4.证: 设ξ为一次试验中事件A 发生的次数, 当然最多只能发生1次, 最少为0次, 即ξ服从0-1分布, P {ξ=1}=P (A )=p , P {ξ=0}=1-p =q ,则4121412124141)1(222≤⎪⎭⎫ ⎝⎛--=-⋅+-=-=-=p p p p p p p D ξ19. 证明对于任何常数c , 随机变量ξ有 D ξ=E (ξ-c )2-(Eξ-c )2证: 由方差的性质可知D (ξ-c )=Dξ, 而2222)()()]([)()(c E c E c E c E c D ---=---=-ξξξξξ证毕.20. (ξ,η)的联合概率密度φ(x ,y )=e -(x +y )(x ,y >0), 计算它们的协方差cov (ξ,η). 解: 由φ(x ,y )=e -(x +y )(x ,y >0)可知ξ与η相互独立, 因此必有cov (ξ,η)=0.21. 袋中装有标上号码1,2,2的3个球, 从中任取一个并且不再放回, 然后再从袋中任取一球, 以ξ, η分别记为第一,二次取到球上的号码数, 求ξ与η的协方差.,P {ξ=2}=P {η=2}=2/3, P {ξ=1}=P {η=1}=1/3, E ξ=E η=35322311=⨯+⨯38314312312},{)(2121=⨯+⨯+⨯====∑∑==i j j i ijP E ηξξη则913538)(),cov(22-=-=⋅-=ηξξηηξE E E22. (ξ , η)只取下列数组中的值:)0,2()31,1()1,1()0,0(--且相应的概率依次为1/6, 1/3, 1/12, 5/12. 求ξ与η的相关系数ρ, 并判断ξ与η是否独立? 解: ξ与的联合分布表及各边缘分布计算表如下表所示: 因此1212260121=⨯+⨯+⨯-=ξE 1225125412512=⨯+⨯=ξE 144275144251225)(22=-=-=ξξξE E D 3613311121311270=⨯+⨯+⨯=ηE 1083731121912=+⨯=ηE 129627512961691237129616910837)(22=-⨯=-=-=ηηηE E D 36133112131)(-=-⨯-=ξηE则4322211236171336131253613)(),cov(-=⨯⨯-=⋅--=⋅-=ηξξηηξE E E 相关系数804.027522127543236122211296275144275432221),cov(-=-=⨯⨯⨯-=⨯-==ηξηξρD D, 计算ξ与η的相关系数ρ, 并判断ξ与η是否独立? 解: 由上表的数据的对称性可知与η的边缘分布一样, 算出为 P (ξ=-1)=P (η=-1)=3/8 P (ξ=0)=P (η=-0)=2/8P (ξ=1)=P (η=1)=3/8 由对称性可知Eξ=Eη=0831831=⨯+⨯-. 081818181)(=+--=ξηE 因此cov (ξ,η)=E (ξη)-E (ξ)E (η)=0 则ρ=0而P (ξ=0,η=0)=0≠P {ξ=0}P {η=0}=1/16因此ξ与η不独立. 这是一个随机变量间不相关也不独立的例子.24. 两个随机变量ξ与η, 已知Dξ=25, Dη=36, ρξη=0.4, 计算D (ξ+η)与D (ξ-η). 解:374.065236252),cov(2)]()[()]([)(854.065236252),cov(2)]()[()]([)(2222=⨯⨯⨯-+=-+=-+=---==---=-=⨯⨯⨯++=++=++=-+-==+-+=+ξηξηρηξηξηξηξηηξξηξηξηξρηξηξηξηξηηξξηξηξηξD D D D D D E E E E E D D D D D D D E E E E E D《概率论与数理统计》复习资料一、填空题(15分)题型一:概率分布的考察 【相关公式】(P379)【相关例题】 1、设(,)XU a b ,()2E X =,1()3D Z =,则求a ,b 的值。
概率论课后习题答案第三章
概率论课后习题答案第三章第三章概率论课后习题答案概率论是一门研究随机现象的数学学科,它在现代科学和工程领域中有着广泛的应用。
而习题则是巩固和加深对概率论知识的理解和应用的重要手段。
在第三章的习题中,我们将探讨一些与随机变量和概率分布相关的问题,并给出相应的答案和解析。
1. 设随机变量X服从参数为λ的指数分布,即X~Exp(λ),其概率密度函数为f(x) = λe^(-λx),x≥0。
求以下概率:(a) P(X > 2)(b) P(X ≤ 1)(c) P(1 ≤ X ≤ 3)答案:(a) P(X > 2) = ∫[2,∞] λe^(-λx) dx = e^(-2λ)(b) P(X ≤ 1) = ∫[0,1] λe^(-λx) dx = 1 - e^(-λ)(c) P(1 ≤ X ≤ 3) = ∫[1,3] λe^(-λx) dx = e^(-λ) - e^(-3λ)解析:根据指数分布的性质,我们可以利用概率密度函数求解概率。
对于(a),我们计算X大于2的概率,即求解X在区间[2,∞]上的概率密度函数的积分。
对于(b),我们计算X小于等于1的概率,即求解X在区间[0,1]上的概率密度函数的积分。
对于(c),我们计算X在1到3之间的概率,即求解X在区间[1,3]上的概率密度函数的积分。
2. 设随机变量X服从参数为μ和σ^2的正态分布,即X~N(μ,σ^2),其概率密度函数为f(x) = (1/(σ√(2π))) * e^(-(x-μ)^2/(2σ^2)),-∞<x<∞。
求以下概率:(a) P(X > μ)(b) P(X ≤ μ)(c) P(μ-σ ≤ X ≤ μ+σ)答案:(a) P(X > μ) = 1 - P(X ≤μ) = 1 - 0.5 = 0.5(b) P(X ≤ μ) = 0.5(c) P(μ-σ ≤ X ≤ μ+σ) = P(X ≤ μ+σ) - P(X ≤ μ-σ) = 0.6827 - 0.3173 =0.3654解析:对于正态分布,我们可以利用概率密度函数求解概率。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1⎛ 1 1 ⎞ = ⎜ 6 xy − x 2 y − xy 2 ⎟ 9⎝ 2 2 ⎠ P{ X ≤ 0.5, Y ≤ 1.5}=F ( 0.5,1.5 ) − F ( 0.5, 0 ) + F ( 0, 0 ) − F ( 0,1.5 ) = 5 12
(3) 8.
8 . 27
(1)
⎧2e − ( 2 x + y ) , f ( x, y ) = ⎨ ⎩0,
pij p i⋅
, j = 1,2, "
在 X = 2 的条件下, Y 的条件分布律;
P{Y = 1| X = 2} = 0 P{Y = 2 | X = 2} = 1 6
P{Y = 3 | X = 2} = 0 P{Y = 4 | X = 2} = 1 6
1 =0. 3 1 1 = . 3 2 1 = 0. 3 1 1 = . 3 2
∫∫ 4dxdy
y⎞ ⎛ = 4 S梯形 = 2 y ⎜ 1 − ⎟ ⎝ 2⎠
三角形
∫∫
4dxdy = 4S三角形 = 1
1 ⎧ 0, x < − 或y < 0; ⎪ 2 ⎪ 1 ⎪ y (4 x + 2 − y ), − ≤ x < 0,0 ≤ y < 2 x + 1; ⎪ 2 . F ( x, y ) = ⎨ y (2 − y ), x ≥ 0,0 ≤ y < 1; ⎪ 1 ⎪ (2 x + 1) 2 , − ≤ x < 0, y ≥ 2 x + 1; ⎪ 2 ⎪ 1 x ≥ 0, y ≥ 1. ⎩
14. 由 x 轴, y 轴以及直线 y = 2(1 − x) 所围成的三角形区域的面积 B = 1 , 因此 ( X , Y ) 的概率密度函数为:
1 = 0. 6 1 = 1. 6 1 =0. 6 1 = 0. 6
3 0 4 0
X
P
1 0
2 1
(2) X 的边缘分布律 P{ X = 2} = p2⋅ = p21 + p22 + p23 + p24 = 0 + 由条件分布率
1 1 1 +0+ = 6 6 3
P{Y = y j | X = xi } =
1 16 1 12 1 48 1 12
Y
X
1 2 3 4
1
2
3
4
1 6
0
0
1 6
0 0 0
0
1 6
0
1 6
0 0
1 6
0
1 6
(1) Y 的边缘分布律 P{Y = 4} = p⋅4 = p14 + p24 + p34 + p44 = 0 + 由条件分布率
1 1 +0+0 = 6 6
P{ X = xi | Y = y j } =
F ( x, y ) = ∫ y x
当x > 0, y > 0时, 其它,
f (u , v) dudv −∞ ∫ −∞
⎧ y x − (2u + v ) dudv = (1 − e −2 x )(1 − e − y ), y > 0, x > 0 2e ⎪ = ⎨∫ 0 ∫ 0 ⎪ 0 其它 ⎩
1 . 3 P{ X < Y } = ∫∫ f ( x, y )dxdy =
∫
⎡⎛ 1 1 = a ⎢⎜ 6 y − y 2 − 2 2 ⎣⎝
= 9a
⎞ 2⎤ y ⎟ |0 ⎥ ⎠ ⎦
9a =1,a =
(2)
1 9
5 ; 12
x y F ( x, y ) = ∫ −∞ ∫ −∞ f (u , v)dudv
= =
1 x y ∫ 0 ∫ 0 ( 6 − u − v ) dudv 9 1 y⎛ 1 ⎞ ∫ 0 ⎜ 6 x − x 2 − vx ⎟ dv 9 ⎝ 2 ⎠
1 时, F ( x, y ) = P {Φ} = 0 2
(b)
当−
1 < x ≤ 0 时, 2
y ≤ 0时,f ( x, y ) = 0, 所以,F ( x, y ) = 0
0 < y ≤ 2 x + 1时, F ( x, y ) =
梯形
∫∫ 4dxdy
y⎞ ⎛ = 4 S梯形 = 2 y ⎜ 2 x + 1 − ⎟ 2⎠ ⎝ 1⎞ ⎛ = 4⎜ x + ⎟ 2⎠ ⎝
所以
1 ⎧ ⎧2(1 − y ), 0 ≤ y < 1 ⎪4(2 x + 1), − ≤ x < 0 f X ( x) = ⎨ ; f Y ( y) = ⎨ ;1. 2 0, 其它 ⎩ ⎪ 0 , 其它 ⎩
12.
⎧3 2 ⎪ xy , f ( x, y ) = ⎨ 2 ⎪ ⎩0,
+∞
当0 ≤ x ≤ 2,0 ≤ y ≤ 1时, 其它,
1
x2 fY ( y ) = ∫ f ( x , y ) dx = ∫ 4.8 y (2 − x ) dx = 4.8 y (2 x − ) y −∞ 2
所以
= 2.4 y (3 − 2 y +
y
y2 ) 2
⎧2.4 x 2 (2 − x), 0 ≤ x ≤ 1 ⎧2.4 y (3 − 4 y + y 2 ), 0 ≤ y ≤ 1 ; f Y ( y) = ⎨ . f X ( x) = ⎨ 0, 其它 0, 其它 ⎩ ⎩
3 10 3 10 3 5
3 10 1 10 2 5
3 5 2 5
此结果说明不同的联合分布律可以确定相同的边缘分布律,因此边缘分布不能唯一确定联合分布. 4. (1) ( X , Y ) 的联合分布律为
Y
X
-1 0 (2) 离散型随机变量 X 和 Y 的联合分布函数为
0
1 0
1 2 1 3
F ( x, y ) = P{ X ≤ x, Y ≤ y} F ( x, y ) = ∑ ∑ pij
(2)
D
x< y
∫∫ f ( x, y)dxdy
=∫ =∫
+∞ ⎡ y − (2 x + y ) ⎤ +∞ − y e dx dy = e [1 − e−2 y ]dy 2 ⎢ ⎥ ∫ ∫ 0 ⎣ 0 0 ⎦ +∞ 0 e − y dy − ∫ +∞ 1 2 e −3 y dy = 1 − = 0 3 3
{
X 2 +Y2 < z
}
∫∫
f (u, v)dudv
1 dudv 2 2 2 ) + v 2 2 2 π (1 + u u +v < z
∫∫
令⎨
⎧ x = r cos θ ,则变换的雅可比行列式为 ⎩ y = r sin θ ∂x cos θ ∂θ = ∂y sin θ ∂θ −r sin θ = r, r cos θ
1
13 2 xy 3 f X ( x) = ∫ f ( x , y ) dy = ∫ xy dy = 02 −∞ 2 +∞ 23
2
=
0 2
x , 2 = 3y2,
3x2 y 2 fY ( y ) = ∫ f ( x , y ) dx = ∫ xy dx = 02 −∞ 4
所以
0
⎧x ⎧3 y 2 , 0 ≤ y ≤ 1 ⎪ , 0≤ x≤2 f X ( x) = ⎨ 2 ; f Y ( y) = ⎨ . 0 , 其它 ⎩ ⎪ 其它 ⎩ 0,
y=2x+1
-1/2
由 x 轴, y 轴以及直线 y = 2 x + 1 所围成的三角形区域的面积 B = 因此 ( X , Y ) 的概率密度函数为:
1 , 4
1 ⎧ ⎪4, (− < x < 0, 0 < y < 2 x + 1) f ( x, y ) = ⎨ ; 2 ⎪ ⎩0, 其他
(2)分布函数为: F ( x, y ) = P { X < x, Y < y} (a)当ቤተ መጻሕፍቲ ባይዱx ≤ −
9. 由题意知命中点与靶心(坐标原点)的距离为 Z = 当 z ≤ 0 时, Fz ( Z ) = P {Z < z} = P 当 z > 0 时,
X 2 + Y 2 ,先求 Z 的分布函数,
{
X 2 +Y2 < z = 0
}
Fz ( Z ) = P {Z < z} = P = =
u 2 + v2 < z
1⎫ 1⎫ 1 1 ⎧ ⎧ P ⎨ X = -2, Y = - ⎬ = P { X = -2} ⋅ P ⎨Y = - ⎬ = ⋅ 2⎭ 2⎭ 4 2 ⎩ ⎩
以此类推,得到下表
Y
X
-
1 2
1
3
-2 -1 0
1 2
6. ( X , Y ) 的分布律
1 8 1 6 1 24 1 6
1 16 1 12 1 48 1 12
z
∂x ∂r J= ∂y ∂r
故 Fz ( Z ) =
∫
2π
0
dθ ∫
z
0
r 1 dr = 2π ⋅ 2 2 π (1 + r ) 2π
1 ⎤ 1 z2 ⎡ − = − = 1 2 ⎢ 1+ z2 1+ z2 ⎣ 1+ r ⎥ ⎦0
a2 Fz ( a ) = 1 + a2
a2 . 1+ a2
10. (1)
2
y > 2 x + 1时, F ( x, y ) =
(c)
三角形
∫∫
4dxdy = 4 S三角形
当 x > 0 时,
