§7—2机械系统的等效动力学模型
机械系统的动力学建模与仿真分析

机械系统的动力学建模与仿真分析一、引言机械系统是由多个相互作用的部件组成的复杂系统,其动力学行为是研究的核心问题之一。
动力学建模与仿真分析可以帮助工程师深入理解机械系统的运动规律,预测系统的性能,并优化设计。
本文将介绍机械系统的动力学建模方法以及仿真分析技术。
二、动力学建模1. 基本原理机械系统的动力学建模是基于牛顿力学的基本原理进行的。
通过分析受力、受力矩以及质量、惯性等因素,可以建立机械系统的运动方程。
在建立方程时,需要考虑系统的自由度、刚体或者弹性体的运动特性以及约束条件等因素。
2. 运动学建模运动学建模是机械系统动力学建模的前提。
通过研究机械系统的几何结构和运动规律,可以得到系统的等效长度、转动角度等信息。
基于运动学建模,可以计算系统的速度、加速度以及运动的轨迹等。
3. 动力学建模动力学建模是机械系统分析的核心部分。
基于受力和受力矩的平衡条件,可以建立机械系统的运动方程。
通常采用牛顿第二定律和力矩平衡条件,可以得到刚体的平动和旋转方程。
对于复杂的非线性系统,也可以采用拉格朗日方程或者哈密顿原理进行建模。
三、仿真分析1. 数值解算方法为了求解机械系统的运动方程,需要采用适当的数值解算方法。
常见的方法包括欧拉法、龙格-库塔法、变步长积分法等。
这些方法可以将微分方程离散化,然后通过迭代计算求解系统的状态变量。
2. 动力学仿真动力学仿真是建立在动力学模型的基础上。
通过将模型转化成计算机程序,可以在计算机上模拟机械系统的运动行为。
通过仿真分析,可以研究系统的稳定性、动态响应以及力学性能等。
3. 优化设计动力学仿真还可以应用于优化设计。
通过改变系统参数、构型和控制策略等,可以研究不同设计方案的性能差异,并选择最佳方案。
通过仿真分析,可以避免实际试验的成本和时间消耗。
四、案例分析以汽车悬挂系统为例,进行动力学建模与仿真分析。
汽车悬挂系统是一个典型的机械系统,包含减震器、弹簧、悬挂臂等部件。
首先进行运动学建模,分析车轮的运动状态和轨迹。
第七章 机械系统的动力学分析

§7-2 单自由度机械系统动力学分析
3、等效动力学模型的意义
等效力学模型
等效构件 + 等效质量(转动惯量) + 等效力(力矩)
Je
Me
注意: 、、S、V是某构件的真实运动;
Me是系统的等效力矩;
Je是系统的等效转动惯量。
Fe
me
ve
Fe是系统的等效力; me是系统的等效质量。
例题:图示机构。已知z1=20,J1;z2=60,质量中心在B点,
§7-1 概 述
机构力分析的目的和方法
目的: 1)求驱动力。用以确定所需功率,选择合适的电动机。
2)求生产阻力。根据原动件上驱动力的大小,确定机
械所能克服的生产阻力。 3)求机构运动副中的反力。该力大小和性质是零件设
计计算和强度计算的重要依据。
方法:图解法和解析法
§7-1 概 述
二、机械的运转过程 机械运转中的功能关系 Wd - Wc = E2 – E1 其中:Wc = Wr+ Wf 1、 起动阶段: ω=0,↗ωm , 则:E1 =0,↗E2, W= E=E2-E1 >0 故:Wd > Wc = Wr +Wf 主动件作加速运动。
启
动
Wd-Wc=E2-E1>0
稳定运行
Wd-Wc=E2-E1=0
停
车
原动件速度从正常工作速 度值下降到零
Wd-Wc=E2-E1<0
§7-2 单自由度机械系统动力学分析
为了便于讨论机械系统在外力作用下作 功和动能变化,将整个机械系统多个构件运
动问题根据能量守恒原理转化成对某个构件
的运动问题进行研究。为此引入等效转动惯
等效力可以根据等效前后功率相等的原则求取。
第7章机械动力学
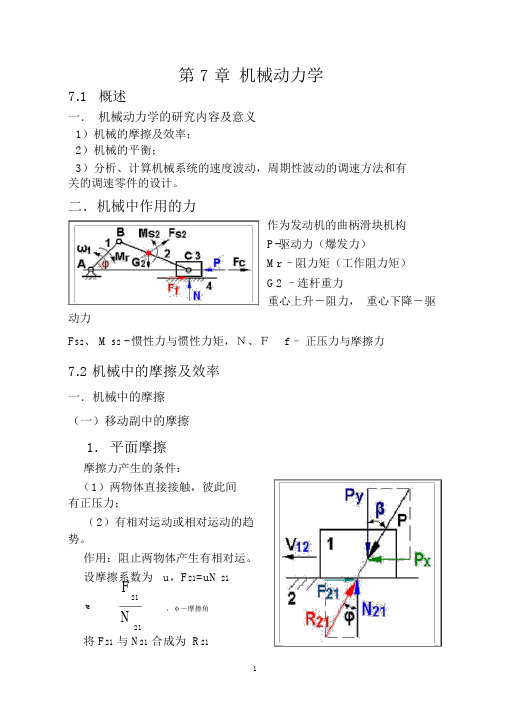
第 7 章机械动力学7.1概述一.机械动力学的研究内容及意义1)机械的摩擦及效率;2)机械的平衡;3)分析、计算机械系统的速度波动,周期性波动的调速方法和有关的调速零件的设计。
二.机械中作用的力作为发动机的曲柄滑块机构P-驱动力(爆发力)Mr –阻力矩(工作阻力矩)G2 –连杆重力重心上升-阻力,重心下降-驱动力F S2、 M S2 - 惯性力与惯性力矩,N、F f –正压力与摩擦力7.2 机械中的摩擦及效率一.机械中的摩擦(一)移动副中的摩擦1.平面摩擦摩擦力产生的条件:(1)两物体直接接触,彼此间有正压力;(2)有相对运动或相对运动的趋势。
作用:阻止两物体产生有相对运。
设摩擦系数为u,F21=uN 21F21tg,φ-摩擦角N21将 F21与 N21合成为 R21R21-总反力(全反力)P X P分解为 P和 P ,tgX Y P Y( P X P sin、 P Y P cos )F21P X,有F21tgY 方向平衡: Py=N 21,即:tg tg P Xtg讨论:①总反力 R21恒与相对速度V 12成 90° +φ②当β >φ, P X > F21,滑块作加速运动;当β =φ, P X = F21,动则恒动,静则恒静;当β <φ, P X < F21,原来运动,作减速运动,原来静止,永远静止,称自锁。
③ 自锁条件:β≤φβ=φ,条件自锁(静止);β<φ,无条件自锁。
2.斜面摩擦斜面机构如图,滑块置于升角α的斜面上,摩擦角为φ,作用于滑块上的铅垂力为Q,求滑块等速上升和下降时所需水平平衡力P 和 P’。
(1)求等速上升水平平衡力 PP-驱动力, Q-阻力PQ R 21 0 ,tg ()P,P Qtg () (1)Q( 2)求等速下降水平平衡力 P ’Q -驱动力, P ’-阻力P'Q R 21 0 ,tg () P ',P 'Qtg () (2)Q讨论:① 欲求下滑 (反行程) P ’,只需将式 ( 1)中 P →P ’,φ→ (-φ )② 下滑时,当α >φ, P ’为平衡力α <φ, P ’为负,成为驱动力的一部分,该条件下,若无 P ’,则无论 Q 多大,滑块不下滑,称自锁,自锁条件:α≤φ。
机械原理速度波动

9J1 J 2 m3 l 2 m4 l 2 sin2 2
2)求M e
瞬时功率不变 Me2 M11 F4 cos180(v4 ) Me M1 (1 / 2 ) F4 cos180(v4 / 2 )
说明
M1(z2 / z1 ) F4 (2l sin2 /2 ) 3M1 F4l sin2
Fr r3 144
整个传动系统的等效力矩为
Me
Med
Mer
Md
Fr r3 144
三、其他形式表达的机械运动方程式
1. 以回转构件为等效构件时
1)力矩形式的机械运动方程式
d[ J e
( 1 2
)
2 1
]
Me
(1 ,1
,
t ) 1dt
2
d(Je
2
2
)
M edt
M ed
d(Je 2
d
)
Me
2
Je
d( 2
me
dv dt
v2 2
dme ds
Fe
2)动能形式的机械运动方程式:
1
2
me v 2
1 2
me
v
2 0
s
S0 Feds
§7-3 机械运动方程的求解
(一) 机械运动方程 利用等效动力学模型方法,只要能解出等效构件的运动 规律,即可以用运动分析方法求出整个系统中所有构件的运 动规律。
(二)运动方程求解 方法 图解法、解析法、数值方法 数值方法已成为机械系统真实运动规律分析的常用方 法。
2 Si
/
2
J
Si
2 i
/
2)]
[
(Fi vi cos i M i i )]dt
机械原理》机械的运转及其速度波动的调节

动可通过建立等效构件的运动方程式求解。
2. 能量形式的运动方程式
➢以回转构件为等效构件时
d[
1 2
Je ( ) 2 ]
Me ( , , t)dt
d
J
e
2
2
Me ( , , t)dt
Med
d
J
e
2
2
Me ( , , t)dt
Med
d (Je 2 d
/ 2)
Me
Je
d( 2 / d
2)
2
功能关系: Wd=Wc
ωm
启动
稳定运转
匀速稳定运转时,速度不需要调节。
后两种情况由于速度的波动,会产生以下不良后果:
①在运动副中引起附加动压力,加剧磨损,使工作可靠性降低。 ②引起弹性振动,消耗能量,使机械效率降低。 ③影响机械的工艺过程,使产品质量下降。 ④载荷突然减小或增大时,发生飞车或停车事故
ω
ωm
此阶段分三种情况: ① =常数——等速稳定运转
t
启动 稳定运转 停止
② 常数,但在正常工作速度的平均值m上下作周期性速度 波动——周期变速稳定运转
ω
ω
起动
稳定运转 图11-1
停车
③非周期变速稳定运转
ω
❖功(率)特征:Wd-WcT=0 ❖动能特征:E= Wd-WcT=0 ❖速度特征:t=T+t
1. 起动阶段——原动件的速度由零逐渐上升到开始稳定的过程。
❖功(率)特征:外力对系统做正功 Wd-Wc>0
❖动能特征:系统的动能增加 E=Wd-Wc>0 ❖速度特征:系统的速度增加 =0m
功能关系: Wd=Wc+E
2. 稳定运转阶段 ——原动件速度保持常数或在正常工作速度的平均
飞轮的转动惯量

Me — 等效力
me— 等效
质量
故其运动方程式为:
1 2 d ( me v3 ) FeV3 dt 2
取转动构件为等效构件,则:
取移动构件为等效构件,则:
Je
Me Fe me ve
转动构件为等效构件
移动构件为等效构件
§7—4 机械运转和速度波动的调节
1、机械速度波动产生原因
以曲柄滑块机构为例。 取曲柄1为等效构件。 t 令 J e J1 J S 2 (
vS 2 2 v3 2 2 2 ) m2 ( ) m3 ( ) 1 1 1
Me — 等效力矩
Je— 等效转 动惯量
Me = M1-F3(v3/ω1)
故其运动方程式为: d ( 1 J e 12 ) M e 1 dt 2
第七章 机械动力学分析
提示:本章介绍机械运转时产生速度波动的原因
及调节的方法;机械系统的等效力学模型 的建立;飞轮的设计。 重点:机械系统的等效力学模型的建立;机械运 转时产生速度波动的原因及调节的方法。 难点:等效转动惯量、等效力的计算;最大盈亏功 的计算。
§7—1 概述
一、本章研究的内容及目的
图示某一机械在稳定运转
过程中,等效构件在一个周期
T中所受等效驱动力矩Mer() 与等效阻抗力矩Mer()的变化 曲线。驱动功与阻抗功为:
Wd ( )
Wr ( )
M
a
d
( )d
M
a
r
( ) d
则机械动能的增量为:
E Wd Wr [ M d ( ) M r ( )]d J e ( ) 2 / 2 J ea ( ) a2 / 2
机械系统的等效力学模型
温馨小提示:本文主要介绍的是关于机械系统的等效力学模型的文章,文章是由本店铺通过查阅资料,经过精心整理撰写而成。
文章的内容不一定符合大家的期望需求,还请各位根据自己的需求进行下载。
本文档下载后可以根据自己的实际情况进行任意改写,从而已达到各位的需求。
愿本篇机械系统的等效力学模型能真实确切的帮助各位。
本店铺将会继续努力、改进、创新,给大家提供更加优质符合大家需求的文档。
感谢支持!(Thank you for downloading and checking it out!)机械系统的等效力学模型一、引言随着科技的不断发展,机械系统在工程领域的应用越来越广泛,但其复杂性也随之增加。
为了更好地理解和优化这些系统,等效力学模型应运而生。
这种模型能够将复杂的机械系统简化为等效的力学模型,从而便于分析和研究。
背景及意义等效力学模型在机械系统的研究中具有重要的背景及意义。
首先,等效力学模型可以有效地简化复杂的机械系统,使之更易于理解和分析。
其次,通过等效力学模型,研究人员可以更方便地探索机械系统的性能和稳定性,从而为设计和优化提供有力的支持。
此外,等效力学模型还可以为机械系统故障诊断和预测提供重要的参考依据。
研究目的与任务本文的主要目的是研究机械系统的等效力学模型,并探讨其在工程领域的应用。
具体任务包括:首先,对等效力学模型的基本原理进行介绍和阐述;其次,通过实例分析,展示等效力学模型在机械系统研究中的应用;最后,对等效力学模型的优缺点进行总结和评价,并提出未来的研究方向和应用前景。
通过本文的研究,希望能为机械系统的设计、分析和优化提供一定的参考价值,同时也为等效力学模型在工程领域的应用提供新的思路和方向。
二、机械系统等效力学模型的建立方法等效力学模型的定义等效力学模型是指将实际的机械系统通过一定的简化与变换,建立一个在数学描述上等效的系统,以方便研究和分析。
等效力学模型能够保持原系统的主要动态特性,同时简化系统的复杂性,使问题易于处理和分析。
机械原理第7章 机械的运转及其速度波动的调节 (1)
(3)一般形式
对于具有 n 个运动构件的机械系统,各运动构件的质量 为 mi ,其质心的速度为 vS i ;各运动构件对质心轴线的转动惯
n
对于该机械系统,作用在构件上的外力为Fi ,力作用点的 速度为vi ,Fi 的方向与vi 的方向间的夹角为i ;作用在构件上 的机械系统的外力矩为Mi ,构件的角速度为 i 。 则作用在 该机械上的所有外力和外力矩在dt时间内所作之功为:
n d W Fi v i cos i M i i d t i 1
2、机械运转的三个阶段
(1)起动阶段 机械的角速度 由零渐增至 m 其功能关系为: Wd = Wc + ∆E
驱动功 (2)稳定运转阶段 阻抗功 输出功 周期变速稳定运转 Wr和损 失功Wf m = 常数,而 作周期性变化 之和 动能 增量
ω
ωm
t 起动 稳定运转 停止
机械原动件的角速度随时间变化曲线
对于具有 n 个运动构件的机械系统,作用在构件
上的外力为Fi ,力作用点的速度为vi ,Fi 的方向与vi 的方向间的夹角为i ;作用在构件上的机械系统的外 力矩为Mi ,构件的角速度为 i 。 则作用在机械上的 所有外力和外力矩所产生的功率之和为:
P Fi v i cos i M i i
6、实例分析
例1:曲柄滑块机构的等效动力学模型
y
ω1 A
1 1 1 1 2 2 2 2 E J S 11 m2vS 2 J S 22 m3v3 2 2 2 2
2
机械原理 西工大第八版第7章 机械的运转及其速度波动的调节
把具有等效转动惯量,作用有等效力矩的等效构件称
为机械系统的等效动力学模型。
13
Je Je (1)
Me Me (1,1,t)
d
[
J
e
(1
)
12
2
]
M
e
(1
,
1,
t
)1dt
Me
1
Je
个等对效于转一动个构单件自的由运度动机的械研系究统。的该运构动件学具研有究等,效Fi可转g.简动1化惯1-为量1 对Je,其其一
上作用有等效力矩Me。
等效转动惯量是等效构件具有的假想转动惯量,等效构件的 动能应等于原机械系统中所有运动构件的动能之和。
等效力矩是作用在等效构件上的一个假想力矩,其瞬时功率 应等于作用在原机械系统上的所有外力在同一瞬时的功率之和。
把具有等效转动惯量,其上作用有等效力矩的等效构件就称为 原机械系统的等效动力学模型。
(,) / 2]
M
Med () M
e (,)d
er
(
)
d
[
J
e
2
2
]
M
e
dt
非线性微分方程
32
d[Je ()2 / 2] M e (,)d
1 2
2dJe ()
Je
( )d
Me
( , )d
i1 i
J ei J e (i1 ) J ei
29
选取齿轮3为等效构件,Je为常数
* Je
d
dt
2
2
dJ e
d
Me
Me ()
机械原理07(本科)-运转及速度波动调节
3
Y
2 1
S1 M1
S2
3
S3 F3
X
4
1 2 E1 = J1ω1 , 2 1 2 E3 = m 3v 2
1 1 2 2 E 2 = J s 2ω 2 + m 2v s2 , 2 2 1 1 2 1 2 1 2 2 则:dE = d ( J1ω1 + Js2ω2 + m2vs2 + m3v3 ) 2 2 2 2
dW = (M1ω1 − F3v3 )dt
Y
2 1
S1 M1
S2
3
S3 F3
X
4
则曲柄滑块机构的运动方程式为: 则曲柄滑块机构的运动方程式为:
1 1 2 1 2 1 2 2 d ( J1ω1 + Js2ω2 + m2vs2 + m3v3 ) 2 2 2 2 = ( M1ω1 − F3v3 )dt
对于具有n个活动构件的机械, 设第i个构件 对于具有 个活动构件的机械, 设第 个构件 个活动构件的机械 的作用力为Fi、力矩为Mi,力Fi的作用点的速度 的作用力为 力矩为 构件的角速度为ω 为vi、构件的角速度为 i, Fi与vi间的夹角为 i。 间的夹角为α 机械运动方程式的一般表达式为
机器在稳定运 转阶段, 转阶段,其等效力 矩一般是机械位置 的周期性函数
Me d
Me r
φ
Med= Med (φ) φ Mer= Mer (φ) φ
φ
则等效驱动力矩和等效阻力矩所作的功分别为: 则等效驱动力矩和等效阻力矩所作的功分别为 :
Wd (ϕ ) = ∫ Med (ϕ )dϕ
ϕa
ϕ
Me d
取转动构件为等效构件时, 取转动构件为等效构件时,有:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
∴ 当Fi、Mi是常数或位置的函数时,Me、Fe是等效构件位 置的函数或常数;当Fi、Mi是速度(或时间)的函数时, Me、Fe是等效构件位置、速度的函数。 注意:1)Me、Fe是等效动力学模型中使用的假想力或力矩,而不
是机械上各力的合力或合力矩。 2)有时为了求解的需要,我们可以分别对驱动力矩和阻力 矩求其等效驱动力矩和等效阻力矩, 即 :Md→Med 、 Mr→Mer 。则:Me= Med - Mer
Me= [Ficosαi(vi /ω)±Mi(ωi /ω)]
i 1
n
2)等效构件为以v移动的滑块时,则Ne=Fev。 由Ne=N可得Fe的一般表达式: Fe= [Ficosαi(vi /v)±Mi(ωi / v)]
i 1 n
∵ Me、Fe与外力Fi、外力矩Mi及速比有关,而速比是等效 构件位置的函数或常数。
效力Fe或等效力矩Me的等效构件称为原机械系统的等效动
力学模型。
在建立等效动力学模型时,通常取连架杆作为等效构 件,如图7-4即为两种常用的等效动力学模型:
a)
图7-4
b)
图a的模型中,等效构件是回转构件(曲柄),其ω与 原机构中该构件本身的ω相同,但其具有的转动惯量为Je, 其上作用的力矩为Me。 图b的模型中,等效构件是移动构件(滑块),其v与 原机构中该构件本身的v相同,但其具有的质量为me,其 上作用的力为Fe。
统等效转化为只有一个独立运动的等效构件(Equivalent
link) ,等效构件的运动与机械中该构件本身的运动相同。
等效转化的原则是:使机械系统转化前后的动力学效果保 持不变。即:
1)等效构件的等效质量me或转动惯量Je所具有的动能等
于原机械系统的总动能,即Ee=E;
2)等效构件上作用的等效力Fe或等效力矩Me所产生的瞬 时功率等于原机械系统所有外力或外力矩产生的瞬时 功率,即Ne=N。 把这种具有等效质量me或转动惯量Je,其上作用有等
则该系统具有的总动能为: E= (mivSi2/2+ JSiωi2/2)
i 1 n
1)等效构件为以ω转动的回转构件时,则Ee= Jeω2/2。 由Ee=E得Je的一般表达式: Je= [mi(vSi /ω)2+ JSi(ωi /ω) 2]
i 1 n
2)等效构件为以v移动的滑块时,则Ee= mev 2/2。 由Ee=E可得me的一般表达式: me= [mi(vSi /v)2+ JSi(ωi / v) 2]
例1:图7-3所示的曲柄滑块机构中,曲柄1的角速度为ω1,其质心 在O点,转动惯量为J1,其上作用有驱动力矩M1;连杆2的角速度为 ω2,质量为m2,相对于质心S2的转动惯量为JS2,质心S2的速度为 vS2;滑块3的质量为m3,其质心在B点,速 度为v3,其上作用有工作阻力F3。求分别以 曲柄1和滑块3为等效构件时的等效参数。 解:1)以曲柄1为等效构件: 图7-3 由Ee=E:Jeω12/2 = J1ω12/2 +JS2ω22/2 +m2vS22/2 +m3v32/2 则: Je= J1+ JS2(ω2/ω1)2+m2(vS2/ω1)2+ m3(v3/ω1)2 由Ne=N: eω1=M1ω1 + F3 v3cosα3 (α3=180°) M 则:Me= M1- F3 (v3/ω1) 2)以滑块3为等效构件: 同理可求得: me= J1(ω1/ v3)2+ JS2(ω2/ v3)2+m2(vS2/ v3)2+ m3 Fe=M1(ω1/ v3) -F3 cosα3
例2:图7-5所示为一由齿轮驱动的连杆机构。设已知齿轮1的齿数 Z1=20,转动惯量为J1;齿轮2的齿数Z2=60,它与曲柄2′的质量中心 在B点,其对B轴的转动惯量为J2,曲柄长为L;滑块3和构件4的 质量分别为m3、 m4 ,其质心
分别在C、D点。在轮1上作用 有驱动力矩M1,在构件4上作 用有阻抗力F4。现取曲柄2′为 等效构件,求在图示位置时的 等效转动惯量Je及等效力矩Me。
v4= v4P24 = v2P24 = ω2 lBP24
= ω2 L sinψ2
∴ Je= J1 (Z2/ቤተ መጻሕፍቲ ባይዱ1)2 + J2+m3(ω2 L /ω2)2+ m4(ω2 L sinψ2 /ω2)2
= 9J1 + J2+m3L 2+ m4L2 sin2ψ2 由Ne=N:Meω2=M1ω1 + F4 v4cos 180° ∴ Me= M1(ω1 /ω2) -F4 (v4/ω2) = M1(Z2 /Z1) -F4 (ω2 L sinψ2 /ω2) = 3M1-F4 L sinψ2
图7-5
解: e=E:Jeω22/2 = J1ω12/2 +J2ω22/2+ m3v32/2+ m4v42/2 由E ∴ Je= J1 (ω1/ω2)2 + J2+m3(v3/ω2)2 + m4(v4/ω2)2
Je= J1 (ω1/ω2)2 + J2+m3(v3/ω2)2 + m4(v4/ω2)2 用瞬心法求v3 /ω2 、 v4 /ω2 : v3 = v3P23 = v2P23 = ω2 L
对于具有n个活动构件的机械系统,构件i上的作用力 为Fi,力矩为Mi,力Fi作用点的速度为vi,角速度为ωi。 则该系统产生的总瞬时功率为: N = ivicosαi±Miωi) (F
i 1 n
其中:αi为Fi与速度vi方向的夹角;Mi与ωi同向时取“+”、 反向时取“-”。 1)等效构件为以ω转动的回转构件时,则Ne= Meω。由 Ne=N得Me的一般表达式:
i 1 n
∵ Je、me与各构件的质量mi、转动惯量JSi及速比有关,一
般情况下,mi、JSi是常数,而速比是等效构件位置的
函数或常数。
∴ Je、me是等效构件位置的函数或常数,即 Je= Je(ψ)或C、 me=m e(s)或C 。
2、等效力矩(Moment ——根据Ne=N来求
of force) Me和等效力(force ) Fe
二、等效参数(Equivalent parameter) 的确定 1、等效转动惯量(Moment of inertia) Je和质量(Mass) me ——根据Ee=E来求 对于具有n个活动构件的机械系统,构件 i 的质量为 mi,相对于质心Si的转动惯量为JSi ,质心Si的速度为vSi, 角速度为ωi。
§7—2 机械系统的等效动力学模型
(Dynamically Equivalent Model of a Mechanical System)
一、等效动力学模型的建立
机械系统是复杂多样的,在进行动力学研究时,通常 将复杂的机械系统按一定的原则简化为一个便于研究的等 效动力学模型。 为了研究单自由度机械系统的真实运动,可将机械系
