理论力学试题(动力学 ) (3)
理论力学复习题(含答案)
《理论力学》复习题A一、填空题1、二力平衡和作用反作用定律中的两个力,都是等值、反向、共线的,所不同的是 二力平衡是作用在一个物体上,作用效果能抵消、作用力与反作用力是作用在两个物体上,作用效果不能抵消。
2、平面汇交力系平衡的几何条件是顺次将表示各个力Fi 的有向线段首尾相接,可以构成闭合n 边形;平衡的解析条件是 ∑Fxi=0;且∑Fyi=o 。
3、静滑动摩擦系数与摩擦角之间的关系为 tanφ=fs 。
4、点的切向加速度与其速度的 方向 变化率无关,而点的法向加速度与其速度 大小 的变化率无关。
5、点在运动过程中,满足0,0=≠n a a 的条件,则点作 牵连 运动。
6、动点相对于的 定系 运动称为动点的绝对运动;动点相对于 动系 的运动称为动点的相对运动;而 动系 相对于 定系 的运动称为牵连运动。
7、图示机构中,轮A (只滚不滑)作 平面 运动;杆DE 作 定轴转动 运动。
题7图 题8图8、图示均质圆盘,质量为m ,半径为R ,则其对O 轴的动量矩为 。
9、在惯性参考系中,不论初始条件如何变化,只要质点不受力的作用,则该质点应保持 静止或等速直线 运动状态。
10. 任意质点系(包括刚体)的动量可以用 其质心 的动量来表示。
二、选择题1. 在下述公理、规则、原理和定律中,对所有物体都完全适用的有( D )。
A.二力平衡公理B.力的平行四边形规则C.加减平衡力系原理D.力的可传性2. 分析图中画出的5个共面力偶,与图(a )所示的力偶等效的力偶是(B )。
A. 图(b ) B. 图(c ) C.图(d ) D. 图(e )题2图3. 平面力系向点1简化时,主矢0='RF ,主矩01≠M ,如将该力系向另一点2简化,则( D )。
A. 12,0M M F R≠≠' B. 12,0M M F R ≠='C. 12,0M M F R=≠' D. 12,0M M F R ==' 4. 将大小为100N 的力F 沿x 、y 方向分解,若F 在x 轴上的投影为86.6 N ,而沿x 方向的分力的大小为115.47 N ,则F 在y 轴上的投影为( B )。
《理论力学 动力学》 第三讲 第二类拉格朗日方程的应用

2、第二类拉格朗日方程的应用例1质量为m 1的物块C 以细绳跨过定滑轮B 联于点A, A ,B 两轮皆为均质圆盘,半径为R ,质量为m 2, 弹簧刚度为k ,质量不计。
ACOxAOCx例2已知:如图所示的运动系统中,重物M 1的质量为m 1,可沿光滑水平面移动。
摆锤M 2的质量为m 2,两个物体用长为l 的无重杆连接。
M 1M 2φC 求:此系统的运动微分方程。
2、第二类拉格朗日方程的应用解:系统有两个自由度,选M 1的水平坐标x 1和φ为广义坐标, 并将质点位置用广义坐标表示:111212,0;sin ,cos x x y x x l y l j j===-=将上式两端对时间t 求导数得:111212,0;cos sin x x yx x l y l j j j j ===-=-&&&&&&&&,系统的动能为:222122211()22T m x m x y =++&&&22212111()(2cos )22m l m m x l x j j j =++-&&&&选质点M 2在最低处时的位置为系统的零势能位置,则系统的势能为:)cos 1(2j -=gl m V 系统的主动力为有势力,此为保守系统,可写出系统的动势,运用保守系统的拉格朗日方程求解,此处我们运用一般形式的第二类拉格朗日方程求解。
d 0(12)d k T TQ k N t q q æö¶¶--==ç÷¶¶L &,,,注意:零势能位置的选取不是唯一的。
选取原则:计算方便代入拉格朗日方程得到:1212110()cos T Tm m xm l x xj j ¶¶==+-¶¶&&&,2121221d ()()cos sin d T m m x m l m l t x j j j j¶=+-+׶&&&&&&10x V Q x ¶=-=¶先计算)cos 1(2j -=gl m V 22212111()(2cos )22m l T m m x l xj j j =++-&&&&221221sin cos T T m lx m l mlx j j jj j j¶¶==-¶¶&&&&&,222121d ()cos sin d T m l m lx m lx t jj j j j ¶=-+׶&&&&&&&2sin V Q m gl j j j¶=-=-¶212122()cos sin 0m m xm l m l j j j j +-+×=&&&&&(cos sin )sin 0m l l x x m gl jj j j j -+×+=&&&&&&2、第二类拉格朗日方程的应用x 1φ再计算如果质点M 2摆动很小,可以近似地认为1cos sin »»j j j ,且可以忽略含和的高阶小量,2j &1xj &&微分方程可改写为:1212()0m m xm l j +-=&&&&1l x g jj -=-&&&&从以上两式中消去,得到1x&&1210m m gm lj j ++=&&这是自由振动的微分方程,其通解为:)sin(0q w j +=t A 固有角频率:lgm m m 1210+=w 摆动周期:如果21m m >>则质点M 1的位移x 1将很小,质点M 2的摆动周期将趋于普通单摆的周期:1lim 2m T ®¥=也可以从微分方程中消去,得到:j&&可见质点M 1沿x 方向也作自由振动。
理论力学复习题

Total Review of Theoretical Mechanics一、静力学(STATICS )1、由AC 和CD 构成的组合梁通过铰链C 连接。
它的支承和受力如图所示。
已知均布载荷强度q =10KN/m ,力偶矩M = 40 KN •m ,不计梁重。
求支座A ,B ,D 的约束力和铰链C 处所受的力。
1. Beams AC and CD are joined by a smooth pin C , Knowing q =10KN/m, M =40KNm, other conditions are shown as figure. Determine the reaction forces at points A , B , D , C. Neglect the weights of the beams.2、水平梁AB 由铰链A 和杆BC 所支持,如图所示。
在梁上D 处用销子安装半径为r=0.1m 的滑轮。
有一跨过滑轮的绳子,其一端水平地系于墙上,另一端悬挂有重P =1800N 的重物。
如AD =0.2m , BD =0.4m , ,且不计梁、杆、滑轮和绳的重量。
求铰链A 处的约束力和杆BC 的内力。
2. A bracket consists of members AB , CB and pulley D as shown in figure. A string supporting a weight P =1800N passes through over pulley D , the other end of the string is secured to the wall. r =0.1m , AD =0.2m , BD =0.4m, . Determine the reaction forces at points A and the internal force of rod BC . The weight of themembers and pulley are negligible.3、在图示连续梁中,已知q ,a 及。
《理论力学》动力学典型习题+答案
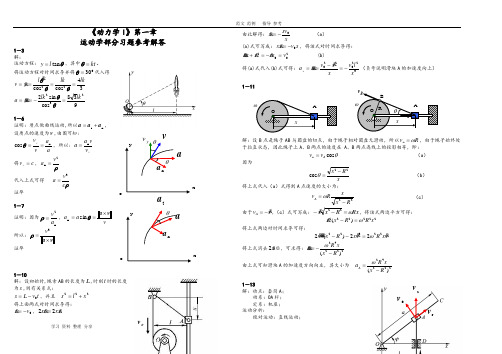
学习 资料 整理 分享《动力学I 》第一章 运动学部分习题参考解答1-3 解:运动方程:θtan l y =,其中kt =θ。
将运动方程对时间求导并将030=θ代入得34cos cos 22lklk l y v ====θθθ 938cos sin 2232lk lk y a =-==θθ1-6证明:质点做曲线运动,所以n t a a a +=, 设质点的速度为v ,由图可知:a a v v yn cos ==θ,所以: yv va a n =将c v y =,ρ2n v a =代入上式可得 ρc v a 3=证毕 1-7证明:因为n2a v =ρ,v a a v a ⨯==θsin n所以:va ⨯=3v ρ证毕1-10解:设初始时,绳索AB 的长度为L ,时刻t 时的长度 为s ,则有关系式:t v L s 0-=,并且 222x l s +=将上面两式对时间求导得: 0v s-= ,x x s s 22= 由此解得:xsv x-= (a ) (a)式可写成:s v x x 0-= ,将该式对时间求导得: 2002v v s x x x =-=+ (b)将(a)式代入(b)式可得:3220220xlv x x v x a x -=-==(负号说明滑块A 的加速度向上)1-11解:设B 点是绳子AB 与圆盘的切点,由于绳子相对圆盘无滑动,所以R v B ω=,由于绳子始终处于拉直状态,因此绳子上A 、B 两点的速度在 A 、B 两点连线上的投影相等,即: θcos A B v v = (a ) 因为xR x 22cos -=θ (b ) 将上式代入(a )式得到A 点速度的大小为: 22Rx x Rv A -=ω (c )由于x v A -=,(c )式可写成:Rx R x xω=--22 ,将该式两边平方可得: 222222)(x R R x xω=- 将上式两边对时间求导可得:x x R x x R x xx 2232222)(2ω=-- 将上式消去x2后,可求得:22242)(R x xR x --=ω由上式可知滑块A 的加速度方向向左,其大小为 22242)(R xxR a A -=ω1-13解:动点:套筒A ;动系:OA 杆; 定系:机座; 运动分析:绝对运动:直线运动;o vo va ve vr vxovxot学习 资料 整理 分享 相对运动:直线运动; 牵连运动:定轴转动。
理论力学简答题

答:在非惯性系中a =a—65x r f简答题答案1、说明科里奥利加速度产生的原因。
答:(1)质点具有相对速度B时,致使质点在活动参考系中的位置发生变化,从而改变了速度的大小;(2)质点跟随活动参考系转动时,相对速度方向的变化2、试推导出质点在非惯性系中的动力学方程,并说明方程中各项的含义。
动力学方程为ma'=ma—m(6x r'一m6x(6x r')—2m6x v fma表示外力;m6x r'是由非惯性系的加速转动引起的,与非惯性系的角加速度有关;m6x(6x r')成为惯性离心力;2m6x v'科里奥利惯性力。
3.试举两例说明由于地球自转而产生的力学效应,并简述其原因.答:①如物体的重力随地理纬度的增大而增大,这是地球自转产生惯性离心力的影响。
②自由落体的偏东。
地球上物体的运动方程为:X的正方向向南,y的正方向向东,Z的正方向竖直向上。
自由落体的运动方向mx=F+2m6y sin九x<my=F—2m6(x sin九+z cos九)mz=F—mg+2m6y cos九z向着z轴的负方向,'小于零,从运动方程知,物体向东方向受到附加的科里奥利力的作用,即自由落体的偏东。
4.为什么落体会偏东答:地球上物体的运动方程为:d d t-dr')r x m iii"dT 丿—艺r'x F(e)+r xCiii—1艺m rd d tM ‘—dL 1dtmx —F +2m W ysin 九x<my —F —2m 3(x sin 九+z cos 九)mz —F —mg +2m W ycos 九zX 的正方向向南,y 的正方向向东,Z 的正方向竖直向上。
自由落体的运动方向向着Z 轴的负方向,z小于零,从运动方程知,物体向东方向受到附加的科里奥利力的作用,即自由落体的偏东。
5、应用非惯性系动力学方程导出质点组对质心的角动量定理.答:在非惯性系中d 2r '--二m L —F (e)+F (i)+(—m r )id t 2iiiC工r 'x F(e)iii —1艺mr '—0iii—16、分别说明质点组动量守恒定律、动量矩守恒定律、机械能守恒定律成立条件。
理论力学--动力学习题+答案

A
B
2g 5r
aC
4 5
g
(2)选圆柱A为研究对象
1 2
P g
r 2 A
M
Tr
(1)
选圆柱B为研究对象
1 2
P g
r
2
B
T
'r
(2)
P g
aC
T 'P
(3)
运动学关系:
aC ae ar r A r B (4)
由(1)~(4)式得:
B
4gM 2g 5 Pr2
mv1x
py 0
mv2x mv3x
5 2
ml1()
所以
p
px
5 2
ml1
A
方向水平向左
B
O
例9-5在静止的小船中间站着两个人,其中甲m1=50kg,面向船首方向走动1.5m。 乙m2=60kg,面向船尾方向走动0.5m。若船重M=150kg,求船的位移。水的阻力不计。
【解受】力有三个重力和一个水的浮力,因无水平力,水平方向质心运动守恒,
0 3.67rad/s
如图所示,均质杆AB质量为m,长为l,由图示位置( )无初速度地倒下4,5求0 该瞬
时A端所受到地面的约束反力。
B
C C
A
例10-13 如图所示均质细长杆,质量为M,长为l,放置在光滑水平面上。若在A 端 作用一垂直于杆的水平力F,系统初始静止,试求B端的加速度。
Pr
A
6gM 5
2g Pr2
Pr
aC
理论力学总复习(3).

R ,质量为
m的匀质圆盘在其自身平面内作平面运动。
点速度大小为 B
在图示位置时,若已知图形上 A、B 二点的速度方向如图所示。
45 ,且知
v B ,则圆轮的动能为
②
2、已知匀质杆长L,质量为m,端点B的速度为v,则杆的动能为 ②
3、图示三棱柱重P,放在光滑的水平面上,重Q的匀质圆柱体静止释放后
(a 0 g ) sin / L 0
1、倾角为 的楔形块A质量为 m1 ,置于光滑水平面上,物块B的 质量为 m2 ,放置在楔块斜面上。系统由静止开始运动。求A、 B的相互作用力。(不计两物块之间的摩擦)
第九章 质点系动力学基础
一、是非题
1、任意质点系(包括刚体)的动量可以用其质心(具有系统的质量)的动量来 表示。 (√ ) 2、质点系中各质点都处于静止时,质点系的动量为零。于是可知如果质点系的 动量为零,则质点系中各质点必须静止。 ( ×) 3、不管质点系作什么样的运动,也不管质点系内各质点的速度如何,只要知道 质点系的总质量和质点系质心的速度,即可求得质点系的动量。 (√ ) √ 4、冲量的量纲与动量的量纲相同。 ( ) 5、质点系对某轴的动量矩等于质点系中各质点的动量对同一轴之矩的代数和。 (√ ) 6、刚体的质量是刚体平动时惯性大小的度量,刚体对某轴的转动惯量则是刚体 绕该轴转动时惯性大小的度量。 ( ) √
1、半径为r,质量为M的光滑圆柱放在光滑水平面上,如图所示。一质 量为m的小球从圆柱顶点无初速下滑,试求小球离开圆柱前的轨迹。
2、重为 W1 的物体A,沿三棱体D的光滑斜面下降,同时借一绕过滑轮 C的绳子使重为 W2 的物块B运动。三棱体D重为 W 0 ,斜面与水平 面成 角,如略去绳子和滑轮的重量,求三棱体D给凸出部分E
理论力学

相对坐标
r r01 r02 r1 r2
01 02 1 2
与坐标系无关
B、 两粒子体系拉格朗日函数 体系动能 体系势能
L T V 1 2 m 1 ( r0 C
T
1 2
m 1r
(e )
2 01
1 2
m 2 r02
(i)
x
(2)平面极坐标
m ( r 2 ) F r r m ( r 2 r ) F
(3)球坐标
m ( r 2 r 2 sin 2 ) F r , r 2 m ( r 2 r r sin cos ) F , m ( r sin 2 r sin 2 r cos ) F .
H
s
p q L
1
H T V
(2) 正则方程
H q , p . 1, 2 , , s . H p , q
H t
L t
C、哈密顿作用量及哈密顿原理
(1) 哈密顿作用量: (2) 哈密顿原理: D. 正则变换 (1) F1(q,Q,t)称为第一类正则变换母函数
(2) 主动力为保守力时:
V q 0 , 1 ,2 , , s.
(3) 虚功原理 理想约束力学体系处于平衡状 态,则主动力在任意虚位移中所做 的虚功之和等于零。
n
F i ri 0
i 1
E、 对称性和守恒定律 在运动过程中保持不变的广义坐标和广义速度的 函数叫做运动积分.
(4)柱坐标
m (R R 2 ) FR , m ( R 2 R ) F , m F . z z
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、一、填空题(每小题5分,共10分)1、如图,若弹簧在Q作用下的静位移st20=∆冲击时的最大动位移mmd60=∆为:3Q。
2、在其它条件相同的情况下,用内直径为d实心轴,若要使轴的刚度不变的外径D。
二、二、选择题(每小题5分,共10分)1、置有四种答案:(A)截面形心;(B)竖边中点A(C)横边中点B;(D)横截面的角点正确答案是:C2、足的条件有四种答案:(A);zyII=(A);zyII>(A);zyII<(A)yzλλ=。
正确答案是: D 三、1、(15P=20KN,[]σ解:AB20000Mn=ABmaxM=危险点在A2、图示矩形截面钢梁,A 端是固定铰支座,B 端为弹簧支承。
在该梁的中点C 处受到的重解:(1)求st δ、max st σ。
将重力P 按静载方式沿铅垂方向加在梁中心C 处,点C 的挠度为st δ、静应力为max st σ,惯性矩 )(12016.004.012433m bh I ⨯==由挠度公式)2(21483K PEI Pl st +=δ得, 83339310365.112)10(104010210488.040---⨯⨯⨯⨯⨯⨯⨯=st δmm m 1001.01032.25240213==⨯⨯⨯+mm m 1001.0==根据弯曲应力公式z st W M =max σ得,其中4Pl M =, 62bh W z =代入max st σ得, MPa bhPlst 12401.004.068.0406422max =⨯⨯⨯⨯==σ(2)动荷因数K d12160211211=⨯++=++=K std hδ(3)梁内最大冲击应力M P a st d d 1441212max =⨯=K =σσ3、(10分)图中的1、2杆材料相同,均为园截面压杆,若使两杆在大柔度时的临界应力相等,试求两杆的直径之比d 1/d 2,以及临界力之比21)/()(cr cr P P 。
并指出哪根杆的稳定性较好。
解:由222212λπλπσEE cr == 即:22221111i l i l μλμλ===;∴又:4、(15分)等截面钢架如图所示,各杆段的抗弯刚度EI 相同。
试求钢架横截面上的最大弯矩,基本静定系。
多余的约束反力为X 1。
由01111=∆+p X δ 应用图乘法求系数:EI aa a a a a a EI3112)()33221(1=⎥⎦⎤⎢⎣⎡⨯⨯+⨯⨯⨯=δ EI qa a a qa EI p 3221)2231(1421-=⎥⎦⎤⎢⎣⎡⨯⨯⨯-=∆ 将计算结果代入方程:01111=∆+p X δ;得:022413=-EI qa X EI a因此解得:qa X 311=将计算结果代入方程:01111=∆+P X δ得:M q 图aaa2qa 2M 图022413=-EI qa X EI a ;因此解得:qa X 311=如图:最大弯矩为2qa 在AD 32)2(22maxqa a q M =-= 5、(15分)一根在A p 均为已知:杆在B 端有一不计自重的刚性臂,在C 截面处有一固定指针。
当杆未受载荷时,刚性臂及指针均处于水平位置。
如在刚性臂端部加一向下的载荷P ,同时在D 、E 处作用有扭转力偶矩T D 和T E ,当刚性臂与指针仍保持水平时,试确定此时的T D 和T E 。
M由0==CA BC φφ;及P GI Ml=φ; ;)()(0;3;2)(0PD E P E CA E P P E BC GI a T T Pb GI a T Pb Pb T GI a Pb GI a T Pb +-+-===∴⋅+-==φφpb T D 4=∴6、(10应力圆。
2/)();(3072.735(72.773542401531max 32122MPa R R R =-=-=-=-==+==+=σστσσσM n Pb-T E材料力学模拟试题(二)解答一、一、填空题(共15分) 1、 1、 (5分)一般钢材的弹性模量E = 210 GPa ;吕材的弹性模量E = 70 GPa2、 2、 (10分)图示实心圆锥杆受扭转外力偶作用,材料的剪切弹性模量为G ,该杆的man τ1、(5(A )各向同性材料;(B (C )向异性。
正确答案是 A 。
2、(5分)边长为d 杆(1)是等截面,杆(2荷系数d k 和杆内最大动荷应力d σ论:(A )()(,)()(1max 21d d d k k σ<<(B )()(,)()(1max 21d d d k k σ><(C )()(,)()(1max 21d d d k k σ<>(D )2max 1max 21()(,)()(d d d d k k σ>>。
正确答案是 A 。
三、三、计算题(共75分)(1)直径比21/d d ; (2)扭BC AB φφ/。
AC 轴的内力图:)(105);(10355Nm M Nm BC ⨯=⨯=由最大剪应力相等:8434.05/3/;16/1050016/10300321323313max==⨯=⨯==d d d d W M n n ππτ由594.0)(213232;41221242411=∙∙=∙=⇒∴⋅=d d M M M d G d G a M GI l M n n n n BC AB P n ππφφφ;(2)2、(15分)直径为d 的圆截面钢杆处于水平面内,AB 垂直与CD ,铅垂作用力P 1=2KN ,P 2=6KN,如图。
已知d =7cm ,材料MPa 110][=σ。
试用第三强度理论校核该杆的强度。
解:1.作内力图,确定危险截面杆AB 的 A弯矩分别为)(18003.02Nm P M n =⨯=(30003.060006.02000M A =⨯+⨯=2.强度计算32/07.018003000322223πσ+=+=W M M nr 9.1031002.107754.11196=⨯=MPa110][=≤σMPa3、(15分)用图乘法求图示刚架铰链B 处左右两截面的相对转角B 。
EI =常数。
略去轴力及剪力对变形的影响。
解:各构件受力如图:2/qa y y B A == 2/2qa分别作出原载荷和单位力的弯矩图 由图乘法:)]431()231[()321()221[()]21()832{(1232+⨯⨯⨯++⨯⨯⨯+-⨯⨯=∆qa a qa a qa a EI B θ)]}2(2)22[(2⨯⨯⨯+qa aEI qa 3143=j d σ和st d hδ211++=K:zz st W PaW M 2max ==σ;EI Pa EI j 64833==δ将上式子整理得:31211211Pa EIhhstd ++=++=K δz st d d W PaPaEIh K 2)1211(3max max ++==σσ m ax d σ与P 不成线性关系,所以结论不正确。
5、(20分)AB 和BD 材料相同,直径均为d ,且1/30/=d l ,BD 杆P λ=100,求当BD杆达到临界状态时P 的数值。
点挠度为零。
解除B 由力法: 111+X δ确定系数EI l EI l 383)2(3311==δl Pl l P ()(21[1+⨯⨯-=∆代入上式:31X =计算BD 由==i lμλp λλ≥∴)(221l EI X μπ=临界状态时:P cr6、(10分)泊松比ν解 A 其中t PD 21=σt PD 42=σ (122σεε==E x 所以)21(4νε-=D Et P xσ2四、一、填空题(每小题512、简支梁AC 在B 点与钢索钢索中轴力所需的变形EI l N EA Nl Tl 48)2(3=-α。
五、二、选择题(每小题51、 1、(A) (B) 正确方式是 D 。
2个柔度最大,哪个柔度最小?有四种答案:正确答案是 B 。
(A )a λ大,c λ(B )b λ大,d λ(C )b λ大,c λ(D )a λ大,b λ六、三、证明题(重物Q 证明:g v 22=d K +=∴1即: K1、(2、(15分)矩形截面简支梁如图。
测得在载荷P 作用下,点A 处纵向线应变4101-⨯-=x ε。
已知材料的E =200Gpa ,试求P 值。
解:梁的内力如图:A 点处正应力: IPl IMy 16/02.0-=-=σ忽略切应力影响,由虎克定律:E x x /1014σε=⨯-=-(KN) 7.2 1.002.011206.004.01020035=⨯⨯⨯=∴P3、(15分)如图示砂轮传递的力偶矩m =20.5N.m ,砂轮直径D =25cm ,砂轮重量Q=275N 磨削力P y :P z =3:1用第四强度理论选择砂轮轴直径。
解:(1)外力分析。
轴受力如图,由扭转平衡有m =2DP z=20.5N.m ,则P z =D M2= 41/0.25 =164(N ) P y = 3P z =1643⨯= 492(N )(2)画内力图确定危险截面由内力图知,截面A 弯矩:M ZA = )275492(13.0-⨯=28.21(NmM YA = 13.0164⨯= 21.32(Nm ))(36.3522Nm M M M YAZAAMAX =+=扭矩:M x = 20.5(Nm ) (3)强度计算在圆轴弯扭组合变形下,根据第四强度理论的强度条件有[]σ≤+WM M x2275.0 []σ2275.0xM M W +≥622310605.2075.036.353214.3⨯⨯+≥⨯d 63106057.393214.3⨯≥⨯d )(10887.1106014.33257.39236m d -⨯=⨯⨯⨯≥ 取d =19mm.4、(15分)图示结构,1、2两杆长度、截面积相同,1杆为圆截面,2杆为圆环截面(7.022=d D )。
l =1200mm,A =900mm 2,材料的E =200Gpa ,λP =100,λS =61.4,临界应力经验公式)(12.1304MPa cr λσ-=,求两杆的临界应力及结构失稳时的载荷P cr。
解: (1)研究AB221P Q Q ==(2)计算Q 1Crmm d mm A d 9.3314.3900490041221=⨯=∴==πKN A E Q d lCrp 6.889006.141102001006.141914.331200129222111=⨯⨯⨯=⨯=∴==⨯==πλπλμλ(3)计算Q 2CrmmD mm A D D 4.47)7.01(14.39004900)7.01(4)1(422222222=-⨯⨯=∴==-=-παπKN N A Q D i lcr p s 19010190900)8312.1304()12.1304(1004.61837.0174.412004141200132222222=⨯=⨯⨯-=-=∴=<<==+⨯⨯=+⨯==λλλλαμλ(4)结构失稳载荷为: KN P cr 2.177Q 21cr ==5、(10解: (1(2 (3 (4) (5 y ∴σ xy ∴τ材料力学模拟试题(四)解答八、一、 填空题(3道题,共15分)1.(5分)表示交变应力情况的5个量值:σm 、σa 、r 及σmax 、σmin ,其中只有 2 个(A )“平面假设”给出了横截面上内力与应力的关系A ;(B )“平面假设”给出了圆轴扭转时的变形规律; (C )“平面假设”使物理方程得到简化; (D )“平面假设”是建立剪应力互等定理的基础。
