高等数学_第一章函数与极限习题课

合集下载

高等数学第1章函数与极限练习册解答(10月19修改)

时,就有
2. 极限 l i m f (x ) A的定义是 : 对于 0 , 存在 X 0 , 当 x
f x A .
时,就有
3. 对于任意的正数 , 存在正数 =
，当
时 5x 2 12 , 因此
lim (5x 2) 12.
x2
解答：
1、当 0 x x0 时； 2、 x X 时；
1.设
xn
n n
1 ,则当 1
n
大于正整数
N
时, | xn 1| 104 , 对于任意正数 ,
当 n 大于正整数 N
时,
|
xn
1|
,所以
lim
n
xn
1.
2. 对于任意正数 , 存在正整数 N
cos n
, 当 n N 时,
2 0 , 所以
n
cos n lim 2 0 . n n
3. 设 xn 为任一数列, 又设对于任意正数 , 存在正整数 N1, N2 , 当 n N1 时,
第 1 章函数与极限
V.同步练习
第 1 章函数、极限与连续
1.1 函数及其性质
一、填空题
1.已知 f x ax2 bx 5 且 f x 1 f x 8x 3 , 则 a
；b
；
2. y cos 2x 1 的周期为
；
3.
函数
f
(x)
sin
1 x
,
x
0;
的定义域为
；值域为
.
解. 设圆锥的半径与高分别为r, h , 则 2 r R 2 , 即 r R 2 , 从而
2
h
R2 r2

高等数学课后习题答案--第一章

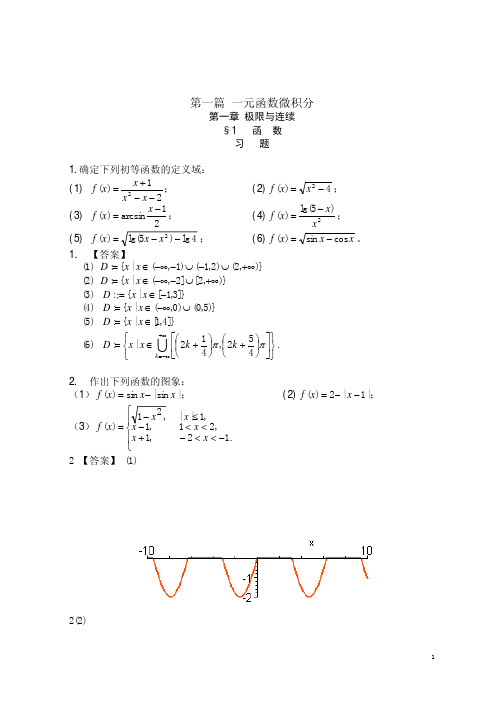
《高等数学》习题参考资料第一篇一元函数微积分第一章极限与连续§1 函数习题1.确定下列初等函数的定义域：(1) 21)(2−−+=x x x x f ；(2)4)(2−=x x f ；(3) 21arcsin )(−=x x f ；(4)2)5lg()(x x x f −=；(5) 4lg )5lg()(2−−=x x x f ；(6)x x x f cos sin )(−=。

1．【答案】(1) )},2()2,1()1,(|{:+∞∪−∪−−∞∈=x x D (2) )},2[]2,(|{:+∞∪−−∞∈=x x D (3) ]}3,1[|{:;−∈=x x D (4) )}5,0()0,(|{:∪−∞∈=x x D (5) ]}4,1[|{:∈=x x D (6)+ +∈=+∞−∞=U k k k x x D ππ452,412|:.2. 作出下列函数的图象：（1）|sin |sin )(x x x f −=；(2)|1|2)(−−=x x f ；（3）+−−=,1,1,21)(x x x x f .12,21,1||−<<−<<≤x x x 2 【答案】 (1)2(2)2 (3)3.判断下列函数的奇偶性：（1）x x x f ++−=11)(；（2）xxx f x x +−+−=11lg110110)(；（3）x x a a x f x x sin )(++=−；（4）)1lg()(2x x x f ++=。

3. 【答案】 (1) 偶函数; (2) 偶函数; (3) 偶函数; (4) 奇函数 .4.证明:两个奇函数的乘积是偶函数;一个奇函数与一个偶函数的乘积是奇函数。

4．【答案】设)(x f ,)(x h 是奇函数, )(x g 是偶函数,)()()(x h x f x f =,)()()(x g x f x G =, 于是)()()(x h x f x F −−=−))())(((x h x f −−=)()()(x F x h x f ==, 因此)(x F 是偶函数.)()()(x g x f x G −−=−)()(x g x f −=)(x G −=, 因此)(x G 是奇函数.5．设函数f 满足：D （f ）关于原点对称，且()xc x bf x af =+1)(，其中a ,b ,c 都是常数，||||b a ≠,试证明f 是奇函数。

高等数学第一章课后习题答案

高等数学（本）第一章函数与极限1. 设 ⎪⎩⎪⎨⎧≥<=3||,03|||,sin |)(ππϕx x x x , 求).2(446ϕπϕπϕπϕ、、、⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛6sin )6(ππϕ=21=224sin )4(==ππϕ ()0222)4sin()4(==-=-ϕππϕ2. 设()x f 的定义域为[]1,0，问：⑴()2x f ； ⑵()x f sin ； ⑶()()0>+a a x f ； ⑷()()a x f a x f -++ ()0>a 的定义域是什么？（1）][；，－的定义域为所以知－11)(,111022x f x x ≤≤≤≤[]ππππ)12(,2)(sin ),()12(21sin 0)2(+∈+≤≤≤≤k k x f Z k k x k x 的定义域为所以知由][a a a x f ax a a x -+-≤≤≤+≤1,)(110)3(－的定义域为所以知－由][φ时，定义域为当时，定义域为当从而得－知由211,210111010)4(>-≤<⎩⎨⎧+≤≤-≤≤⎩⎨⎧≤-≤≤+≤a a a a a x a ax a a x a x班级姓名学号3. 设()⎪⎩⎪⎨⎧>-=<=111011x x x x f ，()x e x g =，求()[]x g f 和()[]x f g ，并做出这两个函数的图形。

⎪⎪⎩⎪⎪⎨⎧>=<==⎪⎩⎪⎨⎧>-=<=⎪⎩⎪⎨⎧>-=<=-1,1,11,)]([.)20,10,00,1)]([1)(,11)(,01)(,1)]([.)11)(x e x x e e x f g x x x x g f x g x g x g x g f x f 从而得4. 设数列{}n x 有界, 又,0lim =∞→n n y 证明: .0lim =∞→n n n y x{}结论成立。

北科大高数课件第一章

第一章
习题课
8/24
1 2 n ⎛ ⎞ lim ⎜ 2 + 2 + + 2 例5 求极限 ⎟. n→∞ n + n + 1 n +n+2 n +n+n⎠ ⎝ n( n + 1) 1 2 n < 2 + 2 + + 2 解 2 n + n+1 n + n+ 2 n +n+n 2 n +n+n
(
)
n( n + 1) 1 = , 而 lim n→∞ 2 n 2 + n + n 2 n( n + 1) 1 lim = , n→∞ 2 n 2 + n + 1 2
3 ⎛ ⎛ 1 + tan x tan x − sin x ⎞ x 3 ⎞⎞x ⎛ 1 − 1 ⎟ ⎟ = lim ⎜ 1 + 原式 = lim ⎜ 1 + ⎜ x →0 x →0 1 + sin x 1 + sin x ⎟ ⎠⎠ ⎝ ⎠ ⎝ ⎝
1
解
1
∞
1
⎛⎛ tan x − sin x ⎞ = lim ⎜ ⎜ 1 + x →0 ⎜ 1 + sin x ⎟ ⎠ ⎝⎝
第一章
习题课
7/24
x− y x+ y sin x − sin y = 2sin cos 2 2 x+ y x− y sin x + sin y = 2sin cos 2 2 x+ y x− y cos x − cos y = −2sin sin 2 2 x+ y x− y cos x + cos y = 2cos cos 2 2

北大版高等数学第一章函数及极限答案习题1.3

习题1.31.(1,2,),lim 1,0,,2|-1|,:n n n n n x n x N n n N x εε→∞===>+>< 设证明即对于任意求出正整数使得当时有并填下表220,1,|-1||1|,2,2222,,|-1|.2.lim ,lim ||||.0,,,||,||||||||,lim ||||.3.{},(1),n n n n n n n n n n n n nx n n n N n N x a l a l N n N a l a l a l a l a l N εεεεεεεεε→∞→∞→∞∀><=-=<>-++⎡⎤=-><⎢⎥⎣⎦==∀>∃>-<-≤-<=不妨设要使只需取则当时就有设证明使得当时此时故设有极限证明存在一个自然数证证1||||1;(2){},,||(12,).(1)1,,,||1,|||||||||| 1.(2)m ax {||1,||,,||},||(12,).-313(1)lim23n n n n n n n N n n n N a l a M a M n N n N a l a a l l a l l l M l a a a M n N n n εε→∞<<+≤==∃>-<=-+≤-+<+=+≤=+=- 是一个有界数列即存在一个常数使得对于使得当时此时令则 4.用说法证明下列各极限式:证23/23/2; (2)lim0;21!(3)lim 0(||1); (4)lim0;111(5)lim 1;1223(1)11(6)lim 0.(1)(2)31311(1),2322(23)n nnn n n n n n n q q nn n n n n n n n εεε→∞→∞→∞→∞→∞=+=<=⎛⎫+++= ⎪-⎝⎭⎛⎫++= ⎪+⎝⎭+∀-=<-- 不妨设要使只需证>0,<1,3113,2113133133,,,lim .22322321(2),,,n n n N n N n n n εεεεεεε→∞>+++⎡⎤=+>-<=⎢⎥--⎣⎦∀<≤<>取当时故要使由于只需>0,32222333331,.1(3)||(0).41||(1)(1)(2)(1)1266242424,,m ax {4,}.(1)(2)!111(4),,.11(5)1223nnnnN n N q n nnn q n n n n n n nn N n n n n n N nnεεαααααααεααεαεαεεε⎡⎤=><⎢⎥⎣⎦=>>+==---++++++⎡⎤<<<>=⎢⎥--⎣⎦⎡⎤≤<>=⎢⎥⎣⎦+++ 取当时3/23/23/22211(1)1111111111,,.1223(1)1111(6),,.(1)(2)(1)5.lim 0,{},,||(1,2,),lim n n n n n n n n N n n n n n N n n n a b M b M n εεεεεε→∞⎛⎫- ⎪-⎝⎭⎛⎫⎛⎫⎛⎫⎛⎫⎡⎤=-+-++--=<>=⎪ ⎪ ⎪ ⎪⎢⎥-⎝⎭⎝⎭⎣⎦⎝⎭⎝⎭⎡⎤++≤<<>=⎢⎥++⎣⎦=<= 设是有界数列即存在常数使得证明2222220.0,,||,||||||,lim 0.6.lim1.0,11, 1.(1)24444,1,,.(1)(1)(1)127.:(1)l n n n n n n n n n n n nna b N a a b a b M MMa b n n n n N n n n n n n εεεεεεεεεεεεεεε→∞→∞→∞=∀>∃<=≤===∀><<+⎡⎤=<<<>=⎢⎥-+-⎣⎦++正整数使得故证明要使|只需而只需求下列各极限的值证证32232244432221im lim0.310013/100/1(2)limlim.4241/2/4(210)(210/)(3)limlim16.11/11(4)lim 1lim 1.n n n n n n nnn n n n n n n n n nn n n nne n n →∞→∞→∞→∞→∞→∞---→∞→∞==+-+-==-+-+++==++⎡⎤⎛⎫⎛⎫+=+=⎢⎥⎪⎪⎝⎭⎝⎭⎢⎥⎣⎦21111(5)lim 1lim 11111111.11lim 1lim 1111111(6)lim 1lim 1,(,1),,,1101nn n n n n n nnnnn n nn n n en n q N n N q n n e n n -→∞→∞-→∞→∞→∞→∞⎛⎫-= ⎪⎝⎭⎛⎫⎛⎫++ ⎪ ⎪--⎝⎭⎝⎭==⎛⎫⎛⎫++ ⎪ ⎪--⎝⎭⎝⎭⎡⎤⎛⎫⎛⎫⎛⎫-=-∈∃>-<⎢⎥ ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭⎢⎥⎣⎦⎡⎤⎛⎫<-⎢ ⎪⎝⎭⎢⎣⎦取当时2211,lim 0,lim10,lim 10.1111(7)lim 1lim 1lim 1 1.nnnnn nn n n nnnn n n q q n n e n n n e →∞→∞→∞→∞→∞→∞⎡⎤⎛⎫⎛⎫<=-=-=⎥⎢⎥ ⎪ ⎪⎝⎭⎝⎭⎥⎢⎥⎣⎦⎛⎫⎛⎫⎛⎫-=+-== ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭ 即12221212218.1111(1),,12(1)11112 2.12(1)1111(2),,21212121111111111121222222221n n n n n n n n n n nn nn n n x x x x nn x x n n nx x x x x +++-=+++=+>+<+++=-<-=+++=+>++++-⎛⎫=+++=++++= ⎪⎝⎭ 利用单调有界序列有极限证明下列序列极限的存在性:单调增加有上界，故有极限.111 1.12111111(3).0,1222122,0,111(4)11.0,2!!(1)!111111213 3.2231n n n n n n n n n n n n n x x x x n n n nn n n x x x x x x x n n x n n n x +++<-=+++-=-=-<++++++<>=++++-=>+⎛⎫⎛⎫⎛⎫≤+-+-++-=-< ⎪ ⎪ ⎪-⎝⎭⎝⎭⎝⎭ 单调增加有上界，故有极限.单调减少有下界，故有极限.单调增加有上界，故11lim 11.2!!n e n →∞⎛⎫++++ ⎪⎝⎭ 有极限.9.证明=211(1)1(1)(1)1112!!(1)(1)1!111111112111112!!!1111111.lim 1lim 112!!2!!nknnn n n n n n n k n n n n k n n n n n n nk n n k n n n n n e n n n →∞→∞---+⎛⎫+=+++++ ⎪⎝⎭--++--⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫=+-+--+-- ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎛⎫<++++=+≤++++ ⎪⎝⎭ 证1.,11111112111,2!!1111,2!!1111lim 11lim 11.2!!2!!10.:||||,1,2,,nk n n n k n k k n n k n n n e k e k n x k x n →∞→∞+⎛⎫ ⎪⎝⎭>-⎛⎫⎛⎫⎛⎫⎛⎫+>+-+-- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎛⎫→∞≥++++ ⎪⎝⎭⎛⎫⎛⎫≥++++=++++ ⎪ ⎪⎝⎭⎝⎭≤= 对于固定的正整数,由上式,当时令得设满足下列条件其中是小于211111.lim 0.||||||||0(),lim 0.n n n n n n n n x x k x k x k x n x →∞-+-→∞=≤≤≤→→∞= 的正数证明由得证。

高等数学(同济第七版)课后答案解析

(2)不同，因为对应法贝J不同・g⑴=7? ={.：
(3)相同、因为定义域、对应法则均相同.
(4)不同、因为定义域不同.
际3.设
求。(寻)“仔)・9(-骨)顽-2).并作出函数L)的囲形.
TT
S,,,T i
1(、)的,形如图丨・1所示.
S4.试让F列陥数在指定区间内的单Wi性:
第一章函故与扱限
（2）j = x+In n（0, *8）.证（I） y=/（^）=rL-=-丨+宀（-8』）.
F（-T）=/|（-X）+/2（F=/|（对+人（x） =F（x）,
枚，（大）为偶函数.
设幻（T）,&2（愛）均为奇函数.则幻（-工）=-们（*）,幻（-X）=-g2（■*）•令。（]）=g]（））+&《]）,于是
G（-X）=X|（-X）+评2（-X）=■•幻（x） -&2（1）=f）,
故c（x）为奇函数.
解因为AC= 20= 15,所以,Ali= /^后IF=25.
Ih20 <2-15 <20・25可知，点P、Q在斜边AH上相讷.
令a + 2% = 15+20 + 25J!；x = 20.即当x= 2()时•点七。相遇.因此•所求函數的定义域为(0.20).
(I )当Ov — vIO时，点P在CR上•点Q在CA上(图1-5).
洎6.&卜血所考虑的函救都是定义在区间U）上的.i止明：
（1）两个偶函数的和是偶函数.两个奇函数的和是奇函数；
（2）两个偶函数的乘枳是偶函数，两个奇函数的乘枳是偶函数，偶函数与奇丽数的乗积是奇函数.
证（1）设J|（X）./2（X）均为偶函数，则乂（-X）”（'），（-X）=6（x）.今/⑴=/|（^）+/i（x）,于是

高数函数与极限习题【优质PPT】

第一章函数与极限习题课
一、主要内容
（一）函数的定义（二）极限的概念（三）连续的概念
（一）函数
基本初等函数
复合函数
函数的定义
初等函数反函数隐函数
双曲函数与反双曲函数
反函数与直接函数之间关系
函数的性质
奇偶性单调性有界性周期性
1.函数的定义函数的分类 2.函数的性质有界、单调、奇偶、周期 3.反函数 4.隐函数 5.基本初等函数
原 li 式 ( 1 m x )1 (x )1 (x 2 )1 (x 4 ) ( 1 x 2 n )
n
1 x
(1 x 2 )1 ( x 2 )1 ( x 4 ) (1 x 2 n)
lim
n
1 x
(1x2n)1(x2n)

1 x2n1
lim
lim
n
1x
n 1 x
1 . ( 当 x 1 时 ,lix m 2 n 10 .)
证明必 [0 有 ,1]使一 f(得点 1)f().
2
证明令 F (x)f(x1)f(x),
2
则F(x)在[0,1]上连. 续 2
F(0)f(1)f(0), 2
F(1)f(1)f(1),
2
2
讨论: 若 F(0)0, 则0, f(01)f(0);
2
若F(1) 0, 则 1 , f(11)f(1);
xn11 2(xnxan) a
xn1xn12(xanxn)
1 a xn2 0 2 xn
即xn单调减，有下界
故由单调有界原理得 ln imxn存在
设 ln i m xnA ，A 则 0
在xn1 12(xnxan)两边取极限得

北大版高等数学第一章函数及极限答案习题1.3-推荐下载

习题1.31.(1,2,),lim 1,0,,2|-1|,:n n n n nx n x N n n N x εε→∞===>+>< 设证明即对于任意求出正整数使得当时有并填下表220,1,|-1||1|,2,2222,,|-1|.2.lim ,lim ||||.0,,,||,||||||||,lim ||||.3.{},(1),n n n n n n n n n n n n n x n n n N n N x a l a l N n N a l a l a l a l a l N εεεεεεεεε→∞→∞→∞∀><=-=<>-++⎡⎤=-><⎢⎥⎣⎦==∀>∃>-<-≤-<=不妨设要使只需取则当时就有设证明使得当时此时故设有极限证明存在一个自然数证证1||||1;(2){},,||(12,).(1)1,,,||1,|||||||||| 1.(2)max{||1,||,,||},||(12,).-313(1)lim 23nn n n n n n N n n n N a l a M a M n N n N a l a a l l a l l l M l a a a M n N n n εε→∞<<+≤==∃>-<=-+≤-+<+=+≤=+=- 是一个有界数列即存在一个常数使得对于使得当时此时令则 4.用说法证明下列各极限式:证23/23/2; (2)0;2!(3)lim 0(||1); (4)lim0;111(5)lim 1;1223(1)11(6)lim 0.(1)(2)31311(1),2322(23)nn nn n n nn n q qn n n n nn n n n εεε→∞→∞→∞→∞==<=⎛⎫+++= ⎪-⎝⎭⎛⎫++= ⎪+⎝⎭+∀-=<-- A A A 不妨设要使只需证>0,<1,3113,2113133133,,,lim.22322321(2),,,n n n N n N n n n εεεεεεε→∞>+++⎡⎤=+>-<=⎢⎥--⎣⎦∀<>取当时故>0,ε0.10.010.0010.0001N1819819981999832222333331,.1(3)||(0).41||(1)(1)(2)(1)1266242424,,max{4,}.(1)(2)!111(4),,.11(5)1223nnnn N n Nq n nn n q n n n n n n n n N n n n n n N n n εεαααααααεααεαεαεεε⎡⎤=>⎢⎥⎣⎦=>>+==---++++++⎡⎤<<<>=⎢⎥--⎣⎦⎡⎤≤<>=⎢⎥⎣⎦+++ A A取当时3/23/23/22211(1)1111111111,,.1223(1)1111(6),,.(1)(2)(1)5.lim 0,{},,||(1,2,),lim n n nn n n nn N n n n n n N n n n a b M b M n εεεεεε→∞⎛⎫- ⎪-⎝⎭⎛⎫⎛⎫⎛⎫⎛⎫⎡⎤=-+-++--=<>= ⎪ ⎪ ⎪ ⎪⎢⎥-⎝⎭⎝⎭⎣⎦⎝⎭⎝⎭⎡⎤++≤<<>=⎢⎥++⎣⎦=<=A 设是有界数列即存在常数使得证明2222220.0,,||,||||||,lim 0.6. 1.0,11,1.(1)24444,1,,.(1)(1)(1)127.:(1)l nn n n n n n n n n nnn a b N a a b a b M MM a b nn n n N n n n n n n εεεεεεεεεεεεεεε→∞→∞=∀>∃<=≤===∀>-<<+⎡⎤=<<<>=⎢⎥-+-⎣⎦++A 正整数使得故证明要使而只需求下列各极限的值证证32232244432220.310013/100/1(2)lim lim .4241/2/4(210)(210/)(3)lim lim 16.11/11(4)lim 1lim 1.n n n n n n nn n n n n n n n n n n n n n n n e n n →∞→∞→∞→∞→∞---→∞→∞==+-+-==-+-+++==++⎡⎤⎛⎫⎛⎫+=+=⎢⎥ ⎪ ⎪⎝⎭⎝⎭⎢⎥⎣⎦21111(5)lim 1lim 11111111.11lim 1lim 1111111(6)lim 1lim 1,(,1),,,1101nn n n n n n n n n nn n n n n n e n n q N n N qn n e n n -→∞→∞-→∞→∞→∞→∞⎛⎫-= ⎪⎝⎭⎛⎫⎛⎫++ ⎪ ⎪--⎝⎭⎝⎭==⎛⎫⎛⎫++ ⎪ ⎪--⎝⎭⎝⎭⎡⎤⎛⎫⎛⎫⎛⎫-=-∈∃>-<⎢⎥ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎢⎥⎣⎦⎡⎤⎛⎫<-⎢ ⎪⎝⎭⎢⎣⎦取当时2211,lim 0,lim 10,lim 10.1111(7)lim 1lim 1lim 1 1.nnn n n nn n n nnnn n n q q n n e n n n e →∞→∞→∞→∞→∞→∞⎡⎤⎛⎫⎛⎫<=-=-=⎥⎢⎥ ⎪ ⎪⎝⎭⎝⎭⎥⎢⎥⎣⎦⎛⎫⎛⎫⎛⎫-=+-== ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭A 即12221212218.1111(1),,12(1)11112 2.12(1)1111(2),,21212121111111111121222222221n n n n n n n n n n n n nn n n x x x x n n x x n n n x x x x x +++-=+++=+>+<+++=-<-=+++=+>++++-⎛⎫=+++=++++= ⎪⎝⎭ A A 利用单调有界序列有极限证明下列序列极限的存在性:单调增加有上界，故有极限.111 1.12111111(3).0,1222122,0,111(4)11.0,2!!(1)!111111213 3.2231n n n n n n n n n n n n n x x x x n n n n n n n x x x x x x x n n x n n n x +++<-=+++-=-=-<++++++<>=++++-=>+⎛⎫⎛⎫⎛⎫≤+-+-++-=-< ⎪ ⎪ ⎪-⎝⎭⎝⎭⎝⎭单调增加有上界，故有极限.单调减少有下界，故有极限.单调增加有上界，故11lim 11.2!!n e n →∞⎛⎫++++ ⎪⎝⎭ 有极限.9.证明=211(1)1(1)(1)1112!!(1)(1)1!111111112111112!!!1111111.lim 1lim 112!!2!!nknnn n n n n n n k n n n n k n n n n n n n k n n k n n n n n e n n n →∞→∞---+⎛⎫+=+++++ ⎪⎝⎭--++--⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫=+-+--+-- ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎛⎫<++++=+≤++++ ⎪⎝⎭ A A 证1.,11111112111,2!!1111,2!!1111lim 11lim 11.2!!2!!10.:||||,1,2,,nk n n n k n k k n n k n n n e k e k n x k x n →∞→∞+⎛⎫ ⎪⎝⎭>-⎛⎫⎛⎫⎛⎫⎛⎫+>+-+-- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎛⎫→∞≥++++ ⎪⎝⎭⎛⎫⎛⎫≥++++=++++ ⎪ ⎪⎝⎭⎝⎭≤= 对于固定的正整数,由上式,当时令得设满足下列条件其中是小于211111.lim 0.||||||||0(),lim 0.n n n n n n n n x x k x k x k x n x →∞-+-→∞=≤≤≤→→∞= 的正数证明由得证。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

可求得最终结果。
4 3 3 x3 4 x2 5 x 6 x lim 解： lim x 4 x 3 5 x 2 x 8 x 5 4 x 5 6 3 2 x x 3 1 8 4 3 x2 x
2 【例3】计算 lim x( x 1 x ) x
f ( x) g( x )
也连续( g( x ) 0 时).
4．复合性质：若 u g( x ) 在点 x x 0 连续; y f (u) 在
u g( x 0 )连续, 则 y f [ g( x )]在 x x 0连续.
三、闭区间上连续函数的性质
f ( x )在[a, b]连续
一、函数连续的基本概念
1．函数连续的定义
（1）f ( x )在 x 0点连续:
f （2） ( x )在 x 0点左连续:
x x0
lim f ( x ) f ( x 0 )
lim f ( x ) f ( x 0 ) lim f ( x ) f ( x 0 )
x x0 0
右连续:
有界性定理
最值定理
介值定理
f (a ) A, f (b) B AC B
零点定理
f (a) f (b) 0
K 0, x [a , b] 有 | f ( x ) | K
最小值m , 最大值M x [ a , b ] 有m f ( x ) Mபைடு நூலகம்
(a, b), 使f ( ) C
x( x 1) 2 lim x 2 x3 5
3x3 4x2 5x 6 【例2】计算 lim x 4 x 3 5 x 2 x 8
分析对形如 lim
f ( x) 的极限，分子、分母可同除以 x g ( x ) 1 f ( x ), g( x )中x的最高次，再利用 lim k 0( k 0) x x
lim f ( x ) A
x
2．函数的左右极限
左极限: 0, 0, 使当x 0 x x 0时,
恒有 f ( x ) A .
记作 lim f ( x ) A 或
x x0 0 ( x x0 )
f ( x 0 0) A.
右极限: 0, 0, 使当x 0 x x 0 时, 恒有 f ( x ) A .
f ( x ) lim f ( x ) A ( 3) lim ( B 0时) g( x ) lim g( x ) B
5．函数极限的主要性质
(1) 唯一性：若limf ( x ) A, lim f ( x ) B, 则A B
( 2) 局部有界性：若lim f ( x ) A，则M 0, 0
( 2) lim f ( x ) A lim f ( x ) lim f ( x ) A
x x x
4．函数极限的运算法则
(1) lim[af ( x ) bg( x )] a lim f ( x ) b lim g( x ) aA bB
(2) lim[ f ( x ) g( x )] lim f ( x ) lim g( x ) AB
m( x )
f (x ) 为复合函数 f ( x ) g(h( x ))
应用连续函数的极限运算准则
应用极限的四则运算法则求极限
g( x ), h( x )为无穷小, 且 g( x ) ~ g1 ( x ) h( x ) ~ h1 ( x )
应用等价无穷小代换
f ( x ) [1 m( x )]
n n
则 lim x n A
n
( 2)单调有界收敛原理
x n x n1 , x n M lim x n A
n
x n x n1 , x n M lim x n A
n
二、函数的极限
1．函数极限的定义
x x0
lim f ( x ) A
第一章函数与极限习题课
Ⅰ 数列与函数的极限
一、数列极限
1．数列极限的定义
lim x n a
n
0, N 0, 使n N时, 恒有 x n a .
几何解释:
a x 2 x1 x N 1
2
a
xN 2
a
x3
x
当n N时, 所有的点 x n 都落在 (a , a )内, 只有有限个 (至多只有N个 ) 落在其外.
n
3．数列极限的主要性质
(1)有界性：若lim x n A, 则M 0, 使得 | x n | M
n
( 2)唯一性：若lim x n A, lim x n B，则A B
n n
4．数列极限的存在准则
(1)夹逼准则：若 n x n z n , lim yn A, lim z n A y
比低阶
与同阶
与等价
2．无穷小的主要性质
(1) 若 | f ( x ) | M , g( x ) 0, 则 f ( x ) g( x ) 0
(2) 若～ 0( )
(3) 若～，～，且 lim 存在，则 lim lim
(a, b), 使f ( ) 0
函数极限典型例题
x3 3x2 2x lim 【例1】计算 x 2 x2 x 6
分析经过计算可得分子分母的极限都为零，说明分子分母都有致零因子，可以将分子分母的致零因子约去，再求极限。
x3 3 x2 2 x x( x 1)( x 2) 解： lim lim 2 x 2 x 2 ( x 3)( x 2) x x6
1 1 lim arctan x lim lim arctan x 0 0 x x x x x 2
1 1 lim arctan x lim arctan x 0 因为 x x x x
所以
1 lim arctan x 0 x x
分析
由于函数中含有根式，可利用分子有理化变形，

可变成的形式。解：lim x( x 2 1 x ) lim
x
x x2 1 x
x
lim
1 1 2 1 ( ) 1 x
x
思考
如果改为： x
1 2
结果如何？
【例4】计算 lim x 解法1: 因为 lim x
x x0 0
3．函数连续与极限的关系
连续极限存在
4．间断点的分类
第一类间断点（左右极限都存在）
lim lim 可去间断点： x 0 f ( x ) x x 0 f ( x ) x
0 0
间断点
lim lim 跳跃间断点： x 0 f ( x ) x x 0 f ( x ) x
可找到数列 bn和 cn 满足 bn an cn
lim bn a
n n
an 1 g ( a n )
验证 a n单调有界
lim cn a
应用极限的四则运算法则求极限
lim an a
n
应用单调有界准则
a lim an1
n
应用夹逼准则
lim an a
x x0
使得0 | x x0 | 时， f ( x ) | M |
,则在 (3) 局部保号性：若 lim f ( x ) A （0或0）
U ( x , ) 内有
x x0
f ( x ) 0(或 0)
（4）夹逼准则：若 g( x ) f ( x ) h( x )
【例 5】*计算 lim
x0
2e 1 e
1 x 2 x
分析本题含 e ，当 x 0 与(－0)时，有不同的结果，需要用左右极限求之。 1
0 0
第二类间断点
（左右极限至少有一个不存在）

无穷间断点：左右极限至少有一个是
振荡间断点：
二、连续函数的运算法则
1．若 f ( x ), g( x ) 都连续; 则 af ( x ) bg( x ) 也连续. 2．若 f ( x ), g( x ) 都连续; 则 f ( x ) g( x )也连续. 3．若 f ( x ), g( x ) 都连续; 则
2．数列极限的运算法则
(1) lim(axn byn ) a lim x n b lim yn aA bB
n n n
( 2) lim( x n yn ) lim x n lim yn AB
n n n
xn lim xn A ( 3) lim n ( B 0时) n y lim yn B n
limg( x ) lim h( x ) A
则 limf ( x ) A
三、无穷小与无穷大
1．无穷小的基本概念（1）无穷小的定义（2）无穷小阶的比较
lim ( x ) 0
0, 0，比较它们的阶
lim A
A0
A＝
A＝ c 0
c1
比高阶
n
lim g(an ) g(a )
n
lim an a
n
函数极限解题方法流程图
求 lim f ( x )
判别 f (x ) 的形式
f ( x ) g( x )h( x )
恒等变形
f ( x)
g( x ) h( x )
f (x ) 为未定式
f ( x) sin m( x ) 或 m( x ) 1