中点模型的构造(1)

合集下载

第1讲中点模型(经典难题)

基础知识回顾
1. 倍长中线已知任意三角形一边上的中点，可以连出过中点的线段并加倍延长，从而达到构造全等三角形的目的，如图 B 倍长中线法构造全等三角形，可以得到一组平行且相等的边，从而可知，倍长中线的本质是“构造平行四边形”
D A
D A
M
C
B
M E
C
几何辅助线秘诀拔高班·第1讲·学生版
E
F
B
【例2】如图，点 D 、 E 三等分 △ ABC 的 BC 边．求证： AB AC AD AE ．
A
D
C
B
D
E
C
2
几何辅助线秘诀拔高班·第1讲·学生版
【例3】分别以 △ ABC 的边 AB ，AC 为边，向三角形的外侧作正方形 ABDE 和正方形 ACFG ， M 为 BC 中点，求证： EG 2 AM ．
A
A M C B
A 30
B
D
C
B
A
C
D
E
B 图
C
A O M N
B
版块一：倍长中线
典题精练
【例1】 ⑴ 如下图，已知在 △ ABC 中， AD 是 BC 边上的中线， E 是 AD 上一点，且 BE AC ，延长 BE 交 AC 于 F ．求证： AF EF ． ⑵ 已知 △ ABC 中， AB 12 ， AC 30 ，求 BC 边上的中线 AD 的范围． A
A G F
D B
H E C
【例8】如图 1 所示， P 是 △ ABC 内的一点， PAC PBC ，过点 P 分别作 PM AC 于点 M ， PL BC 于点 L ， D 为线段 AB 的中点，求证： DM DL .

2021届中考数学精品冲刺复习“中点”之六大模型

跟踪训练 5．如图，在△ABC 中，AB＝12，AC＝8，AD 是 BC 边上的中线，则 AD 的取值范围是_2_＜__A_D_＜__1_0_______．
6．如图，已知在△ABC 中，AD 是 BC 边上的中线，E 是 AD 上一点，连接 BE 并延长交 AC 于点 F，AF＝EF，求证：AC＝BE．证明：延长 AD 至点 G，使 AD＝DG，连接 CG，BG． ∵AD 是中线，∴BD＝CD，∴四边形 ABGC 是平行四边形， ∴∠FAG＝∠BGE，AC＝BG．又∵AF＝EF，∴∠FAG＝∠AEF＝∠BEG， ∴∠BEG＝∠BGE． ∴BE＝BG，∴AC＝BE．
AC＝8，点 D 是 AB 的中点，过点 D 作 DE⊥AB 交 BC 的延 7
长线于点 E，则 CE 的长为____3____．【思路点拨】根据勾股定理易求得 AB＝10，则 BD
＝5，易证△ABC∽△EBD，则 BC∶BD＝AB∶(BC＋CE)，
从而求得 CE 的长．
跟踪训练 4．如图，在△ABC 中，AB＝AC．∠A＝120°，BC＝6 cm，AB，AC 的垂直平分线分别为 ME 与 NF，交 BC 边于点 M，N，则 NM 的长为___2_____cm．
数，再由 G 为 EF 中点，易得∠EOD＝∠DOF．
跟踪训练 7．★如图，⊙O 中，AB 是直径，AB＝10，BC＝8，E 是BC 的中点，连接 AE 交 BC 于点 D，则 AD＝__3__5____．
四边形 EGDF 为平行四边形，则 DF＝GE．再根据中位线定理可求得在边长为 8 的等边三角形 ABC 中，D，E 分别为 AB，BC 的中点， EF⊥AC 于点 F，G 为 EF 的中点，连接 DG，则 DG 的长为___1_9____．

中点模型的构造.docx1

中点模型的构造1.已知任意三角形一边上的中点，可以考虑：。

（1）倍长中线或类中线（与中点有关的线段）构造全等三角形。

（2）三角形中位线定理。

2 已知直角三角形斜边中点，可以考虑构造斜边中线。

3 已知等腰三角形底边中点，可以考虑与顶点连接用“三线合一”。

4 有些题目的中点不直接给出，此时需要我们挖掘题目中的隐含中点，例如直角三角形斜边中点，等腰三角形底边上的中点，当没有这些条件的时候，可以用辅助线添加。

一倍长中线或倍长类中线1如图，△ABC中，AD是BC边上的中线，E是AD上的一点。

连接BE并延长线交AC 于F，且AF=EF,求证：BE=AC.2 在△ABC 中，AD 交BC 于点D ，点E 是BC 中点，EF//AD 交CA的延长线于点F ，交AB 于点G，若AD为△ABC的角平分线，求证；BG=CF3 已知M为△ABC的边BC的中点，∠AMB、∠AMC的平分线分别与AB,AC交于点E、F,连接EF。

求证:EF<BE+CF.4 在△ABC中，D是BC的中点, DM⊥DN，如果BM²+CN²=DM²+DN²，求证AD²=¼（AB²+AC²）二直角三角形斜边中线1 如图，在△ABC中,BE,CF分别是AC,AB上的高,D是BC的中点，DM⊥EF于点M,求证：FM=EM.2已知：△ABD和△ACE都是直角三角形，且∠ABD=∠ACE=90°．如图甲，连接DE，设M为DE的中点．（1）说明：MB=MC；（2）设∠BAD=∠CAE，固定△ABD，让Rt△ACE绕顶点A在平面内旋转到图乙的位置，试问：MB=MC是否还能成立？并证明其结论．三一题多解题，利用中点作中线，倍长中线，中位线等辅助线是常用解法。

如图，在△ABC中，AB=AC，CE是AB边上的中线，延长AB至D，使BD=AB，联结CD。

求证:CD=2CE四利用三角形中位线的性质问题一如图1 在四边形ABCD中，AB=CD，E、F分别是BC、AD的中点，连接EF并延长，分别与BA、CD的延长线交于点M、N，求证∠BME=∠CNE 问题二：如图2，在四边形ADBC中，AB与CD相交于点O，AB=CD，E、F 分别是BC、AD的中点，连接EF，分别交DC、AB于点M、N，判断△OMN的形状，请直接写出结论；问题三：如图3，在△AB C中，AC＞AB，D点在AC上，AB=CD，E、F分别是BC、AD的中点，连接EF并延长，与BA的延长线交于点G，若∠EFC=60°，连接GD，判断△AGD的形状并证明．。

中点四大模型

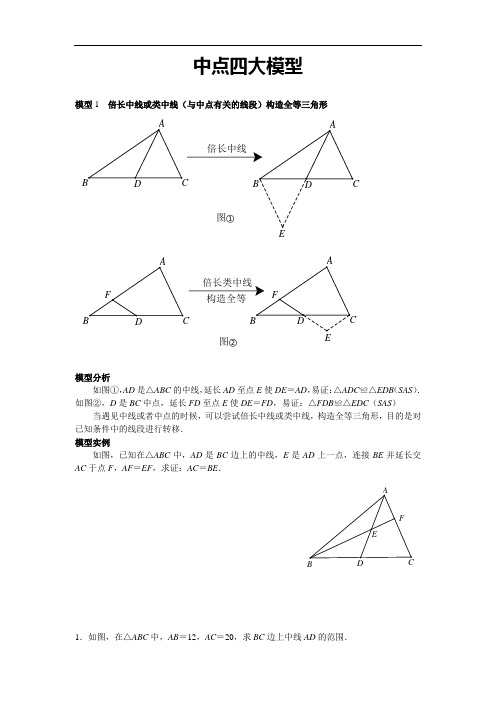
中点四大模型模型1 倍长中线或类中线（与中点有关的线段）构造全等三角形②图①图构造全等倍长类中线倍长中线DC BAFF ABCABCDCBA模型分析如图①，AD 是△ABC 的中线，延长AD 至点E 使DE ＝AD ，易证：△ADC ≌△EDB （SAS ）．如图②，D 是BC 中点，延长FD 至点E 使DE ＝FD ，易证：△FDB ≌△EDC （SAS ）当遇见中线或者中点的时候，可以尝试倍长中线或类中线，构造全等三角形，目的是对已知条件中的线段进行转移．模型实例如图，已知在△ABC 中，AD 是BC 边上的中线，E 是AD 上一点，连接BE 并延长交AC 于点F ，AF ＝EF ，求证：AC ＝BE ．FECA1．如图，在△ABC 中，AB ＝12，AC ＝20，求BC 边上中线AD 的范围．BA解：延长AD 到E ，使AD ＝DE ，连接BE ， ∵AD 是△ABC 的中线， ∴BD ＝CD ，在△ADC 与△EDB 中，⎪⎩⎪⎨⎧=∠=∠=DE AD BDE ADC CD BD ， ∴△ADC ≌△EDB （SAS ）， ∴EB ＝AC ＝20，根据三角形的三边关系定理：20－12＜AE ＜20＋12， ∴4＜AD ＜16，故AD 的取值范围为4＜AD ＜16．EABCD2．如图，在△ABC 中，D 是BC 的中点，DM ⊥DN ，如果BM 2＋CN 2＝DM 2＋DN 2．求证：AD 2＝41(AB 2＋AC 2)．NMA证明：如图，过点B 作AC 的平行线交ND 的延长线于E ，连ME ． ∵BD ＝DC ， ∴ED ＝DN ．在△BED 与△CND 中，∵⎪⎩⎪⎨⎧=∠=∠=DN ED CDN BDE DC BD ∴△BED ≌△CND （SAS ）． ∴BE ＝NC ． ∵∠MDN ＝90°，∴MD 为EN 的中垂线． ∴EM ＝MN ．∴BM 2＋BE 2＝BM 2＋NC 2＝MD 2＋DN 2＝MN 2＝EM 2， ∴△BEM 为直角三角形，∠MBE ＝90°． ∴∠ABC ＋∠ACB ＝∠ABC ＋∠EBC ＝90°． ∴∠BAC ＝90°． ∴AD 2＝(21BC )2＝41（AB 2＋AC 2）． ABCD MN模型2 已知等腰三角形底边中点，可以考虑与顶点连接用“三线合一”．连接中线ABCDDCBA模型分析等腰三角形中有底边中点时，常作底边的中线，利用等腰三角形“三线合一”的性质得到角相等，为解题创造更多的条件，当看见等腰三角形的时候，就应想到： “边等、角等、三线合一”．模型实例如图，在△ABC 中，AB ＝AC ＝5，BC ＝6，M 为BC 的中点，MN ⊥AC 于点N ，求MN 的长度．NM CB AAN解答：连接AM ．∵AB ＝AC ＝5，BC ＝6，点M 为BC 中点， ∴AM ⊥BC ，BM ＝CM ＝21BC ＝3． ∵AB ＝5， ∴AM ＝4352222=-=-BM AB ．∵MN ⊥AC ，∴S △ANC ＝21MC ·AM ＝21AC ·MN ．即：21×3×4＝21×5×MN ．∴MN ＝512小猿热搜1．如图，在△ABC 中，AB ＝AC ，D 是BC 的中点，AE ⊥DE ，AF ⊥DF ，且AE ＝AF ，求证：∠EDB ＝∠FDC ．FCA证明：连结AD ，∵AB ＝AC ，D 是BC 的中点， ∴AD ⊥BC ，∠ADB ＝∠ADC ＝90° 在Rt △AED 与Rt △AFD 中，⎩⎨⎧==ADAD AFAB ， ∴Rt △AED ≌Rt △AFD ．（HL ） ∴∠ADE ＝∠ADF ， ∵∠ADB ＋∠ADC ＝90°， ∴∠EDB ＝∠FDC ．AB C2．已知Rt △ABC 中，AC ＝BC ，∠C ＝90°，D 为AB 边的中点，∠EDF ＝90°，∠EDF 绕D 点旋转，它的两边分别交AC 、CB （或它们的延长线）于E 、F ．（1）当∠EDF 绕D 点旋转到DF ⊥AC 于E 时（如图①），求证：S △DEF ＋S △CEF ＝21S △ABC ；（2）当∠EDF 绕D 点旋转到DE 和AC 不垂直时，在图②和图③这两种情况下，上述结论是否成立？若成立，请给予证明；若不成立， S △DEF 、S △CEF 、S △ABC 又有怎样的数量关系？请写出你的猜想，不需要证明．③图②图①图ABDEFACDF DCA解：（1）连接CD ；如图2所示： ∵AC ＝BC ，∠ACB ＝90°，D 为AB 中点， ∴∠B ＝45°，∠DCE ＝21∠ACB ＝45°，CD ⊥AB ，CD ＝21AB ＝BD ， ∴∠DCE ＝∠B ，∠CDB ＝90°，∵∠EDF ＝90°， ∴∠1＝∠2，在△CDE 和△BDF 中，⎪⎩⎪⎨⎧∠=∠=∠=∠B DCB BD CD 21， ∴△CDE ≌△BDF （ASA ），∴S △DEF ＋S △CEF ＝S △ADE ＋S △BDF ＝21S △ABC ；（2）不成立；S △DEF −S △C EF ＝21S △ABC ；理由如下：连接CD ，如图3所示：同（1）得：△DEC ≌△DBF ，∠DCE ＝∠DBF ＝135° ∴S △DEF ＝S 五边形DBFEC ，＝S △CFE ＋S △DBC ，＝S △CFE ＋21S △ABC ， ∴S △DEF －S △CFE ＝21S △ABC ．∴S △DEF 、S △CEF 、S △ABC 的关系是：S △DEF －S △CEF ＝21S △ABC ． 21ACDEABCDEF模型3 已知三角形一边的中点，可考虑中位线定理构造中位线取另一边中点EADDC模型分析在三角形中，如果有中点，可构造三角形的中位线，利用三角形中位线的性质定理： DE ∥BC ，且DE ＝21BC 来解题．中位线定理中既有线段之间的位置关系又有数量关系，该模型可以解决角问题，线段之间的倍半、相等及平行问题．模型实例如图，在四边形ABCD 中，AB ＝CD ，E 、F 分别是BC 、AD 的中点，连接EF 并延长，分别与BA 、CD 的延长线交于点M ，N ．求证：∠BME ＝∠CNE ．NM FEDCBAHABDEFM N解答如图，连接BD ，取BD 的中点H ，连接HE 、HF ． ∵E 、F 分别是BC 、AD 的中点， ∴FH ＝21AB ，FH ∥AB ，HE ＝21DC ，HE ∥NC ．又∵AB ＝CD ，∴HE ＝HF ．∴∠HFE ＝∠HEF ． ∵FH ∥MB ，HE ∥NC ，∴∠BME ＝∠HFE ，∠CNE ＝∠FEH ． ∴∠BME ＝∠CNE ．练习：1.（1）如图1，BD ，CE 分别是△ABC 的外角平分线，过点A 作AD ⊥BD ，AE ⊥CE ，垂足分别为D ，E ，连接DE ，求证：DE ∥BC ，DE =12（AB +BC +AC ）；（2）如图2，BD ，CE 分别是△ABC 的内角平分线，其他条件不变，上述结论是否成立？（3）如图3，BD 是△ABC 的内角平分线，CE 是△ABC 的外角平分线，其他条件不变，DE 与BC 还平行吗？它与△ABC 三边又有怎样的数量关系？请写出你的猜想，并对其中一种情况进行证明.E D CBA图1G FEDCBA图2FED BA图31.解答（1）如图①，分别延长AE ，AD 交BC 于H ，K . 在△BAD 和△BKD 中，ABD DBK BD BDBDA BDK ∠=∠⎧⎪=⎨⎪∠=∠⎩∴△BAD ≌ △BKD （ASA ） ∴AD =KD ，AB =KB .同理可证，AE =HE ，AC =HC . ∴DE =12HK .又∵HK =BK +BC +CH =AB +BC +AC . ∴DE =12（AB +AC +BC ）.HKED C BA图1（2）猜想结果：图②结论为DE =12（AB +AC -BC ）证明：分别延长AE ，AD 交BC 于H ，K . 在△BAD 和△BKD 中ABD DBK BD BDBDA BDK ∠=∠⎧⎪=⎨⎪∠=∠⎩∴△BAD ≌△BKD （ASA ） ∴AD =KD ，AB =KB同理可证，AE =HE ，AC =HC . ∴DE =12HK . 又∵HK =BK +CH -BC =AB +AC -BC∴DE =12（AB +AC -BC ）GABCDEKHF 图2（3）图③的结论为DE =12（BC +AC -AB ）证明：分别延长AE ，AD 交BC 或延长线于H ，K . 在△BAD 和△BKD 中，ABD DBK BD BDBDA BDK ∠=∠⎧⎪=⎨⎪∠=∠⎩∴△BAD ≌△BKD （ASA ） ∴AD =KD ，AB =KB .同理可证，AE =HE ，AC =HC . ∴DE =12KH . 又∵HK =BH -BK=BC +CH -BK =BC +AC -AB∴DE =12（BC +AC -AB ）.ABCD EKHF图32.问题一：如图①，在四边形ABCD 中，AB 与CD 相交于点O ，AB =CD ，E ，F 分别是BC ，AD 的中点，连接EF ，分别交DC ，AB 于点M ，N ，判断△OMN 的形状，请直接写出结论.问题二：如图②，在△ABC 中，AC >AB ，D 点在AC 上，AB =CD ，E ，F 分别是BC ，AD 的中点，连接EF 并延长，与BA 的延长线交于点G ，若∠EFC =60°，连接GD ，判断△AGD 的形状并证明.图1NMO F E DC BAE图2G ABCDF2.证明（1）等腰三角形（提示：取AC 中点H ，连接FH ，EH ，如图①）图1ABC DE FNMO H（2）△AGD 是直角三角形如图②，连接BD ，取BD 的中点H ，连接HF ，HE . ∵F 是AD 的中点， ∴HF ∥AB ，HF =12AB . ∴∠1=∠3.同理，HE ∥CD ，HE =12CD ， ∴∠2=∠EFC ， ∴AB =CD ，∴HF =HE . ∴∠1=∠2.∵∠EFC =60°，∴∠3=∠EFC =∠AFG =60°. ∴△AGF 是等边三角形. ∴AF =FG . ∴GF =FD .∴∠FGD =∠FDG =30°.∴∠AGD =90°，即△AGD 是直角三角形.图2321G A BCDF H模型4 已知直角三角形斜边中点，可以考虑构造斜边中线构造直角三角形斜边上的中线DCBADA模型分析在直角三角形中，当遇见斜边中点时，经常会作斜边上的中线，利用直角三角形斜边上的中线等于斜边的一半，即CD =12AB ，来证明线段间的数量关系，而且可以得到两个等腰三角形：△ACD 和△BCD ，该模型经常会与中位线定理一起综合应用. 模型实例如图，在△ABC 中，BE ，CF 分别为AC ，AB 上的高，D 为BC 的中点，DM ⊥ EF 于点M ，求证：FM =EM .M FEDCBA证明连接DE ，DF .BE ，CF 分别为边AC ，AB 上的高，D 为BC 的中点， DF =12BC ，DE =12BC .DF =DE ，即△DEF 是等腰三角形. DM ⊥EF ，点M 是EF 的中点，即FM =EM .ABCEFM练习：1.如图，在△ABC 中，∠B =2∠C ，AD ⊥BC 于D ，M 为BC 的中点，AB =10，求DM 的长度.MD A1.解答取AB 中点N ，连接DN ，MN .在Rt △ADB 中，N 是斜边AB 上的中点， ∴DN =12AB =BN =5.∴∠NDB =∠B .在△ABC 中，M ，N 分别是BC ，AB 的中点， ∴MN ∥AC∴∠NMB =∠C ，又∵∠NDB 是△NDM 的外角， ∴∠NDB =∠NMD +∠DNM .即∠B =∠NMD +∠DNM =∠C +∠DNM . 又∵∠B =2∠C ，∴∠DNM =∠C =∠NMD . ∴DM =DN . ∴DM =5.N MD CBA2.已知，△ABD 和△ACE 都是直角三角形，且∠ABD =∠ACE =90°，连接DE ，M 为DE 的中点，连接MB ，MC ，求证：MB =MC .MEDCBA2.证明延长BM 交CE 于G ，∵△ABD 和△ACE 都是直角三角形， ∴CE ∥BD .∴∠BDM =∠GEM .又∵M 是DE 中点，即DM =EM ，且∠BMD =∠GME ， ∴△BMD ≌△GME . ∴BM =MG .∴M 是BG 的中点，∴在Rt △CBG 中，BM =CM .ABCDEMG3.问题1：如图①，三角形ABC 中，点D 是AB 边的中点，AE ⊥ BC ，BF ⊥AC ，垂足分别为点E ，F .AE 、BF 交于点M ，连接DE ，DF ，若DE =kDF ，则k 的值为 . 问题2：如图②，三角形ABC 中，CB =CA ，点D 是AB 边的中点，点M 在三角形ABC 内部，且∠MAC =∠MBC ，过点M 分别作ME ⊥BC ，MF ⊥ AC ，垂足分别为点E ，F ，连接DE ，DF ，求证：DE =DF .问题3：如图③，若将上面问题2中的条件“CB =CA ”变为“CB ≠CA ”，其他条件不变，试探究DE 与DF 之间的数量关系，并证明你的结论.图1MF E DCBA图2ABCDE FM图3ABCDE F M3.解答∵（1）AE ⊥BC ，BF ⊥AC ，∴△AEB 和△AFB 都是直角三角形， ∵D 是AB 的中点， ∴DE =12AB ，DF =12AB . ∴DE =DF . ∵DE =KDF ， ∴k =1.图1MF E DCBA（2）∵CB =CA ， ∴∠CBA =∠CAB . ∵∠MAC =∠MBC ，∴∠CBA -∠MBC =∠CAB -∠MAC ，即∠ABM =∠BAM . ∴AM =BM .∵ME ⊥BC ，MF ⊥AC ， ∴∠MEB =∠MF A =90°. 又∵∠MBE =∠MAF ，∴△MEB ≌△MF A （AAS ） ∴BE =AF .∵D 是AB 的中点，即BD =AD ，又∵∠DBE =∠DAF ，∴△DBE ≌△DAF （SAS ） ∴DE =DF .图2ABCDFM（3）DE =DF .如图，作AM 的中点G ，BM 的中点H ，连DG ，FG ，DH ，EH . ∵点D 是边AB 的中点， ∴DG ∥BM ，DG =12BM . 同理可得：DH ∥AM ，DH =12AM . ∵ME ⊥BC 于E ，H 是BM 的中点.∴在Rt △BEM 中，HE =12BM =BH . ∴∠HBE =∠HEB . ∴∠MHE =2∠HBE .又∵DG =12BM ，HE =12BM ，∴DG =HE .同理可得：DH =FG . ∠MGF =2∠MAC . ∵DG ∥BM ，DH ∥GM ，∴四边形DHMG 是平行四边形. ∴∠DGM =∠DHM .∵∠MGF =2∠MAC ， ∠MHE =2∠MBC ， ∠MBC =∠MAC ， ∴∠MGF =∠MHE .∴∠DGM +∠MGF =∠DHM +∠MHE . ∴∠DGF =∠DHE . 在△DHE 与△FGD 中DG HE DGF DHE DH FG =⎧⎪∠=∠⎨⎪=⎩∴△DHE ≌ △FGD （SAS ） ∴DE =DF .A BCDEFMHG。

2021年中考复习第07讲—中点五大模型

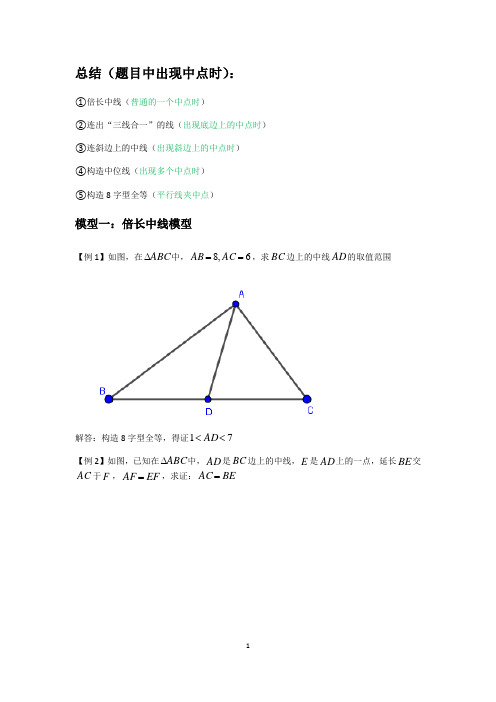
总结（题目中出现中点时）：①倍长中线（普通的一个中点时）②连出“三线合一”的线（出现底边上的中点时） ③连斜边上的中线（出现斜边上的中点时） ④构造中位线（出现多个中点时） ⑤构造8字型全等（平行线夹中点）模型一：倍长中线模型【例1】如图，在ABC ∆中，6,8==AC AB ，求BC 边上的中线AD 的取值范围解答：构造8字型全等，得证71<<AD【例2】如图，已知在ABC ∆中，AD 是BC 边上的中线，E 是AD 上的一点，延长BE 交AC 于F ，EF AF =，求证：BE AC =解答：①方法一：倍长中线【DG AD =构造8字型全等+集散思想】 ②方法二：类倍长中线【DE DG =构造8字型全等+集散思想】可证【例3】如图，在ABC ∆中，AD 交BC 于点D ，点E 是BC 中点，AD EF //交CA 的延长线于点F ，交AB 于点G ，若CF BG =，求证：AD 为ABC ∆的角平分线解答：类倍长中线+集散思想，可证模型二：平行线夹中点模型【例1】如图，在菱形ABCD 中，110=∠A ，F E ,分别是边AB 和BC 的中点，CD EP ⊥于点P ，则=∠FPC （）A.35 B.45 C.50 D.55解答：构造8字型全等【延长EF 和DC 交于点G 】，得证D【例2】如图，在平行四边形ABCD 中，AD BE AD CD ⊥=,2于点F E ,为DC 的中点，连接BF EF ,，下列结论 ①ABF ABC ∠=∠2 ②BF EF =③EFB DEBC S S ∆=2四边形 ④DEF CFE ∠=∠3 其中正确结论有（）A.1个B.2个C.3个D.4个解答：双平模型+平行线夹中点模型，得证D【例3】如图，在菱形ABCD 和正三角形BGF 中，60=∠ABC ，点F 在AB 的延长线上，点P 是DF 的中点，连接PC PG ,，求证：PC PG 3=解答：①方法一：延长CP 交AB 于点E ，连接EG CG ,②方法二：延长GP 交AD 于点E ，连接CG CE , 可证模型三：三线合一模型【例1】如图，在等腰三角形ABC 中，BC AC =，D 是BC 的中点，过C 作CE DE ⊥，CF DF ⊥，且CE CF =，求证：EDA FDB ∠=∠解答：可证【例2】如图，在ABC ∆中，5,6AB AC BC ===，M 为BC 中点，MN AC ⊥于点N ，则MN 的长度（） A.165 B.125 C.95 D.65解答：得证B【例3】如图，在ABC ∆中，,,,AB AC BAD CAD BD BE AM BM >∠=∠==，E 为AD 延长线上一点，N 在DE 上，//MN AC ，求证：ND NE =解答：双平模型+三线合一，可证【例4】如图所示，在ABC ∆中，AB AC =，90BAC ∠=，D 是AC 的中点，AF BD ⊥于点E ，交BC 于点F ，连接DF ，求证：ADB CDF ∠=∠解答：①方法一：三线合一模型 ②方法二：十字型三垂直模型可证模型四：斜边中线模型【例1】如图，在ABC ∆中，BD 和CE 是高，M 为BC 的中点，P 为DE 的中点，求证：PM DE ⊥解答：可证【例2】如图，在ABC ∆中，2B C ∠=∠，AD BC ⊥于点D ，M 是BC 中点，10AB =，求DM 的长度解答：可证【例3】已知，ABD ∆和ACE ∆都是直角三角形，且90ABD ACE ∠=∠=，如图甲，连接DE ，设M 为DE 的中点（1）说明：MB MC =（2）设BAD CAE ∠=∠，固定ABD ∆，让Rt ACE ∆绕顶点A 在平面内旋转到图乙位置，试问：MB MC =是否还能成立？并证明其结论解答：（1）①方法一：斜边中线模型【方程思想用字母表示角】 ②方法二：平行夹中点模型③方法三：相似【作MF BC ⊥交BC 于点M 1DM BFEM CF==得证】（2）成立，同理可证【例4】已知Rt ABC ∆中，AC BC =，90C ∠=，D 为AB 边的中点，90EDF ∠=，EDF ∠绕D 点旋转，它的两边分别交,AC CB （或它们的延长线）与,E F（1）当EDF ∠绕D 点旋转到DE AC ⊥于E 时（如图1），易证12DEF CEF ABC S S S ∆∆∆+=（2）当EDF ∠绕D 点旋转到和DE AC 不垂直时，在图2和图3这两种情况下，上述结论是否成立？若成立，请给予证明，若不成立,,DEF CEF ABC S S S ∆∆∆又有怎样的数量关系？请写出你的猜想，不需证明解答：（1）可证（2）图2成立，同理可证；图3不成立12DEF CEF ABC S S S ∆∆∆-=模型五：中位线模型【例1】已知四边形ABCD 是梯形，//AD BC ，如图，,E F 是,BD AC 中点，试写出EF 与,AD BC 之间的关系解答：①方法一：中位线+三点共线，得证1()2EF BC AD =- ②方法二：平行线夹中点模型，构造8字型全等，得证1()2EF BC AD =- 【例2】如图，在四边形ABCD 中，CD AB =，F E ,分别是AD BC ,的中点，连结EF 并延长，分别与CD BA ,的延长线交于点N M ,，证明：CNE BME ∠=∠解答：【等对边四边形（方法连接对角线）】可证【例3】在ABC ∆中，AB AC >，D 点在AC 上，CD AB =，F E ,分别是AD BC ,的中点，连结EF 并延长，与BA 的延长线交于点G ，若60=∠EFC ，连结GD ，判断AGD ∆的形状并证明解答：【类等对边四边形（方法连接对角线）】可证【例4】如图，在四边形ABCD 中，AC 与BD 相交于点O ，BD AC =，F E ,分别是CD AB ,的中点，连结EF ，分别交BD AC ,于点N M ,，判断OMN ∆的形状解答：【中点四边形（方法连接对角线）】可证。

初中数学常见模型之中点四大模型

巩固练习
1.（1）如图①，BD、CE 分别是△ABC 的外角平分，过点 A 作AD⊥BD、AE⊥CE，垂足分别为D、 E，连接DE。求证：DE∥BC，
（2）如图②，BD、CE 分别是△ABC 的内角平分，其它条件不变。上述结论是否成立？
（3）如图③，BD 是△ABC 的内角平分，CE 是△ABC 的外角平分，其它条件不变。DE 与BC 还平行吗？它与△ABC 三边又有怎样的数量关系？请写出你的猜想BD 中，AB 与CD 相交于点O，AB=CD，E、F 分别是BC、AD 的中点，连接 EF 分别交DC、AB 于点M、N，判断△OMN 的形状，请直接写出结论；
问题二：如图②，在△ABC 中，AC>AB，点D 在AC 上，AB=CD，E、F 分别是 BC、AD 的中点，连接EF 并延长，与BA 的延长线交于点 G，若 ∠EFC=60°，连接GD，判断△AGD 的形状并证明。
3.问题 1：如图①，△ABC 中，点D 是AB 边的中点，AE⊥BC，BF⊥AC，垂足分别为点E、F， AE、BF 交于点M，连接DE、DF。若 DE =kDF ，则k 的值为；
问题 2 ：如图 ② ， △ ABC 中， CB=CA ，点 D 是 AB 边的中点，点 M 在 △ ABC 内部，且 ∠MAC=∠MBC。过点 M 分别作ME⊥BC，MF⊥AC，垂足分别为点E、F，连接DE、DF。若 DE=DF；
模型实例
例 1:如图，已知在△ABC 中，AD 是BC 边上的中线，E 是AD 上一点，连接BE
并延长 AC 于点F，AF=EF。求证：AC=BE
巩固练习
1.如图，在△ABC 中，AB=12，AC=20，求BC 边上中线AD 的范围
2.如图，在△ABC 中，D 是BC 的中点，DM⊥DN，如果求证：

八年级数学第八章中点四大模型

第八章中点四大模型模型1【倍长中线或类中线（与中点有关的线段）构造全等三角形】模型分析如图①，AD是△ABC的中线，延长AD至点E使DE=AD，易证：△ADC≌△EDB（SAS）。

如图②，D是BC中点，延长FD至点E使DE=FD，易证：△FDB≌△FDC（SAS）。

当遇见中线或者中点的时候，可以尝试倍长中线或类中线，构造全等三角形，目的是对已知条件中的线段进行转移。

模型实例例1．如图，已知在△ABC中，AD是BC边上的中线，E是AD上一点，连接BE并延长AC于点F，AF=EF。

求证：AC=BE。

热搜精练1．如图，在△ABC 中，AB=12，AC=20，求BC 边上中线AD 的范围。

2．如图，在△ABC 中，D 是BC 的中点，DM⊥DN，如果2222B M C N D M D N +=+。

求证：()22214A D AB AC =+。

模型2【已知等腰三角形底边中点，可以考虑与顶点连接用“三线合一”】模型分析等腰三角形中有底边中点时，常作底边的中线，利用等腰三角形“三线合一”的性质得到角相等或边相等，为解题创造更多的条件，当看见等腰三角形的时候，就应想到：“边等、角等、三线合一”。

模型实例例1．如图，在△ABC中，AB=AC-5，BC=6，M为BC的中点，MN⊥AC于点N，求MN的长度。

热搜精练1．如图，在△ABC中，AB=AC，D是BC的中点，AE⊥DE，AF⊥DF，且AE=AF。

求证：∠EDB=∠FDC。

2．已知Rt△ABC 中，AC=BC，∠C=90°，D 为AB 边的中点，∠EDF=90°，∠EDF 绕点D 旋转，它的两边分别交AC、CB（或它们的延长线）于E、F。

（1）当∠EDF 绕点D 旋转到DE⊥AC 于E 时（如图①），求证：12DEF CEF ABC S S S += ；（2）当∠EDF 绕点D 旋转到DE 和AC 不垂直时，在图②和图③这两种情况下，上述结论是否成立？若成立，请给予证明；若不成立，DEF S 、CEF S 、ABC S 又有怎样的数量关系？请写出你的猜想，不需证明。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

EDN是等腰三角形 M是DN的中点
EM⊥DN

DM 1 EM
B
D
C
G
例题讲解
例1 如图所示，已知在∆ABC中，AD是BC边上的中线，E是AD上一点，连接BE并延长交AC于点F， AF=EF，求证:AC=BE
证法二：延长ED至点G，使DG=DE,连接CG A E F
点D是BC的中点 DB DC BDE CDG BED CGD G BED, BE CG 又 AF EF FAE AEF BED G DAC,即G EAF AC CG AC BE
E
F
例题讲解
例1 如图所示，已知在∆ABC中，AD是BC边上的中线，E是AD上一点，连接BE并延长交AC于点F， AF=EF，求证:AC=BE
证法一：延长AD至点G，使DG=AD,连接BG
A
E F
DB DC, BDG CDA, AD GD ADC GDB AC GB, G EAF 又 AF EF EAF AEF AEF BED G BED BE BG AC BE
B
D
C
G
∴
尝试应用
思路：中点构造八字全等
四边形ABCD和四边形CEFH都是正方形，连接AF，M是 AF中点，连接DM和EM.探究线段DM与EM的位置关系，并求 DM 的值. EM （1）如图，当点B、C、H在一条直线上时，线段DM与EM的位置关系是， DM = ；
EM 解题思路：延长DM与EF交于点N 证明△ADM≌△FNM 又 ∵∠DEN＝90° DM＝NM DM=MN,
D
C
(2)三角形中位线定理 2、已知直角三角形斜边上中点，可以考虑构造斜边中线。 3、已知等腰三角形底边中点，可以考虑与顶点连接用“三线合一” 4、有些题目的中点不直接给出，此时需要我们挖掘题目中的隐含中点，例如直角三角形中斜边中点，等腰三角形底边上的中点，当没有这些条件的时候，可以用辅助线添加。
几何辅助线添加技巧之
中点模型的构造（1）
珠海市夏湾中学
梁淑妍
核心纲要
线段的中点是几何图形中一个特殊的点，它关联着三角形中线、直角三角形斜边上中线、中心对称图形、三角形中位线等丰富的知识，恰当地利用中点，处理中点是解与中点有关问题的关键。
常见的联想路径
1、已知任意三角形一边上的中点，可以考虑：（1）倍长中线或类中线（与中点有关的线段）构造全等三角形（八字全等） A

中点模型的构造(1)

第1讲 中点模型(经典难题)