中点模型地构造、等积模型
平面几何五种模型

平面几何五种模型 TYYGROUP system office room 【TYYUA16H-TYY-TYYYUA8Q8-平面几何五种模型等积,鸟头,蝶形,相似,共边1、等积模型等底等高的2个三角形面积相等2个三角形高相等,面积比=底之比2个三角形底相等,面积比=高之比夹在一组平行线之间的等积变形(方方模型)等积模型是基本应用应是烂熟于心的都是利用面积公式得到的推定比例如下:1等底等高的2个平行四边形面积相等2三角形面积等于它等底等高的平行四边形面积的一半3 2个平行四边形高相等,面积比=底之比;2个平行四边形底相等,面积比=高之比2、鸟头模型(共角定理)鸟头定理:2个三角形中,有一个角相等或互补,这2个三角形叫做共角三角形。
共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比(夹角2边)鸟头定理的使用要火眼金睛,经常需要自己补一条辅助线同时经过2次以上转换对应才能得到结果。
A B C DE如图,浅紫色的三角形ADE 跟大三角形ABC 是公用A 角的,等于浅紫色三角形是“嵌入”在大三角形ABC 里面,注意,鸟头定理用的是乘积比!不是单独的线段比~记忆上用夹角2边 最好记,这里等于鸟头定理的证明,写出来是因为很多题目的解题过程,都需要补这么一条辅助线来过度连接2个看起来无关的图形。
证明的途径其实跟我们日常解题途径重合,所以写出来,仔细看。
经由媒介的ABE ,联系了ADE 和大三角形ABCBE 辅助线很重要!鸟头定理是用等高(等于是用等积推算而得) 第二种的证明方式将对顶角压回来ABC 内,对顶角性质是相等的,所以压回来的新跟ADE 是全等,再做一条辅助线就能用共角的方式证明出对角的鸟头定理互补角的鸟头定理证明S△ADE=S△AD'E,因为同底等高AD=AD',高相等,所以面积相等D'A B C D E 写了这几个证明,其实说的目的只有一个:连接小三角形和大三角形过度的那条辅助线,特别重要!3蝴蝶模型 任意四边形中的比例关系(“蝴蝶定理”)任蝴蝶①1243::S S S S =或者1324S S S S ⨯=⨯②()()1243::AO OC S S S S =++ 【上下比】= = = 【上上比】 = ==由上述比例可以按数学运算原则推出很多规则:如面积交叉相乘的乘积相等 == 1324S S S S ⨯=⨯ 梯形蝴蝶定理(梯蝴蝶)①2213::S S a b =→上:下=22:a b②221324::::::S S S S a b ab ab =→上:下:左:右=22:::a b ab ab ③S 的对应份数为()2a b +→a 2+2ab+b 2=a 2+b 2+ab+ab 有木有↑4 相似三角形形状相同,大小不同的三角形,只要形状不变,无论大小怎么改变,他们都相似。
中点模型的构造、等积模型

几何综合题型一:中点模型的构造中点模型 ①中线(点):倍长(类)中线 ②两中点:中位线③等腰三角形底边中点:三线合一④直角三角形斜边中点:斜边中线=斜边一半⇒构造两等腰 ⑤中垂线:中垂线上的点连两端点有些题目的中点没有直接给出,此时需要挖掘题目中隐含的中点条件,并适时添加辅助线.典题精练【例1】 如图,在平行四边形ABCD 中,点M 为边AD 的中点,过点C 作AB 的垂线交AB 于点E ,若∠EMD = 3∠MEA .求证:BC =2AB .DCBA E M【解析】证法一:如右图(a ),延长EM 交CD 的长线于点E ',连结CM ∵AB ∥CD ,∴∠ME'D =∠MEA .又AM = DM ,∠AME =∠DME' ∴△AFM ≌△DE M '. ∴EM =E M '∵AB ∥CD ,CE ⊥AB , ∴EC ⊥CD .∴CM 是Rt △ECE '斜边EE '的中线, ∴ME '=MC .∴ME D E CM '=',∴∠EMC = 2ME D ∠'= 2∠AEM . ∵∠EMD =3∠MEA , ∴∠CMD =∠DCM , ∴MD = CD .∵AD = 2DM ,AB = CD ,AD = BC , ∴BC = 2AB .证法二:(a )E’ME A BCD如右图(b ),过点M 作MM AB '∥交BC 于M ',过点M '作M E ME ''∥交AB 的延长线于点E ',连接EM '.∴点M '是BC '的中点,EE AB '=,E BM EAM ∠''=∠,M E B M EA ''=∠,M MD EAM E BM '=∠=∠'' ∵点M '是Rt △EBC 斜边BC 的中点, ∴M E BM '=',∴BEM M BE ∠'=∠'.∴180E BM BEM ∠''=︒-∠'.∵∠EMD = 3∠MEA ,∴2M MD MEA ∠'=∠, ∴2E BM M E B ∠''=∠''∴1802BEM M E B ︒-∠'=∠'',1902M E B BEM ∠''=︒-∠'.∴E EM E ∠=∠''.∴EM EE '=',∴BM AB '=. ∴BC = 2AB .【例2】 如图所示,分别以△ABC 的边AB 、AC 为边,向三角形的外侧作正方形ABDE 和正方形ACFG ,点M 为BC 中点,⑴ 求证:AM ⊥EG ;⑵ 求证:EG = 2AM .GF E DCBAM【解析】⑴ 如图所示,延长AM 到N ,使MN = AM ,延长MA 交EG 于点P ,连接BN 、NC .∵BM = CM ,∴四边形ABNC 是平行四边形. ∴BN = AC = AG .∵∠EAG +∠BAC = 180︒, ∠ABN +∠BAC = 180︒, ∴∠EAG =∠ABN . ∵AE = AB ,∴△EAG ≌△ABN .∴∠AEG =∠BAN . 又∵∠EAB = 90︒,∴∠EAP +∠BAN = 90︒. ∴∠AEP +∠EAP = 90︒. ∴MA ⊥EG .⑵ 证明:∵△EAG ≌△ABN ,∴EG = AN = 2AM .题型二:平移及等积变换典题精练(b )M’E’ME A B CDN P M A B C DE F G【例3】 已知:如图,正方形ABCD 中,E 是AB 上一点,FG ⊥DE 于点H .⑴ 求证:FG = DE .⑵ 求证:FD + BG.HG FE DC B APAB C DEFG H【解析】延长GC 到点P ,使得GP = DF ,连接EP ,DP .⑴ ∵DF ∥GP ,GP = DF∴四边形DFGP 为平行四边形 ∴FG = DP ,FG ∥DP 又∵FG ⊥DE ,∴DP ⊥DE ∴∠ADE =∠CDP 在△ADE 和△CDP 中 DAE DCP DA DCADE CDP ∠=∠⎧⎪=⎨⎪∠=∠⎩∴△ADE ≌△CDP ∴DE = DP = FG⑵ 由⑴知道△DEP 为等腰直角三角形∴EP ==在△EGP 中,EG + DF = EG + GP ≥PE当EG ∥FD 时,取到等号【例4】 如下图,过平行四边形ABCD 内的一点P 作边的平行线EF 、GH ,若△PBD 的面积为8平方分米,求平行四边形PHCF 的面积比平行四边形PGAE 的面积大多少平方分米?D【解析】根据差不变原理,要求平行四边形PHCF 的面积与平行四边形PGAE 的面积差,相当于求平行四边形BCFE 的面积与平行四边形ABHG 的面积差. 如右图,连接CP 、AP .可得:12BCP ADP S S ABCD +=△△12ABP BDP ADP ABCD S S S S ++=△△△所以BCD ABP BDP S S S -=△△△而12BCP BCFE S S =△,12ABP ABHG S S =△,所以()2216BCFE ABHG BCP ABP BDP S S S S S -=-==△△△(平方分米).题型三:旋转典题精练【例5】 已知△ABC 和△ADE 都是等腰直角三角形,∠ABC =∠ADE =90°,点M 是CE 的中点,连接BM .⑴ 如图①,点D 在AB 上,连接DM ,并延长DM 交BC 于点N ,可探究得出BD 与BM 的数量关系为 .⑵ 如图②,点D 不在AB 上,⑴中的结论还成立吗?如果成立,请证明;如果不成立,说明理由.图1NMED CBA图2M DCBE【解析】⑴ BD⑵ 结论成立,证明:连接DM ,过点C 作CF ∥ED ,与DM 的延长线交于点F ,连接BF ,可证得△MDE ≌△MFC ,∴DM = FM ,DE = FC , ∴AD = ED = FC , 作AN ⊥EC 于点N ,由已知∠ADE =90°,∠ABC =90°, 可证得∠1 =∠2,∠3 =∠4, ∵CF ∥ED , ∴∠1 =∠FCM ,∴∠BCF =∠4 +∠FCM = ∠3 +∠1 =∠3 +∠2 =∠BAD . ∴△BCF ≌△BAD ,∴BF = BD ,∠5 =∠6,∴∠DBF =∠5 +∠ABF =∠6 +∠ABF =∠ABC = 90°, ∴△DBF 是等腰三角形, ∵点M 是DF 的中点, 则△BMD 是等腰三角形,∴BD【例6】 已知正方形ABCD ,在BC 边上取一点E ,作EF AE ⊥交BCD ∠的外角平分线于F ,求证:AE EF =.D F CE B AGDFCE BA 【解析】 法一:如图,连接AC ,过E 作EG BC ⊥,交AC 于G .∵90AEG GEF ∠=︒-∠,90FEC GEF ∠=︒-∠, ∴AEG FEC ∠=∠.又∵GEC △为等腰直角三角形,∴GE CE =.又9045135ECF ∠=︒+︒=︒,18045135EGA ∠=︒-︒=︒, ∴ECF EGA ∠=∠,∴AEG FEC △≌△,故AE EF =. 法二:如图,过E 作EG BC ⊥,交FC 的延长线于G ,连接AC , 则45ECG DCF ∠=∠=︒,∴45EGF ∠=︒,∴EG EC =.而45ACE ∠=︒,∴EGF ECA ∠=∠.又90FEG FEC ∠=︒+∠,90AEC FEC ∠=︒+∠,∴FEG AEC ∠=∠,有EFG EAC △≌△, ∴AE EF =.法三:在AB 上截取BN =BE ,证明ANE ECF △≌△即可;思维拓展训练(选讲)训练1. 如图所示 ,等腰梯形ABCD 中,AB ∥CD ,AD = BC ,AC 与BD 交于点O ,∠AOB =60︒,P 、Q 、R 分别是OA 、OB 、OC 的中点,求证:△PQR 是正三角形.DCB AR Q P O【解析】证明:如右图,连接BP 、CR .∵四边形ABCD 是等腰梯形, ∴AD = BC ,OA = OB ,OC = OD . ∵∠AOB = 60°,∴△AOB 、△COD 都是正三角形. ∵P 是OA 的中点,R 是OD 的中点, ∴BP ⊥OA ,CR ⊥OD . ∵PR 是△ODA 的中位线,∴PR = 1122AD BC =.∴PR = PQ = QR .GDFCE BAO P QR ABCD∴△PQR 是正三角形.训练2. 如图⑴,四边形EFGH 中,若12∠=∠,则3∠必然等于4∠.请运用结论证明下述问题:如图⑵,在平行四边形ABCD 中取一点P ,使得56∠=∠,求证:78∠=∠.4321HGE F (1)(2)A BCDP5678【分析】此题为信息题,难点在于如何理解已知条件,经观察我们.....发现,若....1∠和.2∠,位置为....时可得出....3∠和.4∠相等..(.本质为...四点共圆....)..图⑵中,5∠与6∠关系并不像条件所示,因此,需要改变角位置,而这点可以通过构造平行四边形来解决.而构造平行四边形,恰可以达到改变角位置作用,为使5∠与6∠成形,我们可有如下四种方法.【解析】分别过点B 、P 作BK AP ∥,PK AB ∥,交于点K ,连接CK .∵BK AP ∥,PK AB ∥∴BK AP =,PK AB =,5BKP ∠=∠,7BPK ∠=∠∵AB CD =,AB CD ∥ ∴PK CD ∥,PK CD =∴四边形PKCD 为平行四边形 ∴PD CK = ∵AD BC = ∴ADP △≌BCK △∴8BCK ∠=∠ 在四边形BKCP 中,56BKP ∠=∠=∠ ∴BPK BCK ∠=∠ ∴78∠=∠A BCDP 5678K(∠5,∠6不动移)A BCDP 5678K(∠5,∠6不动移)ABC D P5678K(∠5不动移∠6)(∠5不动移∠6) (∠5,∠6不移动) (∠5,∠6不移动)(∠6不动移∠5)K8765P DC B A训练3. 已知:在△ABC 中,BC = a ,AC = b ,以AB 为边作等边三角形ABD .探究下列问题:⑴ 如图(a ),当点D 与点C 位于直线AB 的两侧时,a = b = 3,且∠ACB =60°,则CD = ________;⑵ 如图(b ),当点D 与点C 位于直线AB 的同侧时,a = b = 6,且∠ACB =90°,则CD = ________;⑶ 如图(c ),当∠ACB 变化,且点D 与点C 位于直线AB 的两侧时,求CD 的最大值及相应的∠ACB 的度数.(a )D C BA(b )DCBA(c )ABCD【解析】⑴⑵⑶ 如图(d ),以点D 为中心,将△DBC 逆时针旋转60°,则点B 落在点A ,点C 落在点E ,连接AE 、CE 、DE . ∴CD = ED ,∠CDE = 60°. ∴△CDE 为等边三角形. ∴CE = CD .当点E 、A 、C 不在一条直线上时,有CD = CE < AE + AC = a + b ;如图(e ),当点E 、A 、C 在一条直线上时,CD 有最大值,CD = CE = a + b ; 此时∠CED =∠BCD =∠ECD =60°,∴∠ACB =120°. 因此当∠ACB =120°时,CD 有最大值是a + b .ED CBA(d )(e )ED CBA。
中考必会几何模型:中点四大模型

2
9
Wang
2.问题一:如图①,在四边形 ABCD 中,AB 与 CD 相交于点 O,AB=CD,E,F 分别是 BC, AD 的中点,连接 EF,分别交 DC,AB 于点 M,N,判断△OMN 的形状,请直接写出结论. 问题二:如图②,在△ABC 中,AC>AB,D 点在 AC 上,AB=CD,E,F 分别是 BC,AD 的 中点,连接 EF 并延长,与 BA 的延长线交于点 G,若∠EFC=60°,连接 GD,判断△AGD 的形状并证明.
1
1
∴∠B=45°,∠DCE= ∠ACB=45°,CD⊥AB,CD= AB=BD,
2
2
∴∠DCE=∠B,∠CDB=90°,
∵∠EDF=90°,
5
Wang
∴∠1=∠2, 在△CDE 和△BDF 中,
1 2
CD BD
,
DCB B
∴△CDE≌△BDF(ASA),
1
∴S△DEF+S△CEF=S△ADE+S△BDF= S△ABC;
2 又∵HK=BK+CH-BC =AB+AC-BC ∴DE= 1 (AB+AC-BC)
2
Wang
(3)图③的结论为 DE= 1 (BC+AC-AB) 2
证明:分别延长 AE,AD 交 BC 或延长线于 H,K. 在△BAD 和△BKD 中, ABD DBK BD BD BDA BDK ∴△BAD ≌△BKD(ASA) ∴AD=KD,AB=KB. 同理可证,AE=HE,AC=HC. ∴DE= 1 KH.
10
Wang
初中数学必背几何模型
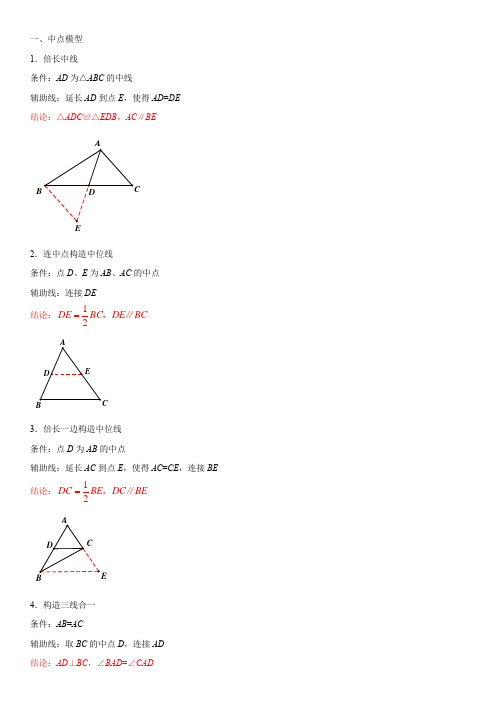
一、中点模型1.倍长中线条件:AD 为△ABC 的中线辅助线:延长AD 到点E ,使得AD =DE结论:△ADC ≌△EDB ,AC ∥BE2.连中点构造中位线条件:点D 、E 为AB 、AC 的中点辅助线:连接DE 结论:12DE BC DE BC =,∥3.倍长一边构造中位线条件:点D 为AB 的中点辅助线:延长AC 到点E ,使得AC =CE ,连接BE 结论:12DC BE DC BE =,∥4.构造三线合一条件:AB =AC辅助线:取BC 的中点D ,连接AD结论:AD ⊥BC ,∠BAD =∠CADB5.构造斜边中线条件:∠ABC =90°辅助线:取AC 的中点D ,连接BD 结论:12BD AC AD CD ===二、角平分线模型6.往角两边作垂线条件:AD 平分∠BAC辅助线:过点D 作AB 、AC 的垂线,垂足分别为E 、F结论:△ADE ≌△ADF7.在角的两边截取等长线段条件:AD 平分∠BAC辅助线:在AB 、AC 上取点E 、F ,满足AE =AF ,连接DE 、DF 结论:△ADE ≌△ADF8.过角平分线上一点作垂线条件:AD 平分∠BAC辅助线:过点D 作EF ⊥AD ,交AB 、AC 于点E 、FD CBB CCC结论:△ADE ≌△ADF三、双角平分线模型9.内内模型条件:BD 、CD 平分∠ABC 、∠ACB 结论:1902D A ∠=︒+∠10.内外模型条件:BD 、CD 平分∠ABC 、∠ACE 结论:12D A ∠=∠11.外外模型条件:BD 、CD 平分∠CBE 、∠BCF 结论:1902D A ∠=︒-∠四、平行线模型12.猪蹄模型CA BCC ED条件:AB ∥CD辅助线:过点E 作EF ∥AB结论:∠B +∠D =∠BED13.铅笔头模型条件:AB ∥CD辅助线:过点E 作EF ∥AB结论:∠B +∠D +∠BED =360°14.鸟头模型条件:AB ∥CD辅助线:过点E 作EF ∥AB结论:∠D +∠BED =∠B15.平行线+角平分线模型条件:AB ∥CD ,CE 平分∠ACD结论:AC =AE五、等积模型16.等底等高条件:AD ∥BCFAFBC结论:ABC DBC S S =,ADB ADC S S =17.等高模型条件:B 、C 、D 共线结论:::ABD ADC S S BD CD =18.等底模型条件:AE 、DE 为△ABC 、△DBC 边BC 上的高结论:::ABC DBC S S AE DE =六、对称半角模型19.对称半角模型-含45°角的三角形条件:∠BAC =45°,AD ⊥BC辅助线:作点D 关于AB 的对称点E ,关于AC 的对称点F , 连接AE 、AF 、BE 、CF 、EF结论:△AEF 是等腰直角三角形20.对称半角模型-含30°角的三角形B CB C DED条件:∠BAC =30°,AD ⊥BC辅助线:作点D 关于AB 的对称点E ,关于AC 的对称点F , 连接AE 、AF 、BE 、CF 、EF结论:△AEF 是等边三角形七、旋转半角模型21.旋转半角模型-等腰直角三角形条件:AB =AC ,∠BAC =90°,∠MAN =45°辅助线:将△ABM 绕点A 逆时针旋转90°,得到△ACM ' 结论:ANM ANM '≌,222BM CN MN +=22.旋转半角模型-等边三角形条件:△ABC 是等边三角形,BD =CD ,∠BDC =120°, ∠MDN =60°辅助线:将△BDM 绕点D 顺时针旋转120°,得到△DCM ' 结论:NDM NDM '≌,BM CN MN +=23.旋转半角模型-正方形条件:正方形ABCD ,∠MAN =45°,FEAM'M CAB辅助线:将△ABM 绕点A 逆时针旋转90°,得到△ADM ' 结论:NAM NAM '≌,BM DN MN +=八、自旋转模型24.自旋转模型-等边三角形条件:△ABC 是等边三角形,点P 为其内任意一点辅助线:将△BAP 绕点B 顺时针旋转60°,得到△BCP ' 结论:△BPP '是等边三角形25.自旋转模型-等腰直角三角形条件:△ABC 中,∠BAC =90°,AB =AC ,点P 为△ABC 内任 意一点辅助线:将△BAP 绕点A 逆时针旋转90°,得到△ACP ' 结论:△APP '是等腰直角三角形26.自旋转模型-等腰三角形条件:△ABC 中,AB =AC ,点P 为△ABC 内任意一点,∠BAC =α 辅助线:将△BAP 绕点A 逆时针旋转α,得到△ACP ' 结论:△APP '是等腰三角形M'DNCBAB九、手拉手模型29.手拉手模型-等边三角形条件:△ABC和△CDE都是等边三角形结论:△ACE≌△BCD27.手拉手模型-等腰直角三角形条件:△ABC和△CDE都是等腰直角三角形结论:△ACE≌△BCD,AE⊥BDEE28.手拉手模型-等腰三角形条件:△ABC 和△CDE 都是等腰三角形,CA =CB , CD =CE ,且∠ACB =∠DCE结论:△ACE ≌△BCD30.手拉手模型-正方形条件:四边形ABCD 和AEFH 都是正方形结论:△ABE ≌△ADH ,BE ⊥DH十、最短路程模型31.直线同侧两线段之和最小(将军饮马)条件:点A 、B 在直线l 同侧,点P 为l 上一点辅助线:作点A 关于直线l 的对称点A ',连接A 'B 结论:点P 为A 'B 和l 交点时,AP +BP 最小C32.直线异侧两线段之差最小条件:点A 、B 在直线l 异侧,点P 为l 上一点辅助线:作线段AB 的垂直平分线m结论:点P 为m 和l 交点时,|AP -BP |最小33.直线同侧两线段之差最小条件:点A 、B 在直线l 同侧,点P 为l 上一点辅助线:作线段AB 的垂直平分线m结论:点P 为m 和l 交点时,|AP -BP |最小34.过桥模型(将军饮马)条件:A 、B 为定点,l 1∥l 2,MN 为定长线段且MN ⊥l 1 辅助线:将点A 向上平移MN 的长度得到A ',连接A 'B 结论:点N 为A 'B 与l 1交点时,AM +MN +BN 最小35.四边形周长最小(将军饮马)条件:A 、B 为定点,M 、N 为角两边上的动点辅助线:作点A 、B 关于角两边的对称点A '、B ',连接 lAlAll 1l 2A'B'结论:M、N为A'B'与角两边交点时,四边形ABMN的周长最小B'36.三角形周长最小(将军饮马)条件:A为定点,B、C为角两边上的动点辅助线:作点A关于角两边的对称点A'、A",连接A'A"结论:B、C为A'A"与角两边交点时,△ABC的周长最小37.旋转类最短路程模型条件:线段OA=a,OB=b(a>b),OB绕点O在平面内旋转结论:点B与点N重合时,AB最小;点B与点M重合时,AB最大十一、基本相似模型38.A字型条件:BC∥DE结论:△ABC∽△ADE条件:∠ABC =∠ADE结论:△ABC ∽△ADE39.8字型条件:AB ∥CD结论:△AOB ∽△DOC条件:∠BAO =∠DCO结论:△AOB ∽△COD40.母子型条件:△ABC 中,∠ACB =90°,CD ⊥AB结论:△ABC ∽△ACD ∽△CBD41.一线三等角模型条件:∠B =∠D =∠ACE结论:△ABC ∽△CDECBCC A42.手拉手相似模型条件:△ABC ∽△ADE结论:△ACE ∽△ABD十二、对角互补模型43.对角互补模型-90°全等型条件:∠AOB =∠DCE =90°,OC 平分∠AOB辅助线:过点C 作CM ⊥AO ,CN ⊥BO ,垂足分别为M 、N 结论:△CDM ≌△CEN ,CD =CE ,OD +OEOC ,212OECD S OC 四边形CB ACE AB D CDD44.对角互补模型-120°全等型条件:∠AOB =120°,∠DCE =60°,OC 平分∠AOB辅助线:过点C 作CM ⊥AO ,CN ⊥BO ,垂足分别为M 、N 结论:△CDM ≌△CEN ,CD =CE ,OD +OE =OC ,24OECD S =四边形45.对角互补模型-任意角全等型条件:∠AOB =2α,∠DCE =180°-2α,OC 平分∠AOB辅助线:过点C 作CM ⊥AO ,CN ⊥BO ,垂足分别为M 、N 结论:△CDM ≌△CEN ,CD =CE ,2cos OD OE OC α+=⋅, 2sin cos OEC OCD S S OC αα+=⋅46.邻边相等的对角互补模型条件:四边形ABCD 中,AB =AD ,∠ABC +∠ADC =180°D BAN E OB辅助线:延长CD 到E ,使得DE =BC ,连接AE结论:△ABC ≌△ADE ,CA 平分∠BCD十三、隐圆模型47.动点定长模型条件:AB =AC =AP ,点P 为动点结论:点B 、C 、P 三点共圆,点A 为圆心,AB 为半径48.直角圆周角模型条件:点C 为动点,∠ACB =90°结论:点A 、B 、C 三点共圆,线段AB 的中点为圆心,线段 AB 为直径49.定弦定长模型条件:点P 为动点,固定线段AB 所对的动角∠APB 为定值 结论:点A 、B 、P 三点共圆,线段AB 和BP 的中垂线的交点 为圆心BA50.四点共圆模型①条件:点A 、C 为动点,∠BAD +∠BCD =180°结论:点A 、B 、C 、D 四点共圆,线段AB 和BC 的中垂线的 交点为圆心当∠BAD =∠BCD =90°,BD 为直径51.四点共圆模型②条件:线段AB 为固定长度,点D 为动点,∠C =∠D结论:点A 、B 、C 、D 四点共圆,线段AB 和BC 的中垂线的 交点为圆心CCA当∠C=∠D=90°,AB为直径。
2021年中考复习第07讲—中点五大模型

解答:类倍长中线+集散思想,可证
模型二:平行线夹中点模型
【例1】如图,在菱形ABCD中,ZA = 110°,仗尸分别是边A3和BC的中点,EP丄CD
于点P,
则ZFPC=(
)
A・35°
B・45°
C.50c
D・55°
D
解答:构造8字型全等【延长EF和DC交于点G】,得证D
【例2】如图,在平行四边形ABCD中,CD=2AD.BE丄4D于点6尸为DC的中点, 连接E0BF,下列结论
1ZABC=2ZABF
2 EF = BF
解答:构造8字型全等,得证1&l中,4D是BC边上的中线,E是ADL的一点,延长BE交
AC于F,AF=EF,求证:AC=BE
解答:
1方法一:倍长中线【AD=DG构造8字型全等+集散思想】
2方法二:类倍长中线【DG = DE构造8字型全等+集散思想】
可证
【例3】如图,在AABC中,AD交BC于点D,点疋是BC中点,EF//AD交C4的延 长线于点尸,交43于点G,若BG=CF,求证:4D为MBC的角平分线
总结(题目中出现中点时):
1倍长中线(普通的一个中点时)
2连出“三线合一”的线(出现底边上的中点时)
3连斜边上的中线(出现斜边上的中点时)
4构造中位线(出现多个中点时)
5构造8字型全等(平行线夹中点)
模型一:倍长中线模型
【例1】如图,在MBC中,4F = &AC=6,求BC边上的中线AD的取值范围
DC
初中数学中点模型

初中数学中点模型
中点模型是初中数学中的一个重要概念,它在解决几何问题时经常被使用。
中点模型指的是利用线段的中点来研究线段的性质和几何图形的性质的模型。
其基本思想是:在一个线段上找到中点,从而将原本的线段分成两个相等的部分,这两个部分之间具有一些特殊的性质。
中点模型可以应用于多种几何问题,如证明线段的平分线垂直于线段、证明三角形的垂心、证明四边形的对角线相等等。
此外,中点模型还可以用来求解一些有趣的几何题目,如如何用直线把正方形分成相等的两部分、如何用直线把正六边形分成相等的三部分等。
在学习中点模型时,学生需要掌握线段的中点的定义和性质,了解如何利用中点模型解决几何问题,同时还需要掌握一些基本的几何定理和推理方法。
通过练习和实践,学生可以逐渐掌握中点模型的应用技巧,提高几何证明和问题解决的能力。
- 1 -。
五年级奥数 五个几何模型
直线形面积计算的五个模型知识点精讲一、 等积变换模型(1) 等底等高的两个三角形面积相等;(2) 两个三角形的底相等,面积比等于他们高的比;(或者两个三角形的高相等,面积比等于他们底的比)AB 为公共边,所以 21::ABC ABD s s h h ∆∆=1h 为公共的高,所以 12::BD DC s s =(3) 两个三角形面积的比等于这两个三角形底与各自对应高的乘积的比。
底和高均不同,所以()21::)(ABD CDE BD DC h s s h ∆∆=⨯⨯比如:两个三角形的底的比是5:3,与各自底对应的高的比是7:6,那么他们的面积的比是(5×7):(3×6)二、 鸟头模型(共角模型)两个三角形中有一个角相等或者互补,这两个三角形叫做共角三角形。
共角三角形的面积比等于对应角(相等角或互补角)两条夹边的乘积之比。
BAC DAC ∠∠和互补,::DAC BAC DA AC BA AC s s ∆∆=⨯⨯所以E :E:DA BAC DA A BA AC s s ∆∆∠=⨯⨯A 为公共角,所以推理过程:连接BE ,运用等积变换模型证明。
三、 蝴蝶定理模型1.任意四边形中的比例关系(蝴蝶定理)1243::s s s s =或者1342s s s s ⨯=⨯14231243+AO:OC s s s s s s s s ===::():(+) 蝴蝶定理为我们提供了解决不规则四边形的面积问题的一个途径。
通过构造模型,一方面可以是不规则四边形的面积关系与四边形内三角形相联系;另一方面也可以得到与面积对应的对角线被分割的两段之间的比例关系。
2.梯形中比例关系(梯形蝴蝶定理)2213:a b s s =:221324::a b s s s s=:::ab :ab整个梯形对应的面积份数为: 2(a+b)四、 相似模型相似三角形性质:(金字塔模型) (沙漏模型)下面的比例关系适用如上两种模型:1、AD AE DE AF AB AC BC AG ===2、 22::ADE ABC s s AF AG ∆∆=所谓的相似三角形,就是形状相同,大小不同的三角形(只要其形状不改变,不论大小怎样改变,他们都是相似的),与相似三角形相关的常用的性质以及定理如下:(1) 相似三角形的一切对应线段的长度成比例,并且这个比例等于他们的相似比; (2) 相似三角形的面积比等于他们的相似比的平方。
【小升初奥数专题】几何之五大模型(已更新完)
【⼩升初奥数专题】⼏何之五⼤模型(已更新完)在⼩学奥数知识体系中,⼏何五⼤模型是⼏何专题中⾮常重要的⼀块知识点,⽅法性很强,掌握了⼏何的五⼤模型,对于我们解决组合型直图形或者⾮规则图形是⾮常有帮助的,所以⼏何五⼤模型在⼩学⼏何体系中的重中之重!⼏何五⼤模型的难点在于我们要在掌握各个模型适⽤的题型、相应的⽅法、公式的基础上学会灵活运⽤,还有就是有时要根据题意同时运⽤多种模型,从⽽更好的解决问题!接下来e 度徐丽⽼师会针对⼏何五⼤模型进⾏解析,希望能帮助到各位家长,让您的孩⼦在这次⼩升初中⼤战全胜!ps:对于不同题型均会有例题讲解分析以及精选练习题,以供⼤家有针对性学习巩固,相信⼤家对于应⽤题的攻克将不在话下!【⼏何五⼤模型知识点】【⼏何五⼤模型经典例题详解】【⼏何五⼤模型巩固练习】【⼏何五⼤模型巩固练习详解】标签:⼏何 模型 五⼤ ⼩升初 奥数回复 收藏1~3年级奥数每⽇⼀题汇总,含试题详解【每⽇不断更新中】4~5年级奥数每⽇⼀题汇总,含试题详解【每⽇不断更新中】⼩升初奥数天天练汇总,含试题详解【每⽇不断更新中】【徐丽⽼师】⼩升初奥数应⽤题专题汇总【徐丽⽼师】⼩升初奥数⾏程专题汇总【徐丽⽼师】⼩升初奥数⼏何专题汇总【徐丽⽼师】⼩升初奥数数论专题汇总【徐丽⽼师】⼩学数学毕业总复习专题汇总⼏⼏何五⼤模型⼀、五⼤模型简介(1)等积变换模型1、等底等⾼的两个三⾓形⾯积相等;2、两个三⾓形⾼相等,⾯积之⽐等于底之⽐,如图①所⽰,S[sub]1[/sub]:S[sub]2[/sub]=a:b ;3、两个三⾓形底相等,⾯积在之⽐等于⾼之⽐,如图②所⽰,S[sub]1[/sub]:S[sub]2[/sub]=a:b ;4、在⼀组平⾏线之间的等积变形,如图③所⽰,S[sub]△ACD[/sub]=S[sub]△BCD[/sub];反之,如果S[sub]△ACD[/sub]=S[sub]△BCD[/sub],则可知直线AB 平⾏于CD 。
初中数学中点模型归纳总结
初中数学中点模型归纳总结中点模型是初中数学中一个重要的概念,常用于几何图形的证明和计算中。
通过对中点模型的归纳总结,可以更好地理解和运用这一概念。
本文将分别从数轴中点、线段中点和三角形中点三个方面进行归纳总结。
一、数轴中点数轴中点是指数轴上离两个点距离相等的点。
在数轴上,如果A、B两个点的坐标分别为a和b,那么它们的中点的坐标可以通过以下公式计算:中点坐标 = (a + b) / 2通过这个公式,我们可以很方便地求解两个点的中点坐标。
同时,我们还可以推广到三个点的情况:三点中点坐标 = (a + b + c) / 3这个公式也可以以类似的方式计算。
二、线段中点线段中点是指线段上距离两个端点相等的点。
在线段AB上,如果A、B两个点的坐标分别为(x1,y1)和(x2,y2),那么它们的中点的坐标可以通过以下公式计算:中点坐标 = ((x1 + x2) / 2, (y1 + y2) / 2)通过这个公式,我们可以计算出线段AB的中点坐标。
同样地,我们还可以推广到三维空间中的情况:三维空间中点坐标 = ((x1 + x2 + x3) / 3, (y1 + y2 + y3) / 3, (z1 + z2 +z3) / 3)这个公式在三维几何场景中也能帮助我们求解线段的中点坐标。
三、三角形中点三角形中点是指连接三角形三个顶点与对边中点的线段所构成的三个线段的交点。
三角形的三个中点分别是三边中点、三角形重心和三角形外心。
下面我们分别来介绍它们的特点和计算方法。
1. 三边中点:连接三角形三个顶点与对边中点的线段的交点,分别记为M1、M2、M3。
这三个点构成的线段M1M2、M2M3和M3M1分别平分三角形的三条边,且交于三角形的重心G。
2. 三角形重心:三角形重心是连接三角形三个顶点与对边中点的线段的交点,记为G。
三角形的重心是三条中线的交点,其中中线是连接三角形的一个顶点与对边中点的线段。
3. 三角形外心:三角形外心是三角形三边垂直平分线的交点,记为O。
平面几何部分五大模型
平面几何部分知识点拨一、等积模型①等底等高的两个三角形面积相等;②两个三角形高相等,面积比等于它们的底之比; 两个三角形底相等,面积比等于它们的高之比; 如右图12::S S a b =③夹在一组平行线之间的等积变形,如右图ACDBCD S S =△△;反之,如果ACD BCD S S =△△,则可知直线AB 平行于CD .④等底等高的两个平行四边形面积相等(长方形和正方形可以看作特殊的平行四边形); ⑤三角形面积等于与它等底等高的平行四边形面积的一半;⑥两个平行四边形高相等,面积比等于它们的底之比;两个平行四边形底相等,面积比等于它们的高之比.二、鸟头定理两个三角形中有一个角相等或互补,这两个三角形叫做共角三角形. 共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比.如图在ABC △中,,D E 分别是,AB AC 上的点如图 ⑴(或D 在BA 的延长线上,E 在AC 上), 则:():()ABC ADE S S AB AC AD AE =⨯⨯△△图⑴ 图⑵三、蝴蝶定理任意四边形中的比例关系(“蝴蝶定理”):①1243::S S S S =或者1324S S S S ⨯=⨯②()()1243::AO OC S S S S =++蝴蝶定理为我们提供了解决不规则四边形的面积问题的一个途径.通过构造模型,一方面可以使不规则四边形的面积关系与四边形内的三角形相联系;另一方面,也可以得到与面积对应的对角线的比例关系. 梯形中比例关系(“梯形蝴蝶定理”): ①2213::S S a b = ②221324::::::S S S S a b ab ab =; ③S 的对应份数为()2a b +.EDCBAEDCB ADC BA S 4S 3S 2S 1O DCB A A BC D Ob aS 3S 2S 1S 4四、相似模型(一)金字塔模型 (二) 沙漏模型①AD AE DE AFAB AC BC AG===; ②22:ADE ABC S S AF AG =△△:.所谓的相似三角形,就是形状相同,大小不同的三角形(只要其形状不改变,不论大小怎样改变它们都相似),与相似三角形相关的常用的性质及定理如下:⑴相似三角形的一切对应线段的长度成比例,并且这个比例等于它们的相似比; ⑵相似三角形的面积比等于它们相似比的平方;⑶连接三角形两边中点的线段叫做三角形的中位线.三角形中位线定理:三角形的中位线长等于它所对应的底边长的一半.相似三角形模型,给我们提供了三角形之间的边与面积关系相互转化的工具. 在小学奥数里,出现最多的情况是因为两条平行线而出现的相似三角形. 五、燕尾定理 在三角形ABC 中,AD ,BE ,CF 相交于同一点O ,那么::ABO ACO S S BD DC ∆∆=. 上述定理给出了一个新的转化面积比与线段比的手段,因为ABO ∆和ACO ∆的形状很象燕子的尾巴,所以这个定理被称为燕尾定理.该定理在许多几何题目中都有着广泛的运用,它的特殊性在于,它可以存在于任何一个三角形之中,为三角形中的三角形面积对应底边之间提供互相联系的途径.GF E ABCD AB CDEF G O F ED CB A。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
几何综合题型一:中点模型的构造中点模型①中线(点):倍长(类)中线 ②两中点:中位线③等腰三角形底边中点:三线合一④直角三角形斜边中点:斜边中线=斜边一半⇒构造两等腰 ⑤中垂线:中垂线上的点连两端点有些题目的中点没有直接给出,此时需要挖掘题目中隐含的中点条件,并适时添加辅助线.典题精练【例1】 如图,在平行四边形ABCD 中,点M 为边AD 的中点,过点C 作AB 的垂线交AB 于点E ,若∠EMD = 3∠MEA .求证:BC =2AB .DCBA E M【解析】证法一:如右图(a ),延长EM 交CD 的长线于点E ',连结CM∵AB ∥CD ,∴∠ME'D =∠MEA .又AM = DM ,∠AME =∠DME' ∴△AFM ≌△DE M '. ∴EM =E M '∵AB ∥CD ,CE ⊥AB , ∴EC ⊥CD .∴CM 是Rt △ECE '斜边EE '的中线, ∴ME '=MC . ∴ME D E CM '=',∴∠EMC = 2ME D ∠'= 2∠AEM . ∵∠EMD =3∠MEA , ∴∠CMD =∠DCM , ∴MD = CD .∵AD = 2DM ,AB = CD ,AD = BC , ∴BC = 2AB . 证法二:如右图(b ),过点M 作MM AB '∥交BC 于M ',过点M '作M E ME ''∥交AB 的延长线于点E ',连接EM '.∴点M '是BC '的中点,EE AB '=,E BM EAM ∠''=∠,M E B M EA ''=∠,M MD EAM E BM '=∠=∠''∵点M '是Rt △EBC 斜边BC 的中点, ∴M E BM '=',∴BEM M BE ∠'=∠'. ∴180E BM BEM ∠''=︒-∠'.∵∠EMD = 3∠MEA ,∴2M MD MEA ∠'=∠, ∴2E BM M E B ∠''=∠'' ∴1802BEM M E B ︒-∠'=∠'',1902M E B BEM ∠''=︒-∠'.∴E EM E ∠=∠''.∴EM EE '=',∴BM AB '=.∴BC = 2AB .【例2】 如图所示,分别以△ABC 的边AB 、AC 为边,向三角形的外侧作正方形ABDE 和正方形ACFG ,点M 为BC 中点,⑴ 求证:AM ⊥EG ;⑵ 求证:EG = 2AM .(a )E’M E A BD(b )M’E’ME AB CDGF E DCAM【解析】⑴ 如图所示,延长AM 到N ,使MN = AM ,延长MA 交EG 于点P ,连接BN 、NC .∵BM = CM ,∴四边形ABNC 是平行四边形. ∴BN = AC = AG . ∵∠EAG +∠BAC = 180︒, ∠ABN +∠BAC = 180︒, ∴∠EAG =∠ABN . ∵AE = AB ,∴△EAG ≌△ABN .∴∠AEG =∠BAN . 又∵∠EAB = 90︒, ∴∠EAP +∠BAN = 90︒. ∴∠AEP +∠EAP = 90︒. ∴MA ⊥EG .⑵ 证明:∵△EAG ≌△ABN ,∴EG = AN = 2AM .题型二:平移及等积变换典题精练【例3】 已知:如图,正方形ABCD 中,E 是AB 上一点,FG ⊥DE 于点H .⑴ 求证:FG = DE .⑵ 求证:FD + BG.NP M ABC DEFGHG FE D C B APA B C DEFG H【解析】延长GC 到点P ,使得GP = DF ,连接EP ,DP .⑴ ∵DF ∥GP ,GP = DF ∴四边形DFGP 为平行四边形 ∴FG = DP ,FG ∥DP 又∵FG ⊥DE ,∴DP ⊥DE ∴∠ADE =∠CDP 在△ADE 和△CDP 中 DAE DCP DA DCADE CDP ∠=∠⎧⎪=⎨⎪∠=∠⎩∴△ADE ≌△CDP ∴DE = DP = FG⑵ 由⑴知道△DEP 为等腰直角三角形∴EP ==在△EGP 中,EG + DF = EG + GP ≥PE= FG当EG ∥FD 时,取到等号【例4】 如下图,过平行四边形ABCD 内的一点P 作边的平行线EF 、GH ,若△PBD 的面积为8平方分米,求平行四边形PHCF 的面积比平行四边形PGAE 的面积大多少平方分米?D【解析】根据差不变原理,要求平行四边形PHCF 的面积与平行四边形PGAE 的面积差,相当于求平行四边形BCFE 的面积与平行四边形ABHG 的面积差. 如右图,连接CP 、AP .可得:12BCP ADP S S ABCD +=△△12ABP BDP ADP ABCD S S S S ++=△△△所以BCD ABP BDP S S S -=△△△而12BCP BCFE S S =△,12ABP ABHG S S =△,所以()2216BCFE ABHG BCP ABP BDP S S S S S -=-==△△△(平方分米).题型三:旋转典题精练【例5】 已知△ABC 和△ADE 都是等腰直角三角形,∠ABC =∠ADE =90°,点M 是CE 的中点,连接BM .⑴ 如图①,点D 在AB 上,连接DM ,并延长DM 交BC 于点N ,可探究得出BD 与BM 的数量关系为 .⑵ 如图②,点D 不在AB 上,⑴中的结论还成立吗?如果成立,请证明;如果不成立,说明理由.图1NMED CB图2M DCBE【解析】⑴ BD⑵ 结论成立,证明:连接DM ,过点C 作CF ∥ED ,与DM 的延长线交于点F ,连接BF ,可证得△MDE ≌△MFC , ∴DM = FM ,DE = FC , ∴AD = ED = FC , 作AN ⊥EC 于点N ,由已知∠ADE =90°,∠ABC =90°, 可证得∠1 =∠2,∠3 =∠4, ∵CF ∥ED , ∴∠1 =∠FCM ,∴∠BCF =∠4 +∠FCM = ∠3 +∠1 =∠3 +∠2 =∠BAD . ∴△BCF ≌△BAD ,GDFCEBA∴BF = BD ,∠5 =∠6,∴∠DBF =∠5 +∠ABF =∠6 +∠ABF =∠ABC = 90°, ∴△DBF 是等腰三角形, ∵点M 是DF 的中点, 则△BMD 是等腰三角形, ∴BD【例6】 已知正方形ABCD ,在BC 边上取一点E ,作EF AE ⊥交BCD ∠的外角平分线于F ,求证:AE EF =.【解析】 法一:如图,连接AC ,过E 作EG BC ⊥,交AC 于G .∵90AEG GEF ∠=︒-∠,90FEC GEF ∠=︒-∠, ∴AEG FEC ∠=∠.又∵GEC △为等腰直角三角形,∴GE CE =.又9045135ECF ∠=︒+︒=︒,18045135EGA ∠=︒-︒=︒, ∴ECF EGA ∠=∠,∴AEG FEC △≌△,故AE EF =.法二:如图,过E 作EG BC ⊥,交FC 的延长线于G ,连接AC , 则45ECG DCF ∠=∠=︒, ∴45EGF ∠=︒,∴EG EC =. 而45ACE ∠=︒,∴EGF ECA ∠=∠.又90FEG FEC ∠=︒+∠,90AEC FEC ∠=︒+∠, ∴FEG AEC ∠=∠,有EFG EAC △≌△, ∴AE EF =.法三:在AB 上截取BN =BE ,证明ANE ECF △≌△即可;GDFCEBADFCEBA思维拓展训练(选讲)训练1. 如图所示 ,等腰梯形ABCD 中,AB ∥CD ,AD = BC ,AC 与BD交于点O ,∠AOB =60︒,P 、Q 、R 分别是OA 、OB 、OC 的中点,求证:△PQR 是正三角形.DCB AR Q P O【解析】证明:如右图,连接BP 、CR .∵四边形ABCD 是等腰梯形, ∴AD = BC ,OA = OB ,OC = OD . ∵∠AOB = 60°,∴△AOB 、△COD 都是正三角形. ∵P 是OA 的中点,R 是OD 的中点, ∴BP ⊥OA ,CR ⊥OD . ∵PR 是△ODA 的中位线,∴PR = 1122AD BC =.∴PR = PQ = QR . ∴△PQR 是正三角形.训练2. 如图⑴,四边形EFGH 中,若12∠=∠,则3∠必然等于4∠.OPQ R ABCD请运用结论证明下述问题:如图⑵,在平行四边形ABCD 中取一点P ,使得56∠=∠,求证:78∠=∠.4321HGE F (1)(2)A BCDP5678【分析】此题为信息题,难点在于如何理解已知条件,经观察我们.....发现,若....1∠和.2∠,位置为....时可得出....3∠和.4∠相等..(.本质为四点共圆.......)..图⑵中,5∠与6∠关系并不像条件所示,因此,需要改变角位置,而这点可以通过构造平行四边形来解决.而构造平行四边形,恰可以达到改变角位置作用,为使5∠与6∠成形,我们可有如下四种方法.【解析】分别过点B 、P 作BK AP ∥,PK AB ∥,交于点K ,连接CK .∵BK AP ∥,PK AB ∥∴BK AP =,PK AB =,5BKP ∠=∠,7BPK ∠=∠ ∵AB CD =,AB CD ∥ ∴PK CD ∥,PK CD =∴四边形PKCD 为平行四边形 ∴PD CK = ∵AD BC = ∴ADP △≌BCK △ ∴8BCK ∠=∠在四边形BKCP 中,56BKP ∠=∠=∠ ∴BPK BCK ∠=∠ ∴78∠=∠A BCDP 5678K(∠5,∠6不动移)A BCDP 5678K(∠5,∠6不动移)ABC D P5678K(∠5不动移∠6)(∠5不动移∠6) (∠5,∠6不移动) (∠5,∠6不移动)(∠6不动移∠5)K8765P DCB A训练3. 已知:在△ABC 中,BC = a ,AC = b ,以AB 为边作等边三角形ABD .探究下列问题:⑴ 如图(a ),当点D 与点C 位于直线AB 的两侧时,a = b = 3,且∠ACB =60°,则CD = ________;⑵ 如图(b ),当点D 与点C 位于直线AB 的同侧时,a = b = 6,且∠ACB =90°,则CD = ________;⑶ 如图(c ),当∠ACB 变化,且点D 与点C 位于直线AB 的两侧时,求CD 的最大值及相应的∠ACB 的度数.(a )DC BA(b )DCBA(c )ABCD【解析】⑴⑵⑶ 如图(d ),以点D 为中心,将△DBC 逆时针旋转60°,则点B 落在点A ,点C 落在点E ,连接AE 、CE 、DE . ∴CD = ED ,∠CDE = 60°. ∴△CDE 为等边三角形. ∴CE = CD .当点E 、A 、C 不在一条直线上时,有CD = CE < AE + AC = a + b ; 如图(e ),当点E 、A 、C 在一条直线上时,CD 有最大值,CD = CE = a + b ; 此时∠CED =∠BCD =∠ECD =60°,∴∠ACB =120°. 因此当∠ACB =120°时,CD 有最大值是a + b .ED CBA(d )(e )ECBA。
