2简谐振动的合成
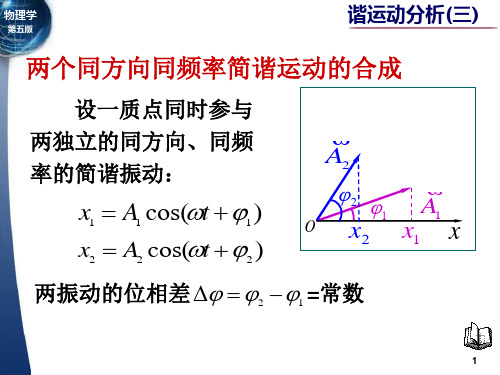
谐振动分析(三)两个同方向同频率简谐运动的合成
o
o
A1
A2
A
T
t
A A1 A2
x (A A )cos(t )
1
2
2 1 2k π
3
物理学
第五版
谐运动分析(三)
(2)相位差 (2k 1) π(k 0,1, )
2
1
x
x
A1
2 o
o
Tt
A
A2
A A1 A2
x (A2 A1)cos(t )
2
1
(2k
1)π
4
物理学
第五版
小结
(1)相位差
2
1
2k
π
A A1 A2
谐运动分析(三)
(k 0,1, ) 加强
(2)相位差
2
1
(2k 1) π
(k 0,1, )
A A A
1
2
减弱
(3)一般情况
A1 A2 A A1 A2
5
物理学
第五版
谐运动分析(三)
二 两个相互垂直的同频率的简谐
运动的合成 x A1 cos(t 1)
x 阻尼振动位移时间曲线
A
Ae t
Aet cost
O
T A
t
( 0)
21
物理学
第五版
三种阻尼的比较
谐运动分析(三)
(a)欠阻尼
2 0
2
(b)过阻尼
2 0
2
(c)临界阻尼
2 0
2
x
b
oc
t
a
22
物理学
第五版
谐运动分析(三)
例 有一单摆在空气(室温为 20C)中来 回摆动. 摆线长l 1.0 m,摆锤是半径r 5.0103 m 的铅球.求(1)摆动周期;(2)振幅减小 10%所需的时间;(3)能量减小10%所需 的时间;(4)从以上所得结果说明空气的 粘性对单摆周期、振幅和能量的影响.
大物习题集答案解析第4章机械振动

第4章 机械振动4.1基本要求1.掌握描述简谐振动的振幅、周期、频率、相位和初相位的物理意义及之间的相互关系2.掌握描述简谐振动的解析法、旋转矢量法和图线表示法,并会用于简谐振动规律的讨论和分析3.掌握简谐振动的基本特征,能建立一维简谐振动的微分方程,能根据给定的初始条件写出一维简谐振动的运动方程,并理解其物理意义4.理解同方向、同频率简谐振动的合成规律,了解拍和相互垂直简谐振动合成的特点4.2基本概念1.简谐振动 离开平衡位置的位移按余弦函数(或正弦函数)规律随时间变化的运动称为简谐振动。
简谐振动的运动方程 cos()x A t ωϕ=+2.振幅A 作简谐振动的物体的最大位置坐标的绝对值。
3.周期T 作简谐振动的物体完成一次全振动所需的时间。
4.频率ν 单位时间内完成的振动次数,周期与频率互为倒数,即1T ν=5.圆频率ω 作简谐振动的物体在2π秒内完成振动的次数,它与频率的关系为22Tπωπν==6.相位和初相位 简谐振动的运动方程中t ωϕ+项称为相位,它决定着作简谐振动的物体状态;t=0时的相位称为初相位ϕ7.简谐振动的能量 作简谐振动的系统具有动能和势能。
弹性势能222p 11cos ()22E kx kA t ωϕ==+ 动能[]22222k 111sin()sin ()222E m m A t m A t ωωϕωωϕ==-+=+v弹簧振子系统的机械能为222k p 1122E E E m A kA ω=+==8.阻尼振动 振动系统因受阻尼力作用,振幅不断减小。
9.受迫振动 系统在周期性外力作用下的振动。
周期性外力称为驱动力。
10.共振 驱动力的角频率为某一值时,受迫振动的振幅达到极大值的现象。
4.3基本规律1.一个孤立的简谐振动系统的能量是守恒的物体做简谐振动时,其动能和势能都随时间做周期性变化,位移最大时,势能达到最大值,动能为零;物体通过平衡位置时,势能为零,动能达到最大值,但其总机械能却保持不变,且机械能与振幅的平方成正比。
大物习题答案第4章机械振动

第4章 机械振动4.1基本要求1.掌握描述简谐振动的振幅、周期、频率、相位和初相位的物理意义及之间的相互关系2.掌握描述简谐振动的解析法、旋转矢量法和图线表示法,并会用于简谐振动规律的讨论和分析3.掌握简谐振动的基本特征,能建立一维简谐振动的微分方程,能根据给定的初始条件写出一维简谐振动的运动方程,并理解其物理意义4.理解同方向、同频率简谐振动的合成规律,了解拍和相互垂直简谐振动合成的特点4.2基本概念1.简谐振动 离开平衡位置的位移按余弦函数(或正弦函数)规律随时间变化的运动称为简谐振动。
简谐振动的运动方程 cos()x A t ωϕ=+2.振幅A 作简谐振动的物体的最大位置坐标的绝对值。
3.周期T 作简谐振动的物体完成一次全振动所需的时间。
4.频率ν 单位时间内完成的振动次数,周期与频率互为倒数,即1T ν=5.圆频率ω 作简谐振动的物体在2π秒内完成振动的次数,它与频率的关系为22Tπωπν== 6.相位和初相位 简谐振动的运动方程中t ωϕ+项称为相位,它决定着作简谐振动的物体状态;t=0时的相位称为初相位ϕ7.简谐振动的能量 作简谐振动的系统具有动能和势能。
弹性势能222p 11cos ()22E kx kA t ωϕ==+ 动能[]22222k 111sin()sin ()222E m m A t m A t ωωϕωωϕ==-+=+v弹簧振子系统的机械能为222k p 1122E E E m A kA ω=+== 8.阻尼振动 振动系统因受阻尼力作用,振幅不断减小。
9.受迫振动 系统在周期性外力作用下的振动。
周期性外力称为驱动力。
10.共振 驱动力的角频率为某一值时,受迫振动的振幅达到极大值的现象。
4.3基本规律1.一个孤立的简谐振动系统的能量是守恒的物体做简谐振动时,其动能和势能都随时间做周期性变化,位移最大时,势能达到最大值,动能为零;物体通过平衡位置时,势能为零,动能达到最大值,但其总机械能却保持不变,且机械能与振幅的平方成正比。
第2节_简谐振动的合成

x = ( A1 cosϕ1 + A2 cosϕ2 ) cosωt − ( A1 sinϕ1 + A2 sinϕ2 ) sinωt = A cos ϕ ⋅ cos ωt − A sin ϕ ⋅ sin ωt = A cos(ωt + ϕ ) ∴ x = A cos(ωt + ϕ )
两个同方向、 两个同方向、同频率的简谐振动合成后仍然是一个 简谐振动,且频率不变。 简谐振动,且频率不变。 由
若 A1 = A2 , A = 2A1
= A1 + A2
合振动振幅最大。 合振动振幅最大。
( ) 2.当 ∆ϕ=ϕ2 −ϕ1 = 2k +1 π ( k = 0,±1,±2,⋯) 时, 当
2 2 A = A1 + A2 + 2A1A2 cos( 2 −ϕ1 ) ϕ
A2
=| A1 − A2 |
A
A2 A1
2 2
ϕ 2 − ϕ1 = π / 2
2 2
x y + =1 A1 A2
•当 当
16
A1 = A2 ,
x +y =A
2
为圆方程
2.
∆ϕ = π / 2
y
8
1 2
y
7 6 5
4
7 6 5
4
8
1 2 2 1
x
3
3
4
播 放 动 画
17
3
5 6 7
x
8
4.
3π (ϕ 2 − ϕ1 ) = 2
9
由于余弦函数绝对值的周期为π。 ω 2 − ω1 t ) 的频率的两倍。 所以, 的频率的两倍。 所以,拍频是振动 cos( 2 即拍频为: 即拍频为:
简谐振动的合成实验

简谐振动的合成实验一、实验目的1.掌握谐振动的表达与合振动的分析2.掌握信号的相位、幅度、频率等参数的物理含义3.掌握用示波器观察波形以及测量电压、周期和频率的方法。
4.掌握使用信号发生器。
5.利用李萨茹图分析待测信号的相位频率等信息二、实验仪器Waveace1012型数字示波器1台、DG4062型数字信号发生器一台、传输线2条等。
三、示波器的使用(三四节的内容在实验报告中仅需概述即可)示波器就是显示波形的机器,它还被誉为“电子工程师的眼睛”。
它的核心功能就是为了把被测信号的实际波形显示在屏幕上,以供工程师查找定位问题或评估系统性能等等。
它的发展同样经历了模拟和数字两个时代,如图1和图2所示。
图1 模拟示波器图2 数字示波器模拟示波器采用的是模拟电路(示波管,其基础是电子枪)电子枪向屏幕发射电子,发射的电子经聚焦形成电子束,并打到屏幕上。
屏幕的内表面涂有荧光物质,这样电子束打中的点就会发出光来。
而数字示波器则是数据采集,A/D转换,软件编程等一系列的技术制造出来的高性能示波器。
数字示波器一般支持多级菜单,能提供给用户多种选择,多种分析功能。
还有一些示波器可以提供存储,实现对波形的保存和处理。
模拟示波器显示的波形是连续的,是信号真实的波形,而且反应速度特快。
而数字示波器显示的波形是经过数字电路采样得来的点组成的,是个不连续的波形,采样率越高的示波器,越与真实波形接近,但显示速度没有模拟机快。
反应速度快是模拟示波器最大的优点之一,是数字机很难取代的,比如,在测试某一信号时,模拟示波器能在瞬间显示波形,几乎没有延时,而数字机还需要将测试的信号进过数字电路处理后,再显示出模拟的波形,在显示时间上落后模拟示波器。
在此,我们仅介绍数字示波器的使用情况。
示波器可以将输入的波形在屏幕上显示出来,waveace1012型示波器具有两个输入通道,可以同时测量并显示2路信号的变化波形。
示波器的屏幕可以设置成横坐标为时间t,纵坐标为输入信号的电压量的大小,称为“Y-T”时基,如图所示。
第二节 两个简谐振动的合成

A12 A22 2A1A2 cos(02 01)
A A12 A22 2A1A2 cos
[注:cos( ) cos cos sin sin ]
A值的讨论,有三种情况:
(1) 2k
cos 1
A A1 A2
A值最大
(2) (2k 1) cos 1
A A1 A2 (3) 为其它值
波器显示屏上出现合成结果的图形,见右图。求x ?
解:
x y
m n
Y方向切点数 X方向切点数
x 3 x y 2 1000
x 1500 Hz
本节小结
同方向
1
2
简谐振动 A A12 A22 2A1A2 cos
同方向 1 2 拍 2 1
垂直方向
x m y n
李萨如图
x y
两个简谐振动的步调比较
同相:若两个简谐振动的频率相同、初相位相同,则两个简谐 振动的位移同时达到最大和最小。
x
1
2
t3
t1
t2
t4
t
0 ,同相
反相:若两个简谐振动的频率相同、初相位相差π,则一个振
动到达最大位移处时,另一个振动到达反向最大位移处。
1
x
t1
t2
t3
t4
t
2
,反相
超前与落后:若两个简谐振动的频率相同,初相位之差为
Y2 B2
1
X 0 t1 0 Y B
t2
2
X A Y 0
X 0 t3 Y B
t4
3 2
X A Y 0
t4 t3
t2
t1 Y超前π/2
右旋振动
t1 t2
t3
t4 Y落后π/2
5.2 简谐振动的能量与合成

第5章 机械振动
4
2.简 谐 振 动 的 微 分 方 程 (动力学方程) 动力学方程)
k F
m
o x
x
dx 2 +ω x = 0 2 dt
2
a = −ω x
2
作者 杨 鑫
k ω = m
2
5.2 简谐振动的能量与合成
第5章 机械振动
5
3.简谐振动的运动方程(振动方程) 3.简谐振动的运动方程 振动方程)
ω
2 0 2
5.2 简谐振动的能量与合成
第5章 机械振动
8
1 ω ν= = T= ω = 2πν T 2π ω 1 1 k 弹簧 2π m k ω = T = = 2π ν = T= 2π m 振子 k m ω
2.周期 2.周期 (T )
2π
频率 ( ) ν
圆频率 (ω)
单 摆
作者 杨
鑫
g l 1 1 g 2π ω = T = = 2π ν = = g T 2π l l ω
5.2 简谐振动的能量与合成
第5章 机械振动
9
求一个振动系统固有ω,T,ν的方法 求一个振动系统固有 的方法 2 ( 1 ) 建立振动系 d x + Bx = 0 统的微分方程 2
dt
x前的系数的开方就是振
( 2 ) 利用公式
ω = 2πν = 2π T 2 (3)利用速度 vm = ωA am = ω A 和加速度幅值
5.2 简谐振动的能量与合成
第5章 机械振动
1
作者
杨
鑫
5.2 简谐振动的能量与合成
第5章 机械振动
2
一、简谐振动 的特征方程 1.回复力 1.回复力
高二物理竞赛两个同方向同频率简谐运动的合成PPT(课件)

x2 5 cos(20 t ) cm
由旋转矢量法
4 -5 振动合成
A2 4
AOx
A A12 A22 5 2 cm
A1
5
4
x 5 2 cos (20 t 5 ) cm
4
11
物理学
第五版
4 -5 振动合成
两个简谐运动方向相同,频率相同,振
3
x A co t s ( ) n n 当木块位于平衡位置下方时,x>0
一 两个同方向同频率简谐运动的合成
n
A 例2 已知两谐振动的曲线(如图),它们是同频率的谐振动,求它们的合振动方程。
1、图示,木块上放置一质量为 m 的砝码,木块沿竖直方向作简谐运动,问砝码脱离木块的可能位置将发生在
2
x x x x 1 2 (b)在平衡位置上方(向上运动)(向下运动)
两振动步调反0 向,
1
12
2
(2)若另有一简谐运动
xAco t s() 多个同方向同频率简谐运动合成仍为简谐运动
例3、两个同方向、同频率简谐运动方程分别为
当 一
N两≥个0同时方,向砝同码2 频不率脱简离谐木运块动2 的合成
2
合位移 xx1x2
(SI)求:合成谐振动方程
(b)在平衡位置上方(向上运动)(向下运动)
0.4 (4)推广到 多个同方向同频率简谐运动的合成
(2)若另有一简谐运动
则合振幅为
则合振幅为
6
A2
x
0.12 x 0 .5 co 3 t s0 .1 ( 2 )
3
14
物理学
x 第五版 1
0.4cos3t()
3
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
简谐振动的合成
1. 两个不同的轻质弹簧分别挂上质量相同的物体1和
2, 若它们的振幅之比A 2 /A 1=2, 周期之比T 2 / T 1=2, 则它们的总振动能量之比E 2 / E 1 是( A )
(A) 1 (B) 1/4 (C) 4/1 (D) 2/1
解:振动能量22
2
22221T
A m A m E E E p
k πω==+= 即 2
12
1
212T A m E π= 2222222T A m E π=
121222222112222
121222
2
222212
12
2
1=⎪⎭⎫ ⎝⎛⨯=⎪⎪⎭⎫ ⎝⎛⋅=⋅==∴T T A A T T A A T A m T A m E E ππ 2.有两个同方向的谐振动分别为X 1=4COS(3t+π/4)cm ,
X 2 =3COS(3t -3π/4)cm, 则合振动的振幅为A=1cm, 初周相为φ=π/4.
∵φ2-φ1=-π ∴A=|A 1-A 2|=|4-3|=1cm φ=φ1=π/4
3. 一质点同时参与两个两个同方向, 同频率的谐振动,
已知其中一个分振动的方程为X 1=4COS3t cm, 其合振动的方程为 X=4COS (3t+π/3)cm, 则另一个分振动的振幅为A 2 =4cm , 初位相φ=2π/3.
3 , 0 ,411π
ϕϕ=
===cm A A
解:根据题意作旋转矢量图
21A A A 及平行四边形中和
4. 一质点同时参与了三个简谐振动, 它们的振动方程分别为X 1=A COS(ω
t+π/3), X 2 =A COS (ωt+5π/3), X 3 =A COS(ωt+π), 其合成运动的运动方程为X=0.
解: 作旋转矢量图 已知A 1=A 2=A 3=A,
A 3 且 A A A A =+='21
A 合=0 ∴ x = 0
5. 频率为v 1和v 2的两个音叉同时振动时,可以听到拍
音,若v 1>v 2,则拍的频率是( B )
(A)v 1+v 2 (B)v 1-v 2 (C)(v 1+v 2)/2 (D)(v 1-v 2)/2
O
1
A :
形的对边组成一个正三角
m
A A A 4c 12===∴ππ
π
π
ϕϕ3
2
3
3
32=
+
=
+
=20
)(321=++=∴A A A A
合。
