2018齐鲁名校教科研协作体
齐鲁名校教科研协作体山东、湖北部分重点中学2018年高二高三新起点联考数学文试题 含答案 精品
齐鲁名校教科研协作体山东、湖北部分重点中学2018年高二（高三新起点）联考文科数学试题命题：湖北随州一中（虞川 吴晓旭） 审题：湖北恩施高中（陈芳立） 湖北巴东一中（张世林） 湖北潜江中学（周超豹）一、选择题：本大题共12小题，每小题5分，共60分. 在每小题给出的四个选项中，只有一项是符合题目要求的.1.(原创，容易)在平面直角坐标系中，向量AD AB 与所对应的复数分别为i i +-5,32，则=（ ）A. 22B. 3C. 4D. 5 [答案] D[解析=,-所对应的复数为i 43+，其模长为54322=+ [考点]复数的几何意义，复数的运算，复数的模2. (原创，容易)命题“0ln 1,0≥-->∀x x x ”的否定是（ ） A.0ln 1,0<-->∀x x x B.0ln 1,0≥--≤∃x x x C.0ln 1,0<-->∃x x x D.0ln 1,0<--≤∃x x x [答案]C[解析]00≤>x x 不能改为[考点]全称命题的否定3.(原创，容易)阅读右边程序框图，任意输入()22x x -≤≤与()11y y -≤≤，则能够输出“2019高考必胜”的概率为（ ）A.8π B.18π- C.16π D.116π- [答案]A [解析]428P ππ==⨯[考点]程序框图、几何概型4.(原创，容易)已知命题:p “27不是7的倍数”，命题:q “27是3的倍数”，则命题“中某一个数的倍数和至少是7327”应该表示为（ ）A.q p ∨⌝B.q p ∧⌝C.q p ⌝∧D.q p ⌝∨ [答案]A[解析] 表示的倍数用是""727p ⌝，表示中某一个数的倍数用“或者是"7327q p ∨⌝ [考点]逻辑联结词“或”的意义5.(原创，容易)已知点1F 是椭圆)0(12222>>=+b a b y a x 的左焦点，过点1F 作圆16222a y x =+的切线与椭圆交于P 点，切点为M ，若切点M 恰好为线段1PF 的中点，则椭圆的离心率e 为（ ） A.210 B.410 C. 25 D.45[答案] B[解析]取椭圆的右焦点2F ，连接2,PF OM ,由中位线定理计算出22aPF =，由椭圆的定义计算出231a PF =,在直角三角形21F PF 中由勾股定理建立等量关系，计算得到e =410 [考点]椭圆的定义，椭圆的简单几何性质6.(原创，容易)在同一直角坐标系中，下列原函数)(x f y =与其导函数)('x f y =对应一定错误的是（ ）A .B .C . D.[答案] D[解析]原函数单调递增，则0)('≥x f 恒成立，选项D 显然错误。
【全国省级联考】齐鲁名校教科研协作体湖北、山东部分重点中学2019届高三上学期第一次联考化学试题-
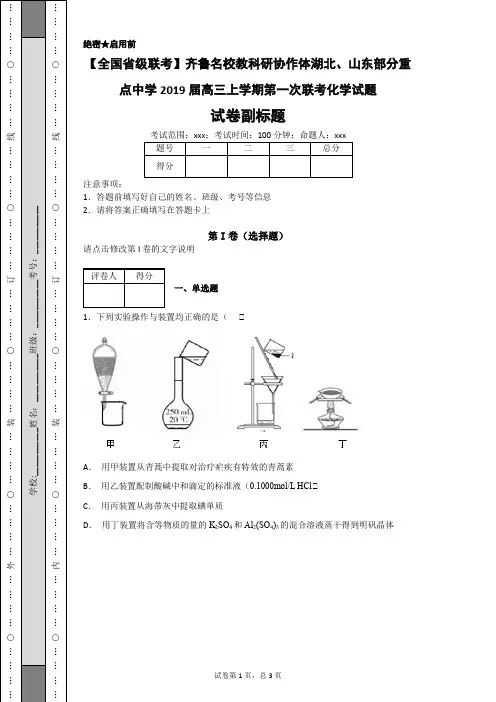
……装…………○……________姓名：___________班级：_……装…………○……绝密★启用前 【全国省级联考】齐鲁名校教科研协作体湖北、山东部分重点中学2019届高三上学期第一次联考化学试题 试卷副标题 注意事项： 1．答题前填写好自己的姓名、班级、考号等信息 2．请将答案正确填写在答题卡上 第I 卷（选择题） 请点击修改第I 卷的文字说明 一、单选题 1．下列实验操作与装置均正确的是（ ） A ． 用甲装置从青蒿中提取对治疗疟疾有特效的青蒿素 B ． 用乙装置配制酸碱中和滴定的标准液（0.1000mol/L HCl ） C ． 用丙装置从海带灰中提取碘单质 D ． 用丁装置将含等物质的量的K 2SO 4和Al 2(SO 4)3的混合溶液蒸干得到明矾晶体……※※在……第II 卷（非选择题） 请点击修改第II 卷的文字说明 二、综合题 2．碳族元素包括碳、硅、锗（Ge ）、锡（Sn ）、铅等，它们的单质及化合物广泛应用于我们生活的各个领域。
锗和锡以前曾被用于半导体材料，铅被用来制造蓄电池。
碳族元素在化合物中只有铅以低价形式存在时较稳定，其它元素在化合物中都是以高价形式存在比较稳定，回答下列问题：I ．（1）高岭土的成分中含Al 2(Si 2O 5)(OH)4，请改写成氧化物的形式_________________.（2）实验室用单质锡粉制取少量二氯化锡溶液，制取和保存的方法是(用文字叙述)_______________________________（3）铅有多种氧化物，写出四氧化三铅与浓盐酸反应的离子方程式_____________________ .二氧化铅在空气中强热会得到一系列铅的其它氧化物。
若把239g 二氧化铅强热，当质量变为231g 时，写出反应的化学方程式____________________________.II ．CH 4–CO 2催化重整不仅可以得到合成气（CO 和H 2），还对温室气体的减排具有重要意义。
齐鲁名校教科研协作体山东、湖北部分重点中学2018版高二(高三新起点)联考物理试题 Word版含答案
齐鲁名校教科研协作体山东、湖北部分重点中学2018年高二（高三新起点）联考物理试题命题：湖北天门中学（钟大鹏曹博）审题：山东临沂一中（王桂昕）山东莱芜一中（孟昭）湖北郧阳中学（张立克）一、选择题（每题5分共50分，1—5题为单选题，6—10题为多选题）1、（原创，容易）电阻R1与R2并联在电路中,通过R1与R2的电流之比为1∶3,则当R1与R2串联接入电路中时,R1与R2两端电压之比U1∶U2为 ()A.1∶9B9∶1 C.1∶3D.3∶1答案：D解析：由并联时的电流与电阻成反比可知R1：R2的电流之比为3∶1，再由串联时电压与电阻成正比可知答案为D2、（原创，容易）质量为M=50 kg的人站在地面上,人抓住绳的末端通过滑轮让质量为m=30 kg的重物以5m/s2的加速度匀加速下落,忽略人的重心变化、绳子和定滑轮的质量及一切摩擦,则地面对人的支持力大小为(g取10 m/s2) ()A.200 N B350 N C.400 N D.920 N答案：B解析：设人对绳的拉力大小为F,对重物进行分析,由牛顿第二定律得mg-F=ma;由牛顿第三定律可知,绳对人向上的拉力F'与人对绳的拉力F等大反向；设地面对人的支持力为F N,对人进行分析,由平衡条件可得F'+F N=Mg；解得F N=Mg-mg+ma=350 N。
3、（原创，中档）如图所示，ABC为一正三角形匀强磁场区域，边长为L，AE为BC边的中线。
现有一边长也为L的正方形导体框MNQP，在外力的作用下从图示位置沿AE匀速向右运动，A 与PQ中点重合。
导体框穿过磁场过程中感应电流i随时间变化的图象正确的是（规定逆时针电流为正）（）答案：A解析： 此题需分析线框的有效切割长度。
线框进入磁场时有效切割长度线性增加，产生的感应电流线性增加；完全进入后有一小段时间内磁通量不变，无感应电流产生；出磁场时，有效切割长度也在线性增加，产生的感应电流线性增加，A 选项正确。
山东、湖北部分重点中学2018届高三高考冲刺模拟考试理科数学试题(解析版)
齐鲁名校教科研协作体山东、湖北部分重点中学2018年高考冲刺模拟试卷（一）数学（理科）试题一、选择题：本大题共12小题，每小题5分，共60分. 在每小题给出的四个选项中，只有一项是符合题目要求的.1. 已知全集1=|0,A={1,2,4},5x U x N CuA x +⎧⎫∈≤=⎨⎬-⎩⎭则（ ） A. {3}B. {0，3，5}C. {3，5}D. {0，3} 【答案】D【解析】 因为全集1=|05x U x N x +⎧⎫∈≤⎨⎬-⎩⎭{}0,1,2,3,4=，{},A=1,2,4，所以{}0,3U A =，故选D.2. 已知i 为虚数单位，现有下面四个命题p 1：复数z 1=a +bi 与z 2=－a +bi ，（a ，b R ∈）在复平面内对应的点关于实轴对称；p 2：若复数z 满足(1-i )z =1+i ，则z 为纯虚数；p 3：若复数z 1，z 2满意z 1z 2R ∈，则z 2=1z ；p 4：若复数z 满足z 2+1=0，则z ＝±i .其中的真命题为（ ）A. p 1，p 4B. p 2，p 4C. p 1，p 3D. p 2，p 3 【答案】B【解析】对于11:p z 与2z 关于虚轴对称，所以1p 错误；对于2:p 由()1i 1i 1i i 1iz z +-=+⇒==-，则z 为纯虚数，所以2p 正确；对于3:p 若122,3z z ==，则126z z =，满足12z z R ∈，而它们实部不相等，不是共轭复数，所以3p 不正确；4p 正确,故选B.3. 已知2:2,:,10p a q x R x ax p q >∀∈++≥是假命题,则是的( )A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件 【答案】A。
齐鲁名校教科研协作体
齐鲁名校教科研协作体山东、湖北部分重点中学2018届高三第三次调研联考英语试题命题:山东德州一中(王平)审题:山东沂水一中(王国其)湖北黄冈中学(吕琴)湖北沙市中学(陈蓓)注意事项：1.本试卷由四个部分组成。
其中,第一、二部分和第三部分的第一节为选择题。
第三部分的第二节和第四部分为非选择题。
2.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
3.回答选择题时,选出每小题答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑;回答非选择题时,将答案写在答题卡上,写在本试卷上无效。
4.考试结束后,将本试卷和答题卡一并交回。
第一部分听力(共两节,满分30分)做题时,先将答案标在试卷上。
录音内容结束后,你将有两分钟的时间将试卷上的答案转涂到答题卡上。
第一节听下面5段对话。
每段对话后有一个小题,从题中所给的A、B、C三个选项中选出最佳选项,并标在试卷的相应位置。
听完每段对话后,你都有10秒钟的时间来回答有关小题和阅读下一小题。
每段对话仅读一遍。
1. What will the man do during the vacation?A. Work in a clothes storeB. Travel around with SamC. Go to the countryside2. what's the probable relationship between the speakers?A. Husband and wifeB. Customer and waitressC. Workmates3. How does the woman sound?A. Excited.B. Confused.C. Annoyed.4. What does the woman think Tom needs?A. Punishment.B. Suggestions.C. Encouragement.5. Where does the woman find her mobile phone?A. On the tableB. On the chairC. In her bag.第二节听下面5段对话或独白。
复合函数的零点问题
复合函数的零点问题I ．题源探究·黄金母题【例1】设函数()1,0,()11,11x x a af x x a x a⎧≤≤⎪⎪=⎨⎪-<≤⎪-⎩（a 为常数且()0,1a ∈）．若0x 是()()ff x x -的零点但不是()f x x -的零点，则称0x 为()f x 的二阶周期点，求函数()f x 的二阶周期点．【答案】函数()f x 有且仅有两个二阶周期点，121a x a a =-++，2211x a a =-++． 【解析】2222221,0,1(),,(1)(())1(),1,(1)1(1),1 1.(1)x x a a a x a x a a a f f x x a a x a a a x a a x a a ⎧≤≤⎪⎪⎪-<≤⎪-⎪=⎨⎪-<<-+-⎪⎪⎪--+≤≤-⎪⎩当20x a ≤≤时，由21x x a=解得0x =，由于()00f =，故0x =不是()f x 的二阶周期点； 当2a x a <≤时，由1()(1)a x x a a -=-解得21a x a a =-++2(,),a a ∈因222211()1111a a af a a a a a a a a a =⋅=≠-++-++-++-++，故21ax a a =-++是()f x 的二阶周期点；当21a x a a <<-+时，由21()(1)x a x a -=-解得12x a=-2(,1)a a a ∈-+，因精彩解读【试题来源】2013年高考江西卷改编． 【母题评析】本题以新定义的形式考查复合函数、分段函数的零点，难度较大．新定义（信息题）是近几年来高考的一个热点．【思路方法】理解定义，写出复合函数的解析式，再利用函数与方程思想、分类分类讨论思想、数形结合思想解题．111112122f a a a a ⎛⎫⎛⎫=⋅-= ⎪ ⎪----⎝⎭⎝⎭故12x a =-不是()f x 的二阶周期点；当211a a x -+≤≤时，1(1)(1)x x a a -=-解得211x a a =-++ 2(1,1)a a ∈-+，因22221111()(1)11111a f a a a a a a a a a =•-=≠-++--++-++-++， 故211x a a =-++是()f x 的二阶周期点．综上：函数()f x 有且仅有两个二阶周期点，121a x a a =-++，2211x a a =-++． II ．考场精彩·真题回放【例2】【2017年高考江苏卷】设()f x 是定义在R 且周期为1的函数，在区间[0,1)上，2,,(),,x x D f x x x D ⎧∈⎪=⎨∉⎪⎩ 其中集合1,*n D x x n n -⎧⎫==∈⎨⎬⎩⎭N ，则方程()lg 0f x x -=的解的个数是 ▲ ． 【答案】8【解析】由于()[0,1)f x ∈ ，则需考虑110x ≤< 的情况 在此范围内，x Q ∈ 且x ∈Z 时，设*,,,2qx p q p p=∈≥N ，且,p q 互质 若lg x Q ∈ ，则由lg (0,1)x ∈ ，可设*lg ,,,2nx m n m m=∈≥N ，且,m n 互质 因此10n mq p =，则10()nm q p= ，此时左边为整数，右边非整数，矛盾，因此lg x Q ∉因此lg x 不可能与每个周期内x D ∈对应的部分相等，只需考虑lg x 与每个周期x D ∉的部分的交点，画出函数图象，【命题意图】本题主要考查复合函数的零点．本题能较好的考查学生的运算能力、动手作图能力以及观察能力等．【考试方向】这类试题在考查题型上，通常基本以选择题或填空题的形式出现，综合性强，难度大． 【难点中心】解答此类问题，关键在于 “抽茧剥丝”，把复合函数问题转化为单函数问题，准确作出函数图象，利用图象解决问题．图中交点除()1,0外其它交点横坐标均为无理数，属于每个周期x D ∉的部分，且1x =处()11lg 1ln10ln10x x '==<，则在1x =附近仅有一个交点，一次方程解的个数为8． 【例3】【2015年高考天津】已知函数()()22,2,2,2,x x f x x x ⎧-≤⎪=⎨->⎪⎩ 函数()()2g x b f x =-- ，其中b R ∈，若函数()()y f x g x =- 恰有4个零点，则b 的取值范围是 （ ） A ．7,4⎛⎫+∞⎪⎝⎭ B ．7,4⎛⎫-∞ ⎪⎝⎭ C ．70,4⎛⎫ ⎪⎝⎭ D ．7,24⎛⎫ ⎪⎝⎭【答案】D ． 【解析】由()()22,2,2,2,x x f x x x -≤⎧⎪=⎨->⎪⎩得222,0(2),0x x f x x x --≥⎧⎪-=⎨<⎪⎩， 222,0()(2)42,0222(2),2x x x y f x f x x x x x x x ⎧-+<⎪∴=+-=---≤≤⎨⎪--+->⎩，即222,0()(2)2,0258,2x x x y f x f x x x x x ⎧-+<⎪=+-=≤≤⎨⎪-+>⎩()()()(2)y f x g x f x f x b =-=+--，所以()()y f x g x =-恰有4个零点等价于方程()(2)0f x f x b +--=有4个不同的解，即函数y b =与函数()(2)y f x f x =+-的图象的4个公共点，由图象可知724b <<． III ．理论基础·解题原理1．复合函数定义：设()y f t =，()t g x =，且函数()g x 的值域为()f t 定义域的子集，那么y 通过t 的联系而得到自变量x 的函数，称y 是x 的复合函数，记为()y f g x =⎡⎤⎣⎦．2．复合函数函数值计算的步骤：求()y g f x =⎡⎤⎣⎦函数值遵循“由内到外”的顺序，一层层求出函数值．例如：已知()()22,x f x g x x x ==-，计算()2g f ⎡⎤⎣⎦． 【解析】()2224f ==，()()2412g f g ∴==⎡⎤⎣⎦．3．已知函数值求自变量的步骤：若已知函数值求x 的解，则遵循“由外到内”的顺序，一层层拆解直到求出x 的值．例如：已知()2x f x =，()22g x x x =-，若()0g f x =⎡⎤⎣⎦，求x ．由上例可得，要想求出()0g f x =⎡⎤⎣⎦的根，则需要先将()f x 视为整体，先求出()f x 的值，再求对应x 的解，这种思路也用来解决复合函数零点问题，先回顾零点的定义．4．函数的零点：设()f x 的定义域为D ，若存在0x D ∈，使得()00f x =，则称0x x =为()f x 的一个零点．5．复合函数零点问题的特点：考虑关于x 的方程()0g f x =⎡⎤⎣⎦根的个数，在解此类问题时，要分为两层来分析，第一层是解关于()f x 的方程，观察有几个()f x 的值使得等式成立；第二层是结合着第一层()f x 的值求出每一个()f x 被几个x 对应，将x 的个数汇总后即为()0g f x =⎡⎤⎣⎦的根的个数． IV ．题型攻略·深度挖掘 【考试方向】这类试题在考查题型上，通常基本以选择题或填空题的形式出现，一般综合性强，难度大． 【技能方法】求解复合函数()y g f x =⎡⎤⎣⎦零点问题的技巧：（1）此类问题与函数图象结合较为紧密，在处理问题的开始要作出()(),f x g x 的图像（2）若已知零点个数求参数的范围，则先估计关于()f x 的方程()0g f x =⎡⎤⎣⎦中()f x 解的个数，再根据个数与()f x 的图像特点，分配每个函数值()i f x 被几个x 所对应，从而确定()i f x 的取值范围，进而决定参数的范围． 【易错指导】1．函数零点—忽视单调性的存在．例如：若函数f(x)在区间[－2，2]上的图象是连续不断的曲线，且f(x)在(－2，2)内有一个零点，则f(－2)·f （2）的值 ( ) A ．大于0 B ．小于0 C ．等于0 D ．不能确定解答：若函数f(x)在(－2，2)内有一个零点，该零点可分两种情况：（1）该零点是变号零点，则f(－2)·f （2）<0；（2）该零点是非变号零点，则f(－2)·f（2）>0，因此选D ．易错警示： 警示1：错误认为该零点是变号零点；警示2：不知道非变号零点这种情况．方法剖析：方程的根或函数零点的存在性问题，可以根据区间端点处的函数值的正负来确定，但要确定零点的个数还需进一步研究函数在区间上的单调性，在给定的区间上，如果函数是单调的，它至多有一个零点，如果不是单调的，可继续细分出小的单调区间，再结合这些小的区间的端点处函数值的正负，作出正确判断．本题的解答错误在于没有正确理解函数零点的含义及存在性，事实上，当f(x)在(－2，2)内有一个零点时，f(－2)·f（2）的符号不能确定．2．要注意对于在区间[a ，b]上的连续函数f(x)，若x 0是f(x)的零点，却不一定有f(a)·f(b)<0，即f(a)·f(b)<0仅是f(x)在[a ，b]上存在零点的充分条件，而不是必要条件． 注意以下几点：①满足零点存在性定理的条件的零点可能不唯一； ②不满足零点存在性定理条件时，也可能有零点．③由函数)(x f y =在闭区间[],a b 上有零点不一定能推出)(a f ·)(b f 0<，如图所示．所以)(a f ·)(b f 0<是)(x f y =在闭区间[],a b 上有零点的充分不必要条件．注意：①如果函数()f x 在区间[],a b 上的图象是连续不断的曲线，并且函数()f x 在区间[],a b 上是一个单调函数，那么当)(a f ·)(b f 0<时，函数()f x 在区间),(b a 内有唯一的零点，即存在唯一的(,)c a b ∈，使0)(=c f ．②如果函数()f x 在区间[],a b 上的图象是连续不断的曲线，并且有)(a f ·)(b f 0>，那么，函数()f x 在区间),(b a 内不一定没有零点．③如果函数()f x 在区间[],a b 上的图象是连续不断的曲线，那么当函数()f x 在区间),(b a 内有零点时不一定有)(a f ·)(b f 0<，也可能有)(a f ·)(b f 0>． V ．举一反三·触类旁通 【例1】【2018四川绵阳一诊】函数满足，且当时，．若函数的图象与函数（，且）的图象有且仅有4个交点，则的取值集合为（ ） A ．B ．C ．D ．【答案】C【例2】【2018南宁高三毕业班摸底联考】设函数是定义在上的偶函数，且，当时，，若在区间内关于的方程（且）有且只有4个不同的根，则实数的取值范围是（ ） A ．B ．C ．D ．【答案】D【解析】由题意可得函数f(x)的对称轴为x=2，周期为T=4，原方程变形为，，所以只需画出，两个函数在区间(-2，6)的图像，根据图像求a 的范围，图像如下，一定过（-1，0）点，当时，显然只有一个交点，所以，只需要对数从点B ，点C 下面穿过就有4个零点，所以解得，选D ．【点睛】对于求不同类的两个函数构成的方程，我们常把方程变形为f(x)=g(x)，然后根据y=f(x)与y=g(x)的两个图像交点个数来判断原方程根的个数．如本题把方程变形为，再画出两个函数的图像，根据两个图像有4个交点，求出参数a 的范围．【例3】【2018河南天一大联考】已知函数若关于的方程有3个实数根，则实数的取值范围是（ ） A ．B ．C ．D ．【答案】D【解析】作图如下： 因此要使方程有3个，实数的取值范围是，选D ．【名师点睛】对于方程解的个数(或函数零点个数)问题，可利用函数的值域或最值，结合函数的单调性、草图确定其中参数范围．从图象的最高点、最低点，分析函数的最值、极值；从图象的对称性，分析函数的奇偶性；从图象的走向趋势，分析函数的单调性、周期性等． 【例4】【2018广西桂林柳州高三综合模拟】已知函数()3log ,03{4,3x x f x x x <≤=->，若函数()()2h x f x mx =-+有三个不同的零点，则实数m 的取值范围是（ ）A ．1,12⎛⎫⎪⎝⎭B ．()1,1,2⎛⎫-∞⋃+∞ ⎪⎝⎭C ．[)1,1,2⎛⎫-∞⋃+∞ ⎪⎝⎭D ．1,12⎛⎤ ⎥⎝⎦【答案】AA （0，﹣2），B （3，1），C （4， 0），则g （x ）的图象介于直线AB 和AC 之间，介于k AB ＜m ＜k AC ，可得12＜m ＜1．故答案为：（12，1）． 点睛:函数h （x ）=f （x ）﹣mx+2有三个不同的零点，即为f （x ）﹣mx +2=0有三个不同的实根，可令y=f （x ），y =g （x ）=mx ﹣2，分别画出y=f （x ）和y=g （x ）的图象，通过图象观察，结合斜率公式，即可得到m 的范围．【例5】【2018广东珠海一中等六校第一次联考】已知函数()()222,12{log 1,1x x f x x x +≤=->，则函数()()()322F x f f x f x =--的零点个数是（ ）A ．4B ．5C ．6D ．7 【答案】A【解析】解：令t=f （x ），F （x ）=0，则f （t ）﹣2t ﹣32=0， 【名师点睛】本题关键是找出内外层函数的对应关系，找准一个t 对应几个x ． 【例6】【2018安徽阜阳临泉一中上学期二模】已知，若关于的方程恰好有 个不相等的实数根，则实数的取值范围是______________．【答案】【解析】∵，∴，∴∴当或时，，当时，∴在上单调递增，在上单调递减，在上单调递增可作出大致函数图象如图所示： 令，则当时，方程有一解；当时，方程有两解；时，方程有三解∵关于的方程，恰好有4个不相等实数根 ∴关于的方程在和上各有一解∴，解得，故答案为【名师点睛】已知函数有零点求参数取值范围常用的方法和思路：①直接法：直接根据题设条件构建关于参数的不等式，再通过解不等式确定参数的范围；②分离参数法：先将参数分离，转化成求函数值域问题加以解决；③数形结合法：先对解析式变形，在同一平面直角坐标系中画出函数的图象，然后数形结合求解．【例7】【2018湖南株洲醴陵第二中学、醴陵第四中学高三上学期两校期中联考】已知函数()2log ,02{2,22x x f x x x x<<=+≥，若0＜a ＜b ＜c ，满足f （a ）=f （b ）=f （c ），则()abf c 的范围为__． 【答案】（1，2）0a b c Q ＜＜＜，满足()()()f a f b f c ==，22log log a b ∴-=，即1ab =，()21122c f c c c+==+Q ，()112f c ∴<<，故()()112ab f c f c <=<，故答案为()12，．【名师点睛】画出函数()f x 的图象，由图象可知有相等时的取值范围，这里2log x 由的图象和计算得1ab =，可以当作结论，这样三个未知数就只剩下c ，由反比例即可求出结果．【例8】【2018江西宜春丰城九中、高安二中、宜春一中、万载中学、樟树中学、宜丰中学六校联考】已知函数()ln 1||f x x =-， ()f x m -的四个零点1x ， 2x ， 3x ， 4x ，且12341111k x x x x =+++，则()kf k e -的值是__________． 【答案】2e -【例9】【2018山西山大附中等晋豫名校第四次调研】已知函数()()21,0{11,0x x f x f x x -≤=-+>，把方程()0f x x -=的根按从小到大顺序排成一个数列，则该数列的前n 项和n S =__________．【答案】()12n n -【解析】当01x <≤时，有110x -<-≤，有()()1112x f x f x -=-+= ，当12x <≤时，有011x <-≤ ，有()()21121x f x f x -=-+=+ 当23x <≤时，有112x <-≤ ，有()()31122x f x f x -=-+=+ 当34x <≤时，有213x <-≤ ，有()()31123x f x f x -=-+=+依次类推，当()1n x n n N <≤+∈时，则()()1112x n f x f x n --=-+=+ ，所以()()12x n g x f x x n x --=-=+- ，故21n a n +=+ ，所以通项公式1n a n =-， ()12n n n S -=．【点睛】本题考查对分段函数的处理方法，分段函数要分段处理，根据分段函数的解析式找出各段函数的零点，从而得出各个零点与项数的关系，写出数列的通项公式，根据数列是特殊的等差数列，利用等差数列求和公式，求出数列的前n 项的和．【例10】【2018江苏南通如皋第一次联考】已知函数()211{ 52128lnx x xf x m x mx x +>=-++≤，，，，若()()g x f x m =-有三个零点，则实数m 的取值范围是________．【答案】714⎛⎤ ⎥⎝⎦，【例11】【2018齐鲁名校教科研协作体山东、湖北部分重点中学第一次调研】已知定义在R 上的函数()()2,0{1,0x x x f x ln x x +≤=+>，若函数()()()1g x f x a x =-+恰有2个零点，则实数a 的取值范围是_________．【答案】()1,1,1e ⎛⎫-∞-⋃ ⎪⎝⎭．【解析】数形结合，由直线()1y a x =+与曲线()y f x =的位置关系可得当()1,1,1a e ⎛⎫∈-∞-⋃ ⎪⎝⎭时有两个交点，即函数()y g x =恰有两个零点．【名师点睛】涉及函数的零点问题、方程解的个数问题、函数图像交点个数问题，一般先通过导数研究函数的单调性、最大值、最小值、变化趋势等，再借助函数的大致图象判断零点、方程根、交点的情况，归根到底还是研究函数的性质，如单调性、极值，然后通过数形结合的思想找到解题的思路．【例12】【2018江苏淮安盱眙中学第一次学情调研】已知函数()22f x x m =+的图象与函数()ln g x x =的图象有四个交点，则实数m 的取值范围为________． 【答案】1,ln22⎛⎫-∞-- ⎪⎝⎭数()22ln h x x m x =+-最小值为21112ln 222h m ⎛⎫⎛⎫=+- ⎪ ⎪⎝⎭⎝⎭，令102h ⎛⎫< ⎪⎝⎭ ，可得1ln22m <-，此时函数()22ln h x x m x =+-有两个零点，故函数()22f x x m =+的图象与函数()ln g x x =的图象有四个交点，实数m 的取值范围为1,ln22⎛⎫-∞-- ⎪⎝⎭，故答案为1,ln22⎛⎫-∞-- ⎪⎝⎭． 【方法点睛】本题主要考查函数图象的交点、函数的零点、方程的根，属于难题．函数图象的交点、函数的零点、方程的根往往是“知一求二”，解答时要先判断哪个好求解就转化为哪个，判断函数()y f x =零点个数的常用方法：（1） 直接法： 令()0,f x =则方程实根的个数就是函数零点的个；（2） 零点存在性定理法：判断函数在区间[],a b 上是连续不断的曲线，且()()0,f a f b <再结合函数的图象与性质(如单调性、奇偶性、周期性、对称性) 可确定函数的零点个数；（3） 数形结合法：转化为两个函数的图象的交点个数问题，画出两个函数的图象，其交点的个数就是函数零点的个数，在一个区间上单调的函数在该区间内至多只有一个零点，在确定函数零点的唯一性时往往要利用函数的单调性，确定函数零点所在区间主要利用函数零点存在定理，有时可结合函数的图象辅助解题． 【跟踪练习】1．【2018辽宁庄河高中、沈阳二十中高三上学期第一次联考】函数()()()820{ 1022sin x x f x f x x π-≤=⎛⎫-> ⎪⎝⎭，则函数()()4log h x f x x =-的零点个数为（ ） A ．2个 B ．3个 C ．4个 D ．5个 【答案】D【解析】函数的零点满足： ()4log f x x =，则原问题等价于考查函数4log y x =与函数()f x 的交点的个数．()114sin22sin22222f x f x x x ππ⎛⎫⎛⎫=-=⨯-=- ⎪ ⎪⎝⎭⎝⎭； 当32x ππ<≤时， 22x πππ<-≤，据此可得： ()112sin2sin22222f x f x x x ππ⎡⎤⎛⎫⎛⎫=-=⨯--= ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦；当54x π=时， 55sin 2144f ππ⎛⎫⎛⎫=⨯= ⎪ ⎪⎝⎭⎝⎭， 而445log log 414π<=， 则函数4log y x =与函数()f x 在区间3,2ππ⎛⎫⎪⎝⎭上有2个交点， 很明显，当32x π>时，函数图象没有交点，绘制函数图象如图所示，观察可得： 函数()()4h x f x log x =-的零点个数为5个． 【名师点睛】函数零点的求解与判断方法：（1）直接求零点：令f (x )＝0，如果能求出解，则有几个解就有几个零点．（2）零点存在性定理：利用定理不仅要函数在区间[a ，b ]上是连续不断的曲线，且f (a )·f (b )＜0，还必须结合函数的图象与性质(如单调性、奇偶性)才能确定函数有多少个零点．（3）利用图象交点的个数：将函数变形为两个函数的差，画两个函数的图象，看其交点的横坐标有几个不同的值，就有几个不同的零点．2．【2018江西上饶高三下学期一模】已知()f x 是定义域为()0,+∞的单调函数，若对任意的()0,x ∈+∞，都有()13log 4f f x x ⎡⎤+=⎢⎥⎣⎦，且方程()323694f x x x x a -=-+-+在区间(]0,3上有两解，则实数a 的取值范围是（ ）A ．05a <≤B ．5a <C ．05a <<D ．5a ≥ 【答案】A即有3213log 694x x x x a =-+-+在区间(]0,3上有两解，由()32694g x x x x a =-+-+，可得()23129g x x x =-+'，当13x <<时， ()0g x '<， ()g x 递减；当01x <<时， ()0g x '>， ()g x 递增． ()g x 在1x =处取得最大值a ， ()04g a =-， ()34g a =-，分别作出13log y x =，和32694y x x x =-+-的图象，可得两图象只有一个交点()1,0，将32694y x x x =-+-的图象向上平移，至经过点()3,1，有两个交点，由()31g =，即41a -=，解得5a =，当05a <≤时，两图象有两个交点，即方程两解．故选A ．3．【201甘肃兰州西北师范大学附属中学一调】若函数()3,0{ ,0xx e x f x e x x+≤=>，则方程()()330f f x e -=的根的个数为（ ） A ．1 B ．2 C ．3 D ．4 【答案】C【解析】【方法点睛】本题主要考查分段函数的解析式及图象、函数与方程思想、数形结合思想的应用，属于难题．数形结合是根据数量与图形之间的对应关系，通过数与形的相互转化来解决数学问题的一种重要思想方法，是中学数学四种重要的数学思想之一，尤其在解决选择题、填空题是发挥着奇特功效，大大提高了解题能力与速度．运用这种方法的关键是正确作出函数图象以及熟练掌握函数图象的几种变换．充分利用数形结合的思想方法能够使问题化难为简，并迎刃而解．4．【2018安徽滁州高三9月联合质量检测】已知()()11,011{ ,10x f x f x x x +<<-=-<≤，若方程()()200f x ax a a -+=≠有唯一解，则实数a 的取值范围是__________．【答案】1,3⎡⎫+∞⎪⎢⎣⎭【解析】当01x <<时， 110x -<-<，所以()11f x x -=-．()()111111f x f x x =+=+--．若方程()()200f x ax a a -+=≠有唯一解，即() 2f x ax a =-，有唯一解． 作出()y f x =和y 2ax a =-的图象，根据题意两函数图象有唯一交点． 由图可知： 13a ≤． 【名师点睛】根据函数零点求参数取值，也是高考经常涉及的重点问题， （1）利用零点存在的判定定理构建不等式求解；（2）分离参数后转化为函数的值域（最值）问题求解，如果涉及由几个零点时，还需考虑函数的图象与参数的交点个数；（3）转化为两熟悉的函数图象的上、下关系问题，从而构建不等式求解． 5．【2018山西45校高三第一次联考】已知(),01,{ 11,1.x e x f x e x e x<≤=+-<≤若方程()f x kx e =+有且仅有3个实数解，则实数k 的取值范围是__________． 【答案】211,4e e -⎛⎤-⎥⎝⎦设()0,A e ，AB 为()y f x =的切线，B 为切点， 1,1C e e e ⎛⎫+- ⎪⎝⎭，观察可知，当位于切线AB 和割线AC 之间时， y kx e =+图象与()y f x =的图象有三个交点，设()00,B x y ．由2111'e x x ⎛⎫+-=-⎪⎝⎭，可得切线AB: ()02001110y e x x x ⎛⎫-+-=--⎪⎝⎭，解得02x =，故14AB k =-，又2111AC e ee e k e e+---==，所以当方程()f x kx e =+在(]0,e 上有三个实数解，实数k 的取值范围为211,4e e -⎛⎤-⎥⎝⎦． 【名师点睛】根据函数零点求参数取值，也是高考经常涉及的重点问题， （1）利用零点存在的判定定理构建不等式求解；（2）分离参数后转化为函数的值域（最值）问题求解，如果涉及由几个零点时，还需考虑函数的图象与参数的交点个数；（3）转化为两熟悉的函数图象的上、下关系问题，从而构建不等式求解．6．【2018齐鲁名校教科研协作体山东、湖北部分重点中学第一次调研】已知()2,0{2,0lnx x f x x x x ->=+≤，若()=f x a 有4个根1234,,,x x x x ，则1234x x x x +++的取值范围是________________．【答案】10,2e e ⎛⎫+- ⎪⎝⎭【解析】因为1234342x x x x x x +++=-++，所以，故答案为10,2e e ⎛⎫+- ⎪⎝⎭． 7．【2018河郑州一中模拟】已知函数()222,0{ 2,0x x x f x x x x -+≥=-<，若关于x 的不等式()()220f x af x b ⎡⎤+-<⎣⎦恰有1个整数解，则实数a 的取值范围是__________． 【答案】38a <≤【解析】画出()f x 的图象如图所示 当()0f x =时，得x 0=或x 2=此时()()220f x af x b ⎡⎤+-<⎣⎦化为， 20b -< 若b 0≠，则此时有两解x 0=或x 2=，违背题意， 故b 0=此时()()a 0f x f x ⎡⎤+<⎣⎦若a 0>，则关于的不等式()a 0f x -<<恰有一个整数解．结合图象可知()()33{48a f a f -<=--≥=-，可得3a 8<≤若a 0<，则关于的不等式()0a f x <<-恰有一个整数解． 结合图象可知()()11{13a f a f ->=-≤-=，可得3a 1-≤<-综上， 3a 13a 8-≤<-<≤或．8．【2018江苏南京高三数学上学期期初学情调研】已知函数()22,0{,313,0x x f x x x ≤=--+>若存在唯一的整数x ，使得()0f x a x->成立，则实数a 的取值范围为______．【答案】[0，2]∪[3，8]满足()00f x a x ->-符合题意，当8a >时，至少存在两点()()()()1,1,2,2f f ----满足()00f x a x ->-不合题意，故答案为[][]0,23,8⋃【名师点睛】对于方程解的个数(或函数零点个数)问题，可利用函数的值域或最值，结合函数的单调性、草图确定其中参数范围．从图象的最高点、最低点，分析函数的最值、极值；从图象的对称性，分析函数的奇偶性；从图象的走向趋势，分析函数的单调性、周期性等 9．【2018浙江温州一模】已知函数有六个不同零点，且所有零点之和为3，则的取值范围为__________． 【答案】单调递增，且取值范围是，当时，函数的导函数，考虑到是上的单调递增函数，且，于是在上有唯一零点，记为，进而函数在上单调递减，在上单调递增，在处取得极小值，如图：接下来问题的关键是判断与的大小关系，注意到，，函数，在上与直线有个公共点，的取值范围是，故答案为．10．【2018湖南永州高三上学期一模】定义函数()()(),{,f x x a h x g x x a≤=>， ()f x x =， ()224g x x x =--，若存在实数b 使得方程()0h x b -=无实数根，则实数a 的取值范围是__________． 【答案】()(),54,-∞-⋃+∞【解析】11．【2018河北石家庄二中八月高三模拟】已知()22,{ 2,x x a f x x x a -≥=+<，若函数()1ln g x f x a x ⎛⎫=+- ⎪⎝⎭有零点，则实数a 的取值范围是__________． 【答案】[][)1,23,-⋃+∞ 综上可得： 1a 2-≤≤或a 3≥ 故答案为： [][)1,23,-⋃+∞【名师点睛】已知函数有零点求参数取值范围常用的方法和思路（1）直接法：直接根据题设条件构建关于参数的不等式，再通过解不等式确定参数范围； （2）分离参数法：先将参数分离，转化成求函数值域问题加以解决；（3）数形结合法：先对解析式变形，在同一平面直角坐标系中，画出函数的图象，然后数形结合求解． 12．【2018广东茂名高三五大联盟学校9月份联考】若函数至少有3个零点，则实数的取值范围是__________． 【答案】【解析】由可得，则问题转化为函数的图像有至少三个交点，结合图像可以看出当时，即时满足题设，应填答案．【名师点睛】本题的求解过程体现了数形结合的数学思想的巧妙运用，求解时先在同一平面直角坐标系中画出两个函数的图像，进而借助图像的直观建立不等式，进而通过解不等式求出参数的取值范围．13．【2018山东齐河晏婴学校一模】已知()1x f x e =-，又()()()()2g x f x tf x t R =-∈，若满足()1g x =-的x 有三个，则t 的取值范围是__________．【答案】()2,+∞【解析】由题意作函数()1x f x e =-的图象：【名师点睛】本题考查方程根的个数问题的转化，一元二次方程根的分布问题，以及换元法的应用，考查数形结合思想，转化思想；由题意作函数()1x f x e =-的图象，令()m f x =，由图求出m 的范围，代入方程()1g x =-化简，由条件和图象判断出方程的根的范围，由一元二次方程根的分布问题列出不等式，求出t 的取值范围．14．【2018浙江名校协作体上学期考试】已知函数()()22,0{,14,0x x f x x ln x x +>=-+≤则关于x 的方程()246f x x -=的不同实根的个数为________．【答案】4个【解析】函数 ()f x 图像如图所示， ()22424t x x x =-=--，由图15．【2018河南郑州一中模拟】已知函数()f x 满足()()22f x f x +-=，当(]0,1x ∈时， ()2f x x = ，当(]1,0x ∈-时，()()21f x fx +=+，若定义在()1,3-上的函数()()()1g x f x t x =-+有三个不同的零点，则实数t 的取值范围是__________． 【答案】()0,627-【解析】当(]1,0011x x ∈-⇒<+≤时，则11f x x +=+，故()221f x x =-+；当(]1,2021x x ∈⇒≤-<时，则()()222f x x -=-，故()()222f x x =--；当()2,3120x x ∈⇒-<-<时，则()()()()22224213f x f x f x f x⎡⎤⎥=--=--=⎥-+-⎦，又因为()2,3031x x ∈⇒<-<，所以()33fx x -=-，则()224433f x x x =-=+--．所以()222+1{ 2(243xx x f x x -=-+-，(](](](),1,0,0,1,1,2,2,3x x x x ∈-∈∈∈，画出函【名师点睛】解答本题的关键是充分运用题设条件先将函数()y f x =在区间()1,3-上的解析表达式求出来，再画出其图像数形结合，从而将问题转化为方程()()()2212242=0t x x x t x t +=--⇒+-++有唯一解，可求得627t =-0627t <<-()y f x =在区间()1,3-上的图像与直线()1y t x =+的图像有且只有三个不同的交点，即定义在()1,3-上的函数()()()1g x f x t x =-+有三个不同的零点．16．【2018江苏南京师范大学附属中学模拟】函数()()()({ 4x x x t f x x x t ≤=>其中0t >，若函数()()1g x f f x ⎡⎤=-⎣⎦有6个不同的零点，则实数t 的取值范围是__________．【答案】()3,4【解析】314{ 34127t t t<⇒<<>时，两直线1,1y t y =+=与函数()y f x =共有六个不同交点，应填答案()3,4． 【名师点睛】解答本题的关键关节有两个：其一是将函数的零点问题进行等价转化；其二是要巧妙运用数形结合思想建立不等式组．求解时还要综合运用导数知识确定函数的极值点和极值．灵活运用所学知识和重要是数学思想进行分析问题和解决问题是本题一大特征，体现了数学思想在解决数学问题中四两拨千斤的功能．。
xAB+yAC解题探秘
专题26 应用AD x AB y AC =+ 解题探秘【热点聚焦与扩展】高考对平面向量基本定理的考查，往往以选择题或填空题的形式出现。
常以平面图形为载体，借助于向量的坐标形式等考查共线、垂直等问题;也易同三角函数、解析几何等知识相结合,以工具的形式出现．用平面向量基本定理解决问题的一般思路是：先选择一组基底，再用该基底表示向量,其实质就是利用平行四边形法则或三角形法则进行向量的加减运算和数乘运算．要特别注意基底的不唯一性—-—-—只要两个向量不共线，就可以作为平面的一组基底，对基底的选取不唯一，平面内任意向量a都可被这个平面的一组基底12e e ，线性表示，且在基底确定后，这样的表示是唯一的．1、平面向量基本定理：若平面上两个向量12,e e 不共线，则对平面上的任一向量a ，均存在唯一确定的()12,λλ，（其中12,R λλ∈)，使得1122a e e λλ=+.其中12,e e 称为平面向量的一组基底。
（1）不共线的向量即可作为一组基底表示所有的向量 （2)唯一性：若1122a e e λλ=+且1122a e e μμ=+,则1122λμλμ=⎧⎨=⎩2、“爪”字型图及性质:B(1）已知,AB AC 为不共线的两个向量，则对于向量AD ，必存在,x y ，使得AD x AB y AC =+。
则,,B C D 三点共线⇔1x y +=当01x y <+<，则D 与A 位于BC 同侧，且D 位于A 与BC 之间 当1x y +>,则D 与A 位于BC 两侧1x y +=时，当0,0x y >>，则D 在线段BC 上；当0xy <，则D 在线段BC 延长线上（2)已知D 在线段BC 上,且::BD CD m n =,则n mAD AB AC m n m n=+++ 3、AD x AB y AC =+中,x y 确定方法（1）在几何图形中通过三点共线即可考虑使用“爪”字型图完成向量的表示，进而确定,x y（2)若题目中某些向量的数量积已知,则对于向量方程AD x AB y AC =+，可考虑两边对同一向量作数量积运算，从而得到关于,x y 的方程,再进行求解（3）若所给图形比较特殊（矩形，特殊梯形等），则可通过建系将向量坐标化，从而得到关于,x y 的方程，再进行求解【经典例题】例1。
【新人教版】2019-2020高中语文 第四专题 心连广宇 滕王阁序并诗试题 苏教版必修5
登高能赋滕王阁序并诗一、基础夯实1.下列各句中没有通假字的一项是( )A.云销雨霁,彩彻区明B.不顾恩义,畔主背亲C.俨骖马非于上路,访风景于崇阿D.北海虽赊,扶摇可接;东隅已逝,桑榆非晚解析:D A项,“销”同“消”;B项,“畔”通“叛”;C项,“俨”同“严”。
2.下列句中加点词的含义相同的一项是( )解析:A A项,旧,形容词。
B项,名望,声望,名词/指望,期望,动词;C项,才华出众,形容词/盛大,形容词;D项,写作,动词/古时臣子向君主陈述意见的一种文体,名词。
3.从词类活用看,下列各句中加点词的用法与例句中的“雾”相同的一项是( )例句:雄州雾．列,俊采星驰A.纤歌凝而白云遏．B.襟．三江而带五湖C.四美．具,二难并D.有好事者船．载以入解析:D 例句中的“雾”是名词作状语。
A项,无词类活用。
B项,名词“襟”用作意动词,“以……为襟”。
C项,形容词“美”用作名词,美好的事物。
D项,名词“船”作状语。
4.下列句子中加点的词语的古今意义相同的一项是( )A.孟尝高洁．．,空余报国之情B.千里逢迎．．,高朋满座C.所赖君子见机．．,达人知命D.阮籍猖狂．．,岂效穷途之哭解析:A B项,古,迎接;今,说话和做事故意迎合别人的心意(含贬义)。
C项,古,看到细微的预兆;今,看机会,看形势。
D项,古,狂放,不拘礼法,不含贬义;今,狂妄而放肆,含贬义。
5.下列各句中与其他三句句式不同的一项是( )A.宇文新州之懿范B.蚓无爪牙之利,筋骨之强C.舍簪笏于百龄,奉晨昏于万里D.都督阎公之雅望解析:C C项为介宾短语后置句;A、B、D三项都是定语后置句。
6.下列对课文内容分析概括不正确的一项是( )A.作为一篇优秀的骈文,作者调动了对偶、用典等艺术手法,在精美严整的形式之中,表现了自然变化之趣;尤其是景物描写部分,文笔瑰丽,手法多样,令人叹赏。
B.本文的用典信手拈来,用典除了能加强论证外,还能借古抒怀,使文章内容充实,联想丰富,语言简练,风格典雅。
山东省、湖北省部分重点中学2018届高三第一次(9月)联考语文试卷(解析版)
齐鲁名校教科研协作体山东、湖北部分重点中学2018届高三第一次调研联考语文试题注意事项：1．答卷前，考生务必将自己的姓名和座位号填写在答题卡上。
2．回答选择题时，选出每小题答案后，用铅笔把答题卡对应题目的答案标号涂黑。
如需改动，用橡皮擦干净后，再选涂其它答案标号。
回答非选择题时，将答案写在答题卡上。
写在本试卷上无效。
3．考试结束后，将本试卷和答题卡一并交回。
一、现代文阅读（35分）（一）论述类文本阅读（本题共3小题，9分）阅读下面的文字，完成1—3题。
从“抵制韩流”看消费型民族主义■梁文道韩剧风猛烈吹袭大陆后，就有很多人看不过去要出来说话，这种事我们大可以引为茶余饭后的闲谈话题，一笑置之。
但是我们也应认真思索，为什么我们可以这么轻易地把爱韩剧就等于汉奸、看国产片就等于爱国的逻辑理直气壮地宣之于口，而且竟还有市场？很多人之所以能够不假思索地说出这种话，是因为近年有一股更大的潮流，这股潮流就是‚消费型民族主义‛。
首先，我们要注意它与抵制日货的理路不尽相同。
不管你同意与否，提倡抵制日货的人至少还试图搬出一套罢买日货可以打击日本商界然后日本企业会抱怨日本政府外交政策的推理。
‚消费型民族主义‛却是诉诸感情直觉，要大家以抵制某产品的方式直接表达爱国情怀。
当然，实际操作起来，‚消费型民族主义‛又会和抵制日货运动相混杂，成为后者的指导精神。
其次，‚消费型民族主义‛不是一种经济政策上的保护主义。
奉行保护主义的国家如韩国，会硬性规定电影院每年要有一定日数放映韩片，以保证电影生产数量的稳定，以阻挡外来电影带来的竞争压力，目的是扶持自己国家的特定产业。
保护政策好还是不好，各有各的观点，但它起码也是套言之成理的说法。
‚消费型民族主义‛着眼的却不是这么深层次的产业发展问题，它只不过是一种浮浅的情绪表达和标签。
‚消费型民族主义‛的出现，靠的是两种逻辑。
一个是民族主义本身的空洞，另一个是市场营销的文化转向。
什么叫民族主义的空洞呢？难道民族主义不是很强大很澎湃的一种意识形态吗？的确，它是的。
02或且非命题的真假判断-2018版高人一筹之高二数学特色训练(2-1)含解析
一、选择题1．【河北省邢台市2018届高三上学期第二次月考】已知()2x f x e ax =-.命题:p 对1a ∀≥， ()y f x =有三个零点，命题:q a R ∃∈,使得()0f x ≤恒成立.则下列命题为真命题的是（ ）A 。
p q ∧B . ()()p q ⌝∧⌝C 。
()p q ⌝∧D .()p q ∧⌝【答案】B2．【北京市海淀首经贸2016-2017学年高二上学期期中】若命题“且”为假，且“”为假,则( )．A 。
或为假B . 为假C 。
为真D 。
为假【答案】D【解析】“”为假，则为真， 又“且”为假，为真， 故为假， 故选．3．【北京市西城鲁迅中学2016-2017学年高二上学期期中】命题的值不超过，命题是无理数，则( ）．A. 命题“”是假命题B. 命题“"是假命题C。
命题“”是假命题D. 命题“”是真命题【答案】B【解析】命题为假，，命题为真,是无理数，“”为真命题,“”为真命题，“”为假命题,“”为假命题．故选．点睛:若要判断一个含有逻辑联结词的命题的真假，需先判断构成这个命题的每个简单命题的真假,再依据“或”：一真即真，“且”：一假即假，“非"：真假相反,做出判断即可。
以命题真假为依据求参数的取值范围时，首先要对两个简单命题进行化简，然后依据“p∨q”“p∧q”“非p”形式命题的真假，列出含有参数的不等式(组）求解即可。
4．【北京西城13中2016—2017学年高二上期期中】已知互不重合的三个平面α，β，γ，命题p：若αβ⊥, γβ⊥，则αγ;命题q：若α上不共线的三点到β的距离相等,则αβ,下列结论中正确的是（）．A。
命题“p且q”为真B. 命题“p或q⌝"为假C。
命题“p或q”为假D。
命题“p且q⌝”为假【答案】C5．【甘肃省会宁县第一中学2018届高三上学期第二次月考】已知命题，命题，若命题“"是真命题,则实数的取值范围是（）A. B。
齐鲁名校教科研协作体
7、（改编）下列是关于成语包含的化学原理的叙述，不合理的是（ ） A．钻木取火--摩擦生热，使可燃物的温度达到着火点而燃烧 B．煽风点火--使空气流通，为燃烧补充空气或氧气 C．釜底抽薪—取出可燃物使燃烧更旺 D．百炼成钢--多次提炼，使生铁中碳、硅、锰等杂质的含量调节至钢的标准 8、 （原创）设 NA 表示阿伏伽德罗常数，下列说法正确的是： A、10mL 质量分数为 98%的 H2SO4，加水至 100mL，H2SO4 的质量分数为 9.8% B、常温常压下，28gN2 所含电子数为 14NA C、标准状况下，0.01mol/LNaOH 溶液的 pH=12 D、60gSiO2 含有硅氧键的数目为 2NA 9、（原创）每逢春节期间，一种“本宝宝福禄双全”的有机物就会刷爆朋友圈，其结构简式如下：
-1
是 发， Ⅱ.乳酸亚铁晶体纯度增强，说明 HR 为弱酸 B、b 点溶液 PH=7，此时 HR 与氨水恰好完全反应 C、c 点溶液中存在 c(NH4 )>c(R )、c(OH )>c(H )
+ +
（4）该兴趣小组用 KMnO4 滴定法测定样品中亚铁含量进而计算产品中乳酸亚铁的质量分数，发现产 品的质量分数总是大于 100%，其原因可能是 ．
10、 （改编）电致变色玻璃以其优异的性能将成为市场的新宠，如图所示五层膜的玻璃电致变色系统， 其工作原理是在外接电源下，通过在膜材料内部发生氧化还原反应，实现对器件的光透过率进行多级 可逆性调节。 (已知:WO3 和 Li4Fe4[Fe(CN)6]3 均为无色透明， LiWO3 和 Fe4[Fe(CN)6]3 均为蓝色)下列有关 说法正确的是（ ）
A．当 B 外接电源负极时，膜由无色变为蓝色 B．当 B 外接电源负极时，离子储存层发生反应为： Fe4[Fe(CN)6]3+4Li++4eˉ=Li4Fe4[Fe(CN)6]3 C．当 A 接电源的负极时，此时 Li+得到电子被还原 D．当 A 接电源正极时，膜的透射率降低，可以有效阻挡阳光 11、(改编)已知 X、Y、Z、W 四种元素分别是元素周期表中三个连续短周期的主族元素，且原子序数 依次增大。X、W 同主族，Y、Z 为同周期的相邻元素，W 原子的质子数等于 Y、Z 原子的最外层电子 数之和。下列有关说法正确的是 A、Y、Z 分别与 X 形成化合物的稳定性前者大于后者
山东省、湖北省部分重点中学2018届高三第二次(12月)联考化学试卷+Word版含解析
齐鲁名校教科研协作体山东、湖北部分重点中学2018届高三第二次调研联考理科综合（化学）试题命题学校：宜昌一中命题人：王宝玉可能用到的相对原子质量：H 1 C 12 N 14 O 16 S 32 K 39 Fe 56（容易）7．黑火药是中国古代伟大发明之一，配方是“一硫二硝三炭”。
孙思邈在《丹经内伏硫磺法》中记载：“硫磺、硝石各二两，研成粉末。
将皂角点着夹入其里，起烧烟火。
”下列说法不正确的是（）A．黑火药是混合物B．皂角的作用是提供炭C．反应原理是首先生成NH4NO3，然后NH4NO3分解爆炸D．大量燃放用黑火药制造的鞭炮会造成环境污染答案：C解析：火药成分“一硫二硝三炭”，是混合物。
皂角提供“炭”。
反应生成大量气体，并放热产生爆炸，不会生成铵盐。
鞭炮燃烧会产生SO2污染大气。
考点：化学常识，传统文化，氧化还原，环境保护（容易）8．设N A为阿伏加德罗常数的值。
下列有关叙述正确的是（）A．向FeI2溶液中通入一定量Cl2，当1molFe2+被氧化时，转移的电子数不小于3N AB．一定质量的某单质，若含质子数为n N A，则中子数一定小于nN AC．22.4LHF含有的共价键数为N AD．2 L 0.5 mol·L-1CH3COOH溶液中，CH3COO- 的数目为N A答案：A解析：A：先氧化I-，再氧化Fe2+。
原来I-不少于2mol。
B：质子数与中子数无必然数目关系，H质子数多，K中子数多（试题开头给出K相对原子质量39）。
C：没给条件。
D：CH3COOH在溶液中存在电离平衡，部分变为CH3COO-考点：同位素、物质状态、共价键数、氧化还原、弱电解质电离（容易）9．尿素是一种常见的化肥，在酸、碱或酶作用下水解。
其结构简式为CO(NH2)2。
关于尿素的说法正确的是（）A．含氮质量分数比碳酸氢铵低B．所有原子一定共平面C．可以发生取代反应D．将尿素加热到160℃分解，产物为CO2、NH3和H2O答案：C解析：A：可以硬算；可以比分数大小（巧算）；也可以是能记住尿素是含氮质量分数最高的常用化肥B：NH3分子是三角锥形，所以含氨基的物质所有原子不可能共平面，考查迁移能力（从甲烷结构迁移到氨分子结构）C：水解是取代反应；-NH2也可以和-COOH发生取代（理科综合，生物有学习过）。
语文试题参考答案及评分标准
齐鲁名校教科研协作体山东、湖北部分重点中学2018年高考冲刺模拟试卷（二）语文试题参考答案及评分标准一、现代文阅读（一）1.B A“首要原因”错，“方言的差异”及“方言基础上两地民间曲调风格的差异”是其成因，但二者并无主次之分；C“南曲的单一来源”说法有误，它受到了宋人词调及民间曲调的影响；D“脱离了乐器的伴奏”有误，原文是说南曲不用管弦乐器伴奏。
2.B “论述了……异同”说法有误，文中只是论述了南曲与北曲在唱腔等方面的具体差异，并不涉及相同点。
3.C 北曲在唱腔方面“一直领先于南曲”与原文不符，原文“约从成化年间开始，戏文在东南几省陆续变化出诸多新的腔种来”说明此时南曲在唱腔方面已经取得了对北曲的明显优势。
（二）4.C “文中的‘娘’形象非常丰满，性格复杂，具有多面性”有些言过其实；“旨在展现其武断的一面”也有误，写“娘”常去数西瓜，催促家人查出原因，旨在展现她对年成的关心，这种关心与期望背后蕴含着她对整个家的负责以及对“我”的爱。
5.①知恩图报。
尽管自家缺吃少喝，孩子瘦弱如猴，疯子仍用一篮鸡蛋报送瓜之恩。
②舐犊情深。
父爱如山，母爱如水。
如父亲塞馒头给我、娘对我的期望与关爱、疯婶对瘦猴的疼爱等。
③宽容善良，有同情心，帮扶弱势人群。
在物质匮乏的时代，更是难能可贵。
主要体现在“我”的爹娘身上。
④自尊与尊人。
如爹对疯婶偷瓜的宽容，爹娘第二天悄悄送瓜在门口等是维护他人尊严，疯婶第一次不接受母亲送瓜，多是出于自尊⑤舍身救人。
主要体现为老邢叔救人殒命的事迹。
（每条2分，立足给分，但须言之有理、有据。
答出3条方可得满分。
）6.①情节再添波澜，疯子也知报恩，出人意料之外，但又在情理之中，结尾以鸡蛋报送瓜之恩，与前文瓜主的善行、疯婶的病情、家中养鸡等内容形成照应，使文章结构严密。
②结尾处描写鸡蛋上泛起亮光，语含双关，以景衬情，折射出的是人性的光辉。
③结尾处内容拓宽了主题，增添了知恩图报这一新的主题。
同时，深化了主旨，揭示了人间有大爱、好人有好报的主题。
2020届一轮复习人教版：第7讲 美国联邦共和制的建立【作业】
第7讲美国联邦共和制的建立一、选择题1．当时，美国各州之间关税壁垒的存在阻碍着经济发展，如果某州为了维护自己的政府和资源而征收关税，它的邻近州就有许多诱惑去采取自由贸易制度，将更大份额的国内外贸易吸引到自己那里去。
这种状况表明当时美国()A．邦联政府软弱无力B．采取了贸易保护政策C．具有浓厚的重商主义思想D．尚未完成国家的统一答案 A解析根据题目中“美国各州之间关税壁垒的存在阻碍着经济发展”得出：美国刚建国时期实行邦联制，邦联政府权力小，各州权力大，故A项正确。
2．(2019·肇庆模拟)18世纪末，有个美国政治家认为，危险的野心多半为热心于人民权利的漂亮外衣所掩盖，很少用热心拥护政府坚定而有效率的严峻面孔作掩护。
该论断的意图是()A．为强化联邦政府权力做辩护B．呼吁美国人民正确行使自己的权利C．论证民主社会导致多数人的暴政D．主张政府权力要分权与制衡答案 A解析该政治家批判邦联制的拥护者，期望建立联邦政府，故A项正确；该政治家反对过分倡导人民权利，故B项错误；材料否定邦联制，主张建立联邦制，而非强调多数人的暴政，故C项错误；材料未提及分权与制衡，故D项错误。
3．(2019·武汉高三调研)在美国宪法的背后，有一种与众不同的政治文化。
在美国形成初期，美国人清醒地意识到自己是“第一个新型国家”的公民。
这不是一个法国大革命时宣扬的准宗教性的乌托邦社会，而是根据政府的首要原则建立起来的新型自由共和国。
这种新型自由共和制既希望避免导致共和国崩溃的离心危险，又希望避免随心所欲的集中权力。
这说明()A．美国首创共和政体B．美国人的政治追求与法国人有本质差别C．美国新型共和国的首要原则是三权分立D．美国联邦共和制的建立有着很深的文化背景答案 D解析共和政体古已有之，美国首创共和政体这种说法是错误的，故A项错误；美国人的政治追求与法国人没有本质差别，他们都追求民主，故B项错误；材料中没有涉及三权分立的原则，故C项错误。
22第一部分 板块二 专题六 函数与导数 第3讲 导数的简单应用(小题)
第3讲 导数的简单应用(小题)热点一 导数的几何意义应用导数的几何意义解题时应注意：(1)f ′(x )与f ′(x 0)的区别与联系，f ′(x 0)表示函数f (x )在x ＝x 0处的导数值，是一个常数； (2)函数在某点处的导数值就是对应曲线在该点处切线的斜率； (3)切点既在原函数的图象上也在切线上．例1 (1)已知函数f (x )＝x ＋1，g (x )＝a ln x ，若函数f (x )与g (x )的图象在x ＝14处的切线平行，则实数a 的值为( ) A.14 B.12C ．1D ．4 (2)(2019·东莞调研)设函数f (x )＝2x 3＋(a ＋3)x sin x ＋ax ，若f (x )为奇函数，则曲线y ＝f (x )在点(0,0)处的切线方程为( ) A ．y ＝x B ．y ＝2x C ．y ＝－3xD ．y ＝4x跟踪演练1 (1)(2019·六安联考)曲线f (x )＝a ln x 在点P (e ，f (e))处的切线经过点(－1，－1)，则a 的值为( )A ．1B ．2C ．eD ．2e(2)若直线y ＝kx ＋b 是曲线y ＝ln x ＋1的切线，也是曲线y ＝ln(x ＋2)的切线，则实数b ＝________.热点二 利用导数研究函数的单调性 利用导数研究函数单调性的关键：(1)在利用导数讨论函数的单调区间时，首先要确定函数的定义域； (2)单调区间的划分要注意对导数等于零的点的确认； (3)已知函数单调性求参数范围，要注意导数等于零的情况．例2 (1)(2019·郑州质检)函数f (x )是定义在[0，＋∞)上的函数，f (0)＝0，且在(0，＋∞)上可导，f ′(x )为其导函数，若xf ′(x )＋f (x )＝e x (x －2)且f (3)＝0，则不等式f (x )<0的解集为( ) A ．(0,2) B ．(0,3) C ．(2,3)D ．(3，＋∞)(2)(2019·江西红色七校联考)若函数f (x )＝2x 3－3mx 2＋6x 在区间(1，＋∞)上为增函数，则实数m 的取值范围是( ) A ．(－∞，1] B ．(－∞，1) C ．(－∞，2]D ．(－∞，2)跟踪演练2 (1)(2019·上饶模拟)对任意x ∈R ，函数y ＝f (x )的导数都存在，若f (x )＋f ′(x )>0恒成立，且a >0，则下列说法正确的是( ) A ．f (a )<f (0) B ．f (a )>f (0) C ．e a ·f (a )<f (0)D ．e a ·f (a )>f (0)(2)(2019·临沂质检)函数f (x )＝12ax 2－2ax ＋ln x 在(1,3)上不单调的一个充分不必要条件是( )A ．a ∈⎝⎛⎭⎫－∞，－12 B ．a ∈⎝⎛⎭⎫－12，16 C ．a ∈⎝⎛⎭⎫16，12D ．a ∈⎝⎛⎭⎫12，＋∞热点三 利用导数研究函数的极值、最值 利用导数研究函数的极值、最值应注意的问题： (1)不能忽略函数f (x )的定义域；(2)f ′(x 0)＝0是可导函数在x ＝x 0处取得极值的必要不充分条件； (3)函数的极小值不一定比极大值小；(4)函数在区间(a ，b )上有唯一极值点，则这个极值点也是最大(小)值点，此结论在导数的实际应用中经常用到．例3 (1)(2019·东北三省三校模拟)若函数f (x )＝e x －ax 2在区间(0，＋∞)上有两个极值点x 1，x 2(0<x 1<x 2)，则实数a 的取值范围是( ) A ．a ≤e 2 B ．a >e C ．a ≤e D ．a >e2(2)(2019·丹东质检)直线y ＝m 与直线y ＝2x ＋3和曲线y ＝ln 2x 分别相交于A ，B 两点，则|AB |的最小值为________．跟踪演练3 (1)(2019·天津市和平区质检)已知函数f (x )＝x 3＋ax 2＋bx ＋c ，若f (1)＝0，f ′(1)＝0，但x ＝1不是函数的极值点，则abc 的值为________． (2)已知a >0，f (x )＝x e xe x ＋a ，若f (x )的最小值为－1，则a 等于( )A.1e 2B.1eC ．eD ．e 2真题体验1．(2017·山东，文，10)若函数e x f (x )(e ＝2.718 28…是自然对数的底数)在f (x )的定义域上单调递增，则称函数f (x )具有M 性质，下列函数中具有M 性质的是( ) A ．f (x )＝2－x B ．f (x )＝x 2 C ．f (x )＝3－xD ．f (x )＝cos x2．(2019·全国Ⅱ，文，10)曲线y ＝2sin x ＋cos x 在点(π，－1)处的切线方程为( ) A ．x －y －π－1＝0 B ．2x －y －2π－1＝0 C ．2x ＋y －2π＋1＝0 D ．x ＋y －π＋1＝0押题预测1．曲线y ＝2x ln x 在x ＝e 处的切线与坐标轴围成的三角形的面积为( ) A.e 24 B.e 22C ．e 2D ．2e 2 2．已知定义在R 上的函数f (x )的导函数为f ′(x )，若f (x )＋f ′(x )<0，f (0)＝1，则不等式e x f (x )<1的解集为( ) A ．(－∞，0) B ．(0，＋∞) C ．(－∞，1)D ．(1，＋∞) 3．已知函数f (x )＝(x －3)e x ＋a (2ln x －x ＋1)在(1，＋∞)上有两个极值点，且f (x )在(1,2)上单调递增，则实数a 的取值范围是( ) A ．(e ，＋∞) B ．(e,2e 2)C ．(2e 2，＋∞)D ．(e,2e 2)∪(2e 2，＋∞)A 组 专题通关1．设函数y ＝x sin x ＋cos x 的图象在点()t ，f (t )处切线的斜率为g (t )，则函数y ＝g (t )的图象一部分可以是( )2．(2019·甘青宁联考)若直线y ＝kx －2与曲线y ＝1＋3ln x 相切，则k 等于( ) A ．3 B.13 C ．2 D.123．(2019·沈阳模拟)已知函数f (x )＝2e f ′(e)ln x －xe，则f (x )的极大值点为( )A.1eB ．1C ．eD ．2e 4．(2019·全国Ⅲ)已知曲线y ＝a e x ＋x ln x 在点(1，a e)处的切线方程为y ＝2x ＋b ，则( ) A ．a ＝e ，b ＝－1 B ．a ＝e ，b ＝1 C ．a ＝e －1，b ＝1D ．a ＝e －1，b ＝－15．已知定义在R 上的可导函数f (x )的导函数为f ′(x )，满足f ′(x )<f (x )，且f (0)＝12，则不等式f (x )－12e x <0的解集为( )A.⎝⎛⎭⎫－∞，12 B ．(0，＋∞) C.⎝⎛⎭⎫12，＋∞ D ．(－∞，0)6．已知函数f (x )＝e xx 2＋2k ln x －kx ，若x ＝2是函数f (x )的唯一极值点，则实数k 的取值范围是( ) A.⎝⎛⎦⎤－∞，e24 B.⎝⎛⎦⎤－∞，e2 C ．(0,2]D.[)2，＋∞7．若函数f (x )＝e x －x 2－ax (其中e 是自然对数的底数)的图象在x ＝0处的切线方程为y ＝2x ＋b ，则函数g (x )＝f ′(x )－bx 在(0，＋∞)上的最小值为( )A ．－1B ．eC ．e －2D ．e 28．若曲线y ＝x －ln x 与曲线y ＝ax 3＋x ＋1在公共点处有相同的切线，则实数a 等于( ) A.e 23 B ．－e 23C ．－e 3D.e 39．(2019·岳阳模拟)已知M ＝{α|f (α)＝0}，N ＝{β|g (β)＝0}，若存在α∈M ，β∈N ，使|α－β|<n ，则称函数f (x )与g (x )互为“n 度零点函数”．若f (x )＝32－x －1与g (x )＝x 2－a e x 互为“1度零点函数”，则实数a 的取值范围为( ) A.⎝⎛⎦⎤1e 2，4e B.⎝⎛⎦⎤1e ，4e 2 C.⎣⎡⎭⎫4e 2，2eD.⎣⎡⎭⎫1e 3，2e 210．设直线x ＝t 与函数f (x )＝x 2，g (x )＝ln x 的图象分别交于点M ，N ，则当|MN |达到最小时t 的值为( )A ．1 B.12 C.52 D.2211．(2019·吉林调研)设函数f (x )在R 上存在导函数f ′(x )，对任意实数x ，都有f (x )＝f (－x )＋2x ，当x <0时，f ′(x )<2x ＋1，若f (1－a )≤f (－a )＋2－2a ，则实数a 的最小值为( ) A ．－1 B ．－12 C.12D ．112．(2019·江淮联考)若对∀x 1，x 2∈(m ，＋∞)，且x 1<x 2，都有x 1ln x 2－x 2ln x 1x 2－x 1<1，则m 的最小值是( )注：(e 为自然对数的底数，即e ＝2.718 28…) A.1e B ．e C ．1 D.3e13．(2018·齐鲁名校教科研协作体模拟)已知函数f (x )＝sin x －x cos x ，现有下列结论： ①当x ∈[0，π]时，f (x )≥0； ②当0<α<β<π时，α·sin β>β·sin α；③若n <sin x x <m 对∀x ∈⎝⎛⎭⎫0，π2恒成立，则m －n 的最小值等于1－2π； ④已知k ∈[]0，1，当x i ∈()0，2π时，满足|sin x i |x i ＝k 的x i 的个数记为n ，则n 的所有可能取值构成的集合为{0,1,2,3}． 其中正确的序号为________．14．已知函数f (x )＝2ln x 和直线l ：2x －y ＋6＝0，若点P 是函数f (x )图象上的一点，则点 P 到直线l 的距离的最小值为________．15．(2019·衡水调研)已知函数f (x )＝12x 2＋tan θx ＋3⎝⎛⎭⎫θ≠π2，在区间⎣⎡⎦⎤－33，1上是单调函数，其中θ是直线l 的倾斜角，则θ的所有可能取值区间为________．16．(2019·厦门模拟)若实数a ，b ，c 满足(a －2b －1)2＋(a －c －ln c )2＝0，则|b －c |的最小值是________．B 组 能力提高17．已知a ∈Z ，若∀m ∈(0，e)，∃x 1，x 2∈(0，e)且x 1≠x 2，使得(m －2)2＋3＝ax 1－ln x 1＝ax 2－ln x 2，则满足条件的a 的取值个数为( ) A ．5 B ．4 C ．3 D ．218．(2019·洛阳统考)若函数f (x )＝e x －(m ＋1)ln x ＋2(m ＋1)x －1恰有两个极值点，则实数m 的取值范围为( ) A ．(－e 2，－e) B.⎝⎛⎭⎫－∞，－e2 C.⎝⎛⎭⎫－∞，－12 D.()－∞，－e －1。
山东、湖北部分重点中学2018届高三高考冲刺模拟考试(二)数学(理)试卷
齐鲁名校教科研协作体山东、湖北部分重点中学2018年高考冲刺模拟试卷（二）理科数学试题本试卷共4页，23题（含选考题）。
全卷满分150分。
考试用时120分钟。
一.选择题：本题共12个小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1. （原创.容易）已知集合(,1][1,)A =-∞-+∞ ，21{|log ,[,4]}2B y y x x ==∈，则A B = （ ）A.[1,2]-B. [1,2]C. {1}[1,2]-D. [1,1]{2}- 【答案】C【解析】，由B 可得[1,2]B =-，(,1][1,)A =-∞-+∞ {1}[1,2]A B ∴=- .故选C. 【考点】考查对数不等式的解法及集合运算.2. (原创.容易)已知复数z 满足||2z z z +=，（z 为z 的共轭复数）.下列选项（选项中的i 为虚数单位）中z =（ ）.A. 1i +B. 1i -C.1i +或1i -D.1i -+或1i -- 【答案】C【解析】设(,)z a bi a b R =+∈，则z a bi =-，所以22222a b a ⎧+=⎨=⎩得11a b =⎧⎨=±⎩，所以1z i =+或1z i =-.故选C.（用验证法2z z +=即可得C ） 【考点】考查复数的模的运算.3. (原创.容易)正项等比数列{}n a 中，34,a a 的等比中项为11eed x x⎰，令123n n T a a a a =⋅⋅⋅⋅ ，则6T =（ ）A.6B.16C.32D.64 【答案】D【解析】因为1111ln |ln ln 2ee eedx x e x e ==-=⎰，即344a a =， 又1625344a a a a a a ===，所以33612634()464T a a a a a =⋅⋅⋅=== .故选D. 【考点】考查积分的运算及等比数列的性质.4. （原创.容易） 一个几何体的三视图如图所示，正视图与俯视图外框为全等的长与宽分别为2，1的长方形，侧视图为正方形.则这个几何体的体积为A.13 B.53 C.54D.2 【答案】B【解析】依题意几何体是长方体截去了一个三棱锥部分而成.长方体的体积为1122⨯⨯=，三棱锥的体积为111112323⨯⨯⨯⨯=, 所以几何体的体积为15233-=.故选B. 【考点】考查立体几何三视图及体积运算.5. (原创.容易)已知如图所示的程序框图中输出的结果为a ，则二项式6()a x x-展开式中的常数项为（ ）A.15B.-15C.20D.-20 【答案】C 【解析】由11a a=-赋值运算，a 输入值为-1，则第1次运算结果为12，第2次结果为2，第3次结果为-1，结果数字以3为周期循环出现，要运算12次，此时输出的数为-1.这样二项式6()a x x-的展开通项为6161()k k kk T C x x-+=，当3k =时为常数项，所以常数项为3620C =.故选C.【考点】考查算法框图及二项式定理的展开式. 6.(原创.容易)函数sin |sin |()x x f x x+=的部分图象为几何体i <13?【答案】A【解析】当[,0)x π∈-时，()0f x =，所以排除C,D ；当(2,)x ππ∈--时sin 0x >，2sin ()0xf x x=<.故选A. 【考点】考查三角函数的值的变化及图象.7.(原创.容易)一个圆形电子石英钟由于缺电，指针刚好停留在8:20整，三个指针(时针、分针、秒针)所在射线将时钟所在圆分成了三个扇形，一只小蚊子（可看成是一个质点）随机地飞落在圆面上，则恰好落在时针与分针所夹扇形内的概率为（ ） A.1136 B.13 C.1336 D.718【答案】C【解析】观察时钟所在圆被12个刻度十二等分，指针转过一等分就旋转30，时针转过一等分就是1小时，分针转过一等分就是5分钟，所以8:20的时候秒针指向12，分针指向4，时针的指向是从刻度8再转过一等分的三分之一即10.这样分针与时针这间的扇形的圆心角为43010130⨯+=.又同圆中扇形面积比等于其圆心角的度数的比，所以1301336036P ==.故选C. 【考点】考查几何概率8. (原创.容易)在ABC ∆中，,1CA CB CA CB ⊥==，D 为AB 的中点，将向量CD绕点C 按逆时针方向旋转90得向量CM ，则向量CM在向量CA 方向上的投影为（ ）A.1-B.1C.12-D.12【答案】C121110987654321【解析】如图，以,CA CB 为,x y 轴建立平面直角坐标系，则11(1,0),(,)22CA CD == ，得11(,)22CM =- ，所以向量CM 在向量CA 方向上的投影为11212||CA CM CA -⋅==-.故选C. 【考点】考查平面向量的投影的定义及计算.9. (原创.中等) 在三棱锥S ABC -中，,,AB AC AB AC SA SA ⊥==⊥平面ABC ，D 为BC 中点，则异面直线AB 与SD 所成角的余弦值为（ ）A.以上结论都不对 【答案】B【解析】如图，取AC 中点为E ，连结,DE SE ，因为,D E 分别为,BC AC 的中点，所以DE ∥AB ，所以SDE ∠就是异面直线AB 与SD 所成角，令2AB AC SA ===，由勾股定理得SE =1DE =.易证BA ⊥平面SAC ，DE ∴⊥平面SAC ，DE SE ∴⊥，SD ∴=在Rt SDE ∆中，cos 6DE SDE SD ∠===.故选B. 【考点】考查空间异面直线所成角的大小. 10. (原创.中等) 下面有四个命题：①设(1,1),X N (13)0.9544P X -≤≤=，则(3)0.0228P X ≥=. ②已知lg 2a =，则aaa a a a <<. ③将2tan()6y x π=+的图象向右平移6π个单位，再将所得图象的横坐标不变，纵坐标缩短到原来的12，可得到tan y x =的图象. ④设03a <<，则函数3()(01)f x x ax x =-<<有最小值无最大值. 其中正确命题的个数为（ ）A.1B.2C.3D.4 【答案】CCS【解析】①(1,1),X N 曲线关于1X =对称，所以0.9544(3)0.50.02282P X ≥=-=，正确. ②可知0101,a a a a a <<∴>>，即1a a a >>，所以aa a a a a <<，错误. ③正确.④'201,()30x f x x a <<∴=-= 得x =，又03a <<，01∴<，可知()f x 在单调递减，在单调递增，所以正确.故选C. 【考点】考查了正态分布的概率计算，用指数函数的单调性比较大小，图象变换及函数的最值的求解.11. (原创.中)已知双曲线22221(0,0)x y a b a b-=>>的左、右顶点分别为,A B ，右焦点为F .过点F 且垂直于x 轴的直线l 交双曲线于,M N 两点，P 为直线l 上一点，当APB ∠最大时，点P 恰好在M （或N ）处.则双曲线的离心率为（ ）2【答案】A【解析】当过,A B 的圆与直线l 相切于P 点时，直线上其它点都在圆外，此时APB ∠最大，由切割线定理得2222||||||()()FP FB FA c a c a c a b ==-+=-=，点P 恰好在M 处，所以||FM b =，由双曲线可知2||b FM a =，所以2,b b a b a=∴=，所以双曲线的离心率为e =故选A.（也可用正切的和差公式求解）【考点】考查求双曲线的离心率. 12. （改编，难）已知函数ln ,0()ln(),0mx x x f x mx x x ->⎧=⎨+-<⎩.若函数()f x 有两个极值点12,x x ，记过点11(,())A x f x 和22(,())B x f x 的直线斜率为k ，若02k e <≤，则实数m 的取值范围为（ ）A.1(,2]eB.1(,]e eC.(,2]e eD.1(2,]e e+ 【答案】B【解析】当0x >时，函数()ln f x mx x =-的导函数为'11()mx f x m x x-=-=， 由函数()f x 有两个极值点得0m >，又()f x 为奇函数，不妨设210x x =->，则有21x m=，1(,1ln )B m m ∴+可得：1(,(1ln ))A m m--+ . 由直线的斜率公式得2121()()(1ln )f x f x k m m x x -==+-，0m >，又0k >，11ln 0,m m e∴+>∴>，（当10m e <≤时，0k ≤，不合题意）令1()(1ln ),k h m m m m e==+>得'()2ln 1(1ln )0h m m m =+=++>，()h m ∴在1(,)e +∞上单调递增，又1()0,()2h h e e e==，由02k e <≤得：1()()()h h m h e e<≤，所以1m e e <≤.故选B.【考点】利用导数研究函数的极值、零点及不等式问题. 二.填空题：本题共4个题，每小题5分，共20分.13. (书本题改编.容易)已知抛物线22y px =的准线方程为2x =-，点P 为抛物线上的一点，则点P 到直线3y x =+的距离的最小值为_________.【解析】由题设得抛物线方程为28y x =，设P 点坐标为(,)P x y ，则点P 到直线3y x =+的距离为d=222===≥，当4y =. 【考点】考查抛物线的性质，点到直线的距离及最值的求解.14. (原创.容易) 我国古代著名的数学家刘徽著有《海岛算经》.内有一篇：“今有望海岛,立两表齐,高三丈,前后相去千步,令后表与前表相直.从前表却行百二十三步,人目著地取望岛峰,与表末参合.从后表却行百二十七步,人目著地取望岛峰,亦与表末参合.问岛高及去表各几何?”请你计算出海岛高度为__________步.（参考译文：假设测量海岛,立两根标杆，高均为5步,前后相距1000步,令前后两根标杆和岛在同一直线上,从前标杆退行123 步, 人的视线从地面(人的高度忽略不计)过标杆顶恰好观测到岛峰,从后标杆退行127步, 人的视线从地面过标杆顶恰好观测到岛峰,问岛高多少？ 岛与前标杆相距多远?）（丈、步为古时计量单位，当时是“三丈=5步”） 【答案】1255步【解析】如图，设岛高x 步，与前标杆相距y 步，则有512312351271271000x y x y⎧=⎪+⎪⎨⎪=⎪++⎩，解得：1255x =步. 【考点】考查解直角三角形，利用相似成比例的关系.15. (原创.容易)若实数,x y 满足3||3y x ay x ≥+⎧⎨≤-+⎩.若z x y =+的最小值为7-，则________a =. 【答案】2-【解析】作出可行域如图所示，过点C 时取最小值.由33y x y x a=+⎧⎨=+⎩得333(,)22a a C --，则333722a a --+=-得2a =-. 【考点】考查利用线性规划求字母的值.16. (改编.难) 已知数列{}n a 的前n 项和为n S （*n N ∈），且满足212n n S S n n ++=+，若对*1,n n n N a a +∀∈<恒成立，则首项1a 的取值范围是__________． 【答案】13(,)44-【解析】因为212n n S S n n ++=+，所以212(1)1,(2)n n S S n n n -+=-+-≥， 两式作差得141,2n n a a n n ++=-≥，所以145,3n n a a n n -+=-≥两式再作差得114,3n n a a n +--=≥，可得数列{}n a 的偶数项是以4为公差的等差数列，从3a 起奇数项也是以4为公差的等差数列.若对*1,n n n N a a +∀∈<恒成立，当且仅当1234a a a a <<<.1271000又12213213,32,742a S a a a a a +=∴=-∴=-=+，4311172a a a =-=-， 所以1111324272a a a a <-<+<-，解得：11344a -<<. 【考点】数列递推的应用.三.解答题：共70分.解答应写出文字说明、证明过程或演算步骤.第17-21题为必考题，每个试题考生都必须作答.第22、23题为选考题，考生根据要求作答. （一）必考题：共60分. 17.（本小题满分12分）（原创.易）已知ABC ∆中，2AB BC CA ===，P 为ABC ∆内一点，且90BPC ∠= .（Ⅰ）当BP =AP 的长；（Ⅱ）若150APC ∠= ，令PCB θ∠=，求tan θ的值.解析：（Ⅰ）如图，在PBC ∆中，90BPC ∠=，2BP BC ==，45PBC ∴∠= .所以15ABP ∠=，cos15cos(4530)=-=.……………2分 由余弦定理得：2222cos15AP BA BP BA BP =+-⋅⋅424=+-=-4分1AP ∴=.……………6分(另解：取BC 中点为D ，连PD ，证明,,A P D 三点共线，求出1PD =，又AD =则1AP =.此法请酌情给分)（Ⅱ）PCB θ∠=，60ACP θ∠=-，150APC ∠=由内角和定理得30PAC θ∠=-.……………8分在直角PBC ∆中，cos 2cos PC BC θθ=⋅=，……………9分 在APC ∆中，由正弦定理得：sin sin AC PCAPC PAC =∠∠即22cos sin150sin(30)θθ=-，……………11分CACA解得tan 3θ=.……………12分 18. （本小题满分12分）（原创.中）如图，五边形ABSCD 中，四边形ABCD 为长方形，三角形SBC 为边长为2的正三角形，将三角形SBC 沿BC 折起，使得点S 在平面ABCD 上的射影恰好在AD 上.（Ⅰ）当AB =时，证明：平面SAB ⊥平面SCD ；（Ⅱ）若1AB =，求平面SCD 与平面SBC 所成二面角的余弦值的绝对值.解析：（Ⅰ）作SO AD ⊥，垂足为O ，依题意得SO ⊥平面ABCD ，,SO AB SO CD ∴⊥⊥， 又AB AD ⊥，AB ∴⊥平面SAD ，,AB SA AB SD ⊥⊥.……………2分利用勾股定理得SA ==SD =在SAD ∆中，2,AD SA SD SA SD ==⊥……………4分SD ∴⊥平面SAB ，又SD ⊂平面SCD ，所以平面SAB ⊥平面SCD .……………5分（Ⅱ）连结,BO CO ，SB SC = ，Rt SOB Rt SOC ∴∆≅∆，BO CO =，又四边形ABCD 为长方形，,Rt AOB Rt DOC OA OD ∴∆≅∆∴=.取BC 中点为E ，得OE ∥AB ，连结,SE SE ∴=其中1OE =，1OA OD ==，OS =……………7分由以上证明可知,,OS OE AD 互相垂直，不妨以,,OA OE OS 为,,x y z 轴建立空间直角坐标系. 1,OE OS =∴(0,1,0),(1,1,(2,0,0)DC SC BC ∴==-=-,……………8分设111(,,)m x y z =是平面SCD 的法向量，则有00m DC m SC ⎧⋅=⎪⎨⋅=⎪⎩即111100y x y =⎧⎪⎨-+=⎪⎩， 令11z =得(m =.……………9分设222(,,)n x y z =是平面SBC 的法向量，则有00n BC n SC ⎧⋅=⎪⎨⋅=⎪⎩即2222200x x y -=⎧⎪⎨-+=⎪⎩ 令11z =得n =.……………10分则||1|cos ,|3||||m n m n m n ⋅===⋅……………11分所以平面SCD 与平面SBC 所成二面角的余弦值的绝对值为13.……………12分 19. （本小题满分12分）（原创.易）我校为了更好地管理学生用手机问题，根据学生每月用手机时间（每月用手机时间总和）的长短将学生分为三类： 第一类的时间区间在(0,30]，第二类的时间区间在(30,60]，第三类的时间区间在(60,720]（单位：小时），并规定属于第三类的学生要进入“思想政治学习班”进行思想和心理的辅导.现对我校二年级1014名学生进行调查，恰有14人属于第三类，这14名学生被学校带去政治学习.由剩下的1000名学生用手机时间情况，得到如图所示频率分布直方图.(I) 求这1000名学生每月用手机时间的平均数； (II)利用分层抽样的方法从1000名选出10位学生代表，若从该10名学生代表中任选两名学生，求这两名学生用手机时间属于不同类型的概率； (III)若二年级学生长期保持着这一用手机的现状，学校为了鼓励学生少用手机，连续10个月，每个月从这1000名学生中随机抽取1名，若取到的是第一类学生，则发放奖品一份，设X 为获奖学生人数，求X 的数学期望()E X 与方差()D X .x用手机时间解析：(Ⅰ) 平均数为: 50.01010150.03010250.04010350.01010⨯⨯+⨯⨯+⨯⨯+⨯⨯450.00610550.0041023.4+⨯⨯+⨯⨯=（小时）. ……………………4分(Ⅱ) 由频率分布直方图可知，采用分层抽样抽取10名学生，其中8名为第一类学生，2名为第二类学生，则从该10名学生代表中抽取2名学生且这两名学生不属于同一类的概率为118221016.45C C C =…………8分 (Ⅲ) 由题可知，这1000名学生中第一类学生80%，则每月从1000名学生中随机抽取1名学生，是第一类学生的概率为0.8，则连续10个月抽取，获奖人数(10,0.8)X B ，其数学期望()100.88E X np ==⨯=（小时），方差()(1)100.80.2 1.6D X np p =-=⨯⨯=.……………12分 20. （本小题满分12分）（原创.中难）已知椭圆2222:1(0)x y C a b a b +=>>的离心率为2，12,F F 分别为椭圆的左、右焦点，点P 为椭圆上一点，12F PF ∆（Ⅰ）求椭圆C 的方程； （Ⅱ）过点(4,0)A 作关于x 轴对称的两条不同直线12,l l 分别交椭圆于11(,)M x y 与22(,)N x y ，且12x x ≠，证明直线MN 过定点，并求AMN ∆的面积S 的取值范围.解：（Ⅰ）设222a b c -=，则c a =.……………1分 设(,)P x y，则1212||,||F PF F PF S c y y b S bc ∆∆=≤∴≤= .……………3分 解得21a b =⎧⎨=⎩.所以椭圆C 的方程为2214x y +=.……………4分 （Ⅱ）设MN 方程为,(0)x ny m n =+≠，联立22440x ny m x y =+⎧⎨+-=⎩，得222(4)240n y nmy m +++-=，212122224,44nm m y y y y n n --∴+==++，……………5分因为关于x 轴对称的两条不同直线12,l l 的斜率之和为0 即1212044y y x x +=--，即1212044y y ny m ny m +=+-+-，……………7分 得1212122()4()0ny y m y y y y ++-+=，即222222(4)280444n m nm nmn n n --+=+++.解得：1m =.……………8分 直线MN 方程为：1x ny =+，所以直线MN 过定点(1,0)B .……………9分又12||y y -===令211,(0,)44t t n =∴∈+12||y y ∴-=……………11分又121213||||||(0,222S AB y y y y =-=-∈.……………12分 （其它解法酌情给分） 21. （本小题满分12分）（原创.难）已知函数()ln(),0f x ax a a =->.（Ⅰ）若函数()()xh x e f x =为单调函数，求a 的取值范围；（Ⅱ）当1a =时，证明：()sin 0xe f x x +>.解：（Ⅰ）()(ln ),0x h x e ax a x =->'1()(ln )x h x e ax a x∴=+-， ()h x 为单调函数等价为'()0h x ≥恒成立或'()0h x ≤恒成立，令1()ln x ax a x ϕ=+-得/22111()x x x x xϕ-=-=， 所以()x ϕ在(0,1)单调递减，在(1,)+∞单调递增，……………………2分 又1()0aϕ=，当01a <≤时11a ≥，1(,)x a ∴∈+∞时，1()()0x a ϕϕ>=； 当1a >时11a <，1(0,)x a ∴∈时，1()()0x aϕϕ>=；'()0h x ∴≤不可能恒成立，归纳得'()0h x ≥恒成立. ……………………3分又min ()(1)ln 1x a a ϕϕ==-+，所以ln 10a a -+≥ . 令()ln 1,0p a a a a =-+>，'1()1p a a=-， 得()p a 在(0,1)单调递增，在(1,)+∞单调递减，()(1)0p a p ≤=，即ln 10a a -+≤， ……………………5分所以ln 10a a -+=，即1a =. ……………………6分 （Ⅱ）令()(ln 1)sin x F x e x x =+-， (1)当x e ≥时，sin 1x ≥-，所以()(ln 1)sin ln 1x x F x e x x e x =+-≥-+，0x >. ……………………7分因为'[(1)]10x x e x e -+=-≥，所以0(1)(01)0x e x e -+>-+=即1x e x >+；因为'1[(1)l n ]1x x x--=-，可知函数(1)l nx x --在1x =处取最小值即(1)ln 0x x --≥，即ln 1x x -≥-.由不等式的性质得ln 1(1)(1)130xe x x x -+>++-+=>，所以()(ln 1)sin 0xF x e x x =+->. ……………………9分(2)当0x e <<时，()(ln 1)sin 1(ln 1)sin xF x e x x x x =+->+-， 因为/(sin )1cos 0x x x -=-≥，所以sin 0sin 00x x ->-=，即sin x x <，ln 10,(ln 1)sin (ln 1)x x x x x -<∴->- ，即1()1(ln 1)(ln 1)F x x x x x x>+-=+- 由（Ⅱ）证明可知1ln 10x x+-≥，所以()0F x >. ……………………11分由（1）（2）得()sin 0x e f x x +>. ……………………12分 （二）选考题：共10分.请考生在第22、23题中任选一题作答.如果多做，则按所做的第一题计分.22. （本小题满分10分）[选修4-4：坐标系与参数方程] （原创.易）在直角坐标系xOy 中，直线l 的参数方程为5cos sin x t y t αα=+⎧⎨=⎩，（t 为参数，α为直线倾斜角）.以平面直角坐标系的原点为极点，x 轴的正半轴为极轴，建立极坐标系，曲线C 的极坐标方程是4cos ρθ=.（Ⅰ）当45α= 时，求直线l 的普通方程与曲线C 的直角坐标方程；（Ⅱ）已知点C 的直角坐标为(2,0)C ，直线l 与曲线C 交于,A B 两点，当ABC ∆面积最大时，求直线l 的普通方程.解：（Ⅰ）当45α= 时，直线l的参数方程为52x y ⎧=+⎪⎪⎨⎪=⎪⎩， 消去t 得直线l 的普通方程为50x y --=. ……………………2分曲线C 的极坐标方程是4cos ρθ=，两边乘以ρ为24cos ρρθ=，由cos sin x y ρθρθ=⎧⎨=⎩得：2240x y x +-=，所以曲线C 的直角坐标方程为2240x y x +-=. ……………………5分 （Ⅱ）曲线C 是以(2,0)C 为圆心，2为半径的圆，1||||sin 2sin 2ABC S CA CB ACB ACB ∆=∠=∠. ……………………7分 当90ACB ∠=时面积最大.此时点C 到直线:(5)l y k x =-的距离为，所以|，解得：k =， ……………………9分 所以直线l的普通方程为5)7y x =±-. ……………………10分23. （本小题满分10分）[选修4-5：不等式选讲] （原创.易）设()|1||3|f x a x x =-++. （Ⅰ）当1a =时，求()f x 的最小值；（Ⅱ）若()g x 为奇函数，且(2)()g x g x -=，当[0,1]x ∈时，()5g x x =.若()()()h x f x g x =-有无数多个零点，作出()g x 图象并根据图象写出a 的值（不要求证明）.解：（Ⅰ）当1a =时，()|1||3||(1)(3)|4f x x x x x =-++≥--+=， 当且仅当(1)(3)0x x -+≤，即31x -≤≤时等号成立.()f x ∴的最小值为4. ……………………4分（Ⅱ）()g x 的图象是夹在5y =-与5y =之间的周期为4的折线，如图，…………6分又(1)3,3()(1)3,31(1)3,1a x a x f x a x a x a x a x -++-≤-⎧⎪=-++-<<⎨⎪+-+≥⎩， ()f x 的图象是两条射线与中间一段线段组成. ……………………8分若()()()h x f x g x =-有无数多个零点，则()f x 的图象的两条射线中至少有一条是平行于x 轴的，所以(1)0a -+=或(1)0a +=得1a =-.此时4,3()22,314,1x f x x x x -≤-⎧⎪=+-<<⎨⎪≥⎩，经验证符合题意，1a ∴=- ……………………10分。
秒词邦-全网唯一的高中单词微信程序-山东、湖北部分重点中学2018届高三高考冲刺模拟考试(三)化学试题
齐鲁名校教科研协作体山东、湖北部分重点中学2018年高考冲刺模拟试卷（三）理科综合化学试题命题学校：宜昌一中命题人：王宝玉可能用到的相对原子质量：H 1 C 12 N 14 O 16 S 32 Ca 40 Fe 56 Cu 64 Pb 207（容易，改编）7．《新修本草》是中国古代著名的中药学著作，记载药物844种。
其中有关用“青矾”制备“绛矾”的描述：“本来绿色，新出窟未见风者，正如瑠璃……烧之赤色，故名绛矾矣。
”据此推测，“青矾”的主要成分为（）A．Fe2O3B．FeSO4·7H2OC．Na2SO4·10H2O D．CuSO4·5H2O答案：B解析：FeSO4·7H2O为绿色，高温灼烧得到Fe2O3红色。
考点：Fe元素物理性质，传统文化，Fe2+的还原性。
（容易，原创）8．设N A为阿伏加德罗常数的值。
下列有关叙述正确的是（）A．用浓盐酸分别和MnO2、KClO3反应制备1mol氯气，转移的电子数均为2N AB．1molH2O最多可形成4N A个氢键C．常温下，pH=2的H2SO4溶液1L中，硫酸和水电离的H+总数为0.01N AD．常温常压下，O2与O3的混合气体16g，分子总数为N A答案：C解析：A：用KClO3时小于2 N A。
B：1个水分子最多可形成4个氢键，但每个氢键被两个水分子公用，所以1mol最多形成2N AC：pH计算的就是整个溶液中的c(H+)。
D：原子总数为N A考点：氢键、氧化还原、pH含义（较难，原创）9．有机物X分子式为C3H6O，有多种同分异构体。
其中之一丙醛（液态）的燃烧热为1815kJ/mol。
下列说法不正确的是（）A．X的同分异构体中，含单官能团的共5种B．X的同分异构体其中之一CH2=CHCH2OH可以发生取代反应、加成反应、加聚反应、氧化反应C．1molX最多能和1molH2加成D．表示丙醛燃烧热的热化学方程式为：C3H6O（l）+4O2(g) = 3CO2(g)+3H2O(l) △H=+1815 kJ/mol答案：D解析：A：有丙醛【CH3CH2CHO】、丙酮【CH3COCH3】以及(注意：烯醇、烯醚为多官能团)。
物理二
齐鲁名校教科研协作体山东、湖北部分重点中学2018年高考冲刺模拟试卷理科综合物理试题湖北襄阳五中（李琴、熊杨爽、刘荣沛）审题：湖北夷陵中学（国建云）山东泰安一中（罗凯）山东莱芜一中（亓建芃）一、选择题：（共8小题，14~18为单选，19~21为多选，每题6分，共48分）14、（原创，容易）如图所示，电源电动势为4V，内阻内阻1Ω，电阻R1=3Ω，R2=R3=4Ω，R4=8Ω，电容器C=6.0μF，闭合S电路达稳定状态后，电容器极板所带电量为：（）A．1.5×10-5C；B．3.010-5C；C．2.0×10-5C；D．2.1×10-5C。
【答案】A【解析】由电路结构可知，电容器两极板间的电势差为2.5V，由CUQ 可知A项正确。
【考点】恒定电流、电容器15.（改编，简单）如图所示为用位移传感器和速度传感器研究某汽车刹车过程得到的速度—位移图像，汽车刹车过程可视为匀变速运动，则：（）10A.汽车刹车过程中的加速度大小为2m/s2；B.汽车刹车过程所用时间为10s；C.当汽车运动的位移为5m 时，其速度为5m/s ；D.当汽车的速度为5m/s 时，运动的位移为7.5m 【答案】D【解析】由图可知物体做匀减速运动，结合匀变速直线运动的规律ax v v 2202=-可得到图线的解析式为m /s 10100x v -=，故汽车的加速度为2m/s 5，A 错；初速度m/s 100=v ，故运动时间为2s ，B 错；当汽车位移为5m 时，带入解析式有m /s 25=v ，C 错，同理，D 对。
【考点】匀变速直线运动，运动图像16.（原创，中档）如图所示，边长为a 2的正方形ABCD 的四个顶点分别固定电荷量为+q 的点电荷，直线MN 过正方形的几何中心O 且垂直正方形平面，P 与O 点相距为a ，P 点的电场强度为E ，若将A 点的电荷换为-q 的点电荷，则P 点的电场强度的大小为（ ）MNA.2E B.43E C. E 2 D.22E【答案】D【解析】由几何关系及场强的叠加原理可知，每一个+q 点电荷在P 点的场强为E 42，将A 点的点电荷换位-q 后，该点电荷在P 点的场强大小没变，但方向反向，由叠加原理可知，D 选项正确。
2020版高考(人民版)历史一轮复习试题 ：新民主主义革命
新民主主义革命一、选择题(共12小题，每小题4分，共48分)1.(2018·齐鲁名校教科研协作体)二十八日，和约签字；我国代表拒绝签字，不出席会场；而发电报告北京政府，说：“……不料大会专横至此……若再隐忍签字，我国……将更无外交之可言。
”下列选项与该会议相关的是( )A.割让台湾及附属岛屿B.将德国在山东的权益让与日本C.提出“求同存异”方针D.提出“两个中国”的席位2.(2019·山西大同、阳泉模拟)下表为不同报刊对同一事件的历史叙述。
据此能够被认定的历史事实是( )A.火烧曹汝霖宅是事件的导火线B.学生在运动中发挥了重要作用C.波及全国所有的大中型城市D.学生展开盲目的排日行为3.(2018·江西六校大联考)费正清说：“这是一个大约12个二十几岁年轻人参加的会议。
会议是在上海法租界的一所女子学校(暑假放假)里召开的，成员们担心巡捕的监视，乘火车转移到(嘉兴南湖)湖上的一艘游艇中继续讨论。
”这次会议( )A.标志着国共两党合作的形成B.给思想紊乱的中共指明了方向C.成为中共历史上重要的转折点D.使得中国革命面貌焕然一新4.(2018·广东珠海模拟)胡适指出：民国十三年以后，国民党一度成为中国“一个簇新的社会重心……这四五年来，又逐渐失去做社会重心的资格了”。
国民党成为中国“一个簇新的社会重心”的主要原因是( )A.北伐战争的胜利B.国民党的改组C.黄埔军校的建立D.共产国际帮助5.(2019·广西南宁模拟)1924年后，共产党一方面推动国民党中央先后设立了农民部、工人部、青年部、妇女部和商人部，工运、农运计划及相关政策、法规也相继出台；另一方面积极从事国民党不愿意做的下层民众动员工作，这说明( )A.共产党主导群众运动B.国共合作在基层未实现C.国民党不愿发动民众D.中共掌握了革命领导权6.(2019·河北邯郸模拟)1926年，共产国际指示中共说：“在城市中退却并收缩工人争取改善其地位的斗争的政策是不正确的，必须在农村中展开斗争，但同时必须利用有利的时机来改善工人的物质生活状况和法权地位，用一切方法使工人的斗争具有组织性。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
齐鲁名校教科研协作体山东、湖北部分重点中学2018年高考冲刺模拟试卷（五）文科科综合地理试题2014年9月，广东省东莞市在全国率先启动了“机器换人”计划。
根据计划，到2020年，东莞工业机器人在电子、机械、食品、纺织、家具等行业普及应用，服务机器人在家政服务、养老助残、医疗康复、教育娱乐等领域初步应用；每万名员工使用机器人台数从30多台提升至超过120台；将建成1－2个机器人产业园和6－8个智能制造装备产业基地。
截至2015年底，东莞企业申报“机器换人”项目总数达到了1262个；同时，东莞已聚集了400多家机器人智能装备企业。
据此回答下列各题。
1. 东莞机器换人计划的背景不包括( )A. 我国中西部经济发展B. 人口老龄化C. 东部沿海产业升级D. 交通运输发展2. 东莞机器人智能装备企业聚集的区位优势主要是( )A. 位于珠三角，技术水平高B. 地方政府政策扶持C. 产业协作条件好D. 市场需求量大3. 机器换人计划将导致东莞( )A. 劳动力素质总体提升B. 单位产品成本长期来说上升C. 劳动密集型产业转移D. 劳动力价格下降【解析】1. 机器换人计划主要应用在电子、机械、食品、纺织、家具、家政服务、养老助残、医疗康复、教育娱乐等领域，这与中西部经济发展，劳动密集型产业转移，东部地区产业升级、人力成本上升，人口老龄化等都有关系，但与交通运输业关系不大，选D。
2. 根据材料中“率先”、“申报”等字眼可知，东莞机器人智能装备企业聚集获得了地方政府政策扶持，选B。
3. 机器换人计划是在该地劳动密集型产业转移、当地产业升级时的应对措施，该计划将导致东莞低端产业的劳动力被机器人大量取代，而整体产业级别提升，迫使当地劳动力素质总体提升，劳动力成本上升，选A。
【答案】1. D 2. B 3. A【点睛】机器换人计划是“工业4.0”的直接应用。
“工业4.0”概念即是以智能制造为主导的第四次工业革命，或革命性的生产方法。
该战略旨在通过充分利用信息通讯技术和网络空间虚拟系统—信息物理系统（Cyber-Physical System）相结合的手段，将制造业向智能化转型。
“工业4.0”项目主要分为两大主题，一是“智能工厂”，重点研究智能化生产系统及过程，以及网络化分布式生产设施的实现；二是“智能生产”，主要涉及整个企业的生产物流管理、人机互动以及3D技术在工业生产过程中的应用等。
该计划将特别注重吸引中小企业参与，力图使中小企业成为新一代智能化生产技术的使用者和受益者，同时也成为先进工业生产技术的创造者和供应者。
我国中部某地校园内有很多香樟树、玉兰、石楠等常绿阔叶树，常绿阔叶树中间点缀着几棵落叶阔叶树，而校园外的天然植被却正好相反。
2018年初的一次暴风雪过境，香樟树等大量枝条折断，但落叶树基本毫发无损。
据此回答下列各题。
4. 该校园最有可能位于( )A. 黄河以北B. 黄淮之间C. 江淮之间D. 长江以南5. 香樟树等大量枝条折断的原因是( )A. 枝干细小，被大风吹折B. 枝多叶密，被积雪压折C. 气温骤降，被冻结折断D. 保护树木，被人为折断6. 依据材料，下列叙述正确的是( )A. 校内外植被受灾差异可在一定程度上反映自然地理环境的整体性。
B. 校园内外植被差异大致体现了自然地理环境的区域差异性。
C. 该校所在地不适合种植常绿阔叶树，校内应全面改种落叶树。
D. 该校应在冬春季对常绿树采取严密防冻措施，防止树木冻死。
【解析】4. 根据材料，该地的天然植被以常绿林为主，间杂落叶阔叶林，因此该地应位于温带与亚热带之间的过渡部位，并稍微偏南，秦岭-淮河为温带与亚热带的界线，据此该地应位于该线附近或稍微偏南部位，结合选项选C。
5. 香樟树、玉兰、石楠等苗木属于常绿阔叶林，冬季，当降雪量过大，这些林木由于枝多叶密，会被积雪压折，大量枝条折断，选B。
6、校内外植被受灾差异的直接原因是校内外树种的差异，由于校内树种是人为的常绿林为主，与当地以阔叶林为主的自然规律不符，故导致了校内树木面对暴风雪时的损失较大，这说明一种因素的变化会引起其他因素的变化，这在一定程度上是自然地理环境整体性的反映，故选A。
【答案】4. C 5. B 6. A地下水位过高导致会土壤过湿，不利于农业生产，需要排水。
下图示意某地等潜水位线及拟建的排水井和排水沟的位置(图中等潜水位线单位：m)。
据此回答下列各题。
7. 土壤过湿对农作物的危害是( )A. 气温日较差小，不利营养物质积累B. 土质黏重，不利农作物根系发育C. 土壤空气少，不利农作物根系呼吸D. 导致土壤中营养元素减少8. 图中排水沟4的排水效率是最低的，其原因最可能是( )A. 沟底是倾斜的B. 延伸方向是和等潜水位线垂直的C. 沟较浅D. 潜水是向两侧分流的9. 综合考虑排水效率和工程量，图中排水沟5的沟底最适宜的海拔高度是( )A. 79mB. 80mC. 81mD. 82m【解析】7. 土壤中的水分、空气比例相当才能保证土壤保温透气，作物生长好。
土壤过湿时，土壤中的空隙被水占用，由于空气少，不利农作物根系呼吸，作物生长会受到影响，据此选C。
8. 据图可知，排水沟4沟底平深，潜水位高，潜水向两侧分流，这导致大量水体滞留，不能有效排水，据此选D。
9. 图中排水沟5处的潜水位是（81,83），为保证本水位段的排水并综合考虑排水效率和工程量，沟底最适宜的海拔高度应接近最低水位，即81米，选C。
建水县位于云南省南部，早在唐代就是南方丝绸之路的交通要道。
“建水紫陶”是建水县的传统手工艺品，始于元末明初，为中国四大名陶之一。
其主要用建水近郊五彩山五色陶土（红黄青褐白）手工拉坯制作成型，经过书画、雕刻、填刮、烧炼、磨光等工序制成，其工艺以手口相传为主。
目前“建水紫陶”产业仍以个体作坊生产经营为主，并未形成规模化生产。
据此完成下列各题。
【答案】7. C 8. D 9. C10. “建水紫陶”产业规模化发展的主要限制因素是( )A. 工艺复杂独特B. 交通不便C. 知名度较低D. 工业基础差11. 建水县拟大幅扩大“建水紫陶”的产业规模，推测此举产生的影响最可能是( )A. 吸纳大量劳动力B. 导致水土流失加剧C. 迅速提升旅游业D. 有利可持续发展【解析】10. 根据材料分析，“建水紫陶”的生产需要复杂的工艺，且工艺以手口相传为主，制作工艺独特神秘，掌握工艺的人口数量受到限制，成为该产业规模化发展的主要限制因素，选A。
11. “建水紫陶”主要用建水近郊五彩山五色陶土（红黄青褐白）手工拉坯制作成型，大幅扩大“建水紫陶”的产业规模，会导致建水近郊的陶土大量挖掘，地表植被破坏，由于该地降水多，会加剧水土流失，选B。
【答案】10. A 11. B【点睛】复杂独特的工艺可以提升产品的知名度但会对产业规模造成一定的限制。
大幅发展与表土及表土覆盖物有关的产业，在湿润地区会导致水土流失，在干旱地区会导致土地荒漠化。
12. 阅读图文材料，完成下列要求。
材料一：桑树，落叶乔木。
喜温暖湿润气候，气温12℃以上开始萌芽，生长适宜温度25-30℃，气温降到12℃以下则停止生长。
耐旱，不耐涝。
耐瘠薄，对土壤的适应性强。
桑蚕是以桑叶为主要食料的吐丝结茧的经济昆虫，生长适宜温度为22～28℃，自孵化至吐丝结茧，24～25℃下约需24～26日，26～28℃下约需21～23日，结茧过程约需2～3日。
桑蚕茧可缫丝，蚕丝主要用于丝绸生产。
材料二：广西宜州市域面积3869平方公里，其中山地、丘陵面积占89.80％。
总人口62万，其中农业人口49万。
地处黔桂交通要冲，又是西南出海大通道的要地，种桑养蚕历史悠久。
近年来，江浙等东部地区种桑面积日渐缩小，随着国家实施“东桑西移”战略，广西宜州市的桑蚕产业突飞猛进，已成为“中国第一大桑蚕基地”，茧丝绸相关企业也已有20多家。
但目前宜州绝大多数养蚕户还是在自家院子里养殖，加工企业缫制出来的生丝大多为中低档，丝绸加工行业的关键技术和装备研发还有待提升，印染后整理技术、产品设计等水平较差。
如何完成从“东桑西移”到“东绸西移”的“破茧化蝶”问题一直困扰着宜州桑蚕产业。
下图示意宜州在广西的位置。
(1)与江浙相比，说明宜州有利于种桑养蚕的气候条件。
(2)从市场角度说明宜州桑蚕养殖业迅猛发展的原因。
(3)当地政府应如何促进从“东桑西移”到“东绸西移”的转变。
【答案】(1)与江浙相比，宜州纬度低，热量条件好，桑叶生长的时间长，一年内桑蚕养殖的次数多；雨季更长，更适宜桑树生长，以山地丘陵为主，利于排水；受伏旱、台风、寒潮等灾害性天气影响相对较小 (2)蚕茧产量大，国内外市场需求量大；土地、劳动力等成本低，市场竞争力强；交通运输便利，便于产品输出(3)引导农户进行规模化养殖，对养殖户进行技术培训和技术扶持，以提高桑蚕的产量和品质；整合桑蚕加工企业，加大产品推广力度，打造本地品牌；为企业引进高素质管理、技术和设计人才提供便利和支持；加强基础设施建设；为养殖户和加工企业提供融资支持（答案合理即可给分）【解析】（1）农作物生长的气候条件一般从光热水的组合及气象灾害方面分析。
与江浙相比，宜州纬度较低，热量条件好，桑叶生长的时间长，一年内桑蚕养殖的次数多；雨季更长，更适宜桑树生长，以山地丘陵为主，利于排水；受伏旱、台风、寒潮等灾害性天气影响相对较小。
（2）市场条件一般考虑产品质量、品牌知名度、价格、外运成本等。
近年，国内外市场对桑蚕产品需求量大；宜州土地、劳动力等成本低，市场竞争力强；交通运输便利，便于产品输出，这些条件促使宜州桑蚕业迅猛发展。
（3）从“东桑西移”到“东绸西移”是一种蚕茧产业的升级，当地政府需要引导农户进行规模化养殖，提高桑蚕的产量；对养殖户进行技术培训和技术扶持，以提高桑蚕的品质；加大宣传推广，打造本地品牌；为企业引进人才提供便利和支持；加强基础设施建设；为养殖户和加工企业提供融资支持等。
【点睛】产业转移是发生在不同经济发展水平的区域之间的一种重要的经济现象，是指在市场经济条件下，发达区域的部分企业顺应区域比较优势的变化，通过跨区域直接投资，把部分产业的生产转移到发展中区域进行，从而在产业的空间分布上表现出该产业由发达区域向发展中区域转移的现象。
产业转移对于区域经济结构调整及区域间经济关系的优化具有重要意义，并进而影响部分企业的战略决策。
产业转移影响因素：1.劳动力因素2.内部交易成本3.市场因素4.国家政策的调整5.原生产地用地紧张6.地价昂贵7.环境污染8.国际经济形势的变化等。
产业转移产生的影响：1.促进区域产业结构调整2.促进区域产业分工与合作3.改变了区域地理环境4.改变了劳动力就业的空间分布。
我国的产业转移主要是从劳动密集型产业、加工制造业和资源型加工业开始，产业转移从发达地区向欠发达地区渐次推进。