材料力学实验竞赛模拟题
材料力学模拟试题(一)

模拟试题(一)一、选择题(每题2分,共12分)1. 对图1-1所示梁,给有四个答案,正确答案是( c )。
(A )静定梁; (B )一次静不定梁; (C )二次静不定梁; (D )三次静不定梁。
2. 图1-2所示正方形截面偏心受压杆,其变形是( c )。
(A) 轴向压缩和斜弯曲的组合; (B) 轴向压缩、平面弯曲和扭转的组合; (C) 轴向压缩和平面弯曲的组合;(D) 轴向压缩、斜弯曲和扭转的组合。
3. 关于材料的冷作硬化现象有以下四种结论,正确的是(d ) (A )由于温度降低,其比例极限提高,塑性降低; (B )由于温度降低,其弹性模量提高,泊松比减小; (C )经过塑性变形,其弹性模量提高,泊松比减小; (D )经过塑性变形,其比例极限提高,塑性降低。
4. 细长压杆的( a ),则其临界应力cr σ越大。
(A )弹性模量E 越大或柔度λ越小;(B )弹性模量E 越大或柔度λ越大; (C )弹性模量E 越小或柔度λ越大;(D )弹性模量E 越小或柔度λ越小;5. 受力构件内一点的应力状态如图1-5所示,若已知其中一个主应力是5MPa ,则另一个主应力是( a )。
(A )85M Pa -;(B )85M Pa ;(C )75M Pa -;(D )75M Pa6. 已知图示AB 杆为刚性梁,杆1、2的面积均为A ,材料的拉压弹性模量均为E ;杆3的面积为A 3,材料的拉压弹性模量均为E 3,且E 3=2E 。
若使三根杆的受力相同,则有__________b_________。
(A ) A=A 3/2 (B ) A=A 3 (C ) A=2A 3 (D )A=4A 3二、填空题(共18分)1. (每空1分,共2分)平面弯曲时,梁的中性轴是梁的 横截面 和 中性层 的交线。
2.(每空2分,共4分)图示变截面梁,用积分法求挠曲线方程时,应分___4______段,有__8____个积分常数。
材料力学竞赛试题

8、T 形截面铸铁悬臂梁受力如图,轴 Z 为中性轴,横截面合理布置的方案应为( )
2、图示刚性梁 AB 由杆 1 和杆 2 支承,已知两杆的材料相同,长度不等,横截面积分
别为 A1 和 A2,若载荷 P 使刚梁平行下移,则其横截面面积( )。
F
A、A1〈A2 B、A1 〉A2 C、A1=A2 D、A1、A2 为任意
学号
姓名
3、悬臂梁 ACB 由铸铁材料制成,其许用拉应力[σt]=40MPa,许用压应力[σc]=160MPa, 载荷 FP=44kN,梁截面为 T 型,Iz=101.8×106mm4,尺寸如图(单位为 mm),(1)画 出梁的内力图;(2)试校核其强度。(20 分)
4、已知结构如下图(16 分)(1)、试列出求解 AB 梁弯曲变形所需的挠曲线近似微分 方程。(不必积分)(10 分)(2)、列出确定积分常数所需的全部条件。(6 分)
一、 选择题(每题 3 分,共 30 分)
A、提高到原来的 2 倍 B、提高到原来的 4 倍 C、降低到原来的 1/2 倍 D、降低到原来的 1/4 倍
1、工程构件要正常安全的工作,必须满足一定的条件。下列除( )项,其他各项是
必须满足的条件。 A、强度条件 B、刚度条件
C、稳定性条件 D、硬度条件
材料分别是( )
(A)a、b、c; (B)b、c、a;
y (D)
(C)b、a、c; (D)c、b、a。
5、以下正确的说法是: (A) 集中力作用处,剪力和弯矩值都有突变; (B) 集中力作用处,剪力有突变,弯矩不光滑; (C) 集中力偶作用处,剪力和弯矩值都有突变;
(D)集中力偶作用处,剪力图不光滑,弯矩有突变。
(2) 在最大允许载荷 q 作用下,梁中的最大剪应力。(30 分)
材料力学模拟考试题

材料力学模拟考试题1一、计算题(共6题,70分)1.(10分)图示水平放置圆截面直角钢杆(2ABC π=∠),直径mm 100d =,m l 2=,m N k 1q =,[]MPa 160=σ,试校核该杆的强度。
2.(10分)悬臂梁受力如图,试作出其剪力图与弯矩图。
3.(10分)图示三角架受力P 作用,杆的截面积为A ,弹性模量为E ,试求杆的内力和A 点的铅垂位移Ay δ。
4.(15分)图示结构中CD 为刚性杆,C ,D 处为铰接,AB 与DE 梁的EI 相同,试求E 端约束反力。
5. (15分) 作用于图示矩形截面悬臂木梁上的载荷为:在水平平面内P 1=800N ,在垂直平面内P 2=1650N 。
木材的许用应力[σ]=10MPa 。
若矩形截面h/b=2,试确定其尺寸。
6.(10分) 某塑性材料,其屈服极限为MPa 300s =σ,用其制成的构件中有图a 和b 所示的两种应力状态。
试按第四强度理论比较两者的危险程度(σ与τ的数值相等)。
二、是非题 (共2题,2分):(正确请划“√”,不正确的划“×)1.(1分)悬臂架在B 处有集中力P 作用,则AB ,BC 都产生了位移,同时AB ,BC 也都发生了变形。
( )(1) (2)2.(1分)微元体在受力过程中变成虚线所示,则其剪切应变为α案:( )三.填空题 (共3题,20分)1.(4分)设单元体的主应力为321σσσ、、,则单元体只有体积改变而无形状改变的条件是( ) ;单元体只有形状改变而无体积改变的条件是( )。
2.(3分)杆件的基本变形一般有( ) 、( ) 、( ) 、( ) 四种;而应变只有( ) 两种。
3.(6分)影响实际构件持久极限的因素通常有( ) 、( ) 、( ) ,它们分别用( ) 、( ) 、( ) 来加以修正。
4.(5分)平面弯曲的定义为( ) 。
5.(2分)低碳钢圆截面试件受扭时,沿( ) 截面破坏;铸铁圆截面试件受扭时,沿( ) 面破坏。
材料力学实验竞赛

材料力学实验试题(江苏科技大学 2008.08)1 碳钢制成的构件,某点的应力状态如图,已知0>x σ、0=y σ、0<xy τ、31=μ,若在该点贴直角应变花,定性分析得出的三个应变值为( )。
(A) 00>ε、045<ε、390εε≈(B) 00>ε、045>ε、090=ε(C)00>ε、045<ε、390εε-≈(D)00>ε、045>ε、390εε-≈ε答案:(D)2某材料的应力应变曲线1如图所示,弹性模量为E1,条件屈服极值为12.0σ。
在图上绘出另一种材料的应力应变曲线2,已知其E2< E1,12.022.0σσ>,并在图上标出22.0σ点的位置。
σ答案:σ3 三根不同材料的拉伸试件,所得的σ-ε曲线如图所示,则塑性最好的是杆 ,刚度最好的是杆 ,强度最好的是杆 。
4 低碳钢的拉伸应力—应变曲线如图所示,若加载至C 点,然后卸载,则应力回到零值的路径是沿(C )A :曲线cbao;B :曲线cbf(bf ∥oa);C :曲线ce(ce ∥oa);D :曲线cd(cd ∥oσ);5在电测实验中,应变片的灵敏系数为片K ,若将应变仪的灵敏系数旋钮指向任意值仪K ,在加载后,测点的实际应变ε与应变仪读数ds ε(设在半桥单片测量情况下)之间的关系为 。
答案:ds K K εε片仪=6 若静态应变仪标定的应变片灵敏系数比实际所用的应变片灵敏系数小时,则应变仪的读数比实际应变值是大还是小?作简单说明。
7由同一种材料分别制成的短试件(l=5d)和长试件(l=10d),则两者的延伸率之间的关系为 。
答案:105δδ>8 拉伸试件的延伸率%100%1001⨯∆=⨯-=l l l l l δ,而试件的纵向线应变ll∆=ε,可见, δ与ε的表达式相同,因此是否可说,延伸率就等于试件的纵向线应变?答案:不能,ε是一点处的线应变,当在全长l 范围内为均匀变形时才有意义,且其伸长∆l 包含弹性变形和塑性变形。
材料力学模拟试题-1(附答案)

d 4
32
(2
分) ;而对竖直形心轴 y 的惯性矩 I y
y
5d 4 (2 分) 。 32
z
F
d
d
1m
1m
3. 分)上右图中外伸梁的截面为 b h 20 mm 60 mm 的矩形,载荷 F 2 kN 可在全梁移动,则梁 (4 中的最大弯曲正应力 max 167 MPa (2 分) ,最大切应力 max 2.5 MPa (2 分) 。 4. 分) (4 下左图直径为 d 的实心圆轴两端固定, 在轴中间承受扭矩 m 作用, 材料的剪切弹性模量为 G , 轴长为 2L , 则圆轴两端的力偶矩 m A
RL 500 66.7 0.167 mm EA1 200 10 3
杆件中间截面向右移动了 u 0.167 mm (5 分) 。
三. (10 分) 画出图示梁的剪力图和弯矩图。
q
m qa2
2a
a
RA
解:求支反力
RB
mA 0
R B 2a
3qa (1 分) 2 3qa qa (1 分) R A 2qa RB 2qa 2 2 RB
d1
。
B
d2
m
A
C
a
填空题4图
a
5. 分) 矩形截面梁受一定的横向载荷作用,若将其横截面的高度增加一倍,其余条件不变,则梁 (5 的最大正应力变化到原来的 。最大挠度变化到原来的 。
二. (15 分)如图所示结构中的横梁为刚性梁,两圆形竖杆的长度和材料均相同,直径 d 20 mm , 材料的许用拉应力 [ t ] 35 MPa 。不计刚性梁的重量,求结构能承受的最大载荷 Fmax 。
材料力学试题带参考答案解析
1 / 20材料力学模拟试题(一)解答一、 一、 填空题(每小题5分,共10分)1、 如图,若弹簧在Q 作用下的静位移mm st 20=D ,在Q 自由下落冲击时的最大动位移mm d 60=D ,则弹簧所受的最大冲击力d P 为:3Q 。
2、 在其它条件相同的情况下,用内直径为d 的实心轴代替直径d 的实心轴,若要使轴的刚度不变(单位长度的扭转角j 相同),则实心轴的外径D = d 42 。
二、 二、 选择题(每小题5分,共10分)1、 图示正方形截面杆承受弯扭组合变形,图示正方形截面杆承受弯扭组合变形,在进行强度计算时,在进行强度计算时,其任一截面的危险点位置有四种答案:置有四种答案:(A)截面形心;截面形心; (B )竖边中点A 点;点;(C )横边中点B ;(D )横截面的角点D 点。
点。
正确答案是:正确答案是:C2、 若压杆在两个方向上的约束情况相同;若压杆在两个方向上的约束情况相同;且且z y m m >。
那么该正压杆的合理截面应满足的条件有四种答案:足的条件有四种答案:(A );z y I I =(A );z y I I >(A );z y I I <(A )y z l l =。
正确答案是:。
正确答案是: D三、 三、 计算题(共80分) 1、(15分)图示拐轴受铅垂载荷P 作用。
试按第三强度理论确定AB 轴的直径d 。
已知:P=20KN,[]MPa 160=s 。
解:AB 梁受力如图:梁受力如图: )(280014.020000Nm M n =´= AB 梁内力如图:梁内力如图:)(300015.020000max Nm M =´=危险点在A 截面的上下两点截面的上下两点由圆轴弯扭组合第三强度理论的强度条件:由圆轴弯扭组合第三强度理论的强度条件:[])(64)(0639.01016014.3101.4321016032/28003000363632222mm m d d W M M n ==´´´´³\´=£+=+s pM 图0.14PM x 图2、图示矩形截面钢梁,A 端是固定铰支座,B 端为弹簧支承。
材料力学全国比赛试题

3、图4-1 是一个吊装设备的示意图。水平平面内的 直角刚架由塑性材料的实心圆杆制成,其两个短杆的端 面A 和G 牢固地固定在竖直的刚性壁上。吊装的重物一 直不变,但可以吊挂在刚架的任意部位。已知刚架各部 分圆杆横截面的直径均为d ,其他尺寸如图所示。材料 的弹性模量为E ,泊松比 ν = 0.25。不考虑刚架的自重。
(3) 在图示AB 区段的中截面J 处,如果要利用电测法 测算出在各种吊挂情况下该截面的全部内力,同时要求应 变片要用得尽可能地少,效果要尽可能地好,在理论上应 该贴多少个应变片?应在该截面外圆的何处粘贴?沿着什 么方向粘贴?如何利用这些应变片的读数来求得J 截面上 各个内力的数值?
首先,可以由直觉确定,当挂钩位于刚架左边角点 B 处时, A 截面最上点沿轴线方向上的应变为εmax 。
(1) 暂不考虑金属片的变形,如果在匀速转动时O′处轴 套向上升起的高度 H = L 是额定的工作状态,那么相应的 转速ω0是多少?
(2) 当转速恒定于ω0 时,只考虑金属片弯曲变形的影 响,试计算图示角度 ∠OAO′相对于把金属片视为刚体的 情况而言的变化量。
2023年材料力学竞赛答案
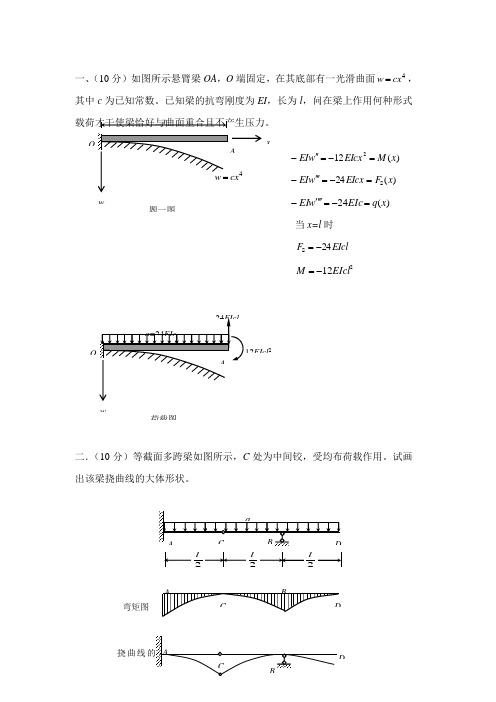
一、(10分)如图所示悬臂梁OA ,O 端固定,在其底部有一光滑曲面4cx w =,其中c 为已知常数。
已知梁的抗弯刚度为EI ,长为l ,问在梁上作用何种形式)(122x M EIcx w EI =-=''-)(24S x F EIcx w EI =-='''-)(24x q EIc w EI =-=''''-当x=l 时 EIcl F 24S -= 212EIcl M -=二.(10分)等截面多跨梁如图所示,C 处为中间铰,受均布荷载作用。
试画出该梁挠曲线的大体形状。
弯矩图挠曲线4cx Ax w 题一图w荷载图EIcl 2三、(10分)图示梁AB 弯曲刚度为EI ,抗弯截面系数为W ,B 端由拉压刚度为EA 的杆BD 连接,已知231Aa I =。
若重量为P 的重物以水平速度v 冲击在梁的中点C 处,求杆BD 和梁AB 内的最大冲击动应力。
EIPa EA aPEI a P 422148)2(33=⋅⋅+=∆st APA P 22st ==杆σWPaW aP 242st =⋅=梁σ 3224gPa EIv g v K =∆=std 杆杆st d d σσK = 梁梁st d d σσK =四.(10分)图示钢筋AD 长度为3a ,总重量为W ,对称地放置于宽为a 的刚性平台上。
试求钢筋与平台间的最大间隙δ。
设EI 为常量。
题三图EI Wa EI aa W EI a a W EI ql EI l M 115219384352166384521634442e =-⨯=-⨯=δ五.(10分)以绕带焊接而成的圆管如图所示,焊缝为螺旋线。
管的内径d =300mm ,壁厚t =1mm ,内压p =0.5MPa 。
求沿焊缝斜面上的正应力和切应力。
焊缝斜面上一点单元体MPa 5.37101410300105.04336=⨯⨯⨯⨯⨯==--t pd x σ MPa 752==tpdy σ,0=xy τ 沿焊缝斜面上的正应力和切应力MPa53)80cos(2755.372755.372sin 2cos 22=⎥⎦⎤⎢⎣⎡--++=--++=ατασσσσσαxy yx yx MPa 5.18)80sin(2755.372cos 2sin 2=⎥⎦⎤⎢⎣⎡--=--=ατασσταxy yxy σ 26a aW 26a aW W q =六.(10分)两根钢轨铆接成组合梁,其连接情况如图所示。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
材料力学实验竞赛模拟题
(中国矿业大学)
一、试说明铸铁试件单轴拉伸、单轴压缩、扭转破坏的断口形状及破坏原因。
二、用标距50 mm 和100 mm 的两种拉伸试样,测得低碳钢的屈服极限分别为s1σ、
s2σ,伸长率分别为5δ和10δ。
比较两试样的结果,则有以下结论,其中正确的是哪一个?
(A) s2s1σσ<,105δδ>; (B) s2s1σσ<,105δδ=;
(C) s2s1σσ=,105δδ>; (D) s2s1σσ=,105δδ=。
三、三根圆棒试样,其面积和长度均相同,进行拉伸试验得
到的εσ-曲线如图所示,其中强度最高、刚度最大、塑性最好的
试样分别是___________。
(A) a , b , c (B) b , c , a
(C) c , b , a (D) c , a , b
四、测力传感器的圆筒表面沿径向和轴向分别贴有8枚应变片,接成全桥如图所示,则力F 与应变读数εd 之间的关系为__________。
(A) )1(2μ-=EA F d ε (B) )
1(2μ+=EA F d ε (C) )1(4μ-=
EA F d ε (D) )
1(4μ+=EA F d ε
五、在材料伸长率%100001⨯-=l l l δ的计算公式中,1l 的量取与断口部位有关。
若断口 发生在0l 之外或在0l 的两端,而与其头部之距离等于或小于 时,则实验无效,应重做。
若断口到邻近标距点的距离小于 ,则必须经过折算,将断口移中,具体方法如下: 。
六、低碳钢Q235的屈服极限MPa 235s =σ。
当拉伸应力达到MP a 320=σ时,测得试件的应变为3106.3-⨯=ε。
然后卸载至应力MP a 260=σ,此时测得试件的应变为3103.3-⨯=ε。
试求:
(1) 试件材料的弹性模量E ;
(2) 以上两种情形下试件的弹性应变e ε和塑性应变p ε。
七、如图所示的悬臂梁,在同一横截面
的上下表面已粘贴有四枚相同的应变片,梁
端部受有力F 的作用。
试设计相应的桥路联
接方式,以分别测出F 引起的弯曲应变和压
应变,并给出计算公式。
(不计温度效应,
桥臂可接入固定电阻)
八、图示一圆轴,在其两端除受扭转力偶矩e1M 外,还受有轴向力F 和弯曲力偶矩e2M 作用。
欲用4枚应变片测出该圆轴的扭转力偶矩e1M ,而排除轴向力F 和弯曲力偶矩e2M 的影响。
试设计应变片的布置方式、桥路联接图,并给出分析计算公式。
已知圆轴直径d ,弹性模量E 及泊松比μ。
九、用直角应变花测试平面应力状态下的主应力,已知E 、μ、︒0ε、︒45ε、︒90ε,推导主应力大小和主方向的计算公式。
十、在受扭圆轴表面上一点K 处的线应变值为:610375-⨯=u ε,610500-⨯=v ε。
若已知GPa 200=E ,25.0=μ,直径mm 100=D ,试求作用于轴上的外力偶矩e M 的值。
【解答】
一、解:单轴拉伸时,沿横截面破坏,是拉坏的;
单轴压缩时,沿︒45斜截面破坏,是剪坏的;
扭转时,沿︒45螺旋面破坏,是拉坏的。
二、解:C
三、解:C
四、解:B
五、直径的两倍时;3/0l ;略
六、解:(1) GPa 200103.0MPa 603
=⨯=∆∆=
-εσE
(2) 当拉伸应力达到MP a 320=σ时 3e 106.1-⨯==E σ
ε, 3e p 102-⨯=-=εεε
卸载至应力MP a 260=σ时 3p 102-⨯=ε, 3p e 103.1-⨯=-=εεε
七、解:按图(a)所示方式接桥,F 引起的弯曲应变等于输出读数除以4 按图(b)所示方式接桥,F 引起的压应变等于输出读数除以2
八、解:在圆轴的同一条母线上沿与轴线成︒±45方向贴4枚应变片,按图示方式接桥,设应变仪输出读数为读ε。
由 t e114W M E με+=读
得 )1(64π3e1με+=读Ed M
九、解:⎥⎦
⎤⎢⎣⎡-+--±++-=︒︒︒︒︒︒290452045900231)()(21)(211εεεεμεεμμσσE )
()(2tan 45900450900︒︒︒︒︒︒----=εεεεεεα 十、解:首先在K 点处取一单元体,其应力状态如图所示
α
τατασσσσσσατατασσσσσα2sin )90(2sin )90(2cos 222sin )(2sin )(2cos 2290x x y
x y
x u x x y
x y
x u -=-︒--︒-++===----++=-︒⊥ 由广义胡克定律 610375)1(2sin )]2sin (2sin [1)(1-⊥⨯=+=--=-=
ματατματμσσεE
E E x x x u u u 由此可得 MPa 602sin =ατx 用同样的方法,由610500-⨯=v ε可求得 MPa 802cos =ατx
因此 MPa 1008060)2cos ()2sin (2222=+=+=αταττx x x 由 t
e W M x =τ 得 m kN 6.19t e ⋅==W M x τ。
