江西省赣州市2014-2015学年高二上学期期末联考数学(文)试题 Word版含答案
试题精选_江西省赣州市2014-2015学年高二上学期十二县(市)期中联考语文调研试卷_精校完美版

江西省赣州市2014-2015学年高二上学期十二县(市)期中联考语文试题第Ⅰ卷一、(每小题3分,共18分)1.下列词语中,加点字读音全都正确....的一项是A.迤.逦(yǐ)提.防(dī) 朔.风(sù) 不省.人事(xǐng)B.央浼.(miǎn) 熟稔.(rěn) 傩.神(nuó) 家给.人足(jǐ)C.尴尬.(gà) 泥淖.(nào) 上乘.(chéng) 涸.辙之鲋(hé)D.蒿.草(hāo) 叨.扰(tāo) 坍.塌(tān) 如椽.大笔(yuán)2.下列词语中,没有..错别字的一项是A.撰写庇佑噩梦墨守成规 B.通宵惦量辐射食不果腹C.讥诮连袂逋逃殒身不恤 D.岑寂案牍蕴籍不落言荃3.下列各句中,加点成语使用恰当..的一项是A.得知将要征用村里的土地建新开发区的消息,村民们为了多得拆迁补偿款,突击装修、非法建房在村里蔚然成风....。
B.碳酸饮料含磷酸,它会潜移默化....地影响人体骨骼。
常喝碳酸饮料,大量磷酸的摄入会影响钙的吸收,引起钙、磷的比例失调,影响骨骼健康。
C.随着经济的发展,人们的腰包越越鼓,借助适度的物质消费以提升生活质量本无.可厚非...,但若消费旨在炫富,精神境界就未免太低了。
D.这是罗森行文的一贯风格——切中要害但并不妨碍生机盎然,学富五车....但决不“掉书袋”,文笔犀利而又不失优雅。
4.下列各句,没有..语病的一项是A.《中国通史》共拍摄了100集,再现了中国上下五千年的浩瀚历史图景和变迁,全面而系统地展示了丰富灿烂的包括敦煌文化在内的中华文明。
B. 电视节目《爸爸去哪儿》的热播, Kimi、王诗龄、田雨橙、天天等“星二代”的“同款服饰”顿成热销品,有文化品味的童装也成了服饰行业的“新增长点”。
C.日前颁布的《国务院关于促进民航业发展的若干意见》明确把民航业定为战略性产业,把发展民航业提升为国家战略,这将对中国民航的发展起到巨大的推动作用。
2014-2015学年高一上学期期末考试数学试题(文科班)

2014-2015学年高一上学期期末考试数学试题(文科班)一、选择题(每小题4分,共40分)1.已知集合{}1,0,1-=A ,{}11<≤-=x x B 则B A ⋂等于( )A. {}0B. {}1-C. {}0,1-D. {}1,0,1-2.若,54cos ,53sin -==αα则在角α终边上的点是( ) A. )3,4(- B. )4,3(- C. )3,4(- D. )4,3(-3.已知函数的定义域为[]2,0,值域为[]4,1,则函数的对应法则可以为( )A. x y 2=B. 12+=x yC. xy 2= D. x y 2log =4.已知)(x f 是偶函数,且0>x 时,ax x x f +=2)(,若2)1(=-f ,则)2(f 的值是( )A. -1 B . 1 C . 3 D . 65.函数),0,0(),sin()(R x A x A x f ∈>>+=ωϕω的部分图象如右图所示,则函数的表达式为( ) A. )834sin(4)(ππ+=x x f B. )834sin(4)(ππ-=x x f C. )438sin(4)(ππ-=x x f D. )88sin(4)(ππ+=x x f 6.若0cos 2sin =-αα,则αα2sin cos 12+的值为( ) A . -2 B . -1 C . 1 D . 27.若函数)1(log )(++=x a x f a x 在[]1,0上的最大值和最小值之和为a ,则a 的值是( )A. 4B.41 C. 2 D. 21 8.已知0>ω, πϕ<<0,直线4π=x 和45π=x 是函数B x A x f ++=)sin()(ϕω图像的两条相邻的对称轴,则ϕ为( ) A. 2π B. 3π C. 4π D. 43π 9.已知函数x x m x f sin 3sin log )(2+-=在R 上的值域为[]1,1-,则实数m 的值为( ) A . 1 B . 2 C . 3 D . 4二、填空题(每小题4分,共20分)11.对于函数m x y =,若21)41(=f ,则m =________. 12.已知31)4cos(-=-απ,则)43cos(απ+的值为____ ____. 13.函数)4sin()(x x f -=π的单调增区间为________.14.已知函数⎥⎦⎤⎢⎣⎡-∈=2,2,sin )(ππx x x f ,若0)21(cos )(sin =-+ααf f ,则=⋅ααcos sin ____________.15.已知函数⎩⎨⎧≤++>=m x x x m x x f ,24,2)(2,若函数x x f x F -=)()(恰有三个不同的零点, 则实数m 的取值范围是____________.三、解答题(本大题共4题,共40分)17.已知函数)0,0(,11)(>>-=x a ax x f . (1)若)(x f 在[]2,1上的最小值为41,求实数a 的值; (2)若存在),0(,+∞∈n m ,使函数)(x f 在[]n m ,上的值域为[]m n --,,求实数a 的取值范围;19. 设是R 上的奇函数,且当时,,. (1)若1)1(=f ,求的解析式;(2)若,不等式0)14()2(>++⋅x x f k f 恒成立,求实数的取值范围; (3)若的值域为,求的取值范围.。
江西省赣州市四所重点中学2013-2014学年高二数学上学期期末联考试题 文
赣州市四所重点中学(赣州一中、平川中学、瑞金中学、赣州三中) 2013~2014学年度第一学期期末联考试卷高二数学试题(文科)一、选择题(每小题5分,共50分。
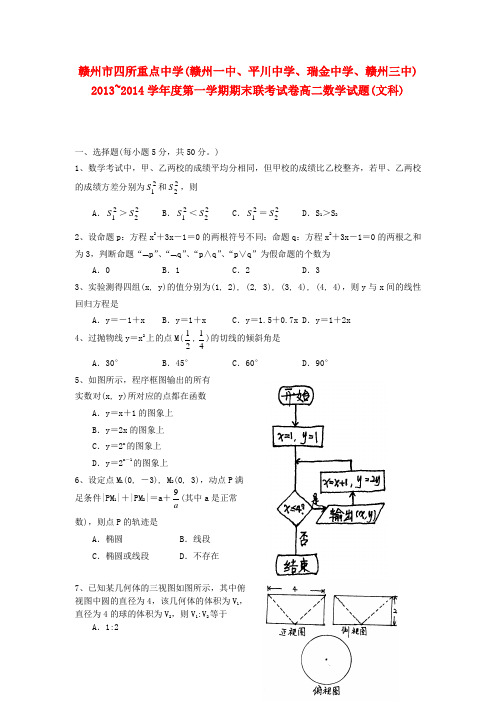
)1、数学考试中,甲、乙两校的成绩平均分相同,但甲校的成绩比乙校整齐,若甲、乙两校的成绩方差分别为21S 和22S ,则 A .21S >22S B .21S <22S C .21S =22S D .S 1>S 2 2、设命题p :方程x 2+3x -1=0的两根符号不同;命题q :方程x 2+3x -1=0的两根之和为3,判断命题“⌝p ”、“⌝q ”、“p ∧q ”、“p ∨q ”为假命题的个数为A .0B .1C .2D .33、实验测得四组(x, y)的值分别为(1, 2), (2, 3), (3, 4), (4, 4),则y 与x 间的线性回归方程是A .y =-1+xB .y =1+xC .y =1.5+0.7xD .y =1+2x4、过抛物线y =x 2上的点M(21,41)的切线的倾斜角是 A .30° B .45° C .60° D .90° 5、如图所示,程序框图输出的所有实数对(x, y)所对应的点都在函数A .y =x +1的图象上B .y =2x 的图象上C .y =2x 的图象上D .y =2x -1的图象上6、设定点M 1(0, -3), M 2(0, 3),动点P 满足条件|PM 1|+|PM 2|=a +a9(其中a 是正常 数),则点P 的轨迹是A .椭圆B .线段C .椭圆或线段D .不存在7、已知某几何体的三视图如图所示,其中俯视图中圆的直径为4,该几何体的体积为V 1,直径为4的球的体积为V 2,则V 1:V 2等于A .1:2B .2:1C .1:1D .1:48、设A, B 两点的坐标分别为(-1, 0), (1, 0), 条件甲:²>0;条件乙:点C 的坐 标是方程)0(13422≠=+y y x 的解,则甲是乙的 A .充分不必要条件 B .必要不充分条件C .充要条件D .既不充分也不必要条件9、已知直线l 1: 4x -3y +6=0和直线l 2: x =-1,抛物线y 2=4x 上一动点P ,P 到直线l 1和直线l 2的距离之和的最小值是A .2B .3C .511 D .1637 10、已知函数f(x)=-x 3+ax 2-4在x =2处取得极值,若m, n ∈[-1, 1],则f(m)+f ' (n)的最小值为A .-13B .-15C .10D .15二、填空题(每小题5分,共25分)11、某学校共有师生2400人,现用分层抽样方法,从所有师生中抽取一个容量为160的样本,已知从学生中抽取的人数为150,那么该学校的教师人数是 。
江西省赣州市2014-2015学年高二上学期期末联考数学(理)试卷及答案

江西省赣州市2014~2015学年度第一学期期末联考高二数学(理科)试题一、选择题1~5.ACBAD ; 6~10.BCDBC 11~12.AC二、填空题13.10; 14.83; 16.3(1)n n +. 三、解答题17.解:由题意:232p x -≤-≤因为15x ≤≤,所以非:1p x <或5x >……………………………………………………3分 :11q m x m -≤≤+所以非:1q x m <-或1x m >+………………………………………………………………6分又因为非p 是非q 的充分不必要条件,所以1115m m -≥⎧⎨+≤⎩……………………………………8分所以24x ≤≤…………………………………………………………………………………10分18.解:(1)设(,)x y 表示一个基本事件,则抛掷两次骰子包括:(1,1),(1,2),(1,3),(1,4),(1,5),(1,6),(2,1)L L (6,5),(6,6),共36个基本事件……………………………2分用A 表示事件“3x y +≤”,则A 包含(1,1),(1,2),(2,1),共3个基本事件…………3分 所以31()3612P A ==,即事件“3x y +≤”的概率为112…………………………………6分 (2)用B 表示事件“2x y -=”,则B 包含(1,3),(3,1),(2,4),(4,2),(3,5),(5,3),(4,6),(6,4),共8个基本事件……………………………………………………………9分 所以82()369P B ==,即事件“2x y -=”的概率为29………………………………12分 19.解:(1)1(0.020.0160.0060.004)100.54-+++⨯=……………………………2分 所以27500.54n ==人………………………………………………………………………4分 (2)成绩在区间[)40,50的学生人数是:500.042⨯=人……………………………5分成绩在区间[)50,60的学生人数是:500.063⨯=人……………………………………6分设成绩在区间[)40,50的学生分别是12,A A ,成绩在区间[)50,60的学生分别是123,,B B B ,从成绩在[)40,60的学生中随机选取2人的所有结果有:12(,)A A ,11(,)A B ,12(,)A B ,13(,)A B ,21(,)A B ,22(,)A B ,23(,)A B ,12(,)B B ,13(,)B B ,23(,)B B 共10种情况…………………………………………………………………………8分至少有1人成绩在[)40,50内的结果有:12(,)A A ,11(,)A B ,12(,)A B ,13(,)A B ,21(,)A B ,22(,)A B ,23(,)A B 共7种情况………………………………………………………………10分所以至少有1人成绩在[)40,50内的概率710P =…………………………………………12分 20.解:过点(1,0)A -且斜率为(0)k k ≠的直线方程为(1)y k x =+……………………1分将(1)y k x =+代入24y x =,化简得2222(24)0k x k x k +-+=………………………4分设1122(,),(,)M x y N x y ,则有212242k x x k-+=,121x x =……………………………6分 又2114y x =,2224y x =,所以221216y y =……………………………………………………7分 因为120y y >,所以124y y =………………………………………………………………8分 从而有21212284(1)(1)k FM FN x x y y k-⋅=--+=uuu r uuu r ………………………………………9分12(1)(1)FM FN x x ⋅==++uuu r uu u r 24k=…………………10分 因为cos ,FM FN FM FN FM FN⋅<>=uuu r uuu r uuu r uuu r uuu r uuu r ,所以22284142k k k -=-⨯…………………………11分 解得12k =±…………………………………………………………………………………12分 21.(1)证明:因为四边形ABCD 为菱形,60ABC ∠=,所以ABC △为正三角形……………………………………………………………………1分因为E 为BC 的中点,所以AE BC ⊥……………………………………………………2分又BC AD ∥,所以AE AD ⊥……………………………………………………………3分因为PA ⊥平面ABCD ,AE ⊂平面ABCD ,所以PA AE ⊥………………………………………………………………………………4分而PA ⊂平面PAD ,AD ⊂平面PAD 且PA AD A =,所以AE ⊥平面PAD .又PD ⊂平面PAD ……………………………………………5分所以AE PD ⊥……………………………………………………………………………6分(2)解法一∵PA ⊥平面ABCD ,PA ⊂平面PAC ,∴平面PAC ⊥平面ABCD ………………………………………………………………7分过E 作EO AC ⊥于O ,则EO ⊥平面PAC ,过O 作OS AF ⊥于S ,连接ES ,则ESO ∠为二面角E AF C --的平面角……………8分在Rt AOE △中,3sin 30EO AE =⋅=3cos302AO AE =⋅=, 又F 是PC 的中点,在Rt ASO △中,32sin 45SO AO=⋅= (10)分又SE ===11分 在Rt ESO △中,cos SO ESO SE∠===12分 解法二:由(1)知AE AD AP ,,两两垂直,以A 为坐标原点,建立如图所示的空间直角坐标系,又E F ,分别为BCPC ,的中点,所以(000)10)0)(020)A B C D-,,,,,,,,,,1(002)0)12P E F ⎫⎪⎪⎭,,,,,,,……………………7分所以31(300)12AE AF ⎛⎫== ⎪⎪⎭,,,,,. 设平面AEF 的一法向量为111()m x y z =,,,则00m AE m AF⎧⋅=⎪⎨⋅=⎪⎩,所以11110102x y z =++=……………………………………………8分 取11z =-,则(021)m =-,,………………………………………………………………9分D BE CF A O S P∵BD AC ⊥,BD PA ⊥,PA AC A =,∴BD ⊥平面AFC …………………………………………………………………………10分故BD 为平面AFC 的一法向量又(0)BD =,,所以cos 5m BDm BD m BD ⋅<>===⋅,11分 因为二面角E AF C --为锐角,12分 22.解:(1)依题意,c =1b =………………………………………………………2分 所以a =………………………………………………………………………3分故椭圆C 的方程为2213x y +=………………………………………………………………5分 (2)①当直线l 的斜率不存在时,由22113x x y =⎧⎪⎨+=⎪⎩解得1,x y==…………………6分 不妨设A,(1,B , 所以122233222k k ++=+=…………………………………………………………8分 ②当直线l 的斜率存在时,设直线l 的方程为(1)y k x =-.将(1)y k x =-代入2213x y +=, 整理化简得,2222(31)6330k x k x k +-+-=………………………………………9分 设11(,)A x y ,22(,)B x y ,则2122631k x x k +=+,21223331k x x k -=+……………………10分 又11(1)y k x =-,22(1)y k x =-……………………………………………………11分所以12211212[2(1)](3)[2(1)](3)3()9k x x k x x x x x x ---+---=-++ 121212122(42)()6123()9kx x k x x k x x x x -++++=-++222222223362(42)6123131336393131k k k k k k k k k k k -⨯-+⨯++++=--⨯+++222(126)2126k k +==+……………………12分 所以122k k +=。
高中高二数学上学期第二次月考试卷 文(含解析)-人教版高二全册数学试题

2014-2015学年某某省某某市安吉县上墅私立高中高二(上)第二次月考数学试卷(文科)一、选择题:(本大题共10小题,每小题3分,共30分.)1.在△ABC中,“A=”是“cosA=”的()A.充分而不必要条件 B.必要而不充分条件C.充分必要条件 D.既不充分也不必要条件2.已知命题p:∃x∈R,x﹣2>0,命题q:∀x∈R,>x,则下列说法中正确的是() A.命题p∨q是假命题 B.命题p∧q是真命题C.命题p∨(¬q)是假命题 D.命题p∧(¬q)是真命题3.直线x﹣2y+2=0经过椭圆的一个焦点和一个顶点,则该椭圆的离心率为()A. B. C. D.4.若直线(m+2)x+3y+3=0与直线x+(2m﹣1)y+m=0平行,则实数m=() A.﹣或1 B. 1 C. 1或2 D.﹣5.直线2x+3y+1=0与直线4x+my+7=0平行,则它们之间的距离为() A. 4 B. C. D.6.设l,m是不同的直线,α,β,γ是不同的平面()A.若l⊥α,l⊥m,则m∥α B.若l⊂α,m⊂β,α∥β,则l∥mC.若l∥α,m⊥α,则l⊥m D.若α∩β=l,l⊥γ,m⊥β,则m∥γ7.过P(2,0)的直线被圆(x﹣2)2+(y﹣3)2=9截得的线段长为2时,直线l的斜率为()A. B. C.±1 D.8.若双曲线的离心率为,则其渐近线方程为()A. y=±2x B. C. D.9.直线l:x+y﹣4=0与圆C:x2+y2=4的位置关系是()A.相交过圆心 B.相交不过圆心 C.相切 D.相离10.下列结论正确的是()A.命题“若a>b>0,则a2>b2”的逆命题是假命题B.若函数f(x)=sinx,则函数f(x)为周期函数的逆命题是真命题C.向量,的夹角为钝角的充要条件是•<0D.“x2>2”是“x2﹣3x+2≥0”的充分不必要条件二、填空题:(本大题共7小题,每小题3分,共21分.)11.由命题“存在x∈R,使x2+2x+m≤0”是假命题,则实数m的取值X围为.12.已知命题p:m<0,命题q:∀x∈R,x2+mx+1>0成立,若“p∧q”为真命题,则实数m 的取值X围是.13.两直线l1:ax+2y﹣1=0,l2:(a﹣1)x+ay+1=0垂直,则a=.14.两圆x2+y2﹣4x+6y=0和x2+y2﹣6x=0的连心线方程为.15.已知动圆M与圆C1:(x+3)2+y2=9外切且与圆C2:(x﹣3)2+y2=1内切,则动圆圆心M的轨迹方程是.16.一个几何体的三视图如图所示(单位:m),则该几何体的体积为m3.17.下列四个命题:①“∃x∈R,x2﹣x+1≤0”的否定;②“若x2+x﹣6≥0,则x>2”的否命题;③在△ABC中,“A>30°”是“sinA>”的充分不必要条件④“函数f(x)=tan(x+φ)为奇函数”的充要条件是“φ=kπ.(k∈Z)”,其中真命题的序号是.三、解答题:(本大题共5小题,共49分.)18.设p:实数x满足x2+2ax﹣3a2<0(a>0),q:实数x满足x2+2x﹣8<0,且q是p的必要不充分条件,求a的取值X围.19.求满足下列条件的椭圆方程:(1)长轴在x轴上,长轴长等于12,离心率等于;(2)椭圆经过点(﹣6,0)和(0,8);(3)椭圆的一个焦点到长轴两端点的距离分别为10和4.20.如图,正方形ACDE所在的平面与平面ABC垂直,M是CE和AD的交点,AC⊥BC,且AC=BC.(1)求证:AM⊥平面EBC;(2)求直线AB与平面EBC所成角的大小.21.已知在平面直角坐标系中的一个椭圆,它的中心在原点,左焦点为,且过点D(2,0).(1)求该椭圆的标准方程;(2)设点,若P是椭圆上的动点,求线段PA的中点M的轨迹方程.22.已知圆C:x2+y2=4和直线l:3x+4y+12=0,点P是圆C上的一动点,直线与坐标轴的交点分别为点A、B,(1)求与圆C相切且平行直线l的直线方程;(2)求△PAB面积的最大值.2014-2015学年某某省某某市安吉县上墅私立高中高二(上)第二次月考数学试卷(文科)参考答案与试题解析一、选择题:(本大题共10小题,每小题3分,共30分.)1.在△ABC中,“A=”是“cosA=”的()A.充分而不必要条件 B.必要而不充分条件C.充分必要条件 D.既不充分也不必要条件考点:必要条件、充分条件与充要条件的判断.专题:简易逻辑.分析:根据充分必要条件的定义结合三角形的性质,分别证明充分性和必要性,从而得到答案.解答:解:在△ABC中,若A=,则cosA=,是充分条件,在△ABC中,若cosA=,则A=或A=,不是必要条件,故选:A.点评:本题考查了充分必要条件,考查了三角形中的三角函数值问题,是一道基础题.2.已知命题p:∃x∈R,x﹣2>0,命题q:∀x∈R,>x,则下列说法中正确的是() A.命题p∨q是假命题 B.命题p∧q是真命题C.命题p∨(¬q)是假命题 D.命题p∧(¬q)是真命题考点:复合命题的真假.专题:简易逻辑.分析:容易判断命题p是真命题,q是假命题,所以根据p∨q,p∧q,¬q的真假和p,q的关系即可找出正确选项.解答:解:∃x∈R,x﹣2>0,即不等式x﹣2>0有解,∴命题p是真命题;x<0时,无解,∴命题q是假命题;∴p∨q为真命题,p∧q是假命题,¬q是真命题,p∨(¬q)是真命题,p∧(¬q)是真命题;∴D正确.故选D.点评:考查真命题,假命题的概念,以及p∨q,p∧q,¬q的真假和p,q真假的关系.3.直线x﹣2y+2=0经过椭圆的一个焦点和一个顶点,则该椭圆的离心率为()A. B. C. D.考点:椭圆的简单性质.专题:计算题.分析:直线x﹣2y+2=0与坐标轴的交点为(﹣2,0),(0,1),依题意得.解答:直线x﹣2y+2=0与坐标轴的交点为(﹣2,0),(0,1),直线x﹣2y+2=0经过椭圆的一个焦点和一个顶点;故.故选A.点评:本题考查了椭圆的基本性质,只需根据已知条件求出a,b,c即可,属于基础题型.4.若直线(m+2)x+3y+3=0与直线x+(2m﹣1)y+m=0平行,则实数m=() A.﹣或1 B. 1 C. 1或2 D.﹣考点:直线的一般式方程与直线的平行关系.专题:直线与圆.分析:由直线的平行可得m的方程,解得m代回验证可得.解答:解:∵直线(m+2)x+3y+3=0与直线x+(2m﹣1)y+m=0平行,∴(m+2)(2m﹣1)﹣3×1=0,解得m=﹣或1经验证当m=1时,两直线重合,应舍去,故选:D点评:本题考查直线的一般式方程和平行关系,属基础题.5.直线2x+3y+1=0与直线4x+my+7=0平行,则它们之间的距离为() A. 4 B. C. D.考点:两条平行直线间的距离.专题:直线与圆.分析:通过直线的平行求出m,然后利用平行线之间的距离求解即可.解答:解:直线2x+3y+1=0与直线4x+my+7=0平行,所以m=6,直线4x+my+7=0化为直线4x+6y+7=0即2x+3y+3.5=0,它们之间的距离为:d==.故选:C.点评:本题考查两条平行线之间是距离的求法,基本知识的考查.6.设l,m是不同的直线,α,β,γ是不同的平面()A.若l⊥α,l⊥m,则m∥α B.若l⊂α,m⊂β,α∥β,则l∥mC.若l∥α,m⊥α,则l⊥m D.若α∩β=l,l⊥γ,m⊥β,则m∥γ考点:空间中直线与平面之间的位置关系.专题:空间位置关系与距离.分析:利用空间中线线、线面、面面间的位置关系求解.解答:解:若l⊥α,l⊥m,则m∥α或m⊂α,故A错误;若l⊂α,m⊂β,α∥β,则l与m平行或异面,故B错误;若l∥α,m⊥α,则由直线与平面平行的性质得l⊥m,故C正确;若α∩β=l,l⊥γ,m⊥β,则m∥γ或m⊂γ,故D错误.故选:C.点评:本题考查命题真假的判断,是基础题,解题时要注意空间思维能力的培养.7.过P(2,0)的直线被圆(x﹣2)2+(y﹣3)2=9截得的线段长为2时,直线l的斜率为() A. B. C.±1 D.考点:直线与圆的位置关系.专题:直线与圆.分析:设直线l的方程为:y=kx﹣2k,由已知条件结合圆的性质和点到直线的距离公式推导出=2,由此能求出直线的斜率.解答:解:设直线l的斜率为k,则直线l的方程为:y=kx﹣2k,(x﹣2)2+(y﹣3)2=9的圆心C(2,3),半径r=3,∵过P(2,0)的直线被圆(x﹣2)2+(y﹣3)2=9截得的线段长为2,∴圆心C(2,3)到直线AB的距离d==2,∵点C(2,3)到直线y=kx﹣2k的距离d==2,∴•2=3,解得k=±.故选:A.点评:本题考查直线的斜率的求法,是中档题,解题时要认真审题,注意点到直线的距离公式的合理运用.8.若双曲线的离心率为,则其渐近线方程为()A. y=±2x B. C. D.考点:双曲线的简单性质.专题:圆锥曲线的定义、性质与方程.分析:通过双曲线的离心率,推出a、b关系,然后直接求出双曲线的渐近线方程.解答:解:由双曲线的离心率,可知c=a,又a2+b2=c2,所以b=a,所以双曲线的渐近线方程为:y==±x.故选B.点评:本题考查双曲线的基本性质,渐近线方程的求法,考查计算能力.9.直线l:x+y﹣4=0与圆C:x2+y2=4的位置关系是()A.相交过圆心 B.相交不过圆心 C.相切 D.相离考点:直线与圆的位置关系.专题:直线与圆.分析:求出圆心(0,0)到直线l:x+y﹣4=0的距离d正好等于半径,可得直线和圆相切.解答:解:由于圆心(0,0)到直线l:x+y﹣4=0的距离为d==2=r(半径),故直线和圆相切,故选:C.点评:本题主要考查直线和圆的位置关系,点到直线的距离公式的应用,属于基础题.10.下列结论正确的是()A.命题“若a>b>0,则a2>b2”的逆命题是假命题B.若函数f(x)=sinx,则函数f(x)为周期函数的逆命题是真命题C.向量,的夹角为钝角的充要条件是•<0D.“x2>2”是“x2﹣3x+2≥0”的充分不必要条件考点:命题的真假判断与应用.专题:简易逻辑.分析: A.“若a>b>0,则a2>b2”的逆命题为“若a2>b2,则a>b>0”是假命题;B.函数f(x)=sinx,则函数f(x)为周期函数的逆命题为“函数f(x)为周期函数,则f (x)=sinx”,显然不正确;C.向量,的夹角为钝角⇒•<0,反之不成立,由于非零向量反向共线时,满足<0;D.“x2>2”⇒或x,而x2﹣3x+2=﹣≥﹣,反之也不成立.解答:解:A.“若a>b>0,则a2>b2”的逆命题为“若a2>b2,则a>b>0”是假命题,正确;B.函数f(x)=sinx,则函数f(x)为周期函数的逆命题为“函数f(x)为周期函数,则f (x)=sinx”是假命题,不正确;C.向量,的夹角为钝角⇒•<0,反之不成立,由于向量反向共线时,其<0,因此不正确;D.“x2>2”⇒或x,此时x2﹣3x+2=﹣≥﹣,反之也不成立,因此“x2>2”是“x2﹣3x+2≥0”的既不充分也不必要条件,不正确.综上可得:只有A.故选:A.点评:本题考查了函数的性质、简易逻辑的判定、向量的数量积及其夹角公式,考查了推理能力,属于基础题.二、填空题:(本大题共7小题,每小题3分,共21分.)11.由命题“存在x∈R,使x2+2x+m≤0”是假命题,则实数m的取值X围为(1,+∞).考点:特称命题.专题:计算题.分析:原命题为假命题,则其否命题为真命题,得出∀x∈R,都有x2+2x+m>0,再由△<0,求得m.解答:解:∵“存在x∈R,使x2+2x+m≤0”,∴其否命题为真命题,即是说“∀x∈R,都有x2+2x+m>0”,∴△=4﹣4m<0,解得m>1.∴m的取值X围为(1,+∞).故答案为:(1,+∞)点评:本题考查了存在命题的否定,不等式恒成立问题.考查转化、计算能力.12.已知命题p:m<0,命题q:∀x∈R,x2+mx+1>0成立,若“p∧q”为真命题,则实数m 的取值X围是﹣2<m<0 .考点:复合命题的真假.专题:简易逻辑.分析:根据复合命题的真假性判断出命题p、q都是真命题,再逐一求出m的X围,最后求它们的交集.解答:解:因为“p∧q”为真命题,所以命题p、q都是真命题,若命题q是真命题,则∀x∈R,x2+mx+1>0横成立,所以△=m2﹣4<0,解得﹣2<m<2,又命题p:m<0,也是真命题,所以实数m的取值X围是:﹣2<m<0,故答案为:﹣2<m<0.点评:本题考查了复合命题的真假性,以及二次函数的性质,属于基础题.13.两直线l1:ax+2y﹣1=0,l2:(a﹣1)x+ay+1=0垂直,则a= 0或﹣1 .考点:直线的一般式方程与直线的垂直关系.专题:直线与圆.分析:由已知得a(a﹣1)+2a=0,由此能求出a.解答:解:∵两直线l1:ax+2y﹣1=0,l2:(a﹣1)x+ay+1=0垂直,∴a(a﹣1)+2a=0,解得a=0或a=﹣1.故答案为:0或﹣1.点评:本题考查实数值的求法,是基础题,解题时要认真审题,注意直线与直线垂直的性质的合理运用.14.两圆x2+y2﹣4x+6y=0和x2+y2﹣6x=0的连心线方程为3x﹣y﹣9=0 .考点:圆与圆的位置关系及其判定.专题:计算题;直线与圆.分析:求出圆心坐标,利用点斜式,可得方程.解答:解:两圆x2+y2﹣4x+6y=0和x2+y2﹣6x=0的圆心坐标分别为(2,﹣3),(3,0),∴连心线方程为y﹣0=(x﹣3),即3x﹣y﹣9=0.故答案为:3x﹣y﹣9=0.点评:本题考查圆与圆的位置关系及其判定,考查直线方程,比较基础.15.已知动圆M与圆C1:(x+3)2+y2=9外切且与圆C2:(x﹣3)2+y2=1内切,则动圆圆心M的轨迹方程是﹣=1(x≥2).考点:直线与圆的位置关系.专题:直线与圆.分析:找出两圆圆心坐标与半径,设设动圆圆心M(x,y),半径为r,根据动圆M与圆C1外切且与圆C2内切,即可确定出M轨迹方程.解答:解:由圆C1:(x+3)2+y2=9,圆心C1(﹣3,0),半径r1=3,圆C2:(x﹣3)2+y2=1,圆心C2(3,0),r2=1,设动圆圆心M(x,y),半径为r,根据题意得:,整理得:|MC1|﹣|MC2|=4,则动点M轨迹为双曲线,a=2,b=,c=3,其方程为﹣=1(x≥2).故答案为:﹣=1(x≥2)点评:此题考查了直线与圆的位置关系,以及动点轨迹方程,熟练掌握双曲线定义是解本题的关键.16.一个几何体的三视图如图所示(单位:m),则该几何体的体积为m3.考点:由三视图求面积、体积.专题:立体几何.分析:几何体是圆锥与圆柱的组合体,判断圆柱与圆锥的高及底面半径,代入圆锥与圆柱的体积公式计算.解答:解:由三视图知:几何体是圆锥与圆柱的组合体,其中圆柱的高为4,底面直径为2,圆锥的高为2,底面直径为4,∴几何体的体积V=π×12×4+×π×22×2=4π+π=π.故答案为:.点评:本题考查了由三视图求几何体的体积,根据三视图判断几何体的形状及数据所对应的几何量是解题的关键.17.下列四个命题:①“∃x∈R,x2﹣x+1≤0”的否定;②“若x2+x﹣6≥0,则x>2”的否命题;③在△ABC中,“A>30°”是“sinA>”的充分不必要条件④“函数f(x)=tan(x+φ)为奇函数”的充要条件是“φ=kπ.(k∈Z)”,其中真命题的序号是①②.考点:命题的真假判断与应用.专题:简易逻辑.分析:①按照特称命题的否定要求改写,然后判断真假;②先写出原命题,然后再按照否条件、否结论进行改写;③双向推理,然后进行判断,此例可以举反例;④结合奇函数的性质进行推导,从左推右,然后反推化简.解答:解:①原命题的否定是:∀x∈R,x2﹣x+1>0;因为,故①为真命题;②原命题的否命题是:若x2+x﹣6<0,则x≤2.由x2+x﹣6<0,得(x+3)(x﹣2)<0,所以﹣3<x<2,故②为真命题;③当A=150°时,.所以故在△ABC中,“A>30°”是“sinA>”的不充分条件.故③是假命题;④若函数f(x)为奇函数,则f(0)=tanφ=0,或y轴为图象的渐近线,所以φ=kπ(k∈Z);或tanφ不存在,则φ=,(k∈Z)所以前者是后者的不充分条件.故④为假命题.故答案为:①,②点评:本题以简易逻辑为载体,考查了命题的否定及否命题的写法以及真假判断,充分必要性的判断方法,属于基础题,难度不大.三、解答题:(本大题共5小题,共49分.)18.设p:实数x满足x2+2ax﹣3a2<0(a>0),q:实数x满足x2+2x﹣8<0,且q是p的必要不充分条件,求a的取值X围.考点:必要条件、充分条件与充要条件的判断.专题:不等式的解法及应用.分析:先分别化简两个不等式,再利用q是p的必要不充分条件,转化为,然后某某数a的取值X围.解答:解:由x2+2ax﹣3a2<0得(x+3a)(x﹣a)<0,又a>0,所以﹣3a<x<a,(2分)x2+2x﹣8<0,∴﹣4<x<2,p为真时,实数x的取值X围是:﹣3a<x<a;q为真时,实数x的取值X围是:﹣4<x<2(6分)因为q是p的必要不充分条件,所以有(10分)所以实数a的取值X围是≤a≤2.(14分)点评:本题考查一元二次不等式的解法,必要条件、充分条件与充要条件的判断,考查计算能力,转化思想,是中档题.19.求满足下列条件的椭圆方程:(1)长轴在x轴上,长轴长等于12,离心率等于;(2)椭圆经过点(﹣6,0)和(0,8);(3)椭圆的一个焦点到长轴两端点的距离分别为10和4.考点:椭圆的简单性质.专题:圆锥曲线的定义、性质与方程.分析:(1)设椭圆方程为+=1(a>b>0),运用离心率公式和a,b,c的关系,解得a,b,即可得到椭圆方程;(2)设椭圆方程为mx2+ny2=1,(m,n>0),由题意代入点(﹣6,0)和(0,8),解方程即可得到椭圆方程;(3)讨论椭圆的焦点的位置,由题意可得a﹣c=4,a+c=10,解方程可得a,c,再由a,b,c 的关系解得b,即可得到椭圆方程.解答:解:(1)设椭圆方程为+=1(a>b>0),由题意可得,2a=12,e=,即有a=6,=,即有c=4,b===2,即有椭圆方程为+=1;(2)设椭圆方程为mx2+ny2=1,(m,n>0),由题意代入点(﹣6,0)和(0,8),可得36m+0=1,且0+64n=1,解得m=,n=,即有椭圆方程为+=1;(3)当焦点在x轴上时,可设椭圆方程为+=1(a>b>0),由题意可得a﹣c=4,a+c=10,解得a=7,c=3,b==2,即有椭圆方程为+=1;同理,当焦点在y轴上时,可得椭圆方程为+=1.即有椭圆方程为+=1或+=1.点评:本题考查椭圆的方程和性质,主要考查椭圆的方程的求法,注意运用椭圆的方程的正确设法,以及椭圆性质的运用,属于基础题.20.如图,正方形ACDE所在的平面与平面ABC垂直,M是CE和AD的交点,AC⊥BC,且AC=BC.(1)求证:AM⊥平面EBC;(2)求直线AB与平面EBC所成角的大小.考点:直线与平面所成的角;平面与平面垂直的判定.专题:空间位置关系与距离;空间角;空间向量及应用.分析:(1)建立空间直角坐标,利用向量法证明线面垂直.(2)利用向量法求线面角的大小.解答:解:∵四边形ACDE是正方形,所以EA⊥AC,AM⊥EC,∵平面ACDE⊥平ABC,∴EA⊥平面ABC,∴可以以点A为原点,以过A点平行于BC的直线为x轴,分别以直线AC和AE为y轴和z轴,建立如图所示的空间直角坐标系A﹣xyz.设EA=AC=BC=2,则A(0,0,0),B(2,2,0),C(0,2,0),E(0,0,2),∵M是正方形ACDE的对角线的交点,∴M(0,1,1) (3)=(0,1,1),=(0,2,0)﹣(0,0,2)=(0,2,﹣2),=(2,2,0)﹣(0,2,0)=(2,0,0),∴,,∴AM⊥EC,AM⊥CB,∴AM⊥平面EBC.…(5分)(2)∵AM⊥平面EBC,∴为平面EBC的一个法向量,∵=(0,1,1),=(2,2,0),∴cos.∴=60°.∴直线AB与平面EBC所成的角为30°.…(12分)点评:本题主要考查向量法证明线面垂直以及利用向量法求线面角的大小,运算量较大.21.已知在平面直角坐标系中的一个椭圆,它的中心在原点,左焦点为,且过点D(2,0).(1)求该椭圆的标准方程;(2)设点,若P是椭圆上的动点,求线段PA的中点M的轨迹方程.考点:轨迹方程;椭圆的标准方程.专题:计算题;圆锥曲线的定义、性质与方程.分析:(1)设椭圆方程为,根据题意可得a=2且c=,从而b==1,得到椭圆的标准方程;(2)设点P(x0,y0),线段PA的中点为M(x,y),根据中点坐标公式将x0、y0表示成关于x、y的式子,将P(x0,y0)关于x、y的坐标形式代入已知椭圆的方程,化简整理即可得到线段PA的中点M的轨迹方程.解答:解:(1)由题意知椭圆的焦点在x轴上,设椭圆的标准方程是∵椭圆经过点D(2,0),左焦点为,∴a=2,,可得b==1因此,椭圆的标准方程为.(2)设点P的坐标是(x0,y0),线段PA的中点为M(x,y),由根据中点坐标公式,可得,整理得,∵点P(x0,y0)在椭圆上,∴可得,化简整理得,由此可得线段PA中点M的轨迹方程是.点评:本题给出椭圆满足的条件,求椭圆方程并求与之有关的一个轨迹方程,着重考查了椭圆的标准方程、简单几何性质和轨迹方程的求法等知识点,属于中档题.22.已知圆C:x2+y2=4和直线l:3x+4y+12=0,点P是圆C上的一动点,直线与坐标轴的交点分别为点A、B,(1)求与圆C相切且平行直线l的直线方程;(2)求△PAB面积的最大值.考点:直线和圆的方程的应用.专题:直线与圆.分析:(1)根据题意设所求方程为3x+4y+a=0,根据直线与圆相切时,圆心到直线的距离d=r求出a的值,即可确定出所求直线方程;(2)当直线与AB平行,且与圆相切时,△PAB面积的最大值,如图所示,求出|AB|与|MN|的长,即可确定出△PAB面积的最大值.解答:解:(1)设所求直线方程为3x+4y+a=0,由题意得:圆心(0,0)到直线的距离d=r,即=2,解得:a=±10,则所求直线方程为3x+4y±10=0;(2)当直线与AB平行,且与圆相切时,△PAB面积的最大值,此时直线方程为3x+4y﹣10=0,∵点C到直线AB的距离||=,CM=2,∴|MN|=+2=,∵A(﹣4,0),B(0,3),即OA=4,OB=3,∴|AB|=5,则△PAB面积最大值为×5×=11.点评:此题考查了直线与圆的方程的应用,涉及的知识有:点到直线的距离公式,两直线平行时斜率的关系,以及直线与圆相切的性质,熟练掌握公式及性质是解本题的关键.。
【解析版】江西省赣州市六校2014届高三上学期期末联考试题(数学文)

江西省赣州市六校2014届高三上学期期末联考试题高三数学试题(文科) 第Ⅰ卷(共50分)一、选择题:本大题共12个小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知复数满足i Z i 213+=,则Z 等于( )A .i --2B .i +-2C .i +2D .i -23.甲、乙两名同学在某项测试中的6次成绩的茎叶图如图所示,1x ,2x 分别表示甲乙两名同学这项测试成绩的平均数,12,s s 分别表示甲乙两名同学这项测试成绩的标准差,则有( ) A .1212,x x s s ><B .1212,x x s s =<C .1212,x x s s ==D .1212,x x s s =>【答案】B 【解析】4.已知函数2()f x x bx c =++,其中04b ≤≤,04c ≤≤,记函数()f x 满足条件:12)2(≤f 为事件A ,则事件A 发生的概率为( )A.14 B.21 C. 38 D. 435.在ABC ∆中, AD=3,点P 在AD 上且满足,3AP AD =则=+⋅)(PC PB DA ( ) A .6B .6-C .-12D . 126.某几何体的三视图如右图所示,则它的表面积是( ) A. π524+ B.π-24 C.()π1524-+D.()π1520-+7.已知πcos sin 6αα⎛⎫-+= ⎪⎝⎭⎪⎭⎫ ⎝⎛∈3,0πα,则⎪⎭⎫ ⎝⎛+πα125sin 的是( )A . C .1027 D .15278.阅读右侧程序框图,输出的结果s 的值为( ) A.0B.23C.3D.23-9.已知双曲线C 的方程为)0,0(12222>>=-b a by a x ,它的左、右焦点分别21,F F ,左右顶点为21,A A ,过焦点2F 先作其渐近线的垂线,垂足为P ,再作与x 轴垂直的直线与曲线C 交于点R Q ,,若1212,,QF A A PF 依次成等差数列,则离心率e=( )A 、2B 、5C 、2或5D 、215+P x y的轨迹方程是10.如图放置的边长为1的正方形PABC沿x轴正方向滚动.设顶点(),()x fy=,设()x=从=在其两个相邻零点间的图象与x轴所围区域为S,则直线ty f xt到所匀速移动扫过区域S的面积D与的函数图象大致为().=t0=4A B C D第Ⅱ卷(共100分)二、填空题(每题5分,满分25分,将答案填在答题纸上)11.已知过原点的直线与圆22(2)1x y ++=相切,若切点在第二象限,则该直线的方程为 .13.设y x ,满足约束条件⎪⎩⎪⎨⎧≥≥≥+-≤--,0,0,02,063y x y x y x 若目标函数)0,0(>>+=b a by ax z 的最大值为,12则ba 32+的最小值为______________ .考点:简单线性规划的应用;基本不等式. 14.已知定义在R 上的函数()()f x g x 、满足()()x b x g x f =,且'()()()'()f x g x f x g x <, 25)1()1()1()1(=--+g f g f ,若{}n a 是正项等比数列,且()()4421248675g f a a a a a a =++,则86a a +等于 .15.函数()x f 的定义域为D ,若存在闭区间[]D n m ⊆,,使得函数()x f 满足以下两个条件:(1)()x f 在[m ,n]上是单调函数;(2) ()x f 在[m ,n]上的值域为[2m ,y=的“倍值区间”.下列函数中存在“倍值区间”2n],则称区间[m,n]为()x f的有(填上所有正确的序号)①()x f=x2(x≥0);②()x f=e x(x∈R);③()x f=;④()x f=.三、解答题 (本大题共6小题,共75分.解答应写出文字说明、证明过程或演算步骤.)16.(本题满分为12分)在ABC ∆中,角A ,B ,C 所对边分别为a ,b ,c ,且向量()B A m sin ,sin = ,()A B n cos ,cos =,满足C n m 2sin =⋅(1)求角C 的大小;(2)若sin ,sin ,sin A C B 成等差数列,且()18AC AC AB ⋅-=,求边c 的长17.(本题满分为12分)数列{}n a 的前n 项和记为n S ,11=a ,点1(,)n n S a +在直线12+=x y 上,n ∈N *.(1)求证:数列{}n a 是等比数列,并求数列{}n a 的通项公式n a ;(2)设31log n n b a +=,n T 是数列11n n b b +⋅{}的前n 项和,求2014T 的值.18.(本题满分为12分)某公司研制出一种新型药品,为测试该药品的有效性,公司选定2000个药品样本分成三组,测试结果如下表:已知在全体样本中随机抽取个,抽到B 组药品有效的概率是35.0.(1)现用分层抽样的方法在全体样本中抽取360个测试结果,问应在C 组抽取样本多少个?(2)已知425≥b ,68≥c ,求该药品通过测试的概率(说明:若药品有效的概率不小于90%,则认为测试通过).Rt 中,AB=2BF=4,C,E分别是AB,AF的中点19.(本题满分为12分)在ABF(如下左图).将此三角形沿CE对折,使平面AEC⊥平面BCEF(如下右图),已知D是AB的中点.(1)求证:CD∥平面AEF;(2)求证:平面AEF⊥平面ABF;(3)求三棱锥C-AEF的体积,20.(本题满分为13分)已知动圆M 与直线21:-=x l 相切且与圆F :()41122=+-y x 外切。
江西省赣州市六校2013-2014学年高二上学期期末联考数学(文)试题含答案
2013-2014学年度第一学期期末联考高二数学试题(文科)(共150分.考试时间120分钟)一、选择题:本大题共10小题,每小题5分,共50分,在每一小题给出的四个选项中,只有一项是符合题目要求的,答案填写在答题卷上.1.椭圆221x y +=的焦距为( ) A B .2 2 C .4 D .4 22.已知x 与y 之间的一组数据(如表所示):则关于y 与x 的线性回归方程y =bx +a 必过定点( )A .(2,2)B .(1.5,0)C .(1,2)D .(1.5,4)3.执行右边程序语句的过程中,执行循环体的次数是( ) A .0 B .1 C .2 D .34.从甲乙两个城市分别随机抽取16台自动售货机,对其销售额进行统计,统计 数据用茎叶图表示(如图所示),设甲乙两组数据的平均数分别为x 甲,x 乙,中位 数分别为m 甲,m 乙,则( )A . x x <甲乙,m 甲>m 乙B .x x <甲乙,m 甲<m 乙C .x x >甲乙,m 甲>m 乙D .x x >甲乙,m 甲<m 乙5.已知函数f (x )=ax 2+3x -2在点(2,f (2))处的切线斜率为7,则实数a 的值为( )A .-1B .1C .±1D .-26.设函数f (x )=x e x ,则( )A .x =1为f (x )的极大值点B .x =1为f (x )的极小值点C .x =-1为f (x )的极大值点D .x =-1为f (x )的极小值点 7.下列说法错误..的是( ) A .“0<ab ”是“方程122=+by ax 表示双曲线”的充分不必要条件 B .命题“若0=a ,则0=ab ”的否命题是:“若0≠a ,则0≠ab ”C .若命题p :存在01,2=+-∈x x R x ,则命题p 的否定:对任意01,2≠+-∈x x R xD .若命题“非p ”与命题“p 或q ”都是真命题,那么命题q 一定是真命题i=1 Doi=i+1 i=i *iLoop while i <10 输出 i8.如图所示22⨯方格,在每一个方格中填入一个数字,数字可以是4,3,2,1中的任何 一个,允许重复,则填入A 方格的数字大于D 方格的数字的概率为( )A .21 B .41 C .43D .83 9.设F 为抛物线x y 82=的焦点,A ,B ,C 为该抛物线上三点,若0FA FB FC ++=,则||||||FA FB FC ++= ( )A .6B .9C .12D .1610.如图,在棱长为1的正方体1111ABCD A BC D -的对角线1AC 上任取一点P ,以A 为球心,AP 为半径作一个球.设AP x =,记该球面与正方体表面的交线的长度和为()f x ,则函数()f x 的图象最有可能的是( )A .B .C .D .二、填空题:本大题共5小题,每小题5分,共25分,答案填写在答题卷上.11. 如图的程序框图所示,若输入4=a ,3=b ,则输出的值是 ;12.设函数f (x )的导数为'()f x ,且()'()sin cos 2f x f x x π=+,则'()4f π=___.13. 设函数,[5,5]()2x f x x ∈-=-+ .若从区间[5,5]-内随机选取一个实数0x ,则所选取的实数0x 满足0()0f x ≤的概率为 . 14. 一个半径为2的球体经过切割后,剩余部分几何体的三视图如图所示, 则该几何体的表面积为 ;15.已知双曲线()222210,0x y a b a b-=>>的两条渐近线与抛物线24y x =的准线分别交于,A B 两点,O 为坐标原点.若AOB ∆则双曲线的离心率为_________.三、解答题:共6小题,共75分。
江西省赣州市四所重点中学2014届高三上学期期末联考数学(理)试题 Word版含答案
江西省赣州市四所重点中学(赣州一中、平川中学、瑞金中学、赣州三中)2013-2014学年度第一学期期末联考高三数学试题(理科)一、选择题(每小题5分,共50分)1、已知x, y ∈R , i 为虚数单位,且(x ―2)i ―y =-1+i ,则(1+i)x +y 的值为 A .4 B .-4 C .4+4i D .2i 2、下列命题中正确的是 A .若命题p 为真命题,命题q 为假命题,则命题“p 且q ”为真命题B .“sin α=21”是“α=6π”的充分不必要条件C .l 为直线,α,β为两个不同的平面,若l ⊥β,α⊥β, 则l ∥αD .命题“∀x ∈R , 2x >0”的否定是“∃x 0∈R ,02x ≤0”3、平面α∥平面β,点A, C ∈α, B, D ∈β,则直线AC ∥直线BD 的充要条件是 A .AB ∥CD B .AD ∥CB C .AB 与CD 相交 D .A, B, C, D 四点共面4、已知向量a , b 的夹角为60°,且|a |=2, |b |=1,则向量a 与向量a +2b 的夹角等于 A .150° B .90° C .60° D .30°5、一个空间几何体的三视图及其相关数据如图所示,则这个空间几何体的表面积是A .211πB .211π+6C .11πD .211π+33 6、过抛物线y 2=4x 的焦点F 的直线交该抛物线于A, B 两点,O 为坐标原点。
若|AF|=3,则△AOB 的面积为A .22 B .2 C .223 D .227、已知函数f(x)=ax 3+21x 2在x =-1处取得极大值, 记g(x)=)('1x f 。
程序框图如图所示,若输出的结果 S =20142013,则判断框中可以填入的关于n 的判断条件是 A .n ≤2013 B .n ≤2014C .n >2013D .n >20148、已知双曲线)0,0(12222>>=-b a by a x 的左焦点为F 1,左、右顶点分别为A 1、A 2,P 为双曲线上任意一点,则分别以线段PF 1,A 1A 2为直径的两个圆的位置关系为 A .相交 B .相切 C .相离 D .以上情况都有可能9、已知函数f(x)=2||4+x -1的定义域是[a, b](a, b ∈Z ),值域是[0, 1],则满足条件的整数对(a, b)共有A .2个B .5个C .6个D .无数个10、设D ={(x, y)|(x -y)(x +y)≤0},记“平面区域D 夹在直线y =-1与y =t(t ∈[-1,1])之间的部分的面积”为S ,则函数S =f(t)的图象的大致形状为二、填空题(每小题5分,共25分)11、设O 为坐标原点,C 为圆(x -2)2+y 2=3的圆心,且圆上有一点M(x, y)满足OM ²CM =0,则x y=。
江西省赣州市赣县中学北校区2014-2015学年高二1月月考数学(文)试题
正视图俯视图江西省赣州市赣县中学北校区2014-2015学年高二1月月考数学(文)试题2015-1一、选择题:(本大题共10小题,每小题5分,共50分,在每小题给出的四个选项中,有且只有一项是符合题目要求的 )1.设向量a =()21x ,-,b =()14x ,+,则“3x =”是“a //b ”的( ) A .充分而不必要条件 B .必要而不充分条件C .充分必要条件D .既不充分也不必要条件 2.下列四种说法中,错误的个数是( ) ①A={0,1}的子集有3个②“若22bm am <,则b a <”的逆命题为真③“命题q p ∨为真”是“命题q p ∧为真”的必要不充分条件④命题“R x ∈∀,均有0232≥--x x ”的否定是:“R x ∈∃0,使023020≤--x x ”A.0个B.1个C.2个D.3个3.如图是某赛季甲、乙两名篮球运动员每场比赛得分的茎叶图,则甲、乙两人这几场比赛得分的中位数之和是( )A .62B .63C .64D .564.在区间,22ππ⎡⎤-⎢⎥⎣⎦上随机取一个x ,sin x 的值介于12-与12之间的概率为( ) (A)13 (B)2π(C)12 (D)23 5.三棱锥的三视图如图,正视图是等边三角形,侧视图是直角三角形,俯视图是等腰直角三角形,则此三棱锥的体积为 ( ) A6.已知直线3x +4y -3=0与直线6x +my +14=0平行,则它们之间的距离是( )A.1B.2C.12 D.4 7.已知双曲线221()my x m R -=∈与椭圆2215yx +=有相同的焦点,则该双曲线的渐近线方程为( )(A)y = (B )y x = (C )13y x =± (D )3y x =±8.已知圆221:()(2)4C x a y -++=与圆222:()(2)1C x b y +++=相外切, 则ab 的最大值为 ( )A.2B.32C.94 D.9.设椭圆()0>>b a 的左、右焦点分别为21,F F ,以2F 为圆心,2OF (O 为椭圆中心)CD C B为半径作圆2F ,若它与椭圆的一个交点为M ,且1MF 恰好为圆2F 的一条切线,则椭圆的离心率为( )A .13-B .32-C .22D .2310.如图,正方体1111ABCD A B C D -的棱长为1,点M 在棱AB 上,且13AM =,点P 是平面ABCD 上的动点,且动点P 到直线11A D 的距离与点P 到点M 的距离的平方差为1,则动点P 的轨迹是 ( )A .圆 B .抛物线 C .双曲线 D .椭圆二、填空题(本大题共5小题,每小题5分,共25分,将各小题的结果写在横线上)11.一个正方体的各顶点均在同一球的球面上,若该球的体积为π34,则该正方体的 表面积为 .12. .执行如图所示的程序框图,若输入的5a =,则输出的结果是 .13.设抛物线y x122=的焦点为F ,经过点()12,P 的直线l 与抛物线相交于BA,两点且点P 恰为AB 的中点,则=+BF AF .14.已知P 是双曲线1366422=-y x 上一点,F 1,F 2是双曲线的两个焦点,若|PF 1|=17,则|PF 2|的值为________.15.以下四个关于圆锥曲线的命题中:①设A B 、为两个定点,k 为非零常数,||||PA PB k -=,则动点P 的轨迹为双曲线;②过定圆C 上一定点A 作圆的动点弦AB ,O 为坐标原点,若1(),2OP OA OB =+则动点P 的轨迹为圆;③04πθ<<,则双曲线22122:1cos sin x y C θθ-=与222222:1sin sin tan y x C θθθ-=的离心率相同;④已知两定点12(1,0),(1,0)F F -和一动点P ,若212||||(0)PF PF a a ⋅=≠,则点P 的轨迹关于原点对称.其中真命题的序号为 (写出所有真命题的序号).三、解答题:(本大题共6小题,共75分.解答应写出文字说明,证明过程或演算步骤 )16.命题p “方程22133x y k k +=-+表示双曲线” (R k ∈);命题q )1(log 22++=kx kx y 定义域为R ,若命题p q ∨为真命题,p q ∧为假命题,求实数k 的取值范围.nBOCDA17.某校50名学生参加2013年全国数学联赛初赛,成绩全部介于90分到140分之间.将成绩结果按如下方式分成五组:第一组[)100,90,第二组[)110,100, ,第五组[]140,130.按上述分组方法得到的频率分布直方图如图所示.(1)若成绩大于或等于100分且小于120分认为是良好的,求该校参赛学生在这次数学联赛中成绩良好的人数;(2)若从第一、五组中共随机取出两个成绩,求这两个成绩差的绝对值大于30分的概率.0.0.0分数.0..018.平面内动点(,)P x y 到定点(1,0)F 的距离比它到y 轴的距离大1。
江西省吉安县中、新余一中2014-2015学年高二上学期12月联考数学文试题
江西省吉安县中、新余一中2014-2015学年高二上学期12月联考数学文试题一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.若R c b a ∈,,,b a >,则下列不等式成立的是 ( )A .b a 11< B .1122+>+c b c a C .22b a > D .c b c a >2. 已知等比数列{}n a 的公比13q =-,则13572468a a a aa a a a ++++++等于 ( )A.3-B.13-C.3D. 133. 在ABC ∆中,内角,,A B C 所对的边分别为,,a b c ,若sin sin sin a A b B c C +<,则ABC ∆的形状是( )A.锐角三角B.直角三角形C.钝角三角形D.正三角形4. 已知函数⎩⎨⎧≤->-=)0(1)0(log )(22x x x x x f ,则不等式0)(>x f 的解集为( ) A.}10|{<<x x B }01|{≤<-x x C. }1|{->x x D. }11|{<<-x x5. 在等差数列{}n a 中,912162a a =+,则数列{}n a 的前11项和S 11等于 ( ) A.24B.48C.66D.1326. 设定点12(0,3),(0,3),M M -动点P 满足条件129PM PM a a+=+(a 为大于0的常数),则点P 的轨迹是( )A.椭圆B.线段C.椭圆或线段D.不存在7. 在ABC ∆中,80,100,45a b A ︒===,则此三角形解的情况是 ( )A.一解B.两解C.一解或两解D.无解8. 已知变量,x y 满足1,2,0.x y x y ≥⎧⎪≤⎨⎪-≤⎩则x y +的最小值是( )A. 2B. 3C. 4D. 59. “方程22221x y m n+=表示焦点在y 轴上的椭圆” 是“0n m >>”的( )A .充分而不必要条件B .必要而不充分条件C .充要条件D .既不充分也不必要条件10.下列说法错误的是( )A .若命题2:,10p x R x x ∃∈-+=使得,则 2:,10p x R x x ⌝∀∈-+≠都有;B .命题“若0232=+-x x ,则1=x ”的否命题为假命题;C .命题“若0a =,则0ab =”的否命题是:“若0a ≠,则0ab ≠”;D .已知:,cos 1p x R x ∃∈=使得,2:,10q x R x x ∀∈-+>都有,则“q p ⌝∧”为假命题.11. 已知)0,(),0,(21c F c F -为椭圆12222=+by a x 的两个焦点,P 为椭圆上的一点,且221c PF PF =⋅,则此椭圆离心率的取值范围是( )A .B .11[,]32C . 2D .(0,]212. 设1a >,定义111()122f n n n n=+++++,如果对任意的2n N n *∈≥且,不等式()1127log 77log a a f n b b ++>+恒成立,则实数b 的取值范围是( )A .29217⎛⎫ ⎪⎝⎭, B .()0,1 C .()0,4 D .()1,+∞二、填空题:本大题共4小题,每小题5分.13.已知数列{}n a 满足12324n n n n a a a a +++=,且1231,2,3,a a a ===则12320132014a a a a a +++⋅⋅⋅++=________.14. 已知O 为原点,椭圆221259x y +=上一点P 到左焦点1F 的距离为4,M 是1PF 的中点.则OM = .15. 在ABC ∆中,内角,,A B C 所对的边分别为,,a b c ,若s i n ,A C 30,2,B b ==则ABC ∆的面积是 .16. 已知正实数,x y 满足3x y x y ++=,若对任意满足条件的,x y ,都有2()()10x y a x y +-++≥恒成立,则实数a 的取值范围是 .三、解答题:本大题共6小题,共70分,解答应写出文字说明,证明过程或演算步骤.17.(本小题满分10分)已知全集U R =,非空集合{23x A x x -=-<}0,{}()(4)0B x x a x a =---<. (1)当32a =-时,求A B ⋂; (2)命题:p x A ∈,命题:q x B ∈,若p ⌝是q ⌝的必要不充分条件,求实数a 的取值范围.18.(本小题满分12分)在ABC ∆中,内角,,A B C 所对的边分别为,,a b c ,若(cos ,sin ),(cos ,sin ),m B C n C B ==-且1.2m n ⋅=(1)求角A 的大小;(2)若a =ABC ∆的面积S =求b c +的值.19.(本小题满分12分) 在等差数列{}n a 中,31=a ,其前n 项和为n S ,等比数列{}n b 的各项均为正数,11=b ,公比为q ,且1222=+S b ,22b S q =. (1)求n a 与n b ;(2)设数列{}n c 满足n n n c a b =⋅,求{}n c 的前n 项和n T .20.(本小题满分12分)新余到吉安相距120千米,汽车从新余匀速行驶到吉安,速度不超过120kmh ,已知汽车每小时的运输成本(单位:元)由可变部分和固定部分两部分组成:可变部分与速度v (kmh )的平方成正比,比例系数为b ,固定部分为a 元,(1)把全程运输成本y (元)表示为速度v (kmh )的函数;并求出当150,200a b ==时,汽车应以多大速度行驶,才能使得全程运输成本最小; (2)随着汽车的折旧,运输成本会发生一些变化,那么当1691,2200a b ==,此时汽车的速度应调整为多大,才会使得运输成本最小.21.(本小题满分12分)在平面直角坐标系中,椭圆2222:1(0)x y C a b a b+=>>的上顶点到焦点的距离为2,离心(1)求椭圆C 的方程;(2)设P 是椭圆C 长轴上的一个动点,过点P 作斜率为k 的直线l 交椭圆C 于A 、B 两点.若22PA PB +的值与点P 的位置无关,求k 的值.22.(本小题满分12分) 已知数列{}na 是各项均不为0的等差数列,公差为d ,n S 为其前n 项和,且满足221n n a S -=,n *N ∈.数列{}n b 满足11n n n b a a +=⋅,n *N ∈, n T 为数列{}n b 的前n 项和.(1)求数列{}n a 的通项公式n a ;(2)若对任意的*n N ∈,不等式8(1)n n T n λ<+⨯-恒成立,求实数λ的取值范围; (3)是否存在正整数,(1)m n m n <<,使得1,,m n T T T 成等比数列?若存在,求出所有,m n 的值;若不存在,请说明理由.2014~2015学年度上学期 吉安县中新余一中高二年级联考数学试卷(文)参考答案二、填空题(本大题共5小题,每小题5分,共25分.)13. 5033 14. 3 15 16. 37,6⎛⎤-∞ ⎥⎝⎦三、解答题:(本大题共6小题,共70分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
赣州市2014~2015学年度第一学期期末考试 高二数学(文科)试题一、选择题(本大题共12小题,每小题5分,满分60分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1、如果一个几何体的三视图都是等腰三角形,那么这个几何体可能是( ) A .圆锥 B .正四棱锥 C .正三棱锥 D .正三棱台2、若a ,b 是异面直线,b ,c 是异面直线,则a ,c 的位置关系是( ) A .异面 B .相交或平行 C .相交、平行和异面 D .平行或异面3、设双曲线22221x y a b -=(0a >,0b >)的虚轴长为2,焦距为方程为( )A.y = B .2y x =± C.2y x=±D .12y x =± 4、用α表示一个平面,m 表示一条直线,则α内一定有无数多条直线与m ( )A .平行B .相交C .垂直D .异面5、一批热水器共有98台,其中甲厂生产的有56台,乙厂生产的有42台,用分层抽样从中抽取一个容量为14的样本,那么甲、乙两厂各抽取的热水器的台数是( ) A .9,5 B .8,6 C .10,4 D .7,76、某程序框图如图所示,该程序运行后,输出的x 的值为31,则a 等于( )A .3B .2C .1D .0 7、如果一个命题的逆命题是真命题,那么这个命题的否命题是( )A .真命题B .假命题C .与所给的命题有关D .无法判断8、已知a ,b 是实数,则“0a >,且0b >”是“0a b +>且0ab >”的( ) A .充分不必要条件 B .必要不充分条件C .充要条件D .既不充分也不必要条件 9、如图,在矩形CD AB 中,4AB =,C 2B =,随机向矩形内丢一粒豆子(豆子的体积忽略不计),则豆子落入圆内的概率为( )A .14B .12C .8πD .4π10、已知线性回归方程的系数b 的估计值是1.23,5y =,4x =,则线性回归方程是( ) A . 1.234y x =+ B .0.94 1.23y x =+ C . 1.230.08y x =+ D .0.08 1.23y x =+11、垂直于直线2610x y -+=,且与曲线3231y x x =+-相切的直线方程是( ) A .320x y ++= B .320x y -+= C .320x y +-= D .320x y --=12、已知C ∆AB 的顶点B ,C 在椭圆2213x y +=上,顶点A 是椭圆的一个焦点,且椭圆的另一个焦点在C B 边上,则C ∆AB 的周长为( )A. B .6 C .12 D.二、填空题(本大题共4小题,每小题5分,共20分.) 13、函数2sin y x x =+的单调递增区间为 .14、某校举行2015年元旦汇演,七位评委为某班的小品打出的分数如右茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的平均数为 ,方差为 . 15、若曲线()2ln f x ax x=+存在垂直于y 轴的切线,则实数a 的取值范围是 .16、将双曲线22221x y a b -=(0a >,0b >)的实轴、虚轴互换,所得双曲线方程为22221x y b a -=(0a >,0b >),我们称这两双曲线是互为共轭的双曲线,若两共轭双曲线的离心率分别为1e ,2e ,则221211e e +=.三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.) 17、(本小题满分10分)已知命题:p 46x -≤,命题:q 22210x x a -+-≥(0a >),若p ⌝是q的充分不必要条件,求实数a 的取值范围.18、(本小题满分12分)某超市在2015年元旦期间举行抽奖活动,规则是:从装有编号为0,1,2,3四个小球的抽奖箱中同时抽出两个小球,两个小球号码之和等于5中一等奖,等于4中二等奖,等于3中三等奖.()1求中三等奖的概率; ()2求中奖的概率.19、(本小题满分12分)某汽车制造厂为了检测A ,B 两种轮胎的性能,分别从这两种轮胎中随机抽取8个进行测试,下面记录的是每个轮胎行驶的最远路程数(单位:100km ): 轮胎A :96,112,97,108,100,103,86,98; 轮胎B :108,101,94,105,96,93,97,106.()1分别计算A ,B 两种轮胎行驶最远路程的平均数、极差; ()2比较A ,B 两种轮胎的性能,估计哪一种较为稳定.20、(本小题满分12分)在如图所示的几何体中,C ∆AB 为正三角形,AE 和CD 都垂直于平面C AB ,且2AE =AB =,CD 1=,F 为BE 的中点.()1求证:DF//平面C AB ; ()2求证:平面D BE ⊥平面ABE .21、(本小题满分12分)已知函数()223x f x e x x=+-(e 为自然对数的底数).()1求曲线()f x 在点()()1,1f 处的切线方程;()2当1x ≥时,若关于x 的不等式()f x ax ≥恒成立,求实数a 的取值范围.22、(本小题满分12分)如图,F 为抛物线22y px =(0p >)的焦点,()4,2A 为抛物线内一定点,P 为抛物线上一动点,且FPA +P 的最小值为8.()1求抛物线的方程;()2如果过点F 的直线l 交抛物线于M ,N 两点,且32MN ≥,求直线l 的倾斜角的取值范围.赣州市2014~2015学年度第一学期期末考试 高二数学(文科)试题参考答案 一、选择题1~5. CCCCB ; 6~10. AACCC 11~12. AD 二、填空题13.(,)-∞+∞; 14.85,1.6; 15.(,0)-∞; 16.1 三、解答题 17.解:p ⌝即46x ->,解得10x >或2x <-,记{}102A x x x =|><-或22:210q x x a -+-≥,解得1x a ≥+或1x a ≤-,记{}11B x x a x a =|≥+≤-或p q ⌝⇒即A 是B 的真子集所以1211011a a a a -≥-⎧⎪+≤⎨⎪+>-⎩,解得03a <≤,即实数a 的取值范围是(]0,318.解:(1)从四个小球任选两个共有(0,1),(0,2),(0,3),(1,2),(1,3),(2,3)六种结果 两个小球号码之和等于3的取法有两种:(0,3),(1,2)所以两个小球号码之和等于3的概率12163P ==(2)两个小球号码之和等于的取法有一种(0,1);两个小球号码之和等于2的取法有一种(0,2),故中奖的概率为222163P =-=19.解:(1)轮胎A 的平均最远路程为1(9611298)1008A x =+++=L 轮胎B 的平均最远路程为1(108101106)1008B x =+++=L轮胎A 的平均最远路程的极差为1128626-= 轮胎B 的平均最远路程的极差为1089315-=(2)轮胎A 的最远路程的方差为22221(4122)55.258A s =+++=L轮胎B的最远路程的方差为22221(816)29.58Bs=+++=L由于22B As s<,所以B种轮胎的性能较为稳定.20.证明:(1)取AB的中点G,连接,CG FG 因为F为BE的中点,所以GF∥AE,且12 GF AE=又AE⊥平面ABC,CD⊥平面ABC所以CD∥AE,且12 CD AE=所以GF∥CD且GF CD=所以四边形CDFG为平行四边形所以DF∥CG,又DF⊄平面ABC,CG⊆平面ABC所以DF∥平面ABC(2)由(1)知四边形CDFG为平行四边形,所以CG∥DF 又AE⊥平面ABC,AE⊆平面ABE所以平面ABE⊥平面ABC,交线为AB又ABC∆为正三角形,G为AB的中点所以CG AB⊥,所以CG⊥平面ABE又CG∥DF,所以DF⊥平面ABE而DF⊆平面DBE,所以平面DBE⊥平面ABE21.解:(1)因为2()e23xf x x x=+-,所以()e43xf x x'=+-则(1)e1f'=+,又(1)e1f=-,所以曲线()f x在点(1,(1))f处的切线方程(e1)20x y+--=HG EDCBFA(2)由()f x ax ≥,得2e 23x ax x x ≤+-,因为1x ≥,所以2e 23x x x a x +-≤ 令2e 23()x x x g x x +-=,则22(1)e 2()x x x g x x -+'=,因为1x ≥,所以()0g x '>所以函数()g x 在区间[)1,+∞内是增函数,所以函数()g x 的最小值为(1)e 1g =-故实数a 的取值范围为(],e 1-∞-22.解:(1)设P 点到抛物线的准线为2px =-的距离为d由抛物线的定义知d PF=,所以min min ()()482pPA PF PA d +=+=+=即8p =,所以抛物线的方程为216y x = (2)由(1)得(4,0)F ,易知当直线的斜率不存在时不合题意,设其斜率为k 则直线的方程为(4)y k x =-,显然0k ≠将直线的方程代入抛物线方程整理得:2222(816)160k x k k -++= 设1122(,),(,)M x y N x y ,则2122816k x x k ++=,1216x x ====2216(1)32k k +=≥所以2111k k ≤⇒-≤≤所以直线的倾斜角的取值范围是[)(]1,00,1-U ,倾斜角的范围是30,,44ππ⎛⎤⎡⎫π ⎪⎥⎢⎝⎦⎣⎭U。
