随机变量练习题(答案)
(完整版)多维随机变量及其分布习题及答案

第三章多维随机变量及其分布一、填空题1、随机点落在矩形域的概率为),(Y X ],[2121y y y x x x ≤<≤< .),(),(),(),(21111222y x F y x F y x F y x F -+-2、的分布函数为,则 0 .),(Y X ),(y x F =-∞),(y F3、的分布函数为,则),(Y X ),(y x F =+),0(y x F ),(y x F4、的分布函数为,则),(Y X ),(y x F =+∞),(x F )(x F X5、设随机变量的概率密度为),(Y X ,则.⎩⎨⎧<<<<--=其其042,20)6(),(y x y x k y x f =k 816、随机变量的分布如下,写出其边缘分布.),(Y X 7、设是的联合分布密度,是的边缘分布密度,则1 .),(y x f Y X ,)(x f X X =⎰∞+∞-)(x f X8、二维正态随机变量,和相互独立的充要条件是参数 0.),(Y X X Y =ρXY0123jP ⋅10838308638108182⋅i P 818383819、如果随机变量的联合概率分布为),(Y X YX12316191181231αβ则应满足的条件是 ;若与相互独立,则 , .βα,186=+βαX Y =α184=β18210、设相互独立,,则的联合概率密度Y X ,)1.0(~),1,0(~N Y N X ),(Y X,的概率密度.=),(y x f 22221y x e +-πY X Z +==)(Z f Z 42221x e-π12、 设 ( ξ 、 η ) 的 联 合 分 布 函 数 为则 A =__1___。
()()()()⎪⎩⎪⎨⎧≥≥+-+-+++= y x y x y x A y x F 00,0111111,222二、证明和计算题1、袋中有三个球,分别标着数字1,2,2,从袋中任取一球,不放回,再取一球,设第一次取的球上标的数字为,第二次取的球上标的数字,求的联合分布律.X Y ),(Y X 解: 031}1,1{⋅===Y X P 31131}2,1{=⋅===Y X P 312132}1,2{=⋅===Y X P 312132}2,2{=⋅===Y X P 2、三封信随机地投入编号为1,2,3的三个信箱中,设为投入1号信箱的信数,为投入2X Y 号信箱的信数,求的联合分布律.),(Y X 解:的可能取值为0,1,2,3的可能取值为0,1,2,3X Y331}0,0{===Y X P 333}1,0{===Y X P 3323333}2,0{====C Y X P XY 12103123131331}3,0{===Y X P 333}0,1{===Y X P 3323}1,1{⨯===Y X P3313}2,1{⨯===Y X P 0}3,1{===Y X P 3233}0,2{C Y X P === 333}1,2{===Y X P 0}2,2{===Y X P 0}3,2{===Y X P 331}0,3{===Y X P 0}3,3{}2,3{}1,3{=========Y X P Y X P Y X P X Y123271273273271127327627322732730032710003、设 函 数 F(x , y) = ;问 F(x , y) 是 不 是 某 二 维 随 机 变 量 的⎩⎨⎧≤+>+120121y x y x 联 合 分 布 函 数 ? 并 说 明 理 由 。
(完整版)概率论习题答案随机变量的数字特征

(完整版)概率论习题答案随机变量的数字特征第3章随机变量的数字特征1,在下列句⼦中随机地取⼀单词,以X 表⽰取到的单词所包含的字母个数,试写出X 的分布律并求)(X E .“They found Peking greatly changed ”解:根据题意,有1/5的可能性取到5个单词中的任意⼀个。
它们的字母数分别为4,5,6,7,7。
所以分布律为5/29)77654(51)(=++++=X E .2,在上述句⼦的29个字母中随机地取⼀个字母,以Y 表⽰取到的字母所在的单词所包含的字母数,写出Y 的分布律并求)(Y E 。
解:5个单词字母数还是4,5,6,7,7。
这时,字母数更多的单词更有可能被取到。
分布律为29/175)147665544(291)(=?+?+?+?=Y E .3,在⼀批12台电视机中有2台是次品,若在其中随即地取3台,求取到的电视机中包含的次品数的数学期望。
解:根据古典概率公式,取到的电视机中包含的次品数分别为0,1,2台的概率分别为1163123100==C C p , 229312210121==C C C p , 221312110222==C C C p 。
所以取到的电视机中包含的次品数的数学期望为)(21222112290116台=?+?+?=E 。
4,抛⼀颗骰⼦,若得6点则可抛第⼆次,此时得分为6+(第⼆次所抛的点数),否则得分就是第⼀次所抛的点数,不能再抛。
求所得分数的分布律,并求得分的数学期望。
解:根据题意,有1/6的概率得分超过6,⽽且得分为7的概率为两个1/6的乘积(第⼀次6点,第2次1点),其余类似;有5/6的概率得分⼩于6。
分布律为得分的数学期望为)(1249)121110987(361)54321(61点=++++++++++=E 。
5,(1)已知)(~X λπ,}6{}5{===X P X P ,求)(X E 。
(2)设随机变量X 的分布律为Λ,4,3,2,1,6}{22--===k k k X P π,问X 的数学期望是否存在?解:(1)根据)(~X λπ,可得}6{!6!5}5{65=====--X P e e X P λλλλ,因此计算得到6=λ,即)6(~X π。
概率论与数理统计教程习题(第二章随机变量及其分布)(1)答案

概率论与数理统计练习题系 专业 班 姓名 学号第六章 随机变量数字特征一.填空题1. 若随机变量X 的概率函数为1.03.03.01.02.043211pX-,则=≤)2(X P ;=>)3(X P ;=>=)04(X X P .2. 若随机变量X 服从泊松分布)3(P ,则=≥)2(X P 8006.0413≈--e.3. 若随机变量X 的概率函数为).4,3,2,1(,2)(=⋅==-k c k X P k则=c1516. 4.设A ,B 为两个随机事件,且A 与B 相互独立,P (A )=,P (B )=,则()P AB =____________.() 5.设事件A 、B 互不相容,已知()0.4=P A ,()0.5=P B ,则()=P AB6. 盒中有4个棋子,其中2个白子,2个黑子,今有1人随机地从盒中取出2个棋子,则这2个棋子颜色相同的概率为____________.(13) 7.设随机变量X 服从[0,1]上的均匀分布,则()E X =____________.(12) 8.设随机变量X 服从参数为3的泊松分布,则概率密度函数为 __.(k 33(=,0,1,2k!P X k e k -==L )) 9.某种电器使用寿命X (单位:小时)服从参数为140000λ=的指数分布,则此种电器的平均使用寿命为____________小时.(40000)10在3男生2女生中任取3人,用X 表示取到女生人数,则X 的概率函数为11.若随机变量X 的概率密度为)(,1)(2+∞<<-∞+=x xa x f ,则=a π1;=>)0(X P ;==)0(X P 0 .12.若随机变量)1,1(~-U X ,则X 的概率密度为 1(1,1)()2x f x ⎧∈-⎪=⎨⎪⎩其它13.若随机变量)4(~e X ,则=≥)4(X P ;=<<)53(X P .14..设随机变量X 的可能取值为0,1,2,相应的概率分布为 , ,,则()E X =15.设X 为正态分布的随机变量,概率密度为2(1)8()x f x +-=,则2(21)E X -= 916.已知X ~B (n,p ),且E (X )=8,D (X )=,则n= 。
随机变量及其分布列习题(含解析)
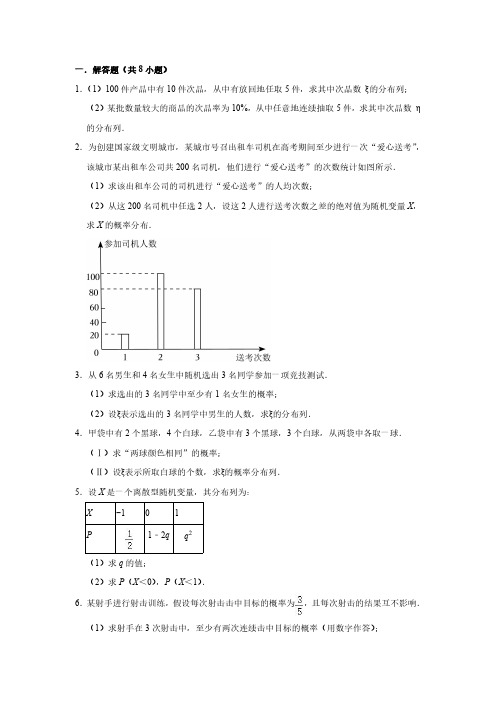
一.解答题(共8小题)1.(1)100件产品中有10件次品,从中有放回地任取5件,求其中次品数ξ的分布列;(2)某批数量较大的商品的次品率为10%,从中任意地连续抽取5件,求其中次品数η的分布列.2.为创建国家级文明城市,某城市号召出租车司机在高考期间至少进行一次“爱心送考”,该城市某出租车公司共200名司机,他们进行“爱心送考”的次数统计如图所示.(1)求该出租车公司的司机进行“爱心送考”的人均次数;(2)从这200名司机中任选2人,设这2人进行送考次数之差的绝对值为随机变量X,求X的概率分布.3.从6名男生和4名女生中随机选出3名同学参加一项竞技测试.(1)求选出的3名同学中至少有1名女生的概率;(2)设ξ表示选出的3名同学中男生的人数,求ξ的分布列.4.甲袋中有2个黑球,4个白球,乙袋中有3个黑球,3个白球,从两袋中各取一球.(Ⅰ)求“两球颜色相同”的概率;(Ⅱ)设ξ表示所取白球的个数,求ξ的概率分布列.5.设X是一个离散型随机变量,其分布列为:X−101P1﹣2q q2(1)求q的值;(2)求P(X<0),P(X<1).6.某射手进行射击训练,假设每次射击击中目标的概率为,且每次射击的结果互不影响.(1)求射手在3次射击中,至少有两次连续击中目标的概率(用数字作答);(2)求射手第3次击中目标时,恰好射击了4次的概率(用数字作答);(3)设随机变量ξ表示射手第3次击中目标时已射击的次数,求ξ的分布列.7.袋中有3个红球,4个黑球,从袋中任取4个球.(1)求红球个数X的分布列;(2)若取到一个红球得2分,取到一个黑球得1分,求得分不小于6分的概率.8.从5名男生和3名女生中任选2人去参加学校组织的“低碳杯”知识抢答赛,用ξ表示选出的女生的人数.(1)求随机变量ξ的分布列;(2)求事件“选出的2学生至少有一女生”的概率.参考答案与试题解析一.解答题(共8小题)1.(1)100件产品中有10件次品,从中有放回地任取5件,求其中次品数ξ的分布列;(2)某批数量较大的商品的次品率为10%,从中任意地连续抽取5件,求其中次品数η的分布列.【解答】解:(1)由题意知ξ的可能取值为0,1,2,3,4,5,每次取出次品的概率为:,相当于5次独立重复实验,ξ~B(5,),P(ξ=0)==0.59059,P(ξ=1)==0.32805,P(ξ=2)==0.07329,P(ξ=3)==0.0081,P(ξ=4)==0.00045,P(ξ=5)==0.00001,∴ξ的分布列为:ξ012345P0.590590.328050.07290.00810.000450.00001(2)由题意知η的可能取值为0,1,2,3,4,5,且η~B(5,0.1),∴η的分布列为:η012345P0.590590.328050.07290.00810.000450.000012.为创建国家级文明城市,某城市号召出租车司机在高考期间至少进行一次“爱心送考”,该城市某出租车公司共200名司机,他们进行“爱心送考”的次数统计如图所示.(1)求该出租车公司的司机进行“爱心送考”的人均次数;(2)从这200名司机中任选2人,设这2人进行送考次数之差的绝对值为随机变量X,求X的概率分布.【解答】解:(1)由统计图得200名司机中送考1次的有20人,送考2次的有100人,送考3次的有80人,∴该出租车公司的司机进行“爱心送考”的人均次数为;(2)从该公司任选两名司机,记“这两人中﹣人送考1次,另一人送考2次”为事件A,“这两人中一人送考2次,另一人送考3次“为事件B,“这两人中﹣人送考1次,另一人送考3次”为事件C,“这两人送考次数相同”为事件D,由题意知X的所有可能取值为0,1,2,,,,所以X的分布列为:X012P3.从6名男生和4名女生中随机选出3名同学参加一项竞技测试.(1)求选出的3名同学中至少有1名女生的概率;(2)设ξ表示选出的3名同学中男生的人数,求ξ的分布列.【解答】解:(1)由意可知,选出的3名同学全是男生的概率为=,∴选出的3名同学中至少有1名女生的概率为P=1﹣=.(2)根据题意,ξ的可能取值为0,1,2,3,P(ξ=0)==,P(ξ=1)==,P(ξ=2)==,P(ξ=3)==,∴ξ的分布列为:ξ0123P4.甲袋中有2个黑球,4个白球,乙袋中有3个黑球,3个白球,从两袋中各取一球.(Ⅰ)求“两球颜色相同”的概率;(Ⅱ)设ξ表示所取白球的个数,求ξ的概率分布列.【解答】解:(I)从甲中取出黑球的概率为,取出白球的概率为,从乙中取出黑球的概率为,取出白球的概率为,故“两球颜色相同”的概率P=.(II)由题意可得,ξ所有可能取值为0,1,2,P(ξ=0)==,P(ξ=1)=,P(ξ=2)=,故ξ的分布列为:ξ012P5.设X是一个离散型随机变量,其分布列为:X−101P1﹣2q q2(1)求q的值;(2)求P(X<0),P(X<1).【解答】解:(1)依题意,得,解得或(舍去),所以.(2)由(1)得,,所以,.6.某射手进行射击训练,假设每次射击击中目标的概率为,且每次射击的结果互不影响.(1)求射手在3次射击中,至少有两次连续击中目标的概率(用数字作答);(2)求射手第3次击中目标时,恰好射击了4次的概率(用数字作答);(3)设随机变量ξ表示射手第3次击中目标时已射击的次数,求ξ的分布列.【解答】解:(1)设事件该射手第i次射击,击中目标为A i,i=1,2,3,则,所以,事件射手在3次射击中,至少有两次连续击中目标可表示为,因为事件,,A1A2A3互斥,所以又事件A1,A2,A3相互独立,所以==;(2)事件射手第3次击中目标时,恰好射击了4次等于事件前3次中恰好击中两次目标且第四次击中目标,又各次击中目标的概率为,所以前3次中恰有两次击中目标的概率为,第四次击中目标的概率为,所以事件射手第3次击中目标时,恰好射击了4次的概率;(3)由已知ξ的取值有3,4,5,⋅⋅⋅,n,⋅⋅⋅,又,,,⋅⋅⋅,,所以随机变量ξ的分布列为:ξ345…n…P……7.袋中有3个红球,4个黑球,从袋中任取4个球.(1)求红球个数X的分布列;(2)若取到一个红球得2分,取到一个黑球得1分,求得分不小于6分的概率.【解答】解:(1)由题意可得,X可能取值为0,1,2,3,P(X=0)=,P(X=1)=,P(X=2)=,P(X=3)=,故X的分布列为:X0123P(2)设得分为Y,则得分Y可以取4,5,6,7,分别对应4个黑球,3黑1红,2黑2红,1黑3红四种情况,P(Y≥6)=P(Y=6)+P(Y=7)=,故得分不小于6分的概率为.8.从5名男生和3名女生中任选2人去参加学校组织的“低碳杯”知识抢答赛,用ξ表示选出的女生的人数.(1)求随机变量ξ的分布列;(2)求事件“选出的2学生至少有一女生”的概率.【解答】解:(1)由题意得ξ的可能取值为0,1,2,P(ξ=0)==,P(ξ=1)==,P(ξ=2)==,∴随机变量ξ的分布列为:ξ012P(2)事件“选出的2学生至少有一女生”的概率为:P=P(ξ=1)+P(ξ=2)==.。
高中数学离散型随机变量的期望与方差练习(含答案)

高中数学离散型随机变量的期望与方差练习(含答案)1.事件A为“三个点数都不同”,事件B为“至少出现一个6点”,求条件概率P(A|B)和P(B|A)。
2.已知随机变量ξ服从正态分布N(1,1),若P(ξ<3)=0.977,则求P(-1<ξ<3)。
3.随机变量X的取值为1和2,若P(X=0)=0,E(X)=1,则求D(X)。
4.已知随机变量X服从正态分布N(3,1),且P(X≥4)=0.1587,则求P(2<X<4)。
5.甲乙等人参加米接力赛,在甲不跑第一棒的条件下,乙不跑第二棒的概率是多少?6.不透明袋子中装有大小、材质完全相同的2个红球和5个黑球,现从中逐个不放回地摸出小球,直到取出所有红球为止,则摸取次数的数学期望是多少?7.下面说法中正确的是:A.离散型随机变量ξ的均值E(ξ)反映了ξ取值的概率的平均值;B.离散型随机变量ξ的方差D(ξ)反映了ξ取值的平均水平;C.离散型随机变量ξ的均值E(ξ)反映了ξ取值的平均水平;D.离散型随机变量ξ的方差D(ξ)反映了ξ取值的概率的平均值。
8.每次试验的成功率为p,重复进行10次试验,其中前7次都未成功,后3次都成功的概率是多少?9.设随机变量X服从二项分布B(n,p),则P(X=k)的分布列为多少。
10.现在有10张奖券,其中7张未中奖,3张中奖,某人从中随机无放回地抽取1张奖券,则此人得奖金额的数学期望为多少?11.已知X~B(n,p),E(X)=2,D(X)=1.6,则n和p的值分别为多少?12.袋中有大小相同的5个球,分别标有1、2、3、4、5五个号码,现在在有放回抽取的条件下依次取出两个球,则它们的和的数学期望为多少?1.一个球,设两个球号码之和为随机变量,则所有可能取值的个数是()A。
5B。
9C。
10D。
25.答案:C。
10.2.电灯泡使用时数在1 000小时以上的概率为0.2,则三个灯泡在1 000小时以后最多有一个坏了的概率是()A。
概率与数理统计第2章一维随机变量习题及答案

第2章一维随机变量 习题2一. 填空题:1.设 离 散 型 随 机 变 量 的 分 布 函 数 是 (){}x P x F ≤=ξ, 则 用 F (x) 表 示 概 {}0x P =ξ = __________。
解:()()000--x F x F 2.设 随 机 变 量 的 分 布 函 数 为 ()()+∞<<∞-+=x arctgx x F π121 则 P{ 0<<1} = ____14_____。
解: P{ 0<<1} = =-)0(F )1(F 143.设 服 从 参 数 为 的 泊 松 分 布 , 且 已 知 P{ = 2 } = P{ = 3 },则 P{ = 3 }= ___2783e - 或 。
4.设 某 离 散 型 随 机 变 量 的 分 布 律 是 {}⋅⋅⋅===,2,1,0,!k k C k P Kλξ,常 数 >0, 则 C 的 值 应 是 ___ e _____。
解:{}λλλλξ-∞=∞=∞==⇒=⇒=⇒=⇒==∑∑∑e C Ce k C k Ck P KK KK K 11!1!105 设 随 机 变 量 的 分 布 律 是 {}4,3,2,1,21=⎪⎭⎫⎝⎛==k A k P kξ则 ⎭⎬⎫⎩⎨⎧<<2521ξP = 。
解:()A A k P k 161516181412141=⎪⎭⎫ ⎝⎛+++==∑=ξ 令15161A = 得 A =1615()()212521=+==⎪⎭⎫ ⎝⎛<<ξξξp p P 8.041211516=⎥⎦⎤⎢⎣⎡+=6.若 定 义 分 布 函 数 (){}x P x F ≤=ξ, 则 函 数 F(x)是 某 一 随 机 变 量 的 分 布 函 数 的 充 要 条 件 是F ( x ) 单 调 不 减 , 函 数 F (x) 右 连 续 , 且 F (- ) = 0 , F ( + ) = 17. 随机变量) ,a (N ~2σξ,记{}σ<-ξ=σa P )(g ,则随着σ的增大,g()σ之值 保 持 不 变 。
随机变量与数字特征练习题及答案
1 第8章 随机变量与数字特征一、填空题⒈ 设随机变量X 的概率分布为则a = . ⒉ 设X 服从区间[1,5]上的均匀分布,当5121<<<x x 时,}{21x X x P ≤≤= .⒊ 设),(~p n B X ,且6)(=X E ,6.3)(=X D ,则n = .4.设)10,5(~2N X ,若5.0)5(=<-a X P ,则a = .5. 设随机变量X 的期望方差分别为E X ()和D X (),令Y aX b =+,则有E Y ()= ,D Y ()= .二、单项选择题⒈ 设X 是连续型随机变量,其密度函数为 ⎩⎨⎧∉∈=],1(0],1(ln )(b x b x x x f 则常数b =( ).A . eB . e + 1C . e - 1D . e 2⒉ 设)10,50(~2N X ,则随机变量( )~)1,0(N . A .10050-X B . 1050-X C . 50100-X D . 5010-X ⒊ 设),2(~2σN X ,已知4.0)42(=≤≤x P ,则=≤)0(x P ( ). A . 0.4 B . 0.3 C . 0.2 D . 0.14. 已知X N ~(,)222,若aX b N +~(,)01,则有( )A . a b ==-22,B . a b =-=-21,C . a b ==-121, D . a b ==122, 5. 已知1)(-=X E ,3)(=X D ,则=-)]2(3[2X E ( ). A . 30 B . 9 C . 6 D . 366. 设随机变量X 的密度函数为f x (),则E X ()2=( )A .xf x x ()-∞+∞⎰d B . x f x x 2()-∞+∞⎰d C . xf x x 2()-∞+∞⎰d D . (())()x E X f x x --∞+∞⎰2d 三、解答题1.设随机变量X 的密度函数为f x x x ()()=-≤≤⎧⎨⎩311202其它, 求:⑴ P X (..)1525<<; ⑵ E X ().2.盒中装有分别标12345,,,,数字的球,从中任取2个,用X 表示所取2球中最大的数字. 求X 的概率分布.3.设)5.0,3(~2N X ,求)6.32(≤≤X P .已知9772.0)2(,8849.0)2.1(=Φ=Φ.4.在一次数学考试中,其分数服从均值为65,标准为10的正态分布,求分数在60~75的概率. (6915.0)5.0(=Φ,8413.0)1(=Φ)。
概率论与数理统计教程习题(第二章随机变量及其分布)答案
15.设X为正态分布的随机变量,概率密度为 ,则 9
16.已知X~B(n,p),且E(X)=8,D(X)=4.8,则n=。
17.设随机变量X的密度函数为 ,则 0
二、单项选择题
1.甲、乙、丙三人射击的命中率分别为0.5、0.6、0.7,则三人都未命中的概率为(D)
解:设同一时刻被使用的供水设备的套数为 则 (二项分布).
于是, ,( 0,1,2,3,4,5),即
.,Biblioteka ,.3.若某型号电子元件的使用寿命 (单位: ),(1)写出概率密度 ;(2)求概率 ;(3)求这样的5个独立使用的元件在15000小时后至多有两个能使用的概率。.
解:(1)随机变量 的概率密度为
C.1/3D.1/2
4.设随机变量X的概率密度为 ,则X服从(A)
A.正态分布B.指数分布
C.泊松分布D.均匀分布
5.设随机变量 ,且 ,则参数 的值分别为(B)
A.4和0.6B.6和0.4
C. 8和0.3D.3和0.8
6.设随机变量X的概率密度为 则 ( B )
A. B.
C. D.
7. 设 为随机变量且 , 为常数,则下列各式中不正确的是( D )
(2)
(3)用 表示5个这样独立使用的元件在15000小时后仍能使用的个数,
则 服从二项分布 .于是
4.甲、乙两台自动机床,生产同一种标准件,生产2000只所出的次品数分别用X、Y来表示,经过一段时间的考察,X、Y的分布律分别为:
X
0
1
2
3
P
0.6
0.2
0.1
随机变量练习题(答案)
随机变量练习题(答案)1.袋中有2个黑球6个红球,从中任取两个,可以作为随机变量的是(B )(A )取到的球的个数 (B )取到红球的个数(C )至少取到一个红球 (D )至少取到一个红球的概率提示:(A )的取值不具有随机性,(C )是一个事件而非随机变量,(D )是概率值而非随机变量,而(B )满足要求.2.抛掷两颗骰子,所得点数之和记为ξ,那么ξ=4表示的随机试验结果是(D )(A )一颗是3点,一颗是1点 (B )两颗都是2点(C )两颗都是4点 (D )一颗是3点,一颗是1点或两颗都是2点提示:对(A )、(B )中表示的随机试验的结果,随机变量均取值4,而(D )是ξ=4代表的所有试验结果.掌握随机变量的取值与它刻划的随机试验的结果的对应关系是理解随机变量概念的关键.提示(A )、(D )不满足分布列的基本性质②,(B )不满足分布列的基本性质①,正确选择是(C ). 4.在三次独立重复试验中,若已知A 至少出现一次的概率等于1927,则事件A 在一次试验中出现的概率为31 。
提示:1927=1-(1-p )3, ⇒P (A )=p =31. 5.设随机变量ξ的分布列为P (ξ=k )=(1)c k k +,k =1,2,3,c 为常数,则P (0.5<ξ<2.5)= 98 . 提示:1=c ·(111122334++⨯⨯⨯)=43c , 故c =34. 所以P (0.5<ξ<2.5)=p (1)+p (2)=32+92=98. 6.设随机变量ξ~B (2,p ),η~B (4,p ),若 P (ξ>1)=95,则 P (η≥1)= 6581· 提示:95=P (ξ≥1)=1-P (ξ=0)=1-(1-p )2, 即(1-p )2=94, p =31,故P (η≥1)=1-P (η=0)=1-(1-p )4=1-(32)4=6581. 7.一名学生每天骑自行车上学,从家到学校的途中有5个交通岗,假设他在各交通岗遇到红灯的事件是相互独立的,并且概率都是31。
随机变量及其分布期末练习题及答案
随机变量及其分布期末练习题及答案随机变量及其分布期末练习题及答案1.在事件A 发⽣的概率为p 的伯努利试验中,若以ξ记第r 次A 发⽣时的试验的次数,求ξ的分布。
[解] {}发⽣次试验次⽽第恰好出现了次试验中前A k r A k P k P 11-)(-==ξ),1,(,)1()1(11111 +=-=?-=-------r r k p p Cp p pC rk r r k r k r r k⼩结求离散型随机变量的分布律时,⾸先应该搞清随机变量取可能值时所表⽰的随机事件,然后确定其分布列。
为验证所求分布是否正确,通常可计算⼀下所求得的“分布列”之和是否为1,若不是,则结果⼀定是错误的。
2.设随机变量X 的分布函数为>≤≤<=.1,1;10.0,1)(2x x Ax x x F求(1)A 的值;(2)X 落在)21,1(-及)2,31(内的概率;(3)X 的概率密度函数。
[解] (1)有分布函数的右连续性,在1=x 点处有1)01()1(=+==F A F ,即1=A (2)由分布函数的性质知,41)1()21())21,1((=--=-∈F F X P ;98311)31()2())2,31((2=??-=-=-∈F F X P ;(3)由于)(x F 最多除1=x 和0点外处处可导,且在1,0=x 处连续,若取≤≤><=.10,2;10,0)(x x x x x f 或则0)(≥x f ,且对⼀切x 有?∞-=xdt t f x F )()(,从⽽)(x f 为随机变量X 的密度函数。
3.设),2(~2σN X ,且3.0)42(=<[解] 因为 )0(2)42(3.0Φ-??Φ=<<=σX P 所以 8.05.03.02=+=??Φσ于是 2.0212202)0(=??Φ-=??? ??-Φ=-<-=<σσσσX P X P4.⼀批鸡蛋,优良品种占三分之⼆,⼀般品种占三分之⼀,优良品种蛋重(单位:克))5,55(~21N X ,⼀般品种蛋重)5,45(~22N X 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
随机变量练习题(答案)
1.袋中有2个黑球6个红球,从中任取两个,可以作为随机变量的是(B )
(A )取到的球的个数 (B )取到红球的个数
(C )至少取到一个红球 (D )至少取到一个红球的概率
提示:(A )的取值不具有随机性,(C )是一个事件而非随机变量,(D )是概率值而非随机变量,而(B )满足要求.
2.抛掷两颗骰子,所得点数之和记为ξ,那么ξ=4表示的随机试验结果是(D )
(A )一颗是3点,一颗是1点 (B )两颗都是2点
(C )两颗都是4点 (D )一颗是3点,一颗是1点或两颗都是2点
提示:对(A )、(B )中表示的随机试验的结果,随机变量均取值4,而(D )是ξ=4代表的所有试验结果.掌握随机变量的取值与它刻划的随机试验的结果的对应关系是理解随机变量概念的关键.
提示(A )、(D )不满足分布列的基本性质②,(B )不满足分布列的基本性质①,正确选择是(C ).
4.在三次独立重复试验中,若已知A 至少出现一次的概率等于1927
,则事件A 在一次试验中出现的概率为
31 。
提示:1927
=1-(1-p )3, ⇒P (A )=p =31. 5.设随机变量ξ的分布列为P (ξ=k )=(1)
c k k +,k =1,2,3,c 为常数,则P (0.5<ξ<2.5)= 98 . 提示:1=c ·(111122334++⨯⨯⨯)=43c , 故c =34. 所以P (0.5<ξ<2.5)=p (1)+p (2)=32+92=9
8. 6.设随机变量ξ~B (2,p ),η~B (4,p ),若 P (ξ>1)=9
5,则 P (η≥1)= 6581
· 提示:95=P (ξ≥1)=1-P (ξ=0)=1-(1-p )2, 即(1-p )2=9
4, p =31,
故P (η≥1)=1-P (η=0)=1-(1-p )4=1-(32)4=6581. 7.一名学生每天骑自行车上学,从家到学校的途中有5个交通岗,假设他在各交通岗遇到红灯的事件是相互独立的,并且概率都是3
1。
(1)求这名学生在途中遇到红灯的次数ξ的分布列;(2)求这名学生在首次遇到红灯或到达目的地停车前经过的路口数η的分布列;(3) 这名学生在途中至少遇到一次红灯的概率.
解:(1)ξ~B (5, 31),ξ的分布列为P (ξ=k )=5512()()33
k k k C -,k =0,1,2,3,4,5;
(2)η的分布列为P (η=k )=p (前k 个是绿灯,第k +1个是红灯)=21()33
k ⋅,k =0,1,2,3,4;P (η=5)=P (5个均为绿灯)=52()3
; (3)所求概率=P (ξ≥1)=1-P (ξ=0)=1-52211()3243
=≈0.8683. 8.设ξ的分布列为P (ξ=k )=2
k a ,(k =0,1,2,……,10),求: (1) a ;(2) P (ξ≤2);(3) P (9<ξ<20).
解:(1)由P (ξ=0)+P (ξ=1)+……+P (ξ=10)=1, 即210111(1)222a ++++ =1,解得10242047
a =. (2)P (ξ≤2)=P (ξ=0)+P (ξ=1)+P (ξ=2)=1024111792(1)2047242047
++=. (3)P (9<ξ<20)=P (ξ=10)=102411204710242047⋅=.。
