认证杯数学建模A题第二阶段试题
2016数学建模网络挑战赛第二阶段A题论文

数学建模网络挑战赛承诺书我们仔细阅读了第九届“认证杯”数学中国数学建模网络挑战赛的竞赛规则。
我们完全明白,在竞赛开始后参赛队员不能以任何方式(包括电话、电子邮件、网上咨询等)与队外的任何人(包括指导教师)研究、讨论与赛题有关的问题。
我们知道,抄袭别人的成果是违反竞赛规则的, 如果引用别人的成果或其他公开的资料(包括网上查到的资料),必须按照规定的参考文献的表述方式在正文引用处和参考文献中明确列出。
我们郑重承诺,严格遵守竞赛规则,以保证竞赛的公正、公平性。
如有违反竞赛规则的行为,我们接受相应处理结果。
我们允许数学中国网站()公布论文,以供网友之间学习交流,数学中国网站以非商业目的的论文交流不需要提前取得我们的同意。
我们的参赛队号为:2202参赛队员(签名) :队员1:王奕队员2:丁梦清队员3:庄亚勤参赛队教练员(签名):教练组参赛队伍组别(例如本科组):本科组数学建模网络挑战赛编号专用页参赛队伍的参赛队号:(请各个参赛队提前填写好):2202 竞赛统一编号(由竞赛组委会送至评委团前编号):竞赛评阅编号(由竞赛评委团评阅前进行编号):2016年第九届“认证杯”数学中国数学建模网络挑战赛第二阶段论文题目洗衣机关键词传动系统优化、悬挂系统模型、“活塞式”洗衣机摘要:洗衣机在生活中有着广泛的应用,较为普及的是波轮式洗衣机、滚筒式洗衣机和搅拌式洗衣机。
本文主要针对为了能尽量提高净衣效能和减小洗涤过程对衣物的机械损伤而提出优化方案。
本文首先分别对波轮式洗衣机和滚筒式洗衣机的结构和工作原理进行分析,再在此基础上对波轮式洗衣机的传动系统优化改进,即用多楔带取代三角皮带;其次对滚筒式洗衣机建立悬挂系统数学模型,列出参数外筒、内筒、上配重、下配重、吊簧、减振器以及电机,计算滚筒洗衣机的势能和动能,得出系统的总动能。
再进行悬挂系统关键参数优化结果理论分析,分析之前和改进后筒体质心垂向(y方向)和侧向(x方向)的振幅最大值的变化。
数学建模试卷A参考答案
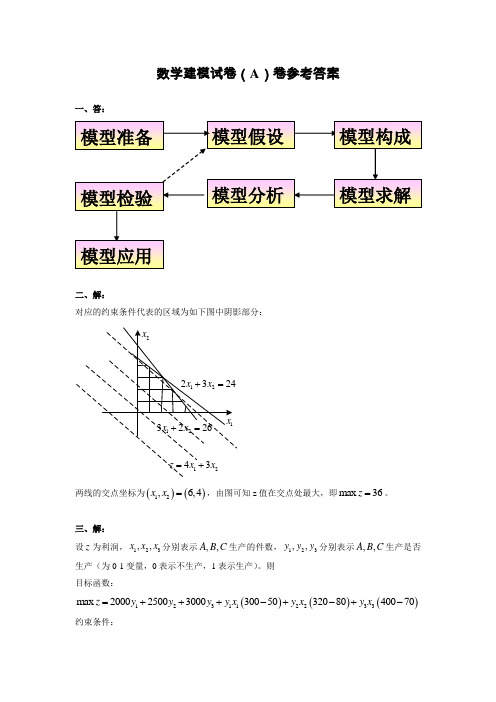
数学建模试卷(A )卷参考答案一、答:二、解:对应的约束条件代表的区域为如下图中阴影部分:两线的交点坐标为()()12,6,4x x =,由图可知z 值在交点处最大,即max 36z =。
三、解:设z 为利润,123,,x x x 分别表示,,A B C 生产的件数,123,,y y y 分别表示,,A B C 生产是否生产(为0-1变量,0表示不生产,1表示生产)。
则 目标函数:()()()123112233max 200025003000300503208040070z y y y y x y x y x =+++-+-+-约束条件:1231231231231232350024000350000,0,0;,0 1;x x x x x x x x x x x x y y or ++≤⎧⎪++≤⎪⎨++≤⎪⎪≥≥≥=⎩四、解:(一)(二)目标层准则层方案层11/2433217551/41/711/21/31/31/52111/31/5311A ⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦1(),0,ij n n ij ji ijA a a a a ⨯=>=层次分析法的基本步骤成对比较阵和权向量元素之间两两对比,对比采用相对尺度设要比较各准则C 1,C 2,… , C n 对目标O 的重要性:i j ijC C a ⇒A ~成对比较阵 A 是正互反阵要由A 确定C 1,… , C n 对O 的权向量选择旅游地(三)111122221212n n n n n n w w w w w w w w w w w w A w w w w w w ⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎤⎥⎢⎥⎢⎥⎣⎦23a =一致比较允许不一致,但要确定不一致的允许范围考察完全一致的情况12(1),,nW w w w =⇒/ij i ja w w =令12(,,)~T n w w w w =权向量“选择旅游地”中准则层对目标的权向量及一致性检验11/2433217551/41/711/21/31/31/52111/31/5311A ⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦准则层对目标的成对比较阵最大特征根λ=5.073权向量(特征向量)w =(0.263,0.475,0.055,0.090,0.110)T 5.07350.01851CI -==-一致性指标随机一致性指标 RI=1.12 (查表) 一致性比率CR =0.018/1.12=0.016<0.1通过一致性检验五、解:()221max ni i i a bx y =+-∑,对,a b 分别求偏导数,可以求解得0.9726,0.0500b a ==。
认证杯a题问题二分析

四、问题二的分析与建模4.1问题二的分析绳索的直径,软硬和表面的摩擦系数等机械性能都会影响打的绳结是否容易自动松脱。
不同的打结方法下,绳索的机械性能与绳结是否容易自动松脱之间存在一定的关系。
绳子的材质、结绳的力度等因素不同,是否容易自动松脱的性质可能也有区别,但本文不考虑这些因素,假设绳索的材质相同,结绳的力度相同且适宜。
为了使绳索最不易松脱,我们通过改变绳索的机械性能的不同因素,从而找出其与绳结是否容易自动松脱之间的关系。
可采用的改变绳索机械性能的方法有(1)减小绳索的横截面积(直径);(2)降低绳索的硬度;(3)增加绳与绳相接处表面的摩擦力;(4)减小绳子的弹性。
在制定方案时,主要考虑的因素有:减小绳子的张力,增大绳子相接处的摩擦力。
对于这个问题可以采用层次分析法进行分析。
上述的各项方法:减小绳索的横截面积(直径);降低绳索的硬度;增加绳与绳相接处表面的摩擦力;减小绳子的弹性。
其目的都是为了减小绳子的张力,增大绳子相接处的摩擦力。
而这一切最终目的都是为了提高绳索的机械性能,使绳结最不易松脱。
4.2模型建立与算法设计4.2.1 根据上述分析,我们可以构建如图(4.1)所示的层次分析结构。
目标层A准则层B方案层C图(4.1) 4.2.2符号说明及相关定义 1)记A 为一致矩阵入m a x =n ,其中n 为rank(A)2)一致性指标1max--=n nCI 入3)平均随机一次性指标1'max--=n nRI 入最不易自动松脱的绳结 B1减小张力B2增大摩擦力C1减小直径C2减小硬度C3增大表面摩擦系数 C4降低弹性4)一致性比例RICI CR注:当CR<0.10时,认为判断矩阵的一致性成立,否则需要修改 4.2.3设立标度采用对因子通过两两比较方式,确定层次中诸因素相对重要性,然后综合判断。
设两个因子对Z 的影响之比为a ij ,为了确定aij 的值及一致性检验,引入Saaty 等建议采用表4-2所示的标度和平均随机一致性指标RI 标准值表4-3。
大学生数学建模竞赛A题参考答案

2018高教社杯全国大学生数学建模竞赛题目<请先阅读“全国大学生数学建模竞赛论文格式规范”)A题城市表层土壤重金属污染分析随着城市经济的快速发展和城市人口的不断增加,人类活动对城市环境质量的影响日显突出。
对城市土壤地质环境异常的查证,以及如何应用查证获得的海量数据资料开展城市环境质量评价,研究人类活动影响下城市地质环境的演变模式,日益成为人们关注的焦点。
按照功能划分,城区一般可分为生活区、工业区、山区、主干道路区及公园绿地区等,分别记为1类区、2类区、……、5类区,不同的区域环境受人类活动影响的程度不同。
现对某城市城区土壤地质环境进行调查。
为此,将所考察的城区划分为间距1公里左右的网格子区域,按照每平方公里1个采样点对表层土<0~10 厘M深度)进行取样、编号,并用GPS记录采样点的位置。
应用专门仪器测试分析,获得了每个样本所含的多种化学元素的浓度数据。
另一方面,按照2公里的间距在那些远离人群及工业活动的自然区取样,将其作为该城区表层土壤中元素的背景值。
附件1列出了采样点的位置、海拔高度及其所属功能区等信息,附件2列出了8种主要重金属元素在采样点处的浓度,附件3列出了8种主要重金属元素的背景值。
现要求你们通过数学建模来完成以下任务:(1> 给出8种主要重金属元素在该城区的空间分布,并分析该城区内不同区域重金属的污染程度。
(2> 通过数据分析,说明重金属污染的主要原因。
(3> 分析重金属污染物的传播特征,由此建立模型,确定污染源的位置。
(4> 分析你所建立模型的优缺点,为更好地研究城市地质环境的演变模式,还应收集什么信息?有了这些信息,如何建立模型解决问题?题目A题城市表层土壤重金属污染分析摘要:本文研究的是某城区警车配置及巡逻方案的制定问题,建立了求解警车巡逻方案的模型,并在满足D1的条件下给出了巡逻效果最好的方案。
在设计整个区域配置最少巡逻车辆时,本文设计了算法1:先将道路离散化成近似均匀分布的节点,相邻两个节点之间的距离约等于一分钟巡逻路程。
2023mathercup数学建模a题

2023mathercup数学建模a题摘要:一、引言1.介绍2023年Mather Cup数学建模竞赛2.分析A题的背景和意义二、A题的题目解析1.题目概述2.题目要求三、解题思路1.建立数学模型2.选择合适的算法求解四、案例分析1.应用解题思路进行具体分析2.结果展示与讨论五、总结与展望1.总结解题过程与收获2.对未来数学建模竞赛的建议和期望正文:一、引言2023年Mather Cup数学建模竞赛作为一项面向全球高校大学生的数学竞赛活动,旨在提高学生的创新思维能力和实际问题解决能力。
本次竞赛的A题涉及到实际问题的数学建模,具有很高的挑战性和实用性。
本文将对A题进行具体的分析和解答。
二、A题的题目解析1.题目概述A题:“某电商平台在双十一期间推出优惠活动,用户购买指定商品可以获得一定金额的返利。
假设用户购买一件商品的价格为p,平台返利金额为r,且用户购买商品的总金额满足p1 + p2 + ...+ pn ≤ 1000。
请建立数学模型,求解在满足上述条件下,用户可以获得的最大返利金额。
”2.题目要求(1) 建立用户购买商品的数学模型。
(2) 求解在满足题目给定条件下,用户可以获得的最大返利金额。
(3) 对所建立的模型进行解释和分析。
三、解题思路1.建立数学模型假设用户购买n件商品,每件商品的价格分别为p1, p2, ..., pn。
用户购买商品的总金额满足p1 + p2 + ...+ pn ≤ 1000。
设用户可以获得的最大返利金额为R。
我们需要求解在满足上述条件下,用户可以获得的最大返利金额R。
2.选择合适的算法求解我们可以使用线性规划的方法来求解这个问题。
首先,将目标函数最大化,即求解R的最大值。
然后,建立约束条件,包括购买商品的总金额不超过1000和返利金额不超过购买商品金额的限制。
最后,利用线性规划求解器求解该问题。
四、案例分析我们通过一个具体的案例来分析这个问题。
假设某用户购买了三件商品,分别为商品A、B和C,价格分别为300元、400元和300元。
2016数学建模第二阶段问题

2016 年“认证杯”数学中国数学建模网络挑战赛第二阶段B 题低分辨率下看世界数码摄像技术被广泛使用于多种场合中。
有时由于客观条件的限制,拍摄设备只能在较低的分辨率下成像。
为简单起见,我们只考虑单色成像。
假设成像的分辨率为32 _ 64,成像方式是将整个矩形视野划分成32 _ 64 个相同大小的矩形格子,图像中每个像素的取值为对应格子的亮度平均值。
每间隔一定时间拍摄一帧图像,运动的画面体现为图像的序列。
第一阶段问题:现在整个视野区域向某个方向缓慢运动,拍摄到的系列图像实时地传输到计算机中。
请你建立合理的数学模型和算法,通过分析实时拍摄的图像,使用尽量少的时间,以判断出运动的方向。
第二阶段问题:对一副静态的图像而言,每个像素对应于视野中的一个格子,每个格子内部的细节信息已经无法还原。
但如果在视野移动的过程中拍摄系列图像,我们通过对多帧图像进行对比分析,仍然有可能还原出来一些在单张照片中无法体现的细节。
请建立合理的数学模型和算法,通过对多帧图像进行分析,尽可能多地还原出被摄物的细节。
A 题洗衣机洗衣机是普及率极高的家用电器,它给人们的生活带来了很大的方便。
家用洗衣机从工作方式来看,有波轮式、滚筒式、搅拌式等若干种类。
在此基础上,各厂商也推出了多种具体方案,设计了不同的几何及运转参数,诸如波轮的外形、内筒的内壁形状、旋转方式和转速等。
不同设计方案的净衣效能和对衣物的损伤程度各不相同。
第一阶段问题:1. 请你建立合理的指标,衡量洗衣机的净衣效能和对衣物的损伤程度。
2. 请你建立合理的数学模型,对典型的波轮式和滚筒式家用洗衣机的工作方式进行分析,并分别估算这两种工作方式的净衣效能和对衣物的损伤程度。
为简单起见,我们可以只考虑洗涤过程,不考虑漂洗和脱水过程。
第二阶段问题:用户总是希望洗衣机能尽量提高净衣效能,而且能够尽量减小洗涤过程对衣物的机械损伤。
为此,请你建立合理的数学模型,对典型的家用洗衣机进行优化的设计。
2023深圳杯数学建模a题第二题

2023深圳杯数学建模a题第二题一、引言数学建模是一门应用数学的学科,旨在将数学理论和方法应用于实际问题的求解过程中。
深圳杯数学建模竞赛是一个国际性的数学建模比赛,吸引了来自全球各地的优秀学子积极参与。
本文将就2023深圳杯数学建模a题的第二题展开讨论,以此展示数学建模的魅力和实用性。
二、题目介绍2023深圳杯数学建模a题第二题是一个实际问题,涉及到社会经济发展中的相关数据分析和预测。
具体来说,题目要求参赛者利用给定的数据,建立数学模型,预测未来某项经济指标的发展趋势,并提出相应的应对措施。
三、数据分析在开始建立数学模型之前,首先需要对给定的数据进行分析。
这些数据可能包括历史经济指标、相关产业发展情况、人口变化趋势等。
通过对数据的分析,可以发现数据之间的内在联系和规律,为模型的建立提供重要的信息和依据。
四、数学模型的建立建立数学模型是解决实际问题的关键步骤。
在建立模型时,需要考虑到问题的具体背景和要求,选择合适的数学工具和方法进行建模。
可能涉及到的数学知识有统计学、微积分、线性代数等,具体的建模方法可以包括回归分析、时间序列分析、神经网络模型等。
五、模型的验证与修正建立完数学模型之后,需要对模型进行验证和修正。
这一步是非常重要的,因为一个好的模型需要能够准确地反映出实际情况,并能够对未来的变化做出合理的预测。
验证模型可以采用历史数据进行拟合,并通过一定的检验方法来评估模型的拟合程度和预测能力。
六、结果分析与应对措施建立好的数学模型可以用来进行进一步的结果分析和应对措施的提出。
通过对模型得到的预测结果进行分析,可以得出一些有益的结论和建议,为相关部门的决策提供参考。
这些应对措施可能涉及到政策调整、资源配置、产业转型等方面。
七、总结通过对2023深圳杯数学建模a题第二题的讨论,我们可以看到数学建模在实际问题求解中的重要性和价值。
数学建模不仅可以锻炼学生的数学思维和解决问题的能力,还可以为社会经济发展提供重要的支持和促进作用。
认证杯数学建模A题第二阶段试题

2012年第五届认证杯
数学中国数学建模网络挑战赛
A题:蜘蛛网
1第一阶段问题
世界上生存着许多种类的蜘蛛,而其中的大部分种类都会通过结网来进行捕食。
请你建立合理的数学模型,说明蜘蛛网织成怎样的结构才是最合适的。
2第二阶段问题
现在我们假设一个具体的环境。
假设有一个凸多边形的区域,蜘蛛准备在这个区域(或其一部分)上结一张网。
问题一:在区域的边界上安置有若干支撑点,蛛丝可以连结在支撑点上,不能连结到区域边界的其它点1。
请建立合理的数学模型,对不同的情况都设计出合适的蛛网结构。
问题二:如果蛛丝可以连结在区域边界的任何点上,请建立合理的数学模型,设计出合适的蛛网结构。
1区域的形状和支撑点的设定都是随机的,示意图只对一种可能的情况做了示例。
1
图1:多边形区域和支撑点的示意图
仅需针对第二阶段问题提交解决方案,内容中可以包含对于第一阶段论文的改进。
2。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2012年第五届认证杯
数学中国数学建模网络挑战赛
A题:蜘蛛网
1第一阶段问题
世界上生存着许多种类的蜘蛛,而其中的大部分种类都会通过结网来进行捕食。
请你建立合理的数学模型,说明蜘蛛网织成怎样的结构才是最合适的。
2第二阶段问题
现在我们假设一个具体的环境。
假设有一个凸多边形的区域,蜘蛛准备在这个区域(或其一部分)上结一张网。
问题一:在区域的边界上安置有若干支撑点,蛛丝可以连结在支撑点上,不能连结到区域边界的其它点1。
请建立合理的数学模型,对不同的情况都设计出合适的蛛网结构。
问题二:如果蛛丝可以连结在区域边界的任何点上,请建立合理的数学模型,设计出合适的蛛网结构。
1区域的形状和支撑点的设定都是随机的,示意图只对一种可能的情况做了示例。
1
图1:多边形区域和支撑点的示意图
仅需针对第二阶段问题提交解决方案,内容中可以包含对于第一阶段论文的改进。
2。
