2020年深国交G1入学考试数学复习资料:真题训练4
2020年最新深圳国际交流学院G1入学考试数学训练2
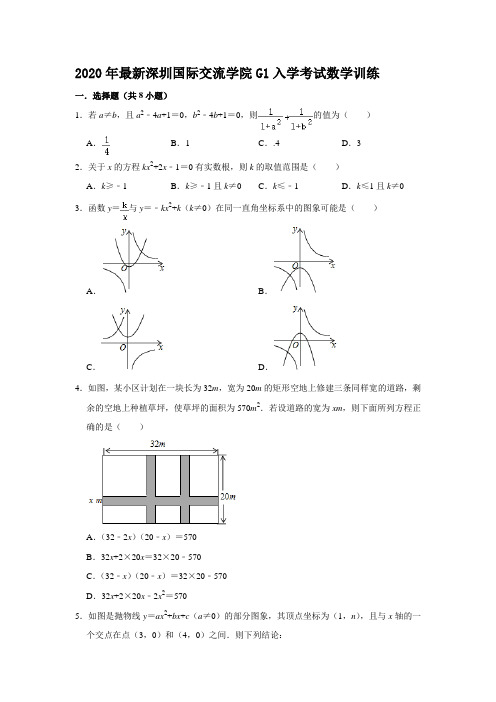
2020年最新深圳国际交流学院G1入学考试数学训练一.选择题(共8小题)1.若a≠b,且a2﹣4a+1=0,b2﹣4b+1=0,则的值为()A.B.1 C..4 D.32.关于x的方程kx2+2x﹣1=0有实数根,则k的取值范围是()A.k≥﹣1 B.k≥﹣1且k≠0 C.k≤﹣1 D.k≤1且k≠0 3.函数y=与y=﹣kx2+k(k≠0)在同一直角坐标系中的图象可能是()A.B.C.D.4.如图,某小区计划在一块长为32m,宽为20m的矩形空地上修建三条同样宽的道路,剩余的空地上种植草坪,使草坪的面积为570m2.若设道路的宽为xm,则下面所列方程正确的是()A.(32﹣2x)(20﹣x)=570B.32x+2×20x=32×20﹣570C.(32﹣x)(20﹣x)=32×20﹣570D.32x+2×20x﹣2x2=5705.如图是抛物线y=ax2+bx+c(a≠0)的部分图象,其顶点坐标为(1,n),且与x轴的一个交点在点(3,0)和(4,0)之间.则下列结论:①a﹣b+c>0;②3a+b=0;③b2=4a(c﹣n);④一元二次方程ax2+bx+c=n﹣1有两个不相等的实数根.其中正确结论的个数是()A.1 B.2 C.3 D.46.甲、乙两车间同时开始加工一批服装.从开始加工到加工完这批服装甲车间工作了9小时,乙车间在中途停工一段时间维修设备,然后按停工前的工作效率继续加工,直到与甲车间同时完成这批服装的加工任务为止.设甲、乙两车间各自加工服装的数量为y (件).甲车间加工的时间为x(时),y与x之间的函数图象如图所示,则下列结论错误的是()A.甲车间每小时加工服装80件B.这批服装的总件数为1140件C.乙车间每小时加工服装为60件D.乙车间维修设备用了4小时7.如图,在平面直角坐标系中,A(1,2),B(1,﹣1),C(2,2),抛物线y=ax2(a≠0)经过△ABC区域(包括边界),则a的取值范围是()A.a≤﹣1或a≥2 B.≤a≤2C.﹣1≤a<0或1<a≤D.﹣1≤a<0或0<a≤28.如图,在单位为1的方格纸上,△A1A2A3,△A3A4A5,△A5A6A7,…,都是斜边在x轴上,斜边长分别为2,4,6,…的等腰直角三角形,若△A1A2A3的顶点坐标分别为A1(2,0),A2(1,1),A3(0,0),则依图中所示规律,A2019的坐标为()A.(﹣1008,0)B.(﹣1006,0)C.(2,﹣504)D.(1,505)二.填空题(共5小题)9.因式分解:x3﹣9x=.10.已知=+,则实数A=.11.如图,菱形ABCD的顶点A,B的横坐标分别为1,4,BD∥x轴、双曲线y=(x>0)经过A,B两点,则菱形ABCD的面积为.12.如图是抛物线型拱桥,当拱顶离水面2m时,水面宽4m,水面下降2m,水面宽度增加m.13.已知直线y=kx(k≠0)经过点(12,﹣5),将直线向上平移m(m>0)个单位,若平移后得到的直线与半径为6的⊙O相交(点O为坐标原点),则m的取值范围为.三.解答题(共4小题)14.计算:+﹣﹣()﹣1.15.如图,AB为⊙O的直径,弦CD∥AB,E是AB延长线上一点,∠CDB=∠ADE.(1)DE是⊙O的切线吗?请说明理由;(2)求证:AC2=CD•BE.16.某中学计划购买A型和B型课桌凳共200套.经招标,购买一套A型课桌凳比购买一套B型课桌凳少用40元,且购买4套A型和5套B型课桌凳共需1820元.(1)求购买一套A型课桌凳和一套B型课桌凳各需多少元?(2)学校根据实际情况,要求购买这两种课桌凳总费用不能超过40880元,并且购买A 型课桌凳的数量不能超过B型课桌凳数量的,求该校本次购买A型和B型课桌凳共有几种方案?哪种方案的总费用最低?17.如图,二次函数y=ax2+2x+c的图象与x轴交于点A(﹣1,0)和点B,与y轴交于点C(0,3).(1)求该二次函数的表达式;(2)过点A的直线AD∥BC且交抛物线于另一点D,求直线AD的函数表达式;(3)在(2)的条件下,在x轴上是否存在一点P,使得以B、C、P为顶点的三角形与△ABD相似?若存在,求出点P的坐标;若不存在,请说明理由.参考答案与试题解析一.选择题(共8小题)1.若a≠b,且a2﹣4a+1=0,b2﹣4b+1=0,则的值为()A.B.1 C..4 D.3【分析】根据根与系数的关系即可求出答案.【解答】解:由题意可知:a、b是方程x2﹣4x+1=0的两个不同的实数根,∴由根与系数的关系可知:ab=1,a+b=4,∴a2+1=4a,b2+1=4b,∴原式=+===1,故选:B.2.关于x的方程kx2+2x﹣1=0有实数根,则k的取值范围是()A.k≥﹣1 B.k≥﹣1且k≠0 C.k≤﹣1 D.k≤1且k≠0 【分析】由于k的取值范围不能确定,故应分k=0和k≠0两种情况进行解答.【解答】解:(1)当k=0时,﹣6x+9=0,解得x=;(2)当k≠0时,此方程是一元二次方程,∵关于x的方程kx2+2x﹣1=0有实数根,∴△=22﹣4k×(﹣1)≥0,解得k≥﹣1,由(1)、(2)得,k的取值范围是k≥﹣1.故选:A.3.函数y=与y=﹣kx2+k(k≠0)在同一直角坐标系中的图象可能是()。
2020年深国交G1入学考试数学冲刺 题型专练 几何综合与实践专题(含答案)

2020年深国交G1入学考试数学冲刺 题型专练 几何综合与实践专题(1. 综合与实践问题探究:(1)如图①,点A 是线段BC 外一动点,若AB =a ,BC =b ,求线段AC 长的最大值(用含a ,b 的式子表示);(2)如图①,点A 是线段BC 外一动点,且AB =1,BC =4,分别以AB 、AC 为边作等边①ABD 、等边①ACE ,连接CD 、BE .①求证:CD =BE ;①求线段BE 长的最大值;问题解决:(3)如图①,在平面直角坐标系中,已知点A (2,0)、B (5,0),点P 、M 是线段AB 外的两个动点,且P A =2,PM =PB ,①BPM =90°,求线段AM 长的最大值及此时点P 的坐标.第1题图(1)解:①点A 是线段BC 外一动点,且AB =a ,BC =b , 则AC ≤AB +BC ,且当点A 位于CB 的延长线上时,线段AC 的长取得最大值,此时AC 的长的最大值为:AB +BC =a +b ;(2)①证明:①①ABD ,①ACE 都是等边三角形,①AD =AB ,AC =AE ,①BAD =①EAC =60°,①①DAC =①BAE ,在①CAD 和①EAB 中,⎩⎪⎨⎪⎧AD =AB ①CAD =①EAB AC =AE,①①CAD ①①EAB (SAS),①CD =BE ;①解:①CD =BE ,①线段BE 长的值最大值即为线段CD 长的最大值,此时BE 的最大值为:BD +BC=AB +BC =5;(3)解:如解图①,连接BM ,①PB =PM ,①MPB =90°,第1题解图①①可以将①APM 绕点P 顺时针旋转90°得到①PBN ,连接AN ,则①APN 是等腰直角三角形,①PN =P A =2,BN =AM ,①线段AM 的长的最大值即为线段BN 长的最大值, 由(1)的结论可知,当点N 在线段BA 的延长线上时,线段BN 的值最大,且此时的最大值为AB +AN 的值.①A (2,0),B (5,0),①OA =2,OB =5,AB =3,①AN =2AP =22,①最大值为22+3;如解图①中,作PE ①x 轴于点E ,第1题解图①①①APN 是等腰直角三角形,①PE =AE =12AN =2, ①OE =OA -AE =2-2,①P (2-2,2), 即线段AM 的最大值为22+3,此时P 的坐标为(2-2,2).2.综合与探究问题背景在综合实践课上,老师让同学们根据如下问题情境,写出两个教学结论:如图①,点C在线段BD上,点E在线段AC上.①ACB=①ACD=90°,AC=BC;DC=CE,M,N分别是线段BE,AD上的点.“兴趣小组”写出的两个教学结论是:①①BCE①①ACD;①当CM,CN分别是①BCE和①ACD 的中线时,①MCN是等腰直角三角形.解决问题(1)请证明“兴趣小组”所写的两个结论的正确性.类比探究受到“兴趣小组”的启发,“实践小组”的同学们写出如下结论:如图②,当①BCM=①ACN时,①MCN是等腰直角三角形.(2)“实践小组”所写的结论是否正确?请说明理由.感悟发现“奋进小组”认为:当点M,N分别是BE,AD的三等分点时,①MCN仍然是等腰直角三角形请你思考:(3)“奋进小组”所提结论是否正确?答:.(填“正确”、“不正确”或“不一定正确”.)(4)反思上面的探究过程,请你添加适当的条作,再写出使得①MCN是等腰直角三角形的数学结论.(所写结论必须正确,写出1个即可,不要求证明)图①图②备用图。
2020年深国交G1入学考试 数学模拟试卷9(初三)

3.若方程组
的解 x 与 y 的和为 0,则 m 的值为( )
A.﹣2 B.0 C.2 D.4
4.如图,有四个平面图形分别是三角形、平行四边形、直角梯形、圆,垂直于 x 轴的直线 l:x=t(0≤t≤a)从原点 O 向右平行移动,l 在移动过程中扫过平面图形的面积为 y(图中阴 影部分),若 y 关于 t 函数的图象大致如图,那么平面图形的形状不可能是 ()
A. a(x1﹣x2)=d C. a(x1﹣x2)2=d
B. a(x2﹣x1)=d D. a(x1+x2)2=d
10.在平面直角坐标系中,函数 y=x2﹣2x(x≥0)的图象为 C1,C1 关于原点对称的图象为 C2,则直线 y=a(a 为常数)与 C1、C2 的交点共有( ) A.1 个 B.1 个或 2 个 C.1 个或 2 个或 3 个 D.1 个或 2 个或 3 个或 4 个
中阴影部分的面积为
.
16.方程 x=
的解是
三.解答题(共 3 小题,共 36 分) 17.(10 分)若 x1,x2 是关于 x 的方程 x2+bx+c=0 的两个实数根,且|x1|+|x2|=2|k(| k 是整数), 则称方程 x2+bx+c=0 为“偶系二次方程”.如方程 x2﹣6x﹣27=0,x2﹣2x﹣8=0,x2+3x﹣ =0, x2+6x﹣27=0,x2+4x+4=0,都是“偶系二次方程”. (1)判断方程 x2+x﹣12=0 是否是“偶系二次方程”,并说明理由; (2)对于任意一个整数 b,是否存在实数 c,使得关于 x 的方程 x2+bx+c=0 是“偶系二次方 程”,并说明理由.
二.填空题(共 6 小题,每题 4 分)
2020年最新深圳国际交流学院G1入学考试数学训练试题

2020年最新深圳国际交流学院G1入学考试数学训练知识点1 :函数的定义与自变量的取值范围1.(3分)下列图象能表示y是x的函数的是()A.B.C.D.2.(3分)在函数y=+中,自变量x的取值范围是()A.x≥1B.x≥1且x≠3C.x≠3D.1≤x≤3知识点2 :一次函数的定义,图像与性质3.(3分)若y=(m﹣1)x2﹣|m| +3是关于x的一次函数,则m的值为()A.1 B.﹣1 C.±1 D.±24.(3分)以下关于直线y=2x﹣4的说法正确的是()A.直线y=2x﹣4与x轴的交点坐标为(0,﹣4)B.坐标为(3,3)的点不在直线y=2x﹣4上C.直线y=2x﹣4不经过第四象限D.函数y=2x﹣4中,y的值随x的增大而减小5.(3分)A(x1,y1)和B(x2,y2)是一次函数y=(k2+1)x+2图象上的两点,且x1<x2,则y与y2的大小关系是()1A.y1=y2B.y1<y2C.y1>y2D.不确定6.(3分)已知正比例函数y=kx(k≠0)的图象经过二、四象限,则一次函数y=kx﹣k的图象大致是()A.B.C.D.7. (3分)将函数y=2x-3的图象向上平移2个单位得到的函数解析式为。
知识点3 :一次函数图像与不等式,方程(组)的关系8.(3分)函数y=kx+b(k、b为常数,k≠0)的图象如图,则关于x的不等式kx+b<0的解集为()A.x>0 B.x<0 C.x<2 D.x>29.(3分)如图,一次函数y=x+1与y=2x﹣1图象的交点是(2,3),观察图像,直接写出方程组 y=x+1 的解为()y=2x﹣1A. B.C. D.知识点4 :观察图像,获取信息10.(3分)电话卡上存有4元话费,通话时每分钟话费0.4元,则电话卡上的余额y(元)与通话时间t(分钟)之间的函数图象是图中的()A.B.C.D.11.(3分)甲、乙两同学骑自行车从A地沿同一条路到B地,已知乙比甲先出发,他们离出发地的距离s/km和骑行时间t/h之间的函数关系如图所示.根据图象信息,以下说法错误的是()A.他们都骑了20kmB.两人在各自出发后半小时内的速度相同C.甲和乙两人同时到达目的地D.相遇后,甲的速度大于乙的速度12. (3分)一台印刷机每年可印刷的书本数量y(万册)与它的使用时间x(年)成反比例关系,当x=2时,y=20.则y与x的函数图象大致是()A. B. C. D.知识点5: 分段函数的定义与图像13.(3分)如图是一个运算程序的示意图,若输出y的值为2,则输入的x值可能为()A.3 B.±1C.1或3 D.±1或314.(3分)小刘下午5点30分放学匀速步行回家,途中路过鲜花店为过生日的妈妈选购了一束鲜花,6点20分到家,已知小刘家距学校3千米,下列图象中能大致表示小刘离学校的距离S(千米)与离校的时间t(分钟)之间的关系的是()A. B.C. D.15.(9分)某城市出租车的收费标准为:3千米以内(含3千米)收费8元,超过3千米时,超过的部分每千米收费1.4元.(1)写出车费y(元)和行车里程x(千米)之间的关系式;(2)甲乘坐13千米需付多少元钱?若乙付的车费是36元,则他乘坐了多少里程?知识点6: 反比例函数的定义,图像与性质16. (3分)在下列函数中,y是x的反比例函数的是()A.y=3x B.y=C.y=D.y=17.(3分)已知函数是反比例函数,且当x<0时,y随着x的增大而增大,则m的取值是.18.(3分)若点A(﹣3,y1),B(﹣2,y2),C(1,y3)都在反比例函数y=(k<0)的图象上,则y1,y2,y3的大小关系是()A.y2<y1<y3B.y3<y2<y1C.y1<y2<y3D.y3<y1<y219.(3分)对于反比例函数y=,下列说法不正确的是()A.图象分布在第一、三象限B.当x>0时,y随x的增大而减小C.图象经过点(2,3)D.若点A(x1,y1),B(x2,y2)都在图象上,且x1<x2,则y1<y220.(3分)已知函数y=图象如图,以下结论,其中正确的有()个:①k<0;②y随x的增大而增大;③若A(﹣1,a),点B(2,b)在图象上,则a<b(﹣x,﹣y)也在图象上.④若P(x,y)在图象上,则点P1A.4个 B.3个 C.2个 D.1个21.(3分)已知A(m+3,2),B(3,)是同一个反比例函数图象上的两个点,则m=知识点7: 反比例函数中K的几何意义22.(3分)反比例函数图象的一支如图所示,△POM的面积为2,则该函数的解析式是()A.y= B.y=C.y=﹣ D.y=﹣23.(3分)如图,在反比例函数y=(x>0)的图象上,有点P1、P2、P3、P4,它们的横坐标依次为1,2,3,4.分别过这些点作x轴与y轴作垂线,图中所构成的阴影部分的面积从左到右依次为S1、S2、S3,则S1+S2+S3=()A.2 B.2.5C.3 D.无法确定知识点 8:反比例函数的应用24. (3分)某种气球内充满了一定质量的气体,当温度不变时,气球内气体的气压P(kPa)是气球体积V的反比例函数,其图象如图所示,当气球内的气压大于160kPa时,气球将爆炸,为了安全,气球的体积应该()A.不小于m3 B.小于m3C.不大于m3 D.小于m3知识点 9: 反比例函数与一次函数结合25.(3分)函数y=﹣2x与函数y=﹣在同一坐标系中的大致图象是()A.B.C.D.26.(3分)如图,正比例函数y1=k1x的图象与反比例函数y2=的图象相交于A,B两点,其中点A的横坐标为2,当y1>y2时,x的取值范围是()A.x<﹣2或x>2 B.x<﹣2或0<x<2C .﹣2<x <0或0<x <2D .﹣2<x <0或x >227.(12分)如图,直线y =kx +b 与反比例函数的图象分别交于点A (﹣1,2),点B (﹣4,n ),直线与x 轴,y 轴分别交于点C ,点D . (1)求此一次函数和反比例函数的解析式; (2)求△AOB 的面积.28.(10分)如图所示,已知一次函数y=kx+b(k≠0)的图象与x 轴、y 轴分别交于A 、B 两点,且与反比例函数y=mx (m≠0)的图象在第一象限交于C 点, CD 垂直于x 轴,垂足为 D.若OA=OB=OD=1,(1)求点A 、B 、D 的坐标;(2)求一次函数和反比例函数的解析式.yOxDC B A29.(14分)为了预防传染病,某学校对教室采用药薰消毒法进行消毒. 已知药物燃烧时,室内每立方米空气中的含药量y(毫克)与时间x(分钟)成正比例,药物燃烧完后,y与x成反比例(如图所示),现测得药物8分钟燃毕, 此时室内空气中每立方米的含药量为6毫克.请根据题中所提供的信息,解答下列问题:(1)分别求出药物燃烧时及药物燃烧后y 关于x 的函数关系式, 并写出自变量x 的取值范围,(2)研究表明,当空气中每立方米的含药量低于 1.6毫克时学生方可进教室,那么从消毒开始,至少需要经过几分钟后,学生才能回到教室?(3)研究表明,当空气中每立方米的含药量不低于3毫克且持续时间不低于10 分钟时,才能有效杀灭空气中的病菌,那么此次消毒是否有效?为什么?参考答案1.D2.B3.B4.B5.B6.C7.y=2x-1,8.D 9.B 10.D 11.C 12.C 13.C 14.C8 x≤315.(1)y = (2)甲需付22元,乙乘坐了23千米。
2020年深国交G1入学考试数学复习资料:真题训练3

⎩2020年深国交G1入学考试数学复习资料真题训练31、有理数a ,b ,c 在数轴上的位置如图所示,化简a -a +b -c -a =.2、如果x 2+x -3=0,那么x 4+7x 3+8x 2-13x -5= .⎧x +y +z =153、已知⎨-3x -y +z =-25,x 、y 、z 为非负数,且N =5x +4y +z ,则N 的取值范围是.4、若一组数据0,-2,8,1,x 的众数是-2,则这组数据的方差是.5、如图,在1×3的小正方形网格中,点A 、B 、C 、D 都在这些小正方形的顶点上,AB 、CD 相交于点P ,则tan ∠APC =.6、已知A ,B ,C 是数轴上的三个点,点A ,B 表示的数分别是1,3,如图所示,若BC =2AB ,则点C 表示的数是。
11325377、按一定规律排成的一列数:,,,,,,3253749,…,则这列数中的第2020个数是。
8、a ,b ,c ,d 是互不相等的正整数,且abcd =441,那么a +b +c +d = 。
9、若x =0是方程(m -2)x 2+3x +m 2+2m -8=0的解,则m =。
11、等腰三角形一腰上的高与另一腰的夹角为36 ,则该等腰三角形的底角的度数为。
12、为了节省材料,某农场主利用围墙(围墙足够长)为一边,用总长为80m的篱笆围成了如图所示的①②③三块矩形区域,而且这三块矩形区域的面积相等,则能围成的矩形区域ABCD的面积最大值是m2.13、如图,矩形ABCD的边长AD=6,AB=4,E为AB的中点,F在边BC上,且BF=2FC,AF分别与DE、DB相交于点M、N,则MN的长为.14、如图,在正方形OABC中,点A的坐标是(-3,1),点B的纵坐标是4,则B点的横坐标是.15、已知点A,B的坐标分别为(1,0),(2,0).若二次函数y=x2+(a-3)x+3的图象与线段AB只有一个交点,则a的取值范围是.16、如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A,B两点,与y轴交于点C,且OA=OC,则下列结论:①abc<0;②b2-4ac4a>0;③ac-b+1=0;④OA⋅OB=-c.其中正确结论的序号是a.。
2020年深国交G1入学考试数学复习资料:新定义问题专题训练(有答案)

例如:因为 ,所以 , .
根据上述规定填空: , ____________, , _____________;
已知 , , , ,求 , 用含m、n的代数式表示 ;
若 , , , ,则a、b的大小关系是:a_______ 填“ ”、“ ”或“ ” .
【学习新知】定义:如果 且 ,即a的n次方等于 且 ,那么数n叫做以a为底M的对数 ,记作 其中a叫做对数的底数,M叫做真数,n叫做以a为底M的对数.例如:因为 ,所以 ;因为 ,所以 ;因为 ,所以 其中零没有对数;在有理数范围内,负数没有对数.
【应用新知】
根据定义计算: _______; _______; ______.
如果 ,那么 _________.
结合上面的知识计算: .
已知 , M、N均为正数 ,求 的值.
答案和解析
1.D
解:由题意可知,原式可化为方程
,
解得 .
2.C
解:由题意可得: ,
3.A
解:由题意得 ,
,
,
,
,
4.C
解:根据题中的新定义得: ,
5.D
解:由题意可得 只有D符合.
6.B
解:由函数 得 ,则 ,
材料二:劳格数有如下运算性质:若m、n为正数,则
根据劳格数的定义,填空: ____, ____;
若 ,求 的值;
已知 , , ,证明: .
24.【知识重现】在七上数学教材p58中,我们已经学习:求n个相同因数a的积的运算叫做乘方 ,乘方的结果叫做幂 ,a叫做底数 ,n叫做指数 , 读作“a的n次幂” 或“a的n次方” ;在 中,已知底数a,指数n,求幂M的运算叫做乘方运算.例如 , .
2020年深国交G1入学考试数学复习资料:限时训练二(2套)

2020年深国交G1入学考试数学复习资料:限时练习题11、如图,将3个12cm×12cm的正方形沿邻边中点剪开,分成两部分,把所得的六片纸片粘在一个边长为62cm正六边形的外面,然后折成多面体,则此多面体的表面积是2、从图形的几何性质考虑,下列字母图形有一个与其他几个不同的是W S T X H3、方程x2+2x-3=0的实数根的和为4、如图,在平行四边形ABCD中,E、F分别是BC边,CD边的中点,AE、AF分别交BD于点G,H,设∆AGH 的面积为S1S1,五边形GHFCE的面积为S2,则S1:S2的值为5、规定[x]表示不大于x的最大整数,例如[2.3]=2,[3]=3,[﹣2.5]=﹣3.那么函数y=x-[x]的图象为(1)(2)(3)(4)⎧,⎬6、一组数据由5个整数组成,中位数是6,唯一的众数是7,那么这5个整数的和最大只可能是7、如图,在正方形ABCD 中,AE =ED ,且EF =2FC ,正方形ABCD 的面积是20,则△ABF 的面积是.8、如图,正方形ABCD 的边长为5,点A 的坐标为(-4,0),点B 在y 轴上,若反比例函数y =k (k >0)的x 图象过点C ,则k =9、如图,直角三角形纸片的两直角边长分别为6,8,按如图所示折叠,使点A 与点B 重合,折痕为DE ,则S △BCE :S △BDE=10、已知函数y =ax 2+2x +1.(1)若函数图象与x 轴只有一个交点,则a =;(2)若方程ax 2+2x +1=0至少有一正根,则a 的取值范围是.11、用min {a ,b ,c }表示a ,b ,c 个数中的最小值,设y =min ⎨-x 2⎩+4x ,-x +43⎫x ⎭(x >0),则y 的最大值是3312、如图,在Rt △ABC 中,∠ACB =90°,sin B =5,D 是BC 上一点,DE ⊥AB 于E ,CD =DE ,AC +CD =9.则BC =.13、如图,点A ,B 为直线y =x 上的两点,过A ,B 两点分别作y 轴的平行线交双曲线y =D 两点.若BD =2AC ,则4OC 2﹣OD 2的值为.1(x >0)于C ,x 14、若关于x的方程(x ﹣4)(x 2﹣6x +m )=0的三个根恰好可以组成某直角三角形的三边长,则m 的值为.15、在n 凸多边形中,除了两个内角外,其余内角之和为2380°,则n =16、如图,AB 为 O 的直径,AB =4,点C 为半圆弧的中点:(1)若 O 的另一条弦AD 长等于2,∠CAD 的度数为;(2)在(1)的条件下,若在直径AB 另一侧有一点E (C ,E 在直线AB 两侧),tan ∠BAE =3,则4CE = .。
2020年最新深圳国际交流学院G1入学考试数学训

2020年最新深圳国际交流学院G1入学考试数学训练1.如图是由 4 个完全一样的小正方体组成的几何体,这个几何体的主视图是()A .B .C .D .2.设 a 为正整数,且 <a +1,则 a 的值为( )A .5B .6C .7D .83.下列图形中,不是轴对称图形的是()A .B .C .D .4.九年级参展作品中有 4 件获得一等奖,其中有 2 名作者是男生,2 名作者是女生.现在要在抽两人去参加学校总结表彰座谈会,求恰好抽中一男一女的概率()A .B .C .D . 5.若在实数范围内有意义,则 x 的取值范围是()A .B .x < 2D .x ≥06.下列事件中,是必然事件的是()A .掷一次骰子,向上一面的点数是 6B .13 个同学参加一个聚会,他们中至少有两个同学的生日在同一个月C .射击运动员射击一次,命中靶心D .经过有交通信号灯的路口,遇到红灯7.如图,l 1∥l 2,等边△ABC 的顶点 A 、B 分别在直线 l 1、l 2,则∠1+∠2=( )A .30°B .40°C .50°D .60°第 7 题 第 8 题第 10 题8.Rt △ABC 中,AB =4,则 cos B 的值是()A .B .C .D .9.《九章算术》是我国古代数学名著,有题译文如下:今有门,不知其高宽;有竿,不知其长短.横放,竿比门宽长出 4 尺;竖放,竿比门高长出 2 尺;斜放,竿与门对角线长恰好相等.问门高、宽和对角线的长各是多少?设门对角线的长为 x 尺,下列方程符合题意的是( ) A .(x +2)2+(x ﹣4)2=x 2 B .(x ﹣2)2+(x ﹣4)2=x 2 C .x 2+(x ﹣4)2=(x ﹣4)2D .(x ﹣2)2+x 2=(x +4)210.如图所示,在平面直角坐标系中,直线 y 1=2x +4 分别与 x 轴,y 轴交于 A ,B 两点,以线段 OB 为一条边向右侧作矩形 OCDB ,且点 D 在直线 y 2=﹣x +b 上,若矩形 OCDB 的面积为 20,直线 y 1=2x +4 与直线 y 2=﹣x +b 交于点 P .则 P 的坐标为( ) A .(2,8)B .C .D .(4,12)11.3x (x ﹣5)+2(5﹣x )分解因式的结果为.12.将抛物线 y =2x 2 向下平移 1 个单位,再向左平移 3 个单位得到的抛物线的解析式是.13.如图:在 Rt △ABC 中,∠B =90°,以顶点 C 为圆心,适当长为半径画弧,分别交 AC 、BC 于点 E 、F ,再分别以点 E 、F 为圆心,大于 EF 的长为半径画弧,两弧交于点 P ,作射线 CP 交 AB 于点 D ,若 BD = 2,AC =6,则△ACD 的面积为.第 13 题 第 14 题14.如图,若△ABC 内接于半径为 6 的⊙O ,且∠A =60°,连接 OB 、OC ,则边 BC 的长为 .15.(每小题 6 分,共 12 分)(2)解不等式组:,并求出所有整数解之和.16.(6 分)已知 x ,y 满足方程组,求代数式(x ﹣y )2﹣(x +2y )(x ﹣2y )的值.17.(本小题 8 分)某校组织学生到恩格贝 A 和康镇 B 进行研学活动,澄澄老师在网上查得,A 和 B 分 别位于学校 D 的正北和正东方向,B 位于 A 南偏东 37°方向,校车从 D 出发,沿正北方向前往 A 地, 行驶到 15 千米的 E 处时,导航显示,在 E 处北偏东 45°方向有一服务区 C ,且 C 位于 A ,B 两地中点处.(1)求 E ,A 两地之间的距离;(2)校车从A地匀速行驶 1 小时 40 分钟到达 B 地,若这段路程限速 100 千米/时,计算校车是否超速? (参考数据 ,cos37°=,tan37°=)18.(本小题 8 分)为了了解本校学生对新闻、体育、动画、娱乐、戏曲五类电视节目的喜爱情况,课题小组随机选取该校部分学生进行了问卷调査(问卷调査表如图 1 所示),并根据调查结果绘制了图 2、图 3两幅统计图(均不完整),请根据统计图解答下列问题.(1)本次接受问卷调查的学生有 名.(2)补全条形统计图.(3)扇形统计图中 B 类节目对应扇形的圆心角的度数为.(4)该校共有 2000 名学生,根据调查结果估计该校最喜爱新闻节目的学生人数.19.(10 分)如图,在平面直角坐标系中,直线 AB 与 y 轴交于点 B (0,7),与反比例函数 y =在第二象限内的图象相交于点 A (﹣1,a ).(1)求直线 AB的解析式;(2)将直线 AB 向下平移 9 个单位后与反比例函数的图象交于点 C 和点 E ,与 y 轴交于点 D ,求△ACD 的面积;(3)设直线 CD 的解析式为 y =mx +n ,根据图象直接写出不等式 mx +n ≤ 的解集.20.(本题10 分)如图,△ABC 内接于⊙O,∠CBG=∠A,CD 为直径,OC 与AB 相交于点E,过点E 作EF⊥BC,垂足为F,延长CD 交GB 的延长线于点P,连接BD.(1)求证:PG 与⊙O 相切;(2)=,的值;(3)在(2)的条件下,若⊙O 的半径为8,PD=OD,求OE 的长.21.已知关于x 的方程a(x+m)2+b=0(a、b、m 为常数,a≠0)的解是x1=2,x2=﹣1,那么方程a(x+m+2)2+b=0 的解.22.有六张正面分别标有数字﹣2,﹣1,0,2,3,4 的不透明卡片,它们除数字不同外其余均相同.现它们背面朝上,洗匀后从中任取一张,将该卡片上的数字记为m,则使关于x 的分式方程有正整数解的概率为.23.如图,在△ABC 中,AB=AC,点A 在y 轴上,点C 在x 轴上,BC⊥x 轴.延长AC 到点D,过点D 作DE⊥x 轴于点G,且DG=GE,连接CE,反比例函数(k≠0)的图象经过点B,和CE 交于点F,且CF:FE=2:1.若△ABE 面积为6,则点D 的坐标为.第23 题第24 题第25 题24.如图,在菱形ABCD 中,∠B=60°,点P 是△ACD 内一点,连接PA、PC、PD,若PA=5,PD=12,PC=13,则AC•BD=.25.矩形ABCD 的边AB=4,边AD 上有一点M,连接BM,将MB 绕M 点逆时针旋转90°得MN,N 恰好落在CD 上,过M、D、N 作⊙O,⊙O 与BC 相切,Q 为⊙O 上的动点,连BQ,P 为BQ 中点,连AP,则AP 的最小值为.26.(本题 8 分)为响应成都市“创建全国文明城市”号召,某单位不断美化环境,拟在一块矩形空地上修建绿色植物园,其中一边靠墙,可利用的墙长不超过18m,另外三边由36m 长的栅栏围成.设矩形ABCD 空地中,垂直于墙的边AB=xm,面积为ym2(如图).(1)求y 与x 之间的函数关系式,并写出自变量x 的取值范围;(2)若矩形空地的面积为160m2,求x 的值;(3)若该单位用8600 元购买了甲、乙、丙三种绿色植物共400 棵(每种植物的单价和每棵栽种的合理用地面积如下表).问丙种植物最多可以购买多少棵?此时,这批植物可以全部栽种到这块空地上吗?请说明理由.甲乙丙单价(元/棵)141628合理用地(m2/棵)0.410.427.(10分)(1)证明推断:如图(1),在正方形ABCD中,点E,Q分别在边BC,AB上,DQ⊥AE于点O,点G,F 分别在边CD,AB 上,GF⊥AE.①求证:DQ=AE;②推断的值为;(2)类比探究:如图(2),在矩形ABCD中,=k(k为常数).将矩形ABCD沿GF折叠,使点A 落在BC 边上的点E 处,得到四边形FEPG,EP 交CD 于点H,连接AE 交GF 于点O.试探究GF 与AE 之间的数量关系,并说明理由;(3)拓展应用:在(2)的条件下,连接CP,当k=时,若tan∠CGP=,GF=2 ,求CP 的长.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
.
x
x
OC 3
3
22.如图,四边形 BDCE 内接于以 BC 为直径的⊙A,已知:BC=10,cos∠BCD= ,∠BCE=30°,则
线段 DE 的长是
.
23. 如图所示,一个半径为 的圆过一个半径为 2 的圆的圆心,则图中阴影部分的面积为
.
24. 如右图是由五个边长都是 1 的正方形纸片拼接而成的,过点 A1 的直线分别与 BC1、BE 交于点 M、N,
7、同时抛掷两枚均匀的骰子 1 次,两枚骰子面朝上的点数之和大于 8 的概率是
.
8、已知实数 x 满足 2x2 x3 x 2 x,则x 的取值为
.
a2 a b a b 3c
9. 若 a、b、c 三个数在数轴上对应点的位置如图所示,化简:
a2 2ac c2
1
12. 若 m,n 是方程 x2﹣2ax+1=0 且 a≥1 的两个实数根,则(m﹣1)2+(n﹣1)2 的最小值是
则 1
1
的值为
.
MB NB
4
个,则 n=
.
15. 如图,在△ABC 中,AB=AC=40, sin A 3 .O 为 AB 上一点,以 O 为圆心,OB 为半径的圆交 BC 5
于 D,且⊙O 与 AC 相切.则 D 到 AC 的距离为
.
2
17.直角坐标系中,点 A(0,0),B(2,0),C(0,2 BC 重合,那么这个三角形的另一个顶点坐标是
.
4.已知
x
1 x
1,则
x4
x2 2007x2
=
1
.
5.分解因式:(a+3)(a﹣3)&不等式组 x m 0 的整数解仅为 1 , 2 , 3 , 若 m , n 为整数, 则代数式
1 n m m2 n2 的值是
.
m 2n m2 4mn 4n2
∠ACB=∠DCE.若 tan∠ACB= ,BC=2,则⊙O 的半径为
.
20. 如图,正六边形 ABCDEF 的边长为 4,两顶点 A,B 分别在 x 轴和 y 轴上运动,则顶点 D 到原点 O 的
距离的最大值为
;最小值为
.
21. 如图所示,矩形 OABC,当点 A 在 y 4 时,点 C 恰好在 y k 上,且 OA 2 ,则 k 的值是
:
2020年深国交G1入学考试数学复习资料 真题训练4
2、实数 a、b、x、y 满足 y x 3 1 a2 , x 3 y 1 b2 那么 2x+y+2a+b 的值是
.
3.(x2﹣x﹣2)6=a12x12+a11x11+a10x10+…+a1x+a0,则 a12+a10+a8+a6+a4+a2=
),若有一三角形与△ABC 全等,且有一条边与 .
18. 如图所示:在平面直角坐标系中,△OCB 的外接圆与 y 轴交于 A(0, ),∠OCB=60°,∠COB=
45°,则 OC=
.
19. 如图,在矩形 ABCD 中,点 O 在对角线 AC 上,以 OA 的半径的⊙O 与 AD、AC 分别交于点 E、F,且
.
a2 2ab b2 b
13. 二次函数 y=ax2+(a﹣b)x﹣b 的图象如图所示,那么化简
的结果是
.
a
14. 在平 面直角坐标系中,横坐标 ,纵坐标都为 整数的点称为整 点.请你观察图 中正方形 A1B1C1D1,
A2B2C2D2,A3B3C3D3…每个正方形四条边上的整点的个数,若累计到正方形 AnBn∁nDn 时,整点共有 1680
