重力坝稳定及应力计算
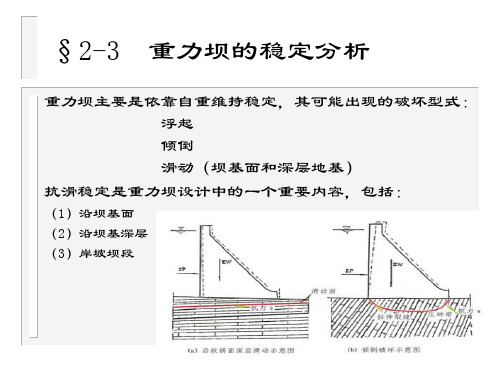
重力坝的抗滑稳定分析
主应力：σ1u=（1+n2) σyu-(pu-puu) n2 σ2u= pu-puu σ1d=(1+ m2) σyd-(pu-pud) m2 σ2d= pd-pud
例1 某重力坝如下图所示，属一级建筑物，基本组合[Ks]=1.10，特殊组合[Ks]=1.05，材料容重为24KN/m3，水的容重为10KN/m3，摩擦系数为f=0.62，试分析该坝的抗滑稳定性。（注：图中高程及尺寸单位均为米）
水工建筑物习题课
重力坝的抗滑稳定分析
沿坝基面的抗滑稳定分析
单一安全系数法、极限状态分析法
抗剪强度公式
Ks=f(∑W-U)/ ∑P
抗剪断公式
Ks’=[f’(∑W-U)+c’A]/ ∑P
刚体极限平衡法
单斜面深层抗滑稳定计算
当整个可能滑动面基本上都由软弱结构面构成
01
01
02
03
04
05
时，宜用抗剪强度公式计算，Ks值用1.05~1.3；
单击此处可添加副标题
校核洪水位情况（特殊组合）抗滑稳定安全系数计算： 扬压力：U=10×25×60.5+10(70-25)×60.5÷2=28737.5(KN) 上游水压力：P1=10×70×70÷2=24500(KN) 下游水压力：P2=10×25×25÷2=3125(KN) 下游水重：W2=10×25×0.7×25÷2=2187.5(KN) 公式：Ｋs=f.(∑W-U)/∑P Ｋs=0.62×(63570+2187.5-28737.5)/(24500-3125)=1.07 ∵基本组合抗滑稳定安全系数：Ｋs=1.24＞[Ｋs]＝１.1０ 特殊组合抗滑稳定安全系数：Ｋs=1.07＞[Ｋs]＝１.05 均符合规范要求 ∴ 该坝的抗滑稳定是安全的。
河海水工建筑物 2-3-1重力坝稳定和应力
分项系数法基本公式
对承载能力验算表达式为：
基本组合：
偶然组合： 0S( GGk , QQk ,k )
1
d
R( fk
m
,k )
0S( GGk , QQk , Ak , ak )
1
d
R( fk
m
, ak )
γG永久作用分项系数； γ0结构重要性系数; γQ可变作用分项系数； φ设计状况系数; GK永久作用标准值； QK可变作用标准值； αK几何参数标准值； fK材料性能标准值； γm材料性能分项系数； AK偶然作用标准值； γd结构系数
具体：
（1）坝基面抗滑稳定的承载能力极限状态：
★按承载能力极限状态校核：应按材料的标准值和荷载的标准值或代表值分别计 算基本组合和偶然组合两种情况。
★ S(*)为作用效应函数，S(*)＝∑PR ∑PR为作用于滑动面之上的全部切向（包括滑动面之上的岩体）作用之和；
★ R(*)为抗力函数，R(*)＝∑f ’R∑WR + c’R AR ∑黏W聚R滑力动。面上全部法向作用之和,f ’R坝基面抗剪断摩擦系数，c’R坝基面抗剪断
评价：该方法有长期的实践经验，目前我国重力 坝设计规范中的强度标准就是以该法为基 础的。
2°弹性理论解析法
该法的力学模型和数学解法均很严密，但前只有 少数边界条件简单的典型结构才有解。
评价：可用于验证其他方法的精确性，有重要 价值。
3°弹性理论差分法
该法力学模型严密，在数学解法上采用差分格式， 是一种近似的方法。
1、单斜面深层抗滑稳定计算
坝基深层单滑动面抗滑稳定计算可参照坝体混凝 土与基岩接触面抗滑稳定计算方法进行，抗滑稳定极 限状态计算应沿软弱结构面进行。
重力坝应力计算的材料力学法基本假定有
重力坝是用来阻挡水流并将水压传递至地基的建筑物。
而在设计重力坝时，对其应力情况进行计算是非常重要的，这涉及到材料力学法的基本假定。
下面将介绍重力坝应力计算所涉及的材料力学法的基本假定。
一、弹性模量与泊松比的假定在重力坝应力计算中，需要用到材料的弹性模量和泊松比。
材料力学法的基本假定之一是材料是具有线弹性性质的材料。
这就意味着材料在应力作用下具有弹性变形，而且在应力消失后能够完全恢复原状。
材料的弹性模量和泊松比假设是常数，不受应力水平和时间的影响。
二、应变与应力的线性关系假定材料力学法的另一个基本假定是应变与应力之间具有线性关系。
这意味着在小应变条件下，应力与应变成正比。
当然，对于某些非线性材料，这个假定是不适用的。
但在重力坝应力计算中，通常可以采用这个假定。
三、应力状态假定材料力学法在重力坝应力计算中通常假定材料处在平面应力状态或平面应变状态。
这意味着材料内部的应力和应变只与一个方向有关，而另外两个方向上的应力和应变可以忽略不计。
这个假定简化了应力计算的复杂性，使得计算更加方便。
四、材料的各向同性假定在重力坝应力计算中，材料力学法通常假定材料是各向同性的。
这意味着材料的力学性能在任何方向上都是相同的。
这个假定在某些实际材料中可能不成立，但在重力坝应力计算中仍然可以采用。
以上就是重力坝应力计算的材料力学法的基本假定。
在实际工程中，设计师需要根据具体情况对这些假定进行合理的适用，以确保重力坝的安全可靠。
五、应力集中与裂纹扩展的假定在重力坝应力计算中还需要考虑应力集中和裂纹扩展的问题。
材料力学法的基本假定包括裂纹尖端的应力场、应力集中系数等问题。
这些假定在重力坝的设计和安全评估中起着重要作用。
应力集中是指在材料中局部区域出现应力增大的现象。
在重力坝的结构中，一些几何形状不规则的部分或者开口处往往容易引起应力集中。
材料力学法的假设需要对这种应力集中进行合理的补偿和计算，以确保结构的安全性。
另外，裂纹扩展是重力坝寿命评估和安全性分析中需要考虑的重要问题。
附录三 用材料力学方法计算坝体应力
附录三 用材料力学方法计算坝体应力一、说明混凝土重力坝一般均用材料力学方法计算坝的应力指标并设计断面，所以本附录仍列入该法的有关计算公式，至于电子计算机的程序另见本规范参考资料。
本法假定坝体各水平截面上的垂直正应力σy 呈直线分布，因此，可以按材料力学中的偏心受压公式来确定σy ，然后依次应用平衡条件确定剪应力τ，水平正应力σx 以及主应力σz 1，σz 2和其方向。
作用在计算截面上的扬压力，通常呈折线形分布(附图6a )，这个图形，可分解为一个在全截面上呈梯形(或三角形)分布的图形(附图6b )和一些在上游部分呈局部三角形或矩形分布的图形，如附图6c 、d 、e 。
当扬压力沿全截面呈直线分布时(即附图6b 所示情况)，其所产生的应力为：=-==τσσvy x p附图6v p 为计算点的扬压力，因此，这种扬压力所产生的应力可以不必专门计算，只须先不考虑扬压力的影响，确定各点上的应力σx ，σy 及τ，然后在正应力中扣去扬压力v p 即可，对于仅作用在截面局部部分上的扬压力(渗透压力)，则必须作专门计算，以确定其所产生的应力。
用材料力学方法计算坝体应力时，以压应力为正，拉应力为负，y 为垂直轴，以向下为正，x 为水平轴，以向上游为正，原点取在计算截面与下游坝面的交点上(附图7)，其余所用符号如下：T ——坝体计算截面沿上、下游方向的长度； n ——上游坝坡，n =tg φs ； m ——下游坝坡，m =tg φxi ； γh ——混凝土容重；γ、'γ——上、下游水的容重('γ在数值上常等于γ)；p 、'p ——计算截面在上、下游坝面所受的水压力(如有泥沙压力时应计入在内)；p y 、'p y ——计算截面在上、下游坝面所受地震动水压力；λ——地震惯性力总系数，λ=k H C z F 以入乘混凝土重量W ，即为地震惯性力，应按《水工建筑物抗震设计规范》计算；vs p 、vxi p ——计算截面在上、下游坝面处的扬压力；ηγH ——在上游的渗透压力(H 为计算截面以上的上游水深，η为扬压力系数)； ΣW ——计算截面上全部垂直力的总和(包括坝体自重、水重、泥沙重及计算的扬压力等)，以向下为正，对于实体重力坝，均切取单位宽度坝体为准(下同)；ΣP ——计算截面上全部水平推力的总和(包括水压力、泥沙压力和地震水压力等)，以指向上游为正；ΣM ——计算截面上全部垂直力及水平力对于计算截面形心的力矩的总和，以使上游面产生压应力者为正；其他符号将在宽缝重力坝计算中再加说明。
重力坝坝体应力计算(好用 未考虑扬压力)
1、计算依据：《混凝土重力坝设计规范》（DL5108-1999）2、计算工况：按正常使用极限状态设计，考虑下列两种作用效应组合：a 、短期组合：持久状况或短暂状况下，可变作用的短期效应永久作用效应的组合。
b 、长期组合：持久状况下，可变作用的短期效应永久作用效应的组合。
3、计算公式：a 、短期组合采用下列公式：b 、长期组合采用下列公式：式中： C 1、C 2—结构的功能限值，Ss （·）、S l （·）—作用效应的短期组合、长期组合时的效应函数，γd3、γd4—正常使用极限状态短期组合、长期组合时的结构系数，ρ—可变作用标准值的长期组合系数，规范取ρ=1G K —永久作用标准值，Q K —可变作用标准值，f k —材料性能的标准值，a k —几何参数的标准值（可作为定值处理）4、计算计算中考虑将正常水位作为长期组合，设计水位和校核水位作为短期组合，计算中不考虑扬压力（因为上游面设置了C20混凝土防渗墙）。
因坝体横剖面有两个折点，因此计算分两个截面进行,分别为1078.770和1066.000高程。
计算内容为各截面在各种组合下上、下面的应力（拉应力和压应力）荷载水平方向以向右为正，垂直方向以向下为正，力矩以顺时针方向为正。
4.1 1078.770m 截面4.1.1荷载计算(1).永久作用标准值（自重）：坝顶宽度 3.000m坝顶高程1083.452则截面高4.682m ，截面以上面积S=14.046m 2坝体材料容重为γ= 2.300t/m 3所以坝体自重G K 为：32.3058t 自重到截面中心的力臂为：0.000m 自重到截面中心的力距为：0t·m (2).可变作用标准值：正常水位1081.500水压力=0.5·γ·H 2=3.726t 水压力到截面中心力臂为：0.91m 水压力到截面中心力距为： 3.391t·m坝体应力计算书()310/,,,d K K K K S C a f Q G S g g £()420/,,,d K K K K l C a f Q G S g r g £设计水位1082.300水压力=0.5·γ·H 2=6.230t 水压力到截面中心力臂为：1.177m 水压力到截面中心力距为：7.331t·m校核水位1082.520水压力=0.5·γ·H 2=7.031t水压力到截面中心力臂为： 1.250m水压力到截面中心力距为：8.789t·m4.1.2应力计算：应力计算参照《土力学》，公式如下：式中：Pmin,Pmax—截面最小、最大压力，Mx —荷载对x—x 轴的力矩，Ix —基础底面积对x—x 轴的惯性矩P=32.3058(正常、设计、校核)A=B×1= 3.000M x= 3.391正常水位7.331设计水位8.789校核水位34.1.1荷载计算(1).永久作用标准值（自重）：永久作用荷载计算分矩形和三角形两部分A 、矩形部分坝顶宽度 3.000m坝顶高程1083.452则截面高17.452m,截面以上矩形面积S 52.356m 2坝体材料容重为γ= 2.300t/m 3所以坝体自重G 1K 为：120.4188t自重到截面中心的力臂L 1为：-5.100m自重到截面中心的力距M 1为：-614.136t·mB 、三角形部分三角形高:12.77截面底宽：13.216则三角形底面宽度=10.216三角形面积S △=65.229坝体材料容重为γ= 2.300t/m 3y I M A P p x x ±=maxmin,所以坝体自重G 2K 为：150.027t自重到截面中心的力臂L 2为：-0.203m自重到截面中心的力距M 2为：-30.405t·m(2).可变作用标准值：正常水位1081.500水压力=0.5·γ·H 2=120.125t水压力到截面中心力臂为： 5.1666667m水压力到截面中心力距为：620.646t·m设计水位1082.300水压力=0.5·γ·H 2=132.845t 水压力到截面中心力臂为：5.433m 水压力到截面中心力距为：721.791t·m校核水位1082.520水压力=0.5·γ·H 2=136.455t水压力到截面中心力臂为： 5.507m水压力到截面中心力距为：751.413t·m4.1.2应力计算：应力计算参照《土力学》，公式如下：式中：Pmin,Pmax—截面最小、最大压力，Mx —荷载对x—x 轴的力矩，Ix —基础底面积对x—x 轴的惯性矩P=120.4188(正常、设计、校核)A=B×1=13.216M x=-23.896正常水位77.250设计水位106.872校核水位3 本工程坝体材料为C10混凝土砌毛石，毛石石料等级为500，查《浆砌石重力坝设计规范》，其允许压力值为，基本组合82.9t/m 2，特殊组合110t/m 2因此，根据上述计算可知，坝体满足最小应力大于0，最大压应力小于坝体允许抗压应力。
有限单元法计算重力坝应力
有限单元法是一种数值分析方法，通过将复杂的结构或系统离散为有限个小的单元，对每个单元进行单独分析，再将这些单元的响应进行组合，得到整体的响应。
这种方法在许多工程领域都有广泛应用，包括重力坝的应力计算。
使用有限单元法计算重力坝的应力，一般会遵循以下步骤：
建立模型：首先，需要建立一个数值模型来表示重力坝。
这个模型通常由一系列的有限单元组成，每个单元代表了坝体的一部分。
这些单元可以是线性的、二次的或更高阶的，取决于问题的复杂性和精度需求。
加载条件：定义重力坝上的载荷，包括坝体的自重、水压力等。
这些载荷将被施加到模型的相应部分。
边界条件：定义模型的边界条件，例如固定边界、自由边界等。
这些条件将影响模型中单元的位移和应力分布。
求解方程：使用有限元方法，将整体的结构方程离散到每个单元上，形成一系列的线性方程组。
然后，使用数值方法（如直接法、迭代法等）求解这些方程，得到每个单元的位移和应力。
后处理：分析求解结果，提取重力坝的应力、应变等信息。
根据这些数据，可以对坝体的安全性进行评估，并进行必要的加固或优化设计。
值得注意的是，使用有限元法进行计算时，需要注意选择合适的单元类型和网格密度，以确保结果的精度和可靠性。
同时，也需要考虑各种因素（如温度变化、材料非线性等）对计算结果的影响。
重力坝的稳定及应力分析
2. 公式：
K'
f ' ( W U ) c ' A
P
3.抗剪断参数的选定
对于大型工程，在设计阶段， f ′,c′应由野外及室内试验 成果决定。在规划阶段，可以参考规范给定的数值选用：
4.安全系数[K′] 设计规范规定： 不分等级,基本荷载组合：采用3.0; 特殊荷载组合：（1）采用2.5；（2）采 用不小于2.3。
地基的接触面、坝体折坡处或坝体断面
削弱的部位（如廊道、泄水管道等部 位）。
1） 基本假定
i.
坝体混凝土为均质、连续、各向同性 的弹性材料； 不考虑两侧坝体的影响，各坝段独立 工作； 假定坝体水平截面上的正应力σy按直 线分布，不考虑廊道等对坝体应力的 影响。
ii.
iii.
2） 边缘应力的计算
一般情况下，坝体的最大应力和 最小应力都出现在坝面，所以应该 首先校核坝体边缘应力是否满足强
坝 踵 坝 踵 坝 趾Fra bibliotek硬 库 满
软
Ec—— Er——
基坝 岩体
2、地基变形弹模对坝体 应力的影响 3、坝体异弹模对坝体应 力的影响 4、纵缝对坝体应力的影 响 5、分期施工对坝体应力 的影响(见下图) 6、坝踵断裂对坝体应力 的影响
坝体主应力分布示意图
影响坝体应力的主要因素有：
1)
地基变形对坝体应力的影响；
2 2
2u Pu
2 d Pd
3）内部应力的计算
1 、坝内水平截面上的正应力 σy 假 定和σy在水平截面上直线分布。 2、坝体内剪应力τ。 3、坝内水平正应力σx。 4、坝内主应力σ1和σ2。 5、考虑扬压力时的计算方法。
考虑扬压力作用时的应力计算
重力坝应力与稳定计算
10
9
校核洪水位
8
设计洪水位
7
正常水位
6
5 前填土 4
反弧段
后填土
3
2
1
0 -2 -1 0 1 2 3 4 5 6 7 8
-2 -1 0 1 2 3 4 5 6 7 8
0.000
0.000 0.900 0.330
0.100
0.006 1.000 0.401
0.200
0.020 1.100 0.478
淤沙压力(Kpa)
坝前土压力(Kpa)
37.39
37.39
37.39
37.39
坝后土压力(Kpa) -29.86 -29.86
-29.86 -29.86
浪压力(Kpa)
冰压力(Kpa)
反弧段离心分力
(Kpa)
地震荷载(Kpa)
2、 ∑W
垂直重力
坝自重
坝上水重
反弧段离心分力
扬压力
α
3 抗滑验算
4
抗剪断强度抗滑 安全系数(K')
-8.84 -3.86
0.00 221.67
-0.37 -0.73 -1.31 -0.13 -493.86
8.16 245.22
8.16 245.22
0.00 221.67
-0.37 -0.73 -1.31 -0.13 -497.73
7.23 246.14
7.23 246.14
式中：X----计算 点到中轴的距 离； J----计算截面的 惯心距
2.02
2.52 2.5
0.7
2110.33
2110.32 2110.3
2108.5
坝前土高
重力坝的荷载与稳定性怎么计算
重力坝的荷载与稳定性怎么计算
重力坝主要依靠自重维持稳定
分类
重力坝的设计内容
①总体布置②稳定分析③剖面设计④应力分析⑤构造设计⑥地基处理
⑦泄水设计⑧监测设计⑨施工设计
作用与荷载
①自重（包括固定设备重）：沿坝基面滑动，仅计坝体重量；沿深层滑动，需计入滑体内岩体重
②静水压力
③扬压力：扬压力=浮力+渗流压力（α：扬压力折减系数）
④动水压力
⑤浪压力
波浪三要素：波高、波长和壅高
⑥泥沙压力
⑦冰压力，⑧土压力，⑨地震作用，⑩温度作用等。
稳定分析
目的：核算坝体沿坝基面或坝基内部缓倾角软弱结构面抗滑稳定的安全度。
失稳机理：首先在坝踵处基岩和胶结面出现微裂松弛区，随后在坝趾处基岩和胶结面出现局部区域的剪切屈服，进而屈服范围逐渐增大并向上游延伸，最后，形成滑动通道，导致坝的整体失稳。
抗剪强度公式（摩擦公式）
抗剪断公式
规范要求：大型工程用抗剪断强度公式；中小型工程可以用摩擦公式。
重力坝设计
溢流坝设计 溢流坝设计 稳定性、应力计算
孔口尺寸
堰顶上游 侧曲线
直线段
堰顶溢流 反弧段曲线 侧曲线
3.溢流坝设计
1.剖面拟定 （1）孔口尺寸：在水文计算中采用孔口总净宽为15m，堤顶高程为 680m进行调洪计算，得此设计下泄流量，设计洪水时Q=317.22m3/s,校 核洪水时Q=406.06m3/s，所以校核洪水时的最大单宽流量 q=406.06/15=27.07[m3/（s·m）]。
堰上最大水头Hmax=685.67-680=5.67m， 取定型水头Hd=Hmax×75%=5.67×75%=5.4m，在规定范围内，是合理的。 1）堰顶上游侧采用椭圆曲线，其方程为
(5)基坑处理
坝基开挖： 坝基面在主河槽挖至659.00m高程，原计划挖至半风化岩石，已是微分 话层。
坝基帷幕灌浆： 在坝址地质剖面图上找出相对隔水层，帷幕深度至645.00m高程。设一 排帷幕孔，钻孔斜向上游，倾斜角控制在5°以内，孔距3m。
坝基排水： 坝基主排水孔设在防渗帷幕下游2m处，间距0.8倍帷幕孔距，即2.4m,深 度645.0m高程。主排水孔之水直接进入排水廊道，次排水管的渗水由横 向排水沟（管）排向下游。
廊道：
基础灌浆廊道采用尺寸为2.5m*3.0（宽*高）上圆下方的标准廊道，廊道 底高程659.00+1.5*2.5=662.75（m）,取663m，距上游边缘距离4m， 坝轴线方向沿地形向两岸逐渐抬高，倾斜角不大于40°，两岸下游洪水位 以上均有进、出口。
坝体排水：
沿坝轴线方向布置一排预制多孔混凝土竖向排水管，间距3.5m，距上游 面2.5m，直径0.15m，并与廊道连通。横向排水管坡降i=1/200，管入 口与廊道的集水沟相连，出口通向下游。管口0.25m，间距在与坝分段相 适应的前提下按30~50m左右进行 布置。
重力坝抗滑稳定及应力计算
项目名称：几内亚凯勒塔（KALETA）水电站工程项目阶段：复核阶段计算书名称：重力坝抗滑稳定及应力计算审查：校核：计算：黄河勘测规划设计有限公司Yellow River Engineering Consulting Co. ,Ltd.二〇一二年四月目录1.计算说明 (1)1.1 目的与要求 (1)1.2 基本数据 (1)2.计算参数和研究方法 (2)2.1 荷载组合 (2)2.2 计算参数及控制标准 (2)2.3 计算理论和方法 (3)3.计算过程 (5)3.1 荷载计算 (5)3.1.1 自重 (5)3.1.2 水压力 (6)3.1.3 扬压力 (10)3.1.4 地震荷载 (14)3.2 安全系数及应力计算 (17)4.结果汇总 (22)1.计算说明1.1 目的与要求下列计算是有关挡水坝段、溢流坝段、进水口、底孔坝段抗滑稳定性和基底应力计算。
1.2 基本数据正常蓄水位：110m；设计洪水位：112.94m；校核洪水位：113.30m；大坝设计洪水标准为100年一遇，校核洪水标准为1000年一遇；坝址区地震动峰值加速度为0.15g（g=9.81m/s²），地震动反应周期为0.25s，相应的地震基本烈度为7度，本工程抗震设计烈度为7度。
计算选取的挡水坝段坝顶高程114.00m，坝基底高程92.00m，坝高22m，坝顶宽5m。
上游坝面竖直，下游坝坡在107.33m高程以上竖直，在107.33m 高程以下坡度为1:0.75。
计算选取的溢流坝段堰顶高程110.00m，坝基底高程96.00m，坝高14m，上游坝面竖直，下游坝坡在108.59m高程以上为Creager剖面，在108.59m 高程以下坡度为1:0.85。
正常蓄水位时，溢流坝段下游无水；设计洪水位112.94m时，下游水位104.80m；校核洪水位113.30m时，下游水位105.42m。
进水口坝段顶高程114.00m，坝基底高程87.80m，坝高26.2m，顶宽13.06m，上游坝坡为1:0.25，下游坝坡在107.33m高程以上竖直，在107.33m 高程以下坡度为1:0.75。
第四节--重力坝的应力分析
Gravity Dam Located onBatholith
第四节重力坝的应力分析
目的：
1、为了检验大坝在施工期和运用 期是否满足强度要求；
2、为解决设计和施工中的某些问 题，如砼分区，某些部位的配 筋等提供依据。
应力分析的过程：
1、进行荷载计算及荷载组合 2、选择合适的方法进行应力计算 3、检验大坝各部位的应力是否满
位等）的局部应力、个别部位（如宽缝重力坝的头部、闸 墩、导墙等）的应力等步骤，必要时分析坝基的上、下游 局部应力及内部应力。
三、材料力学方法
（一）基本假定 1、坝体砼为均质，连续各向同性
的弹性材料。 2、取单宽坝体作为固结在地基上
的悬臂梁计算，且不受两侧坝体的影 响。
3、水平断面上的垂直正应力σy是 直线分布。 （二）**边缘应力的计算
2)短期组合下游坝面的垂直拉应力核算
•施工期属短暂状况，坝体下游面的垂直拉应力应不大于
100kPa，其计算式为
Wc M cTc 100 (kPa)
Ac
Jc
第四节 重力坝的应力分析
其他： 坝体内一般不容许出现主拉应力，但以下情况例外：①宽
缝重力坝离上游面较远的局部区域，可出现拉应力，但不 得超过混凝土的容许拉应力；②当溢流坝堰顶部位出现拉 应力时，可考虑配置钢筋；③廊道及其它孔洞周边的拉应 力区域，宜配置钢筋，以承受拉应力。
坝体主应力 分布示意图
作业2
图与荷载同作业1，砼强度等级C10，标准抗压 强度fkc=10MPa，坝基为较完整的微风化花岗片 麻岩，标准抗压强度fkR=80MPa 试核算基本组合的设计洪水位情况下 (1)计算坝基面A、B及折坡处水平面C、D点的应 力x、y、及主应力； (2)坝趾B抗压强度和坝踵A应力是否满足要求； (3)根据所计算的稳定安全系数及应力情况．讨论 此坝断面设计是否得当；
基于重力坝应力计算及稳定分析的优化设计
基于重力坝应力计算及稳定分析的优化设计重力坝是一种常见的水利工程结构，其稳定性是设计中需要考虑的重要问题。
在设计重力坝时，需要对其应力进行计算和稳定性进行分析，并进行优化设计。
首先，重力坝的应力计算需要考虑以下几个方面。
首先是坝体自重的计算，包括坝体上升水压力和上升地下水压力。
其次是坝顶压力的计算，包括抗倾覆稳定和抗滑移稳定的力学分析。
还需要考虑水侧坝体的压力计算，包括水压头的作用和大坝的承压强度。
最后是岩质坝体的应力分析，考虑岩性、节理的影响及坝体的变形与稳定性。
为了保证重力坝的稳定性，需要进行稳定分析。
稳定分析主要包括抗倾覆稳定和抗滑移稳定两个方面。
抗倾覆稳定分析是为了防止重力坝在承受水压力的作用下发生倾覆。
抗滑移稳定分析是为了防止重力坝在地基土的滑移力的作用下发生移动。
通过合理选择坝体的高度、坝基的强度和选择合适的岩质材料，可以有效地提高重力坝的稳定性。
在重力坝的优化设计中，可以从以下几个方面进行考虑。
首先是合理选择重力坝的形式，可以是三角形、梯形或者圆弧形等不同形式，根据工程实际情况进行选择。
其次是选择合适的坝基处理措施，包括混凝土垫层、防渗墙等，可以提高坝体的稳定性。
另外，可以考虑采用辅助措施，如设置消能防冲设施、阻水排水系统等，提高重力坝的安全性。
最后，可以进行不同形式的优化设计，如遗传算法、模拟退火算法等，寻找最优设计方案，既能满足工程要求，又能提高工程的经济性和可行性。
综上所述，基于重力坝的应力计算及稳定分析的优化设计是一个综合性的工程问题。
通过合理的应力计算和稳定分析，可以提高重力坝的稳定性。
同时，通过优化设计，可以选择合适的形式和措施，提高工程的安全性和经济性。
因此，在重力坝的设计中，需要综合考虑各种因素，进行全面的分析和优化设计。
百色水利枢纽重力坝稳定和应力分析
表 1 坝体抗滑稳定安全系数值
工 况 1
2
3
4
5
6
原断面 3. 058 3. 016 2. 645 2. 533 2. 826 21. 825
现断面 3. 068 3. 026 2. 652 2. 539 2. 843 21. 771
3. 2. 2 坝体应力 各工况下原断面和现断面坝踵和坝趾的竖直向
我们对招标设计阶段的主坝原断面和现断面的 稳定和应力应变情况作了对比分析研究 。本文仅对
非溢流坝段的具有最大坝高的代表坝块 6 号坝块的 对比分析研究情况及主要结果作简要介绍 。6 号坝 块横断面如图 1 。
图 1 6 号坝块横断面 (单位 :m)
2 坝基地质
坝址区出露的地层主要有泥盆系中 、上统的罗 富组 (D2L) 和榴江组 (D3L) ,石炭系 (C) 下 、中 、上统 ,
正常控 原断面 - 0. 432 0. 480 - 0. 790 - 1. 605 - 0. 219 - 2. 887 制泄洪 现断面 - 0. 912 0. 071 - 1. 101 - 2. 572 - 0. 571 - 4. 997
校核洪 原断面 - 0. 172 0. 877 - 0. 664 - 1. 691 - 0. 185 - 3. 044 水水位 现断面 - 0. 655 0. 375 - 0. 928 - 2. 716 - 0. 636 - 5. 229
3 材料力学法分析
材料力学法分析计算坝稳定和应力时采用自编 程序 。抗剪断强度参数 :坝体 RCC 层间 f ′= 1. 1 , c′ = 0. 9 M Pa ;6 号 (6A) 坝块混凝土与辉绿岩间 f ′= 1. 0 , c′= 0. 8 M Pa 3. 1 计算工况
重力坝抗滑稳定计算
104875.62
60591.90
0.00
0.00
8168.33
5051.04
15209.33
10773.53
1865.30
22125.72
0.00
7.33 14.00
0.00
8666.15
5452.18
3589.34
坝面应力计算
上游面垂直正应力Kpa
σyu
下游面垂直正应力Kpa
σyd
上游面剪应力Kpa
校核工况坝体抗滑稳定计算
基本资料
水容重rw(KN/m3) 混凝土容重r(KN/m3) 泥沙容重rs(KN/m3) 泥沙摩擦角Φs(°) 坝顶宽B1(m) 坝底宽B2(m) 上游斜坡段坝高Hx 上游水位高程H1(m) 下游水位高程H2(m) 坝顶高程Hb(m) 坝底高程Ht(m) 堰顶高程 淤沙高程Hs(m) 坝高H(m) 上游坡度系数n 下游坡度系数m 帷幕至上游面距离(m) 上游排水孔距上游面距离(m) 下游排水孔距下游面距离(m) 帷幕扬压力折减系数a1 排水扬压力折减系数a2 浪长L1(m) 波高2h1 波浪中心至静水位高差h0 摩擦系数f 凝聚力c(Mpa) 抗剪断摩擦系数f´ 抗剪断凝聚力c´ 岩层倾角(°)
U4
0.00
0 浪压力(KN) 0.7
PL
3.5 水平淤沙压力(KN)
PsH
5.5 垂直淤沙压力(KN)
PsV
0.00
0
0.25
∑ 15842.47 5839.30
1
#REF! #REF! 抗滑稳定安全系数
∑
10003.17
抗滑稳定计算
K
1.81
考虑倾角
#REF! 抗剪断安全系数
重力坝稳定及应力计算
坝体强度承载能力极限状态计算及坝体稳定承载能力极限状态计算〔一〕、基本资料坝顶高程：m校核洪水位〔P = 0.5 %〕上游：m下游：m正常蓄水位上游：m下游：m死水位：m混凝土容重：24 KN/m3坝前淤沙高程：m泥沙浮容重：5 KN/m3混凝土与基岩间抗剪断参数值：f `c `= 0.2 Mpa坝基基岩承载力：［f］= 400 Kpa坝基垫层混凝土：C15坝体混凝土：C1050年一遇最大风速：v 0 = 19.44 m/s多年平均最大风速为：v 0 `= 12.9 m/s吹程D = 1000 m〔二〕、坝体断面1、非溢流坝段标准剖面(1)荷载作用的标准值计算〔以单宽计算〕 m ，下游水位1094.89m 〕 ① 竖向力〔自重〕W 1 = 24×5×17 = 2040 KN W 2 = 24×× /2 = KN W 3×〔〕2× /2 = KN ∑W = KNW 1作用点至O 点的力臂为： (13.6-5) /2 = 4.3 m W 2作用点至O 点的力臂为：m 067.16.83226.13=⨯- W 3作用点至O 点的力臂为：m 6.58.0)10905.1094(3126.13=⨯-⨯-竖向力对O点的弯矩〔顺时针为“－”，逆时针为“+”〕：M OW1 = 2040×4.3 = 8772 KN·mM OW2 = －×1.067 = －1183.7 KN·mM OW3 = －×5.6 = －445 KN·m∑M OW = 7143.3 KN·m②静水压力〔水平力〕P1 = γH12×－1090)2 /2= －1178.4 KNP2 =γH22×(1094.89-1090)2 /2 = KN∑P = －KNP1作用点至O点的力臂为：－P2作用点至O点的力臂为：－静水压力对O点的弯矩〔顺时针为“－”，逆时针为“+”〕：M OP1 ×5.167 = －6089 KN·mM OP2 ×1.63 = 191.2 KN·m∑M OP = －5897.8 KN·m③扬压力扬压力示意图请见下页附图：H1 = －1090 = 15.5 mH2 = －1090 = m(H1 －H1) = －m计算扬压力如下：U1××= KNU2 = 9.81 ××/2 = KN∑U = KNU1作用点至O点的力臂为：0 mU2作用点至O点的力臂为：13.6 / 2－竖向力对O点的弯矩〔顺时针为“－”，逆时针为“+”〕：M OU1 = 0 KN·mM OU2 = －×2.267 = －1604.6 KN·m∑M OU = －1604.6 KN·m④浪压力〔直墙式〕浪压力计算简图如下：由确定坝顶超高计算时已知如下数据：单位：m使波浪破碎的临界水深计算如下：%1%122ln 4h L h L L H m m m cr πππ-+=将数据代入上式中得到： 013.183.02644.783.02644.7ln 4644.7=-+=πππcr H 由判定条件可知，本计算符合⑴H ≥H cr 和H ≥L m /2，单位长度上的浪压力标准值按下式计算：)(41%1Z m W Wkh h L P +=γ 式中：γw ── KN/m 3 其余计算参数已有计算结果。
重力坝抗滑稳定及应力计算
项目名称：几内亚凯勒塔（KALETA）水电站工程项目阶段：复核阶段计算书名称：重力坝抗滑稳定及应力计算审查：校核：计算：黄河勘测规划设计有限公司Yellow River Engineering Consulting Co. ,Ltd.二〇一二年四月目录1.计算说明 (1)1.1 目的和要求 (1)1.2 基本数据 (1)2.计算参数和研究方法 (1)2.1 荷载组合 (1)2.2 计算参数及控制标准 (2)2.3 计算理论和方法 (3)3.计算过程 (4)3.1 荷载计算 (4)3.1.1 自重 (4)3.1.2 水压力 (4)3.1.3 扬压力 (8)3.1.4 地震荷载 (10)3.2 安全系数及应力计算 (12)4.结果汇总 (17)1.计算说明1.1 目的和要求下列计算是有关挡水坝段、溢流坝段、进水口、底孔坝段抗滑稳定性和基底应力计算。
1.2 基本数据正常蓄水位：110m；设计洪水位：112.94m；校核洪水位：113.30m；大坝设计洪水标准为100年一遇，校核洪水标准为1000年一遇；坝址区地震动峰值加速度为0.15g（g=9.81m/s²），地震动反应周期为0.25s，相应的地震基本烈度为7度，本工程抗震设计烈度为7度。
计算选取的挡水坝段坝顶高程114.00m，坝基底高程92.00m，坝高22m，坝顶宽5m。
上游坝面竖直，下游坝坡在107.33m高程以上竖直，在107.33m 高程以下坡度为1:0.75。
计算选取的溢流坝段堰顶高程110.00m，坝基底高程96.00m，坝高14m，上游坝面竖直，下游坝坡在108.59m高程以上为Creager剖面，在108.59m高程以下坡度为1:0.85。
正常蓄水位时，溢流坝段下游无水；设计洪水位112.94m 时，下游水位104.80m；校核洪水位113.30m时，下游水位105.42m。
进水口坝段顶高程114.00m，坝基底高程87.80m，坝高26.2m，顶宽13.06m，上游坝坡为1:0.25，下游坝坡在107.33m高程以上竖直，在107.33m 高程以下坡度为1:0.75。
重力坝抗滑稳定与应力计算
项目名称：几亚凯勒塔（KALETA）水电站工程项目阶段：复核阶段计算书名称：重力坝抗滑稳定及应力计算审查：校核：计算：黄河勘测规划设计Yellow River Engineering Consulting Co. ,Ltd.二〇一二年四月目录1.计算说明 (1)1.1 目的与要求 (1)1.2 基本数据 (1)2.计算参数和研究方法 (1)2.1 荷载组合 (1)2.2 计算参数及控制标准 (2)2.3 计算理论和方法 (3)3.计算过程 (4)3.1 荷载计算 (4)3.1.1 自重 (4)3.1.2 水压力 (4)3.1.3 扬压力 (6)3.1.4 地震荷载 (7)3.2 安全系数及应力计算 (9)4.结果汇总 (11)1.计算说明1.1 目的与要求下列计算是有关挡水坝段、溢流坝段、进水口、底孔坝段抗滑稳定性和基底应力计算。
1.2 基本数据正常蓄水位：110m；设计洪水位：112.94m；校核洪水位：113.30m；大坝设计洪水标准为100年一遇，校核洪水标准为1000年一遇；坝址区地震动峰值加速度为0.15g（g=9.81m/s²），地震动反应周期为0.25s，相应的地震基本烈度为7度，本工程抗震设计烈度为7度。
计算选取的挡水坝段坝顶高程114.00m，坝基底高程92.00m，坝高22m，坝顶宽5m。
上游坝面竖直，下游坝坡在107.33m高程以上竖直，在107.33m 高程以下坡度为1:0.75。
计算选取的溢流坝段堰顶高程110.00m，坝基底高程96.00m，坝高14m，上游坝面竖直，下游坝坡在108.59m高程以上为Creager剖面，在108.59m高程以下坡度为1:0.85。
正常蓄水位时，溢流坝段下游无水；设计洪水位112.94m 时，下游水位104.80m；校核洪水位113.30m时，下游水位105.42m。
进水口坝段顶高程114.00m，坝基底高程87.80m，坝高26.2m，顶宽13.06m，上游坝坡为1:0.25，下游坝坡在107.33m高程以上竖直，在107.33m 高程以下坡度为1:0.75。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
坝体强度承载能力极限状态计算及坝体稳定承载能力极限状态计算（一）、基本资料坝顶高程：1107.0 m校核洪水位（P = 0.5 %）上游：1105.67 m下游：1095.18 m 正常蓄水位上游：1105.5 m下游：1094.89 m死水位：1100.0 m混凝土容重：24 KN/m3坝前淤沙高程：1098.3 m泥沙浮容重：5 KN/m3混凝土与基岩间抗剪断参数值：f `= 0.5c `= 0.2 Mpa坝基基岩承载力：［f］= 400 Kpa坝基垫层混凝土：C15坝体混凝土：C1050年一遇最大风速：v 0 = 19.44 m/s多年平均最大风速为：v 0 `= 12.9 m/s吹程D = 1000 m（二）、坝体断面1、非溢流坝段标准剖面(1)荷载作用的标准值计算（以单宽计算）A 、正常蓄水位情况（上游水位1105.5m ，下游水位1094.89m ） ① 竖向力（自重）W 1 = 24×5×17 = 2040 KN W 2 = 24×10.75×8.6 /2 = 1109.4 KNW 3 = 9.81×（1094.5-1090）2×0.8 /2 = 79.46 KN ∑W = 3228.86 KNW 1作用点至O 点的力臂为： (13.6-5) /2 = 4.3 m W 2作用点至O 点的力臂为：m 067.16.83226.13=⨯- W 3作用点至O 点的力臂为：m 6.58.0)10905.1094(3126.13=⨯-⨯-竖向力对O点的弯矩（顺时针为“－”，逆时针为“+”）：M OW1 = 2040×4.3 = 8772 KN·mM OW2 = －1109.4×1.067 = －1183.7 KN·mM OW3 = －79.46×5.6 = －445 KN·m∑M OW = 7143.3 KN·m②静水压力（水平力）P1 = γH12 /2 = 9.81×(1105.5－1090)2 /2= －1178.4 KNP2 =γH22 /2 =9.81×(1094.89-1090)2 /2 = 117.3KN∑P = －1061.1 KNP1作用点至O点的力臂为：(1105.5－1090)/3 = 5.167mP2作用点至O点的力臂为：(1094.89－1090)/3 = 1.63m静水压力对O点的弯矩（顺时针为“－”，逆时针为“+”）：M OP1 = 1178.4×5.167 = －6089 KN·mM OP2 = 117.3×1.63 = 191.2 KN·m∑M OP = －5897.8 KN·m③扬压力扬压力示意图请见下页附图：H1 = 1105.5－1090 = 15.5 mH2 = 1094.89－1090 = 4.89 m(H1 －H1) = 15.5－4.89 = 10.61 m计算扬压力如下：U1 = 9.81×13.6×4.89 = 652.4 KNU2 = 9.81 ×13.6×10.61 /2 = 707.8 KN∑U = 1360.2 KNU1作用点至O点的力臂为：0 mU2作用点至O点的力臂为：13.6 / 2－13.6 / 3 = 2.267m 竖向力对O点的弯矩（顺时针为“－”，逆时针为“+”）：M OU1 = 0 KN·mM OU2 = －707.8×2.267 = －1604.6 KN·m∑M OU = －1604.6 KN·m④浪压力（直墙式）浪压力计算简图如下：由确定坝顶超高计算时已知如下数据：单位：m使波浪破碎的临界水深计算如下：%1%122ln 4h L h L L H m m m cr πππ-+=将数据代入上式中得到： 013.183.02644.783.02644.7ln 4644.7=-+=πππcr H 由判定条件可知，本计算符合⑴H ≥H cr 和H ≥L m /2，单位长度上的浪压力标准值按下式计算：)(41%1Z m W Wkh h L P +=γ 式中：γw ── 水的重度 = 9.81 KN/m 3 其余计算参数已有计算结果。
浪压力标准值计算得：KN P Wk 865.20)283.083.0(644.781.941-=+⨯⨯⨯=对坝底中点O 取矩为（顺时针为“－”，逆时针为“+”）：M OPWK = (9.81×1.113×0.862/2)×(15.5+1.113/3)+(9.81×3.822×0.862/2)×(15.5－3.822/3) = －(74.687+229.89) = －304.577 KN ·m⑤ 淤沙压力 淤沙水平作用力：)245(2122S S Sb sk tg h p ψγ-︒=式中：γSb ── 淤沙浮容重 = 5 KN/m 3h S ── 挡水建筑物前泥沙淤积厚度 = 8.3m ψSB ── 淤沙内摩擦角 =18° 代入上式得到淤沙压力标准值P SK = －90.911 KN对O 点的力臂为（1098.3－1090）/3 = 2.767m对O 点取矩 M OPSK = －90.911×2.767 = －251.552 KN ·m 将计算的各荷载进行汇总整理。
结论请见附表1。
B 、校核洪水位情况（上游水位1105.67m ，下游水位1095.18m ） ① 竖向力（自重）W 1 = 24×5×17 = 2040 KN W 2 = 24×10.75×8.6 /2 = 1109.4 KNW 3 = 9.81×（1095.34-1090）2×0.8 /2 = 111.9 KN ∑W = 3261.3 KNW 1作用点至O 点的力臂为： (13.6-5) /2 = 4.3 m W 2作用点至O 点的力臂为：m 067.16.83226.13=⨯- W 3作用点至O 点的力臂为：m 376.58.0)109034.1095(3126.13=⨯-⨯- 竖向力对O 点的弯矩（顺时针为“－”，逆时针为“+”）： M OW1 = 2040×4.3 = 8772 KN ·mM OW2 = －1109.4×1.067 = －1183.7 KN ·mM OW3 = －111.9×5.376 = －601.6 KN·m∑M OW = 6986.7 KN·m②静水压力（水平力）P1 = γH12 /2 = 9.81×(1105.67－1090)2 /2 = －1204.4 KN (→) P2 =γH22 /2 =9.81×(1095.18－1090)2 /2 = 131.6 KN (←)∑P = －1072.8 KN (→)P1作用点至O点的力臂为：(1105.67－1090)/3 = 5.223mP2作用点至O点的力臂为：(1095.18－1090)/3 = 1.727 m静水压力对O点的弯矩（顺时针为“－”，逆时针为“+”）：M OP1 = 1204.4×5.223 = －6290.6 KN·mM OP2 = 131.6×1.727 = 227.3 KN·m∑M OP = －6063.3 KN·m③扬压力扬压力示意图请见下图：H1 = 1105.67－1090 = 15.67 mH2 = 1095.18－1090 = 5.18 m(H1 －H1) = 15.67－5.18 = 10.49 m计算扬压力如下：U1 = 9.81×13.6×5.18 = 691.1 KNU2 = 9.81×13.6×10.49 / 2 = 699.8 KN∑U = 1390.9 KNU1作用点至O点的力臂为：0 mU2作用点至O点的力臂为：13.6 / 2 －13.6 / 3 = 2.267m 竖向力对O点的弯矩（顺时针为“－”，逆时针为“+”）：M OU1 = 0 KN·mM OU2 = 699.8×2.267 = －1586.4 KN·m∑M OU = －1586.4 KN·m④浪压力（直墙式）浪压力计算简图如下：由确定坝顶超高计算时已知如下数据：单位：m使波浪破碎的临界水深计算如下：%1%122ln 4h L h L L H m m m cr πππ-+=将数据代入上式中得到： m H cr 584.05.02069.55.02069.5ln 4069.5=-+=πππ 由判定条件可知，本计算符合⑴H ≥H cr 和H ≥L m /2，单位长度上的浪压力标准值按下式计算：)(41%1Z m W Wkh h L P +=γ 式中：γw ── 水的重度 = 9.81 KN/m 3 其余计算参数已有计算结果。
浪压力标准值计算得：KN P Wk 143.8)155.05.0(069.581.941-=+⨯⨯⨯=对坝底中点O 取矩为（顺时针为“－”，逆时针为“+”）：M OPWK = (9.81×0.655×0.521/2)×(15.98+0.655/3)+(9.81×2.535×0.521/2)×(15.98－2.535/3) = －(27.114+98.048) = －125.162 KN ·m⑤ 淤沙压力淤沙压力标准值 P SK = －90.911 KN对O点的力臂为（1098.3－1090）/3 = 2.767m对O点取矩M OPSK = －90.911×2.767 = －251.552 KN·m将计算的各荷载进行汇总整理。
结论请见附表2。
附表1正常蓄水位情况各项作用力统计表单位：KN、KN·m附表2校核洪水位情况各项作用力统计表单位：KN、KN·m按规范规定作用组合进行作用力的汇总如附表3：附表3 各种工况下的∑↓、∑←、∑M统计表单位：KN、KN·m⑵．由规范8.结构计算基本规定中可知大坝坝体抗滑稳定和坝基岩体进行强度和抗滑稳定计算属于1）承载能力极限状态，在计算时，其作用和材料性能均应以设计值代入。