晶面指数_六方晶系的晶面指数标定
四六方晶系的晶面指数和晶向指数1晶面指数
1-2 晶体学基础
(三)晶向与晶向指数 1. 晶轴:两个以上原子所构成的直线。 2. 晶向:两个以上原子所构成的原子列的方向。 3. 晶向指数及其表示方法
通常也采用密勒指数(Miller Index)来标定晶 向指数
1-2 晶体学基础
(1)已知晶向标定其晶向指数 标定步骤:
1)以待定晶向的始点O为坐标原点,过原点O的三个棱 边为坐标轴x、y、z;
晶系 三斜 单斜
正交
布拉菲点阵
简单六方
简单菱方
简单四方 体心四方 简单立方 体心立方 面心立方
晶系 六方 菱方 四方
立方
1-2 晶体学基础
1-2 晶体学基础
1-2 晶体学基础
(四)晶体结构与晶体点阵 晶体结构:晶体中实际质点
(原子、离子或 分子)的具体排 列情况
1-2 晶体学基础
晶体点阵:晶体中实际原 子、离子或分 子中心的具体 排列情况
1-2 晶体学基础
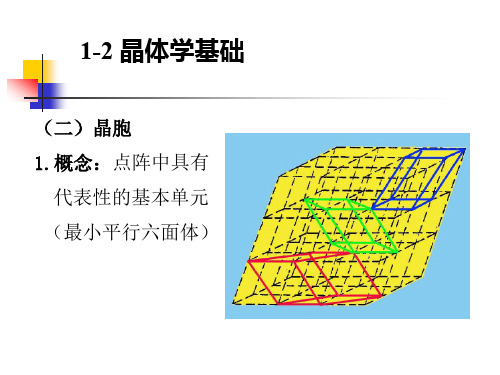
(二)晶胞 1.概念:点阵中具有
代表性的基本单元 (最小平行六面体)
1-2 晶体学基础
2. 晶胞的选取原则 (1) 选取的平行六面体应反映出点阵的最高对称性; (2) 平行六面体内的棱和角相等的数目应最多; (3) 当平行六面体的棱边夹角存在直角时,直角数目
应最多; (4) 在满足上述条件下,晶胞应具有最小的体积。
1-2 晶体学基础
不同的晶体结构类型属于相同的空间点阵
Cu晶体
NaCl晶体
CaF2晶体
1-2 晶体学基础
相似的晶体结构类型属于不同的空间点阵
Cr晶体
CsCl晶体
1-2 晶体学基础
思考题: 说明为何十四种布拉菲点阵中不存在底心
四方点阵和面心四方点阵?
晶面指数六方晶系的晶面指数标定

3° (hkl)中括号代表一组互相平行、面间距相等的晶面。
晶向指数的确定方法
1°在相互平行的结点直线中引出一条过原点的结点直线 2°在该直线上选出距原点最近的结点,确定其坐标 3°消除分数,把它们化为互质的最小整数。负数用上划 线表示。 4°用[ ] 括起来,记为[uvw]
Z
确定距原点最近的结点坐标1/2, 1, 0 消除分数为1、2、0 晶向指数 [120]
晶面指数的确定方法
1°确定平面与晶胞三个坐标轴的交点坐标(平面不能通过原点) 2°取在三个坐标轴上截距的倒数。 3°消除分数,把它们化为互质的最小整数h、k、l。负数用上划 线表示。 4°用()括起来,记为(hkl )
0,0,1
0,1,0 1,0,0
1°确定交点坐标,X轴:1/2、 Y轴:1、 Z轴:1 2°取倒数 2、1、1 3°消除分数 2、1、1 4°晶面指数(211)
2°指数中某一数为“0”,表示晶面与相应的晶轴平行,例 如(hk0)晶面平行于c轴。因交点为,倒数为零。
3° (hkl)中括号代表一组互相平行、面间距相等的晶面。
晶向指数的确定方法
1°在相互平行的结点直线中引出一条过原点的结点直线 2°在该直线上选出距原点最近的结点,确定其坐标 3°消除分数,把它们化为互质的最小整数。负数用上划 线表示。 4°用[ ] 括起来,记为[uvw]
六方晶系一些晶面的指数
六方晶系晶向指数标定
采用4轴坐标时,晶向指数的确定原则仍同前述 晶向指数可用{u v t w}来表示,这里 u + v = - t。
六方晶系晶向指数的表示方法(c轴与图面垂直)
六方晶系中,三轴指数和四轴指数 的相互转化
三轴晶向指数(U V W) 四轴晶向指数(u v t w)
晶面指数 六方晶系的晶面指数标定(经典实用)

晶面指数六方晶系的晶面指数标定(经典实用)晶体学是研究晶体结构和性质的学科,而晶面指数则是描述晶体中晶面的数字表示方法。
晶面指数使用晶体学中的一套标准符号体系,可以精确地表达晶体中每个晶面的表现形式和相对排列位置。
晶面指数标定是晶体学中的基础训练,也是必须掌握的基本技能之一。
本文将针对六方晶系的晶面指数标定进行说明,介绍一些经典实用的方法和技巧。
一、六方晶系的晶面指数表达方式六方晶系是晶体学中的一种晶系,它具有六个等长的轴,其中三个轴共面,呈120度夹角。
在六方晶系中,晶面指数的表达方式是使用Miller指数。
具体来说,对于六方晶系的任何一个晶面,其Miller指数可表示为(h, k, l, i)的形式,其中i表示层数,h、k、l表示垂直于该晶面的三个轴上,分别经过晶面的小整数倍。
这个表示方法又称为(弗兰克-布拉维)符号。
例如,在六方晶系中,垂直于a轴、b轴和c轴的三个晶面分别是(1, 0, 0, 1)、(0, 1, 0, 1)和(0, 0, 1, 1)。
需要注意的是,当晶面不是经过所有轴的整数倍时,需要根据实际情况对其Miller指数进行归一化,即对其进行整数倍处理,使其成为最小的整数倍数。
二、如何确定晶面指数?确定晶面指数的方法通常是从晶体图谱或显微照片中找到可视的晶面,然后测量其与某个特定方向的夹角。
这个方向可以是晶体中的任意方向,但必须是已知的方向,其Miller指数应该是已知的。
此外,需要确定一个基准面,以便进行下一步计算。
基准面通常是顺着已知方向最靠近找到的晶面的面,因为这样可以减少复杂的计算。
在确定了基准面之后,可以按照以下步骤计算该晶面的Miller指数:1、测量该晶面与已知方向的夹角;2、确定该角度的余弦值,并将其化为最简分数形式(如果不是整数);3、利用晶格中的对称性(如果存在)推导该晶面的Miller指数;4、对推导的Miller指数进行检查和归一化,确保其最小。
需要注意的是,计算中需要考虑晶体中的对称性和晶体参数等因素,以避免出现计算错误。
晶面指数六方晶系的晶面指数标定专业知识讲座

d=/(2sin)
2( h2 + k2 + l2 )
∴ sin2 =
4a2
已知晶胞参数的(hkl)晶面,当已知波长,可确定衍射方向;
反之,通过测定衍射方向,可以确定晶胞参数,即可确定晶胞的
大小、形状。【物相分析】
本文档所提供的信息仅供参考之用,不能作为科学依据,请勿模仿。文档如有不 当之处,请联系本人或网站删除。
本文档所提供的信息仅供参考之用,不能作为科学依据,请勿模仿。文档如有不 当之处,请联系本人或网站删除。
晶向指数的确定方法
1°在相互平行的结点直线中引出一条过原点的结点直线 2°在该直线上选出距原点最近的结点,确定其坐标 3°消除分数,把它们化为互质的最小整数。负数用上划
线表示。
4°用[ ] 括起来,记为[uvw]
正交(立方、四方、 斜方晶系)
1 d2
hkl
h2 a2
kb22
cl22
a、b、c为晶胞参数
本文档所提供的信息仅供参考之用,不能作为科学依据,请勿模仿。文档如有不 当之处,请联系本人或网站删除。
单斜
[ 了解 ]
1 h2 k2 l2 2hclo s dh 2k la2si2nb2c2si2nasci2n
本文档所提供的信息仅供参考之用,不能作为科学依据,请勿模仿。文档如有不
(4)衍射方向(当衍之射处角,请θ)联系的本确人定或网站删除。
将布拉格方程和晶面间距公式联系起来,可得到不同晶系 的衍射方向。
如:立方晶系,晶面间距公式为
d12
h2 a2
kb22
cl22
= h2 + k2 + l2 a2
Z
确定距原点最近的结点坐标1/2, 1, 0 消除分数为1、2、0 晶向指数 [120]
金属学基础--晶向指数和晶面指数

U 2u v
V 2v u
W w
25
或
U 2u v
V 2v u
W w
u 1 3 (2U V ) v 1 3 (2V U ) w W t (u v)
26
例如
2 u 3
[100] :
1 v 3 1 t 3
[2 1 1 0]
六方晶系的晶面指数和晶向指数(与“指数”相关共10张)

[UVW]=
[ u v t w ]计算 化简可得 =
在平面上表示一个点只用两个坐标,则
u+v+t=0 t=-(u+v)
(2)
a1+a2+a3=0
(3)
任一晶向中为 ua1+va2+ta3+wC (4)
六方晶系的晶向指数
(3)式代入(4),得到晶向的四轴指数
OR=ua1+va2-t(a1+a2)+wC
=(u-t)a1+(v-t)a2+wC
(5)
六方晶系的晶向指数
六方晶系的晶面指数和晶向指数
六方晶系的晶面指数 取a1、a2、C为晶轴,a1、a2夹角120º,
C⊥a1,C⊥a2
b晶面的晶面指数:(100)
C晶面的晶面指数:
晶面指数上不能明确表示等 同晶面
六方晶系的晶面指数
采用a1、a2、a3及C四 个晶轴 a1、a2、a3之间的 夹角均为120º
晶根轴i= 据不面- (立会指h+体超数k)几过以或何 三(h,个h+在,kki+l三可)i=维证表0 空明示间中独立的坐标 O设即晶六即任六在 采任在=任取1i取六O根在用晶即根取晶任晶任=,(RR∞u晶用面个用一方平用一平一aa个据平四面用据a面一面一--==,111(t-向 三 指 柱 三 晶 晶 面a晶 面 晶 晶 立 面 轴 指 三 立 指 晶 指 晶h)uu、、、1a1+aa,1∞指轴数面轴向系上 向上向面体上坐数轴体数向数向、aaak11+)222,++数坐上的坐中的表 中表中可几表标上坐几以中确中(a、、、或vvv2aa-在标不指标为晶示 为示为归何示,不标何(为定为、CCCt22)ha--为为为三,能数,面一 一并,一能,,方h+atuuutOuu2((kk3aaaaaaa晶晶晶+轴则明可则指个 个为在个明则在法Ri+l及1111111)wi=+++++轴轴轴坐确确数点 点三点确三与=OOO++CC(表vvvvv0aauRRR,,,标表定和只 只维只表维三aaaaa四22aaa-===示t22222))111)晶系示为晶用用空用示空轴++个UUU+++++a、、、wwttttt1aaa面等向两 两间两等间系aaaaa晶[+CCaaa111U33333(222+++族同指个 个中个同中一轴+++++vV夹夹夹VVV(wwwww-W晶数坐 坐独坐晶独致taaaa)CCCCC角角角a22251]面标 标立标面立2+++)、111+WWW(((((, ,的,的222wa000CCC444442则 则坐则坐Cººº,,,)))))、标标((((CCCa轴轴3⊥⊥⊥1115之))))不不aaa间111会会, , ,的超超CCC夹过过⊥⊥⊥角三三aaa222均个个为,,1可可20证证º明明
晶面指数
C D
B
A
o
4
晶向族——晶体中因对称关系而等同的各组晶向为一个
晶向族<uvw>
<111>
5
正交晶系一些重要晶向的晶向指数
晶向族? <100> <110> <111>
6
2.1.2.2 晶面指数的标定
步骤:
2.1 晶体学基础 2.1.1空间点阵和晶胞 2.1.2 晶向指数和晶面指数
(1)在点阵中设定参考坐标系,不能将
( 1 ) 回转对称轴
3次轴
简单立方晶体 <111>
38
2.1.3 晶体的对称性
2.1.3.1 对称元素
a.宏观对称元素
2.1 晶体学基础 2.1.1空间点阵和晶胞 2.1.2 晶向指数和晶面指数
( 2 ) 对称面
晶体通过某一平面作镜像反映而能复 原,则该平面称为对称面或镜面,用符号 m表示。
对称面通常是晶棱或晶面的垂直平分 面或者为多面角的平分面,且必定通过晶 体几何中心。
50
b.微观对称元素
(2) 螺旋轴
回转轴+平移=螺旋轴
由回转轴和平行于该轴的平移
所构成。晶体结构可绕此轴转 360°/n同时沿轴平移一定距离 而复原,此轴称为n次螺旋轴
点1绕轴转360°/3= 120°,沿 轴平移c/3至点2,晶体复原,此 轴称为3次螺旋轴
左(右)旋: 左(右)手四指指向螺旋线旋转方向 左旋 左(右)手拇指指向螺旋线前进方向 下移
39
2.1.3 晶体的对称性
2.1.3.1 对称元素
a.宏观对称元素
( 2 ) 对称面
与m对应的对称 操作是反映
晶体学基本(晶向指数与晶面指数)
1.4晶向指数和晶面指数一晶向和晶面1晶向晶向:空间点阵中各阵点列的方向(连接点阵中任意结点列的直线方向)。
晶体中的某些方向,涉及到晶体中原子的位置,原子列方向,表示的是一组相互平行、方向一致的直线的指向。
2晶面晶面:通过空间点阵中任意一组阵点的平面(在点阵中由结点构成的平面)。
晶体中原子所构成的平面。
不同的晶面和晶向具有不同的原子排列和不同的取向。
材料的许多性质和行为 (如各种物理性质、力学行为、相变、X光和电子衍射特性等) 都和晶面、晶向有密切的关系。
所以,为了研究和描述材料的性质和行为,首先就要设法表征晶面和晶向。
为了便于确定和区别晶体中不同方位的晶向和晶面,国际上通用密勒( Miller )指数来统一标定晶向指数与晶面指数。
二晶向指数和晶面指数的确定1晶向指数的确定方法三指数表示晶向指数[uvw]的步骤如图1所示。
(1)建立以晶轴a, b, c为坐标轴的坐标系,各轴上的坐标长度单位分别是晶胞边长a, b , c,坐标原点在待标晶向上。
(2)选取该晶向上原点以外的任一点P(xa, yb , zc)。
⑶将xa, yb , zc化成最小的简单整数比u , v, w,且u : v : w = xa : yb : zc。
(4)将u , v, w三数置于方括号内就得到晶向指数[uvw]。
图1晶向指数的确定方法图2不同的晶向及其指数当然,在确定晶向指数时,坐标原点不一定非选取在晶向上不可。
若原点不在待标晶向上,那就需要选取该晶向上两点的坐标P(x i, y i ,z i)和Q(x2,y2, Z2),然后将(X1-X2), (y i-y2), (Z1-Z2)三个数化成最小的简单整数u, v,w,并使之满足u : v : w=( X1-X2):(y i-y2):(z i-Z2)。
则[uvw ]为该晶向的指数。
显然,晶向指数表示了所有相互平行、方向一致的晶向。
若所指的方向相反,则晶向指数的数字相同,但符号相反,如图3中[0 10]与[010]。
晶面指数六方晶系的晶面指数标定
晶向指数的确定方法
1°在相互平行的结点直线中引出一条过原点的结点直线 2°在该直线上选出距原点最近的结点,确定其坐标 3°消除分数,把它们化为互质的最小整数。负数用上划
线表示。
4°用[ ] 括起来,记为[uvw]
Z
确定距原点最近的结点坐标1/2, 1, 0 消除分数为1、2、0 晶向指数 [120]
2hk(c ab
osc
osc
os)
2kl(coscoscos)2hl(coscoscos)]
bc
ac
例 : 某 斜 方 晶 体 的 a=0.742nm, b=0.494nm,
c=0.255nm, 计算d110和d200。
1 d2
hkl
h2 a2
kb22
cl22
1
[001]
晶带定律:凡是属于[uvw]晶
带的晶面,它的晶面指数必须
O
符合hu+kv+lw=0
晶面间距:是两个相邻的平行晶面间的垂直距离,通常 用dhkl 或 d 表示。
晶面间距是现代测试中一个重要的参数。在简单点阵中, 通过晶面指数(hkl)可以方便地计算出相互平行的一组 晶面之间的距离d。
正交(立方、四方、 斜方晶系)
晶面指数的确定方法
1°确定平面与晶胞三个坐标轴的交点坐标(平面不能通过原点) 2°取在三个坐标轴上截距的倒数。
3°消除分数,把它们化为互质的最小整数h、k、l。负数用上划
线表示。 4°用()括起来,记为(hkl )
0,0,1 1,0,0
1°确定交点坐标,X轴:1/2、 Y轴:1、 Z轴:1
2°取倒数 2、1、1 3°消除分数 2、1、1 0,1,0 4°晶面指数(211)
• 但是,用三指数表示六方晶系的晶面和晶向 有一个很大的缺点,即晶体学上等价的晶面 和晶向不具有类似的指数。这一点可以从上 图看出。图中六棱柱的两个相邻表面(红面 和绿面)是晶体学上等价的晶面,但其密勒 指数(Miller Indices)却分别是 (110 ) 和(100)。 图中夹角为 60°的两个密排方向 D1 和 D2 是 晶体学上的等价方向,但其晶向指数却分别 是[100]和[110]。
晶向指数与晶面指数
晶向指数与晶面指数2009-09-29 22:24:00 作者:来源:互联网简介:在晶体物质中,原子在三维空间中作有规律的排列。
因此在晶体中存在着一系列的原子列或原子平面,晶体中原子组成的平面叫晶面,原子列表示的方向称为晶向。
晶体中不同的晶面和不同的方向上原子的排列方式和密度不 ...在晶体物质中,原子在三维空间中作有规律的排列。
因此在晶体中存在着一系列的原子列或原子平面,晶体中原子组成的平面叫晶面,原子列表示的方向称为晶向。
晶体中不同的晶面和不同的方向上原子的排列方式和密度不同,构成了晶体的各向异性。
这对分析有关晶体的生长、变形、相变以及性能等方面的问题时都是非常重要的。
因此研究晶体中不同晶向晶面上原子的分布状态是十分必要的。
为了便于表示各种晶向和晶面,需要确定一种统一的标号,称为晶向指数和晶面指数,国际上通用的是密勒(Miller)指数。
一、晶向指数晶向指数是按以下几个步骤确定的:1.以晶胞的某一阵点为原点,三个基矢为坐标轴,并以点阵基矢的长度作为三个坐标的单位长度;2.过原点作一直线OP,使其平行于待标定的晶向AB(见图1-15),这一直线必定会通过某些阵点;3.在直线OP上选取距原点O最近的一个阵点P,确定P点的坐标值;4.将此值乘以最小公倍数化为最小整数u、v、w,加上方括号,[uvw] 即为AB晶向的晶向指数。
如u、v、w中某一数为负值,则将负号标注在该数的上方。
图1-16给出了正交点阵中几个晶向的晶向指数。
显然,晶向指数表示的是一组互相平行、方向一致的晶向。
若晶体中两直线相互平行但方向相反,则它们的晶向指数的数字相同,而符号相反。
如[21]和[ 1]就是两个相互平行、方向相反的晶向。
图1-15 晶向指数的确定图 1-16正交点阵中几个晶向的晶向指数晶体中因对称关系而等同的各组晶向可归并为一个晶向族,用<uvw>表示。
例如,对立方晶系来说,[100]、[010]、[001]和[00]、[00]、[00]等六个晶向,它们的性质是完全相同的,用符号<100>表示。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1°确定平面与晶胞三个坐标轴的交点坐标(平面不能通过原点) 2°取在三个坐标轴上截距的倒数。
3°消除分数,把它们化为互质的最小整数h、k、l。负数用上划
线表示。 4°用()括起来,记为(hkl )
0,0,1 1,0,0
1°确定交点坐标,X轴:1/2、 Y轴:1、 Z轴:1
2°取倒数 2、1、1 3°消除分数 2、1、1 0,1,0 4°晶面指数(211)
六方晶系中,三轴指数和四轴指数 的相互转化
三轴晶向指数(U V W) 四轴晶向指数(u v t w)
三轴晶面指数(h k l) 四轴晶向指数(h k i l)
i =- ( h + k ) 。
和晶向不具有类似的指数。这一点可以从上
图看出。图中六棱柱的两个相邻表面(红面
和绿面)是晶体学上等价的晶面,但其密勒 指数(Miller Indices)却分别是 (110和) (100)。 图中夹角为 60°的两个密排方向 D1 和 D2 是 晶体学上的等价方向,但其晶向指数却分别 是[100]和[110]。
a,c 为单位长); (2)求其倒数并化为最简整数,即得(hkil)指 数,这样得到的晶面指数称为 Miller-Bravais 指数。
六方晶系晶面指数标定
根据六方晶系的对称特点,对六方晶系采用a1, a2,a3及c四个晶轴,a1,a2,a3之间的夹角均 为120度,这样,其晶面指数就以(h k i l)四个 指数来表示。
• 四指数表示是基于4个坐标轴:a1,a2,a3 和 c 轴,其中,a1,a2 和 c 轴就是原胞的 a,b 和c 轴,而 a3 = -(a1+a2)。下面就分别讨论用 四指数表示的晶面及晶向指数。
• 六方晶系晶面指数的标定原理和方法同立方晶 系中的一样,步骤如下:(1)先找出该面在 四个坐标轴上的截距长度(以晶胞的点阵常数
1°确定交点坐标,X轴:1/3、 Y轴:1、 Z轴:1/2
2°取倒数 3、1、2 3°消除分数 3、1、2 4°晶面指数(312)
0,0,1
练习
1,0,0
0,1,0 晶面指数(233)
常见的晶面指数
(001)
(110)
(100)
(010)
(111)
晶面指数的几点说明:
1°h,k,l 三个数分别对应于a,b,c三晶轴方向。 2°指数中某一数为“0”,表示晶面与相应的晶轴平行,例如 (hk0)晶面平行于c轴。因交点为,倒数为零。 3° (hkl)中括号代表一组互相平行、面间距相等的晶面。
O X
晶向符号 [221]
Y
[001] [111]
●
●
常见的晶向指数
O
●
●
[100]
[010]
4、晶带、晶面间距和晶面夹角
晶带:在晶体结构和空间点阵中平行于某一轴向的所有
晶面属于同一晶带。
• 同一晶带中包含不同的晶面,这些晶面的交线互相平行。
• 晶带由所平行的轴向的晶向指数表示。
[001]晶带包含的晶面有: (100)、(010)、(110)、 (110)、(120)等晶面
大小、形状。【物相分析】
4-3 六方晶系指数表示
• 上面我们用三个指数 表示晶面和晶向。这 种三指数表示方法, 原则上适用于任意晶 系。对六方晶系,取 a, b,c 为晶轴,而 a 轴 与 b 轴的夹角为120°, c 轴与 a,b 轴相垂直, 如右图所示。
• 但是,用三指数表示六方晶系的晶面和晶向 有一个很大的缺点,即晶体学上等价的晶面
(001)
(110)
(100)
(010)
(111)
晶面指数的几点说明:
1°h,k,l 三个数分别对应于a,b,c三晶轴方向。 2°指数中某一数为“0”,表示晶面与相应的晶轴平行,例如 (hk0)晶面平行于c轴。因交点为,倒数为零。 3° (hkl)中括号表一组互相平行、面间距相等的晶面。
晶向指数的确定方法
晶向指数的确定方法
1°在相互平行的结点直线中引出一条过原点的结点直线 2°在该直线上选出距原点最近的结点,确定其坐标 3°消除分数,把它们化为互质的最小整数。负数用上划
线表示。
4°用[ ] 括起来,记为[uvw]
Z
确定距原点最近的结点坐标1/2, 1, 0 消除分数为1、2、0 晶向指数 [120]
根据几何学可知,三维空间独立的坐标轴最多 不超过三个。前三个指数中只有两个是独立的, 它们之间存在以下关系:i =- ( h + k ) 。
六方晶系一些晶面的指数
六方晶系晶向指数标定
采用4轴坐标时,晶向指数的确定原则仍同前述 晶向指数可用{u v t w}来表示,这里 u + v = - t。
六方晶系晶向指数的表示方法(c轴与图面垂直)
cos2 )
h2 sin 2
[ a2
k 2 sin 2 b2
l 2 sin 2
c2
2hk ab
(cos cos
cos )
2kl (cos cos cos ) 2hl (cos cos cos )]
bc
ac
例 : 某 斜 方 晶 体 的 a=0.742nm, b=0.494nm,
1 d2
hkl
h2 a2
k2 b2
l2 c2
a、b、c为晶胞参数
单斜
[ 了解 ]
1 d2
hkl
h2 a 2 sin 2
k2 b2
l2 c2 sin 2
2hl cos ac sin 2
三斜
1
1
d
2 hkl
(1 2 cos cos
cos
cos2
cos2
1°在相互平行的结点直线中引出一条过原点的结点直线 2°在该直线上选出距原点最近的结点,确定其坐标 3°消除分数,把它们化为互质的最小整数。负数用上划
线表示。
4°用[ ] 括起来,记为[uvw]
Z
确定距原点最近的结点坐标1/2, 1, 0 消除分数为1、2、0 晶向指数 [120]
O
Y
●
X
Z
练习
●
• 由于等价晶面或晶向不具有类似的指数, 人们就无法从指数判断其等价性,也无法由 晶面族或晶向族指数写出它们所包括的各种 等价晶面或晶向,这就给晶体研究带来很大 的不便。为了克服这一缺点,或者说,为了 使晶体学上等价的晶面或晶向具有类似的指 数,对六方晶体来说,就得放弃三指数表示, 而采用四指数表示。
c=0.255nm, 计算d110和d200。
1 h2 k2 l2
d2 hkl
a2
b2
c2
1
12
12
d2 110
7.4172
4.9452
1 22
d2 200
7.4172
得出:d110 =0.41nm, d200=0.37nm
(4)衍射方向(衍射角θ)的确定
将布拉格方程和晶面间距公式联系起来,可得到不同晶系 的衍射方向。
O
Y
●
X
Z
练习
●
O X
晶向符号 [221]
Y
[001] [111]
●
●
常见的晶向指数
O
●
●
[100]
[010]
1°确定交点坐标,X轴:1/3、 Y轴:1、 Z轴:1/2
2°取倒数 3、1、2 3°消除分数 3、1、2 4°晶面指数(312)
0,0,1
练习
1,0,0
0,1,0 晶面指数(233)
常见的晶面指数
如:立方晶系,晶面间距公式为
1 d 2
h2 a2
k2 b2
l2 c2
= h2 + k2 + l2 a2
d=/(2sin)
2( h2 + k2 + l2 )
∴ sin2 =
4a2
已知晶胞参数的(hkl)晶面,当已知波长,可确定衍射方向;
反之,通过测定衍射方向,可以确定晶胞参数,即可确定晶胞的
[001]
晶带定律:凡是属于[uvw]晶
带的晶面,它的晶面指数必须
O
符合hu+kv+lw=0
晶面间距:是两个相邻的平行晶面间的垂直距离,通常 用dhkl 或 d 表示。
晶面间距是现代测试中一个重要的参数。在简单点阵中, 通过晶面指数(hkl)可以方便地计算出相互平行的一组 晶面之间的距离d。
正交(立方、四方、 斜方晶系)
