晶体学基础(晶向指数与晶面指数)
材料科学基础-第1章

晶面指数及晶面间距
现在广泛使用的用来表示晶面指数的密勒指数是由 英国晶体学家ler于1939年提出的。
z
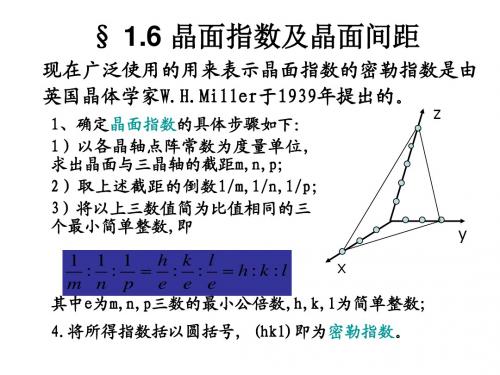
确定晶面指数的具体步骤如下: 1.以各晶轴点阵常数为度量单位,求 出晶面与三晶轴的截距m,n,p; 2.取上述截距的倒数1/m,1/n,1/p; 3. 将以上三数值简为比值相同的三 个最小简单整数,即 1 1 1 h k l (553) : : : : h:k :l x m n p e e e 其中e为m,n,p三数的最小公倍数,h,k,l为简单整数; 4.将所得指数括以圆括号, (hkl)即为密勒指数。
13 体心立方点阵
a=b=c,α=β=γ =90°
14 面心立方点阵
a=b=c,α=β=γ =90°
§ 1.5 晶体结构的对称性
一、对称:对称是指物体相同部分作有规律的 重复。对称操作所依据的几何元素,亦即在对 称操作中保持不动的点、线、面等几何元素称 为对称元素。 二、对称性
1.晶体的宏观对称性 2. 晶体的32种点群 3. 晶体的微观对称性 4.230种空间群
晶体结构=空间点阵+基元
注意:上式并不是一个数学关系式,而只是用来表示这三者之间的 关系。
二、晶体的点阵理论
1 、点阵(Lattice):
将晶体中重复出现的最小单元作为结构基元,用一个数 学上的点来代表 , 称为点阵点,整个晶体就被抽象成一组 点,称为点阵。 1 点阵点必须无穷多; 点阵必须具备的三个条件 2 每个点阵点必须处于相同的环境; 3 点阵在平移方向的周期必须相同。
c
b
a
空间点阵及晶胞的不同取法
选取晶胞的原则: 1.要能充分反映整个空间点阵的周期性和对称性; 2.在满足1的基础上,单胞要具有尽可能多的直角; 3.在满足上条件,晶胞应具有最小的体积。
材料科学导论-第一章 晶体学基础3
3、六方晶系晶面指数标定
根据六方晶系的对称特点,对六方晶系采用a1,a2,a3 及c四个晶轴,a1,a2,a3之间的夹角均为120度,这样, 其晶面指数就以(h k i l)四个指数来表示。 根据几何学可知,三维空间独立的坐标轴最多不超过三 个。前三个指数中只有两个是独立的,它们之间存在以 下关系:i =- ( h + k ) 。
三轴晶面指数(h k l) 四轴晶面指数(h k i l) i=- ( h + k )
立方晶系:
d hkl
a h k l
2 2 2
§ 1.6 晶面指数及晶面间距 范例:
m/l
c
a
m/k
b
m/h
画出晶面 (100),(110),(111),(201),(211),(321)
பைடு நூலகம்
c a
(100)
b
画出晶面 (100),(110),(111),(201),(211),(321)
d V [h b c sin k a c sin l a b sin
2 2 2 2 2 2 2 2 2 2 2 2
2hkabc (cos cos cos )
2
2kla bc(cos cos cos )
2
2hlab c(cos cos cos )]
2
2 2 2
1
2
1 2
V abc(1 cos cos cos 2cos cos cos )
单斜晶系:d=sinβ(h2/a2+k2sin2β/b2+l2/c2-2hlcosβ/ac)-1/2 正交晶系:d=[h2/a2+k2/b2+l2/c2]-1/2 四方晶系:d=[(h2+k2)/a2+l2/c2]-1/2 六方晶系:d=[4(h2+hk+k2)/3a2+l2/c2]-1/2
材料科学基础第二章

y
[111]
x
[111]
例:画出晶向
[112 ]
2.立方晶系晶面指数
晶面指数的确定方法
(a)建立坐标系,结点为原点, 三棱为方向,点阵常数为单位 (原点在标定面以外,可以采 用平移法); (b)晶面在三个坐标上的截距a1 a2 a3 ; (c)计算其倒数 b1 b2 b3 ; (d)化成最小、整数比h:k:l ; 放在圆方括号(hkl),不加逗号, 负号记在上方 。
3.六方晶系晶面和晶向指数
三指数表示六方晶系晶面和晶向的缺点:晶体学上等价的 晶面和晶向不具有类似的指数。 例:
晶面指数
(11 0)
(100)
[010] [100]
从晶面指数上不能明确表示等同晶面,为了克服这一缺点, 采用a1、a2、a3及c四个晶轴, a1、a2、a3之间的夹角均 为120º ,晶面指数以(hkil)表示。 根据立体几何,在三维空间中独立的坐标轴不会超过三 个可证明 : i= - (h+k) 或 h+k+i=0
六方晶系
d hkl
h k l a b c
2 2 2
d hkl
a h2 k 2 l 2
1 l c
2
4 h 2 hk k 2 3 a2
注:以上公式是针对简单晶胞而言的,如为复杂晶胞, 例如体心、面心,在计算时应考虑晶面层数增加的影 响,如体心立方、面心立方、上下底(001)之间还有 一层同类型晶面,实际
[1 00 ]
[0 1 0]
[010]
[1 00]
y
[100]
x
[00 1]
(完整版)材料科学基础基础知识点总结

第一章材料中的原子排列第一节原子的结合方式2 原子结合键(1)离子键与离子晶体原子结合:电子转移,结合力大,无方向性和饱和性;离子晶体;硬度高,脆性大,熔点高、导电性差。
如氧化物陶瓷。
(2)共价键与原子晶体原子结合:电子共用,结合力大,有方向性和饱和性;原子晶体:强度高、硬度高(金刚石)、熔点高、脆性大、导电性差。
如高分子材料。
(3)金属键与金属晶体原子结合:电子逸出共有,结合力较大,无方向性和饱和性;金属晶体:导电性、导热性、延展性好,熔点较高。
如金属。
金属键:依靠正离子与构成电子气的自由电子之间的静电引力而使诸原子结合到一起的方式。
(3)分子键与分子晶体原子结合:电子云偏移,结合力很小,无方向性和饱和性。
分子晶体:熔点低,硬度低。
如高分子材料。
氢键:(离子结合)X-H---Y(氢键结合),有方向性,如O-H—O(4)混合键。
如复合材料。
3 结合键分类(1)一次键(化学键):金属键、共价键、离子键。
(2)二次键(物理键):分子键和氢键。
4 原子的排列方式(1)晶体:原子在三维空间内的周期性规则排列。
长程有序,各向异性。
(2)非晶体:――――――――――不规则排列。
长程无序,各向同性。
第二节原子的规则排列一晶体学基础1 空间点阵与晶体结构(1)空间点阵:由几何点做周期性的规则排列所形成的三维阵列。
图1-5特征:a 原子的理想排列;b 有14种。
其中:空间点阵中的点-阵点。
它是纯粹的几何点,各点周围环境相同。
描述晶体中原子排列规律的空间格架称之为晶格。
空间点阵中最小的几何单元称之为晶胞。
(2)晶体结构:原子、离子或原子团按照空间点阵的实际排列。
特征:a 可能存在局部缺陷;b 可有无限多种。
2 晶胞图1-6(1)――-:构成空间点阵的最基本单元。
(2)选取原则:a 能够充分反映空间点阵的对称性;b 相等的棱和角的数目最多;c 具有尽可能多的直角;d 体积最小。
(3)形状和大小有三个棱边的长度a,b,c及其夹角α,β,γ表示。
材料科学基础(浙大)PPT课件

最新课件
40
§2-3表面、界面结构及不完 整性
一、晶体的表面
• (一)表面力场 固体表面力
分子间引力主要来源 • (二)晶体表面状态 表面能
最新课件
41
§2-3表面、界面结构及不完 整性
一、晶体的表面
• (三)晶体表面的不均匀性
完美晶格结构的晶体表面:
分成两种类型:
紧密堆积表面:表面平坦,没有波折,所有的原 子距离该表面的平行平面的距离都相等
2
最新课件
32
§2-2位错 二、位错的应力场
• (三)位错核心 位错核心错排严重,不能再简化为连续弹性体。以点 阵模型解决 派—纳(Peierls-Nabarro)模型:实际上是不完全的点阵 模型。设晶体由被滑移面隔开的两个半块晶体组成。 衔接处直接考虑原子间相互作用,内部简化成连续弹 性介质。 派-纳模型中位错的能量组成:两部分。一是两半晶 体中的弹性应变能(主要分布于位错核心之外);另 一是滑移面两侧原子互作用能(错排能)(基本集中 于位错核心范围内)
• 晶面间距的概念、特点
•正关交注晶晶系面面间间距距的计计算算式: dhkl
1
h2
k
2
l
2
a b c
立方晶系面间距计算式:
dh kl
a h2 k2 l2
注意:以上对简单晶胞而言;复杂晶胞应考虑层
面增加的影响。如,在体心立方或面心立方晶
胞中间有一层,故实际晶面间距应为d001/2。
最新课件
8
§1-1晶体学基础 三、晶体的对称性
• (一) 高分子晶体的形成 基本形态 、高分子材料特点 、高分子结构单 元连接特点 、结构形态 、结晶特性 (二)高分子晶体的形态 高分子晶体形貌:结晶高分子较多地具有球晶 的形貌。一个球晶由沿半径垂直方向的多层晶 片组成。晶片内是缨束状晶区或折叠链晶区。 晶片间是无定形的非晶区偏振光显微镜下聚乙 烯球晶
潘金生材料科学基础(修订版)知识点笔记课后答案

第1章晶体学基础1.1复习笔记一、空间点阵1.晶体特征和空间点阵概述(1)晶体特征晶体的一个基本特征是具有周期性。
(2)空间点阵空间点阵是指用来描述晶体中原子或原子集团排列的周期性规律的在空间有规律分布的几何点的集合。
2.晶胞、晶系和点阵类型(1)晶胞①晶胞的定义空间点阵可以看成是由最小的单元——平行六面体沿三维方向重复堆积(或平移)而成。
这样的平行六面体称为晶胞。
②点阵常数a.描述晶胞的大小:三条棱的长度a,b和c;b.描述晶胞的形状:棱之间的夹角α,β和γ。
③选取晶胞的条件a.能反映点阵的周期性;b.能反映点阵的对称性;c.晶胞的体积最小。
(2)晶系按照晶胞的大小和形状的特点,或按照6个点阵常数之间的关系和特点,可以将各种晶体归为7种晶系。
表1-1 7种晶系(3)点阵类型①简单三斜点阵(如图1-1(1)所示);②简单单斜点阵(如图1-1(2)所示);③底心单斜点阵(如图1-1(3)所示);④简单斜方点阵(如图1-1(4)所示);⑤底心斜方点阵(如图1-1(5)所示);⑥体心斜方点阵(如图1-1(6)所示);⑦面心斜方点阵(如图1-1(7)所示);⑧六方点阵(如图1-1(8)所示);⑨菱方点阵(三角点阵)(如图1-1(9)所示);⑩简单正方(或四方)点阵(如图1-1(10)所示);⑪体心正方(或四方)点阵(如图1-1(11)所示);⑫简单立方点阵(如图1-1(12)所示);⑬体心立方点阵(如图1-1(13)所示);⑭面心立方点阵(如图1-1(14)所示)。
图1-1 14种空间点阵(4)布拉维点阵与复式点阵①布拉维点阵:由等同点构成的点阵;②复式点阵:由几个布拉维点阵穿插而成的复杂点阵。
二、晶面指数和晶向指数1.晶面指数和晶向指数(1)晶面指数将截距的倒数化成三个互质的整数h,k,l,则(hkl)称为待标晶面的晶面指数。
(2)晶向指数将晶向上除原点以外的任一点的坐标x,y,z化成互质整数u,v,w,得到晶向指数[uvw]。
材料科学基础_第1章_陶杰_主编_化学工业出版社

33
几点说明: 1.hkl分别对应xyz上的截距,不可互换 2.若晶面与对应坐标平行,则在该坐标上的指数为0 3.hkl表示沿三个坐标单位长度范围内所含该晶面的个数,
即晶面线密度。 晶面指数规律: (1)某一晶面指数代表了在原点同一侧的一组相互平行且
无限大的晶面。 (2) 若晶面指数相同,但正负符号相反,则两晶面是以点
材料科学基础
第一章 晶体学基础
❖1.1 晶体的周期性和空间点阵 ❖1.2 布拉菲点阵 ❖1.3 晶向指数与晶面指数 ❖1.4 晶面间距、晶面夹角和晶带定理 ❖1.5 晶体的对称性 ❖1.6 极射投影
2
1.1 晶体的周期性和空间点阵
1.1.1 晶体与晶体学 晶体:是内部质点在三维空间成周期性重复排列的固体, 即晶体是具有格子构造的固体。 非晶体:原子无规则堆积,也称为 “过冷液体” 。
38
a3 =-(a1+a2)
六方晶系的晶面指数与晶向指数
39
三指数系统→四指数系统
(h k l) (h k il) i=-(h+k)
16
3 简单单斜点阵
a≠b≠c α=γ=90°≠β
17
4 简单正交点阵
a≠b≠c,α=β=γ= 90°
18
5 底心正交点阵
a≠b≠c,α=β=γ=90°
19
6 体心正交点阵
a≠b≠c,α=β=γ= 90°
20
7 面心正交点阵
a≠b≠c,α=β=γ= 90°
21
8 简单六方点阵
a=b≠ c,α=β=90°,γ=120°
选取晶胞的原则:
1. 要能充分反映整个空间点成的周期性和对称性; 2. 在满足1的基础上,单胞要具有尽可能多的直角; 3. 在满足上条件,晶胞应具有最小的体积。
晶体学基础-晶体对称性

旋转反映轴的图解
L4s=L4i L6s=L3+C=L31i 6
对称元素--两种符号:
国际符号(International Notation), 圣弗里斯符号(Schoenflies Notation)。
对称元素
对 称 中 心
对称 面
一次 对称 轴
二次 对称 轴
三次 对称 轴
四次 对称 轴
六次 对称 轴
2、对称要素(symmetry element)
在进行对称变换时所凭借的几何要素 ——点、线、面等。
17:14
6
3、宏观晶体中的对称要素及相应对称变换
(1)对称中心(center of symmetry, 符号C):
一假想的几何点; 对称变换:对于这个点的反伸(反演)。
(a)
(b)
(c)
具有对称中心的图形
17:14
18
七种晶系的对称性及点阵常数间的关系
晶族(3) 低级晶族 无高次轴
中级晶族: 只有1个 高次轴
晶系(7) 三斜 单斜
正交
四方 (正方)
六方
对称性
1 (E) 2 (C2) 2个 2(C2) 4 (C4)
6 (C6)
菱方
高级晶族 立方
高次轴>1
3 (C3) 4个3 (C3)
17:14
棱边 /夹角
a = b = c α=β=γ=90°
6L2, 3L4,4L3, 9P,C
? 本质上,决定立方系的主要对称元素? ? 一定有几次轴?
17:14
23
属于立方系,只有三次轴而 没有四次轴的形。
二个三次轴就可以导出立方晶系。
17:14
24
☺立方系主对称元素:4个体对角线方向的
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
i.4晶向指数和晶面指数 一■晶向和晶面 i 晶向
晶向:空间点阵中各阵点列的方向(连接点阵中任意结点列的直线方向)。
晶体中的某 些方向,涉及到晶体中原子的位置,原子列方向,表示的是一组相互平行、方向一致的直线 的指向。
2晶面
晶面:通过空间点阵中任意一组阵点的平面(在点阵中由结点构成的平面)。
晶体中原 子所构成的平面。
不同的晶面和晶向具有不同的原子排列和不同的取向。
材料的许多性质和行为 (如各种 物理性质、力学行为、相变、X 光和电子衍射特性等)都和晶面、
晶向有密切的关系。
所以, 为了研究和描述材料的性质和行为,
首先就要设法表征晶面和晶向。
为了便于确定和区别晶 体中不同方位的晶向和晶面,
国际上通用密勒(Miller )指数来统一标定晶向指数与晶面指 数。
二 晶向指数和晶面指数的确定 i 晶向指数的确定方法 三指数表示晶向指数[uvW ]的步骤如图i 所示。
建立以晶轴a ,b , c 为坐标轴的坐标系,各轴上的坐标长度单位分别是晶胞边长 坐标原点在待标
晶向上。
选取该晶向上原点以外的任一点
P (xa ,yb ,zc )。
将xa , yb , zc 化成最小的简单整数比 u , v , w,且u : v : w = xa : yb : zc 。
将u , v , w 三数置于方括号内就得到晶向指数 图2不同的晶向及其指数 当然,在确定晶向指数时, 坐标原点不一定非选取在晶向上不可。
若原点不在待标晶向 上,那就需要选取该晶向上两点的坐标 Rx i, y i, z i )和Q X 2, y 2, z 2),然后将(X i -X 2),(y i - y 2), ⑴
c , ⑵
⑶
⑷ [iiD]
[101]
{01
Oi]
b
a ,
b ,
[uvW 。
图1晶向指数的确定方法
[00[] £
\ If *
a _________________
m
(Z 1-Z 2)三个数化成最小的简单整数
u,v,w,并使之满足U : V :
w =(x i -X 2):( y i -y 2):(Z 1-Z 2)。
则[uvw ]为该晶向的指数。
显然,晶向指数表示了所有相互平行、方向一致的晶向。
若所指的方向相反,则晶向指
数的数字相同,但符号相反,如图
3中[0 TO]与[010]。
说明:
指数意义:代表相互平行、方向一致的所有晶向。
负值:标于数字上方,表示同一晶向的相反方向。
晶向族:晶体中原子排列情况相同但空间位向不同的一组晶向。
用<uvw>表示,数字 相同,但排列顺序不同或正负号不同的晶向属于同一晶向族。
晶体结构中那些原子密 度相同的等同晶向称为晶向轴,用 <UVW>表示。
<100> : [100] [010] [001] [ 100] [010] [ 001 ]
<111> : [111] [111] [111] [111] [111] [111] [111] [111]
[UTO]
(1)建立一组以晶轴 a , b , 标长度单位分别是晶胞边长 求出待标晶面在a , b
, 取截距的倒数1/xa , 1/yb , 1/zc 。
将这些倒数化成最小的简单整数比 h , k , l ,使h : k : l = 1/ xa : 1/yb : 1/zc o
如有某一数为负值,则将负号标注在该数字的上方, 将h ,k ,l 置于圆括号内,写成(hkl ), 则(hkl )就是待标晶面的晶面指数。
说明:晶面指数所代表的不仅是某一晶面,而是代表着一组相互平行的晶面。
a 指数意义:代表一组平行的晶面;
tt.O.
OJ 图3正交点阵中的几个晶向指数
2晶面指数的确定
国际上通用的是密勒指数,即用三个数字来表示晶面指数( 面
为待确定的晶面,其确定方法如下。
h k l )。
图4中的红色晶
c 为坐标轴的坐标系,令坐标原点不在待标晶面上,各轴上的坐 a , b , c 。
c 轴上的截距xa , yb , zc 。
如该晶面与某轴平行,则截距为》 ⑵ ⑶ ⑷ ⑸
MM
6・。
