10-1 简谐振动的矢量图示法
合集下载
简谐振动最基本最重要的运动

当θ角很小时,有: M mgh —— 谐振
单摆:I mL2 h = L I
I
g
L
2 g
L
T 2 L
g
复摆:
2 mgh
I
T 2 I
mgh
振动周期均取决于系统本身。
七.谐振的能量
Ek
1 mv2 2
1 m 2 A2 sin 2 (
2
t
)
1 kA2 sin 2 (
2
t
)
Ep
1k 2
02 2 A、φ由初始条件决定。
若:
2>
2 0
则为过阻尼振动,物体将缓慢逼近平衡位置。
2 02
称为临界阻尼,物体回到平衡位置,并静止。
应用:电表中的电磁阻尼。临界阻尼。 二. 受迫振动
1.受迫振动 : 振动系统在周期性外力的持续作用 下发生的振动。此外力称驱动力。若强迫力按简谐 振动规律变化,则受迫振动也是谐振,周期为外力 的周期,振幅保持不变。
阻尼越小,振幅越大。
定量分析:
dA d (
f
)0
d p
d p
(
2 0
2 p
)2
4
2
2 p
得: 02 2
A Amax
f
Amax
2
02 2
阻力越小,ωp越接近ω0。同时 Aτ也越大。
β
0
ωτ
ω0
Amax
∞
§6. 谐振的合成
一.两个同方向 同频率的合成
x1 A1 cos( t 1) x2 A2 cos( t 2 )
A = A1- A2 为最小 二.同方向不同频率的合成 拍
合振动的振幅、频率均随时间变化,不是简谐振动。
简谐运动及其旋转矢量表示法简谐运动的能量

解:(1 )A6 1 2 0 m , /3 ,
1 Hz , 2 6
T 2 1 6s, /4
(2)势能 总能
Epkx2/2, EkA 2/2
由题意, k2 x/2k2 A /4, xA/ 24.2 41 02m
(3)从平衡位置运动到 xA/ 2
的最短时间为 T / 8。
即为 6/80.75s
) )
O
A/2
x
(B)
A/2
O
x
A
x 10-2cos( t /3 - /4),(SI)
五、两个同频率简谐运动的相位关系
x 10-2cos( t /3 - /4),(SI)
x2 比 x1 超前
简谐运动及其旋转矢量表示法简谐运动的能量
五、两个同频率简谐运动的相位关系
(或 x1 比 x2 落后 ) 的最短时间为 T / 8。
x Acos( t )
半径
圆周运动小球 角速度
振幅
角频率 简谐振动物体
角坐标
相位
例:一物体做谐振动,振幅为 A,在起始
时刻质点的位移为 A/2 且向 x 轴的正方向
运动,代表此谐振动的旋转矢量图为:
质点运动的周期和振幅。
五、两个同频率简谐运动的相位关系
= 2 v = 2 /T
质点运动的周期和振幅。
A
,振幅A=1 cm. t=0时,速度具有负最O大值,求振动表达式.
(C ) x A/2
(D)
A/2
O
x
A
[D]
四、简谐运动的能量
1. 动能
Ek
1 mv 2
2
1 kA2 sin 2( t )
2
掌握
Ek max
1 Hz , 2 6
T 2 1 6s, /4
(2)势能 总能
Epkx2/2, EkA 2/2
由题意, k2 x/2k2 A /4, xA/ 24.2 41 02m
(3)从平衡位置运动到 xA/ 2
的最短时间为 T / 8。
即为 6/80.75s
) )
O
A/2
x
(B)
A/2
O
x
A
x 10-2cos( t /3 - /4),(SI)
五、两个同频率简谐运动的相位关系
x 10-2cos( t /3 - /4),(SI)
x2 比 x1 超前
简谐运动及其旋转矢量表示法简谐运动的能量
五、两个同频率简谐运动的相位关系
(或 x1 比 x2 落后 ) 的最短时间为 T / 8。
x Acos( t )
半径
圆周运动小球 角速度
振幅
角频率 简谐振动物体
角坐标
相位
例:一物体做谐振动,振幅为 A,在起始
时刻质点的位移为 A/2 且向 x 轴的正方向
运动,代表此谐振动的旋转矢量图为:
质点运动的周期和振幅。
五、两个同频率简谐运动的相位关系
= 2 v = 2 /T
质点运动的周期和振幅。
A
,振幅A=1 cm. t=0时,速度具有负最O大值,求振动表达式.
(C ) x A/2
(D)
A/2
O
x
A
[D]
四、简谐运动的能量
1. 动能
Ek
1 mv 2
2
1 kA2 sin 2( t )
2
掌握
Ek max
第四章 振动学基础§4.2简谐振动的图示法.讲解

cos(t) x 1
A2
t π 或 5π
33
由旋转矢量图可知 t π
3
v A sint
A
o A Ax
2
0.26m s1
(负号表示速度沿 Ox轴负方向)
2019/6/11
重庆邮电大学理学院
17
(3)如果物体在 x 0.05m 处时速度不等于零,而是具有 向右的初速度 v0 0.30m s,1 求其运动方程.
A
aቤተ መጻሕፍቲ ባይዱ
x
由图看出:速度超前位移 π 加速度超前速度 2
位移与加速度 Δ π 称两振动反相
若 0 称两振动同相
8、 在谐振动的合成中,用旋转矢量非常方便。
总之20,19/6旋/11 转矢量法在大学物重庆理邮电,大电学理路学院分析,等学科中有广泛15应用
例4.2.4 如图所示,一轻弹簧的右端连着一物体,弹簧的劲度
22
重庆邮电大学理学院
418
例4.2.5、一作简谐振动的物体,其振动曲
x/m
线如图所示。试写出该振动的表达式。
解:振动方程为 x Acos(t )
0.01
由振动曲线可知,振幅为 A 0.02 m
t = 0 时,
x0
A 2
0.01m
O
1
t/s
且其初始速度 v0 0
0.02
y
作旋转矢量图,如右图。
)
2
0 a v
(t )
2
v Asin(t )
x an r 2 A2
a
an
i
(t ) an i cos
简谐振动的旋转矢量图示法

解:
点 2 在 x = - A / 2 处 向 右 运 动 , 试 用 旋
转 矢 量 法 求 两 质 点 的 相 位 差 。 1
3
x
2
4
3
2
A
2A
O
1
A 2
2143 3
例2、一物体沿x轴作简谐振动,振幅A=0.12m,周期 T=2s。当t=0时,物体的位移x=0.06m,且向x轴正向运
动。求: (1)简谐振动表达式;
向正方向运动,求运动方程。
解:(1) k 0.726.0s-1
m 0.02
由旋转矢量可知初相位 谐振动方程为
0 0
0.05
O
x
x0.05cos(6.0t) m
第一次经过A/2时,相位
(2) v dx 0.056.0sin(6.0t) dt
=0.3sin(6.0t) m/s
6.0t 3
OA
0, x=0.06m可
得0 3
或
3
简谐振动表达式
01
02
03
04
v0Asin00
由于t=0时质点 向x轴正向运动
0 3
因而
可知
x0.12cos(t) m
3
(2)由简谐振动的运动方程可得:
vdx0.12sin(t) m /s
dt
3
adv 0.12 2cos(t)m /s2
dt
3
在t =T/4=0.5s时,可得
A 的长度
振幅A
A 旋转的角速度
角频率ω
A 与参考方向x 的夹角
振动相位ωt+φ0
相位之差为
x1A1cos(t1)
x2A2cos(t2)
简谐振动-旋转矢量法
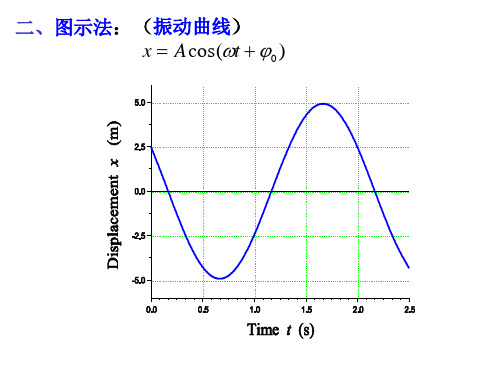
sin2 (2 1)
y
2) 2 1 π
y A2 x A1
3)2 1 π 2
x A2
o A1
x2 A12
பைடு நூலகம்
y2 A22
1
x A1 cost
y
A2
cos(t
π) 2
A2 y
o A1 x
用 旋 转 矢 量 描 绘 振 动 合 成 图
两
相
互 垂 直 同 频 率 不 同 相
简 谐 运 动 的 合 成 图
x
x
A1 o
o
A
A2
A A1 A2
Tt
结论
A A12 A22 2A1 A2 cos(2 1 )
若两分振动同相位:
2 1 2k k 0,1, 2,
A A1 A2
若两分振动反相位:
两分振动相互加强
2 1 (2k 1) k 0,1, 2,
A A1 A2
两分振动相互减弱
再若 A1= A2 , 则 A= 0
M
A
P
x
注意:旋转矢量在第 2 象限
速度v <0
M
PA
x
注意:旋转矢量在第 2 象限
速度v <0
M
PA
x
<
注意:旋转矢量在第 3 象限
速度v 0
P x
MA
<
注意:旋转矢量在第 3 象限
速度v 0
P x
A
M
<
注意:旋转矢量在第 3 象限
速度v 0
P x
A
M
<
注意:旋转矢量在第 3 象限
速度v 0
找到谐振动的特征量,问题就解决了。
1简谐运动

x
x
x A cos( t 0 )
k x A cos( t 0 ) m
定义: 1、物体受线性回复力的作用:
2
F k x
2、物体动力学方程形如: 3、物体运动学方程形如:
x A cos( t 0 )
dx 2x 0 2 dt
的运动叫简谐振动。 一般,习惯推导至形式3。
2π π 1 A 0.08m s T 2 t 0, x 0.04m 代入 x A cos(t ) π 0.04m (0.08m) cos 3 π A v0 0 3
π 3
x/m
0.08 0.04
0.04 0.08 π 1 π x (0.08m) cos[( s )t ] 2 3
(2)由起始位置运动到 的最短时间.
x 0.04m 处所需要
t
时刻
π 3
t
o
起始时刻
vπ 3
0.04 0.08
x/m
0.08 0.04
π t 3
π 1 s 2
2 t s 0.667 s 3
例5 如图所示,一轻弹簧的右端连着一物体,弹 1 簧的劲度系数 k 0.72 N m ,物体的质量 m 20g .
速度幅A,位相比位移超前
/2
四、振动图示法
旋转矢量法、参考圆法
将物理模型转变成数学模型。
矢量 OM,长度A, 以角
速度 逆时针绕O点作匀速转
M A t
o
动,t = 0 时,夹角 0 ,
讨论 M 点在 x 轴上投影点的运 动,
x P
x
10-1 简谐振动的矢量图示法
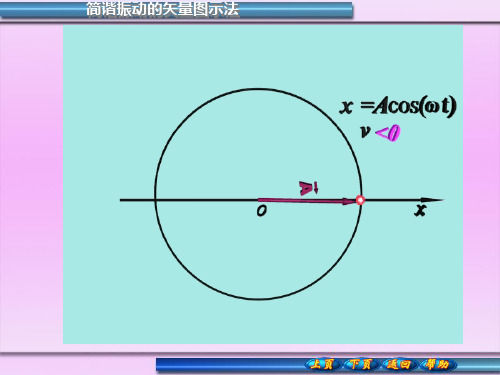
速度v <0
M
PA
x
注意:旋转矢量在第 2 象限
速度v <0
M
PA
x
<
注意:旋转矢量在第 3 象限
速度v 0
P x
MA
<
注意:旋转矢量在第 3 象限
速度v 0
P x
A
M
<
注意:旋转矢量在第 3 象限
速度v 0
P x
A
M
<
注意:旋转矢量在第 3 象限
速度v 0
P x
A
M
<
注意:旋转矢量在第 3 象限
C
x = 0.12 cos (πt-π/3 ) (m)
如不用参考圆只用数学式解题:
由
x = A cos (ωt+ φ)
已知 A= 0.12m , T= 2s → ω= π
则 x = 0.12 cos (πt+ φ) φ= ?
t = 0 时 x=0.06m: 0.06 = 0.12cosφ →
cosφ = 0.5 → φ= ±π/3
简谐振动的矢量图示法
简谐振动的矢量图示法
A 的长度
振幅A
A旋转的角速度
振动圆频率 O
ω
M
A
t 0
P
X
x
A 旋转的方向
逆时针方向
A 与参考方向x 的夹角 振动相位
M 点在 x 轴上投影(P点)的运动规律:
x Acos(t 0 )
矢量OM 的端点 M 所画的圆叫参考圆。 矢量 OM 0 是 t = 0 时刻的位置,它与 x 轴的夹角φ叫初相位。 简谐振动的参考圆和矢量表示方法十分形
x
M
PA
x
注意:旋转矢量在第 2 象限
速度v <0
M
PA
x
<
注意:旋转矢量在第 3 象限
速度v 0
P x
MA
<
注意:旋转矢量在第 3 象限
速度v 0
P x
A
M
<
注意:旋转矢量在第 3 象限
速度v 0
P x
A
M
<
注意:旋转矢量在第 3 象限
速度v 0
P x
A
M
<
注意:旋转矢量在第 3 象限
C
x = 0.12 cos (πt-π/3 ) (m)
如不用参考圆只用数学式解题:
由
x = A cos (ωt+ φ)
已知 A= 0.12m , T= 2s → ω= π
则 x = 0.12 cos (πt+ φ) φ= ?
t = 0 时 x=0.06m: 0.06 = 0.12cosφ →
cosφ = 0.5 → φ= ±π/3
简谐振动的矢量图示法
简谐振动的矢量图示法
A 的长度
振幅A
A旋转的角速度
振动圆频率 O
ω
M
A
t 0
P
X
x
A 旋转的方向
逆时针方向
A 与参考方向x 的夹角 振动相位
M 点在 x 轴上投影(P点)的运动规律:
x Acos(t 0 )
矢量OM 的端点 M 所画的圆叫参考圆。 矢量 OM 0 是 t = 0 时刻的位置,它与 x 轴的夹角φ叫初相位。 简谐振动的参考圆和矢量表示方法十分形
x
简谐振动的旋转矢量图示.ppt
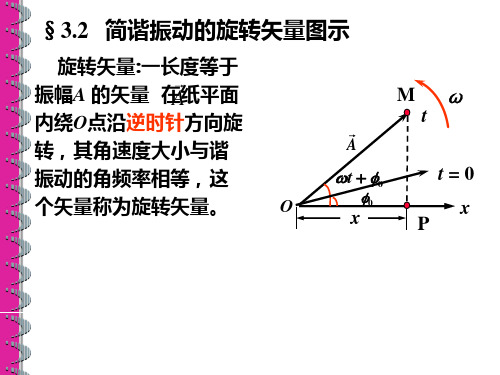
角频率ω
A 与参考方向x 的夹角
振动相位ωt+φ0
3、两个谐振动的相位差
x1 A1 cos(t 1 ) x2 A2 cos(t 2 )
相位差为 (t 2 ) (t 1) 2 1
采用旋转矢量表示为:
A2
2
A1
1
O
x
例1、两个同频率的谐振动,它们都沿x轴振动,且振
幅相等,当t =0时质点1在x=A/2处向左运动,另一质点
F kx m 2x
(0.01kg)(π s1)2 (0.069m) 1.70103 N
2
(2)由起始位置运动到 x 0.04m 处所需要
的最短时间.
v
x/m
0.08 0.04 o 0.04 0.08
解法一 设由起始位置运动到 x 0.04m 处所
需要的最短时间为 t
0.04m (0.08m) cos[(π s1)t π ]
x 0.12cos( 0.5 ) 0.104 m
3
v 0.12 sin( 0.5 ) 0.18 m/s
3 a 0.12 2 cos( 0.5 ) 1.03 m/s2
3
在t =T/4=0.5s时,可得
可得x 0.12cos( 0.5 ) 0.104 m
3
v 0.12 sin( 0.5 ) 0.18 m/s
sin0 0
0
3
简谐振动表达式 x 0.12cos( t ) m
3
因为
(2)由简谐振动的运动方程 x 0.12cos( t ) m
3
可得
v dx 0.12 sin( t ) m/s
dt
3
a dv 0.12 2 cos( t ) m/s2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
简谐振动的矢量图示法
简谐振动的矢量图示法
A 的长度
振幅A
A旋转的角速度
振动圆频率 O
ω
M
A
t 0
P
X
x
A 旋转的方向
逆时针方向
A 与参考方向x 的夹角 振动相位
M 点在 x 轴上投影(P点)的运动规律:
x Acos(t 0 )
矢量OM 的端点 M 所画的圆叫参考圆。 矢量 OM 0 是 t = 0 时刻的位置,它与 x 轴的夹角φ叫初相位。 简谐振动的参考圆和矢量表示方法十分形
x
A 2
A 1.0
0
t
补例 1一谐振动的振动曲线如图所示。
求:ω 、φ 以及振动方程。
x
A 2
A 1.0
0
t
补例 1一谐振动的振动曲线如图所示。
求:ω 、φ 以及振动方程。
x
A 2
A 1.0
0
t
t
=
0时
{
x 0
=
A 2
补例 1一谐振动的振动曲线如图所示
求:ω 、φ 以及振动方程。
x
A 2
A 1.0
解:已知 A = 0.12 m,T = 2s,
ω = 2π/T = π ( rad/s ).
( t =1 s ) B ’
ω
(1) 初态 t = 0 时,
x = 0.06, v >0, 初相 φ = -π/3 ,
-0.06
●
O 0.06
●
φ
Δφ
x (m
运动表达式为:
( t = 5/3 s) B
A(t=0)
速度v 0
P
A
x
M
<
注意:旋转矢量在第 4 象限
速度v 0
A
M Px
<
注意:旋转矢量在第 4 象限
速度v 0
A
M Px
相位差的问题(以两个同频率简谐振动为例)
x 1= A cos(ω t +φ 1 )
AA1
0
2 φ1
x
相位差的问题
x 1= A cos(ω t +φ 1 ) x 2= A cos(ω t +φ 2 )
0
称两振动同步
A2
φ
A1
2 φ1
x
A1 A2
相位差的问题
x 1= A cos(ω t +φ 1 )
x 2= A cos(ω t +φ 2 )
若周相差ΔΦ =φ 2 φ 1> 0 0 称振动 2 超前振动 1
振动 1 滞后振动 2
若周相差Δ Φ = 0
0
称两振动同步
若周相差Δ Φ =π
称两振动反相 A 2
0
t
t
=
0时
{
x 0
=
A 2
v0 >0
补例 1一谐振动的振动曲线如图所示。
求:ω 、φ 以及振动方程。
xπ
x
3
A 2
A 1.0
A
0
t
t
=
0时
{
x 0
=
A 2
v0 >0
补例 1一谐振动的振动曲线如图所示。
求:ω 、φ 以及振动方程。
xπ
x
3
A 2
A 1.0
A
0
t
t
=
0时
{
x 0
=
A 2
v0 >0
...φ
v0 >0
...φ
=
π
3
t =1时
{
x1= 0
v 1
=
dx dt
<
0
补例 1一谐振动的振动曲线如图所示。
求:ω 、φ 以及振动方程。
xπ
x
3
A 2
A 1.0
A
0
t
t
=
0时
{
x 0
=
A 2
v0 >0
...φ
=
π
3
t =1时
{
x1= 0
v 1
=
dx dt
<
0
π
2
x
A
补例 1一谐振动的振动曲线如图所示。
速度v <0
M
PA
x
注意:旋转矢量在第 2 象限
速度v <0
M
PA
x
<
注意:旋转矢量在第 3 象限
速度v 0
P x
MA
<
注意:旋转矢量在第 3 象限
速度v 0
P x
A
M
<
注意:旋转矢量在第 3 象限
速度v 0
P x
A
M
<
注意:旋转矢量在第 3 象限
速度v 0
P x
A
M
<
注意:旋转矢量在第 3 象限
(
5 6
π
t
π
3
)
x = A cos
(
5 6
π
t
π
3
)
本题ω 的另一种求法:
x = A cos
(
5 6
π
t
π
3
)
本题ω 的另一种求法:
(Φ1 - φ) :(2π) = t : T
π
2
+
π
3
2π
=
1 T
x = A cos
(
5 6
π
t
π
3
)
本题ω 的另一种求法:
x
(Φ1 - φ) :(2π) = t : T
C
x = 0.12 cos (πt-π/3 ) (m)
如不用参考圆只用数学式解题:
由
x = A cos (ωt+ φ)
已知 A= 0.12m , T= 2s → ω= π
则 x = 0.12 cos (πt+ φ) φ= ?
t = 0 时 x=0.06m: 0.06 = 0.12cosφ →
cosφ = 0.5 → φ= ±π/3
若相位差ΔΦ =φ 2 φ 1> 0 0 称振动 2 超前振动 1
振动 1 滞后振动 2
A2
φ
A1
2 φ1
x
相位差的问题
x 1= A cos(ω t +φ 1 )
x 2= A cos(ω t +φ 2 )
若周相差ΔΦ =φ 2 φ 1> 0 0 称振动 2 超前振动 1
振动 1 滞后振动 2
若周相差Δ Φ = 0
φ=π/3: t 从 0增加Δt ,相位角增大, x变小 → 向 x轴负向运动 φ= -π/3: t 从 0增加Δt ,相位角绝对值变小 , x增大 →
向 x轴正向运动
∴取 φ= -π/3
运动表达式为: x = 0.12 cos (πt-π/3 ) (m)
其振动曲线 (振动的 x-t 图) 为:
X(m)
0
π
2
π
2
x
Φ1 =ω t 1+ φ =ω × 1 π
A
补例 1一谐振动的振动曲线如图所示。
求:ω 、φ 以及振动方程。
xπ
x
3
A 2
A 1.0
A
0
t
t
=
0时
{
x 0
=
A 2
v0 >0
...φ
=
π
3
t =1时
{
x1= 0
v 1
=
dx dt
<
...Φ 1=
0
π
2
π
2
x
Φ1 =ω t 1+ φ =ω × 1 π =π
0.12
0.06
T/4 T/2 3T/4
T
t(s)
0
1/2
1
3/2
2
Δt=Δφ/ω=(-π/3)/π= -1/3(s)
(2)自学(参见下册书第9页)
(3) 当 x = -0.06 m时,物体在旋转矢量图中
的位置可能在 B 或 B′处,因为物体向 X 轴
负方向运动所以位置应该在B′处。o B′ 与 OC
...φ
=
π
3
t =1时
{
x1= 0
v 1
=
dx dt
<
...Φ 1=
0
π
2
π
2
x
Φ1 =ω t 1+ φ =
A
补例 1一谐振动的振动曲线如图所示。
求:ω 、φ 以及振动方程。
xπ
x
3
A 2
A 1.0
A
0
t
t
=
0时
{
x 0
=
A 2
v0 >0
...φ
=
π
3
t =1时
{
x1= 0
v 1
=
dx dt
<
...Φ 1=
求:ω 、φ 以及振动方程。
xπ
x
3
A 2
A 1.0
A
0
t
t
=
0时
{
x 0
=
A 2
v0 >0
...φ
=
π
3
t =1时
{
x1= 0
v 1
=
dx dt
<
...Φ 1=
0
π
2
π
2
x
A
补例 1一谐振动的振动曲线如图所示。
求:ω 、φ 以及振动方程。
xπ
x
简谐振动的矢量图示法
A 的长度
振幅A
A旋转的角速度
振动圆频率 O
ω
M
A
t 0
P
X
x
A 旋转的方向
逆时针方向
A 与参考方向x 的夹角 振动相位
M 点在 x 轴上投影(P点)的运动规律:
x Acos(t 0 )
矢量OM 的端点 M 所画的圆叫参考圆。 矢量 OM 0 是 t = 0 时刻的位置,它与 x 轴的夹角φ叫初相位。 简谐振动的参考圆和矢量表示方法十分形
x
A 2
A 1.0
0
t
补例 1一谐振动的振动曲线如图所示。
求:ω 、φ 以及振动方程。
x
A 2
A 1.0
0
t
补例 1一谐振动的振动曲线如图所示。
求:ω 、φ 以及振动方程。
x
A 2
A 1.0
0
t
t
=
0时
{
x 0
=
A 2
补例 1一谐振动的振动曲线如图所示
求:ω 、φ 以及振动方程。
x
A 2
A 1.0
解:已知 A = 0.12 m,T = 2s,
ω = 2π/T = π ( rad/s ).
( t =1 s ) B ’
ω
(1) 初态 t = 0 时,
x = 0.06, v >0, 初相 φ = -π/3 ,
-0.06
●
O 0.06
●
φ
Δφ
x (m
运动表达式为:
( t = 5/3 s) B
A(t=0)
速度v 0
P
A
x
M
<
注意:旋转矢量在第 4 象限
速度v 0
A
M Px
<
注意:旋转矢量在第 4 象限
速度v 0
A
M Px
相位差的问题(以两个同频率简谐振动为例)
x 1= A cos(ω t +φ 1 )
AA1
0
2 φ1
x
相位差的问题
x 1= A cos(ω t +φ 1 ) x 2= A cos(ω t +φ 2 )
0
称两振动同步
A2
φ
A1
2 φ1
x
A1 A2
相位差的问题
x 1= A cos(ω t +φ 1 )
x 2= A cos(ω t +φ 2 )
若周相差ΔΦ =φ 2 φ 1> 0 0 称振动 2 超前振动 1
振动 1 滞后振动 2
若周相差Δ Φ = 0
0
称两振动同步
若周相差Δ Φ =π
称两振动反相 A 2
0
t
t
=
0时
{
x 0
=
A 2
v0 >0
补例 1一谐振动的振动曲线如图所示。
求:ω 、φ 以及振动方程。
xπ
x
3
A 2
A 1.0
A
0
t
t
=
0时
{
x 0
=
A 2
v0 >0
补例 1一谐振动的振动曲线如图所示。
求:ω 、φ 以及振动方程。
xπ
x
3
A 2
A 1.0
A
0
t
t
=
0时
{
x 0
=
A 2
v0 >0
...φ
v0 >0
...φ
=
π
3
t =1时
{
x1= 0
v 1
=
dx dt
<
0
补例 1一谐振动的振动曲线如图所示。
求:ω 、φ 以及振动方程。
xπ
x
3
A 2
A 1.0
A
0
t
t
=
0时
{
x 0
=
A 2
v0 >0
...φ
=
π
3
t =1时
{
x1= 0
v 1
=
dx dt
<
0
π
2
x
A
补例 1一谐振动的振动曲线如图所示。
速度v <0
M
PA
x
注意:旋转矢量在第 2 象限
速度v <0
M
PA
x
<
注意:旋转矢量在第 3 象限
速度v 0
P x
MA
<
注意:旋转矢量在第 3 象限
速度v 0
P x
A
M
<
注意:旋转矢量在第 3 象限
速度v 0
P x
A
M
<
注意:旋转矢量在第 3 象限
速度v 0
P x
A
M
<
注意:旋转矢量在第 3 象限
(
5 6
π
t
π
3
)
x = A cos
(
5 6
π
t
π
3
)
本题ω 的另一种求法:
x = A cos
(
5 6
π
t
π
3
)
本题ω 的另一种求法:
(Φ1 - φ) :(2π) = t : T
π
2
+
π
3
2π
=
1 T
x = A cos
(
5 6
π
t
π
3
)
本题ω 的另一种求法:
x
(Φ1 - φ) :(2π) = t : T
C
x = 0.12 cos (πt-π/3 ) (m)
如不用参考圆只用数学式解题:
由
x = A cos (ωt+ φ)
已知 A= 0.12m , T= 2s → ω= π
则 x = 0.12 cos (πt+ φ) φ= ?
t = 0 时 x=0.06m: 0.06 = 0.12cosφ →
cosφ = 0.5 → φ= ±π/3
若相位差ΔΦ =φ 2 φ 1> 0 0 称振动 2 超前振动 1
振动 1 滞后振动 2
A2
φ
A1
2 φ1
x
相位差的问题
x 1= A cos(ω t +φ 1 )
x 2= A cos(ω t +φ 2 )
若周相差ΔΦ =φ 2 φ 1> 0 0 称振动 2 超前振动 1
振动 1 滞后振动 2
若周相差Δ Φ = 0
φ=π/3: t 从 0增加Δt ,相位角增大, x变小 → 向 x轴负向运动 φ= -π/3: t 从 0增加Δt ,相位角绝对值变小 , x增大 →
向 x轴正向运动
∴取 φ= -π/3
运动表达式为: x = 0.12 cos (πt-π/3 ) (m)
其振动曲线 (振动的 x-t 图) 为:
X(m)
0
π
2
π
2
x
Φ1 =ω t 1+ φ =ω × 1 π
A
补例 1一谐振动的振动曲线如图所示。
求:ω 、φ 以及振动方程。
xπ
x
3
A 2
A 1.0
A
0
t
t
=
0时
{
x 0
=
A 2
v0 >0
...φ
=
π
3
t =1时
{
x1= 0
v 1
=
dx dt
<
...Φ 1=
0
π
2
π
2
x
Φ1 =ω t 1+ φ =ω × 1 π =π
0.12
0.06
T/4 T/2 3T/4
T
t(s)
0
1/2
1
3/2
2
Δt=Δφ/ω=(-π/3)/π= -1/3(s)
(2)自学(参见下册书第9页)
(3) 当 x = -0.06 m时,物体在旋转矢量图中
的位置可能在 B 或 B′处,因为物体向 X 轴
负方向运动所以位置应该在B′处。o B′ 与 OC
...φ
=
π
3
t =1时
{
x1= 0
v 1
=
dx dt
<
...Φ 1=
0
π
2
π
2
x
Φ1 =ω t 1+ φ =
A
补例 1一谐振动的振动曲线如图所示。
求:ω 、φ 以及振动方程。
xπ
x
3
A 2
A 1.0
A
0
t
t
=
0时
{
x 0
=
A 2
v0 >0
...φ
=
π
3
t =1时
{
x1= 0
v 1
=
dx dt
<
...Φ 1=
求:ω 、φ 以及振动方程。
xπ
x
3
A 2
A 1.0
A
0
t
t
=
0时
{
x 0
=
A 2
v0 >0
...φ
=
π
3
t =1时
{
x1= 0
v 1
=
dx dt
<
...Φ 1=
0
π
2
π
2
x
A
补例 1一谐振动的振动曲线如图所示。
求:ω 、φ 以及振动方程。
xπ
x
