剪切弹性模量G的测定
实验六金属材料剪切弹性模量G的测量

- 1 -实验六 金属材料剪切弹性模量G 的测量一、实验目的测定金属材料的剪切模量G ,并验证剪切虎克定律。
二、实验原理圆轴扭转时,若最大剪应力不超过材料的比例极限,则扭矩T 与扭转角φ存在线性关系PGI TL 0=φ 式中: 32I p =4d π为圆截面的极惯性矩,为试件的直径 d φ——距离为的两截面之间的相对扭转角0L T ——扭矩由上式可知,若材料符合虎克定律,则T —φ图在比例极限以下成线性关系。
当试件受一定的扭矩增量后,在标距内可量得相应的扭转角增量T Δ0L φΔ,于是由上式可求得G 的公式P I L T G ⋅Δ⋅Δ=φ0实验按照等增量分级加扭矩的方法进行,测得相应的T ΔφΔ,即可求得G RL P T δφΔ=Δ⋅Δ=Δ,,则 δπΔ⋅Δ⋅⋅⋅=4032d PR L L G式中:P Δ--载荷增量 --外载力臂1L δΔ--百分表位移增量 --受扭杆标距 0L R --测量臂长度如图6.1所示:- 2 -受扭杆标距L 0 外载力臂L 1测量臂长R砝码百分表图6.1 JY—2型扭角仪三、实验设备JY—2型扭角仪四、实验步骤1、测量试件的计算长度及直径,取三个直径的平均值作为计算直径;2、在试件上按计算长度安装扭角仪;3、将百分表调节至零点;4、加砝码,使产生扭矩T 及扭转角φ,每增加1㎏砝码后,在百分表上读一个相应的位移量δ,算出位移增量δΔ,注意加载要平稳,实验过程中勿碰仪器;5、重复做几次,卸下载荷;6、根据实验数据,计算剪切弹性模量。
G 五、实验要求1、了解实验目的、原理、步骤及通过实验所求得的数据;2、讨论分析测定的误差情况。
G- 3 -六、实验报告6.1表。
剪切弹性模量g的测定实验报告

剪切弹性模量g的测定实验报告剪切弹性模量G的测定实验报告引言:弹性模量是材料力学性质的重要参数,它描述了材料在受力作用下的变形能力。
剪切弹性模量G是弹性模量的一种,用于描述材料在剪切应力作用下的变形能力。
本实验旨在通过测定剪切弹性模量G的方法,掌握实验技巧,加深对材料力学性质的理解。
实验仪器与材料:1. 剪切弹性模量测定仪器2. 弹性体样品(如橡胶块)实验原理:剪切弹性模量G可以通过测定剪切应力和剪切应变的关系来计算。
实验中,我们将利用剪切弹性模量测定仪器对样品进行测试。
该仪器通过施加剪切力和测量剪切应变,得到剪切弹性模量G的数值。
实验步骤:1. 将弹性体样品放置在剪切弹性模量测定仪器上,并调整仪器使其处于平衡状态。
2. 施加一个恒定的剪切力,记录下施力的数值。
3. 测量样品在施力下产生的剪切应变,记录下剪切应变的数值。
4. 根据施力和剪切应变的数值,计算剪切弹性模量G的数值。
实验结果与分析:根据实验数据计算得到的剪切弹性模量G的数值为X。
通过对实验结果的分析,我们可以得出以下结论:1. 弹性体样品在受力作用下发生剪切变形,剪切弹性模量G描述了材料抵抗剪切应力的能力。
2. 弹性体样品的剪切弹性模量G的数值与材料的性质有关,不同材料的剪切弹性模量G可能存在差异。
3. 实验中所使用的剪切弹性模量测定仪器对于测量剪切弹性模量G具有较高的精确度和准确性。
实验误差与改进:在实验过程中,可能存在一些误差,影响了实验结果的准确性。
可能的误差来源包括:1. 仪器的精度限制:剪切弹性模量测定仪器的精度可能存在一定限制,导致实验结果的误差。
2. 样品的非理想性:实际样品可能存在缺陷或不均匀性,导致实验结果的误差。
3. 实验操作的不精确性:实验过程中操作的不精确性可能导致实验结果的误差。
为了减小误差,提高实验结果的准确性,可以采取以下改进措施:1. 使用更精确的仪器:选择精度更高的剪切弹性模量测定仪器,提高实验结果的准确性。
剪切弹性模量G的测定
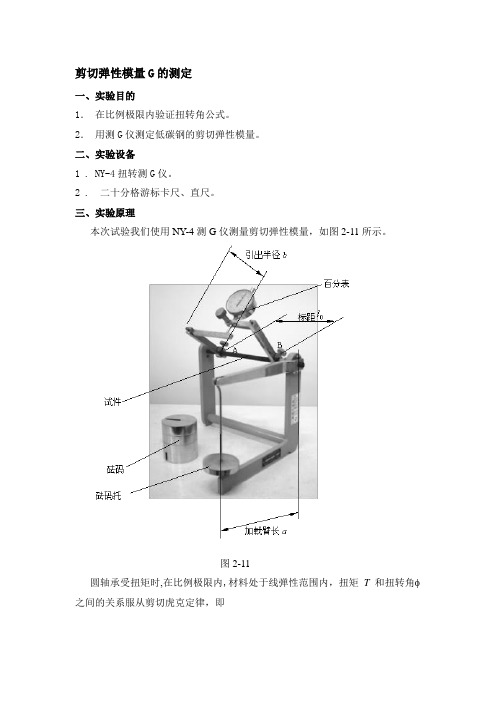
剪切弹性模量G的测定一、实验目的1.在比例极限内验证扭转角公式。
2.用测G仪测定低碳钢的剪切弹性模量。
二、实验设备1 . NY-4扭转测G仪。
2 . 二十分格游标卡尺、直尺。
三、实验原理本次试验我们使用NY-4测G仪测量剪切弹性模量,如图2-11所示。
图2-11圆轴承受扭矩时,在比例极限内,材料处于线弹性范围内,扭矩T和扭转角 之间的关系服从剪切虎克定律,即PGI TL 0=φ 其中,T 为扭矩,0L 是试件的标距长度,P I 为圆轴截面的极惯性矩。
本实验我们采用“增量法”测量剪切弹性模量G ,对试件逐级增加同样大小的扭矩T ∆,相应地由测G 仪测出相距为0L 的两个截面之间的相对扭转角增量i φ∆。
如果每一级扭矩增量所引起的扭转角增量i φ∆基本相等,则说明T ∆和i φ∆成线性关系,这就验证了剪切胡克定律。
根据测得的各级扭转角增量的平均值φ∆,可用下式算出剪切弹性模量PI L T G ⋅∆⋅∆=φ0四、实验步骤1. 按图2-11布置好测量装置。
安装百分表时让百分表有一个初始读数,约为满量程的5%,并记录。
2. 测量试件的直径d 、试件标距L 0、引出半径b 、加载臂长a 。
3. 进行加载。
每级载荷为P ∆=5N ,分四级加载至20N 为止,同时记录每次加载后百分表读数i A 。
五、数据记录及处理1. 根据记录的各级百分表读数求出相应的读数差i A ∆,并求出其算术平均值A ∆。
2.计算: 试件的极惯性矩 4132P I d π= 扭矩增量 T P a ∆∆=扭转角增量 A b ∆∆φ=剪切弹性模量 PI L T G ⋅∆⋅∆=φ0 3. 测量结果φ∆取4为有效数字,G 取3位有效数字。
4. 把实验值和理论值加以比较。
材料剪切弹性模量G的测定

材料 剪切 弹性 模量G 的测
定
(1)原始试件尺寸。参照表15-5。 (2)实验数据。参照表15-6。 (3)根据式(15-15)、式(15-14)计算 出扭转角增量Δφi和材料剪切弹性模量G。
材料 剪切 弹性 模量G 的测
定
1.1实验目的及仪器设备
材料剪切弹性 模量G的测定
1.2实验原理 1.3实验步骤
1.4实验数据处理
材料的剪切弹性模量G是由材料本身 性质来确定的另一力学参数。本节介绍如 何利用实验来测定低碳钢的剪切弹性模量 G值,并验证剪切胡克定律。实验用到的 仪器包括NY-4型扭转测G仪、游标卡尺和 百分表。
材料 剪切 弹性 模量G 的测
定
1.验证胡测量得 出各级扭转角增量Δφi值
材料 剪切 弹性 模量G 的测
定
(1)准确量取试件标距l0。 (2)正确测量试件直径d。 (3)加载。首先挂上砝码托作为初荷载, 记录百分表的初始读数。再分四次加载,每加一 次记录一次读数。加砝码时要缓慢放手,以使之 为静载,并注意防止失落而砸伤人、物。 (4)实验完毕,卸载,整理数据。
剪切弹性模量g的测定实验报告

剪切弹性模量g的测定实验报告实验目的:本实验旨在通过测定金属材料的剪切弹性模量g值,了解材料在受到剪切应力时的变形特性,为材料力学性能的研究提供数据支持。
实验原理:材料在受到剪切应力时,会产生剪切变形。
剪切弹性模量g是描述材料在受到剪切应力时产生的剪切应变与剪切应力之间关系的物理量。
在实验中,通过施加剪切应力,测量材料的剪切应变,从而计算出剪切弹性模量g的数值。
实验仪器和设备:1. 剪切弹性模量测定仪。
2. 金属样品。
3. 电子天平。
4. 温度计。
5. 数据采集系统。
实验步骤:1. 将金属样品放置在剪切弹性模量测定仪上,并调整仪器使其处于水平状态。
2. 施加一定的剪切应力,记录下施加的剪切应力数值。
3. 通过数据采集系统实时监测金属样品的剪切应变,并记录下相应的数据。
4. 在不同的剪切应力下,重复步骤2和步骤3,获取一系列剪切应力与剪切应变的数据。
5. 根据实验数据,计算出金属样品的剪切弹性模量g。
实验数据处理:根据实验所得的剪切应力与剪切应变数据,利用数学方法进行数据处理,得出金属样品的剪切弹性模量g的数值。
同时,还需要考虑温度对实验结果的影响,进行相应的修正。
实验结果分析:根据实验数据处理的结果,得出金属样品的剪切弹性模量g的数值。
通过对实验结果的分析,可以了解材料在受到剪切应力时的变形特性,以及材料的剪切弹性模量与材料性能的关系。
实验结论:通过本次实验,成功测定了金属样品的剪切弹性模量g的数值,并对实验结果进行了分析和讨论。
实验结果对于研究材料的力学性能具有重要的意义,为进一步的材料研究提供了参考数据。
实验注意事项:1. 在实验中要注意安全,避免发生意外伤害。
2. 实验过程中要保持仪器设备的稳定和精准,确保实验数据的准确性和可靠性。
3. 实验结束后要及时清理实验场地和归还实验设备,保持实验室的整洁和安全。
实验改进与展望:在今后的实验中,可以对实验方法和数据处理方法进行改进和优化,提高实验结果的精度和可靠性。
材料力学

力和变形仍按直线规律变化,并留下残余变形o o1,如再重新加载,仍从o1开始沿直线o1e 到e点,过e点才恢复曲线规律。此时就相当于材料的比例极限提高了。这是有利的一面, 而塑性指标(延伸率)却降低了,使材料变脆,这种现象叫冷作硬化。
F
A
B
Fm
0
ΔL
(a)
0
ΔL
(b)
图 1-4 图解方法测定最大力Fm
3.断后塑性指标
表征材料塑性性能的两个指标为断后伸长率 A 和断面收缩率 Z。
断后伸长率 A = L1 − L0 ×100% L0
断面收缩率 Z = S0 − S1 ×100% S0
式中 L0,S0-试验前的标距和横截面积。 L1,S1-拉断后的标距和横截面积。
试件承受的扭矩在剪切比例极限以内时,处于线弹性阶段 OA(图 3-1a),剪应力 和剪应变服从虎克定律,即
τ = Gr
图 3-1 当扭矩超过Mp,试件表面开始形成塑性区,转角越大,塑性区越深入到中心,Mn-φ曲线 开始平坦,一直到B点,这时Mn=Ms,可以近似的认为整个截面剪应力都达到屈服极限τ(s 图 3-2c)。
(a)低碳钢拉伸
(b)铸铁拉伸
图 1-2
图 1-2(a)表示低碳钢静拉伸试验 P-ΔL 曲线。整个过程主要包括:线弹性变形
-4-
阶段(OA),塑性屈服阶段(BC),强化阶段(CD),局部颈缩阶段(DE)。 金属塑性变形是由于晶面间产生滑移的结果。低碳钢塑性屈服阶段,在抛光试件表
面可观察到沿最大剪应力方向(450)的滑移线。 2. 上屈服强度ReH下屈服强度ReL的测定
剪切弹性模量的测定实验报告
剪切弹性模量的测定实验报告一、实验目的1、掌握用扭转实验测定材料剪切弹性模量的方法。
2、观察低碳钢在扭转变形过程中的变形规律和破坏现象。
二、实验设备1、扭转试验机。
2、游标卡尺。
三、实验原理在圆柱形试件的两端施加扭矩,使试件产生扭转变形。
根据材料力学的理论,对于实心圆柱形试件,其扭转时的剪切应力和剪切应变之间的关系为:\\tau = G\gamma\其中,\(\tau\)为剪切应力,\(G\)为剪切弹性模量,\(\gamma\)为剪切应变。
在弹性范围内,扭矩\(T\)与扭转角\(\varphi\)成正比,即:T = K\varphi\其中,\(K\)为扭转刚度。
通过测量扭矩\(T\)和扭转角\(\varphi\),以及试件的几何尺寸,就可以计算出剪切弹性模量\(G\)。
四、实验步骤1、测量试件的直径\(d\),在不同位置测量多次,取平均值。
2、将试件安装在扭转试验机上,确保安装牢固。
3、缓慢加载扭矩,直至达到预定的扭矩值,记录此时的扭矩\(T\)和扭转角\(\varphi\)。
4、继续加载扭矩,观察试件的变形和破坏现象,记录破坏时的扭矩值。
5、卸载扭矩,取下试件。
五、实验数据处理1、计算试件的极惯性矩\(I_p\):\I_p =\frac{\pi d^4}{32}2、根据实验数据,计算剪切弹性模量\(G\):\G =\frac{T L}{I_p \varphi}\其中,\(L\)为试件的有效长度。
3、对实验数据进行整理和分析,计算平均值和标准差。
六、实验结果与分析1、实验结果实验测得的剪切弹性模量为_____,与理论值相比存在一定的误差。
2、误差分析(1)测量误差:在测量试件直径和扭转角时,可能存在测量误差,导致计算结果不准确。
(2)加载误差:在加载扭矩的过程中,加载速度和加载方式可能不均匀,影响实验结果。
(3)材料不均匀性:试件本身的材料可能存在不均匀性,导致实验结果的偏差。
3、实验现象分析在实验过程中,观察到试件在扭转变形初期,变形较小,扭矩与扭转角呈线性关系。
(学)剪切弹性模量G测定实验
33
一、实验目的
1.测定低碳钢材料的剪切弹性模量G
2.学习扭角仪的原理及使用方法 二、实验原理
圆轴扭转时,若最大剪应力不超过材料的比例极限时,则扭矩M n 与扭转角ф存在线性关系:
p
n GI L M 0
=
ϕ 432
d I p π
=
为圆截面的极惯矩,d 为试件直径。
G —低碳钢剪切弹性模量
φ—距离为L 0的两截面之间的相对扭转角 M n —扭矩
当试件受到一定的扭矩增量△M n 后,在标距L 0内可量得相应的扭转角增量于是由上式可求得:
p
n I L M G ϕ∆∆=
试验按照等间隔分级加扭矩△M n 的方法进行,由扭角仪测得相应的扭转角增量△ф,即可求得G 。
JY-2型扭角仪,试件装在支架的AB 间,其标距为L 0,直径d=10mm ,加荷臂长度为L ,测量臂长度为R ,百分表每格0.01mm.
每次加载时由百分表读出的是△δ L P M n ⋅∆=∆ R δ
ϕ∆=∆ δπ∆∆=4
032d P R LL G 三、实验设备
扭角仪、百分表、游标卡尺 四、实验数据整理
1.确定力臂长度L 、测臂长度R
2.每加一级载荷读出百分表下降位移△δ共加4~5级。
卸载后再重复前面操作,共做3次按下式算出平均值 n δδ∑∆=
∆平 R 平δϕ∆=∆ 平
δπϕ∆∆=∆∆=40032d P
R LL I L M G p n 1.。
试验一 弹性模量和泊松比的测定实验
试验一弹性模量和泊松比的测定实验弹性模量和泊松比的测定实验大纲1. 通过材料弹性模量和泊松比的测定实验,使学生掌握测定材料变形的基本方法,学会拟定实验加载方案,验证虎克定律。
2. 电测材料的弹性模量和泊松比,使学生学会用电阻应变计和电阻应变仪测量材料的变形。
主要设备:材料试验机或多功能电测实验装置;主要耗材:低碳钢拉伸弹性模量试样,每次实验1根。
拉伸弹性模量(E)及泊松比(μ)的测定指导书一、实验目的1 、用电测法测量低碳钢的弹性模量 E 和泊松比μ2 、在弹性范围内验证虎克定律二、实验设备1 、电子式万能材料试验机2 、XL 2101C 程控静态电阻应变仪3 、游标卡尺三、实验原理和方法测定材料的弹性模量 E ,通常采用比例极限内的拉伸试验,材料在比例极限内服从虎克定律,其关系式为:(1-1)由此可得(1-2 )式中: E :弹性模量P :载荷:试样的截面积Sε:应变ΔP 和Δε分别为载荷和应变的增量。
由公式(1-2)即可算出弹性模量 E 。
实验方法如图1-1所示,采用矩形截面的拉伸试件,在试件上沿轴向和垂直于轴向的两面各贴两片电阻应变计,可以用半桥或全桥方式进行实验。
1、半桥接法:把试件两面各粘贴的沿轴向(或垂直于轴向)的两片电阻应变计(简称工作片)的两端分别接在应变仪的A、B 接线端上,温度补偿片接到应变仪的B、C 接线端上,然后给试件缓慢加载,通过电阻应变仪即可测出对应载荷下的轴向应变轴r ε值(或横向应变值横r ε)。
再将实际测得的值代入(1-2)式中,即可求得弹性模量 E 之值。
2、全桥接法:把两片轴向(或两片垂直于轴向)的工作片和两片温度补偿片按图1-1中(a)( 或(b)) 的接法接入应变仪的 A 、 B 、 C 、 D 接线柱中,然后给试件缓慢加载,通过电 阻应变仪即可测出对应载荷下的轴向应变值轴r ε(或垂直于轴向横r ε),将所测得的ε值代入(1-2)式中,即可求得弹性模量 E 之值。
剪切弹性模量g的测定实验报告
剪切弹性模量g的测定实验报告实验目的:通过实验测定剪切弹性模量g的数值,了解材料在受剪切应力作用下的变形特性。
实验仪器和材料:1. 剪切弹性模量测定仪。
2. 金属样品。
3. 千分尺。
4. 螺旋测微器。
5. 电子天平。
6. 螺旋压力计。
实验原理:剪切弹性模量g是表征材料在受剪切应力作用下的变形特性的物理量。
在实验中,我们通过对金属样品施加剪切应力,然后测定其应变和应力,最终计算出剪切弹性模量g的数值。
实验步骤:1. 用千分尺测量金属样品的截面积S,并用螺旋测微器测定金属样品的长度L。
2. 将金属样品固定在剪切弹性模量测定仪上,调整仪器使其处于平衡状态。
3. 通过螺旋压力计施加一定的剪切应力,并记录下施加的力F。
4. 根据施加的力F和金属样品的截面积S计算出剪切应力τ=F/S。
5. 通过测微器测量金属样品的位移Δx,计算出金属样品的剪切应变γ=Δx/L。
6. 根据剪切应变γ和剪切应力τ计算出剪切弹性模量g=τ/γ。
实验数据处理:根据实验步骤中得到的数据,我们可以计算出剪切弹性模量g的数值。
为了提高数据的准确性,我们需要进行多次实验,并对数据进行平均处理。
实验结果:经过多次实验和数据处理,我们得到金属样品的剪切弹性模量g的数值为XXX。
实验分析:通过实验测定得到的剪切弹性模量g的数值,可以反映出金属样品在受剪切应力作用下的变形特性。
这对于材料的工程应用具有重要的意义。
实验结论:通过本次实验,我们成功测定了金属样品的剪切弹性模量g的数值为XXX。
这一结果对于深入理解材料的力学性能以及工程应用具有一定的指导意义。
实验注意事项:1. 在实验过程中要注意安全,避免发生意外伤害。
2. 实验数据的准确性对于结果的可靠性具有重要影响,因此需要严格控制实验条件和操作技巧。
实验改进:在今后的实验中,可以进一步改进实验方法,提高数据的准确性和可靠性。
总结:本次实验通过测定剪切弹性模量g的数值,深入了解了材料在受剪切应力作用下的变形特性,为材料力学性能的研究和工程应用提供了重要的参考依据。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
剪切弹性模量G 的测定
(一)实验目的
在比例极限内测定低碳钢的扭转剪切模量以验证虎克定律。
(二)实验仪器
1.NY —4扭转测G 仪 2.KL —150游标卡尺 (三)实验原理
验证扭转变形公式或测定剪变摸量G 都需要准确测定试件的扭转角。
扭角仪的构造原理及按装示意图如图4.1,0l 为按装扭角仪的两个截面A 、B 的距离。
从图中可以看出,测剪切模量实际上是测试件两个截面转角所对的弦长,有了弦长,把弦长近似的当成弧长δ,有了弧长再知道半径b 就可以算出转角。
b
δ
=
Φ
图3-4.1
测剪切模量实际上是测试件两个截面转角所对的弦长,有了弦长,把弦长近似地当成弧长δ,有了弧长再知道半径b 就可以算出转角。
b
δ
=
Φ
由材料力学知,在剪切比例极限内,圆轴的变形公式为
P
GI TL 0
=
Φ 由以上公式可以写成P
I L T G ⋅Φ⋅=
式中T 为扭矩,I P 为圆截面的极惯性矩,L 0为标距。
图3-4.2
以低碳钢试件进行实验时,可以用增量法施加扭矩,每次增加的扭矩T ∆如图3-4.2都相等。
加载过程中,每一个扭矩i T 都对应着相应的扭转角i Φ,这样,只要求出扭矩增量T ∆对应的扭转角增量,再求出扭转角增量的平均值,就可以利用下式计算出剪切弹性摸量。
m
P I L T G ∆Φ⋅⋅∆=
(四) 实验步骤
1. 把扭角仪装到试件上,标距大约在150mm 左右。
2. 把百分表装上,表头预压到小针在1~2格。
3. 旋转表盘使大针指零,而后逐个加法码记下表上的读数。
4. 测两次取线性关系好的一组数据,计算弹性模量G 。
(五) 实验数据及处理
1. 实验数据及计算结果
剪切弹性模量。
平均11
1()n
m i i i n δδδ-=∆=-∑
100m m b b
δ∆∆Φ=
=(mm )
式中:n 为加载级数。
2.作Φ-T 图
以扭矩T 为纵坐标,扭转角Ф为横坐标,作Φ-T 图。
观察各点是否近似在一条直线上,以验证虎克定律。
作图时,应使用坐标纸,并选择合适的比例尺。
