七年级数学第2课时 代数式值的变化课时练习题及答案
2019年秋北师大版深圳专用数学七年级上册同步分层训练第三章整式及其加减2代数式第2课时代数式求值含答案

2第2课时代数式求值知识点代数式求值1.2018·贵阳当x=-1时,代数式3x+1的值是()A.-1B.-2C.4D.-42.若x=-3,y=1,则代数式2x-3y+1的值为()A.-10 B.-8 C.4 D.103.[教材习题3.3第3题变式]如图3-2-1是一个数值转换机的示意图.当输入x的值为-2时,输出的结果为()图3-2-1A.9B.10C.11D.124.某超市购进一批茶杯,进价为每个1.5元,则购进n个茶杯需付款________元;若茶杯的零售价为每个2元,则售完这批茶杯超市收入________元,当n=300时,该超市售完这批茶杯的利润为________元.5.若a,b互为倒数,c,d互为相反数,则2(c+d)2-3ab=________.6.如图3-2-2,在一张边长为x m(x>4)的正方形铁皮上截去一个长4 m,宽3 m的长方形.(1)用含x的代数式表示阴影部分的面积;(2)当x=6时,求阴影部分的面积.图3-2-27.2018·重庆按图3-2-3所示的运算程序,能使输出的结果为12的是()图3-2-3A.x=3,y=3 B.x=-4,y=-2C.x=2,y=4 D.x=4,y=28.2018·岳阳已知a2+2a=1,则3(a2+2a)+2的值为________.9.填写下表,并观察下列两个代数式的值的变化情况.(1)随着m值的逐渐变大,两个代数式的值如何变化?(2)估计一下,哪个代数式的值先超过200.10.2018·宜宾期中某服装厂生产一种西装和领带,西装每套定价500元,领带每条定价40元.厂方在开展促销活动期间,向客户提供两种优惠方案(客户只能选择其中一种):①买一套西装送一条领带;②西装和领带都按定价的90%付款.现某客户要到该服装厂购买西装20套,领带x条(x>20).(1)若该客户按方案①购买,则需付款________元;若该客户按方案②购买,则需付款________元(用含x的代数式表示).(2)若x=30,通过计算说明此时按哪种方案购买较为合算.详解详析1.B 2.B 3.C4.1.5n2n1505.-3[解析] 根据题意得ab=1,c+d=0,所以原式=2×02-3×1=-3.故答案为-3.6.解:(1)S阴影=S正方形-S长方形=x2-3×4=(x2-12)m2.(2)当x=6时,x2-12=36-12=24,即阴影部分的面积为24 m2.7.C[解析] A.当x=3,y=3时,输出的结果为32+2×3=15,不符合题意;B.当x=-4,y=-2时,输出的结果为(-4)2-2×(-2)=20,不符合题意;C.当x=2,y=4时,输出的结果为22+2×4=12,符合题意;D.当x =4,y=2时,输出的结果为42+2×2=20,不符合题意.故选C.8.5[解析] 因为a2+2a=1,所以3(a2+2a)+2=3×1+2=5.9.[解析] 将m的值分别代入代数式6m+8和2m2+1,求值后进行分析.解:表中第二行依次填:14,20,26,32,38,44,50;表中第三行依次填:3,9,19,33,51,73,99.(1)随着m值的逐渐变大,两个代数式的值都逐渐变大.(2)根据表中所求得的代数式的值可知,随着m值的逐渐变大,代数式2m2+1的值比代数式6m+8的值增加得快,所以估计2m2+1的值先超过200.10.解:(1)若该客户按方案①购买,则需付款500×20+40(x-20)=(40x+9200)元;若该客户按方案②购买,则需付款90%×(500×20+40x)=(36x+9000)元.故答案为:(40x+9200),(36x+9000).(2)当x=30时,方案①的费用为40×30+9200=10400(元),方案②的费用为36×30+9000=10080(元).因为10400>10080,所以此时按方案②购买较为合算.。
2022七年级数学上册第2章整式加减2.1代数式第2课时代数式习题课件新版沪科版38

11.甲、乙两地间的公路全长100 km,某人从甲地到乙 地的速度为m km/h,用代数式表示:
(1)此人从甲地到乙地需要用多长时间? 解:此人从甲地到乙地需要用1m00 h.
(2)如果每小时多行5 km,那么此人从甲地到乙地需要用 多长时间?
如果每小时多行 5 km,那么此人从甲地到乙地需要用m1+005 h.
12.[滁州全椒期中]如图,一个3×2的长方形(即长为3,宽为 2)可以用两种不同方式分割成3个或6个边长是正整数的小 正方形,即小正方形的个数最多是6个,最少是3个.
(1)一个5×2的长方形用不同的方式分割后,小正方形的个数 最多是多少个?最少是多少个?
解:一个5×2的长方形最多可分成10个小正方形, 最少可分成4个小正方形.
第2章 整式加减
2.1 代数式
第2课时 代数式
提示:点击 进入习题
核心必知 1 2 (1)数字;字母
(2)幂 (4)假分数
1C 2A 3B 4B
5 见习题
答案显示
6
[(1-a%)m+(1- a%)(1+b%)m]万亿元
7D
8 见习题
9B
10 见习题
11 见习题 12 见习题
答案显示
1.用加、减、乘、除及乘方等运算符号把数或表示数 的字母连接而成的式子,叫做代数式.单个的数或 字母也是代数式.
A.原价降价15元后再打8折
B.原价打8折后再降价15元
C.原价降价15元后再打2折
D.原价打2折后再降价15元
10.用代数式表示. (1)a的平方与b的2倍的差; 解:a2-2b.
(2)m与n的和的平方与m与n的积的和; (m+n)2+mn. (3)x的2倍的三分之一与y的一半的差; 23x-12y. (4)比a除以b的商的2倍小4的数. 2ba-4.
北师大版七年级上册数学《代数式》整式及其加减PPT课时(第2课时)

(0.8x+50)
(2)王老师一次性购物600元,他实际付款________元;
530
(3)王老师第一次购物用了170元,第二次购物用了387元,如
果王老师将这两次的购物换作一次购买可以节省________元.
27
(3)解析:200×0.9=180,500×0.9=450,所以设第二次购
300
小时.
游程3:买票
我们有a个成人, b个学生,买门票需付
(60a 20b)
________ 元钱.
售票处
……
门票价格
成人:每人60元
学生:每人20元
游程4:参观
太和殿占地呈长方形,长m米,宽n米太和殿占地
面积有多少平方米呢?
【
mn
平方米】
游程4:参观
珍宝馆陈列厅呈正方形,边长为a米.地面积有多
(运算符号包括+、-、×、÷、乘方)
典例精析
例1 下列各式中哪些是代数式?哪些不是?
(1) m 5; (2)
a
b
b
a
;
×
√
2
(4)x 3 x 4; (5)x y >1;
√
×
(3)0;
√
1
(6) .
x
√
注意:(1)代数式中不含表示关系的符号.
(“=”,“>”,“<”,“≥”,“≤”,“≠”)
4.5
-15
-6
-3
-1.44
-1
12
24
-30
-21 -18 -16.44 -16
-3
9
3.1代数式+第2课时+代数式的意义与代数式求值2024--2025学年北师大版七年级数学上册

典例精析
例1 某公园的门票价格是:成人10元/张;学生5元/张.
(1)一个旅游团有成人x人、学生y人,那么该旅游团应付多少
门票费?
解:(1)该旅游团应付的门票费是(10x+5y)元。
如果用x(元/kg)表示大米的价格,
用y(元/kg)表示食油的价格,那么
10x+5y就表示小强的妈妈购买10 kg
大米和5 kg食油所用的费用;
(1)设一个人的体重为w(千克),身高为h(米),请用含w,h的
代数式表示这个人的BMI。
解:他的身体质量指数为 2 。
ℎ
思考
(2)张老师的身高是1.75m,体重是65kg,他的体重是否适中?
解:(2)把w=65,h=1.75代入代数式,得
65
=
≈21.22
ℎ2 1.752
由于18.5<21.22<24之间,因此,他的体重适中。
典例精析
例2
若a+2b-7=0,求a+2b-3的值?
解:由题知:
-2a-4b+1=?
a+2b=7
a+2b-3=7-3=4
思考:若2x-y=3,求4x-3-2y=_
=4x-2y-3
整体代值法
①对已知代数式或所求
代数式进行适当变形;
②整体代入求值。
=2(2x-y)-3
=2×3-3
=3
_.
典例精析
例3
5
50岁的人运动时,30秒钟心跳的次数为60次,他有危险吗?请说
明你的理由。
解:他没有危险.
理由:当x=50时,y=(220-x)= ×(220-50)=136(次)。
因为他30秒心跳的次数是60次,
所以他每分钟心跳的次数约是120次,
2024年北师大七年级数学上册1 代数式第2课时 代数式求值(课件)

5. 根据一项科学研究,一个10~50 岁的人每天所需的睡 眠时间t(单位:h)可用公式t=11-1n0计算出来,其中n代表 这个人的年龄。根据这个公式,解答下列问题:
(2) 一个35岁的成年女性每天睡眠时间是7h,她的睡眠时
间够吗? 解:当 n=35 时, t=11-1n0 =11-3150 =7.5 。 因为7<7.5,所以她的睡眠时间不够。
1.代数式6p可以表示什么?
6的p倍
p的6倍
6个p的和
2.求代数式3a2-2ab的值,其中a=6,b=-23 。
解:当a=6,b=-23 时, 3a2-2ab=3×62-2×6×(-23)=116。
3. 华氏温度 f (单位: ℉)与摄氏度c(单位:℃)之间
存在如下的关系:
f=
9 5
c+32。小华对潇潇说:“
(1)设一个人的体重为 w kg,身高为 h m,请
w
用含w,h的代数式表示这个人的BMI。 h2
(2)张老师的身高为 1.75 m,体重是 65 kg,他
的体重是否适中?
你的身体质量
指数是多少?
当w=65,h=1.75时
w h2
65 = 1.752
21.22
张老师体重适中.
对应训练
【课本P79 随堂练习 第1题】
1.填写下表,并观察-8n+5和-n2这两个代数式的值的变化情况。
n
12345678
-8n+5 -3 -11 -19 -27 -35 -43 -51 -59 -n2 -1 -4 -9 -16 -25 -36 -49 -64
(1)随着 n 的值逐渐变大,两个代数式的值如何变化?
七年级数学 第三章 整式及其加减3.2 代数式第2课时 代数式求值作业

解:(1)(6x+2y+18) m2 (2)3 600元
【综合应用】 10.(b)(a-b)的值,并将计算
结果填入下表:
a,b的值
a2-b2 (a+b)(a-b)
当a=3, b=2时
5 5
当a=-5, b=1时
24 24
当a=-2, b=-5时
9.(10 分)小王购买了一套经济适用房,他准备将地面铺上地砖,房屋结构如图 所示,根据图中数据(单位: m),解答下列问题:
(1)用含 x,y 的式子表示房屋总面积; (2)若 x=4,y=1.5 时,且铺 1 m2 地砖的平均费用为 80 元,那么铺地砖的 总费用为多少元?
12/7/2021
12/7/2021
第三章 整式及其加减
3.2 代数式 第2课时 代数式求值
12/7/2021
12/7/2021
用具体数值代替代数式中的字母,求出来的值就是代_数__式__的__值__________.
12/7/2021
12/7/2021
代数式求值 1.(2 分)(2019·海南)当 m=-1 时,代数式 2m+3 的值是( C )
7.(6分)已知a=8,b=-5,c=-3,求下列各式的值: (1)a-b-c;
解:原式=8-(-5)-(-3)=8+5+3=16 (2)a-(c+b).
解:原式=8-[(-3)+(-5)]=8-(-8)=16 12/7/2021
8.(8 分)已知代数式 ax5+bx3+3x+c. (1)当 x=0 时,该代数式的值为-1,求 c 的值; (2)已知当 x=1 时,该代数式的值为-1,求 a+b+c 的值. 解:(1)-1 (2)-4
4.(2 分)(2019·怀化)当 a=-1,b=3 时,代数式 2a-b 的值等于___-__5___.
北师大版数学七年级上册《2 代数式》同步练习含答案解析

2020年~2021年最新北师大版数学七年级上册第三章2代数式课时作业一、选择题1.某厂1月份产量为a吨,以后每个月比上一个月增产x%,则该厂3月份的产量(单位:吨)为()A.a(1+x)2B.a(1+x%)2C.a+a•x% D.a+a•(x%)2答案:B解析:解答:解:∵1月份产量为a吨,以后每个月比上一个月增产x%,∴2月份的产量是a(1+x%),则3月份产量是a(1+x%)2故选:B.分析:元月到三月发生了两次变化,其增长率相同,故由1月份的产量表示出2月份的产量,进而表示出3月份的产量.2.已知x=1,y=2,则代数式x-y的值为()A.1B.-1C.2D.-3答案:B.解析:解答:当x=1,y=2时,x-y=1-2=-1,即代数式x-y的值为-1.故选:B.分析:根据代数式的求值方法,把x=1,y=2代入x-y,求出代数式x-y的值为多少即可.3.a-1的相反数是()A.-a+1 B.-(a+1)C.a-1 D.11 a+答案:A解析:解答:A.-a+1的相反数是a-1;B.-(a+1)的相反数是a+1;C.a-1的相反数是-(a-1)=1-a;D.11a+的相反数是-11a+;故选A.分析:本题是借着相反数的意义列代数式.表示一个数的相反数只需在这个数前面加一个“-”号即可,由此可得对于一个代数式表示它的相反数也是在这个式子前面加“-”号.4.用代数式表示“a与-b的差”,正确的是()A .b-aB .a-bC .-b-aD .a-(-b ) 答案:D解析:解答:被减数-减数=a-(-b ).故选D分析:列代数式的关键是正确理解文字语言中的关键词,比如该题中的“差”等,从而明确其中的运算关系,正确地列出代数式5.设某代数式为A ,若存在实数x 0使得代数式A 的值为负数,则代数式A 可以是( ) A.3x - B. 2x x + C.(4-x )2 D.221x x -+答案:B解析:解答:对于任意的x ,都有|3-x |≥0,(4-x )2≥0,x 2-2x +1=(x -1)2≥0, 因为x 2+x =(x +0.5)2-0.25,所以对于任意的x 的取值,代数式A 的值可以为正数、负数或0, 即存在实数x 0使得代数式A 的值为负数. 故选:B .分析:首先根据对于任意的x ,都有|3-x |≥0≥0,x 2-2x +1=(x -1)2≥0,所以对于任意的实数x 0,代数式A 的值都为非负数;然后判断出x 2+x =(x +0.5)2-0.25,对于任意的x 的取值,代数式A 的值可以为正数、负数或0,即存在实数x 0使得代数式A 的值为负数,据此解答即可.6.苹果的单价为a 元/千克,香蕉的单价为b 元/千克,买2千克苹果和3千克香蕉共需( )A .(a+b )元B .(3a+2b )元C .(2a+3b )元D .5(a+b )元 答案:C解析:解答:买单价为a 元的苹果2千克用去2a 元,买单价为b 元的香蕉3千克用去3b 元,共用去:(2a +3b )元.故选:C分析:用单价乘数量得出买2千克苹果和3千克香蕉的总价,再进一步相加即可. 7.已知多项式x 2+3x =3,可求得另一个多项式3x 2+9x -4的值为( ) A.3 B.4 C.4 D.6 答案:C解析:解答:∵x 2+3x =3,∴3x 2+9x -4=3(x 2+3x )-4=3×3-4=9-4=5. 故选:C .分析:先把3x 2+9x -4变形为3(x 2+3x )-4,然后把x 2+3x =3整体代入计算即可. 8.若代数式5x 2-4x +6的值为26,则x 2−45x +6的值为( ) A.6 B.10 C.14 D.30 答案:B解析:解答:∵5x2-4x+6=26,∴5x2-4x=26-6=20,∴x2−45x+6=15×(5x2-4x)+6=15×20+6=4+6=10故选:B.分析:首先根据代数式5x2-4x+6的值为26,求出5x2-4x的值是多少;然后把它代入x2−4 5x+6,求出算式的值是多少即可.9.已知x-2y=3,则代数式6-2x+4y的值为()A.0B.-1C.-3D.3答案:A解析:解答:∵x-2y=3,∴6-2x+4y=6-2(x-2y)=6-2×3=6-6=0故选:A.分析:先把6-2x+4y变形为6-2(x-2y),然后把x-2y=3整体代入计算即可.10.若2x-1=3y-2,则6y-4x的值是()A.1B.-1C.2D.-2答案:C解析:解答:∵2x-1=3y-2,∴3y-2x=-1+2=1∴6y-4x=2(3y-2x)=2×1=2.故选C.分析:将2x-1=3y-2化为3y-2x=-1+2=1后整体代入求解即可.11.下列式子中代数式的个数有()2a-5,-3,2a+1=4,3x3+2x2y4,1-b.A.2个B.3个C.4个D.5个答案:C解析:解答:由分析可知是代数式的有2a-5;-3;3x3+2x2y4;1-b,而2a+1=4因为有等号,是一元一次方程.代数式有4个,故选C分析:代数式是指用+、-、×、÷把数或表示数的字母连接起来的式子12.对下列代数式作出解释,其中不正确的是()A.a-b:今年小明b岁,小明的爸爸a岁,小明比他爸爸小(a-b)岁B.a-b:今年小明b岁,小明的爸爸a岁,则小明出生时,他爸爸为(a-b)岁C.ab:长方形的长为acm,宽为bcm,长方形的面积为abcm2D.ab:三角形的一边长为acm,这边上的高为bcm,此三角形的面积为abcm2答案:D解析:解答:A.爸爸比小明大(a-b)岁,A项正确;B.此项实际意义与A项相同,B项正确;C、长方形的面积公式为:面积=长*宽,故C项正确;D.根据实际意义分析可得D不正确,三角形面积公式为:面积=12边长 高,此三角形面积应为12ab,故D错;故选D分析:本题主要考查根据题意列代数式的能力,由实际问题的意义进行分析.13.小明的存款是a元,小华的存款是小明存款的一半还多2元,则小华存款()A.12a-2元B.12a+2元C.12(a+2)元D.12(a-2)元答案:C解析:解答:依题意得,小华存款:12a+2.故选C.分析:关键描述语是:小华的存款是小明存款的一半还多2元.则小华存款=12×小明存款+2.14.已知a-3b=5,则2(a-3b)2+3b-a-15的值是()A.25B.30C.35D.40答案:B解析:解答:∵a-3b=5∴2(a-3b)2+3b-a-15=2(a-3b)2-(a-3b)-15=2×52-5-15=30.故答案为B.分析:已知a-3b=5,首先把代数式2(a-3b)2+3b-a-15化为含a-3b的代数式,然后整体代入求值.15.若a,b互为相反数,c,d互为倒数,m的绝对值是1,n是有理数且既不是正数也不是负数,则2014a+b+1+m2-(cd)2014+n(a+b+c+d)的值为()A.1B.-1C.0D.2014答案:D解析:解答:∵a,b互为相反数,c,d互为倒数,m的绝对值是1,n是有理数且既不是正数也不是负数,∴a+b=0,cd=1,|m|=1,n=0,∴2014a+b+1+m2-(cd)2014+n(a+b+c+d)=20140+1+12-12014+0(0+c+d)=2014+1-1+0=2014,故选D.分析:根据已知得出a+b=0,cd=1,|m|=1,n=0,代入后求出即可.二、填空题16.某市出租车收费标准是:起步价7元,当路程超过4km时,每千米收费1.5元,如果某出租车行驶x(x>4km),则司机应收费(单位:元)答案:7+1.5(x-4)解析:解答:司机应收费为:7+1.5(x-4).分析:司机应收费=起步价+超过起步路程的价钱.17.若代数式x2+2x的值是4,则4x2+8x-9的值是答案:7解析:解答:∵代数式x2+2x的值是4,∴x2+2x=4,∴4x2+8x-9=4(x2+2x)-9=4×4-9=7.分析:根据题意得出x2+2x=4,把所求的代数式化成含有x2+2x的形式,代入求出即可.18.不改变代数式a2-(a-b+c)的值,把它括号前面的符号变为相反的符号,应为答案:a2+(-a+b-c)解析:解答:根据题意a2-(a-b+c)=a2+(-a+b-c).分析:把它括号前面的符号变为相反的符号,相当于把-号变成+号,即让括号前的-号看作-1,然后与括号里的字母相乘,仍放在括号里即可.19.体育委员小金带了500元钱去买体育用品,已知一个足球x元,一个篮球y元.则代数式500-2x-3y表示的实际意义为答案:体育委员买了2个足球、3个篮球,剩余的经费解析:解答:∵买一个足球x元,一个篮球y元.∴2x表示委员买了2个足球3y表示买了3个篮球∴代数式500-2x-3y:表示委员买了2个足球、3个篮球,剩余的经费.故答案为:体育委员买了2个足球、3个篮球,剩余的经费.分析:本题需先根据买一个足球x元,一个篮球y元的条件,表示出2x和3y的意义,最后得出正确答案即可.20.若2x2+3x+5=10,则代数式4x2+6x-9=答案:1解析:解答:根据题意得:2x2+3x+5=10,即2x2+3x=5,则原式=2(2x2+3x)-9=10-9=1,故答案为:1.分析:根据题意求出2x2+3x的值,原式前两项提取2变形后,将2x2+3x的值代入计算即可求出值.三、解答题21.已知a、b互为相反数,c、d互为倒数,m的绝对值是5,n是最大的负整数,求代数式2011(a+b)-4cd+2mn的值.答案:-14或6.解答:∵a、b互为相反数,c、d互为倒数,m的绝对值是5,n是最大的负整数,∴a+b=0,cd=1,|m|=5,n=-1,∴m=±5,当m=5时,原式=2011×0-4×1+2×5×(-1)=-14;当m=-5时,原式=2011×0-4×1+2×(-5)×(-1)=6.∴代数式2011(a+b)-4cd+2mn的值是-14或6.解析:分析:根据相反数、倒数、绝对值、最大的负整数求出a+b、cd、m、n的值,代入代数式求出即可.22.已知a与b互为相反数,c与d互为倒数,e为绝对值最小的数,求式子2004(a+b)+cd+e 的值.答案:1解答:∵a与b互为相反数,c与d互为倒数,e为绝对值最小的数,∴a+b=0,cd=1,e=0,∴2004(a+b)+cd+e=2004×0+1+0=1.解析:分析:根据已知求出a+b、cd、e的值,代入代数式即可求出答案.23.已知x=1,求代数式3x+2的值.答案:5.解答:当x=1时,3x+2,=3×1+2,=5,当x=1时,代数式3x+2的值是5.解析:分析:要求代数式的值,知字母x的值是1,代入已知代数式3x+2即可求出所求代数式的值.24.国庆长假里,小华和爸爸、妈妈一家三口去旅游,甲旅行社说:“大人买全票,小孩半价优惠”.乙旅行社说:“大人、小孩全部按票价的八折优惠”.若原票价为α元,问小华家选择哪个旅行社合算,请说出理由.答案:选择乙旅行社比较划算;由题意得:甲旅行社的费用是:2α+0.5α=2.5α(元)乙旅行社的费用是:3α×0.8=2.4α(元)∵2.5α>2.4α∴选择乙旅行社比较划算.解析:分析:由“大人买全票,小孩半价优惠”可得甲旅行社需花费2α+0.5α,由“大人、小孩全部按票价的八折优惠”可得乙旅行社需花费3α×0.8,然后进行比较得出结果.25.已知某船顺水航行2小时,逆水航行3小时,(1)已知轮船在静水中前进的速度是m千米/时,水流的速度是a千米/时,则轮船共航行多少千米?答案:(5m-a)千米解答:轮船共航行路程为:(m+a)×2+(m-a)×3=(5m-a)千米,(2)轮船在静水中前进的速度是70千米/时,水流的速度是2千米/时,则轮船共航行多少千米?答案:348千米解答:把m=70,a=2代入(1)得到的式子得:5×70-2=348千米.答:轮船共航行348千米.解析:解答:(1)轮船共航行路程为:(m+a)×2+(m-a)×3=(5m-a)千米,(2)把m=70,a=2代入(1)得到的式子得:5×70-2=348千米.答:轮船共航行348千米.分析:(1)共航行路程=顺水路程+逆水路程=(静水速度+水流速度)×顺水时间+(静水速度-水流速度)×逆流时间,把相关数值代入,化简即可;(2)把70,2代入(1)得到的式子,求值即可.。
七年级数学上册 3.3代数式的值课时训练2 试题(共3页)
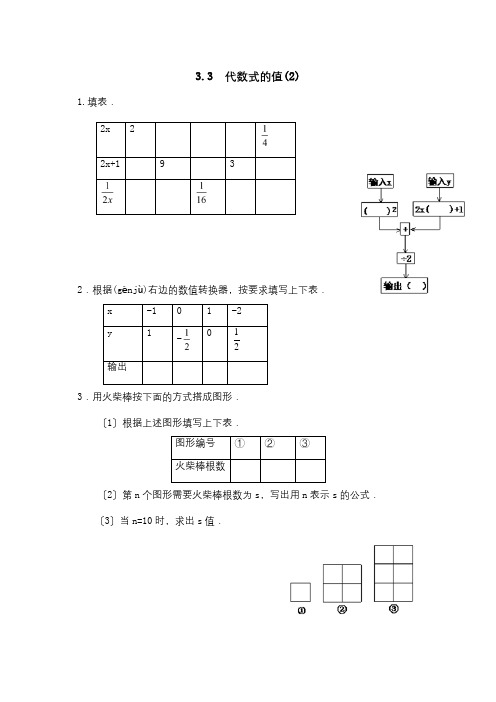
3.3 代数式的值(2)
1.填表.
2.根据(g ēnj ù)右边的数值转换器,按要求填写上下表. x -1 0 1 -2 y
1 - 0 1
2 输出
3.用火柴棒按下面的方式搭成图形.
〔1〕根据上述图形填写上下表.
图形编号 ① ②
③ 火柴棒根数
〔2〕第n 个图形需要火柴棒根数为s ,写出用n 表示s 的公式. 〔3〕当n=10时,求出s 值.
2x 2
2x+1 9
3
4.当x=3,y=1
2
时,求以下(yǐxià)代数式的值:〔1〕2x2-4xy2+4y;〔2〕
.
5.当x-y=2时,求代数式〔x-y〕2+2〔y-x〕+5的值.
6.小明读一本一共m页的书,第一天读了该书的,第二天读了剩下的.〔1〕用代数式表示小明两天一共读了多少页.
〔2〕求当m=120时,小明两天读的页数.
7.当m=2,n=1时,
〔1〕求代数式〔m+2〕2和m2+2mn+n2的值.
〔2〕写出这两个代数式值的关系.
〔3〕当m=5,n=-2时,上述的结论是否仍成立?
〔4〕根据〔1〕、〔2〕,你能用简便(jiǎnbiàn)方法算出,当m=0.125,n=0. 875时,m2+2mn+n2的值吗?
内容总结
(1)3.3 代数式的值(2)
1.填表.
2.根据右边的数值转换器,按要求填写上下表.
3.用火柴棒按下面的方式搭成图形.
〔1〕根据上述图形填写上下表.
〔2〕第n个图形需要火柴棒根数为s,写出用n表示s的公式.〔3〕当n=10时,求出s值.
4.当x=3,y=时,求以下代数式的值:〔1〕2x2-4xy2+4y。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第2课时代数式值的变化
01 基础题
知识点1 求代数式的值
1.(怀化中考)已知m=1,n=0,则代数式m+n的值为()
A.-1B.1 C.-2 D.2
2.当a=3,b=2时,a2+2ab+b2的值是()
A.5 B.13 C.21 D.25
3.当a=2时,代数式3a-1的值是________.
4.当x=-2,y=3时,代数式2x2-3y的值是________.
5.填表:
x-1-1
2
012
x-1
(x-1)2
2
x-4
知识点2 数值转换机
6.下图是一个数值转换机,输入x,输出3(x-2),下面给出了四种转换步骤,其中正确的是()
A.先减去2,再乘以3
B.先减去-2,再乘以3
C.先乘以3,再减去2
D.先乘以3,再加上2
7.按照下图所示的程序计算,当x分别为-3,0时的输出值.
知识点3 代数式的值的简单应用
8.人们通常用c表示摄氏温度(℃),f表示华氏温度(),c与f之间的关系式
为c=5
9(f-32),当华氏温度为59 时,摄氏温度为()
A.-15 ℃ B.15 ℃
C.112.6 ℃ D.95.8 ℃
9.在三角形的面积公式S=1
2ah中,a表示底边长,h表示底边上的高,若a=3.2 cm,h=5 cm,则S=________cm2.
10.研究表明,运动时心跳速率通常和人的年龄有关.用a表示一个人的年龄,用b表示正常情况下这个人在运动时所能承受的每分钟心跳的最高次数,则b=
0.8(220-a).
(1)正常情况下,一个14岁的少年运动时所能承受的每分钟心跳的最高次数是多少?
(2)一个45岁的人运动时,每分钟心跳次数为132次,请问他有危险吗?为什么?
02 中档题
11.当a =1
3,b =9时,下列代数式的值为24的是() A .(3a +2)(b -1)B .(2a +1)(b +10) C .(2a +3)(b -1) D .(a +2)(b +11) 12.下列说法正确的有()
①代数式的值只与代数式本身有关;②一个含有字母的代数式,只有一个值;③代数式x2+x-1的值为-1.
A.0个B.1个 C.2个 D.3个
13.当x=-1时,代数式|5x+2|和代数式1-3x的值分别为M、N,则M、N之间的关系为()
A.M>NB.M=N
C.M<N D.以上三种情况都有可能
14.根据流程图中的程序,当输入数值x为-2时,输出数值y为()
A.4 B.6 C.8 D.10 15.当x=7与x=-7时,代数式3x4-2x2+1的两个值()
A.相等
B.互为倒数
C.互为相反数
D.既不相等也不互为相反数
16.已知2x-5y3=3,则9-4(2x-5y3)的值是________.
17.新定义一种运算:a*b=
ab
1-ab,则2*3=________.
18.某商店出售一批水果,最初以每箱a元的价格出售m箱,后来每箱降价至b 元,又售出m箱,剩下30箱又以每箱再降价5元出售.
(1)用代数式表示这批水果共售多少元?
(2)如果a=20,b=18,m=60,进这批水果共花去1 500元,那么该商店赚了多少元?
03综合题
19.七年级学生在5名教师的带领下去公园秋游,公园的门票为每人30元.现有两种优惠方案,甲方案:带队教师免费,学生按8折收费;乙方案:师生都按7.5折收费.
(1)若有m名学生,用代数式表示两种优惠方案各需多少元?
(2)当m=70时,采用哪种方案优惠?
(3)当m=100时,采用哪种方案优惠?
参考答案
基础题
1.B2.D3.5 4.-1 5.-2 -3
2-1 0 1 4 9
4 1 0 1 -
2
5-
4
9-
1
2
-2
3-1 6.A7.程序对应的代数式为2(5x-2).当x=-3时,2(5x-2)=
2×[5×(-3)-2]=2×(-17)=-34;当x=0时,2(5x-2)=2×(5×0-2)=-4. 8.B9.8 10.(1)当a=14时,b=0.8(220-a)=0.8×(220-14)=164.8(次/分).答:一个14岁的少年运动时所能承受的每分钟心跳的最高次数约是164次.(2)当a=45时,b=0.8(220-a)=0.8×(220-45)=140(次/分).因为140次>132次,所以他无危险.答:他没有危险.
中档题
11.A12.A13.C14.B15.A16.-3 17.-6
518.(1)[am+bm+30(b-5)]元.(2)当a =20,b=18,m=60时,am+bm+30(6-5)=20×60+18×60+30×(18-5)=2 670(元),故这些水果共售2 670元.又因为进这批水果共花去1 500元,所以该商店赚了2 670-1 500=1 170(元).
综合题
19.(1)甲方案:m×30×8
10=24m(元),乙方案:(m+5)×30×
7.5
10=22.5(m+
5)(元).(2)当m=70时,甲方案付费24×70=1 680(元),乙方案付费22.5×75=1 687.5(元).所以采用甲方案优惠.(3)当m=100时,甲方案付费24×100=2 400(元),乙方案付费22.5×105=2 362.5(元).所以采用乙方案优惠.。
