第23讲最值问题一
初中数学“最值问题”集锦(一)

“最值问题”集锦(一)●平面几何中的最值问题 (01)●几何的定值与最值 (07)●最短路线问题 (14)●对称问题 (18)●巧作“对称点”妙解最值题 (22)●平面几何中的最值问题在平面几何中,我们常常遇到各种求最大值和最小值的问题,有时它和不等式联系在一起,统称最值问题.如果把最值问题和生活中的经济问题联系起来,可以达到最经济、最节约和最高效率.下面介绍几个简例.在平面几何问题中,当某几何元素在给定条件变动时,求某几何量(如线段的长度、图形的面积、角的度数)的最大值或最小值问题,称为最值问题。
最值问题的解决方法通常有两种:(1)应用几何性质:①三角形的三边关系:两边之和大于第三边,两边之差小于第三边;②两点间线段最短;③连结直线外一点和直线上各点的所有线段中,垂线段最短;④定圆中的所有弦中,直径最长。
⑵运用代数证法:①运用配方法求二次三项式的最值;②运用一元二次方程根的判别式。
例1、A、B两点在直线l的同侧,在直线L上取一点P,使PA+PB最小。
分析:在直线L上任取一点P’,连结A P’,BP’,在△ABP’中AP’+BP’>AB,如果AP’+BP’=AB,则P’必在线段AB上,而线段AB 与直线L无交点,所以这种思路错误。
取点A关于直线L的对称点A’,则AP’= AP,在△A’BP中A’P’+B’P’>A’B,当P’移到A’B与直线L的交点处P点时A’P’+B’P’=A’B,所以这时PA+PB最小。
1 已知AB是半圆的直径,如果这个半圆是一块铁皮,ABDC是内接半圆的梯形,试问怎样剪这个梯形,才能使梯形ABDC的周长最大(图3-91)?分析本例是求半圆AB的内接梯形的最大周长,可设半圆半径为R.由于AB∥CD,必有AC=BD.若设CD=2y,AC=x,那么只须求梯形ABDC的半周长u=x+y+R的最大值即可.解作DE⊥AB于E,则x2=BD2=AB·BE=2R·(R-y)=2R2-2Ry,所以所以求u的最大值,只须求-x2+2Rx+2R2最大值即可.-x2+2Rx+2R2=3R2-(x-R)2≤3R2,上式只有当x=R时取等号,这时有所以2y=R=x.所以把半圆三等分,便可得到梯形两个顶点C,D,这时,梯形的底角恰为60°和120°.2 .如图3-92是半圆与矩形结合而成的窗户,如果窗户的周长为8米(m),怎样才能得出最大面积,使得窗户透光最好?分析与解设x表示半圆半径,y表示矩形边长AD,则必有2x+2y+πx=8,若窗户的最大面积为S,则把①代入②有即当窗户周长一定时,窗户下部矩形宽恰为半径时,窗户面积最大.3. 已知P点是半圆上一个动点,试问P在什么位置时,PA+PB最大(图3-93)?分析与解因为P点是半圆上的动点,当P近于A或B时,显然PA+PB渐小,在极限状况(P与A重合时)等于AB.因此,猜想P在半圆弧中点时,PA+PB取最大值.设P为半圆弧中点,连PB,PA,延长AP到C,使PC=PA,连CB,则CB是切线.为了证PA+PB最大,我们在半圆弧上另取一点P′,连P′A,P′B,延长AP′到C′,使P′C′=BP′,连C′B,CC′,则∠P′C′B=∠P′BC=∠PCB=45°,所以A,B,C′,C四点共圆,所以∠CC′A=∠CBA=90°,所以在△ACC′中,AC>AC′,即PA+PB>P′A+P′B.4 如图3-94,在直角△ABC中,AD是斜边上的高,M,N分别是△ABD,△ACD的内心,直线MN交AB,AC于K,L.求证:S△ABC≥2S△AKL.证连结AM,BM,DM,AN,DN,CN.因为在△ABC中,∠A=90°,AD⊥BC于D,所以∠ABD=∠DAC,∠ADB=∠ADC=90°.因为M,N分别是△ABD和△ACD的内心,所以∠1=∠2=45°,∠3=∠4,所以△ADN∽△BDM,又因为∠MDN=90°=∠ADB,所以△MDN∽△BDA,所以∠BAD=∠MND.由于∠BAD=∠LCD,所以∠MND=∠LCD,所以D,C,L,N四点共圆,所以∠ALK=∠NDC=45°.同理,∠AKL=∠1=45°,所以AK=AL.因为△AKM≌△ADM,所以AK=AD=AL.而而从而所以 S△ABC≥S△AKL.5. 如图3-95.已知在正三角形ABC内(包括边上)有两点P,Q.求证:PQ≤AB.证设过P,Q的直线与AB,AC分别交于P1,Q1,连结P1C,显然,PQ≤P1Q1.因为∠AQ1P1+∠P1Q1C=180°,所以∠AQ1P1和∠P1Q1C中至少有一个直角或钝角.若∠AQ1P1≥90°,则 PQ≤P1Q1≤AP1≤AB;若∠P1Q1C≥90°,则 PQ≤P1Q1≤P1C.同理,∠AP1C和∠BP1C中也至少有一个直角或钝角,不妨设∠BP1C≥90°,则 P1C≤BC=AB.对于P,Q两点的其他位置也可作类似的讨论,因此,PQ≤AB.6. 设△ABC是边长为6的正三角形,过顶点A引直线l,顶点B,C到l的距离设为d1,d2,求d1+d2的最大值(1992年上海初中赛题).解如图3-96,延长BA到B′,使AB′=AB,连B′C,则过顶点A的直线l或者与BC相交,或者与B′C相交.以下分两种情况讨论.(1)若l与BC相交于D,则所以只有当l⊥BC时,取等号.(2)若l′与B′C相交于D′,则所以上式只有l′⊥B′C时,等号成立.7. 如图3-97.已知直角△AOB中,直角顶点O在单位圆心上,斜边与单位圆相切,延长AO,BO分别与单位圆交于C,D.试求四边形ABCD面积的最小值.解设⊙O与AB相切于E,有OE=1,从而即AB≥2.当AO=BO时,AB有最小值2.从而所以,当AO=OB时,四边形ABCD面积的最小值为●几何的定值与最值几何中的定值问题,是指变动的图形中某些几何元素的几何量保持不变,或几何元素间的某些几何性质或位置关系不变的一类问题,解几何定值问题的基本方法是:分清问题的定量及变量,运用特殊位置、极端位置,直接计算等方法,先探求出定值,再给出证明.几何中的最值问题是指在一定的条件下,求平面几何图形中某个确定的量(如线段长度、角度大小、图形面积)等的最大值或最小值,求几何最值问题的基本方法有:1.特殊位置与极端位置法; 2.几何定理(公理)法; 3.数形结合法等.注:几何中的定值与最值近年广泛出现于中考竞赛中,由冷点变为热点.这是由于这类问题具有很强的探索性(目标不明确),解题时需要运用动态思维、数形结合、特殊与一般相结合、逻辑推理与合情想象相结合等思想方法.【例题就解】【例1】 如图,已知AB=10,P 是线段AB 上任意一点,在AB 的同侧分别以AP 和PB 为边作等边△APC 和等边△BPD ,则CD 长度的最小值为 .思路点拨 如图,作CC ′⊥AB 于C ,DD ′⊥AB 于D ′, DQ ⊥CC ′,CD 2=DQ 2+CQ 2,DQ=21AB 一常数,当CQ 越小,CD 越小,本例也可设AP=x ,则PB=x -10,从代数角度探求CD 的最小值.注:从特殊位置与极端位置的研究中易得到启示,常能找到解题突破口,特殊位置与极端位置是指:(1)中点处、垂直位置关系等; (2)端点处、临界位置等.【例2】 如图,圆的半径等于正三角形ABC 的高,此圆在沿底边AB 滚动,切点为T ,圆交AC 、BC 于M 、N ,则对于所有可能的圆的位置而言, MTN 为的度数( )A .从30°到60°变动B .从60°到90°变动C .保持30°不变D .保持60°不变 思路点拨 先考虑当圆心在正三角形的顶点C 时, 其弧的度数,再证明一般情形,从而作出判断.注:几何定值与最值问题,一般都是置于动态背景下, 动与静是相对的,我们可以研究问题中的变量,考虑当变 化的元素运动到特定的位置,使图形变化为特殊图形时, 研究的量取得定值与最值.【例3】 如图,已知平行四边形ABCD ,AB=a ,BC=b (a >b ),P 为AB 边上的一动点, 直线DP 交CB 的延长线于Q ,求AP+BQ 的最小值.思路点拨 设AP=x ,把AP 、BQ 分别用x 的代数式表示,运用不等式ab b a 222≥+ (当且仅当b a =时取等号)来求最小值.【例4】 如图,已知等边△ABC 内接于圆,在劣弧AB 上取异于A 、B 的点M ,设直线AC 与BM 相交于K ,直线CB 与AM 相交于点N ,证明:线段AK 和BN 的乘积与M 点的选择无关.思路点拨 即要证AK ·BN 是一个定值,在图形中△ABC 的边长是一个定值,说明AK ·BN 与AB 有关,从图知AB 为 △ABM 与△ANB 的公共边,作一个大胆的猜想,AK ·BN=AB 2,⌒⌒从而我们的证明目标更加明确.注:只要探求出定值,那么解题目标明确,定值问题就转化为一般的几何证明问题.【例5】 已知△XYZ 是直角边长为1的等腰直角三角形(∠Z=90°),它的三个顶点分别在等腰Rt △ABC(∠C=90°)的三边上,求△ABC 直角边长的最大可能值.思路点拨 顶点Z 在斜边上或直角边CA(或CB)上,当顶点Z 在斜边AB 上时,取xy 的中点,通过几何不等关系求出直角边的最大值,当顶点Z 在(AC 或CB)上时,设CX=x ,CZ=y ,建立x ,y 的关系式,运用代数的方法求直角边的最大值.注:数形结合法解几何最值问题,即适当地选取变量,建立几何元素间的函数、方程、不等式等关系,再运用相应的代数知识方法求解.常见的解题途径是:(1)利用一元二次方程必定有解的代数模型,运用判别式求几何最值; (2)构造二次函数求几何最值.学力训练1.如图,正方形ABCD 的边长为1,点P 为边BC 上任意一点(可与B 点或C 点重合),分别过B 、C 、D 作射线AP 的垂线,垂足分别是B ′、C ′、D ′,则BB ′+CC ′+DD ′的最大值为 ,最小值为 .2.如图,∠AOB=45°,角内有一点P ,PO=10,在角的两边上有两点Q ,R(均不同于点O),则△PQR 的周长的最小值为 .3.如图,两点A 、B 在直线MN 外的同侧,A 到MN 的距离AC=8,B 到MN 的距离BD=5,CD=4,P 在直线MN 上运动,则PB PA -的最大值等于 .4.如图,A 点是半圆上一个三等分点,B 点是弧AN 的中点,P 点是直径MN 上一动点,⊙O 的半径为1,则AP+BP 的最小值为( )A .1B .22 C .2D .13-5.如图,圆柱的轴截面ABCD 是边长为4的正方形,动点P 从A 点出发,沿看圆柱的侧面移动到BC 的中点S 的最短距离是( )A .212π+B .2412π+C .214π+D .242π+6.如图、已知矩形ABCD ,R ,P 户分别是DC 、BC 上的点,E ,F 分别是AP 、RP 的中点,当P 在BC 上从B 向C 移动而R 不动时,那么下列结论成立的是( )A .线段EF 的长逐渐增大B .线段EF 的长逐渐减小C .线段EF 的长不改变D .线段EF 的长不能确定7.如图,点C是线段AB上的任意一点(C点不与A、B点重合),分别以AC、BC为边在直线AB的同侧作等边三角形ACD和等边三角形BCE,AE与CD相交于点M,BD与CE相交于点N.(1)求证:MN∥AB;(2)若AB的长为l0cm,当点C在线段AB上移动时,是否存在这样的一点C,使线段MN的长度最长?若存在,请确定C点的位置并求出MN的长;若不存在,请说明理由.(2002年云南省中考题)8.如图,定长的弦ST在一个以AB为直径的半圆上滑动,M是ST的中点,P是S对AB作垂线的垂足,求证:不管ST滑到什么位置,∠SPM是一定角.9.已知△ABC是⊙O的内接三角形,BT为⊙O的切线,B为切点,P为直线AB上一点,过点P作BC的平行线交直线BT于点E,交直线AC于点F.(1)当点P在线段AB上时(如图),求证:PA·PB=PE·PF;(2)当点P为线段BA延长线上一点时,第(1)题的结论还成立吗?如果成立,请证明,如果不成立,请说明理由.10.如图,已知;边长为4的正方形截去一角成为五边形ABCDE,其中AF=2,BF=l,在AB上的一点P,使矩形PNDM有最大面积,则矩形PNDM的面积最大值是( )25 D.14A.8 B.12 C.211.如图,AB是半圆的直径,线段CA上AB于点A,线段DB上AB于点B,AB=2;AC=1,BD=3,P是半圆上的一个动点,则封闭图形ACPDB的最大面积是( )A.23+3+ D.21+ C.22+ B.212.如图,在△ABC中,BC=5,AC=12,AB=13,在边AB、AC上分别取点D、E,使线段DE将△ABC分成面积相等的两部分,试求这样线段的最小长度.13.如图,ABCD是一个边长为1的正方形,U、V分别是AB、CD上的点,AV与DU相交于点P,BV与CU相交于点Q.求四边形PUQV面积的最大值.14.利用两个相同的喷水器,修建一个矩形花坛,使花坛全部都能喷到水.已知每个喷水器的喷水区域是半径为l0米的圆,问如何设计(求出两喷水器之间的距离和矩形的长、宽),才能使矩形花坛的面积最大?15.某住宅小区,为美化环境,提高居民生活质量,要建一个八边形居民广场(平面图如图所示).其中,正方形MNPQ与四个相同矩形(图中阴影部分)的面积的和为800平方米.(1)设矩形的边AB=x(米),AM=y(米),用含x的代数式表示y为.(2)现计划在正方形区域上建雕塑和花坛,平均每平方米造价为2100元;在四个相同的矩形区域上铺设花岗岩地坪,平均每平方米造价为105元;在四个三角形区域上铺设草坪,平均每平方米造价为40元.①设该工程的总造价为S(元),求S关于工的函数关系式.②若该工程的银行贷款为235000元,仅靠银行贷款能否完成该工程的建设任务?若能,请列出设计方案;若不能,请说明理由.③若该工程在银行贷款的基础上,又增加资金73000元,问能否完成该工程的建设任务?若能,请列出所有可能的设计方案;若不能,请说明理由.(镇江市中考题)16.某房地产公司拥有一块“缺角矩形”荒地ABCDE,边长和方向如图,欲在这块地上建一座地基为长方形东西走向的公寓,请划出这块地基,并求地基的最大面积(精确到1m2).参考答案111213●最短路线问题通常最短路线问题是以“平面内连结两点的线中,直线段最短”为原则引申出来的.人们在生产、生活实践中,常常遇到带有某种限制条件的最近路线即最短路线问题.在本讲所举的例中,如果研究问题的限制条件允许已知的两点在同一平面内,那么所求的最短路线是线段;如果它们位于凸多面体的不同平面上,而允许走的路程限于凸多面体表面,那么所求的最短路线是折线段;如果它们位于圆柱和圆锥面上,那么所求的最短路线是曲线段;但允许上述哪种情况,它们都有一个共同点:当研究曲面仅限于可展开为平面的曲面时,例如圆柱面、圆锥面和棱柱面等,将它们展开在一个平面上,两点间的最短路线则是连结两点的直线段.这里还想指出的是,我们常遇到的球面是不能展成一个平面的.例如,在地球(近似看成圆球)上A、B二点之间的最短路线如何求呢?我们用过A、B两点及地球球心O的平面截地球,在地球表面留下的截痕为圆周(称大圆),在这个大圆周上A、B两点之间不超过半个圆周的弧线就是所求的A、B两点间的最短路线,航海上叫短程线.关于这个问题本讲不做研究,以后中学会详讲.在求最短路线时,一般我们先用“对称”的方法化成两点之间的最短距离问题,而两点之间直线段最短,从而找到所需的最短路线.像这样将一个问题转变为一个和它等价的问题,再设法解决,是数学中一种常用的重要思想方法.例1 如下图,侦察员骑马从A地出发,去B地取情报.在去B地之前需要先饮一次马,如果途中没有重要障碍物,那么侦察员选择怎样的路线最节省时间,请你在图中标出来.解:要选择最节省时间的路线就是要选择最短路线.作点A关于河岸的对称点 A′,即作 AA′垂直于河岸,与河岸交于点C,且使AC=A′C,连接A′B交河岸于一点P,这时 P点就是饮马的最好位置,连接 PA,此时 PA+PB就是侦察员应选择的最短路线.证明:设河岸上还有异于P点的另一点P′,连接P′A,P′B, P′A′.∵P′A+P′B=P′A′+P′B>A′B=PA′+PB=PA+PB,而这里不等式 P′A′+P′B>A′B成立的理由是连接两点的折线段大于直线段,所以PA+PB是最短路线.此例利用对称性把折线APB化成了易求的另一条最短路线即直线段A′B,所以这种方法也叫做化直法,其他还有旋转法、翻折法等.看下面例题.例2 如图一只壁虎要从一面墙壁α上A点,爬到邻近的另一面墙壁β上的B点捕蛾,它可以沿许多路径到达,但哪一条是最近的路线呢?14解:我们假想把含B点的墙β顺时针旋转90°(如下页右图),使它和含A点的墙α处在同一平面上,此时β转过来的位置记为β′,B点的位置记为B′,则A、B′之间最短路线应该是线段AB′,设这条线段与墙棱线交于一点P,那么,折线4PB就是从A点沿着两扇墙面走到B点的最短路线.证明:在墙棱上任取异于P点的P′点,若沿折线AP′B走,也就是沿在墙转90°后的路线AP′B′走都比直线段APB′长,所以折线APB是壁虎捕蛾的最短路线.由此例可以推广到一般性的结论:想求相邻两个平面上的两点之间的最短路线时,可以把不同平面转成同一平面,此时,把处在同一平面上的两点连起来,所得到的线段还原到原始的两相邻平面上,这条线段所构成的折线,就是所求的最短路线.例3 长方体ABCD—A′B′C′D′中,AB=4,A′A=2′,AD=1,有一只小虫从顶点D′出发,沿长方体表面爬到B点,问这只小虫怎样爬距离最短?(见图(1))解:因为小虫是在长方体的表面上爬行的,所以必需把含D′、B两点的两个相邻的面“展开”在同一平面上,在这个“展开”后的平面上 D′B间的最短路线就是连结这两点的直线段,这样,从D′点出发,到B点共有六条路线供选择.①从D′点出发,经过上底面然后进入前侧面到达B点,将这两个面摊开在一个平面上(上页图(2)),这时在这个平面上D′、B间的最短路线距离就是连接D′、B两点的直线段,它是直角三角形ABD′的斜边,根据勾股定理,D′B2=D′A2+AB2=(1+2)2+42=25,∴D′B=5.②容易知道,从D′出发经过后侧面再进入下底面到达B点的最短距离也是5.③从D′点出发,经过左侧面,然后进入前侧面到达B点.将这两个面摊开在同一平面上,同理求得在这个平面上D′、B两点间的最短路线(上页图(3)),有:D′B2=22+(1+4)2=29.④容易知道,从D′出发经过后侧面再进入右侧面到达B点的最短距离的平方也是29.⑤从D′点出发,经过左侧面,然后进入下底面到达B点,将这两个平面摊开在同一平面上,同理可求得在这个平面上D′、B两点间的最短路线(见图),1516D ′B 2=(2+4)2+12=37.⑥容易知道,从D ′出发经过上侧面再进入右侧面到达B 点的最短距离的平方也是37.比较六条路线,显然情形①、②中的路线最短,所以小虫从D ′点出发,经过上底面然后进入前侧面到达B 点(上页图(2)),或者经过后侧面然后进入下底面到达B 点的路线是最短路线,它的长度是5个单位长度.利用例2、例3中求相邻两个平面上两点间最短距离的旋转、翻折的方法,可以解决一些类似的问题,例如求六棱柱两个不相邻的侧面上A 和B 两点之间的最短路线问题(下左图),同样可以把A 、B 两点所在平面及与这两个平面都相邻的平面展开成同一个平面(下右图),连接A 、B 成线段AP1P2B ,P1、P2是线段AB 与两条侧棱线的交点,则折线AP1P2B 就是AB 间的最短路线.圆柱表面的最短路线是一条曲线,“展开”后也是直线,这条曲线称为螺旋线.因为它具有最短的性质,所以在生产和生活中有着很广泛的应用.如:螺钉上的螺纹,螺旋输粉机的螺旋道,旋风除尘器的导灰槽,枪膛里的螺纹等都是螺旋线,看下面例题.例4 景泰蓝厂的工人师傅要给一个圆柱型的制品嵌金线,如下左图,如果将金线的起点固定在A 点,绕一周之后终点为B 点,问沿什么线路嵌金线才能使金线的用量最少?解:将上左图中圆柱面沿母线AB 剪开,展开成平面图形如上页右图(把图中的长方形卷成上页左图中的圆柱面时,A ′、B ′分别与A 、B 重合),连接AB ′,再将上页右图还原成上页左图的形状,则AB ′在圆柱面上形成的曲线就是连接AB 且绕一周的最短线路.圆锥表面的最短路线也是一条曲线,展开后也是直线.请看下面例题.例5 有一圆锥如下图,A 、B 在同一母线上,B 为AO 的中点,试求以A 为起点,以B 为终点且绕圆锥侧面一周的最短路线.解:将圆锥面沿母线AO剪开,展开如上右图(把右图中的扇形卷成上图中的圆锥面时,A′、B′分别与A、B重合),在扇形中连AB′,则将扇形还原成圆锥之后,AB′所成的曲线为所求.例6 如下图,在圆柱形的桶外,有一只蚂蚁要从桶外的A点爬到桶内的B点去寻找食物,已知A点沿母线到桶口C点的距离是12厘米, B点沿母线到桶口 D点的距离是8厘米,而C、D两点之间的(桶口)弧长是15厘米.如果蚂蚁爬行的是最短路线,应该怎么走?路程总长是多少?分析我们首先想到将桶的圆柱面展开成矩形平面图(下图),由于B点在里面,不便于作图,设想将BD延长到F,使DF=BD,即以直线CD为对称轴,作出点B的对称点F,用F代替B,即可找出最短路线了.解:将圆柱面展成平面图形(上图),延长BD到F,使DF=BD,即作点B关于直线CD 的对称点F,连结AF,交桶口沿线CD于O.因为桶口沿线CD是 B、F的对称轴,所以OB=OF,而A、F之间的最短线路是直线段AF,又AF=AO+OF,那么A、B之间的最短距离就是AO+OB,故蚂蚁应该在桶外爬到O点后,转向桶内B点爬去.延长AC到E,使CE=DF,易知△AEF是直角三角形,AF是斜边,EF=CD,根据勾股定理,AF2=(AC+CE)2+EF2 =(12+8)2+152=625=252,解得AF=25.即蚂蚁爬行的最短路程是25厘米.例7 A、B两个村子,中间隔了一条小河(如下图),现在要在小河上架一座小木桥,使它垂直于河岸.请你在河的两岸选择合适的架桥地点,使A、B两个村子之间路程最短.分析因为桥垂直于河岸,所以最短路线必然是条折线,直接找出这条折线很困难,于是想到要把折线化为直线.由于桥的长度相当于河宽,而河宽是定值,所以桥长是定值.因此,从A点作河岸的垂线,并在垂线上取AC等于河宽,就相当于把河宽预先扣除,找出B、C两点之间的最短路线,问题就可以解决.17解:如上图,过A点作河岸的垂线,在垂线上截取AC的长为河宽,连结BC交河岸于D点,作DE垂直于河岸,交对岸于E点,D、E两点就是使两村行程最短的架桥地点.即两村的最短路程是AE+ED+DB.例8 在河中有A、B两岛(如下图),六年级一班组织一次划船比赛,规则要求船从A岛出发,必须先划到甲岸,又到乙岸,再到B岛,最后回到A岛,试问应选择怎样的路线才能使路程最短?解:如上图,分别作A、B关于甲岸线、乙岸线的对称点A′和B′,连结A′、B′分别交甲岸线、乙岸线于E、F两点,则A→E→F→B→A是最短路线,即最短路程为:AE +EF+FB+BA.证明:由对称性可知路线A→E→F→B的长度恰等于线段A′B′的长度.而从A岛到甲岸,又到乙岸,再到B岛的任意的另一条路线,利用对称方法都可以化成一条连接A′、B′之间的折线,它们的长度都大于线段 A′B′,例如上图中用“·—·—·”表示的路线A→E′→F′→B的长度等于折线AE′F′B的长度,它大于A′B′的长度,所以A→E →F→B→A是最短路线.1819B ●对称问题教学目的:进一步理解从实际问题转化为数学问题的方法,对于轴对称问题、中心对称问题有一个比较深入的认识,可以通过对称的性质及三角形两边之和与第三边的关系找到证明的方法。
八年级数学几何中的最值问题
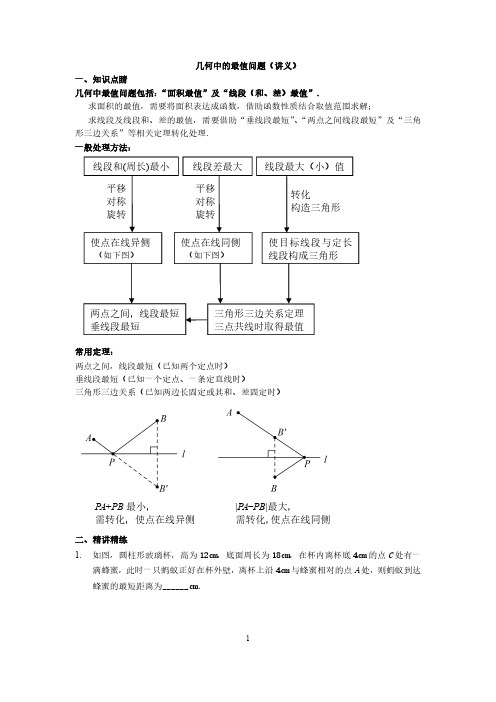
几何中的最值问题(讲义)一、知识点睛几何中最值问题包括:“面积最值”及“线段(和、差)最值”.求面积的最值,需要将面积表达成函数,借助函数性质结合取值范围求解;求线段及线段和、差的最值,需要借助“垂线段最短”、“两点之间线段最短”及“三角形三边关系”等相关定理转化处理.一般处理方法:常用定理:两点之间,线段最短(已知两个定点时)垂线段最短(已知一个定点、一条定直线时)三角形三边关系(已知两边长固定或其和、差固定时)二、精讲精练1.如图,圆柱形玻璃杯,高为12cm,底面周长为18cm,在杯内离杯底4cm 的点C 处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿4cm 与蜂蜜相对的点A 处,则蚂蚁到达蜂蜜的最短距离为______cm.线段和(周长)最小转化构造三角形两点之间,线段最短垂线段最短PA +PB 最小,需转化,使点在线异侧|PA -PB |最大,需转化,使点在线同侧线段差最大线段最大(小)值三角形三边关系定理三点共线时取得最值平移对称旋转使点在线异侧(如下图)使点在线同侧(如下图)使目标线段与定长线段构成三角形平移对称旋转第1题图第2题图2.如图,点P是∠AOB内一定点,点M、N分别在边OA、OB上运动,若∠AOB=45°,OP2,则△PMN周长的最小值为.3.如图,正方形ABCD的边长是4,∠DAC的平分线交DC于点E,若点P,Q分别是AD和AE上的动点,则DQ+PQ的最小值为.第3题图第4题图4.如图,在菱形ABCD中,AB=2,∠A=120°,点P、Q、K分别为线段BC、CD、BD上的任意一点,则PK+QK的最小值为.5.如图,当四边形PABN的周长最小时,a=.第5题图第6题图6.在平面直角坐标系中,矩形OACB的顶点O在坐标原点,顶点A、B分别在x轴、y轴的正半轴上,OA=3,OB=4,D为边OB的中点.若E、F为边OA上的两个动点,且EF=2,当四边形CDEF的周长最小时,则点F的坐标为.7.如图,两点A、B在直线MN外的同侧,A到MN的距离AC=8,B到MN的距离BD=5,CD=4,-的最大值等于.P在直线MN上运动,则PA PB第7题图第8题图8.点A、B均在由面积为1的相同小矩形组成的网格的格点上,建立平面直角坐标系如图-的值最大的点,Q是y轴上使得QA+QB的值最小的所示.若P是x轴上使得PA PB⋅=.点,则OP OQ9.如图,在△ABC中,AB=6,AC=8,BC=10,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为EF中点,则AM的最小值为_________.第9题图第10题图10.如图,已知AB=10,P是线段AB上任意一点,在AB的同侧分别以AP和PB为边作等边△APC和等边△BPD,则CD长度的最小值为.11.如图,点P在第一象限,△ABP是边长为2的等边三角形,当点A在x轴的正半轴上运动时,点B随之在y轴的正半轴上运动,运动过程中,点P到原点的最大距离是________.2,另两边长度不变,则点P到原点的最大距离变为若将△ABP中边PA的长度改为2_________.第11题图第12题图12.动手操作:在矩形纸片ABCD中,AB=3,AD=5.如图所示,折叠纸片,使点A落在BC边上的A′处,折痕为PQ,当点A′在BC边上移动时,折痕的端点P、Q也随之移动.若限定点P、Q分别在AB、AD边上移动,则点A′在BC边上可移动的最大距离为.13.如图,直角梯形纸片ABCD,AD⊥AB,AB=8,AD=CD=4,点E、F分别在线段AB、AD上,将△AEF沿EF翻折,点A的落点记为P.(1)当P落在线段CD上时,PD的取值范围为;(2)当P落在直角梯形ABCD内部时,PD的最小值等于.14.在△ABC中,∠BAC=120°,AB=AC=4,M、N两点分别是边AB、AC上的动点,将△AMN沿MN翻折,A点的对应点为A′,连接BA′,则BA′的最小值是_________.几何中的最值问题(作业)1.如图,在梯形ABCD中,AB∥CD,∠BAD=90°,AB=6,对角线AC平分∠BAD,点E在AB上,且AE=2(AE<AD),点P是AC上的动点,则PE+PB的最小值是__________.第1题图第2题图2.在边长为2cm的正方形ABCD中,点Q为BC边的中点,点P为对角线AC上一动点,连接PB、PQ,则△PBQ周长的最小值为____________cm(结果不取近似值).3.如图,一副三角板拼在一起,O为AD的中点,AB=a.将△ABO沿BO对折于△A′BO,点M为BC上一动点,则A′M的最小值为.第3题图第4题图AB ∠BAC=45°,∠BAC的平分线交BC于点D,点M,4.如图,在锐角△ABC中,42N分别是AD和AB上的动点,则BM+MN的最小值为___________.5.在Rt△ACB中,∠ACB=90°,AC=6,BC=8,P、Q两点分别是边AC、BC上的动点,将△PCQ沿PQ翻折,C点的对应点为C',连接A C',则A C'的最小值是_________.第5题图第6题图6.如图,在△ABC 中,∠ACB=90°,AC=4,BC=2,点A、C 分别在x 轴、y 轴上,当点A 在x 轴上运动时,点C 随之在y 轴上运动,在运动过程中,点B 到原点的最大距离是.7.一次函数y 1=kx -2与反比例函数y 2=m x (m <0)的图象交于A ,B 两点,其中点A 的坐标为(-6,2)(1)求m ,k 的值;(2)点P 为y 轴上的一个动点,当点P 在什么位置时|PA -PB |的值最大?并求出最大值.8.已知点A (3,4),点B 为直线x =-1上的动点,设B (-1,y ).(1)如图1,若点C (x ,0)且-1<x <3,BC ⊥AC ,求y 与x 之间的函数关系式;(2)如图2,当点B 的坐标为(-1,1)时,在x 轴上另取两点E ,F ,且EF =1.线段EF 在x 轴上平移,线段EF 平移至何处时,四边形ABEF 的周长最小?求出此时点E 的坐标.图1图29.如图,已知平面直角坐标系中A,B两点的坐标分别为A(2,-3),B(4,-1).(1)若P(p,0)是x轴上的一个动点,则当p=________时,△PAB的周长最短;(2)若C(a,0),D(a+3,0)是x轴上的两个动点,则当a=________时,四边形ABDC 的周长最短;(3)设M,N分别为x轴和y轴上的动点,请问:是否存在这样的点M(m,0),N(0,n),使四边形ABMN的周长最短?若存在,请写出m和n的值;若不存在,请说明理由.中考数学几何中的最值问题综合测试卷一、单选题(共7道,每道10分)1.如图,圆柱形玻璃杯,高为12cm,底面周长为18cm,在杯内离杯底5cm的点C处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿5cm与蜂蜜相对的点A处,则蚂蚁到达蜂蜜的最短距离为()cmA. B.15 C. D.122.如图,在矩形ABCD中,AB=2,AD=4,E为CD边的中点,P为BC边上的任一点,那么,AP+EP的最小值为()A.3B.4C.5D.63.如图,在锐角△ABC中,AB=6,∠BAC=60°,∠BAC的平分线交BC于点D,点M,N分别是AD和AB上的动点,则BM+MN的最小值为()A. B. C.6 D.34.如图,当四边形PABN的周长最小时,a=().A. B. C. D.5.如图所示,已知A(,y1),B(2,y2)为反比例函数y=图象上的两点,动点P(x,0)在x轴正半轴上运动,当线段AP与线段BP之差达到最大时,点P的坐标是()A. B.(1,0) C. D.6.如图,△ABC是以AB为斜边的直角三角形,AC=4,BC=3,P为边AB上一动点,且PE⊥AC于点E,PF⊥BC于点F,则线段EF长度的最小值是()A. B. C. D.7.如图,正方形ABCD边长为2,当点A在x轴上运动时,点D随之在y轴上运动,在运动过程中,点B到原点O的最大距离为()A. B. C. D.。
高中数学-圆锥曲线中的定点、定值与最值问题

[例 2] 如图,在平面直角
坐标系 xOy 中,椭圆xa22+by22=1(a>b>0)的左、
右焦点分别为 F1(-c,0),F2(c,0).已知点(1,e)
和e,
23都在椭圆上,其中
e
为椭圆的离心率.
(1)求椭圆的方程;
(2)设 A,B 是椭圆上位于 x 轴上方的两点,且直线 AF1 与直
线 BF2 平行,AF2 与 BF1 交于点 P,
法二:同(2)法一假设前内容. 假设平面内存在定点M满足条件,由图形对称性知,点M 必在x轴上. 取k=0,m= 3,此时P(0, 3),Q(4, 3), 以PQ为直径的圆为(x-2)2+(y- 3)2=4, 交x轴于点M1(1,0),M2(3,0); 取k=-12,m=2,此时P1,32,Q(4,0), 以PQ为直径的圆为x-522+y-342=4156, 交x轴于点M3(1,0),M4(4,0).
因为 MP =-4mk-x1,m3 , MQ =(4-x1,4k+m), 由 MP ·MQ =0,得-1m6k+4kmx1-4x1+x12+1m2k+3=0, 整理,得(4x1-4)mk +x12-4x1+3=0.(**) 由于(**)式对满足(*)式的m,k恒成立, 所以4x1x2-1-4x41=+03,=0, 解得x1=1. 故存在定点M(1,0),使得以PQ为直径的圆恒过点M.
圆锥曲线中的最值问题
[例3] 如图,在直角坐标系xOy中,点 P1,12到抛物线C:y2=2px(p>0)的准线的距 离为54.点M(t,1)是C上的定点,A,B是C上的 两动点,且线段AB被直线OM平分.
(1)求p,t的值; (2)求△ABP面积的最大值.
[思路点拨] (1)利用点M(t,1)在曲线上及点P 1,12 到准线的距 离为54求p与t的值;
六年级思维训练23 最值问题(一)(原卷+解析)

六年级思维训练23最值问题(一)1、20个黑球,10个白球装在一个布袋里,至少拿出个才能保证有5个黑球,5个白球.2、司机开车按顺序到五个车站接学生到学校(如下图),每个站都有学生上车,第一站上了一批学生,以后每站上车的人数都是前一站上车人数的一半,车到学校时,车上最少有多少学生?成四位数.问:其中最小的数与最大的数的和是多少?4、用1、2、3、4、5、6、7、8、9这九个数字组成三个三位数(每个数字只用一次),这3个三位数之和最大是。
5、下图是2008年3月的月历,图中用一个方框框住的四个日期的数码之和是5+6+1+2+1+3=18,则在所有可能被框住的四个日期中,数码之和最大是。
6、在10个盒子中放乒乓球,每个盒子中的球的个数不能少于11,不能是13,也不能是5的倍数,且彼此不同,那么至少需要个乒乓球.7、台球桌上有15个红球(每球1分),另有六个高分球;黄色球(2分),棕色球(3分),绿色球(4分),蓝色球(5分),粉色球(6分),黑色球(7分),台球比赛规则:①先打红球,打完所有红球后,再将高分球依次由低分到高分打入袋中,称为打完一局.②在打进两个红球之间可先后连续打进任意两个高分球,然后再取出这两个高分球放回原处,每打进一个球,选手得到该球的分值.问:小白兔打完一局最高能得多少分?8、用一条60米的长绳沿着一道墙围出长方形的三个边(如下图所示,墙是长方形另一个边).请问这条绳子所能围出的最大面积为多少?9、把14分成几个自然数的和,再求出这些数的乘积,要使得到的乘积尽可能大,问这个乘积是几?10、每个星期除了星期天以外,快乐小学每天都要指派8名学生担任纠察队.在这个星期的6天里,每天都恰好只有3名学生在这个星期里只担任一次纠察队.请问这个星期至多有多少名学生会被指派担任纠察队?11、如果100个人共有1000元人民币,且其中任意10个人的钱都不超过190元,那么,一个人最多有元。
12、有一组自然数(数可以重复),其中包含数2003,但不包含数0,这组自然数的平均数是572,如果杷2003去掉,那么剩下的数的平均数就变为413。
专题23 圆锥曲线中的最值、范围问题 微点1 圆锥曲线中的最值问题试题及答案

例7.
7.已知点A(−2,0),B(2,0),动点M(x,y)满足直线AM与BM的斜率之积为− .记M的轨迹为曲线C.
(1)求C的方程,并说明C是什么曲线;
(2)过坐标原点的直线交C于P,Q两点,点P在第一象限,PE⊥x轴,垂足为E,连结QE并延长交C于点G.
(i)证明: 是直角三角形;
最值问题不仅解答题中分量较大,而且客观题中也时常出现.
一、常用方法
解决圆锥曲线中的最值问题,常见的方法有:
(1)函数法:一般需要找出所求几量的函数解析式,要注意自变量的取值范围.求函数的最值时,一般会用到配方法、均值不等式或者函数单调性.
(2)方程法:根据题目中的等量关系建立方程,根据方程的解的条件得出目标量的不等关系,再求出目标量的最值.
题型三、与向量有关的最值问题
例6.
6.如图,已知椭圆C1: + =1(a>b>0)的右焦点为F,上顶点为A,P为椭圆C1上任一点,MN是圆C2:x2+(y-3)2=1的一条直径,在y轴上截距为3- 的直线l与AF平行且与圆C2相切.
(1)求椭圆C1的离心率;
(2)若椭圆C1的短轴长为8,求 · 的最大值.
题型二、与角度有关的最值问题
例5.
5.在平面直角坐标系 中,椭圆 : 的离心率为 ,焦距为 .
(Ⅰ)求椭圆 的方程;
(Ⅱ)如图,动直线 : 交椭圆 于 两点, 是椭圆 上一点,直线 的斜率为 ,且 , 是线段 延长线上一点,且 , 的半径为 , 是 的两条切线,切点分别为 .求 的最大值,并求取得最大值时直线 的斜率.
专题23 圆锥曲线中的最值、范围问题 微点1 圆锥曲线中的最值问题
专题23圆锥曲线中的最值、范围问题
高斯小学奥数四年级上册含答案第23讲_最值问题一

第二十三讲最值问题一最值问题,即求最大值、最小值的问题.这类问题中,有时满足题目条件的情况并不多,这时我们就可以用枚举法将所有可能情况一一列出,再比较大小.例题1(1)在五位数12435的某一位数字后面插入一个同样的数字可以得到一个六位数(例如:在2的后面插入2可以得到122435).请问:能得到的最大六位数是多少?(2)在七位数9876789的某一位数字后面再插入一个同样的数字.请问:能得到的最小八位数是多少?「分析」一共有多少种不同的插入数字的方法?你能将它们全部枚举出来吗?练习1在五位数41729的某一位数字前面插入一个同样的数字(例如:在7的前面插入7得到417729),能得到的最大六位数是多少?直接枚举的优点是不用过多思考,大家都能理直气壮地说,直接比较大小得到的答案一定是正确的.事实上,我们应该多想一想,为什么这个答案是最大或最小的,有没有什么道理,其中有没有什么规律.例题2有9个同学要进行象棋比赛.他们准备分成两组,不同组的任意两人之间都进行一场比赛,同组的人不比赛,那么一共最多有多少场比赛?「分析」把9个同学分成两组,有多少种情况呢?你能算出这些分法各自对应的比赛场数吗?练习2有7个同学要进行乒乓球单打比赛.他们准备分成两组,不同组的任意两人之间都进行一场比赛,同组的人不比赛,那么一共最多有多少场比赛?从例题2我们可以得出:两个数的和相等,当它们越接近时(也就是它们的差越小时),两数乘积越大,也可以简单记成“和同近积大”.“和同近积大”的应用非常广泛,接下来我们分析一下比较典型的“篱笆问题”.例题3墨爷爷要用长20米的篱笆围成一个长方形养鸡场,已知长和宽均为整数米,那么怎样围所得的养鸡场面积最大?(正方形是特殊的长方形)「分析」长方形面积是长、宽的乘积,要想长、宽乘积最大,可以不可以应用“和同近积大”的道理来解决呢?能找到“和同”吗?练习3墨爷爷要用长30米的篱笆围成一个长方形养鸡场,已知长和宽均为整数米,那么怎样围所得的养鸡场面积最大?例题4请将1、2、3、4、5、6这六个数填入下面的方格中,使得乘法算式的结果最大.⨯□□□□□□ 「分析」要使得乘积最大,百位应当填哪两个数?十位呢?个位呢?练习4请将1、2、3、4、5、6、7、8这八个数填入下面的方格中,使得乘法算式的结果最大.⨯□□□□□□□□例题5墨爷爷要用长20米的篱笆围成一个靠墙的直角三角形养鸡场,已知靠墙的恰好为三角形斜边,两条直角边长均为整数米,那么怎样围所得的养鸡场面积最大?「分析」长方形篱笆我们已经解决了,三角形的与长方形的有什么联系吗?养鸡场想一想要用篱笆围一个靠墙的三角形,那么锐角三角形、直角三角形、钝角三角形中的哪一种面积会最大呢?在很多问题中,我们都需要先进行整体的思考,再对局部进行一些调整.千万不能“丢了西瓜捡芝麻”!例题6各位数字互不相同的多位数中,数字之和为23的最小数是多少?最大数是多少?「分析」两个多位数比较大小,首先要比较它们的位数.如果位数相同,还要从高位到低位依次比较.课堂内外动物之最最大的动物:蓝鲸(平均长30米,重达160吨)最大的路上动物:非洲象(平均重达9吨)最高的路上动物:长颈鹿(平均高5米)嘴巴最大的陆生哺乳动物:河马最聪明的动物:海豚(人除外)最大的鸟类:鸵鸟(平均身高2.5米,最重可达155千克)翅膀最长的鸟类:信天翁(翅展2~3米)嘴巴最大的鸟:巨嘴鸟(最长24厘米,宽9厘米)形体最小的鸟:蜂鸟飞得最高的鸟:天鹅(最高能达17000米)最耐寒的鸟:企鹅路上奔跑速度最快的动物:猎豹(可高达时速130公里)速度最快的海洋动物:旗鱼(可高达时速190公里)飞行速度最快的动物:军舰鸟(可高达时速418公里)现存最古老的生物:舌形贝(有4.5亿年历史)牙齿最多的动物:蜗牛(共有25600颗牙齿)飞行能力最强的昆虫:蝗虫(每天能够连续飞行近10小时)力气最大的昆虫:屎壳郎(可以支撑或拖走相当于自己体重1141倍的物体)外形最奇特的鱼:海马最大的两栖动物:大鲵(即娃娃鱼)毒性最强的蛇:海蛇(其毒性为眼镜蛇的2倍)寿命最长的动物:海葵(已发现最年长的海葵有2000多岁了)冬眠时间最长的动物:睡鼠(冬眠时间5~6个月)作业1.在六位数129854的某一位数字前面再插入一个同样的数字(例如:可以在2的前面插入2得到1229854),能得到的最小七位数是多少?2.两个自然数之和等于10,那么它们的乘积最大是多少?3.用20根长1厘米的火柴棒围成一个长方形,这个长方形的面积最大是多少平方厘米?4.请将3,4,5,6,7,8这六个数分别填入算式□□□□□□的方格中,使这个乘法算式的结果最大.5.各位数字互不相同的多位数中,数字之和为32的最小数是多少,最大数是多少?第二十三讲 最值问题一1. 例题1答案:(1)124435;(2)98766789详解:(1)枚举:112435、122435、124435、124335、124355,最大的六位数是124435;(2)枚举:99876789、98876789、98776789、98766789、98767789、98767889、98767899,最小的八位数是98766789.2. 例题2答案:20场详解:如果是(1,8),那么共188⨯=场;如果是(2,7),那么共2714⨯=场;如果是(3,6),那么共3618⨯=场;如果是(4,5),那么共4520⨯=场;所以一共最多有20场比赛.3. 例题3答案:长、宽 都为5米时,面积最大为25平方米详解:长方形周长是20米,长、宽之和为10,是固定不变的;长方形面积为长、宽之积,根据“和同近积大”,可知长、宽越接近,面积越大; 当长、宽相等,即篱笆为正方形时,面积最大,最大面积为5525⨯=平方米.4. 例题4答案:631542⨯详解:要使得乘积最大,那么就要百位上的数字最大、个位上的数字最小;所以百位填5、6,十位填3、4,个位填1、2;在这个前提下,无论怎么填,最后两个三位数的和都固定等于5006003040121173+++++=,所以要想让它们的乘积最大,就要让这两个三位数差最小,尝试可得是631542⨯.5. 例题5答案:两条直角边都为10米时,面积最大为50平方米详解:设两条直角边分别为A 、B ,则20+=A B 米;直角三角形面积为“2⨯÷底高”,即面积大小是由“⨯A B ”决定的;A 、B 之和为20米,越接近则乘积越大,所以当10==A B 米时, “⨯A B ”有最大值; 所以,三角形面积最大为1010250⨯÷=平方米.6. 例题6答案:689;8543210详解:数的大小,首先是要考虑位数,再考虑各个数位上的数的大小.(1)最小:即要位数最少,那么就得要让每个数位上的数字都尽量的大,把23拆开:23986=++,所以最小数为689;(2)最大:即要位数最多,那么就得要让每个数位上的数字都尽量的小,把23拆开:230123458=++++++,所以最大数为8543210.7.练习1答案:441729详解:枚举:441729、411729、417729、417229、417299,最大的六位数为441729.8.练习2答案:12场详解:如果是(1,6),那么共166⨯=场;如果是(2,5),那么共2510⨯=场;如果是(3,4),那么共3412⨯=场;所以一共最多有12场比赛.9.练习3答案:长8米,宽7米时,面积最大为56平方米简答:长、宽和为15米,当长为8米、宽为7米时,长、宽最接近,长、宽乘积最大,最大面积为56平方米.10.练习4答案:76428531⨯简答:要使得乘积最大,那么就要千位上的数字最大、个位上的数字最小;所以千位填7、8,百位填5、6,十位填3、4,个位填1、2;在这个前提下,无论怎么填,最后两个四位数的和都固定等于+++++++=,所以要想让它们的乘积最大,就要让这两个四7000800050060030401216173位数差最小,尝试可得是76428531⨯.11.作业1答案:1129854简答:在原数某一位前面插入相同数一共可以得到1129854、1229854、1299854、1298854、1298554、1298544这些数,对比可知1129854最小.12.作业2答案:25简答:两个数的和为10,根据“和同近积大”的原则,当两个数都为5时乘积最大,为25.13.作业3答案:25平方厘米简答:长、宽的和是10厘米,根据“和同近积大”的原则,正方形的时候面积最大,此时边长为5厘米,面积为25平方厘米.14.作业4答案:853764⨯简答:最高位填8和7,十位填6和5,个位填4和3,相差越小乘积越大,所以应为853764⨯.15.作业5答案:26789;98543210简答:3298762=++++,所以最小为26789;3201234589=+++++++,所以最大为98543210.。
2024年高考数学高频考点(新高考通用)等差数列中Sn的最值问题(精讲+精练)解析版

【一轮复习讲义】2024年高考数学高频考点题型归纳与方法总结(新高考通用)素养拓展19等差数列中Sn 的最值问题(精讲+精练)一、等差数列的通项公式和前n 项和公式1.等差数列的通项公式如果等差数列{}n a 的首项为1a ,公差为d ,那么它的通项公式是1(1)=+-n a a n d .2.等差数列的前n 项和公式设等差数列{}n a 的公差为d ,其前n 项和11()(1)22+-=+=n n n a a n n S na d .注:数列{}n a 是等差数列⇔2=+n S An Bn (、A B 为常数).二、等差数列的前n 项和的最值1.公差0{}>⇔n d a 为递增等差数列,n S 有最小值;公差0{}<⇔n d a 为递减等差数列,n S 有最大值;公差0{}=⇔n d a 为常数列.2.在等差数列{}n a 中(1)若100,><a d ,则满足1+≥0⎧⎨≤0⎩m m a a 的项数m 使得n S 取得最大值m S ;(2)若100,<>a d ,则满足1+≤0⎧⎨≥0⎩m m a a 的项数m 使得n S 取得最小值m S .即若100>⎧⎨<⎩a d ,则n S 有最大值(所有正项或非负项之和);若100<⎧⎨>⎩a d ,则n S 有最小值(所有负项或非正项之和).【典例1】(2022·全国·统考高考真题)记n S 为数列{}n a 的前n 项和.已知221nn S n a n+=+.二、题型精讲精练一、知识点梳理又4a ,7a ,9a 成等比数列,所以2749a a a =⋅,即()()()2111638a a a +=+⋅+,解得112a =-,所以13n a n =-,即有1123210,0a a a a <<<<= .则当12n =或13n =时,()min 78n S =-.【整体点评】(2)法一:根据二次函数的性质求出n S 的最小值,适用于可以求出n S 的表达式;法二:根据邻项变号法求最值,计算量小,是该题的最优解.【题型训练-刷模拟】一、单选题若5,故②正确;当8n =或9n =时,n S 取得最大值,所以211k a b +-=或12,故选:B【点睛】关键点点睛:本题考查的是等差数列的前n 项和最大值问题,思路是不难,大,即确定数列是递减数列,判断前多少项为非负项即可,但关键点在于如何求得正负项分界的项,即求得90a =,100a <,所以这里的关键是利用()217e 1ln 21a bS a b --≤≤-+,构造函数()e 1x f x x =--,利用导数判断函数单调性,结合最值解决这一问题.二、多选题三、填空题1四、解答题32.(2023·全国·高三专题练习)设等差数列{}n a 的前n 项和为n S ,且1121526,a S S =-=.(1)求{}n a 的通项公式;(2)求n S ,并求n S 的最小值.【答案】(1)228n a n =-;(2)227n S n n =-,最小值为182-.【分析】(1)设等差数列{}n a 的公差为d ,根据等差数列前n 项和公式由1215S S =列出方程即可解出d ,从而可得数列{}n a 的通项公式;(2)根据二次函数的性质或者邻项变号法即可判断何时n S 取最小值,并根据等差数列前n 项和公式求出nS。
--四年级第二十三讲-最值问题一教师版

第23讲最值问题一内容概述求最大值与最小值的问题,解题时宜首先考虑起主要作用的量,有时还需要局部调整或者枚举各种可能情形.和为定值的两数的乘积随着两数之差的增大而减小.典型问题兴趣篇1.3个连续奇数相乘,所得乘积的个位数字最小可能是多少? 答案:3分析:乘积的个位数字是由这三个奇数的个位数字决定的。
个位数字可能是:1、3、5、7、9。
通过试验个位是7、9、1的三个连续奇数相乘满足条件,7×9×1=63个位最小是3.2. 用1、2、4可以组成6个没有重复数字的三位数,这些三位数中相差最小的两个数之差是多少?答案:9分析:要使两个数差最小百位数字相同十位与个位数字相近。
满足条件的是412和421.差是421-412=9.3. 用24根长l厘米的火柴棒围成一个矩形,这个矩形的面积最大是多少?如果用22根火柴棒呢?答案:36平方厘米;30平方厘米。
分析:(1)矩形的周长是24厘米。
长和宽的和:24÷2=12(厘米)和为定值的两数的乘积随两数之差的增大而减少。
和是12的两数差为0是积最大。
这两个数相等都是6.即长和宽相等面积是6×6=36(平方厘米)。
(2)周长是22厘米。
长和宽的和是22÷2=11(厘米)和是11差是0时,这样的两个数不是整数。
差是1时两数分别为6和5.积是30.4.三个自然数的和是19,它们的乘积最大可能是多少?答案:252分析:和一定差越小积越大。
19÷3=6……1,6+6+6=18再加1得19,三个数分别是6、6、7时积最大。
最大是6×6×7=252. 5.(1)请将l、2、3、4填人算式“口口×口口”的方格中.要使得算式结果最大,应该怎么填?(2)请将1、2、3、4、5、6填人算式“口口口×口口口”的方格中.要求5、6分别填在百位,4、3分别填在十位,1、2分别填在个位,并使得算式结果最大.应该怎么填?答案:(1)41×32 (2)542×631分析:(1)要使积最大,两个数应尽量大所以4、3分别在十位,1、2在个位。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第23讲最值问题一内容概述求最大值与最小值的问题,解题时宜首先考虑起主要作用的量,有时还需要局部调整或者枚举各种可能情形.和为定值的两数的乘积随着两数之差的增大而减小.典型问题兴趣篇1.3个连续奇数相乘,所得乘积的个位数字最小可能是多少? 答案:3分析:乘积的个位数字是由这三个奇数的个位数字决定的。
个位数字可能是:1、3、5、7、9。
通过试验个位是7、9、1的三个连续奇数相乘满足条件,7×9×1=63个位最小是3.2. 用1、2、4可以组成6个没有重复数字的三位数,这些三位数中相差最小的两个数之差是多少?答案:9分析:要使两个数差最小百位数字相同十位与个位数字相近。
满足条件的是412和421.差是421-412=9.3. 用24根长l厘米的火柴棒围成一个矩形,这个矩形的面积最大是多少?如果用22根火柴棒呢?答案:36平方厘米;30平方厘米。
分析:(1)矩形的周长是24厘米。
长和宽的和:24÷2=12(厘米)和为定值的两数的乘积随两数之差的增大而减少。
和是12的两数差为0是积最大。
这两个数相等都是6.即长和宽相等面积是6×6=36(平方厘米)。
(2)周长是22厘米。
长和宽的和是22÷2=11(厘米)和是11差是0时,这样的两个数不是整数。
差是1时两数分别为6和5.积是30.4.三个自然数的和是19,它们的乘积最大可能是多少?答案:252分析:和一定差越小积越大。
19÷3=6……1,6+6+6=18再加1得19,三个数分别是6、6、7时积最大。
最大是6×6×7=252. 5.(1)请将l、2、3、4填人算式“口口×口口”的方格中.要使得算式结果最大,应该怎么填?(2)请将1、2、3、4、5、6填人算式“口口口×口口口”的方格中.要求5、6分别填在百位,4、3分别填在十位,1、2分别填在个位,并使得算式结果最大.应该怎么填?答案:(1)41×32 (2)542×631分析:(1)要使积最大,两个数应尽量大所以4、3分别在十位,1、2在个位。
有两种情况A:41×32=1×2+2×40+1×30+40×30=1312B:42×31=1×2+1×40+2×30+40×30=1302比较发现区别在划横线部分,当一个数十位上的数字与另一个数个位上的数字较大的与较大的相乘,较小与较小的数字相乘时积最大。
最大是41×32(2)与(1)同理当十位上4与百位上的6相乘,十位上3与百位上5相乘;个位2与百位上6相乘,个位1与百位5相乘时积最大。
其中一个数百位是6十位是3个位是1即631。
另一个是542.6. 在图23-1的中间圆圈内填一个数,计算每一条线段两端的数之差(大减小),然后把这3个差数相加,所得的和最小是多少? 答案:7分析:当中间数是7时和最小,和最小是7。
7. 在所有包含3个相同数码的四位数中,与1389之差(大减小)最小的一个是多少?答案:1411分析:与1389之差(大减小)尽量与1389相近。
所以千位是1,百位是3或4,十位和个位是1.即可能是1311或1411.通过计算与1389之差(大减小)差最小的是1411.8. 把1、2、3、4、5、6填人算式“□□□-□□□”的空格中,要求前一个三位数比后一个三位数大.这个减法算式的结果最大可能是多少?最小可能是多少?答案:最大:531 最小:47分析:满足结果最大,被减数应尽量大,减数应尽量小。
被减数最大是654,减数最小是123。
结果最小,两数应接近。
被减数是412,减数是365时结果最小。
9. 一个自然数是由数字8、9组成的,它的任意相邻两位都可以看成一个两位数,并且这些相邻数字组成的两位数都不相等.请问:满足条件的自然数最大是多少?答案:99889分析:由8和9组成的两位数可能是88、89、99、984种情况。
.要使数最大数的位数尽量大,相邻数字组成的两位数出现以上4种情况。
满足条件的数由高位到低位排列可称为第1位、第2位、第3位…第1位第2位组成的数最大是99,第2位第3位组成的数最大是98第3位第4位组成的数是88,第,4位第5位组成的数是89. 满足条件的自然数最大是99889.10. 有7个盘子排成一排,依次编号为1,2,3,…,7.每个盘子中都放有若干玻璃球,一共放了80个.其中1号盘里放了18个玻璃球,并且任意编号相邻的3个盘子里放的玻璃球组成的数之和都相等.请问:第6个盘子中最多可能放了多少个玻璃球? 答案:12分析:任意编号相邻的3个盘子里放的玻璃球组成的数之和都相等。
1、2、3号盘与2、3、4号盘玻璃球一样多。
所以1号和4号盘都有18个。
依次往后推7号盘也有18个。
前6盘有80-18=62个,相邻的3盘有62÷2=31个。
4、5、6这3个盘,4号盘有18个要使第6个盘子中最多5号应最少最少有1个,第6个盘最多有31-18-1=12个。
拓展篇1.3个连续自然数相乘,所得乘积的个位数字最大可能是多少?答案:6分析:只需考虑3个自然数的个位。
个位上有0----9 十种可能。
通过试验得3个连续自然数个位是1、2、3满足条件。
2. (1)在五位数12435的某一位数字后面再插入一个同样的数字(例如:可以在2的后面插入2得到122435),这样得到的六位数最大可能是多少?(2)在七位数9876789的某一位数字后面再插入一个同样的数字,这样得到的八位数最小是多少?答案:最大124435 最小98766789分析:(1)使结果最大所插数字应尽量大且数位尽量靠前。
试验得出最大是124435.(2)使结果最小,所插数字应尽量小且数位尽量靠后。
试验得出最小是98766789.3.有9个同学要进行象棋比赛.他们准备分成两组,不同组的人相互之间只比赛一场,同组的人之间不比赛.他们一共最多能比赛多少场?答案:20分析:两组比赛的场数是两组人数的乘积。
两组人数的和是9要使乘积最大两组人数应相近。
4+5=9,两组人数分别是4和5时比赛场数最多,一共比赛4×5=20场。
4.3个互不相同的自然数之和是17,它们的乘积最大可能是多少?答案:168分析:三个数和一定,差越小积越大。
6+6+5=17但有相同的数,再做调整得7+6+4=17.积是7×6×4=168。
5.请将2、3、4、5、6、8填人算式“口口口×口口口”的方格中.要使得算式结果最大,应该怎么填?答案:842×653分析:百位最大填8和6,十位填4和5,个位填2和3。
当一个数十位上的5与另一个数百位上的8相乘,一个数个位上的3与另一个数百位上的8相乘时积最大。
所以两个三位数分别是842和653。
6.请将6、7、8、9填人算式“口×口+口口”的方格中.要使得算式结果最大,应该怎么填?答案:7×8+96分析:两数乘积与所加的两位数应尽量大。
9×8+76=148, 8×7+96=152比较发现最大填7×8+96。
7.在图23-2的中间圆圈内填一个数,计算每一条线段两端的数之差(大减小),然后把这5个差数相加,所得的和最小是多少? 答案:19分析:当中间数是19时和最小,和最小是19.8.如果7个互不相同的自然数之和为100,那么其中最小的数最大可能是多少?最大的数最小可能是多少?答案:11;18分析:7个互不相同的自然数最小分别是0、1、2、3、4、5、6这7个数的和是21.100-21=79以上7个数分别加上相同的数也得到7个不同的数。
79÷7=11…2,7个自然数都加上11,得11----17,7个数。
余数2可加到最大的两个数中。
所以最小是11最大是18。
9.一个多位数的各位数字互不相同,而且各位数字之和为23.这样的多位数最小可能是多少?最大可能是多少?答案:最小689 最大8543210分析:要使最小,位数应尽量少。
23可最少拆成3个不同的一位数的和。
即23=6+8+9.所以最小是689.要使最大,位数应尽量多。
6个互不相同的自然数最小是0+1+2+3+4+5+6=21,23-21=2,0+1+2+3+4+5+8=23.最大是8543210。
11.如图23-3,这是一个正方体的展开图.将它折成一个正方体后,相交于同一顶点的3个面上的数之和最大是多少?答案:13分析:1---6个数中3个数的和从大到小分析最大的三个数是6+5+4=15,从图中看出6、5、4不相交于同一顶点。
再次6、5、3也不想交与同一顶点。
6、4、3相交与同一顶点。
6+4+3=13.12.如图23-4,在一个正方体方块的左下角A点处有一只蚂蚁,它要沿着正方体的表面爬行至右上角的B点,去搬运一块食物.为了使得这个蚂蚁所走的路线长度最短,它应该怎么爬行?它可以选择的最短路线一共有几条?答案:6分析:A、B没在同一平面上,不可以连接,蚂蚁只能从表面爬过去,A、B所在的两个面展开就在同一平面上了。
直接连接A、B就是最短路线。
展开A、B所在的两个面有6种情况(正面和上面、正面和右面、下面和后面、下面和右面、左面和上面、左面和后面)。
所以最短路线有6条。
超越篇1.一个两位数除以它的各位数字之和,余数最大是多少?答案:15分析:除法算式中余数小于除数。
要想余数最大,除数应尽量大。
除数最大是18,从最大的除数开始考虑则有:99÷18=5 (9)98÷17=5...13 89÷17=5...4 97÷16=6...1 88÷16=5 (8)79÷16=4…15 观察以上式子发现余数最大是15.2.4个小朋友,每人的体重都是整数千克,而且其中任意3人体重之和都大于99千克.这4个小朋友体重之和最小是多少千克?答案:134千克。
分析:设四个小朋友分别为A、B、C、D。
由题意得任意3人之和最少是100千克。
则:A+B+C=100A+B+D=100A+C+D=100B+C+D=100由以上四式得A+B+C+D=100×4÷3=133…2得数不是整数,不符合题意。
所以最少是134千克。
3.将1至30依次写成一排:123…2930,形成一个多位数.从这个多位数中划掉45个数字,剩下的数最大是多少?如果要求剩下的数首位不为0,这个数最小是多少?答案:最大998930 最小100120分析:要使剩下的数最大每一位最大是9,数位不够再做调整。
要使剩下的数最小,最高位是1后面是0,数位不够再做调整。
