基金持股的小波分解
【国家自然科学基金】_小波-contourlet变换_基金支持热词逐年推荐_【万方软件创新助手】_20140801
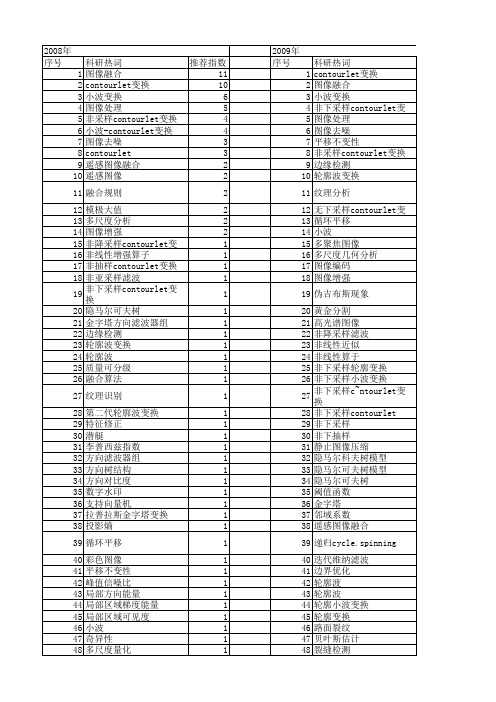
科研热词 推荐指数 图像融合 11 contourlet变换 10 小波变换 6 图像处理 5 非采样contourlet变换 4 小波-contourlet变换 4 图像去噪 3 contourlet 3 遥感图像融合 2 遥感图像 2 融合规则 2 模极大值 2 多尺度分析 2 图像增强 2 非降采样contourlet变换 1 非线性增强算子 1 非抽样contourlet变换 1 非亚采样滤波 1 非下采样contourlet变换 1 隐马尔可夫树 1 金字塔方向滤波器组 1 边缘检测 1 轮廓波变换 1 轮廓波 1 质量可分级 1 融合算法 1 纹理识别 1 第二代轮廓波变换 1 特征修正 1 潜艇 1 李普西兹指数 1 方向滤波器组 1 方向树结构 1 方向对比度 1 数字水印 1 支持向量机 1 拉普拉斯金字塔变换 1 投影熵 1 循环平移 1 彩色图像 1 平移不变性 1 峰值信噪比 1 局部方向能量 1 局部区域梯度能量 1 局部区域可见度 1 小波 1 奇异性 1 多尺度量化 1 多尺度几何分析 1 多分辨率处理 1 多分辨率分析 1 多分辨分析 1
科研热词 推荐指数 contourlet变换 9 图像融合 6 小波变换 4 非下采样contourlet变换 3 轮廓波变换 3 图像处理 3 图像去噪 3 非下采样轮廓波变换 2 纹理检索 2 抗混叠轮廓波变换 2 平移不变性 2 合成孔径雷达 2 非采样contourlet变换 1 非下采样轮廓波 1 隐马尔可夫模型 1 隐马尔可夫树模型 1 阈值去噪 1 阈值 1 遥感影像 1 遥感图像恢复 1 轮廓提取 1 超分辨重构 1 谱直方图 1 计算机应用 1 解析信号 1 融合算子 1 融合 1 脊波变换 1 脉冲耦合神经网络(pcnn) 1 结构相似性 1 纹理图像 1 粒子群优化 1 磁共振图像 1 相干斑噪声 1 相似度 1 灰色关联分析 1 滤波器组 1 混沌粒子群 1 混沌映射 1 正则化 1 椎体ct 1 检索系统 1 检索率 1 极化sar图像 1 有限脊波变换 1 曲波变换 1 时频域 1 无下采样contourlet变换 1 收缩阈值 1 循环平移算法 1 循环平移 1 平稳contourlet变换 1
ETF基金份额拆分原因与解读

ETF基金份额拆分原因与解读基金份额分拆是指将基金份额进行分割,使得基金份额数量增加,单份份额的规模减小,而基金的总份额和资产规模不发生变化。
在实际操作中,基金公司通过将一份大额份额拆分成若干份小额份额的方式来实现基金份额分拆。
例如,将一份面值为100元的基金份额分拆为10份面值为10元的基金份额。
我们先举一个例子来解释基金投资者是如何解读ETF分股的。
2024年4月,市场上一只中证煤炭ETF施基金份额拆分,这也是今年第二只宣布施份额拆分的基金。
公司于4月8日发布公告,股权分置的备案日为4月11日。
股权分置将于4月12日,具体来说,股权分置比例为1:2。
也就是说,每只基金份额分成两份。
截至4月10日,这只中证煤ETF份额净值为2.5724元。
在此之前,3月份,一只中证2000 ETF拆分了旗下基金份额。
该公司还将一份基金份额拆分为两只基金,拆分前的基金份额总数近1.41亿份。
本基金份额净值为1.341元。
基金拆分后,基金份额总数约为2.81亿份,每股净值为0.6705元。
为什么ETF 需要拆股?种操作的目的和影响主要包括以下几个方面。
首先,它降低了投资者的交易门槛。
通过降低单位净值,降低了投资者购买或持有ETF的成本。
从而提高交易的便利性。
这样,就会吸引更多的资金。
申购拆分后,原本高净值的ETF将变得更容易被普通投资者接受和投资。
有利于吸引更多资金流入,增加市场交易活跃度,稳定和扩大基金规模。
此外,基金拆分往往被视为一种积极的行为,因为这反映了基金行业的优秀业绩。
由此可见,截至4月11日,宣布施股份拆细的中证煤炭ETF今年以来累计上涨12.93%。
过去四年都出现了可观的年度增长。
一般来说,ETF基金份额拆分的操作流程包括确定拆分公告和拆分方案。
还有一些关键步骤,如执行拆分操作、调整净值、优化交易流程和投资者参与。
可以看出,这只中证煤炭ETF的公告中提到,基金份额拆分是在保持现有基金份额持有人资产不变的前提下,改变基金份额净值与持有的基金份额之间的对应关系。
基于小波分析理论的证券投资市场预测

2 基 于 小 波 消 噪 的预测 和建 模 方 法
2 1 数据 滤 波 .
一
个 含噪 声 的一 维信号 的模型 可 以表示 成如
下 的形 式 :
s = f + , ( ){ l…, () () / , : , n—1.
() 2
1 小 波理论简介
维普资讯
50 4
东北大学学报( 然科 学版 ) 自
第2 卷 3
收盘 价分 别 为 Y ( )Y ( ) Y ( ) Y ( ; l k , 2 k , 3 k , 4 k) 将 Y( )i , 4 k=1 …, 按下列方式排 ik ,=1…, . , 成一行 Y ( )Y ( )Y ( ) Y ( ) …, 1 k , l1 , 2 1 ,3 1 , 4 1 , Y ( ) y ( )… , 4 k , Y ( ) ( ) 儿 ( , 2k , Y ( ) …, I , , ) 2 Y( ; 4 )并记为 ()…, ( n ; 1, x 4 )
市场 。 望竭 力规 避投资 风险 , 期 同时追求较 高 的预
期 收益 . 内 外 对 证 券 市场 预 测 提 出 了 许 多 方 国 法L- . 些 方 法 在 实 际 工作 中有着 重 要 指 导作 2 这 J
定义 1 设 ( ) R)L ( 表示平方 f ∈L ( ( R) 可积 的实数空 间 , 郎能 量有 限 的信 号 空 问 )其 傅 . 里叶变换为 ( w). 若 ( ) w 满足条件
维普资讯
2 0 年 6月 Leabharlann 2 第2 卷 第6 3 期
东 北 大 学 学 报 ( 自 然 科 学 版 ) Junl f ote t nU i rt( a r c ne ora o N r a e n e i N t a Si c) . hsr v sy ul e
利用小波变换进行时序数据处理与预测的技巧与步骤

利用小波变换进行时序数据处理与预测的技巧与步骤时序数据是指按照时间顺序排列的数据,例如股票价格、气温变化等。
对于时序数据的处理和预测,小波变换是一种常用的方法。
小波变换是一种时频分析方法,可以将时域信号转换为时频域信号,从而提取出信号的特征和规律。
本文将介绍利用小波变换进行时序数据处理与预测的技巧与步骤。
首先,进行小波分解。
小波分解是将时序数据分解为不同尺度的小波系数,从而揭示出数据的不同频率成分。
小波分解的步骤如下:1. 选择小波基函数。
小波基函数是小波变换的基础,不同的小波基函数适用于不同类型的信号。
常用的小波基函数有Daubechies小波、Haar小波等。
选择适合的小波基函数可以更好地提取出信号的特征。
2. 进行多尺度分解。
将时序数据进行多尺度分解,可以得到不同尺度的小波系数。
多尺度分解可以通过连续小波变换或离散小波变换来实现。
连续小波变换适用于连续信号,离散小波变换适用于离散信号。
3. 选择分解层数。
选择合适的分解层数可以平衡时间和频率的分辨率。
分解层数越多,时间分辨率越高,频率分辨率越低;分解层数越少,时间分辨率越低,频率分辨率越高。
根据具体情况选择合适的分解层数。
接下来,进行小波重构。
小波重构是将小波系数重构为原始信号的过程。
小波重构的步骤如下:1. 选择重构层数。
根据小波分解得到的小波系数和分解层数,选择合适的重构层数。
重构层数应与分解层数相等,以保证信号的完整性。
2. 进行小波重构。
利用选定的小波基函数和重构层数,将小波系数进行逆小波变换,得到重构后的信号。
重构后的信号可以用于时序数据的处理和预测。
最后,进行时序数据处理与预测。
通过小波变换得到的重构信号,可以进行以下处理和预测:1. 信号去噪。
利用小波变换的多尺度分解特性,可以将信号的高频噪声去除,从而提高信号的质量和准确性。
2. 信号平滑。
利用小波变换的低频分量,可以对信号进行平滑处理,从而去除信号的突变和波动,得到平滑的曲线。
小波分解 领域泛化

小波分解领域泛化
小波分解是一种信号处理技术,它可以将信号分解成不同尺度的小波系数,从而可以在不同尺度上分析信号的特征。
小波分解可以用于信号压缩、去噪、特征提取等领域。
它的优点在于可以在时域和频域上同时进行分析,能够更好地捕捉信号的局部特征。
在领域泛化方面,小波分解可以应用于不同领域的信号处理。
例如,在地震学领域,可以利用小波分解来分析地震信号的频谱特征,从而帮助地震学家更好地理解地震活动规律。
在医学领域,小波分解可以用于分析生物信号,如心电图和脑电图,从而帮助医生诊断疾病。
在金融领域,小波分解可以用于分析股票价格波动的特征,帮助投资者制定交易策略。
小波分解的领域泛化还可以扩展到图像处理领域。
通过对图像进行小波分解,可以将图像分解成不同尺度和方向的小波系数,从而实现图像的多尺度分析和特征提取。
这对于图像压缩、去噪和图像识别等应用具有重要意义。
总的来说,小波分解在领域泛化方面具有广泛的应用前景,可
以在不同领域的信号处理和图像处理中发挥重要作用,帮助人们更好地理解和处理复杂的信号和图像数据。
【国家自然科学基金】_谐波分解_基金支持热词逐年推荐_【万方软件创新助手】_20140731

1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76
2011年 科研热词 经验模态分解 故障诊断 谐波小波 小波变换 hilbert变换 高频谐波 风电场 频率波动 频带分解 非线性超声 非平稳谐波检测 雷达目标识别 阵列信号处理 阵元域 闪变 进动 转子 贝叶斯准则 谐波检测 谐波小波包 谐波合成法 谐波功率潮流 谐波分解 谐波信号 虚假分量 自旋 脉动风 空域分解 稳态电流特征 瞬时无功功率 电能质量复合扰动 电能质量 电流物理分量法 电压闪变 电压波动 电力谐波分析 电力系统 特征谱 滤波器系数 混沌 混合扰动 波束形成器 模态混叠 模态 本征正交分解 时频分析 数值模拟 摆动 提取 扰动识别 微网 微动 推荐指数 3 3 2 2 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2008年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52
Hale Waihona Puke 2010年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52
小波分解与重构原理
小波分解与重构原理小波分解与重构是一种信号处理技术,它可以将信号分解成不同尺度和频率的成分,从而更好地理解和分析信号的特性。
在本文中,我们将介绍小波分解与重构的原理,以及它在信号处理领域的应用。
首先,让我们来看一下小波分解的原理。
小波分解是通过一组小波基函数对信号进行分解的过程。
这组小波基函数具有不同的尺度和频率特性,可以将信号分解成不同频率成分的系数。
在小波分解中,我们通常使用离散小波变换(DWT)来实现信号的分解。
DWT 是通过一系列的滤波器和下采样操作来实现信号的分解,具体过程是将信号通过低通滤波器和高通滤波器进行滤波,并对滤波后的信号进行下采样,最终得到近似系数和细节系数。
接下来,我们来谈谈小波重构的原理。
小波重构是将分解得到的近似系数和细节系数通过逆小波变换(IDWT)合成为原始信号的过程。
在小波重构中,我们需要使用逆小波变换来将近似系数和细节系数合成为原始信号。
逆小波变换的过程是通过一系列的滤波器和上采样操作来实现信号的合成,具体过程是将近似系数和细节系数通过上采样和滤波器进行滤波,并将滤波后的信号相加得到重构的信号。
小波分解与重构的原理虽然看起来比较复杂,但是它在信号处理领域有着广泛的应用。
首先,小波分解与重构可以用于信号的压缩和去噪。
通过保留重要的近似系数和细节系数,可以实现对信号的高效压缩;同时,通过去除不重要的近似系数和细节系数,可以实现对信号的去噪。
其次,小波分解与重构还可以用于信号的特征提取和模式识别。
通过分析不同尺度和频率的小波系数,可以提取信号的特征并进行模式识别。
此外,小波分解与重构还可以用于信号的分析和合成,例如音频信号的压缩和图像信号的处理等。
综上所述,小波分解与重构是一种重要的信号处理技术,它通过一组小波基函数对信号进行分解和重构,可以实现对信号的压缩、去噪、特征提取、模式识别、分析和合成等功能。
在实际应用中,我们可以根据具体的需求选择合适的小波基函数和分解层数,从而实现对不同类型信号的有效处理和分析。
小波分解与重构原理
小波分解与重构原理小波分解与重构是一种将信号分解为不同频率成分的方法,它是一种新兴的数学理论,近年来在信号处理、图像处理、压缩编码等领域得到广泛应用。
小波可以看作是一种基函数,可以用来表示任意一个非周期函数。
小波分解与重构原理便是利用小波基函数将信号进行分解和重构的过程。
首先,需要选择一个合适的小波基函数。
在小波函数中,常用的有Haar小波、Daubechies小波、Coiflet小波等,不同的小波函数适用于不同的信号特性。
接下来,通过小波基函数对原始信号进行分解。
分解的过程是逐级进行的,每一级都将信号分解为近似系数和细节系数两部分。
近似系数表示信号的低频成分,细节系数表示信号的高频成分。
通过迭代的方式,可以得到多个不同尺度的近似系数和细节系数。
分解后得到的近似系数和细节系数可以用于信号分析和处理。
近似系数表示信号的低频内容,可以用来恢复信号的平滑部分;细节系数表示信号的高频成分,可以用来提取信号的细节特征。
在重构过程中,通过逆变换操作将分解得到的近似系数和细节系数重构为原始信号。
重构的过程是逐级进行的,每一级都将近似系数和细节系数进行逆变换操作得到原始信号的一部分,并将其与上一级的逆变换结果相加得到更精确的重构结果。
小波分解与重构具有多尺度分析的特点,可以适应不同频率成分的信号处理需求。
它具有信号特征提取的能力,可以提取信号中的边缘、纹理等细节信息。
同时,小波变换还具有良好的时频局部性,可以很好地适应信号的时变特性。
小波分解与重构的应用十分广泛。
在图像处理中,可以利用小波分解与重构技术进行图像压缩、边缘提取、图像恢复等操作。
在语音信号处理中,可以提取语音的共振频率、噪声成分等信息。
此外,小波分解与重构还可以用于信号分析、数据压缩、图像处理、模式识别等领域。
总之,小波分解与重构是一种将信号分解为不同频率成分的方法,通过小波基函数的选择和分解重构过程,可以提取信号的不同尺度特征,具有良好的时频局部性和多尺度分析能力,广泛应用于各个领域。
不同小波函数分解
文档:不同小波函数分解一、引言小波变换是一种在信号处理、图像处理、数值分析等领域广泛应用的工具。
它具有多尺度、多方向性和自适应性等优点,可以对信号或数据进行多尺度的分析。
本文档将详细介绍不同类型的小波函数分解,包括一维小波分解、二维小波分解、多维小波分解、连续小波变换、离散小波变换、小波包变换、双小波变换、基于复数的小波变换、基于样条的小波变换和基于多小波的小波变换。
二、一维小波分解一维小波分解是将一维信号分解成不同尺度的小波系数的过程。
通过递归地将信号分解成更小的部分,可以得到信号在不同尺度上的表示。
一维小波分解在信号处理、图像压缩等领域有广泛应用。
三、二维小波分解二维小波分解是将二维信号(如图像)分解成不同尺度的小波系数的过程。
它将二维信号表示为一组一维信号的嵌套,可以得到图像在不同尺度上的表示。
二维小波分解在图像压缩、图像处理等领域有广泛应用。
四、多维小波分解多维小波分解是将多维信号分解成不同尺度的小波系数的过程。
它将多维信号表示为一组低维信号的嵌套,可以得到多维信号在不同尺度上的表示。
多维小波分解在多维数据分析和处理等领域有广泛应用。
五、连续小波变换连续小波变换是将时间连续变化的参数的小波应用到信号上,从而得到信号在不同时间和频率上的表示。
它具有时间和频率的连续性,可以提供更丰富的信息。
连续小波变换在信号处理、图像处理等领域有广泛应用。
六、离散小波变换离散小波变换是将时间离散变化的参数的小波应用到信号上,从而得到信号在不同尺度和位置上的表示。
它具有时间和频率的离散性,便于计算机实现。
离散小波变换在信号处理、图像处理等领域有广泛应用。
七、小波包变换小波包变换是在小波变换的基础上发展起来的一种新的变换方法。
它将信号分解成不同尺度的小波包,可以得到信号在不同尺度和方向上的表示。
小波包变换在信号处理、图像处理等领域有广泛应用。
八、双小波变换双小波变换是将两个不同的小波应用到信号上,从而得到信号在不同尺度和方向上的表示。
小波分解和小波变换
小波分解和小波变换小波分解和小波变换是一种信号解析的数学方法,可以将信号分解成多个不同的频率和幅度的成分,从而更好地了解信号的特性。
小波分解和小波变换的应用广泛,在信号处理、图像处理、数据分析和物理学等领域中都有重要的应用。
一、小波分解小波分解是指将信号分解成一组不同频率和幅度的分量,其中小波函数被用来作为分解的基函数。
这些小波函数可以有不同的特性,例如有限长度和平滑度等。
通常情况下,小波函数是由一个母小波函数递归生成得到的。
小波分解的基本步骤如下:1.选择一个小波基函数,并确定其尺度和位移参数。
2.将这个小波函数与信号进行卷积。
3.将卷积结果分为两部分,一部分是高频成分,另一部分是低频成分。
4.重复以上步骤,递归地对低频成分进行分解,直到无法再进行分解。
小波分解的结果是一个小波系数数组,其中每个小波系数表示了对应频率和振幅的成分的大小。
二、小波变换小波变换是指将信号在小波基函数下的分解。
它将信号分解成不同的频率和振幅成分的过程,可以用于信号去噪、数据压缩和特征提取等应用。
4.对低频成分进行下采样,得到一个新的序列。
三、小波分析的优点相对于傅里叶变换和小波变换,小波分析有一些明显的优点:1.小波分析可以适应各种信号类型,包括非平稳信号和非线性信号。
2.小波分析可以分析信号中的时空分布,而傅里叶变换只能分析信号中的频率分布。
3.小波分析可以将信号分解成有限的、宽带的频率组件,而傅里叶变换需要使用无限多的单色波组成信号。
4.小波分析可以快速地处理并行信号,因为它可以进行高效的多尺度分解。
小波分析在许多领域中都有广泛的应用,例如信号处理、图像处理、音频处理、数据压缩和特征提取等。
以下是一些常见的应用:1.信号去噪:小波分析可以有效地去除信号中的噪声和干扰。
2.数据压缩:小波分析可以将信号分解成有限的频率组件,从而能够进行高效的数据压缩。
3.图像处理:小波分析可以使用不同的小波基函数对图像进行分解,从而能够进行图像去噪、特征提取和边缘检测等处理。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
基金持股行为的小波分析一、 数据说明在此使用数据为2007-2009年基金十大重仓股(万科A 、浦发银行、中国石化、中信证券、歌华有线、中国联通、上海汽车、海螺水泥、北大荒、上海医药)的日交易数据和基金季度报告中的基金持股比例来进行检验。
数据来源为wind 。
根据HS300的走势,我们可以将市场分为3个阶段,2007年1月4日到2007年9月30日为上升期,2007年10月起到2009年1月9日为下降期,2009年1月后又为新一轮的上升期。
时间范围上刚好覆盖了中国股市经历的高峰与低谷,可以比较充分的反映在一个震荡市场周期内每只股票的波动变化情况。
图1:沪深300指数走势图(2007年1月-2009年12月)而在此期间,开放式基金数目日益增加,从2007年1季度的92只偏股型基金增加到2009年第4季度的226只,基金数量迅速扩张,这些基金的股票投资情况如表1所示。
从表1我们可以看到,股票占基金投资组合的比例日益增加,而基金的仓位也随着市场的走势有所变化,有些激进型的基金在市场上升期间持仓比例一度达到90%以上,而在市场下跌期间,基金仓位较低甚至不足40%,可见市场环境不同,基金仓位总体波动较大。
HS300走势图100020003000400050006000700007/1/407/4/407/7/407/10/408/1/408/4/408/7/408/10/409/1/409/4/409/7/409/10/4为了方便研究基金行为对市场波动性的影响,我们对十个样本按基金季报数据中的持股比例变化情况来划分其增减仓阶段,之后的检验也将都建立在所划分的阶段的基础之上。
根据市场上升和下降的不同阶段,对样本的波动性进行统计如表2:表2:基金增减仓阶段划分以及相关描述性统计二、检验步骤显然,仅使用标准差来描述波动率,存在很大局限性而很难将波动率的趋势刻画出来,同时掺杂异质信息(如噪声交易对波动率的影响以及异常事件对波动率影响等)。
利用小波分解技术,可以有效甄别和去除这些杂质信息,进而观察波动是如何产生的,基金行为对波动性如何影响。
进行小波分析前,我们先选择本次研究适合的小波基函数和分解层数。
在实际应用中,时间序列信号涵盖信息的大量性以及所研究问题的侧重的差异性,使相似性对小波基函数的选择判断作用并不明显。
在综合考虑各小波函数紧支性、支撑宽度、对称性、正交性、消失矩等特性(见表3),我们选用db5小波。
由于小波分解后的前三层是周期为1-8天的分量,包含了序列中的随机因素和不规则因素,而我们本身关注的也正是相关时间序列短期的波动性特征,因而,在此使用db5小波进行3层分解。
由于基金持股比重对波动率的影响在不同特质公司表现不同的特征,结合研究样本,我们将以上10只股票中选择权重且强周期类股票,抗周期防御性股票以及小市值股票,即选择代表性的万科A、北大荒和歌华有线依次进行解析:(1)强周期且权重股——万科A为应用小波分析对股价波动率进行分解,在此我们首先选择强周期且权重股——万科A (以下简称万科)。
其小波分解如图 2所示,其中s为原始信号,a3代表小波3层分解后的趋势部分,d1,d2,d3小波分解高频部分的第1层,第2层和第3层。
1Haar,Mexh,morlet,meyer,dbN,symN均为常用小波基函数,其函数表达式,图形可参考小波分析介绍的相关书籍,在此由于篇幅限制,不再过多介绍。
图2:万科A波动率的小波分解从万科小波分解的趋势部分看,万科股价波动总体上较为稳定,个别区间的波动较为明显,如2008年第2季度,波动率明显大幅增加,其股价也由1季度末的25.6元跌至2季度末的9.01元。
最大的一次下跌发生在2008年6月16日,收盘价由16.5元跌至10.6元,图中表现为一个较大的波谷。
观测细节部分,d1和d2在2008年第2季度区间也都出现了较为密集的信号,尤其是6月16日左右的位置。
这意味着波动率增加的同时,也伴随了大量的噪声交易。
此正对应着基金减仓的行为,并且适逢市场开始逐步下跌。
由此可知,市场下跌时,基金的减仓行为不仅造成了股票更大的波动,并且带来更多的噪声交易。
另一个大幅波动的减仓阶段出现在2007年第2季度。
这一区间对应的市场处于一个上升期,但央行在第2季度连续两次加息以及一系列宏观调控措施都使房地产类股票开始走低。
因此,从策略角度看,基金此时的减仓采取的是负反馈策略,促使股票回归其合理的估值区间。
同时,也因为这些政策因素使得这支本来隶属于周期性股票的股价在一定程度上和市场走向产生了不一致。
比较这两次减仓,2008年的减仓造成的波动更大。
但事实上第一次的减持幅度更大: 2007年的一次从35986万股减持到34.99万股,2008年的一次从195879万股减持到193340万股。
之所以发生这种情况,我们考虑主要是受到了市场的影响,市场的下跌在一定程度上引发了羊群效应。
具体来说,基金第二次是在市场下降的时候减仓,这一操作行为对于其他中小投资者来说都是一个消极信号,引发他们过度反应,纷纷跟着减少头寸,从而使股票波动率大幅增加。
并且如果市场继续下跌,则进一步增加股价波动率。
因为当噪声交易者对市场前景感到悲观,价格波动幅度会上升,即噪声交易者的情绪变化会对市场波动率造成影响。
而加仓情况与之相反,观测2009年第1季度区间,可以发现基金的加仓期间股价的波动率比较小,并且此区间的噪声交易也少。
理论上来说,大笔交易的增加也应该引起波动率升高才是。
结合市场,我们发现此时市场处于从下降转为上升的盘整阶段,多空出现分歧,对股票真实价值的评估不一;不一样的价值评估导致了不一样的价格期望,看空的投资者纷纷要求调整自己手中的股票头寸,即结束持有操作而进行买卖操作。
但是,与此同时机构进行了大幅加仓的操作,逢低吸纳,稳定了价格,亦稳定了市场投资者对股价的预期,所以此阶段的股价波动率反而降低了。
至于噪声交易者,仍然表现出受情绪的影响,此刻他们对市场比较乐观,价格波动幅度下降(。
对于加仓阶段的分析说明了两点:第一,机构投资者有自己的价值评估模型,不容易受市场情绪的影响,在市场出现多空分歧的阶段具有稳定市场价格的作用;第二,机构投资者进行加仓操作时没有操纵股票价格,而是实施逢低吸纳的策略,否则此阶段的股价波动不应该是下降,而应该是大幅上升。
综合整个样本区间,机构加仓阶段的噪声信号最少,说明机构在股价盘整阶段加仓确实有促使不知情交易者快速消化新信息,提高新信息传播效率,使股票价格快速回归真实价值的作用。
另一方面,机构平稳持股阶段的噪声信号较少,说明机构持有重仓股票亦有稳定股价作用,与相关理论相符。
总之,机构在股价盘整阶段加仓与机构重仓持有股票均起着稳定股价,减小股市波动的作用,只是相比较而言,前者的作用更为显著。
(2)抗周期防御性股——北大荒由于房地产属于周期性行业,万科股价波动受到经济周期的影响较大;相较而言,属于农业板块的北大荒则是典型的抗周期防御型股票。
从北大荒的趋势图上看,股价大幅度波动产生于2008年第4季度,这一阶段基金开始对其采取减仓操作,即基金持股数量从9609万股逐步减持到2009年第2季度的1945万股(这和基金对万科的加仓操作形成对比)。
到了减仓后期,股票的波动率就相对平稳,几乎不受继续减仓的影响。
这是因为市场已经转入上升期,基金的投资组合调整基本完成,不再出现大幅抛售,股价逐渐下降然后稳定在11-13元附近。
同时,这一区间噪声交易也主要集中在前期,到了后期投资者都能比较理性的进行操作,因而噪声交易相对较少,减仓的利空信息基本消化而股价趋于稳定。
图3:北大荒波动率的小波分解与其他周期性股票相比,北大荒股价波动整体较小,但信号密集的区间比较多。
考虑到农业股本身也容易受季节气候等外在因素的影响,中小投资者仍然会受到各种信息的影响进行频繁操作,进而产生了较多的噪声交易,理论上容易增加波动。
但现实结果表明,机构对这只股票的操作占主导,其负反馈策略已经逐渐减少了波动率。
关于减仓阶段的影响,其他样本基本上也都显示出基金减仓会造成相应阶段的股票波动率增加以及噪声信号的增加的特征,并且市场下跌期的波动也更为显著(3)中小市值股——歌华有线至于加仓阶段的影响,样本中具有显著不同特点的股票为歌华有线。
这只股票市值较小,因而基金操作对股价波动的影响也更为明显。
对应图4,2008年3季度到2009年1季度为基金增仓阶段,这一期间市场逐渐走出低谷,进入上升通道。
从趋势部分a3可以看出,股票的波动也明显增加,但是其细节部分显示此阶段的噪声交易却比较少。
图4:歌华有线波动率的小波分解2此处波动率为小波分析趋势部分a3对应区间的标准差数值以及和前一阶段比较后的描述性结果。
3此处波动率为小波分析高频部分d1+d2观测到的信号密集程度的描述性结果。
4根据表2的划分阶段,基金在市场下降期没有对上海汽车增仓的操作。
考虑到歌华有线市值较小,基金买卖操作对股价容易造成较大冲击,尤其是基金的大幅增仓初期,股价波动率较大,但随着机构投资者所持筹码不断增加,股价波动随之不断减小。
同时我们观测到,此次基金加仓期也较长,到了后期股价波动减小的同时噪音交易也明显减少,即投资者对股票估值到位,使得股价基本平稳。
另外,不同于万科等价值型股票,歌华有线是中小盘成长性股,对其成长性判断投资者存在分歧较大,因而在加仓阶段,由于不同投资者信念和分歧,导致其股价波动性也大幅增加。
在具体分析三个不同特性样本基础上,我们应用小波分解方法对10个股票的进行归纳(见表4)。
从所有研究样本检验结果看,对于权重股而言,基金的加仓和持有行为都使得波动率减小,而且此期间中小投资者也都比较理性,产生的噪声交易也比较少;而同样的操作却使得反周期股票的噪声交易增加,中小市值股票的波动率增加。
但是基金一旦减仓,市场情绪就比较复杂和悲观,股票的波动率和噪声交易都明显增加,中小投资者产生一定的“非理性”投资行为。
尤其是市场下跌期间,基金仓位减少后,中小投资者减仓对股价波动影响的权重上升。
所以,市场下跌期间的股票波动率也更大。
表4:小波分解总结总结上文小波解析结果,发现不同类型股票波动率影响略有差别。
万科这类权重股受基金影响较大,加仓阶段基本能够平抑波动,并且噪声交易也少,但减仓阶段对市场情绪干扰较大,波动率和噪声交易都明显增加,表现出一定的羊群效应。
而北大荒这类股票,虽然抗周期,但基金减仓时也同样波动率增加,不同的是,这只股票在基金加仓期噪声也会增加,主要是这是由于农业股易受天气因素的影响,因而全年噪声交易频繁。
另外对于歌华有线这类成长型中小盘股,首先市值小易受大的交易量影响,其次投资者对其成长性判断的差异导致估值偏差,因而无论基金加仓或减仓,波动率都会增加。
