七年级数学上册4.1 几何图形课时提升作业 湘教版
湘教版七年级上册数学4.1 几何图形同步练习

湘教版七年级上册数学4一、选择题1.将一个正方体的外表沿某些棱剪开,展成一个平面图形,至少要剪开〔〕条棱.A. 3B. 5C. 7D. 9【答案】C2.在3×5的棋盘上,一枚棋子每次可以沿水平或许垂直方向移动一小格,但不可以沿任何斜对角线移动.从某些待定的格子末尾,要求棋子经过全部的小正方格恰恰一次,但不用回到原来动身的小方格上.在这15个小方格中,有( )个可以是这枚棋子动身的小方格.A. 6B. 8C. 9D. 10【答案】B3.如图是一个直三棱柱,那么它的平面展开图中,错误的选项是〔〕A. B. C. D.【答案】D4.以下各图中,可以是一个正方体的平面展开图的是〔〕A. B. C. D.【答案】C5.在市委、市府的指导下,全市人民齐心协力,将我市成功地创立为〝全国文明城市〞,为此小红特制了一个正方体玩具,其展开图如下图,原正方体中与〝全〞字所在的面相对的字应是〔〕A. 文B. 明C. 城D. 市【答案】B6. 如图,矩形ABCD,AB=a,BC=b,a>b;以AB边为轴将矩形绕其旋转一周构成圆柱体甲,再以BC边为轴将矩形绕其旋转一周构成圆柱体乙;记两个圆柱体的体积区分为V甲、V乙,正面积区分为S甲、S乙,那么以下式子正确的选项是〔〕A. V甲>V乙S甲=S乙B. V甲<V乙S甲=S乙C. V甲=V乙S甲=S乙D. V甲>V乙S甲<S乙【答案】B7.以下图形经过折叠不能围成棱柱的是〔〕A. B. C. D.【答案】B8.如下图的平面图形能折叠成的长方体是〔〕A. B. C. D.【答案】D9.将一个圆联系成四个大小相反的扇形,那么每个扇形的圆心角是〔〕度.A.45B.60C.90D.120【答案】C10.以下图形中,可以折叠成一个正方体的是〔〕A. B. C. D.【答案】B11.如图,是一个正方体的外表展开图,那么原正方体中与〝建〞字所在的面相对的面上标的字是〔〕A. 美B. 丽C. 和D. 县【答案】D二、填空题12.硬币在桌面上快速地转动时,看上去象球,这说明了________ .【答案】面动成体13.以下物体出现的是哪一种几何图形?大头针的尖端是________,桌子的边缘是________,桌面是________ .【答案】点;线;面14.从运动的观念看,点动成________,线动成________,面动成________.【答案】线;面;体15.如图1是边长为1的六个小正方形组成的图形,它可以围成图2的正方体,那么图1中小正方形顶点A,B围成的正方体上的距离是________ .【答案】116.假设按图中虚线对折可以做成一个上底面为无盖的盒子,那么该盒子的下底面的字母是________.【答案】C17.①一段烟囱〔无烟囱帽〕;②一段圆钢;③铅锤;④烟囱帽.①②都呈________的外形;③④都呈________的外形.【答案】圆柱;圆锥18.将一个边长为10cm正方形,沿粗黑实线剪下4个边长为________ cm的小正方形,拼成一个大正方形作为直四棱柱的一个底面;余下局部按虚线折叠成一个无盖直四棱柱;最后把两局部拼在一同,组成一个完整的直四棱柱,它的外表积等于原正方形的面积.【答案】2.519. 将一个圆联系成三个扇形,使它们圆心角度数比为2:3:4,那么这3个圆心角中度数最大的为 ________.【答案】160°20.如图是一个正方体的外表展开图,恢复成正方体后,标注了字母A的面是正方体的正面,假定正方体的左面与左面所标注代数式的值相等,那么x的值是________.【答案】1三、解答题21.将以下几何体与它的称号衔接起来.【答案】解:如下图:22.如图是一个正方体的展开图,标注了字母A的面是正方体的正面,假设正方体的左面与左面所标注式子的值相等,求x的值.【答案】解:依据题意得,x﹣3=3x﹣2,解得:x=﹣23.如图,长方形的长和宽区分是7cm和3cm,区分绕着它的长和宽所在的直线旋转一周,回答以下效果:〔1〕如图〔1〕,绕着它的宽所在的直线旋转一周,所失掉的是什么样的几何体?失掉的几何体的体积是多少?〔π取3.14〕〔2〕如图〔2〕,绕着它的长所在的直线旋转一周,所失掉的是什么样的几何体?失掉的几何体的体积是多少?〔π取3.14〕【答案】解:〔1〕失掉的是底面半径是7cm,高是3cm的圆柱,V=3.14×72×3=461.58〔cm3〕,答:失掉的几何体的体积是461.58cm3;〔2〕失掉的是底面半径是3cm,高是7cm的圆柱,V=3.14×32×7=197.82〔cm3〕,答:失掉的几何体的体积是197.82cm3.24.如下图,假定将相似于a、b、c、d四个图的图形称做平面图,那么其顶点数、边数与区域数之间存在某种关系.观察图b和表中对应的数值,探求计数的方法并作答.〔1〕数一数每个图中各有多少个顶点、多少条边,这些边围出多少个区域并填表:〔2〕依据表中数值,写出平面图的顶点数、边数、区域数之间的一种关系;〔3〕假设一个平面图有20个顶点和11个区域,那么应用〔2〕中得出的关系可知这个平面图有________条边.【答案】〔1〕解:〔2〕解:观察表中数据可得;4+3﹣6=1,7+3﹣9=1,8+5﹣12=1,10+6﹣15=1 ∴S+N﹣M=1;〔或顶点数+区域数一边数=1〕〔3〕30。
湘教版-数学-七年级上册-4.1几何图形 练习课件

同一条线段
4. 一个锐角与一个钝角的和( D )
A.一定是平角
B 一定是直角
C 一定是钝角
D 可能是钝角、平角或大于平角
5. 根据直线、射线、线段各自的性质,下面能相交的是
( ) CD
C D
C
C D
D
A
B
(A)
AB (B)
AB (C)
A
B
(D)
6. 同一平面内有四点,过这四点作直线,则直线的条数是( )
③大于直角的角是钝角;
④如图,∠ABD也可用∠B
表示.
A、1个 B、2个 C、3个 D、4个 9 .已知∠A=40°,则∠A的补角等于( ) A、50° B、90° C、140° D. 180°
二.耐心填一填
10. 用一个钉子把一根细木条钉在墙上,木条就可能绕着钉
子
,原因是
当用两个钉子把木条钉在
墙上时,木条就被固定住其依据是
1. 下列几何体中,是圆柱的是( D )
2. 两个锐角的和( D )
A.一定是锐角
B 一定是直角
C 一定是钝角
D 可能是钝角、直角或锐角
3. 下面的语句中不正确的是( D )
A.直线OA和直线AB是同一条直线 B.射线OA和射线OB是
同一条射线
C.射线OA和射线AB是同一条射线 D.线段AB和线段BA是
数.
如图,已知∠1∶∠3∶∠4=1∶2∶4,∠2=80°,求∠1、
∠3、∠4的度数.
A
B
12
4O 3
C
D
已知线段AB被分成2:3:4三部分,且第一部分 与第三部分的中点的距离为4.8cm,求AB的 长。
A
D
【能力培优】七年级数学上册 4.1 几何图形、4.2 线段、射线、直线 (新版)湘教版(1)

第4章图形的熟悉4.1 几何图形4.2 线段、射线、直线专题一线段中点的应用1.如图,点B在线段AC上,M,N别离是AB,AC的中点.试说明:MN.2.如图,点A,B,C是数轴上三点,其中点C是线段AB的中点,点O表示的是原点,线段AC比线段OA 长1个单位,点B表示的有理数是17,求点C表示的有理数.3.已知,点C是线段AB上的一点,点M是线段AC的中点,点N是线段BC的中点,(1)若是AB=10 cm,那么MN等于多少?(2)若是AC∶CB=3∶2,NB=3.5 cm,那么AB等于多少?(要求先依照题意正确画出草图,再列式计算,要有解题进程)专题二探讨题4.在桌面上放了一个正方体的盒子,一只蚂蚁在极点A处,它要尽快爬到极点B处吃食物,请你帮忙蚂蚁设计一条最短的爬行线路吗.5.先阅读下面材料,然后解答问题:材料一:如图(1),直线l上有A1、A2两个点,假设在直线l上要确信一点P,且使点P到点A1、A2的距离之和最小,很明显点P的位置可取在A1和A2之间的任何地址,现在距离之和为A1到A2的距离.如图(2),直线l上依次有A1、A2、A3三个点,假设在直线l上要确信一点P,且使点P到点A1、A2、A3的距离之和最小,不难判定,点P的位置应取在点A2处,现在距离之和为A1到A3的距离.(想一想,这是什么缘故)不难明白,若是直线l上依次有A1、A2、A3、A4四个点,一样要确信一点P,使它到各点的距离之和最小,那么点P应取在点A2和A3之间的任何地址;若是直线l上依次有A1、A2、A3、A4、A5五个点,那么相应点P的位置应取在点A3的位置.材料二:数轴上任意两点a、b之间的距离能够表示为|a﹣b|.问题一:假设已知直线l上依次有点A1,A2,A3,…,A25共25个点,要确信一点P,使它到已知各点的距离之和最小,那么点P的位置应取在;假设已知直线l上依次有点A1,A2,A3,…,A50共50个点,要确信一点P,使它到已知各点的距离之和最小,那么点P的位置应取在.问题二:现要求|x+1|+|x|+|x﹣1|+|x﹣2|+|x﹣3|+…+|x﹣97|的最小值,依照问题一的解答思路,可知当x值为时,上式有最小值为.6.通过阅读所得的启发,回答下列问题(阅读中的结论能够直接利用).阅读:在直线上有n个不同的点,那么此图中共有多少条线段?通过画图尝试,咱们发觉了如下的规律:图形直线上点的个数共有线段条数两者关系211=0+1333=0+1+2466=0+1+2+351010=0+1+2+3+4…………n2)1(-nn2)1(-nn=0+1+2+3+…+(n﹣1)问题:(1)某学校七年级共有8个班级进行辩论竞赛,规定采纳单循环赛制(每两个班之间赛一场),请问该校七年级的辩论赛共需进行多少场辩论赛?(2)来回上海与北京之间的某趟火车,共有15个车站(包括上海与北京),那么共需要预备多少种不同的车票?4.1 几何图形【知识要点】1.长方体、正方体、圆柱、球、点、线段、三角形、四边形等,它们都是从各式各样的物体外形中抽象出来的图形,这种图形统称为几何图形.2.有些几何图形图形的各部份不都在同一平面内,它们是立体图形.3.从不同方向看物体,往往会取得不同形状的平面图形.【温馨提示】1.在平面内画立体图形时,看得见的画实线,看不见的画虚线.2.画长方体、正方体时,有些长方形、正方形要画成平行四边形;画圆柱时,底面圆要画成椭圆.3.把握常见立体图形的几何图形,能够提高解题速度.4.2 线段、射线、直线【知识要点】1.线段有两个端点,线段向一端无穷延长形成了射线,射线有一个端点;线段向两头无穷延长形成了直线,直线没有端点.2.点与直线有两种位置:点在直线上,点在直线外.3.当两条不同的直线只有一个公共点时,咱们说这两条直线相交,那个公共点叫做它们的交点.4.过两点有且只有一条直线.简单地说:两点确信一条直线.5.比较两条线段的长短,能够用刻度尺的方法,也能够把其中一条线段移到另一条上作比较.6.两点之间的所有连线中,线段最短.简单地说:两点之间线段最短.连接两点的线段的长度,叫做这两点间的距离.7.假设B点在线段AC上,且把线段AC分成相等的两条线段AB与BC,这时点B叫做线段AC的中点.【温馨提示】1.表示线段的两个大写字母必需是表示端点的大写字母,表示射线时,表示端点的大写字母要写在前面.2.直线的性质“两点确信一条直线”在实际生活中的应用是确信“直”;线段的性质“两点之间线段最短”在实际生活中的应用是确信最短距离.要注意这二者的区别.【方式技术】1.熟记线段、射线、直线的表示方式、端点个数、性质,有助于提高解题的准确率和速度.2.正确运用“线段的中点”这一条件,由其中的一半乘以2取得“全数”.参考答案1.解:因为M,N别离是AB,AC的中点,因此MA=MB,NA=NC.又因为MN=AN﹣AM,因此MN=NC﹣BM.而NC=NB+BC,BM=MN+NB,因此MN=NB+BC﹣(MN+NB),因此2MN=BC,因此MN.2.解:因为点C是线段AB的中点,因此AC=BC.设OA为x,那么AC=BC=x+1,因此x+x+1+x+1=17,解得x=5,因此x+1=6.因此C表示的数为5+6=11.3.解:如下图,(1)MN=CM+CN;(2)因为NB=3.5 cm,因此BC=2NB=7 cm.因此AB.4.解:蚂蚁可由:点A—点EF的中点(或CE的中点)—B点.5.解:问题一:点A13处;点A25和A26之间的任何地址;问题二:因为|x+1|+|x|+|x﹣1|+|x﹣2|+|x﹣3|+…+|x﹣97|=|x﹣(﹣1)|+|x﹣0|+|x﹣1|+|x﹣2|+ |x﹣3|+…+|x﹣97|,此题相当于数轴上x到点﹣1,0,1,…,97的距离和.因此当x=48时,有最小值为2450.故答案为:48,2450.6.解:(1)场;(2)15个车站看做15,因为车票有起点和终点站之分,因此车票要2×105=210种.。
湘教版-数学-七年级上册-4.1几何图形 作业课件

2
3
且BC=2cm,求BD的长度.
AB C
D
角
1. 角是由 所组成的图形,其中
叫做角的顶点,
叫做角的边.
2. 如图所示:图中共有 个角,它
们分别是
.
A
B
D
C
3. 8.15°= 36°36′=
° ′; °.
4. 8点30时,钟面上时针与分针之
间的夹角是
.
5. 如图:O为直线AB上的一点,OE
平分∠BOC,OF平分∠AOC,则
① 点P在线段AB上
② 点P在线段AB外
③ 点P在直线AB上
④ 点P在在直线AB外
A1
B2 C3 D4
12. 延长AB到C,使得BC=4AB, M为AB中点,N为BC中点,若MN 为5cm,则BN的长度为 ( )
A 3cm
B 4cm
C 5cm D 6cm
13. 按照题中的要求画图或计算:
(1)点M在直线上,点N在直线外, 连接MN并延长.
∠AOF+∠BOE=
.
C
E
F
A
O
B
6. 如图:OD平分∠BOC,则:
① ∠BOD=
;
A
C
② ∠AOD= + ;
D
③ ∠COD= - ; O
B
④ ∠BOC=∠AOD- + .
7. 一个角的补角比它的余角大 度; ∠α的余角的补角为 .
8. 若∠1+∠2=180°,∠2+∠3=
180°,那么∠1=∠3,理由
4. 线段AB上有两点C、D,那么图 中共有 条线段;线段AB上有三 点C、D、E, 那么图中共有 条 线段;线段AB上有四点C、D、E、 F, 那么图中共有 条线段;以此 类推,…,若线段AB上有n个点, 探究图中共有 条线段.
七年级数学上册 4.1 几何图形课时作业 (新版)湘教版
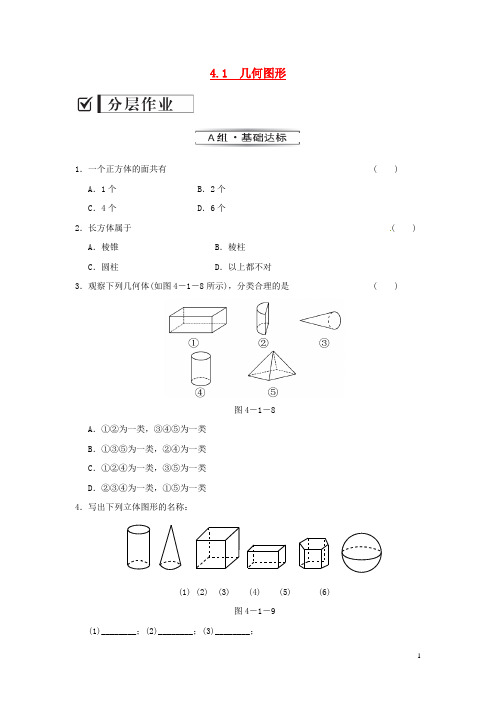
4.1 几何图形1.一个正方体的面共有( ) A.1个B.2个C.4个D.6个2.长方体属于( ) A.棱锥B.棱柱C.圆柱D.以上都不对3.观察下列几何体(如图4-1-8所示),分类合理的是( )图4-1-8A.①②为一类,③④⑤为一类B.①③⑤为一类,②④为一类C.①②④为一类,③⑤为一类D.②③④为一类,①⑤为一类4.写出下列立体图形的名称:(1) (2) (3) (4) (5) (6)图4-1-9(1)________;(2)________;(3)________;(4)________;(5)________;(6)________.5.图4-1-10中哪些图形是立体的,哪些是平面的?图4-1-106.观察图4-1-11,任意写出5种你所熟悉的几何图形的名称.图4-1-117.分别指出图4-1-12中的物体是由哪些立体图形组成的.图4-1-128.分别指出哪种立体图形的表面能展开成如图4-1-13所示的平面图形,请将它们写出来.图4-1-13(1)________;(2)________;(3)________.9.如图4-1-14所示,桌上放着一个茶壶,4名同学从各自的方向观察,请指出实物图右边的四幅图,从左至右分别是由哪个同学看到的?图4-1-14答案解析1.D 【解析】正方体的上、下、左、右、前、后各一个面,共6个面,故选D.2.B 【解析】长方体是四棱柱.3.C【解析】根据柱体、锥体的概念进行分类,①②④是柱体,③⑤是锥体.4.(1)圆柱(2)圆锥(3)正方体(4)长方体(5)六棱柱(6)球5.解析:平面图形的各个部分都在同一平面内,每条边都能看到,用实线表示;立体图形的各部分不都在同一平面内,有一些棱被正面挡住了,所以用虚线表示.解:立体图形有:①④⑤⑥⑦;平面图形有:②③.6.解:答案不唯一,如长方形、正方形、长方体、正方体、球、棱柱、棱锥等7.解:(1)正方体、圆柱、圆锥(2)圆柱、棱柱(3)棱柱、球8.(1)五棱柱(2)圆锥(3)长方体9.略。
湘教版数学七年级上册4.1几何图形、4.2线段、射线、直线(含答案)

初中数学试卷第4章图形的认识4.1 几何图形4.2 线段、射线、直线专题一线段中点的应用1BC.1.如图,点B在线段AC上,M,N分别是AB,AC的中点.试说明:MN=22.如图,点A,B,C是数轴上三点,其中点C是线段AB的中点,点O表示的是原点,线段AC比线段OA长1个单位,点B表示的有理数是17,求点C表示的有理数.3.已知,点C是线段AB上的一点,点M是线段AC的中点,点N是线段BC的中点,(1)如果AB=10 cm,那么MN等于多少?(2)如果AC∶CB=3∶2,NB=3.5 cm,那么AB等于多少?(要求先根据题意正确画出草图,再列式计算,要有解题过程)专题二探究题4.在桌面上放了一个正方体的盒子,一只蚂蚁在顶点A处,它要尽快爬到顶点B处吃食物,请你帮助蚂蚁设计一条最短的爬行路线吗.5.先阅读下面材料,然后解答问题:材料一:如图(1),直线l上有A1、A2两个点,若在直线l上要确定一点P,且使点P到点A1、A2的距离之和最小,很明显点P的位置可取在A1和A2之间的任何地方,此时距离之和为A1到A2的距离.如图(2),直线l上依次有A1、A2、A3三个点,若在直线l上要确定一点P,且使点P到点A1、A2、A3的距离之和最小,不难判断,点P的位置应取在点A2处,此时距离之和为A1到A3的距离.(想一想,这是为什么)不难知道,如果直线l上依次有A1、A2、A3、A4四个点,同样要确定一点P,使它到各点的距离之和最小,则点P应取在点A2和A3之间的任何地方;如果直线l上依次有A1、A2、A3、A4、A5五个点,则相应点P的位置应取在点A3的位置.材料二:数轴上任意两点a、b之间的距离可以表示为|a﹣b|.问题一:若已知直线l上依次有点A1,A2,A3,…,A25共25个点,要确定一点P,使它到已知各点的距离之和最小,则点P的位置应取在;若已知直线l上依次有点A1,A2,A3,…,A50共50个点,要确定一点P,使它到已知各点的距离之和最小,则点P的位置应取在.问题二:现要求|x+1|+|x|+|x﹣1|+|x﹣2|+|x﹣3|+…+|x﹣97|的最小值,根据问题一的解答思路,可知当x值为时,上式有最小值为.6.通过阅读所得的启示,回答问题(阅读中的结论可以直接使用).阅读:在直线上有n个不同的点,则此图中共有多少条线段?通过画图尝试,我们发现了如下的规律:图形直线上点的个数共有线段条数两者关系2 1 1=0+13 3 3=0+1+24 6 6=0+1+2+35 10 10=0+1+2+3+4 …………n2)1(-nn2)1(-nn=0+1+2+3+…+(n﹣1)问题:(1)某学校七年级共有8个班级进行辩论比赛,规定采用单循环赛制(每两个班之间赛一场),请问该校七年级的辩论赛共需进行多少场辩论赛?(2)往返上海与北京之间的某趟火车,共有15个车站(包括上海与北京),则共需要准备多少种不同的车票?4.1 几何图形【知识要点】1.长方体、正方体、圆柱、球、点、线段、三角形、四边形等,它们都是从各式各样的物体外形中抽象出来的图形,这种图形统称为几何图形.2.有些几何图形图形的各部分不都在同一平面内,它们是立体图形.3.从不同方向看物体,往往会得到不同形状的平面图形.【温馨提示】1.在平面内画立体图形时,看得见的画实线,看不见的画虚线.2.画长方体、正方体时,有些长方形、正方形要画成平行四边形;画圆柱时,底面圆要画成椭圆.3.掌握常见立体图形的几何图形,可以提高解题速度.4.2 线段、射线、直线【知识要点】1.线段有两个端点,线段向一端无限延长形成了射线,射线有一个端点;线段向两端无限延长形成了直线,直线没有端点.2.点与直线有两种位置:点在直线上,点在直线外.3.当两条不同的直线只有一个公共点时,我们说这两条直线相交,这个公共点叫做它们的交点.4.过两点有且只有一条直线.简单地说:两点确定一条直线.5.比较两条线段的长短,可以用刻度尺的办法,也可以把其中一条线段移到另一条上作比较.6.两点之间的所有连线中,线段最短.简单地说:两点之间线段最短.连接两点的线段的长度,叫做这两点间的距离.7.若B点在线段AC上,且把线段AC分成相等的两条线段AB与BC,这时点B叫做线段AC的中点.【温馨提示】1.表示线段的两个大写字母必须是表示端点的大写字母,表示射线时,表示端点的大写字母要写在前面.2.直线的性质“两点确定一条直线”在实际生活中的应用是确定“直”;线段的性质“两点之间线段最短”在实际生活中的应用是确定最短距离.要注意这两者的区别.【方法技巧】1.熟记线段、射线、直线的表示方法、端点个数、性质,有助于提高解题的准确率和速度.2.半乘以2得到“全部”.参考答案1.解:因为M,N分别是AB,AC的中点,所以MA=MB,NA=NC.又因为MN=AN﹣AM,所以MN=NC﹣BM.而NC=NB+BC,BM=MN+NB,所以MN=NB+BC﹣(MN+NB),所以2MN=BC,所以MN.2.解:因为点C是线段AB的中点,所以AC=BC.设OA为x,则AC=BC=x+1,所以x+x+1+x+1=17,解得x=5,所以x+1=6.所以C表示的数为5+6=11.3.解:如图所示,(1)MN =CM +CN =BC AC 2121+=AB 21=5 cm ; (2)因为NB =3.5 cm ,所以BC =2NB =7 cm . 所以AB =527÷=17.5 cm .4.解:蚂蚁可由:点A —点EF 的中点(或CE 的中点)—B 点. 5.解:问题一:点A 13处; 点A 25和A 26之间的任何地方;问题二:因为|x +1|+|x |+|x ﹣1|+|x ﹣2|+|x ﹣3|+…+|x ﹣97|=|x ﹣(﹣1)|+|x ﹣0|+|x ﹣1|+|x ﹣2|+|x ﹣3|+…+|x ﹣97|,此题相当于数轴上x 到点﹣1,0,1,…,97的距离和. 所以当x =48时,有最小值为2450. 故答案为:48,2450.6.解:(1)把每一个班级看作一个点,则2)18(8-⨯=28场; (2)15个车站看作15个点,线段条数为2)115(15-⨯=105,因为车票有起点和终点站之分,所以车票要2×105=210种.。
湘教版数学七年级上册4.1几何图形、4.2线段、射线、直线(含答案).docx
初中数学试卷 鼎尚图文**整理制作第4章 图形的认识4.1 几何图形4.2 线段、射线、直线专题一 线段中点的应用1. 如图,点B 在线段AC 上,M ,N 分别是AB ,AC 的中点.试说明:MN =21BC .2.如图,点A ,B ,C 是数轴上三点,其中点C是线段AB 的中点,点O 表示的是原点,线段AC 比线段OA 长1个单位,点B 表示的有理数是17,求点C 表示的有理数.3. 已知,点C 是线段AB 上的一点,点M 是线段AC 的中点,点N 是线段BC 的中点,(1)如果AB =10 cm ,那么MN 等于多少?(2)如果AC ∶CB =3∶2,NB =3.5 cm ,那么AB 等于多少?(要求先根据题意正确画出草图,再列式计算,要有解题过程)专题二探究题4.在桌面上放了一个正方体的盒子,一只蚂蚁在顶点A处,它要尽快爬到顶点B处吃食物,请你帮助蚂蚁设计一条最短的爬行路线吗.5.先阅读下面材料,然后解答问题:材料一:如图(1),直线l上有A1、A2两个点,若在直线l上要确定一点P,且使点P到点A1、A2的距离之和最小,很明显点P的位置可取在A1和A2之间的任何地方,此时距离之和为A1到A2的距离.如图(2),直线l上依次有A1、A2、A3三个点,若在直线l上要确定一点P,且使点P到点A1、A2、A3的距离之和最小,不难判断,点P的位置应取在点A2处,此时距离之和为A1到A3的距离.(想一想,这是为什么)不难知道,如果直线l上依次有A1、A2、A3、A4四个点,同样要确定一点P,使它到各点的距离之和最小,则点P应取在点A2和A3之间的任何地方;如果直线l上依次有A1、A2、A3、A4、A5五个点,则相应点P的位置应取在点A3的位置.材料二:数轴上任意两点a、b之间的距离可以表示为|a﹣b|.问题一:若已知直线l上依次有点A1,A2,A3,…,A25共25个点,要确定一点P,使它到已知各点的距离之和最小,则点P的位置应取在;若已知直线l上依次有点A1,A2,A3,…,A50共50个点,要确定一点P,使它到已知各点的距离之和最小,则点P的位置应取在.问题二:现要求|x+1|+|x|+|x﹣1|+|x﹣2|+|x﹣3|+…+|x﹣97|的最小值,根据问题一的解答思路,可知当x值为时,上式有最小值为.6.通过阅读所得的启示,回答问题(阅读中的结论可以直接使用).阅读:在直线上有n个不同的点,则此图中共有多少条线段?通过画图尝试,我们发现了如下的规律:图形直线上点的个数共有线段条数两者关系2 1 1=0+13 3 3=0+1+24 6 6=0+1+2+35 10 10=0+1+2+3+4…………n2)1(-nn2)1(-nn=0+1+2+3+…+(n﹣1)问题:(1)某学校七年级共有8个班级进行辩论比赛,规定采用单循环赛制(每两个班之间赛一场),请问该校七年级的辩论赛共需进行多少场辩论赛?(2)往返上海与北京之间的某趟火车,共有15个车站(包括上海与北京),则共需要准备多少种不同的车票?4.1 几何图形【知识要点】1.长方体、正方体、圆柱、球、点、线段、三角形、四边形等,它们都是从各式各样的物体外形中抽象出来的图形,这种图形统称为几何图形.2.有些几何图形图形的各部分不都在同一平面内,它们是立体图形.3.从不同方向看物体,往往会得到不同形状的平面图形.【温馨提示】1.在平面内画立体图形时,看得见的画实线,看不见的画虚线.2.画长方体、正方体时,有些长方形、正方形要画成平行四边形;画圆柱时,底面圆要画成椭圆.3.掌握常见立体图形的几何图形,可以提高解题速度.4.2 线段、射线、直线【知识要点】1.线段有两个端点,线段向一端无限延长形成了射线,射线有一个端点;线段向两端无限延长形成了直线,直线没有端点.2.点与直线有两种位置:点在直线上,点在直线外.3.当两条不同的直线只有一个公共点时,我们说这两条直线相交,这个公共点叫做它们的交点.4.过两点有且只有一条直线.简单地说:两点确定一条直线.5.比较两条线段的长短,可以用刻度尺的办法,也可以把其中一条线段移到另一条上作比较.6.两点之间的所有连线中,线段最短.简单地说:两点之间线段最短.连接两点的线段的长度,叫做这两点间的距离.7.若B 点在线段AC 上,且把线段AC 分成相等的两条线段AB 与BC ,这时点B 叫做线段AC 的中点.【温馨提示】1.表示线段的两个大写字母必须是表示端点的大写字母,表示射线时,表示端点的大写字母要写在前面.2.直线的性质“两点确定一条直线”在实际生活中的应用是确定“直”;线段的性质“两点之间线段最短”在实际生活中的应用是确定最短距离.要注意这两者的区别.【方法技巧】1. 熟记线段、射线、直线的表示方法、端点个数、性质,有助于提高解题的准确率和速度.2. 正确运用“线段的中点”这一条件,由“全部”乘以21得到其中的一半,由其中的一半乘以2得到“全部”.参考答案1.解:因为M ,N 分别是AB ,AC 的中点,所以MA =MB ,NA =NC .又因为MN =AN ﹣AM ,所以MN =NC ﹣BM .而NC =NB +BC ,BM =MN +NB ,所以2MN =BC ,所以MN =21BC . 2.解:因为点C 是线段AB 的中点,所以AC =BC .设OA 为x ,则AC =BC =x +1,所以x +x +1+x +1=17,解得x =5,所以x +1=6.所以C 表示的数为5+6=11.3.解:如图所示,(1)MN =CM +CN =BC AC 2121+=AB 21=5 cm ; (2)因为NB =3.5 cm ,所以BC =2NB =7 cm .所以AB =527÷=17.5 cm .4.解:蚂蚁可由:点A —点EF 的中点(或CE 的中点)—B 点.5.解:问题一:点A 13处; 点A 25和A 26之间的任何地方;问题二:因为|x +1|+|x |+|x ﹣1|+|x ﹣2|+|x ﹣3|+…+|x ﹣97|=|x ﹣(﹣1)|+|x ﹣0|+|x ﹣1|+|x ﹣2|+ |x ﹣3|+…+|x ﹣97|,此题相当于数轴上x 到点﹣1,0,1,…,97的距离和.所以当x =48时,有最小值为2450.故答案为:48,2450.6.解:(1)把每一个班级看作一个点,则2)18(8-⨯=28场; (2)15个车站看作15个点,线段条数为2)115(15-⨯=105, 因为车票有起点和终点站之分,所以车票要2×105=210种.。
湘教版数学七年级上册4.1 几何图形.docx
初中数学试卷4.1 几何图形课堂演练:1.把下列立体图形与对应的名称用线连起来。
圆柱圆锥正方体长方体棱柱球2.下面图形中叫圆柱的是()3.长方体共有()个面.A.8 B.6 C.5 D.44.下列说法,不正确的是()A.圆锥和圆柱的底面都是圆. B.棱锥底面边数与侧棱数相等.C.棱柱的上、下底面是形状、大小相同的多边形.D.长方体是四棱柱,四棱柱是长方体.5.正方体有个面,个顶点,经过每个顶点有条棱.这些棱的长度(填相同或不同).棱长为acm的正方体的表面积为 cm2.6.如图,已知一个正方体的六个面上分别写着六个连续的整数,且每两个相对面上的两个数的和都相等,图中所能看到的数是16,19和20,求这6个整数的和.7.如图,小强拿一张正方形的纸,沿虚线对折一次得图②,再对折一次得图③,然后用剪刀沿图③中的虚线剪去一个角,再打开后的形状是()8.在正方体的六个面上分别涂上红、黄、蓝、白、黑、绿六种颜色,现有涂色方式完全相同的四个正方体,如图拼成一个长方体,请判断涂红、黄、白三种颜色的对面分别涂着哪一种颜色?课后达标:9.与新买的铅笔形状近似的图形是( )A.圆锥B.长方形C.球D.圆柱10.在下列所给的几何图形中,属于平面图形的是( )A.三棱柱B.圆C.圆锥D.长方体11.如图,组成这个美丽图案的图形有( )A.三角形和半圆B.圆和四边形C.圆和三角形D.圆和扇形12.下图立体图形中是三棱锥的是( )13.从上面看下列几何体,得到的平面图形相同的是( )A.①②B.①③C.②③D.②④14.把如图中的三棱柱展开,所得到的展开图是( )15.如图是正方体的展开图,则正方体相对两个面上的数字之和的最小值是( )A.4B.6C.7D.816.写出下列几何体的名称.17.下表中是中国部分企业、机构或产品的标志.它们的标志是由简单图形构成的,具有简练、明了、形象、寓意深刻的特点,是企业文化深层次的内涵写照.请找出其中的简单图形.18.如图是一个正方体的平面展开图,标注了A字母的是正方体的正面,如果正方体的左面与右面标注的式子相等,求x的值.19.有一个正方体,将它的各个面上分别标上字母a,b,c,d,e,f.有甲,乙,丙三个同学站在不同的角度观察,结果如图.问这个正方体各个面上的字母a,b,c,d,e,f所对面上各是什么字母?。
初中数学级数学上册 4.1 几何图形课时作业考试卷及答案 (新版)湘教版
xx学校xx学年xx学期xx试卷姓名:_____________ 年级:____________ 学号:______________题型选择题填空题简答题xx题xx题xx题总分得分一、xx题(每空xx 分,共xx分)试题1:下列各组图形都是平面图形的一组是( )A.三角形、圆、球、圆锥B.线段、角、梯形、长方体C.角、三角形、四边形、圆D.直线、圆柱、长方形、圆试题2:下列四个几何体中,从正面看与从左面看相同的几何体有( )A.1个B.2个C.3个D.4个试题3:如图是一个正方体的表面展开图,则原正方体中与“建”字所在的面相对的面上标的字是( )评卷人得分A.美B.丽C.广D.安试题4:下列几种几何图形:①长方形;②梯形;③正方形;④圆柱;⑤圆锥;⑥球.其中是立体图形的是.(只填序号) 试题5:组成下列图案的平面图形有.试题6:如图是某立体图形从三个不同方向看到的图形,则这个立体图形是.试题7:把下列立体图形与其对应的名称用线连起来.试题8:已知由四个大小相同的小正方体搭成的几何体如图所示,请画出从三个方向看到的形状图.试题9:马小虎准备制作一个封闭的正方体盒子,他先用5个大小一样的正方形制成如图所示的拼接图(实线部分),经折叠后发现还少一个面.请你在图中的拼接图形上再接一个正方形,使新拼接成的图形经过折叠后能成为一个封闭的正方体盒子.(注:(1)只需添加一个符合要求的正方形;(2)添加的正方形用阴影表示)试题1答案:C.因为球、圆锥、长方体、圆柱是立体图形,所以A,B,D不符合要求.试题2答案:D.正方体从正面看与从左面看都为正方形;球从正面看与从左面看都是圆;圆锥从正面看与从左面看都是三角形;圆柱从正面看与从左面看都是长方形.试题3答案:D.原正方体中“设”与“丽”,“美”与“广”,“建”与“安”所在的面分别相对.试题4答案:④⑤⑥试题5答案:正方形、长方形、三角形、圆试题6答案:圆柱试题7答案:【解析】试题8答案:【解析】如图所示:【归纳整合】由小正方体组成的立体图形的特点1.从正面与从上面看到的图形列数相同.2.从左面与从正面看到的图形层数相同.试题9答案:【解析】答案不唯一,有下列几种添法,可供参考.。
七年级数学上册4.1 几何图形课时提升作业湘教版
几何图形(30分钟50分)一、选择题(每小题4分,共12分)1.观察下列实物模型,其形状是圆柱体的是( )【解析】选 D.熟悉立体图形的基本概念和特性即可解题.圆柱的上下底面是相同的两个圆,侧面是一个曲面,所以正确的是D项.【知识归纳】根据立体图形的特点识别立体图形(1)若立体图形的表面均是曲面,则该立体图形为球.(2)若立体图形的侧面是曲面,则该立体图形可能是圆柱、圆锥或圆台.(3)若立体图形的侧面是平面,则该立体图形可能是棱柱或棱锥或棱台.2.(2014·无锡实验质检)下列说法中,正确的个数是( )①柱体的两个底面一样大;②圆柱、圆锥的底面都是圆;③棱柱的底面是四边形;④长方体一定是柱体;⑤棱柱的侧面一定是长方形.A.2B.3C.4D.5【解析】选B.①柱体包括圆柱、棱柱,柱体的两个底面一样大,故此选项正确;②圆柱、圆锥的底面都是圆,正确;③棱柱的底面可以为任意多边形,错误;④长方体符合柱体的条件,一定是柱体,正确;⑤棱柱的侧面应是平行四边形,错误,共有3个正确.【易错提醒】1.四棱柱的底面是四边形,但棱柱的底面不一定是四边形.2.直棱柱的侧面都是长方形,但斜棱柱的侧面不一定是长方形.3.(2014·泉州模拟)下列几何体属于柱体的个数是( )A.3B.4C.5D.6【解析】选D.柱体分为圆柱和棱柱,所以柱体有(1)(3)(4)(5)(6)(8),共6个. 【互动探究】上面题目图形中属于棱柱的有哪些?提示:根据棱柱的概念可知,属于棱柱的有:(3)(4)(5)(6)(8).二、填空题(每小题4分,共12分)4.下列图形中, 为柱体,其中为圆柱,为棱柱.【解析】根据棱柱以及圆柱和柱体的定义可得出:C,D为柱体,其中C为圆柱,D为棱柱.答案:C,D C D5.如图所示的图形中,不是锥体的是.【解析】(1)(2)(4)的底面只有一个,属于锥体,(3)的底面有2个,属于柱体. 答案:(3)6.写出下列立体图形的名称.(1) (2) (3)【解析】要根据几何体的特征来判断它的名称:(1)有两个面相互平行,其余各面都是四边形,并且每相邻两个四边形的公共边都相互平行,有四条这样的公共边,是四棱柱.(2)有两个大小相同的圆做底面,曲面是长方形,因此是圆柱体.(3)由6个面组成,每个面都是长方形,且对面相互平行,是长方体.答案:(1)四棱柱(2)圆柱(3)长方体三、解答题(共26分)7.(8分)如图,上面是一些具体的物体,下面是一些立体图形,试从上面找出与下面立体图形相类似的实物(用线连接).【解析】8.(8分)下面画出了8个立体图形(1)找出与图(a)具有相同特征的图形,并说出相同的特征是什么?(2)找出其他具有相同特征的图形,并说明相同的特征是什么?【解析】(1)与图(a)具有相同特征的图形有:(c)(d)(e);它们相同的特征是它们都是柱体.(2)(b)(f)(g)是具有相同特征的图形,它们都是锥体.【培优训练】9.(10分)大家一定知道欧拉公式吧,一定很惊叹欧拉的伟大,其实,你也可以发现公式!如图,试一试!(1)根据上图所示,将所得数值填入下表:图顶点数边数区域数a 4 6 3bcd(2)猜想:顶点数、区域数、边数满足的关系: .(3)验证:请画一个图形验证.【解析】(1)图顶点数边数区域数a 4 6 3b 8 12 5c 6 9 4d 10 15 6(2)顶点数+区域数-边数=1(3)如图顶点数为7,区域数为6,边数为12.7+6-12=1,所以有:顶点数+区域数-边数=1.教学反思在新课改的形式下,如何激发教师的教研热情,提升教师的教研能力和学校整体的教研实效,是摆在每一个学校面前的一项重要的“校本工程”。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
几何图形
(30分钟50分)
一、选择题(每小题4分,共12分)
1.观察下列实物模型,其形状是圆柱体的是( )
【解析】选 D.熟悉立体图形的基本概念和特性即可解题.圆柱的上下底面是相同的两个圆,侧面是一个曲面,所以正确的是D项.
【知识归纳】根据立体图形的特点识别立体图形
(1)若立体图形的表面均是曲面,则该立体图形为球.
(2)若立体图形的侧面是曲面,则该立体图形可能是圆柱、圆锥或圆台.
(3)若立体图形的侧面是平面,则该立体图形可能是棱柱或棱锥或棱台.
2.(2014·无锡实验质检)下列说法中,正确的个数是( )
①柱体的两个底面一样大;
②圆柱、圆锥的底面都是圆;
③棱柱的底面是四边形;④长方体一定是柱体;
⑤棱柱的侧面一定是长方形.
A.2
B.3
C.4
D.5
【解析】选B.①柱体包括圆柱、棱柱,柱体的两个底面一样大,故此选项正确;②圆柱、圆锥的底面都是圆,正确;③棱柱的底面可以为任意多边形,错误;④长方体符合柱体的条件,一定是柱体,正确;⑤棱柱的侧面应是平行四边形,错误,共有3个正确.
【易错提醒】1.四棱柱的底面是四边形,但棱柱的底面不一定是四边形.
2.直棱柱的侧面都是长方形,但斜棱柱的侧面不一定是长方形.
3.(2014·泉州模拟)下列几何体属于柱体的个数是( )
A.3
B.4
C.5
D.6
【解析】选D.柱体分为圆柱和棱柱,所以柱体有(1)(3)(4)(5)(6)(8),共6个. 【互动探究】上面题目图形中属于棱柱的有哪些?
提示:根据棱柱的概念可知,属于棱柱的有:(3)(4)(5)(6)(8).
二、填空题(每小题4分,共12分)
4.下列图形中, 为柱体,其中为圆柱,
为棱柱.
【解析】根据棱柱以及圆柱和柱体的定义可得出:
C,D为柱体,其中C为圆柱,D为棱柱.
答案:C,D C D
5.如图所示的图形中,不是锥体的是.
【解析】(1)(2)(4)的底面只有一个,属于锥体,(3)的底面有2个,属于柱体. 答案:(3)
6.写出下列立体图形的名称.
(1) (2) (3)
【解析】要根据几何体的特征来判断它的名称:
(1)有两个面相互平行,其余各面都是四边形,并且每相邻两个四边形的公共边都相互平行,有四条这样的公共边,是四棱柱.
(2)有两个大小相同的圆做底面,曲面是长方形,因此是圆柱体.
(3)由6个面组成,每个面都是长方形,且对面相互平行,是长方体.
答案:(1)四棱柱(2)圆柱(3)长方体
三、解答题(共26分)
7.(8分)如图,上面是一些具体的物体,下面是一些立体图形,试从上面找出与下面立体图形相类似的实物(用线连接).
【解析】
8.(8分)下面画出了8个立体图形
(1)找出与图(a)具有相同特征的图形,并说出相同的特征是什么?
(2)找出其他具有相同特征的图形,并说明相同的特征是什么?
【解析】(1)与图(a)具有相同特征的图形有:(c)(d)(e);它们相同的特征是它们都是柱体.
(2)(b)(f)(g)是具有相同特征的图形,它们都是锥体.
【培优训练】
9.(10分)大家一定知道欧拉公式吧,一定很惊叹欧拉的伟大,其实,你也可以发现公式!如图,试一试!
(1)根据上图所示,将所得数值填入下表:
图顶点数边数区域数
a 4 6 3
b
c
d
(2)猜想:顶点数、区域数、边数满足的关系: .
(3)验证:请画一个图形验证.
【解析】(1)
图顶点数边数区域数
a 4 6 3
b 8 12 5
c 6 9 4
d 10 15 6
(2)顶点数+区域数-边数=1
(3)如图
顶点数为7,区域数为6,边数为12.
7+6-12=1,所以有:顶点数+区域数-边数=1.
教师个人研修总结
在新课改的形式下,如何激发教师的教研热情,提升教师的教研能力和学校整体的教研实效,是摆在每一个学校面前的一项重要的“校本工程”。
所以在学习上级的精神下,本期个人的研修经历如下:
1.自主学习:我积极参加网课和网上直播课程.认真完成网课要求的各项工作.教师根据自己的专业发展阶段和自身面临的专业发展问题,自主选择和确定学习书目和学习内容,认真阅读,记好读书笔记;学校每学期要向教师推荐学习书目或文章,组织教师在自学的基础上开展交流研讨,分享提高。
2.观摩研讨:以年级组、教研组为单位,围绕一定的主题,定期组织教学观摩,开展以课例为载体的“说、做、评”系列校本研修活动。
3.师徒结对:充分挖掘本校优秀教师的示范和带动作用,发挥学校名师工作室的作用,加快新教师、年轻教师向合格教师和骨干教师转化的步伐。
4.实践反思:倡导反思性教学和教育叙事研究,引导教师定期撰写教学反思、教育叙事研究报告,并通过组织论坛、优秀案例评选等活动,分享教育智慧,提升教育境界。
5.课题研究:立足自身发展实际,学校和骨干教师积极申报和参与各级教育科研课题的研究工作,认真落实研究过程,定期总结和交流阶段性研究成果,及时把研究成果转化为教师的教育教学实践,促进教育质量的提高和教师自身的成长。
6.专题讲座:结合教育教学改革的热点问题,针对学校发展中存在的共性问题和方向性问题,进行专题理论讲座。
7.校干引领:从学校领导开始,带头出示公开课、研讨课,参与本校的教学观摩活动,进行教学指导和引领。
8.网络研修:充分发挥现代信息技术,特别是网络技术的独特优势,借助教师教育博客等平
台,促进自我反思、同伴互助和专家引领活动的深入、广泛开展。
我们认识到:一个学校的发展,将取决于教师观念的更新,人才的发挥和校本培训功能的提升。
多年来,我们学校始终坚持以全体师生的共同发展为本,走“科研兴校”的道路,坚持把校本培训作为推动学校建设和发展的重要力量,进而使整个学校的教育教学全面、持续、健康发展。
反思本学期的工作,还存在不少问题。
很多工作在程序上、形式上都做到了,但是如何把工作做细、做好,使之的目的性更加明确,是继续努力的方向。
另外,我校的研修工作压力较大,各学科缺少领头羊、研修氛围有待加强、师资缺乏等各类问题摆在我们面前。
缺乏专业人员的引领,各方面的工作开展得还不够规范。
相信随着课程改革的深入开展,在市教育教学研究院的领导和专家的亲临指导下,我校校本研修工作一定能得以规范而全面地展开。
“校本研修”这种可持续的、开放式的继续教育模式,一定能使我校的教育教学工作又上一个台阶。
