ACM必做50题——数学

合集下载

acm数学竞赛试题

acm数学竞赛试题
ACM数学竞赛试题通常涉及各种数学领域，包括但不限于代数、几何、概率统计和组合数学等。

以下是一些经典的ACM数学竞赛试题：
1. 平面上n个点的k距离和最小值问题：给定平面上n个点，对于每个点，计算它到其他所有点的距离，然后求出这些距离中的k个最小值。

问题是：如何有效地计算这k个最小值？
2.最长公共子序列问题：给定两个序列，找出它们的最长公共子序列。

例如，对于序列
A = [1, 2, 3, 4] 和
B = [2, 3, 4, 5]，最长公共子序列是[2, 3, 4]。

3. 凸包问题：给定平面上的一组点，找到一个最小的凸多边形，使得这个多边形能够包含这组点中的所有点。

4. 最短路问题：给定一个有向图，其中每条边都有一个非负的权重，找出图中任意两点之间的最短路径。

5. 子集和问题：给定一个正整数数组和一个目标值，判断数组中是否存在和为目标值的两个非空子集。

例如，给定数组[1, 2, 3, 4] 和目标值7，判断是否存在两个子集，它们的和分别为7。

以上只是ACM数学竞赛试题的一部分，实际上还有更多涉及数学各个领域的题目。

要提高解决这类问题的能力，需要不断练习和研究。

ACM题库完整版

#include<stdio.h> int type(int); char week[7][10]={"saturday","sunday","monday","tuesday","wednesday","thursday","friday"}; int year[2]={365,366}; int month[2][12]={31,28,31,30,31,30,31,31,30,31,30,31,31,29,31,30,31,30,31,31,30,31,30,31}; int main(void) { int days,dayofweek; int i=0,j=0; while(scanf("%d",&days)&&days!=-1) { dayofweek=days%7; for(i=2000;days>=year[type(i)];i++) days-=year[type(i)]; for(j=0;days>=month[type(i)][j];j++) days-=month[type(i)][j]; printf("%d-%02d-%02d%s\n",i,j+1,days+1,week[dayofweek]); } return 0; } int type(int m) { if(m%4!=0||(m%100==0&&m%400!=0)) return 0; else return 1; }
登山
1.题目描述五一到了，NUIST-ACM队组织大家去登山观光，队员们发现山上一个有N个景点，并且决定按照顺序来浏览这些景点，即每次所浏览景点的编号都要大于前一个浏览景点的编号。同时队员们还有另一个登山习惯，就是不连续浏览海拔相同的两个景点，并且一旦开始下山，就不再向上走了。队员们希望在满足上面条件的同时，尽可能多的浏览景点，你能帮他们找出最多可能浏览的景点数么？ 2.输入 Line 1： N (2 <= N <= 1000) 景点数 Line 2： N个整数，每个景点的海拔 3.输出最多能浏览的景点数 4.样例输入 8 186 186 150 200 160 130 197 220 5.样例输出 4

(2020年编辑)ACM必做50题的解题-数论

poj 1061 青蛙的约会这题用的是解线性同余方程的方法，之前没接触到过，搜索资料后看到一个人的博客里面讲的很好就拷贝过来了。

内容如下：对于方程：ax≡b(mod m)，a，b，m都是整数，求解x 的值，这个就是线性同余方程。

符号说明：mod表示：取模运算ax≡b(mod m)表示：(ax - b) mod m = 0，即同余gcd(a,b)表示：a和b的最大公约数求解ax≡b(mod n)的原理：对于方程ax≡b(mod n)，存在ax + by = gcd(a,b)，x，y是整数。

而ax≡b(mod n)的解可以由x，y来堆砌。

具体做法如下：第一个问题：求解gcd(a,b)定理一：gcd(a,b) = gcd(b,a mod b)欧几里德算法int Euclid(int a,int b){if(b == 0)return a;elsereturn Euclid(b,mod(a,b));}附：取模运算int mod(int a,int b){if(a >= 0)return a % b;elsereturn a % b + b;}第二个问题：求解ax + by = gcd(a,b)定理二：ax + by = gcd(a,b)= gcd(b,a mod b) = b * x' + (a mod b) * y'= b * x' + (a - a / b * b) * y'= a * y' + b * (x' - a / b * y')= a * x + b * y则：x = y'y = x' - a / b * y'以上内容转自/redcastle/blog/item/934b232dbc40d336349bf7e4.html由这个可以得出扩展的欧几里德算法：int exGcd(int a, int b, int &x, int &y) {if(b == 0){x = 1;y = 0;return a;}int r = exGcd(b, a % b, x, y);int t = x;x = y;y = t - a / b * y;return r;}代码：#include<iostream>#include<cstdlib>#include<cstring>#include<cmath>using namespace std;__int64 mm,nn,xx,yy,l;__int64 c,d,x,y;__int64 modd(__int64 a, __int64 b){if(a>=0)return a%b;elsereturn a%b+b;}__int64 exGcd(__int64 a, __int64 b) {if(b==0){x=1;y=0;return a;}__int64 r=exGcd(b, a%b);__int64 t=x;x=y;y=t-a/b*y;return r;}int main(){scanf("%I64d %I64d %I64d %I64d %I64d",&xx,&yy,&mm,&nn,&l);if(mm>nn) //分情况{d=exGcd(mm-nn,l);c=yy-xx;}else{d=exGcd(nn-mm,l);c=xx-yy;}if(c%d != 0){printf("Impossible\n");return 0;}l=l/d;x=modd(x*c/d,l); ///取模函数要注意printf("%I64d\n",x);system("pause");return 0;}POJ 1142 SmithNumber题意：寻找最接近而且大于给定的数字的SmithNumber什么是SmithNumber？用sum(int)表示一个int的各位的和，那一个数i如果是SmithNumber,则sum（i） =sigma( sum(Pj )),Pj表示i的第j个质因数。

ACM试题及参考答案

1. 给定一个矩阵M(X, Y)，列集为X ，行集为Y 。

如果存在对其列的一个排序，使得每一行的元素都严格递增，称M 是一个次序保持矩阵。

例如下图中存在一个排序x 4，x 1，x 2，x 3，x 5I ⊆X ，满足：子矩阵M(I,Y)是次序保持矩阵。

[测试数据] 矩阵M ：[测试数据结果] I={ x 1，x 3，x 4，x 7，x 8}[解题思路] 将该问题归约为在一个有向图中找一条最长路径的问题。

给定矩阵M=（a ij ），行集Y ，列集X ，行子集J ⊆Y ，定义有向图D A =(V A ,E A )，其中V A 含有|X|个顶点，每个顶点代表X 中的一列，如果顶点u ，v 对应的列x u ，x v 满足，对于任意的j ∈J ，u v ij ij a a <，则有一条从u 到v 的弧（u ，v ）∈E 。

显然，D A 是个无环图，可以在O(|X|2)时间内构造完毕。

对于任意的条件子集J ，A(I,J)是次序保持的当且仅当对应于J 中条件的顶点在D A 中构成一条有向路径。

从而我们只需在有向图D A 中找一条最长路径，该问题可在O(|V A |+| E A |)时间内完成。

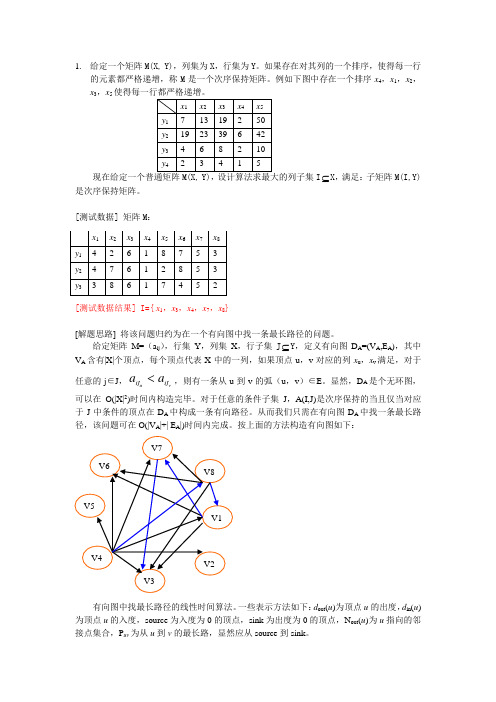
按上面的方法构造有向图如下：有向图中找最长路径的线性时间算法。

一些表示方法如下：d out (u )为顶点u 的出度，d in (u )为顶点u 的入度，source 为入度为0的顶点，sink 为出度为0的顶点，N out (u )为u 指向的邻接点集合，P uv 为从u 到v 的最长路，显然应从source 到sink 。

在每一步为每个顶点关联一个永久的或临时的标签。

v被赋了一个临时标签(v’，i v)表明在当前步，算法找出的最长的从source到v的有向路长度为i v，且经由v’而来。

v被赋了一个永久标签[v’，i v]表明从source到v的最长有向路长度为i v，且经由v’而来，通过回溯每个顶点的永久标签就可以找出最长有向路。

ACM必做50题——动归

1 动态规划——POJ 2479 Maximum sum我觉得这个题目跟2593是一样的题目，就是数据量有些不同。

这个题目数据量是50000，但时间只有1000ms，而2593数据量有100000，但时间有3000ms，所以相对而言，这个题目对算法的要求还要高一些，也难怪好多人都在后面发贴说过了2593但这个却没过得了。

考查点：动态规划思路：在输入的同时，进行一次DP，计算出从左到右的最大值，并把它保存在数组dp的对应的下标元素中，这样之后，对于下标为i的元素，它其中保存的便是前面所有元素可能的最大连续和。

再从右到左进行一次DP，计算从右到左的最大连续和。

假设此时已经算到下标为i的元素，那么将sum+dp[i-1]与ans进行比较，将ans取较大者。

最后当i到2的时候ans中的值即为所求的最大值。

提交情况：记不清是多少Wrong Answer，但肯定是有一次Time Limit Error，因为我有用O(N^2)的DP做过，而且可以通过我想到的所有测试数据。

收获：对动态规划问题如何更好地减少时间有了一点点理解，也复习了一下基本的技能。

经验：做题之前做好充分地分析，包括时间效率、空间效率以及实现地难度。

TLE Code(O(N^2)):（自己想了好久才想出来的，给自己鼓励一下）#include <iostream>using namespace std;int array[50001], num[50001];const int MIN = -999999999;int main(){int tcase, n;cin>>tcase;int tmp, ans, i, sum;while(tcase--){scanf("%d", &n);tmp = MIN; sum = 0;for(i = 1; i <= n; i++){scanf("%d", &num[i]);sum += num[i];if(sum > tmp)tmp = sum;array[i] = tmp;if(sum < 0)sum = 0;}tmp = ans = MIN;sum = 0;for(i = n; i > 1; i--){sum += num[i];if(sum > tmp)tmp = sum;if(ans < (array[i-1]+tmp))ans = array[i-1]+tmp;if(sum < 0)sum = 0;}cout<<ans<<endl;}return 0;}2 POJ 2593 Max Sequence考察点：动态规划思路：虽然题目给出了3000ms的时间，但考虑到数据量可以达到100000，如果用O(N^2)的算法的话，还是极有可能会超时的，于是决定采用这种O(N)时间效率的动规。

ACM竞赛基础训练题.docx

ACM竞赛基础训练题H【题目］】N皇后问题（八皇后问题的扩展）【题ri 2】排球队员站位问题【题H 3］把自然数N分解为若干个自然数之和。

【题H 4］把自然数N分解为若干个自然数之积。

【题H 5】马的遍历问题。

【题H 6】加法分式分解【题H 7】地图着色问题【题H 8］在n和的正方形屮放置长为2,宽为1的长条块，【题H 9】找迷宫的最短路径。

（广度优先搜索算法）【题Fl 10］火车调度问题【题H 11］农夫过河【题FI 12］七段数码管问题。

【题H 13］把1-8这8个数放入下图8个格中，要求相邻的格（横，竖,对角线）上填的数不连续. 【题FI 14］在4X4的棋盘上放置8个棋，要求每一行，毎一列上只能放置2个.【题H 15］迷宫问题.求迷宫的路径.（深度优先搜索法）【题H 16］一笔画问题【题H 17］城市遍历问题.【题H 18］棋子移动问题【题H 19］求集合元索问题（l,2x+l,3X+l类）【题RI N皇后问题(含八皇后问题的扩展，规则同八皇后)：在N粒的棋盘上, 放置N个皇后，要求每一横行每一列，每一对角线上均只能放置一个皇后，问可能的方案及方案数。

const max=8;var i,j:integer;a: array [1.. max] of 0.. max; ｛放皇后数组｝b:array[2.. 2*max] of boolean; ｛/对角线标志数组｝c:array[-(max-1).. max-1 ] of boolean; ｛\对角线标志数组｝col:array [1.. max] of boolean; ｛列标志数组｝total: integer; ｛统计总数｝procedure output; ｛输出｝var i:inte^er;beginwrite (' No.' :4,' [', total+1:2,']');for i :=1 to max do write (a [i] :3) ;write(， ');if (to tal+1) mod 2 =0 t hen writ eln; inc (to tai);end;function ok(i, dep: integer) :boolean; ｛判断第dep 行第i 列可放否｝begin ok:=false;if ( b[i+dep]二true) and ( c[dep-i]二true) ｛and (a[dep]=0)｝ and(col[i]=true) then ok:二trueend;procedure try (dep:integer);var i,j:integer;beginfor i:=l to max do 侮一行均有max种放法｝i f ok (i, dep) then begi na [dep]:=i;b[i+dep]:二false; ｛/对角线已放标志｝c[dep-i]:二false; ｛\对角线已放标志｝col [i]:二false; ｛列已放标志｝if dep二max then outputelse try (dep+1) ; ｛递归下一层｝a[dep] :=0; ｛取走皇后，回溯｝b[i+dep]:二true; ｛恢复标志数组｝c[dep-i]:二true;col[i]:二true;end;end;beginfor i:=1 to max do begin a[i]:=0;col[i]:=true;end;for i:=2 to 2*max do b[i]:二true;for i:=-(max-1) to max~l do c[i]:=true;total:二0;try(l); writelntotal , total);end.【测试数据】n二8八皇后问题No.[ 1] 1 5 8 6 3 7 2 4 No. [ 2] 1 6 83 7 4 2 5 No.[ 3] 1 7 4 6 8 2 5 3 No. [ 4] 1 7 58 2 4 6 3 No.[ 5] 2 4 6 8 3 1 7 5 No. [ 6] 2 5 71 3 8 6 4 No.[ 7] 2 5 7 4 1 8 6 3 No. [ 8] 2 6 17 4 8 3 5 No.[ 9] 2 6 8 3 1 4 7 5 No. [10] 2 7 36 8 5 1 4No. [11] 2 7 5 8 1 4 6 3 No. [12] 2 8 61 3 5 7 4 No. [13] 3 1 7 5 8 2 4 6 No. [14] 3 5 28 1 7 4 6 No. [15] 3 5 2 8 6 4 7 1 No. [16] 3 5 71 4 2 8 6 No. [17] 3 5 8 4 1 7 2 6 No. [18] 3 6 25 8 1 7 4 No. [19] 3 6 2 7 1 4 8 5 No. [20] 3 6 27 5 1 8 4 No. [21] 3 6 4 1 8 5 7 2 No. [22] 3 6 42 8 5 7 1 No. [23] 3 6 8 1 4 7 5 2 No. [24] 3 6 81 5 7 2 4 No. [25] 3 6 8 2 4 1 7 5 No. [26] 3 7 28 5 1 4 6 No. [27] 3 7 2 8 6 4 1 5 No. [28] 3 8 47 1 6 2 5 No. [29] 4 1 5 8 2 7 3 6 No. [30] 4 1 58 6 3 7 2 No. [31] 4 2 5 8 6 1 3 7 No. [32] 4 2 73 6 8 1 5 No. [33] 4 2 7 3 6 8 5 1 No. [34] 4 2 75 1 8 6 3 No. [35] 4 2 8 5 7 1 3 6 No. [36] 4 2 86 1 3 5 7 No. [37] 4 6 1 5 2 8 3 7 No. [38] 4 6 82 7 1 3 5 No. [39] 4 6 8 3 1 7 5 2 No. [40] 4 7 18 5 2 6 3 No. [41] 47 3 8 2 5 1 6 No. [42] 4 7 52 6 1 3 8 No. [43] 4 7 5 3 1 6 8 2 No. [44] 4 8 13 6 2 7 5 No. [45] 4 8 1 5 7 2 6 3 No. [46] 4 8 53 1 7 2 6 No. [47] 5 1 4 6 8 2 7 3 No. [48] 5 1 84 2 7 3 6 No. [49] 5 1 8 6 3 7 2 4 No. [50] 5 2 46 8 3 1 7 No. [51] 5 2 47 3 8 6 1 No. [52] 5 2 61 7 48 3 No. [53] 5 2 8 1 47 3 6 No. [54] 5 3 16 8 2 4 7 No. [55] 5 3 1 7 28 6 4 No. [56] 5 3 84 7 1 6 2 No. [57] 5 7 1 3 8 6 4 2 No. [58] 5 7 14 2 8 6 3 No. [59] 5 7 2 4 8 1 3 6 No. [60] 5 7 26 3 1 4 8 No. [61] 5 7 2 6 3 1 8 4 No. [62] 5 7 41 3 8 6 2 No. [63] 5 8 4 1 3 6 2 7 No. [64] 5 8 41 7 2 6 3 No. [65] 6 1 5 2 8 3 7 4 No. [66] 6 2 71 3 5 8 4 No. [67] 6 2 7 1 4 8 5 3 No. [68] 6 3 17 5 8 2 4 No. [69] 6 3 1 8 4 2 7 5 No. [70] 6 3 18 5 2 4 7 No. [71] 6 3 5 7 1 4 2 8 No. [72] 6 3 58 1 4 2 7 No. [73] 6 3 7 2 48 1 5 No. [74] 6 3 72 8 5 1 4 No. [75] 6 3 7 4 1 8 2 5 No. [76] 6 4 15 8 2 7 3 No. [77] 6 4 2 8 5 7 1 3 No. [78] 6 4 71 3 5 2 8 No. [79] 6 4 7 1 8 2 5 3 No. [80] 6 8 24 1 7 5 3 No. [81] 7 1 3 8 6 4 2 5 No. [82] 7 2 41 8 5 3 6 No. [83] 7 2 6 3 1 4 8 5 No. [84] 7 3 16 8 5 2 4 No. [85] 7 3 8 2 5 1 6 4 No. [86] 7 4 25 8 1 3 6 No. [87] 7 4 2 8 6 1 3 5 No. [88] 7 5 31 6 8 2 4 No. [89] 8 2 4 1 7 5 3 6 No. [90] 8 2 53 1 7 4 6 No. [91] 8 3 1 6 2 5 7 4 No. [92] 8 4 13 6 2 7 5 total:92 对于N皇后:【题H 】排球队员站位问题I ----------------- 1图为排球场的平面图，其屮一、二、三、四、五、六为位置编号， I |二、三、四号位置为前排，一、六、五号位为后排。

acm算法经典例题

acm算法经典例题一、数论1: Wolf and Rabbit描述There is a hill with n holes around. The holes are signed from0 to n-1.A rabbit must hide in one of the holes. A wolf searches the rabbit in anticlockwise order. The first hole he get into is the one signed with 0. Then he will get into the hole every m holes. For example, m=2 and n=6, the wolf will get into the holes which are signed 0,2,4,0. If the rabbit hides in the hole which signed 1,3 or 5, she will survive. So we call these holes the safe holes.输入The input starts with a positive integer P which indicates the number of test cases. Then on the following P lines,each line consists 2 positive integer m and n(0<m,n<2147483648).< bdsfid="69" p=""></m,n<2147483648).<>输出For each input m n, if safe holes exist, you should output "YES", else output "NO" in a single line.样例输入21 22 2样例输出NOYES翻译：描述一座山有n个洞，洞被标记为从0到n-1。

acm数学竞赛试题及答案

acm数学竞赛试题及答案# 题目一：数列问题问题描述：给定一个数列 \( a_1, a_2, a_3, \ldots, a_n \)，数列中每个元素都是正整数，且满足 \( a_i = a_{i-1} + a_{i-2} \) 对于所有\( i \geq 3 \)。

如果 \( a_1 = 1 \) 且 \( a_2 = 1 \)，请找出数列的第 \( n \) 项。

解答：根据题意，这是一个斐波那契数列。

第 \( n \) 项的值可以通过递归关系计算得出。

对于 \( n \) 的值，可以使用以下递归公式：\[ a_n = a_{n-1} + a_{n-2} \]其中，\( a_1 = 1 \) 和 \( a_2 = 1 \)。

因此，数列的前几项为 1, 1, 2, 3, 5, 8, 13, 21, ...。

对于任意的 \( n \)，可以通过递归或动态规划方法计算出 \( a_n \)。

# 题目二：组合问题问题描述：从 \( n \) 个不同的元素中选择 \( k \) 个元素的所有可能组合的个数是多少？解答：这个问题可以通过组合数学中的二项式系数来解决。

从 \( n \) 个不同元素中选择 \( k \) 个元素的组合数 \( C(n, k) \) 可以用以下公式计算：\[ C(n, k) = \frac{n!}{k!(n-k)!} \]其中，\( n! \) 表示 \( n \) 的阶乘。

# 题目三：几何问题问题描述：在一个直角坐标系中，给定三个点 \( A(x_1, y_1) \)，\( B(x_2, y_2) \) 和 \( C(x_3, y_3) \)。

如果 \( \overrightarrow{AB} \) 和 \( \overrightarrow{AC} \) 是垂直的，求证 \( A \) 是直角三角形 \( ABC \) 的直角顶点。

解答：如果 \( \overrightarrow{AB} \) 和 \( \overrightarrow{AC} \) 垂直，那么它们的数量积（点积）应该为零。

ACM必做50题的解题-模拟

break;
}
return 1;
}
int main(){
int i,j,n;
char c;
scanf("%d",&n);
while(n--){
for(i=1; i<=3; i++)
scanf("%s %s %s",left[i],right[i],result[i]);
for(c='A'; c<='L'; c++){
1)选择合适的算法
对于每一枚硬币x逐个试探：
x比真币轻的猜测是否成立？猜测成立则进行输出。
x比真币重的猜测是否成立？猜测成立则进行输出。
2)选择合适的数据结构
以字符串数组存储称量的结果。每次称量时，天平左右最多有6枚硬币。因此，字
符串的长度需要为7，最后一位存储字符串的结束符’\0’，便于程序代码中使用字符串
{
int t,n;
cin>>t;
while(t--){
cin>>n;
int x,y;
int cross[SIZE];
memset(cross,0,sizeof(cross));
for(int i=0;i<n;++i){
cin>>x>>y;
int start,end;
if(x>y){
swapnum(x,y);
case 'u': if( strchr(left[i], x) == NULL) return 0;
break;
case 'e': if(strchr(right[i], x) != NULL || strchr(left[i], x) != NULL) return 0;

ACM必做50题的解题-快速查找 (B-Search, Hash and so on)

{
if(r[x]>r[y])
p[y]=x;
else if(r[x]<r[y])
p[x]=y;
else
{
r[y]++;
char fn[11];
}dict;
dict a[100001];
/* 定义qsort比较函数 */
int q_cmp(const void * a,const void *b)
{
return strcmp(((dict*)a)->fn, ((dict*)b)->fn);
int i, sign;
dict *p;
i = 0;
/* 查询标记记为"未开始" */
sign = 1;
/* 读取字符串直到文件结束 */
while(gets(str))
/* 找到则输出结果 */
if (p)
{
puts(p->en);
}
int id2 = search(s2,root);
degree[id1]++;
degree[id2]++;
if(p[id1]==0)
make_set(id1);
p->next[s[i]-'a']=new TreeNode;
p=p->next[s[i]-'a'];
}
if(p->id==0)//first insert
#include <cstring>
using namespace std;
const int max_size=500001;

ACM必做50题的解题-搜索

POJ1011 Sticks 搜索+强剪枝这个题目是不是贪心的，我就是第一次用了贪心，一直W A，相当的悲剧，贪心错误的sample：7 15 11 8 8 8 4 3 2 1，所以大家还是全部搜索。

但是全部搜索必须剪枝，不然肯定是TLE的，而且本体属于强剪枝，少剪了也是TLE。

经典搜索题，果然是到处充斥着剪枝才能过啊，我的代码离剪到极限还差很多题目给出一大堆小棍子的长度，需要把他们拼成几根长度相等的大棍子，求大棍子的最短长度看自己剪枝方法的效果时候，可以添设一个变量来记录递归次数如剪枝4：没有这个剪枝的情况下对以下数据需要40万次递归，而加上这个剪枝后减少到了4万多次对数据：4515 3 2 4 11 1 8 8 8 15 3 2 4 11 1 8 8 8 15 3 2 4 11 1 8 8 8 15 3 2 4 11 1 8 8 8 15 3 2 4 11 1 8 8 8#include <iostream>#include <algorithm>using namespace std;int sticks[65];int used[65];int n,len;bool dfs(int i,int l,int t)//i为当前试取的棍子序号,l为要拼成一根完整的棍子还需要的长度,t初值为所有棍子总长度{if(l==0){t-=len;if(t==0)return true;for(i=0;used[i];++i); //剪枝1：搜索下一根大棍子的时候，找到第一个还没有使用的小棍子开始used[i]=1; //由于排序过，找到的第一根肯定最长，也肯定要使用，所以从下一根开始搜索if(dfs(i+1,len-sticks[i],t))return true;used[i]=0;t+=len;}{for(int j=i;j<n;++j){if(j>0&&(sticks[j]==sticks[j-1]&&!used[j-1])) //剪枝2：前后两根长度相等时，如果前面那根没被使用，也就是由前面那根continue; //开始搜索不到正确结果，那么再从这根开始也肯定搜索不出正确结果，此剪枝威力较大if(!used[j]&&l>=sticks[j]) //剪枝3：最简单的剪枝，要拼成一根大棍子还需要的长度L>=当前小棍子长度，才能选用{l-=sticks[j];used[j]=1;if(dfs(j,l,t))return true;l+=sticks[j];used[j]=0;if(sticks[j]==l) //剪枝4：威力巨大的剪枝，程序要运行到此处说明往下的搜索失败，若本次的小棍长度刚好填满剩下长度，但是后break; //面的搜索失败，则应该返回上一层}}}return false;}bool cmp(const int a, const int b){return a>b;}int main(){while(cin>>n&&n){int sum=0;for(int i=0;i<n;++i){cin>>sticks[i];sum+=sticks[i];used[i]=0;}sort(sticks,sticks+n,cmp); //剪枝5：从大到小排序后可大大减少递归次数bool flag=false;for(len=sticks[0];len<=sum/2;++len) //剪枝6：大棍长度一定是所有小棍长度之和的因数，且最小因数应该不小于小棍中最长的长度{if(sum%len==0){if(dfs(0,len,sum)){flag=true;cout<<len<<endl;break;}}}if(!flag)cout<<sum<<endl;}return 0;}poj 1033 Defragment题意：磁盘整理，按照从第一个文件到最后一个文件的顺序排放，而且每个文件的碎片按原来的顺序放在一起，要求转移的次数最少。

acm基础试题及答案

acm基础试题及答案1. 题目：给定一个整数数组，请找出数组中第二大的数。

答案：我们可以使用排序的方法，将数组从小到大排序，然后数组中的倒数第二个数就是第二大的数。

或者使用一次遍历的方法，首先初始化两个变量，一个用来存储最大值，一个用来存储第二大的值。

遍历数组，每次比较当前元素与最大值，如果当前元素大于最大值，则更新第二大的值为最大值，并将当前元素赋给最大值；如果当前元素小于最大值但大于第二大的值，则更新第二大的值。

2. 题目：实现一个函数，计算一个字符串中字符出现的次数。

答案：可以使用哈希表来实现，遍历字符串中的每个字符，将其作为键值对存储在哈希表中，键是字符，值是该字符出现的次数。

遍历结束后，哈希表中存储的就是每个字符出现的次数。

3. 题目：给定一个链表，删除链表的倒数第n个节点，并且返回新的链表头节点。

答案：可以使用双指针的方法，首先初始化两个指针，都指向链表的头节点。

然后移动第一个指针，移动n步，此时第一个指针指向倒数第n个节点的前一个节点。

接着同时移动两个指针，直到第一个指针到达链表的末尾，此时第二个指针指向的节点就是需要删除的节点的前一个节点。

然后更新第二个指针的next指针，使其指向第二个指针的next节点的next节点，最后返回链表的头节点。

4. 题目：编写一个函数，判断一个整数是否是回文数。

回文数是指正序和倒序读都一样的数。

答案：首先将整数转换为字符串，然后使用双指针的方法，一个指针从字符串的开始位置，一个指针从字符串的结束位置，向中间移动。

如果两个指针指向的字符不相等，则该整数不是回文数。

如果遍历结束后没有发现不相等的字符，则该整数是回文数。

5. 题目：给定一个字符串，找出其中不含有重复字符的最长子串的长度。

答案：可以使用滑动窗口的方法，维护一个哈希表记录窗口内字符的出现情况，以及一个变量记录不含有重复字符的最长子串的长度。

遍历字符串，每次移动窗口的右端点，如果当前字符不在窗口内，则更新最长子串的长度，并将字符添加到哈希表中。

ACM必做50题的解题-数学

ACM必做50题的解题-数学.txt36母爱是一缕阳光，让你的心灵即便在寒冷的冬天也能感受到温暖如春；母爱是一泓清泉，让你的情感即使蒙上岁月的风尘仍然清澈澄净。

POJ 2249 Binomial Showdown组合数学。

高精度，也可把分子分母的数组进行两两约分#include<iostream>using namespace std;double c(int c,int k){double a=1;int i,j=2;for(i=c;i>c-k;i--)a=a*i/(c-i+1);return a;}int main(){int n,k;while(scanf("%d%d",&n,&k)!=EOF && (n!=0 || k!=0)){if(k>n/2 )k=n-k;printf("%.0lf\n",c(n,k));}return 0;}poj 1023 the fun number system （经典进位制）题意：一种由2进制衍生出来的进制方法（我们暂且称为“类2进制”）；标明'n'的位置上原2进制该位的权重要乘上-1，才是现在进制方法该位的权重；譬如说；pnp对于的能表示的数2来说就是 110；即1*2^2+(-1)*1*2^1+1*2^0=2;算法：这是数论中的进位制问题，我们可以仿照原来的求一个数二进制表示方法；但首先，我们应该考虑几个问题；①k位这种类2进制的表示范围；显然，当给出的'p','n'序列中，我们将所有p的位置都置为1其余位是0，此时最大；当我们将所有n的位置置为1，其余为0，此时最小；不过当我们求最大限max和最小限min时会有一个溢出问题；比如64位全是p的序列，那么max会溢出，值为-1；同理min在全是n 时也会溢出，为1；显然是max>=0,min<=1,溢出时产生异常，依次可以判断；②是否是最大限和最小限之间的数都能表示呢？都可以，而且能够表示的数是2^k个，这个原始2进制是一样的；因为每个位上要么是0，要么是1，而且每个位上的权重唯一的，不能通过其他位的01组合获得；最后，我们就可以仿照原始二进制来算在类2进制下的表示；不断求N的二进制最后一位和右移；如果取余是1，则该位上一定是1，如果该位对于字母为‘n’，则高位应该再加1；这里对2取余可能会出错，因为对于负数，补码的表示，最后一位一定是和原码一样的每次的右移后(有时需先加1）补码表示正好符合要求（可找实例验证）；#include<iostream>using namespace std;__int64 N,M;char s[100],res[100]={'\0'};int main(){int T;scanf("%d",&T);int i,j;__int64 _max,_min;char ch;while(T--){scanf("%I64d",&N);scanf("%s",s);_max=0;_min=0;for(i=0;i<N;i++) //找出能表示的范围；{if(s[i]=='p') _max=2*_max+1,_min*=2;else _min=2*_min-1,_max*=2;}scanf("%I64d",&M);if((M<_min&&_min<=0)||(M>_max&&_max>=0)) puts("Impossible"); //注意防止64位数的溢出；else{memset(res,'\0',sizeof(res));for(i=N-1;i>=0;i--){int flag=0;if(M&1) //这里不能是平常的%2； {res[i]='1';if(s[i]=='n') flag=1;}else res[i]='0';M>>=1;if(flag) M++; //如果是n就需其高位加1；}printf("%s\n",res);}}system("pause");return 0;}POJ2506 Tiling 递推+高精给看似复杂的题找到了合适的规律就会变得简单。

ACM必做50题——动归题

ACM 必做50题——动归 1、POJ 2479 Maximum sumDescription:Given a set of n integers: A={a1, a2,..., an}, we define a function d(A) as below: D(A)=)(max112222111∑∑==<<<<<+t s i t s j nt s t s aj aiYour task is to calculate d(A). InputThe input consists of T(<=30) test cases. The number of test cases (T) is given in the first line of the input.Each test case contains two lines. The first line is an integer n(2<=n<=50000). The second line contains n integers: a1, a2, ..., an. (|ai| <= 10000).There is an empty line after each case. OutputPrint exactly one line for each test case. The line should contain the integer d(A). Sample Input 1 101 -12 23 -34 -45 -5 Sample Output 13 HintIn the sample, we choose {2,2,3,-3,4} and {5}, then we can get the answer. Huge input,scanf is recommended.题意：好题。

ACM必做50题——高精度

ACM必做50题——高精度1 POJ 1001 Exponentiation高精度数的计算，以前在网上看到过一个计算大数阶乘比如10000000！的算法，总体思想就是将结果用数组保存起来，然后将结果的每一位与乘数相乘，当然还有进位...有了这个算法的思想，这个题思路就可以是：先将输入的小数转换成一个整数，当然这个整数肯定能够用int类型的变量保存，比如1.2345, 通过函数removeDot（）将它转化成12345，然后利用大数阶乘的思想计算12345*12345.....*12345, 最后的就是输出了，这个要考虑的情况比较多，因为这个也W A了5次才AC(笨的要死), 情况虽多，但不难.这道题是高精度计算的，不算很难，但是很繁琐，尤其是对输入输出的要求。

被这道题搞了好久，耐心来，一点一点调试，总会成功的。

#include#include#includeusing namespace std;char ans[10];char res[2][205];__int64 ps;//有几位小数点int len;//长度，R的有效长度//计算c = b * avoid Multiply(char * b,int bt,char * a,int at,char * c){int i,j;int up=0;for(i=0;i<at;++i)< p="">{up=0;for(j=0;j<bt;j++)< p="">{int t;if(c[i+j]==0)c[i+j]='0';t=(a[i]-48)*(b[j]-48)+c[i+j]-48+up; if(t>=10){up=t/10;t=t%10;c[i+j]=t+48;if(j==(bt-1) )c[i+j+1]=(up+48);}else{c[i+j]=t+48;up=0;}}}}int main(){string str;int n;int i,j;int s,t;int pos;while(cin>>str>>n){i=5;pos=str.find('.',0);if(pos<0)//没有小数点{ps=0;//zs=zs*n;//后面为0的总数}else//有小数点{ps=(5-pos);ps=ps*n;//小数位总数}memset(ans,0,sizeof(ans)); memset(res[0],0,sizeof(res[0])); memset(res[1],0,sizeof(res[1])); t=5;s=0;while(str[s]=='0' || str[s]=='.') s++;j=0;for(i=t;i>=s;--i){if(str[i]=='.')continue;ans[j]=str[i];j++;}len=j;strcpy(res[0],ans);strcpy(res[1],ans);for(i=2;i<=n;++i){memset(res[(i+1)%2],0,sizeof(res[0]));Multiply(res[i%2],strlen(res[i%2]),ans,len,res[(i+1)%2]); } int L=strlen(res[(n+1)%2]);int d=(n+1)%2;if(ps>0){j=0;while(res[d][j]=='0')j++;if(ps>=L){printf(".");for(i=ps-1;i>=j ;--i){if(i>=L)printf("0");elseprintf("%c",res[(n+1)%2][i]);}}else{if(j>=ps){for(i=L-1;i>=ps;--i)printf("%c",res[(n+1)%2][i]);}else{for(i=L-1;i>=j ;--i){if(i==ps){printf("%c.",res[(n+1)%2][i]);}elseprintf("%c",res[(n+1)%2][i]);}}}}else{for(i=L-1;i>=0;--i)printf("%c",res[(n+1)%2][i]);}printf("\n");}return 0;}2 POJ 1047 Round and Round We Go题意:输入一个数,要求判该数是否为循环数.依次将该数分别于2到len(输入的数的位数)相乘,在乘的过程中,判断数发生了变化没有,如果发生了变化,则直接输出该数不是循环数,没有必要再继续乘下去,而如果是循环数,则一直需要乘下去.#include#include#include#includeusing namespace std;int num[70];int ans[70];char ss[70];bool match[70];int main(){int i,j,k,len;bool flag;while(scanf("%s",ss)!=EOF){len=strlen(ss);for(i=len-1,j=0;i>=0;i--,j++)num[j]=ss[i]-'0';for(i=2;i<=len;i++){memset(ans,0,sizeof(ans));for(j=0;j<len;j++)< p="">//依次将该数与2到len之间的数相乘ans[j]=num[j]*i;for(j=0;j<len;j++)< p="">//循环处理进位if(ans[j]>=10){ans[j+1]+=ans[j]/10;ans[j]%=10;}memset(match,0,sizeof(match)); //match数组用来标记数的匹配情况flag=true;for(j=0;j<len;j++)< p="">{k=0;while(k<len)< p="">{if(ans[k]==num[j]&&!match[k]) //两数字相等且没有进行标记{match[k]=true;break;}k++;}if(k==len)//此时说明相乘后的结果发生了改变{flag=false;break;}}if(!flag){printf("%s is not cyclic\n",ss);break;}}if(flag)printf("%s is cyclic\n",ss);}system("pause");return 0;}3 POJ 1131 Octal Fractions给定一个八进制的小数题目要求你把它转换为十进制小数，转换后小数的位数是转换前八进制小数位数的3倍且不输出末尾无意义的零(即后置零). 我采用的方法是乘10然后对8取整(现在假设将p进制的小数转换为n进制,同样采用乘n取整:),每转换一位,都必须从最低位s[len-1]开始至小数的最高位(即小数点后的一位),每次计算积g=a[j]*n+k(其中k为下一位积的进位),本位进位数k=g/p,积在本位存入s[j]=g%p;最后的整数k作为转换的一位存放于转换结果字符串中。

ACM竞赛数学部分

常用公式 (2)划分问题： (3)Stirling公式 (3)皮克定理 (3)卡特兰数 (4)错排公式 (4)等比数列 (5)等差数列 (5)二次函数 (6)二次方程 (7)约瑟夫环 (7)多边形面积 (7)均值不等式的简介 (8)均值不等式的变形 (8)Lucas 定理 (9)斐波那契数列 (10)欧拉函数 (11)蚂蚁爬绳 (12)(a/b)%m (13)泰勒公式 (13)乘法与因式分解公式 (14)三角不等式 (14)某些数列的前n项和 (15)二项式展开公式 (15)三角函数公式 (16)常用公式划分问题：1、n个点最多把直线分成C(n,0)+C(n,1)份；2、n条直线最多把平面分成C(n,0)+C(n,1)+C(n,2)份；3、n个平面最多把空间分成C(n,0)+C(n,1)+C(n,2)+C(n,3)=(n³+5n+6)/6份；4、n个空间最多把“时空”分成C(n,0)+C(n,1)+C(n,2)+C(n,3)+C(n,4)份. Stirling公式lim(n→∞) √(2πn) * (n/e)^n = n!也就是说当n很大的时候,n!与√(2πn) * (n/e) ^ n的值十分接近这就是Stirling公式.(2πn) ^0.5×n^ n ×e^(-n) =n!;皮克定理一个多边形的顶点如果全是格点，这多边形就叫做格点多边形。

有趣的是，这种格点多边形的面积计算起来很方便，只要数一下图形边线上的点的数目及图内的点的数目，就可用公式算出。

这个公式是皮克(Pick)在1899年给出的，被称为“皮克定理”，这是一个实用而有趣的定理。

给定顶点坐标均是整点（或正方形格点）的简单多边形，皮克定理说明了其面积S和内部格点数目a、边上格点数目b的关系：S=a+ b/2 - 1。

(其中a表示多边形内部的点数,b表示多边形边界上的点数,S表示多边形的面积) 卡特兰数原理:令h(1)＝1,h(0)=1，catalan数满足递归式：h(n)= h(0)*h(n-1)+h(1)*h(n-2) + ... + h(n-1)h(0) (其中n>=2)另类递归式：h(n) = h(n-1)*(4*n-2)/(n+1);该递推关系的解为：h(n)=C(2n,n)/(n+1) (n=1,2,3,...)卡特兰数的应用（实质上都是递归等式的应用）错排公式当n个编号元素放在n个编号位置,元素编号与位置编号各不对应的方法数用M(n)表示,那么M(n-1)就表示n-1个编号元素放在n-1个编号位置,各不对应的方法数,其它类推.第一步,把第n个元素放在一个位置,比如位置k,一共有n-1种方法;第二步,放编号为k的元素,这时有两种情况.1,把它放到位置n,那么,对于剩下的n -2个元素,就有M(n-2)种方法;2,不把它放到位置n,这时,对于这n-1个元素,有M(n-1)种方法;综上得到递推公式：M(n)=(n-1)[M(n-2)+M(n-1)] 特殊地，M(1)=0,M(2)=1通项公式：M(n)=n![(-1)^2/2!+…+(-1)^(n-1)/(n-1)!+(-1)^n/n!]优美的式子：Dn=[n!/e+0.5],[x]为取整函数．公式证明较简单．观察一般书上的公式，可以发现e-1的前项与之相同，然后作比较可得/Dn-n!e-1/<1/(n+1)<0.5,于是就得到这个简单而优美的公式（此仅供参考）等比数列(1) 等比数列：a (n+1)/an=q (n∈N)。

ACM必做50题的解题-计算几何

ACM必做50题的解题-计算几何.txt生活，是用来经营的，而不是用来计较的。

感情，是用来维系的，而不是用来考验的。

爱人，是用来疼爱的，而不是用来伤害的。

金钱，是用来享受的，而不是用来衡量的。

谎言，是用来击破的，而不是用来装饰的。

信任，是用来沉淀的，而不是用来挑战的。

POJ 1113 WALL计算几何，求凸包这题的结果等于这个多边形构成的凸包的周长加上以所给半径为半径的圆的周长步骤如下：1)算法首先寻找最最靠下方的点，如果遇到y坐标相同，则寻找x坐标最小的点firstP2)然后根据所有点相对于firstP的偏角的大小进行排序，遇到偏角相等的，只取距离firstP最远的点(排序利用自己手写的快排)3)然后利用Graham算法求凸包4)最后直接求职#include <iostream>#include <cmath>#define PI 3.1415926#define MAX_N 1000using namespace std;//存储原始输入的坐标值，rad是输入的半径double cord[MAX_N + 2][2], rad;int seq[MAX_N + 2];int stack[MAX_N + 2];int n, top;int firstP;int realN;void swap(int pos1, int pos2){int temp = seq[pos1];seq[pos1] = seq[pos2];seq[pos2] = temp;}int dir(int nodes, int node1, int node2){double x1 = cord[node1][0], y1 = cord[node1][1];double x2 = cord[node2][0], y2 = cord[node2][1];double sx = cord[nodes][0], sy = cord[nodes][1];return (x2 - sx) * (y1 - sy) - (x1 - sx) * (y2 - sy);}double getDist(int node1, int node2){double x1 = cord[node1][0], y1 = cord[node1][1];double x2 = cord[node2][0], y2 = cord[node2][1];double res = sqrt((x1 - x2) * (x1 - x2) + (y1 - y2) * (y1 - y2));return res;}int compare(int node1, int node2){double x1 = cord[node1][0], y1 = cord[node1][1];double x2 = cord[node2][0], y2 = cord[node2][1];double sx = cord[firstP][0], sy = cord[firstP][1];double type = dir(firstP, node1, node2);if(type == 0){double dist1 = (x1 - sx) * (x1 - sx) + (y1 - sy) * (y1 - sy);double dist2 = (x2 - sx) * (x2 - sx) + (y2 - sy) * (y2 - sy);if(dist1 > dist2)return -2;else if(dist1 == dist2)return 0;elsereturn 2;}else if(type > 0)return 1;elsereturn -1;}void fastSort(int start, int end){if(start < end){int curPos = start;int posS = start, posE = end + 1;while(true){while(compare(seq[++posS], seq[curPos]) < 0 && posS < end); while(compare(seq[--posE], seq[curPos]) > 0 && posE > start); if(posS < posE)swap(posS, posE);elsebreak;}swap(curPos, posE);fastSort(start, posE - 1);fastSort(posE + 1, end);}}void sortSeq(){int i, s = 0;for(i = 1; i <= n; i++){//最低最左点不参加排序if(i == firstP)continue;seq[++s] = i;}realN = n - 1;fastSort(1, realN);//清理夹角相同但是距离不同的点，只取举例firstP最远的点i = 1;while(i < realN){s = i + 1;//equal angle but smaller distancewhile(s <= realN && compare(seq[i], seq[s]) == -2) {seq[s] = -1; //置为无效s++;}i = s;}}//寻找凸包void findQ(){int nodes, node1, node2, type;top = 0;stack[top++] = firstP;int s = 1;int c = 0;while(c < 2){if(seq[s] != -1){c++;stack[top++] = seq[s];}s++;}for(; s <= realN; s++){if(seq[s] == -1)continue;while(true){nodes = stack[top - 2];node1 = stack[top - 1];node2 = seq[s];type = dir(nodes, node1, node2);if(type >= 0)top--;elsebreak;}stack[top++] = seq[s];}}double getRes(){double totalDist = 0;int lastNode = firstP;int curNode;while(top > 0){curNode = stack[--top];totalDist += getDist(lastNode, curNode);lastNode = curNode;}//totalDist += getDist(lastNode, firstP);totalDist += 2 * PI * rad;return totalDist;}int main(){int i;cin>>n>>rad;int minX = INT_MAX, minY = INT_MAX;for(i = 1; i <= n; i++){cin>>cord[i][0]>>cord[i][1];if((cord[i][1] < minY) || (cord[i][1] == minY && cord[i][0] < minX)){firstP = i;minX = cord[i][0];minY = cord[i][1];}}sortSeq();findQ();double res = getRes();printf("%.0f\n", res);return 0;}POJ1292 Will Indiana Jones Get There?题目大意：英雄Jones现在在位置1，有人在位置2呼救，所以他要过去救他，但是有个条件，他必须在墙上走，其实就是说他只能在图示的线段上走，但是线段间有空隙，所以要用一个长板搭在线段间才能从一个线段到另外一个线段，问怎么找到一个路径使得要使用的长板最小。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

1、POJ 2249 Binomial Showdown组合数学。

高精度，也可把分子分母的数组进行两两约分#include<iostream>using namespace std;double c(int c,int k){double a=1;int i,j=2;for(i=c;i>c-k;i--)a=a*i/(c-i+1);return a;}int main(){int n,k;while(scanf("%d%d",&n,&k)!=EOF && (n!=0 || k!=0)){if(k>n/2 )k=n-k;printf("%.0lf\n",c(n,k));}return 0;}2、poj 1023 the fun number system （经典进位制）题意：一种由2进制衍生出来的进制方法（我们暂且称为“类2进制”）；标明'n'的位置上原2进制该位的权重要乘上-1，才是现在进制方法该位的权重；譬如说；pnp对于的能表示的数2来说就是110；即1*2^2+(-1)*1*2^1+1*2^0=2;算法：这是数论中的进位制问题，我们可以仿照原来的求一个数二进制表示方法；但首先，我们应该考虑几个问题；①k位这种类2进制的表示范围；显然，当给出的'p','n'序列中，我们将所有p的位置都置为1其余位是0，此时最大；当我们将所有n的位置置为1，其余为0，此时最小；不过当我们求最大限max和最小限min时会有一个溢出问题；比如64位全是p的序列，那么max会溢出，值为-1；同理min在全是n 时也会溢出，为1；显然是max>=0,min<=1,溢出时产生异常，依次可以判断；②是否是最大限和最小限之间的数都能表示呢？都可以，而且能够表示的数是2^k个，这个原始2进制是一样的；因为每个位上要么是0，要么是1，而且每个位上的权重唯一的，不能通过其他位的01组合获得；最后，我们就可以仿照原始二进制来算在类2进制下的表示；不断求N的二进制最后一位和右移；如果取余是1，则该位上一定是1，如果该位对于字母为‘n’，则高位应该再加1；这里对2取余可能会出错，因为对于负数，补码的表示，最后一位一定是和原码一样的每次的右移后(有时需先加1）补码表示正好符合要求（可找实例验证）；#include<iostream>using namespace std;__int64 N,M;char s[100],res[100]={'\0'};int main(){int T;scanf("%d",&T);int i,j;__int64 _max,_min;char ch;while(T--){scanf("%I64d",&N);scanf("%s",s);_max=0;_min=0;for(i=0;i<N;i++) //找出能表示的范围；{if(s[i]=='p') _max=2*_max+1,_min*=2;else _min=2*_min-1,_max*=2;}scanf("%I64d",&M);if((M<_min&&_min<=0)||(M>_max&&_max>=0)) puts("Impossible"); //注意防止64位数的溢出；else{memset(res,'\0',sizeof(res));for(i=N-1;i>=0;i--){int flag=0;if(M&1) //这里不能是平常的%2；{res[i]='1';if(s[i]=='n') flag=1;}else res[i]='0';M>>=1;if(flag) M++; //如果是n就需其高位加1；}printf("%s\n",res);}}system("pause");return 0;}3、POJ2506 Tiling 递推+高精给看似复杂的题找到了合适的规律就会变得简单。

这个题就是这样。

对于n列来说，可以在n-1列的基础上加上一块，或者是在n-2列的基础上加上2块而2块独立的，不依赖于1块的情况有两种，所以得到递推公式f(n)=f(n-1)+2f(n-2)看样例，要用到高精。

#include<iostream>//f(n)=f(n-1)+2f(n-2)using namespace std;int f[251][300];void HPprint(int *a){for (int i=a[0];i>=1;i--) cout<<a[i];cout<<endl;}void HPplus(int *a,int *b,int *c){int i,j;j=0;for(i=1;i<=min(a[0],b[0]);i++){c[i]=a[i]+b[i]+j;j=c[i]/10;c[i]%=10;}if(j!=0) c[i]=j;c[0]=a[0]>b[0]?a[0]+2:b[0]+2;while(c[c[0]]==0 && c[0]>1) c[0]--;}void HPmultyNUM(int *a,int b,int *c) {int i,j,k;for (i=1;i<=a[0];i++)c[i]+=a[i]*b;k=0;for (j=1;j<=a[0];j++){c[j]+=k;k=c[j]/10;c[j]%=10;}//进位if(k!=0) c[j]=k;c[0]=a[0]+3;while (c[c[0]]==0 && c[0]>1) c[0]--; }int main(){int i,j,t[300],test;f[0][0]=1;f[0][1]=1;f[1][0]=1;f[1][1]=1;f[2][0]=1;f[2][1]=3; for(i=3;i<=250;i++){memset(t,0,sizeof(t));HPmultyNUM(f[i-2],2,t);HPplus(t,f[i-1],f[i]);}while(cin>>test)HPprint(f[test]);return 0;}4、POJ 1079 Ratio 分数操作题目大意：给出一个分数，比如1498/902。

求出当分母分别为1, 2, ....的时候，最接近1498/902的分数。

比如：当分母为1的时候，最接近1498/902的分数为1/1。

当分母为2的时候，最接近1498/902的分数为3/2。

当分母为3的时候，最接近1498/902的分数为5/3。

思路：不要用高精度哦，直接模拟分数的操作最好了。

#include <stdio.h>#include <math.h>struct frac {__int64 up, down;};__inline __int64 gcd(__int64 a, __int64 b){__int64 r;if (a < b) {r = a;a = b;b = r;}while (1) {r = a % b;if (!r)return b;a = b;b = r;}}__inline struct frac frac_init(__int64 up, __int64 down){__int64 r, s;struct frac f;r = up ? gcd(up, down) : 1;if (r < 0)r = -r;f.up = up / r;f.down = down / r;return f;}__inline struct frac frac_sub(struct frac fa, struct frac fb){return frac_init(fa.up*fb.down-fa.down*fb.up, fa.down*fb.down); }__inline __int64 frac_cmp(struct frac fa, struct frac fb){return frac_sub(fa, fb).up;}__inline struct frac frac_abs(struct frac f){if (f.up < 0)f.up = -f.up;return f;}int main(){__int64 up, down;struct frac target, min_dis, f, dis;while (scanf("%I64d%I64d", &up, &down) != EOF) {target = frac_init(up, down);min_dis.down = 1;min_dis.up = (__int64)1e15;for (down = 1; down <= target.down; down++) {up = (down*target.up)/target.down;if (((down*target.up)%target.down)*2 >= target.down)up++;f = frac_init(up, down);dis = frac_abs(frac_sub(f, target));if (frac_cmp(dis, min_dis) < 0) {printf("%I64d/%I64d\n", f.up, f.down);min_dis = dis;}}printf("\n");}return 0;}5、poj 1019 Number Sequence (找规律)找规律的题目：先计算出从1到n这个小区间有多长，保存到digit[]数组中，然后计算从112123到n一共有多少位数字，然后根据输入数据查找，其中我在找那一位时比较暴力，把从1开始一直存放，直到存放的比那一位还多，然后取出那一位。

#include <iostream>#include <sstream>#include <string>#include <cmath>using namespace std ;const int MaxSize=100000+10 ;__int64 digit[MaxSize], len[MaxSize] ;stringstream ss ;void init(){int i ;digit[1] = len[1] = 1 ;for( i=2; i<MaxSize; ++i ){digit[i] = digit[i-1] + (int)log10((double)i)+1 ;len[i] = len[i-1] + digit[i] ;}/*for( i=1; i<10; ++i ){cout << i << " 位数" << digit[i] << " 长度" << len[i] << endl ;}*/}char getDigit( int num ){int i ;for( i=1; len[i]<num; ++i );int pos = num-len[i-1] ;// 清空ssss.str("");for( i=1; i<=pos; ++i ){ss << i ;//cout << ss.str() << endl ;}return (ss.str())[pos-1] ;}int main(){int i, sets, num ;init() ;cin >> sets ;while( sets-- ){cin >> num ;cout << getDigit( num ) << endl ;}return 0 ;}6、POJ 1095 Trees Made to Order思路：首先，设拥有N个结点的不同形态的有序二叉树有L[N]棵。