磁路与电路对比
《电机学》 -------电路和磁路的比较
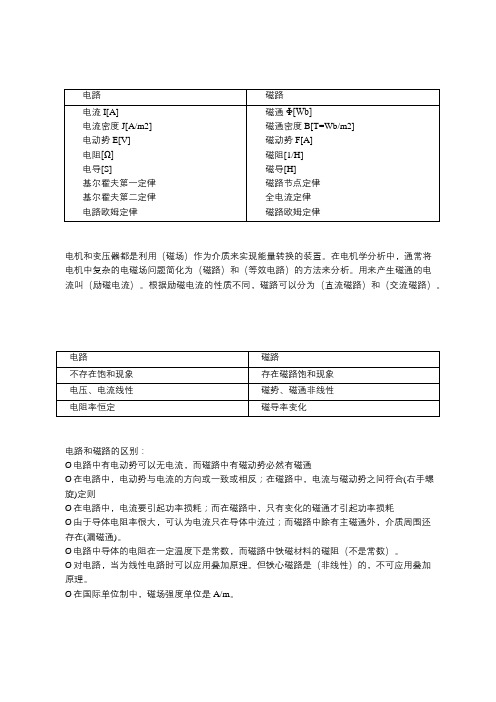
电机和变压器都是利用(磁场)作为介质来实现能量转换的装置。
在电机学分析中,通常将
电机中复杂的电磁场问题简化为(磁路)和(等效电路)的方法来分析。
用来产生磁通的电
流叫(励磁电流)。
根据励磁电流的性质不同,磁路可以分为(直流磁路)和(交流磁路)。
电路和磁路的区别:
Ø电路中有电动势可以无电流,而磁路中有磁动势必然有磁通
Ø在电路中,电动势与电流的方向或一致或相反;在磁路中,电流与磁动势之间符合(右手螺旋)定则
Ø在电路中,电流要引起功率损耗;而在磁路中,只有变化的磁通才引起功率损耗
Ø由于导体电阻率很大,可认为电流只在导体中流过;而磁路中除有主磁通外,介质周围还
存在(漏磁通)。
Ø电路中导体的电阻在一定温度下是常数,而磁路中铁磁材料的磁阻(不是常数)。
Ø对电路,当为线性电路时可以应用叠加原理。
但铁心磁路是(非线性)的,不可应用叠加
原理。
Ø在国际单位制中,磁场强度单位是A/m。
Ø电磁感应定律的物理意义是,当通过闭合线圈的磁通发生变化时,由线圈中的感应电流所
产生的磁场阻碍原来磁通的变化。
一个线圈产生的磁通所经过路径的磁阻越大,说明该线圈
的电感就越小。
啥是磁路啥是电路电路与磁路的差异

啥是磁路?啥是电路?电路与磁路的差异咱们首要来看两个概念:磁路和电路。
那么啥是磁路,啥是电路呢,只需搞了解这两个概念是啥,咱们才干剖析二者之间终究有啥差异。
咱们先来看啥是电路:在电动势或许电压的效果下,电流所流经的途径叫电路。
电路的构成是由电源、负载和开关三有些构造。
而电路又分为直流电路和沟通电路。
流经电路的电流的巨细和方向不随时刻改动的电路,叫做直流电路。
流经电路的电流的巨细和方向随时刻改动的电路,叫做沟通电路。
看完了电路,咱们再来讲讲磁路。
当通电线圈中具有铁芯时,磁动势所发作的磁通,首要会集在由铁芯所规矩的途径内,这种途径就叫做磁路。
而磁路也是分为直流磁路和沟通磁路。
由直流电流励磁的磁路,叫做直流磁路,由沟通电流励磁的磁路,叫做沟通磁路。
电路与磁路一样点的确没有啥可说的。
在电路中,电流是电动势发作的,在磁路中,磁通是由磁动势发作的。
在电路中,电流转过电阻便发作电压降,在磁路中,磁统统过磁阻便发作磁压降。
在电路中,用欧姆规矩来标明电流、电阻和电压降之间的联络,在磁路中,用与电路类似的磁路欧姆规矩来标明磁通、磁阻和磁动势之间的联络。
可是,电路与磁路二者有实质上的差异,首要差异如下:a.在电路中,没有电动势时,电流等于零。
而在磁路没有磁动势时,因为磁滞景象,老是或多或少地存在剩磁。
b.电流代表电荷的移动,而磁通却不代表任何质点移动。
磁统统过滋阻时,不象电流转过电阻那样要耗费能量,坚持安稳磁通也并不需求耗费任何能童。
因而,在电路中可以有断路状况,在磁路中却没有断路的状况,只需有磁动势存在,总会致使相应的磁通,磁通老是接连的。
c.因为铁磁资料具有磁丰满景象,所以磁路的磁阻都对错线性,这与通常状况下电路电阻都是线性电阻是纷歧样的。
因而,磁路欧姆规矩通常只能用来对磁路进行定性剖析。
d.在电路中,导电资料的电导率通常比绝缘资料的电导率大儿千万倍以上,所以电路的漏电十分小,彻底可以疏忽不计。
在磁路中,铁磁资料的磁导率通常比非铁磁资料的磁导率只大几千倍乃至更小。
磁路与电路的相似性探讨

磁路与电路的相似性探讨作者:宋明秋来源:《物理教学探讨》2010年第01期摘要:随着教育教学改革地不断深入,教师应站在科学的高度把握教材。
本文将相似理论的观点赋予电路与磁路的教学中,从磁路与电路中的基本物理量、基本定律、分析方法等方面对磁路问题和电路问题进行了分析比较,得出了磁路与电路具有相似性的结论,并指出了磁路与电路的差异。
可使学习者借用熟悉的电路基础知识和分析方法去理解和掌握磁路,使较难的磁路问题变得简单易懂,并有益于教师提高教学效果。
关键词:磁路;电路;相似性中图分类号:G633.7 文献标识码:A 文章编号:1003-6148(2010)1(S)-0032-2相似理论是站在科学的高度且带有哲学意义的思维理论,具有较高的理论价值和应用价值,物理教学时可以将相似理论赋予其中。
例如:在磁路的教学中将相似理论赋予其中,利用其与电路的相似性进行教学,对提高教学效果十分有益。
下面,我们从磁路与电路的基本物理量、基本定律、分析方法等几个方面,探讨磁路与电路的相似性。
电路是电流流过的回路,它是由电路元件按一定方式连接起来的整体。
磁路是人为造成的磁通易通的路径,它利用具有高磁导率的物质制成一定的形状结构,其周围绕有通有电流的激励磁场的线圈(有些场合也可用永磁体作为磁场激励源)有时还是由适当大小的空气隙组成的整体。
1 磁路与电路的基本物理量的比较(a)在电路中,用电流i这个物理量,描述电流的强弱。
在磁路中,用磁通Φ来描述通过某一面积的磁感应线的多少。
即磁路中的磁通Φ与电路中的电流i相似。
(b)在电路中,有电压U这个物理量,它使某段电路中产生电流。
在磁路中,有磁压降U m这个物理量,它使某段磁路中产生磁通。
即磁路中的磁压降U m相当于电路中的电压降U。
(c)电路中用电源电动势E这个物理量,表示电源把其它形式的能转变为电能的本领。
磁路中,用磁通势F m 这个物理量表示磁源励磁的情况。
即磁路中的磁通势相当于电路中的电源电动势。
磁介质理论的两种观点及其与电介质理论的对照

学苑首页动学堂在线考场电磁课堂科教影院诺贝尔奖科技图库论文集粹物理趣史社区论坛|论坛精华|网络课堂|课堂讨论|科学影院|课件园地|科普之窗首页生命科学概论普物实验精品第一章第二章第三章第四章第五章第六章现在位置电磁学苑->电磁课堂 -> 第七章 -> 第七章学习指南ffdsfdsafdsaffffffsafsafdsaffffffdsafffffffffffffffffffffffffffffffffffffffffffffffffffffffffffd第七章教学指南一、教学目标1.掌握基本概念:(电流观点与磁荷观点对照理解)磁介质(顺、抗、铁磁质),分子环流,磁荷;束缚电流,体磁荷;面磁化电流密度,磁荷面密度;分子磁矩,磁偶极矩;磁化强度,磁极化强度;磁化强度环量,磁极化强度通量;真空磁导率、相对磁导率、绝对磁导率、磁化率(磁极化率);磁化场,磁极化场;退磁化场,退磁化场。
2.理解介质的磁化规律,并与电介质的极化对照3.掌握介质中的高斯定理、安培环路定理,并与电介质的对照4.理解铁磁质的磁化规律及磁滞回线,并与一般介质的磁化规律对照5.掌握简单磁路的串、并联计算,并与电路计算对照6.掌握磁场的能量和能量密度二、本章重点介质的磁化规律、介质中的高斯定理和安培环路定理、铁磁质的磁化规律及磁滞回线、简单磁路计算、磁场的能量和能量密度三、本章内容1.磁介质(1).磁介质的一般分类磁介质:电介质:(2).超导体的抗磁性:在外磁场中B内→0,,,成完全抗磁体。
2.介质的磁化规律(1).磁介质与电介质中两组场量关系的对照电场:磁场:(2).磁介质理论的两种观点及其与电介质理论的对照物理量及规律分子电流观点磁荷观点电介质微观模型分子环流i分子磁矩磁荷磁偶极矩电荷电偶极矩磁化、极化的程度磁化极化后的关系及相关公式宏观效果与平行的界面上出现束缚电流与垂直的界面上出现非自由磁荷与垂直的界面上出现束缚电荷基本场量磁感应强度用电流元受力来定义磁场强应用点磁荷受力来定义(模拟)电场强度用点电荷受力来定义辅助场量磁场强应磁感应强度电位移矢量两种场量间的关系介质对场的影响磁化电流产生附加场磁荷产生附加场极化电荷产生附加场高斯定理环路定理讨算结果殊途同归—————联系磁荷观点公式→→电流观点公式磁荷观点的理论与电荷电场的理论更具有对称性3.铁磁质的磁化规律(1).铁磁质的18个基本概念铁磁质、磁化曲线、起始磁化曲线、-H曲线、磁滞效应、磁滞回线、磁饱和、剩磁、矫顽力、完全退磁曲线、磁畴、居里点、硬磁材料、软磁材料、矩磁材料、永磁体、铁电体、电畴。
磁路的欧姆定律与电路的欧姆定律不同之处

磁路的欧姆定律与电路的欧姆定律不同之处磁路的欧姆定律和电路的欧姆定律是两个不同领域的物理定律,虽然它们都涉及到电流和电压的关系,但在具体应用和理解上存在一些不同之处。
磁路的欧姆定律是用来描述磁场中磁通量密度和磁场强度之间的关系。
根据磁路的欧姆定律,磁通量密度与磁场强度之间呈线性关系,可以表示为B = μH,其中B表示磁通量密度,H表示磁场强度,μ为磁导率。
这个定律类似于电路中的欧姆定律,但不同的是,在磁路中并没有电阻,而是用磁导率来描述材料对磁场的响应能力。
电路的欧姆定律是用来描述电流和电阻之间的关系。
根据电路的欧姆定律,电流与电压之间呈线性关系,可以表示为I = V/R,其中I 表示电流,V表示电压,R表示电阻。
电路的欧姆定律是电学领域中最基本的定律之一,它揭示了电流和电压的关系,为电路的分析和设计提供了重要的理论基础。
在实际应用中,磁路的欧姆定律和电路的欧姆定律也有一些不同之处。
电路的欧姆定律是一个简单的线性关系,只涉及到电流、电压和电阻这三个基本物理量。
而磁路的欧姆定律涉及到磁通量密度、磁场强度和磁导率这些更为复杂的物理量,涉及到更多的物理概念和参数。
电路的欧姆定律适用于封闭的电路系统,可以用来描述电流在电路中的流动情况。
而磁路的欧姆定律适用于磁场中的介质或磁路系统,用来描述磁通量密度和磁场强度之间的关系。
磁路的欧姆定律通常应用在电机、变压器等电磁设备的设计和分析中。
电路的欧姆定律是一种直流电流的定律,适用于恒定电流的情况。
而磁路的欧姆定律可以适用于交流电流的情况,用来描述磁通随时间变化的情况。
磁路的欧姆定律和电路的欧姆定律虽然都涉及到电流和电压的关系,但在具体应用和理解上存在一些不同之处。
磁路的欧姆定律适用于磁场中的磁通量密度和磁场强度之间的关系,而电路的欧姆定律适用于电流和电阻之间的关系。
两者在物理概念、适用范围和应用领域上都存在一些差异,因此需要根据具体情况选择合适的定律进行分析和应用。
磁路和电路的不同点

磁路和电路的不同点英文回答:Differences between magnetic circuits and electric circuits.Magnetic circuits and electric circuits are both used to analyze the flow of energy through a system. However, there are some key differences between the two types of circuits.The type of energy being transported. Magneticcircuits transport magnetic energy, while electric circuits transport electrical energy.The nature of the medium. Magnetic circuits are typically made of ferromagnetic materials, such as iron or steel. Electric circuits are typically made of conductive materials, such as copper or aluminum.The presence of a magnetic field. Magnetic circuits require the presence of a magnetic field in order to operate. Electric circuits do not require a magnetic field.The direction of the flow of energy. In magnetic circuits, the flow of energy is always in the direction of the magnetic field. In electric circuits, the flow of energy is always in the direction of the electric field.中文回答:磁路和电路的区别。
电机学试题(含参考答案)
电机学试题(含参考答案)一、单选题(共40题,每题1分,共40分)1、鼠笼式异步电动机转子磁极数()。
A、与定子磁极数不一定相同B、比定子磁极数小C、与定子磁极数始终保持一致D、比定子磁极数多正确答案:C2、当有交变的磁通通过电机的绕组时,在绕组中会产生()。
A、直流电流B、交流电流C、直流电动势D、交流电动势正确答案:D3、同步发电机的参数中,反映定子漏磁通大小的是(oA、同步电抗XtB、电枢绕组电阻C、电枢漏电抗XQD、电枢反应电抗Xa正确答案:C4、三相交流绕组的对称原则,除了三相绕组完全一样外,还有在电机的圆周空间错开OoA、120B、60C、120D、60度电角度正确答案:C5、当同步发电机的电枢电流I与空载电势E同相位时,其电枢反应性质是(,A、直轴助磁B、纯交轴C、直轴去磁D、直轴去磁兼交轴正确答案:B6、同步发电机进相运行时,有功输出受()限制。
A、电机发热B、转子转速C、静态稳定D、动态稳定正确答案:C7、磁滞损耗的大小与周波()。
A、无关B、成正比C、成反比D、的平方成正比正确答案:B8、电力变压器是常用于改变()的电气设备。
A、交流电源频率大小B、电能大小C、交流电压大小D、直流电压大小正确答案:C9、如果把磁路和电路对比,磁动势比作电动势,磁阳比作电阻,那么应该把O比作电流。
磁感应强度A、磁场强度B、磁导率C、磁通量正确答案:A10、同步电动机负载运行时,励磁磁动势和气隙合成磁动势间的相位关系是().A、同相位B、湍后C、不能确定D、超前正确答案:B11、三相绕线型异步电动机带恒转矩负载运行,当转子回路电阻适当增大,且电机在稳定运行后其定子电流OA、增大B、减小C、不变D、无法判断正确答案:C12、绕线式异步电动机的转子串频敏变阻器起动过程中变阻器阻抗OA、由大变小B、时大时小C、恒定不变D、由小变大正确答案:A13、变压器过负荷运行时,最大负荷不得超过额定负荷的()。
A、10%B、30%C、50%D、20%正确答案:C14、同步发电机不对称运行时,阻尼绕组中会感应()oA、基频感应电动势B、3倍频感应电动势C、不感应电动势D、2倍频感应电动势正确答案:D15、磁路计算时如果存在多个磁动势,则对O磁路可以应用叠加原理。
直交流电磁路异同点
1、直流励磁铁心线圈产生的磁通是恒定的,在线圈和铁芯中不会感应出电动势;
2、在一定电压下,直流励磁铁心线圈中的电流只与线圈本身的电阻有关,功率损耗为P=I2R。
1、交流磁铁心线圈产生的磁通分为主磁通和漏磁通,会分别感应出主磁电动势e和漏磁电动势eΦ;
2、交流磁铁心线圈除电阻R上有功率P=I2R,还有一部分损耗称为铁损,分为磁滞损耗和涡流损耗。
不同点
1、在处理磁路时,离不开磁场的分析;
2、处理磁路是一般要考虑漏磁通;
3、由于剩磁的存在,F=0时,Φ≠0
1、处理电路问题时,一般不涉及电场问题;
2、处理电路是一般可以不考虑漏电流;
3、E=0时,I=0
二.直流励磁铁心线圈与交流磁铁心线圈的异同
直流励磁铁心线圈
交励磁产生磁场
三、交流铁心线圈电路与交流空心线圈电路的异同
交流铁心线圈电路
交流空心线圈电路
相同点
都是通过交流励磁,电路中存在感抗,会产生主磁电动势和漏磁电动势
不同点
1、有铁损
2、产生的磁感应强度较大。
1、无铁损;
2、产生的磁感应强度较小。
四、直流铁心线圈电路与直流空心线圈电路的异同
直流铁心线圈电路
直流空心线圈电路
直交流磁路和电路异同点
一.磁路与电路的异同
磁路
电路
相同点
1磁路与电路都是闭合回路。
2.物理量相似
A、磁路中的磁通与电路中的电流相似;
B、磁路中的磁阻与电路中的电阻相似;
C、磁位差、磁通势分别与电路中的电压、电动势相似。
3.遵循基本定律相似
在任一节点处都遵守基尔霍夫电流定律,电压定律,欧姆定律的约束。
相同点
功率损耗都只有I2R
磁路计算问题及其与电路计算的区别
磁路计算问题及其与电路计算的区别磁路计算问题及其与电路计算的区别1. 引言磁路计算作为电磁学中的重要内容,一直是学习者们所关注的焦点。
它不仅在电机、变压器等电气领域有重要应用,还与电路计算有着一定的联系。
本文将着重探讨磁路计算问题及其与电路计算的区别,帮助读者更深入地理解这一主题。
2. 磁路计算的基础概念磁路计算是指在电磁系统中,通过磁路参数的计算和分析来研究磁场分布、磁通、磁势等问题。
它是电磁学理论的一部分,主要用来描述磁场在磁性材料中的传播和分布规律。
在磁路计算中,需要考虑的因素包括磁通量、磁阻、磁势等。
3. 电路计算的基本原理电路计算是指在电路理论中,通过电流、电压、电阻等参数的计算和分析来研究电路中的电流分布、电压分布、功率分布等问题。
它是电工电子领域的基础课程之一,主要用来描述电流在电路中传播和分布规律。
在电路计算中,需要考虑的因素包括电流、电压、电阻、电感、电容等。
4. 磁路计算与电路计算的区别1) 物理特性不同磁路计算主要研究磁场的传播和分布规律,因此其物理特性主要涉及电磁感应、磁通、磁势等方面;而电路计算主要研究电流的传播和分布规律,因此其物理特性主要涉及电流、电压、电阻等方面。
2) 参数不同在磁路计算中,需要考虑的参数主要包括磁通量、磁阻、磁势等;而在电路计算中,需要考虑的参数主要包括电流、电压、电阻、电感、电容等。
3) 应用范围不同磁路计算主要应用于电机、变压器等电气设备中,用来描述磁场分布和磁通量的变化规律;而电路计算主要应用于电子电路、通信电路、功率电子等领域,用来描述电流、电压、功率的分布和变化规律。
5. 个人观点和理解从个人观点来看,磁路计算与电路计算虽然在物理特性、参数和应用范围上有所不同,但它们都是描述自然界中电磁现象的重要工具。
磁路计算在电气工程中具有重要的应用意义,掌握磁路计算的基本原理对于从事电气工程技术和研究的人员来说是非常必要的。
6. 总结通过本文的讨论,我们深入探讨了磁路计算问题及其与电路计算的区别。
磁路定律及磁路、电路的比较
H1l1 H2l2 H0l0 N i
沿任一闭合磁路,各段磁路上的磁压之和恒等于 磁动势的代数和。
8.3.3 磁路的欧姆定律
这段磁路由磁导率为 的
材料构成,长为 l ,横截面积为
S,穿过的磁通为Φ,其磁压为
Um
Hl
B
l
Sl
l
S
Rm
该段磁路 的磁阻
Rm
l
S
Um
Fm
1/亨利(1/H)
应特别注意:铁磁材料的 值不是常数,导致Rm也
不是常数。所以以下公式仅有定性意义,不便实际计算。
Rm
l
S
Fm Rm
B H
计算时需根据基本磁化曲线,对每一个H 值查对应的B。
8.3.4 交流线圈的电抗
交流线圈的电感系数L为
L N N Fm N N i N 2 N 2 S
i
0
1 2 3 0
1 2 3
进入和穿出任一封闭面磁通的代数和等于零。 进入封闭面的磁通量等于穿出该封闭面的磁通量。
8.3.2 磁路的基尔霍夫第二定律
N i ——磁动势 (磁势 ) Hl ——磁压(磁压降)
磁动势是磁路中有磁场存在的根源。
图示无分支磁路,可按磁路材料不同、横截面积 不同分为三段,每段都为匀强磁场。磁路的基尔霍夫 第二定律表达式为:
内容简介
本教材理论推导从简,计算思路交待详细,概念述 明来龙去脉,增加例题数量和难度档次,章节分 “重计 算”及“重概念”两类区别对待,编排讲究逐步引深的 递进关系,联系工程实际,训练动手能力,尽力为后续 课程铺垫。借助类比及对偶手法,语言朴实简练,图文 印刷结合紧密,便于自学与记忆,便于节省理论教学时 数。适用于应用型本科及高职高专电力类、自动化类、 机电类、电器类、仪器仪表类、电子类及测控技术类专 业。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
N1 2 N1 2 + λ1 R Rl1 c λ = 2 N1 N 2 Rc
N1 N 2 i L Rc 11 1 2 2 = L N2 N i + 2 2 M Rc Rl 2
LM i1 ,即电感矩阵描叙。 很容易说明这 L22 i2
以上的电压电流关系的变压器为理想变压器。 实际中的变压器不可能有去穷大的磁导率,因而必须考虑励磁效应,从而得到非理想变压 器的模型。
此时, Rc > 0 ,电流关系修改成为 N1i1 + N 2 i2 = φ Rc ≠ 0 ,即电流关系出现了一个误差。当副
N1i1 N di di → V1 = 1 1 = Lµ 1 1 。其它线圈也可得到同样的结果。 方开路时候, i2 = 0 , φ c = Rc Rc dt dt
N2
µ c 无关。这种情况下,能量基本存储在气隙之中。
Ni ( lg lc + ) ,它具有与电路理论中的 µ c Ac µ g Ag
φ =
1.2 重 新 回 顾 磁 通 的 计 算 : 磁 阻 模 型
i=
V R1 + R2 的类似的形式。
定义: Ni 为磁势(Magneto-motive Force)
依赖于器件的几何尺寸,材料的性质以及匝数大小。由法拉第定律。 ,
d di =L dt dt
需要注意的几点: 1 电感的大小正比于匝数的平方。一些制造厂商会用 AL 参数定义铁心,其中, A L 为每一匝线圈对应的 nH 大小(或者 1000 匝对应的 mH 数)。因而,电感值的计算公式为:
L = A L× N 2 nH。
2 电感大小正比于导磁材料的磁导率。这是由材料性质决定的。由于磁导率会因为磁 场强度、 环境温度、 时间的变化而变化(非线性),电感值也会因此而改变。 为了稳定电感 L 的大小,我们必须做点其它的工作,其中一种方法就是加入气隙。如下图:
考虑这个加入了气隙的铁心。
H c lc + H g l g = Ni B A = B A = φ φ lg g g φ lc c c ⇒ + = Ni µ c Ac µ g Ag H = Bc , H = B g c g µc µg
B = H ,其中, 为磁导率,是一个由材料性质决定的物理量 (单位 H/m),真空的
磁导率µ0=4π×10H/m。 一般说来,磁通密度与磁场强度的关系都为非线性函数关系。 1.1 让我们考虑设计一个电感,如图。假设外圆半径远远大于环宽,导磁体的磁导率远远大 于真空磁导率,即rc>∆,µ 0。
结论:励磁电感 L 的存在反映了电感在工作时有能量存储在铁心的事实。 可以将励磁电感放在变压器的任何一边,只要按匝数比的平方折算正确即可。 磁化的铁心解释了为什么变压器不能工作在直流环境之中。因为直流感抗为零。
2
V1 = N1
φ 1 dφ 1 ⇒ φ = V1dt ,所以 Bc = = V1 dt ,因为我们要求 B < Bsat ,所以 ∫ dt N1 Ac N 1 Ac ∫
因为只有一条磁路存在,同名端的选取也是显而易见的。我们同样可以允许并联结 构的多绕组线圈。
同理利用无限小磁路阻抗的假设,得到
φ 1 + φ 2 + φ 3 = 0 λ 1 + N 1 V 1 + N1
2 λ N + λ 3 = 0 N 2 3 V V 2 + 3 = 0 N2 N3 N1 i 1 = N2 i 2 = N3 i 3
− LM V1 , 因 而 对 于 实 际 系 统 , 有 L11 V2
LM <
di L11 L22 。否则,如果 V2 = 0 的时候,我们施加一个正的 V1 ,就会发现 1 < 0 ,即 dt L11 L22 ,则两个线圈之间是完美耦 LM − 1 < k < 1。 L11 L22 ,其中
现在让我们考虑变压器,如下图
同名端惯例:流入同名端的电流具有相同的磁通方向。
V1 = V2 =
dλ 1 dφ = N1 dt dt ⇒ V = N 2 V 2 1 dλ 2 dφ N1 = N2 dt dt
电流关系
N i+ φ=1 2,如果 µ c → ∞ ,则 Rc → 0 ,又因为磁通必须为一个有限值,所以 N1i1 = − N 2 i2 。称满足 Rc
无穷多的能量可以从系统中获得。实际中如果 LM =
合的,没有任何的漏电感。故可以定义耦合系数
k=
★ 在理想情况下,考虑多绕组线圈变压器的模型
如果 Rc → 0 ,即不存在漏感成立的话,有
N1i1 + N 2 i2 + N 3i3 = φ Rc = 0
还有
dλ 1 dφ = N1 dt dt dλ 2 V1 V2 V3 dφ V2 = = N2 = = ⇒ dt dt N1 N 2 N 3 dλ 3 dφ V3 = = N3 dt dt V1 =
φ 为磁路中的磁通大小
R= lx µ x Ax 为磁路的磁阻,它反映的是磁路对磁通的阻碍程度。
以上原理对于多绕组线圈(多磁动势)以及并联支路同样适用。因此,它可以用来快速计算结
构较为复杂的磁路系统。 注意到电阻的计算形式为 R =
l l ,磁阻的形式为 µ A ,所以从另一个方面说明了 就 σA
是磁导率,即材料导磁的能力。 1.3 总结:磁路模型 将磁路模型与电路模型进行比较。
电路 电压 EMF 电流 电阻
磁路 磁势 MMF 磁通 磁阻
φ =
如上图所示,
Ni = Rc + Rg
Ni ( lg lc + ) 。求解端电压:每一匝的电动势为 µ c Ac µ g Ag
Vturn =
V=
dφ = N , dt ,整个线圈的电动势就是总匝数的乘积,因而磁链可以定义为
−7
求解此电感的电感值的思路如下: (a) 求出磁场强度 H 大小 (b) 求出磁通 Φ 的大小 (c) 求出磁链大小 ,对于线性电感有 = Li ,这样便可以求解电感值大小。 具体求解的公式: (a) 安培定律:
∮ H⋅d l =∫ J ⋅d A
可以求解出 H 的大小,对于工程上的某些磁路,
我 们可 以简 化为 本质 上的 二维 平面 磁路 ,加 上前 面的 假设 ,此 处可 以简 化为
H⋅l c = N i 。
(b)
B= µH µ A Ni ⇒ φ = µ c Ac H = c c lc φ = bAc
(c) 磁链大小为: λ = Nφ =
µ c Ac N 2 i µ A N2 = Li ⇒ L = c c ,可以看出,电感值大小 lc lc
N2 ( lg lc + µ c Ac µ g Ag di di = L dt dt 。 )
dλ = dt
注意的地方包括: (a) 电感的大小与匝数的平方成正比关系,了解 A L 的电感标定方法。 (b) 为了准确可靠,我们必须要使 µ
c
> > µ 0 , lc > >
Ac , l g < <
Ac 成立
注意到:磁势的方向是由线圈的绕线方向决定的。 绕线端的电器特性是由磁链决定的,参考楞次定律。
∫Vdt=λNφ(+) ∫Vdt=λNφ(+)
1 l1 c 2 l2c
N1 2 N1 2 + V1 Rc Rl1 V = N1 N 2 2 Rc
对应的电路模型为
N1 N 2 d i1 L11 Rc dt = 2 2 L N2 N d + 2 i2 M Rc Rl 2 dt
可以看出,这些关系与串联结构的绕组不同;此时同名端方法不再是一种充分的 描述方法;考虑非理想因素的话,将会有 3 × 3 的矩阵描述。
★ 电感设计技巧 到目前为止,我们只涉及到分析电感。设计电感更加有挑战性,它更是一门艺术。 我们要明确设计中必须满足的种种限制条件,有很多方法可以使这些限制得到满 足。 1 给定一个几何形状已定的铁心,那么电感的大小与线圈绕组匝数的平方成正比。
选择 Ag , l g 要满足 l g < < 3
d LM dt i1 L22 d i2 dt
N1 N N , Lµ 1 = 1 , Ll 2 = 2 。 其中, Ll1 = Rl1 Rc Rl 2
值得注意的是,电感矩阵描述法包含 3 个参数(不包括匝数比),而电路模型包括 4 个参数。 引入物理的匝数比后,我们可以唯一的确定一组电感参数值。 但是这并不重要,有无穷多个 电路模型可以满足电感矩阵描述的端口电气特性。
2
2
2
值得注意的是,在实际的磁路系统中,参数的选择要受到物理限制的。 对于 1 端口网络,为 了保证能量守恒,必须要求电感为正数。同样的道理,在双端口网络中,
V d i1 1 = L− 1 1 = 2 dt i2 V2 L11 L22 − LM
L22 − L M
c 所 以 , φ ( µ A + µ A ) = Ni , 故 c c g g
l
lg
λ = Nφ =
(
N 2i lg , 因 而 , 电 感 大 小 为 lc + ) µ c Ac µ g Ag
L=
λ = i
lg lc lg 。 µ = µ A = A ⇒ lc g 0 c g , 如果 µ > > µ ,电感的大小基本与 ( + ) 因为 0 c µ c Ac µ g Ag
L=
N2 Rc + Rg
