挠度各参数自动计算表
电机转轴的挠度及临界转速计算

b处:f1'= 0.006714438 cm d处:f2'= -0.006606742 cm 5、磁拉力刚度:
转子一:K1= 136812.9233 kg/cm
转子二:K2=
0
kg/cm
6、初始磁拉力:
P1= 1368.129233 kg
P2=
0
kg
7、由磁拉力引起的
挠度:
F0= 1.03954E-12
同步转速:
n=
5781 5000
功率:
P=
300
过载系数:
K=
2.25
2、挠度系数计算:
单位:
cm
cm4
(kg) (kg) (cm) (cm) (cm) (MPa) GS r/min kW
L1=
49
L2=
52.1
L=
126
La=
36
G2=
20
y= 0.388888889
z= 0.285714286
根据y、 z值查图2-119
0 0 0 0
Xi3
91.125 857.375 6331.625 20796.875 34328.125
0 0 0 0 0
Xi3-X(i-1)3
3375 8015.625
7219 18985.75 39170.25 30406.25
0 0 0 0
Kab=
Xi3-X(i-1)3
91.125 766.25 5474.25 14465.25 13531.25
D2无铁心 输入0或 空格
280 2.06E+06
转子二外径: D2=
0
cm
转子一气隙磁密:Bδ1=
挠度计算

h0
ss
sc sc
3、平衡关系:根据裂缝截面的应力分布
C
Ms sc hbh02
Ms ss As hh0
ssAs
10.3 受弯构件的挠度验算
hh0
第十章 变形和裂缝宽度的计算
q 2.0 0.4
Ml 2 (M s M l ) 2 f q S l S l Bs Bs
长期抗弯刚度
Ms 2 f S l Bl
Ms Bl Bs M s (q 1) M l
10.3 受弯构件的挠度验算
第十章 变形和裂缝宽度的计算
六、受弯构件的挠度变形验算 ◆ 由于弯矩沿梁长的变化的,抗弯 刚度沿梁长也是变化的。但按变刚 度梁来计算挠度变形很麻烦。 ◆ 《规范》为简化起见,取同号弯 矩区段的最大弯矩截面处的最小刚 度Bmin,按等刚度梁来计算 ◆ 这样挠度的简化计算结果比按 变刚度梁的理论值略偏大。 ◆ 但靠近支座处的曲率误差对梁 的最大挠度影响很小,且挠度计算 仅考虑弯曲变形的影响,实际上还 存在一些剪切变形,因此按最小刚 度Bmin计算的结果与实测结果的误 差很小。
刚度是反映力与变形之间的关系:
s Ee 应力-应变:
M EI ×f 弯矩-曲率:
EI P 48 × 3 × f 荷载-挠度: (集中荷载) l0 EI V 12 3 d(两端刚接) 水平力-侧移: h
10.3 受弯构件的挠度验算
第十章 变形和裂缝宽度的计算
对钢筋混凝土梁
由于混凝土开裂、弹塑性应力-应变关系和钢筋屈服等影响, 钢筋混凝土适筋梁的M-f 关系不再是直线,而是随弯矩增大, 截面曲率呈曲线变化。
型钢挠度计算公式

型钢挠度计算公式
型钢挠度计算公式是工程计算中常用的一种公式,其计算方法如下:
1. 首先需要知道型钢截面的惯性矩I和弹性模量E,这些参数可以通过型钢的标准参数表或者实验数据得到。
2. 根据型钢的长度L、支撑方式以及施加的载荷P,确定型钢的边界条件。
一般情况下,将型钢固定在一端,另一端受到施加的载荷。
3. 使用欧拉梁理论计算型钢在施加载荷情况下的挠度δ。
欧拉梁理论认为,在弹性区内,型钢在受到轴向压力的作用下,其挠度δ满足以下方程:
δ = (P * L^2)/(π^2 * E * I)
其中,P为施加的载荷,L为型钢的长度,E为型钢的弹性模量,I为型钢的惯性矩。
4. 根据实际情况,可以对计算结果进行修正。
例如,考虑型钢的材料强度、几何形状、温度等因素对挠度的影响,可以通过引入修正系数进行修正。
综上所述,型钢挠度计算公式是一种基于欧拉梁理论的公式,可以用于计算型钢在施加载荷情况下的挠度。
在实际应用中,需要根据具体情况确定边界条件和修正系数,以得到更准确的计算结果。
- 1 -。
转轴的挠度及临界转速计算

转轴的挠度及临界转速计算程序(一)具有集中载荷的两支点轴承的计算(如图2-118)一、绕度及临界转速计算3、轴在b点的柔度:αbb= 4.99225E-06cm/kg4、磁拉力刚度:K0=49554.06333kg/cm5、初始单边磁拉力:P0=991.0812667kg6、由G1重量引起的b点绕度:f1=0.007881595cm7、滑环重量G2引起的b点绕度:f2=0.000163144cm8、单边磁拉力引起的b点绕度:fδ=0.008495762cm9、轴在b点的总绕度:f=0.016540502cm应小于异步电机同步电机10、转轴临界转速:n kp=2802.141933rpm二、轴的强度计算:1、最大转矩:Mmax=10170.75N.m2、bb点处的弯矩:Mbb=8752.669171N.m3、bb处的交变弯矩应力:σbb=9451105.897N/m24、bb处的剪切应力:τbb=5491172.66N/m2τn=2745586.33N/m2脉动循环下的剪切应力:τ∞=6863965.824N/m25、轴在bb处受到的总负荷应力:σ=16.66671863N/mm2应该小于材料许用[σ]=三、轴承计算:1、转子所受最大径向力:W=2301.081267kg2、a处轴承支承力:Pa=1192.429249kg3、c处轴承支承力:Pc=1045.819095kgLh=1456982.883小时 应大于10^5式中:ε=3.33f t=1载荷系数F f=1.1温度系数c=39600轴承额定动负荷P i=1045.82当量动负荷4、轴承寿命:(二)带外伸端的两支点轴承的计算(如图2-120)一、基本参数:电枢重量(G1包括转轴中部重量的2/3和滑环的重量在内)一、绕度及临界转速计算2、柔度系数计算:3、轴的柔度:α11=7.56093E-07cm/kgα22= 2.42497E-06cm/kgα12=-8.91046E-07cm/kgα21=-8.91046E-07cm/kg4、转子重量所引起的挠度:b处:f1'=0.006714438cmd处:f2'=-0.006606742cm5、磁拉力刚度:转子一:K1=136812.9233kg/cm转子二:K2=0kg/cm6、初始磁拉力:P1=1368.129233kgP2=0kg7、由磁拉力引起的挠度:F0= 1.03954E-12E0=0.896556679b处:f1"=0.001153785cmd处:f2"=-0.001359721cm8、总挠度:同步机b处:f1=0.007868222cm应该<0.008d处:f2=-0.007966462cm应该<09、临界转速:一次:n k=3506.387398rpm应该>975(cm)(cm)(cm)(cm)(kg)曲线cmcm-1[X i3-X(i-1)3]/J i0.0158060470.6150555471.00413328510.3702657246.3391216458.34438224[X i3-X(i-1)3]/J i0.0158060474.2301062568.2384035378.674287214.41912717947.9333411973.511071410.02cm0.016cm55N/mm 2小时(cm)(cm)(cm)(cm)Mpa异步机cm应该<0.01cm cm应该<0cmrpm满足要求。
工字钢挠度计算公式

工字钢挠度计算公式工字钢是一种常见的结构钢材,广泛应用于建筑、桥梁、机械制造等领域。
在使用过程中,我们常常需要了解工字钢的挠度情况,以便评估其承载能力和结构稳定性。
工字钢的挠度计算是基于悬臂梁的理论基础上进行的。
悬臂梁是指梁的一端固定,另一端自由悬挂。
工字钢在实际应用中常常处于悬臂状态,因此可以采用相应的悬臂梁挠度计算公式进行计算。
工字钢的挠度计算公式如下:δ = (5 * q * L^4) / (384 * E * I)其中,δ表示工字钢的挠度,q表示悬臂梁上的集中载荷,L表示悬臂梁的长度,E表示工字钢的弹性模量,I表示工字钢截面的惯性矩。
在实际应用中,我们需要根据具体的工字钢尺寸和载荷情况来计算挠度。
首先,我们需要测量工字钢的长度L,并计算出截面的惯性矩I。
惯性矩是描述截面形状对于承载能力的影响的重要参数,可以通过工字钢的几何尺寸计算得出。
接下来,我们需要确定悬臂梁上的集中载荷q。
集中载荷是指作用在悬臂梁上的单点力或集中力,可以通过实际测量或结构设计参数得出。
我们需要知道工字钢的弹性模量E。
弹性模量是描述材料对外力作用下变形程度的物理量,可以通过实验测量或查阅资料得到。
根据上述计算公式,我们可以将具体数值代入进行计算,从而得出工字钢的挠度。
挠度的数值可以帮助我们评估工字钢的承载能力,如果挠度过大,则可能存在结构安全隐患,需要采取相应的加固措施。
工字钢挠度的计算也对工字钢的设计和选型具有重要意义。
通过计算不同尺寸和材质的工字钢的挠度,可以比较不同方案的承载能力和结构稳定性,从而选择合适的工字钢材料和尺寸。
工字钢的挠度计算是工程设计和结构评估中重要的一环。
通过合理计算工字钢的挠度,可以评估其承载能力和结构稳定性,为工程安全提供重要参考。
同时,工字钢挠度的计算也对工字钢的设计和选型具有指导意义,帮助选择合适的工字钢材料和尺寸。
工字钢挠度

工字钢挠度1.什么是工字钢挠度工字钢是建筑、制造等领域中常用的材料,它具有良好的承重能力和稳定性。
然而,在实际应用过程中,工字钢会受到外力的影响,从而发生挠曲变形。
挠度是指杆件在受到一定负载后所产生的弯曲程度,它是衡量工字钢杆件承载能力的重要参数。
2.工字钢挠度的计算方法工字钢挠度的计算一般采用物理方法或数学方法,其中物理方法主要是使用钢尺和测量仪器进行直接测量,而数学方法则是通过公式计算挠度大小。
主要的计算公式如下:①一般静载荷情况下的挠度计算公式:δ=5q*L^4/(384EI)其中,q为单位长度的荷载,L为杆件长度,I为截面惯性矩,E 为弹性模量。
②无固定端支承的工字钢挠度计算公式:δ=qL^4/(8EI)其中,q、L、I、E的含义与上述相同。
根据实际情况选择合适的公式进行计算,可以得到工字钢的挠度大小。
3.工字钢挠度的影响因素工字钢挠度的大小主要受到以下几个因素的影响:①荷载大小:荷载越大,工字钢发生弯曲的程度就越大,从而挠度也会增大。
②杆件长度:杆件长度越长,对荷载的承载能力就越低,挠度也会增大。
③截面惯性矩大小:截面惯性矩越小,工字钢发生弯曲的程度就越大,挠度也会增大。
④材料弹性模量:弹性模量越小,挠度也会越大。
4.工字钢挠度的应用在实际应用中,需要对工字钢的挠度进行评估,以确保其承载能力的安全性。
一般情况下,工程师可以根据工字钢杆件的设计荷载、长度、截面尺寸和材料弹性模量等参数,选择合适的计算公式对其挠度进行计算。
同时,还需比对计算结果与国家标准或行业标准的值,以确认其是否满足规定的安全性要求。
如果工字钢的挠度超标,则需要进行结构优化或采取加固措施来提高其承载能力。
5.工字钢挠度计算的注意事项①所用公式应为经过验证的科学公式。
②物理测量时,需要注意测量仪器的精度,以避免测量误差。
③杆件真实情况与公式中所假设的情况可能存在差异,因此,计算结果仅供参考,不可盲目使用。
④应严格按照设计荷载、设计长度等参数进行计算,以确保计算结果的准确性。
预应力裂缝和挠度计算
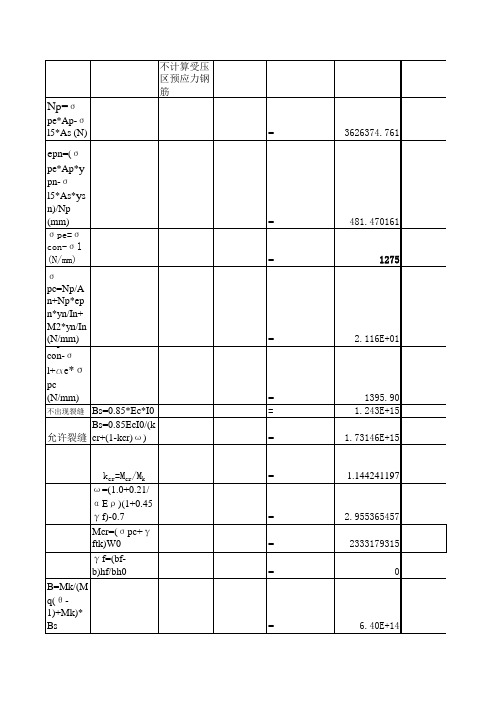
3626374.761 481.470161 1275 2.116E+01 1395.90 1.243E+15 1.73146E+15 1.144241197 2.955365457 2333179315 0 6.40E+14
epn=(σpe*Ap*ypn-σl5*As*ysn)/Np (mm)
三级 标准组合并考虑长期作用的最大裂宽 ωmax≤ω1im ω1im-最大裂缝宽度限值按第3.3.4条采用 ωmax=αcr*ψ*σsk/Es*(1.9c+0.08deq/ρte)= ψ=1.1-0.65ftk/(ρte*σsk)= deq=Σni*(di)^2/Σni*vi*di= V1 V2 按表8.1.2-2 1 ρte=(As+Ap)/Ate= ok Ate=0.5bh+(bf-b)hf= 暂时不考虑bf.hf σsk=(Mk±M2-Np0(z-ep))/((Ap+As)z)=
σpe=σcon-σl (N/mm) σpc=Np/An+Np*epn*yn/In+M2*yn/In (N/mm) σp0=σcon-σl+ae*σpc (N/mm) 不出现裂缝 Bs=0.85*Ec*I0 允许裂缝 Bs=0.85EcI0/(kcr+(1-kcr)ω) kcr=Mcr/Mk ω=(1.0+0.21/αEρ)(1+0.45γf)-0.7 Mcr=(σpc+γftk)W0 γf=(bf-b)hf/bh0 B=Mk/(Mq(θ-1)+Mk)*Bs
C35
3.150E+04
M设计值 2.51E+09 M恒 1.70E+09 M活 3.38E+08 短期弯矩 Ms 2.04E+09 长期弯矩 Ml 1.92E+09 M2 -5.06E+08
不同横截面下挠度计算公式

不同横截面下挠度计算公式
在工程学中,横截面的挠度计算通常涉及到材料力学和结构力
学的知识。
横截面的挠度可以根据不同的载荷情况和横截面形状使
用不同的计算公式。
以下是一些常见情况下的横截面挠度计算公式: 1. 矩形截面梁的挠度计算公式:
对于矩形截面的梁,当受集中力作用时,挠度可以使用以下
公式计算:
δ = (F L^3) / (3 E I)。
其中,δ表示挠度,F表示受到的力,L表示梁的长度,E
表示杨氏模量,I表示横截面的惯性矩。
2. 圆形截面梁的挠度计算公式:
对于圆形截面的梁,当受均布载荷作用时,挠度可以使用以
下公式计算:
δ = (5 F L^4) / (384 E I)。
其中,δ表示挠度,F表示受到的力,L表示梁的长度,E 表示杨氏模量,I表示横截面的惯性矩。
3. 不同载荷组合下的挠度计算:
在实际工程中,梁可能同时受到多种不同的载荷,例如集中力、均布载荷等。
在这种情况下,需要将各种载荷对挠度的影响进行叠加计算,可以使用叠加原理来计算梁的总挠度。
需要注意的是,以上提到的公式仅适用于一些简单的情况,实际工程中可能会涉及到更复杂的载荷和横截面形状,因此在实际工程中,可能需要使用有限元分析等更复杂的方法来计算横截面的挠度。
挠度计算的准确性也受到材料性质、截面形状、边界条件等因素的影响,需要综合考虑多个因素进行分析和计算。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
砼信息 混凝土强度等级 弹性模量Ec ftk .. fcm 钢砼弹模比 ep/ec es/ec 6.190E+00 5.714E+00 2.2 C35 3.150E+04 19.0
短期弯矩 Ms 长期弯矩 Ml M2 准永久系数
荷载 Mk--荷载效应的标准组合 Mq--荷载效应的准永久组合 2.04E+09 (N*mm) 1.92E+09 (N*mm)
不计算受压区预应力钢筋 Np=σpe*Ap-σl5*As (N) epn=(σpe*Ap*ypn-σl5*As*ysn)/Np (mm) σpe=σcon-σl (N/mm) σpc=Np/An+Np*epn*yn/In+M2*yn/In (N/mm) σp0=σcon-σl+ae*σpc (N/mm) 不出现裂缝 允许裂缝 Bs=0.85*Ec*I0 Bs=0.85EcI0/(kcr+(1-kcr)ω) kcr=Mcr/Mk ω=(1.0+0.21/αEρ)(1+0.45γf)-0.7 Mcr=(σpc+γftk)W0 γf=(bf-b)hf/bh0 B=Mk/(Mq(θ-1)+Mk)*Bs = = = = = = = = = = = = 3626374.761 481.470161 1275 2.116E+01 1395.90 1.243E+15 1.73146E+15 1.144241197 2.955365457 2333179315 0 6.40E+14
0 341.470161
αcr-构件受力特征系数按表8.1.2-1 C= 最外层纵向受拉钢筋外边缘至受拉区底边的距离(mm): 当c<20时取c=20;当c>65时取c=65 判断 OK
1.7
60
挠度验算 正常使用极限状态下的挠度fl1=S*Ml*l^2/B= 预应力产生的短期反拱f2l=Np1*epn*l^2/8/Ec/Io= 预应力产生的长期反拱f2l=Np*epn*l^2/8/Ec/Io*2= 挠度限值表3.3.2 [f]=lo/ 构件挠度 f=f1l-f2l= 挠度判断 OK 300 = 1.25E+02 6.706E+01 1.194E+02 66.66666667 5.66E+00
钢筋信息
预应力钢筋 预钢筋数n 钢筋直径d0 单根钢筋Ap 总面积∑Ap 21 fpy 13.5 fpyk 143.1388153 Ep 3005.915121 受力中心ap 1070 1860 195000 140
σcon=fpyk*(0.65~0.75) 取σcon=fpyk*0.75= 1395
普通钢筋 钢筋数n 钢筋直径d0 单根钢筋As 总面积∑As 6 fpy 25 fpyk 490.8738521 Es 2945.243113 受力中心as 180000 35 340
截面信息 (梁长L) (梁宽b) (梁高h) A=bxh
孔道 20000 直径 500 数量 1000 排数 500000 A孔 40 6 2 7539.822369
调整系数 弯矩系数
2 简支&固定 0.5625
计算恒载 计算活载
48 (N/mm) 12 (N/mm)
M设计值 M恒 M活
2.51E+09 1.70E+09 (N*mm) 3.38E+08 (N*mm) 2.04E+09 (N*mm) 1.92E+09 (N*mm) -5.06E+08 (N*mm) 0.65
其他参数 θ Bs= 规范8.2.5 不出现裂缝选1 2 1
1.24312E+15 允许出现裂缝选2 截面抵抗矩塑性影响γ=(0.7+120/h)γm= γm值按表8.2.4= h按表8.2.4上方= ρ=(Ap+As)/(bh0)= 1.55 600 0.013839903 1.395
受拉翼缘截面面积与腹板有效截面面积的比值 γf=(bf-b)hf/(b*h0)= 0
正截面裂缝验算 一级 σck-σpc≤0 σck-σpc= 判断 NO 2.13E+00
二级 短期效应组合 σck=Mk/W0= σck-σpc= 判断 准永久组合 σcq=Mq/W0= σcq-σpc= 判断 NO OK σcq-σpc≤0 19.94531681 9.043E-01 σck-σpc≤ftk 2.12E+01 2.13E+00
(梁高h) A=bxh
换算截面 A0 S0 W0 y4= σl5= σl6= σl=∑σli= 且σl(后张)≥ σl 结果= a*Es/l= σcon*(kx+μθ)= 2Δt= 应力松弛砼规6.2.1 收缩徐变砼规6.2.5 = 70 30 120 80 120 20
换算截面 A0 S0 W0 yp yp-ap= Ip
净截面 5.219E+05 An 2.516E+08 Sn 96310202.43 Wn 482.0693974 yn 342.0693974 yn-as= 46428201248 In 5.063E+05 2.494E+08 8.864E+07 492.6096666 457.6096666 4.366E+10
三级 ωmax≤ω1im
标准组合并考虑长期作用的最大裂宽
ω1im-最大裂缝宽度限值按第3.3.4条采用 ωmax=αcr*ψ*σsk/Es*(1.9c+0.08deq/ρte)= ψ=1.1-0.65ftk/(ρte*σsk)= deq=Σni*(di)^2/Σni*vi*di= V1 V2 按表8.1.2-2 ok 暂时不考虑bf.hf 1
0.2 0.174182263 0.685277071 25.97172237 0.5 0.023804633 250000 144.8493334 764.3561532 617.557324
ρte=(As+Ap)/Ate= Ate=0.5bh+(bf-b)hf=
σsk=(Mk±M2-Np0(z-ep))/((Ap+As)z)= e=ep+((Mk±M2)/Np0)= z=[0.87-0.12(1-r'f)*(h0/e)^2]*h0= γ'f=(b'f-b)*h'f/(b*h0)= ep=epn-ap= 暂时不考虑bf.hf
