解耦控制例题
合集下载
第七章解耦控制系统-(新)
最后，利用对角矩阵法或单位矩阵法，依据 简化后的传递函数矩阵求出解耦装置 。
2.6
2.7s 1
1
4.5s 1
2.74
1.6 2.7s 1
1 4.5s 1
2.6
0
0
0.87
5．解耦控制系统设计举例
两种料液q1和q2经均匀混合后送出，要求对混合液的流量q和成分a进 行控制，流量q和成分a，分别由q1和q2进行控制。
即每一行元素之和为1，每一列元素之和也为1。
推广到一般情况，也成立。
用途： 第一是可以大大减少计算的工作量。
第二是揭示了相对增益矩阵中各元素之间存在某种定性关系。
4．相对增益与耦合特性
(1)当 0.8 ij 1.2
表明其它通道对该通道的关联作用不强，可不必解耦；
(2)当 0.3 ij 0.7或ij 1.5
3）过程的干扰量与输出量无法测量或难以测量；
4）过程的参数模型难以得到，只能获得非参数模型，如阶跃响应曲线 或脉冲响应曲线等；
5）过程的响应曲线ห้องสมุดไป่ตู้难以得到，只能根据经验得到一系列“如果。。。 则。。。”的控制规则等。
上述过程，均具有不同程度的复杂性，所以将它们统称为复杂过程。面 对这些复杂过程，前面讨论的控制策略和系统设计方法已不能满足要求。 本章将讨论针对上述各种复杂过程进行系统设计的相应方法。
4 解耦控制系统的简化设计
比较常用的方法有：
当过程模型的时间常数相差很大时，则可以忽略较小的时间常数；
当过程模型的时间常数相差不大时，则可以让它们相等。
例： 一个三变量控制系统的过程传递函数阵为
2.6
2.7s 1
1
4.5s 1
2.74
1.6 2.7s 1
1 4.5s 1
2.6
0
0
0.87
5．解耦控制系统设计举例
两种料液q1和q2经均匀混合后送出，要求对混合液的流量q和成分a进 行控制，流量q和成分a，分别由q1和q2进行控制。
即每一行元素之和为1，每一列元素之和也为1。
推广到一般情况，也成立。
用途： 第一是可以大大减少计算的工作量。
第二是揭示了相对增益矩阵中各元素之间存在某种定性关系。
4．相对增益与耦合特性
(1)当 0.8 ij 1.2
表明其它通道对该通道的关联作用不强，可不必解耦；
(2)当 0.3 ij 0.7或ij 1.5
3）过程的干扰量与输出量无法测量或难以测量；
4）过程的参数模型难以得到，只能获得非参数模型，如阶跃响应曲线 或脉冲响应曲线等；
5）过程的响应曲线ห้องสมุดไป่ตู้难以得到，只能根据经验得到一系列“如果。。。 则。。。”的控制规则等。
上述过程，均具有不同程度的复杂性，所以将它们统称为复杂过程。面 对这些复杂过程，前面讨论的控制策略和系统设计方法已不能满足要求。 本章将讨论针对上述各种复杂过程进行系统设计的相应方法。
4 解耦控制系统的简化设计
比较常用的方法有：
当过程模型的时间常数相差很大时，则可以忽略较小的时间常数；
当过程模型的时间常数相差不大时，则可以让它们相等。
例： 一个三变量控制系统的过程传递函数阵为
架构师解耦笔试题
架构师解耦笔试题一、架构师解耦笔试题1. 题型概述这是一份关于架构师解耦知识的笔试题，满分为100分哦。
2. 具体题目第一题（20分）：请简要阐述架构师在项目中进行解耦的重要性。
答案：架构师进行解耦可以提高系统的可维护性。
当系统各个模块之间耦合度低时，修改一个模块不会对其他模块产生过多的影响，这样在项目开发过程中，不同的开发人员可以独立地对各个模块进行开发、测试和维护。
而且在系统升级或者功能扩展时，解耦后的系统更容易添加新的功能模块，而不会牵一发而动全身。
解析：这道题主要考查对架构师解耦基本意义的理解，从开发、维护以及功能扩展等方面来回答就比较全面。
第二题（25分）：列举三种常见的架构解耦方法，并分别举例说明。
答案：分层架构解耦，例如在企业级应用中，将业务逻辑层、数据访问层和表示层分开。
以一个电商系统为例，业务逻辑层负责处理订单、库存等业务逻辑，数据访问层负责与数据库交互获取数据，而表示层负责向用户展示界面。
这样当数据库结构发生变化时，只需要修改数据访问层的代码，不会影响到业务逻辑层和表示层。
消息队列解耦，像在一个分布式系统中，不同服务之间通过消息队列进行通信。
例如电商系统中的订单服务和库存服务，当订单生成时，订单服务向消息队列发送消息，库存服务从消息队列获取消息并进行库存的扣减。
这样订单服务和库存服务不需要直接调用，降低了耦合度。
接口解耦，在软件开发中，模块之间通过接口进行交互。
比如一个图形绘制系统，不同形状（圆形、矩形等）的绘制模块都实现一个绘制接口。
当需要添加新的形状绘制功能时，只要新的模块实现这个接口就可以，不需要修改其他模块的代码。
解析：这道题考查对解耦方法的掌握，答案中的举例能更好地说明每种方法的应用场景和解耦效果。
第三题（25分）：在一个已经存在高度耦合的系统中，如何逐步进行解耦？请给出具体步骤。
答案：首先进行系统分析，找出系统中耦合度最高的模块或者功能部分。
例如可以通过分析模块之间的调用关系、数据依赖关系等确定。
现代控制理论系统解耦问题
ഥ 则可表示为：
() = ( − + )− 的两个特征量ҧ 和
ഥ
ҧ
,
ҧ
为满足
(
−
)
≠ 0的最小值
ҧ
= ൝
− 1，当 ( − ) = 0, = 0,1, ⋯ , − 1
ഥ = ( − )
其中： = − = + −1 −1 + ⋯ + 1 + 0
− = , − = + −1 , ⋯ ,
= −1 + −1 −2 + ⋯ + 1
5.4
系统解耦问题
则： () = ( − − + ⋯ + − − + −−1 −− + ⋯ + + )
即 = [11 , 22 , ⋯ , ] 其中 ≠ 0, = 1,2, ⋯ ,
5.4
系统解耦问题
三. 传递函数矩阵的两个结构特征量
1.特征量的定义
设 ()为 × 阶的传递函数矩阵， ()为其第行传递函数向量
即 = [1 , 2 , ⋯ , ]
() = ( − + − )− −
由结构特征量的性质和凯莱－哈密尔顿定理可得：
() = ⋯
() =
+
+
+
⋯
⋯
+
即实现了解耦，充分性得证。
解耦后，各输入输出间的传递函数是多重积分，称为积分型解耦系统。极点在坐
标的原点，其性能在工程上不能被接受。其意义在于理论分析，即可通过简单的
() = ( − + )− 的两个特征量ҧ 和
ഥ
ҧ
,
ҧ
为满足
(
−
)
≠ 0的最小值
ҧ
= ൝
− 1，当 ( − ) = 0, = 0,1, ⋯ , − 1
ഥ = ( − )
其中： = − = + −1 −1 + ⋯ + 1 + 0
− = , − = + −1 , ⋯ ,
= −1 + −1 −2 + ⋯ + 1
5.4
系统解耦问题
则： () = ( − − + ⋯ + − − + −−1 −− + ⋯ + + )
即 = [11 , 22 , ⋯ , ] 其中 ≠ 0, = 1,2, ⋯ ,
5.4
系统解耦问题
三. 传递函数矩阵的两个结构特征量
1.特征量的定义
设 ()为 × 阶的传递函数矩阵， ()为其第行传递函数向量
即 = [1 , 2 , ⋯ , ]
() = ( − + − )− −
由结构特征量的性质和凯莱－哈密尔顿定理可得：
() = ⋯
() =
+
+
+
⋯
⋯
+
即实现了解耦，充分性得证。
解耦后，各输入输出间的传递函数是多重积分，称为积分型解耦系统。极点在坐
标的原点，其性能在工程上不能被接受。其意义在于理论分析，即可通过简单的
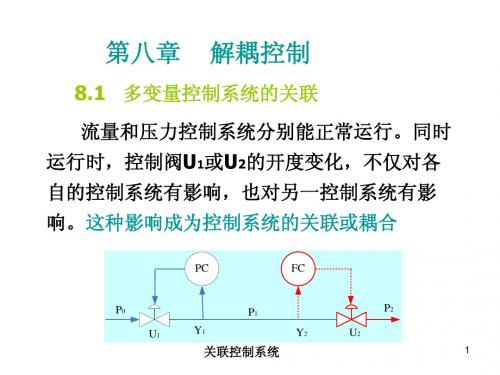
第八章 解耦控制
3
控制系统之间的耦合（关联）程度可用传递函数矩阵表示。 控制系统之间的耦合（关联）程度可用传递函数矩阵表示。
Y( s ) = G ( s ) U( s )
Y1 (s) G 11 (s) G 12 (s) U1 (s) Y (s) = G (s) G (s) U (s) 22 2 21 2
确定各变量之间耦合程度的分析方法有直接法和相对增 确定各变量之间耦合程度的分析方法有直接法和相对增 益法。直接法是采用解析法得到各变量之间的传递函数 益法。直接法是采用解析法得到各变量之间的传递函数 关系，从而确定过程中每个变量相对每个控制作用的耦 关系， 合程度。相对增益法是一种通用的耦合特性分析工具， 合程度。相对增益法是一种通用的耦合特性分析工具， 通过相对增益矩阵，不仅可以确定变量之间的耦合程度， 通过相对增益矩阵，不仅可以确定变量之间的耦合程度， 相对增益矩阵 并且以此去设计解耦控制系统。 并且以此去设计解耦控制系统。
同理
u2
= k11
= k 21，p22 = ∂y2 ∂u2 = k 22
7
p12 =
∂y1 ∂u2
u1
= k12，p21 =
∂y2 ∂u1
u2
u1
第二增益系数 qij 输入 u j 对输出 yi 的第二增益系数指其它控制回路 均为闭环（ Y ( s) = 0, k ≠ j ） 该通道的增益，用
k
∂yi qij = ∂u j
17
v22
vn 2
消除和减弱耦合的方法
（1）被控变量（输出变量）与操纵变量（输入变量） ）被控变量（输出变量）与操纵变量（输入变量） 间的正确匹配 若相对增益矩阵为单位阵，则表明过程通道之间没 有静态耦合，系统的每一个通道均可以构成单回路控制。 如果控制系统的相对增益矩阵中有一个相对增益
动态解耦和静态解耦能否实现例题
动态解耦和静态解耦能否实现例题（最新版）目录1.解耦的概念2.动态解耦和静态解耦的定义3.解耦的实现方式4.解耦的例题演示5.解耦的优缺点分析正文一、解耦的概念解耦，是指将一个系统中的多个变量或方程相互独立，从而简化问题的求解过程。
在数学、物理等领域中，解耦是一种常用的求解方法，它可以将复杂问题转化为多个简单的子问题，便于分析和计算。
二、动态解耦和静态解耦的定义动态解耦和静态解耦是解耦的两种方式。
动态解耦是指在微分方程中，通过变量替换或求解特征方程等方法，将多个变量相互独立，从而简化问题。
而静态解耦则是在代数方程中，通过消元或行列式等方法，将多个变量相互独立。
三、解耦的实现方式解耦的实现方式主要包括以下几种：1.变量替换：在微分方程中，通过引入新的变量，将原来的方程转化为多个简单的子方程。
2.求解特征方程：在微分方程中，通过求解特征方程，得到一组特征根，然后将原方程转化为一组简单的子方程。
3.消元：在代数方程中，通过消元或行列式等方法，将多个变量相互独立。
四、解耦的例题演示例如，考虑以下三元一次微分方程组：dx/dt = x + y + zdy/dt = -x + y + zdz/dt = x - y + z通过变量替换法，我们可以将该方程组转化为以下三个简单的一元一次微分方程：du/dt = udv/dt = -vdw/dt = w这样就实现了解耦。
五、解耦的优缺点分析解耦的优点是可以将复杂问题转化为多个简单的子问题，便于分析和计算。
同时，解耦也有助于理解问题的本质，便于理论分析和实际应用。
然而，解耦也有其缺点。
首先，解耦的实现需要一定的技巧和经验，对于一些复杂的问题，解耦可能会变得非常困难。
其次，解耦可能会丢失一些系统的整体特性，因此在某些情况下，解耦可能不是最佳选择。
总的来说，解耦是一种强大的求解方法，它可以将复杂问题转化为多个简单的子问题，便于分析和计算。
然而，解耦的实现需要一定的技巧和经验，对于一些复杂的问题，解耦可能会变得非常困难。
解耦控制decoupling
( p1 p2 ) ( p0 p2 ) ( p0 p1 ) ( p0 p2 )
2
• 如果p1 p2，则I，说明1 h， 2 p1可行
• 如果p1 p0，则11和22 0，而 21和12 1，此时应 重新匹配变量，即1 p1 ， 2 h可行 • 如果p1=(p0-p2)/2， ij=0.5，只能解耦
2
ij 在0 1之间，因为 p0 p1 p2
p0 p1 p0 p2 ( p1 p2 ) p0 p1 p1 p2 p0 p1 p0 p2 ( p0 p1 ) 1 0 Λ 回路间不耦合 0 1 0.5 0.5 Λ 耦合最严重 0.5 0.5
r1
-
Kc1 gc1
1
K11 g11
K21 g21
+
+
y1
K12 g12 r2
-
Kc2 gc2
调节器
2
K22 g22
过程
+
+
y2
二.求取相对增益的方法
1.利用相对增益定义（7-4）来计算 例7-1
PC QC
p1
PT DT
h p2 2
p0 1
压力--流量系统的数学描述：
1 2 ( p0 p2 ) h 1 ( p0 p1 ) 2 ( p1 p2 ) (7 6) 1 2 y1 h, y2 p1
(7 12) (7 13)
y2
K12 K 21 K11 K 22 (7 14)
11
p11 K11 K 22 q11 K11 K 22 K12 K 21
依此办理可得12， 21， 22。 由上例可知，只要有Kij就可推得相对增益，是否可以 有更方便的计算方法？ 假设有一个矩阵H，它与第二放大系数矩阵Q有如下关 系：
线性系统课件解耦控制问题讲解精品文档
5.5 解耦控制问题
一 .动态解耦问题
对象：p个输入，p个输出
x Ax Bu y Cx G (s) C (sI A)1 B
若系统的初始状态为0，则
y1(s)g11(s)u1(s)g12(s)u2(s)g1p(s)up(s) y2(s)g21(s)u1(s)g22(s)u2(s)g2p(s)up(s) yp(s)gp1(s)u1(s)gp2(s)u2(s)gpp(s)up(s)
w
Bw
Dw
xc
r-xc 来自cxc BceKc{A,B,C,D}
-
y
伺服补偿器
K
镇定补偿器
• 对象
x Ax Bu B w w
y Cx Du D w w { A, B, C}能控 , 能观
•
干扰信号
xw Awxw, xw(0)未知
w(t) Cwxw
• 参考信号 xr Arxr, xr(0)未知 r(t) Crxr
1 (s)
使闭环系统稳定的部分 N c (s) D c (s)
在回路中引入(复制)参考信号和扰动信号的模型
1
(s)
这种方法常称为内模原理.
1 (s)
称为内模.
对象 G(s) N(s)
D(s)
的参数变化称为参数摄动.
• 在以上方法中,对象和补偿器的参数变化即使很大,但只
要 D c (s) D (s) (s) N c (s) N (s) 0
令
r(s),w(s)
(s) 是
分别是 Ar , Aw 的最小多项式
r(s),w(s) 位于右半闭S平面上的根
因式的最小公倍式.
一 .动态解耦问题
对象：p个输入，p个输出
x Ax Bu y Cx G (s) C (sI A)1 B
若系统的初始状态为0，则
y1(s)g11(s)u1(s)g12(s)u2(s)g1p(s)up(s) y2(s)g21(s)u1(s)g22(s)u2(s)g2p(s)up(s) yp(s)gp1(s)u1(s)gp2(s)u2(s)gpp(s)up(s)
w
Bw
Dw
xc
r-xc 来自cxc BceKc{A,B,C,D}
-
y
伺服补偿器
K
镇定补偿器
• 对象
x Ax Bu B w w
y Cx Du D w w { A, B, C}能控 , 能观
•
干扰信号
xw Awxw, xw(0)未知
w(t) Cwxw
• 参考信号 xr Arxr, xr(0)未知 r(t) Crxr
1 (s)
使闭环系统稳定的部分 N c (s) D c (s)
在回路中引入(复制)参考信号和扰动信号的模型
1
(s)
这种方法常称为内模原理.
1 (s)
称为内模.
对象 G(s) N(s)
D(s)
的参数变化称为参数摄动.
• 在以上方法中,对象和补偿器的参数变化即使很大,但只
要 D c (s) D (s) (s) N c (s) N (s) 0
令
r(s),w(s)
(s) 是
分别是 Ar , Aw 的最小多项式
r(s),w(s) 位于右半闭S平面上的根
因式的最小公倍式.
【线性系统课件】解耦控制问题讲解
5.6 跟踪问题:无静差性和鲁棒控制
一.问题的提出 SISO系统:对象 设计补偿器
N c (s) Dc (s)
G (s)
N (s) D (s)
,使输入y(t)跟踪参考输入r(t).
W(s)
R (s) + e
N c (s) Dc (s)
+
N (s)
D
1
Y(s)
(s)
-
渐近跟踪: 扰动抑制: 无静差跟踪:
y K
伺服补偿器
镇定补偿器
• 对象
x Ax Bu B w w y Cx Du D w w { A , B, C} 能控 , 能观
• 干扰信号 x w A w x w , x w ( 0 ) 未知
w (t ) C w x w
• 参考信号 令
x r A r x r , x r ( 0 ) 未知 r (t ) C r x r
5.5 解耦控制问题
一 .动态解耦问题
对象：p个输入，p个输出
x Ax Bu y Cx G ( s ) C ( sI A ) B
1
若系统的初始状态为0，则
y 1 ( s ) g 11 ( s ) u 1 ( s ) g 12 ( s ) u 2 ( s ) g 1 p ( s ) u p ( s ) y 2 ( s ) g 21 ( s ) u 1 ( s ) g 22 ( s ) u 2 ( s ) g 2 p ( s ) u p ( s ) y p ( s ) g p 1 ( s ) u 1 ( s ) g p 2 ( s ) u 2 ( s ) g pp ( s ) u p ( s )
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
+
v2
u2 u1 u 2
y 1 v1 y 2 C 1 (1 v 2 ) C 2 v 2 C 1 ( C 1 C 2 ) v 2
调和过程非线性静态解耦（续）
y1 u 1 u 2 y2 C 1u 1 C 2 u 2 u1 u 2 v1 u 1 u 2
y1 f1 ( u 1 , u 2 ) y 2 f 2 (u1 , u 2 )
+
u 1 g 1 ( v1 , v 2 ) u 2 g 2 ( v1 , v 2 )
v1 u 1 u 2
y 1 h1 ( v 1 ) y 2 h2 (v 2 )
y1 u 1 u 2 y2 C 1u 1 C 2 u 2 u1 u 2
C 1 y 20 C1 C 2 y 20 C 2 C1 C 2
u 10 y 10 u 20 y 10
u 20 y 10 u 10 y 10
变量配对举例（续）
7. 分析结论( 假设C1 >y20 >C2 )：
12
1 1 u 10 u 20 1 1 y 20 C 2 C 1 y 20 C 1 y 20 C1 C 2
y 20 C 2 C1 C 2 C 1 y 20 C1 C 2
C 1 y 20 C1 C 2 y 20 C 2 C1 C 2
耦合过程的控制系统设计
经合适输入输出变量配对后，若关联不大， 则可采用常规的多回路PID控制器； 尽管系统稳态关联严重，但主要控制通道动 态特性差别较大，仍可通过调整PID参数， 使各回路的工作频率拉开； 若系统稳态关联严重，而且动态特性相近， 则需要进行解耦设计。
解耦控制系统的实现 1：初始化问题
为非线性 系统！
变量配对举例（续）
1. 设定稳态工作点：Q0（u10, u20, y10, y20）
y 10 u 10 u 20 y 20 C 1 u 10 C 2 u 20 u 10 u 20
u 10 u 20
y 20 C 2 C1 C 2
y 10 y 10
C 1 y 20 C1 C 2
变量配对举例（续）
6. 进行合适的变量配对 ( 假设C1 >y20 >C2 )：
u 10 y 20 C 2 C1 C 2 y 10 , u 20 C 1 y 20 C1 C 2 y 10
y 20 C 2 C1 C 2 C 1 y 20 C1 C 2
K 21 y 2 u1 y2 u 2
Q0 Q0
K 11
y1 u1 y1 u 2
Q0 Q0
1
K 12
1
(C 1 C 2 )u 2 (u1 u 2 )
2 Q0
( C 2 C 1 ) u 20 ( u 10 u 20 )
2
K 22
(C 2 C 1 )u1 (u1 u 2 )
改进的解耦控制方案
Gc1(s) uc1 D21(s) G21(s) u1 G11(s) y1
r1
D12(s) uc2 r2 Gc2(s) u2
G12(s) y2
G22(s)
调和过程的解耦控制举例
FC FC
调和罐 F1, C1
FC
F, C
AC
F2, C2
2. 稳态工作点 Q0 附近偏差化
y 1 y 1 y 10 y 2 y 2 y 20 u 1 u 1 u 10 u 2 u 2 u 20
变量配对举例（续）
3. 工作点 Q0 附近线性化
y 1 K 11 u 1 K 12 u 2 y 2 K 21 u 1 K 22 u 2
r1 Gc1(s) uc1 D11(s) u1 G21(s) G11(s) y1
D21(s)
D12(s) u2
G12(s) y2
r2
Gc2(s)
uc2
D22(s)
G22(s)
问题：若u1, u2为“手动”时，如何设定基本控制器Gc1输 出的初始值，以便无扰动地投入“自动”？
2 Q0
( C 2 C 1 ) u 10 ( u 10 u 20 )
2
变量配对举例（续）
4. 对于稳态工作点 Q0 计算某一相对增益：
y 1 K 11 u 1 K 12 u 2 y 2 K 21 u 1 K 22 u 2
12
p 12 q 12
K 21
( C 1 C 2 ) u 20 ( u 10 u 20 )
2
0 . 2 , K 22
( C 2 C 1 ) u 10 ( u 10 u 20 )
2
0 .3
相对增益矩阵：
0 .6 0 .4
0 .4 0 .6
问题：如何进行变量配对与解耦控制系统设计？
多回路控制方案#1（F-F1, C-F2）
FC
调和罐 F1 , C1
AC
F, C
F2 , C2
调和过程多回路控制模型#1
多回路控制方案#1的闭环响应
多回路控制方案#2（C-F1, F-F2）
FC AC
调和罐 F1, C1
FC
F, C
FC
F2, C2
调和过程多回路控制模型#2
多回路控制方案#2的闭环响应
+
v2
u2 u1 u 2
y 1 v1 y 2 C 1 (1 v 2 ) C 2 v 2 C 1 ( C 1 C 2 ) v 2
v1 u 1 u 2 v2 u2 u1 u 2
u 1 v1 (1 v 2 ) u 2 v1 v 2
调和过程的非线性完全解耦
K 12 K 12 1 1 u 10 u 20 K 11 K 22 K 21 1
1 1
1 K 11 K 22 K 21 K 12
1
1 K 22 K 21
12
y 20 C 2 C 1 y 20
C 1 y 20 C1 C 2
变量配对举例（续）
5. 利用相对增益的性质计算相对增益矩阵：
调和过程工况举例1
F1= 80 T/hr，F2 = 20 T/hr， F = 100 T/hr； C1= 75 %， C2 = 25 %， C = 64 %。 相对增益矩阵为：
0 . 80 0 . 20 0 . 20 0 . 80
输入输出的正确配对： F1 F , F 2 C
调和过程多回路控制仿真模型#3
调和过程多回路控制响应
调和过程动态线性解耦方案
动态线性解耦闭环响应
调和过程线性静态解耦方案
线性静态解耦系统闭环响应
调和过程的部分静态解耦方案
部分静态解耦系统闭环响应
非线性静态解耦的一般结构
y1, sp PID1 v1 非线性 串级 补偿 解耦器 u1 受控 过程 y2 y1
解耦控制系统的实现 2：约束问题
r1 Gc1(s) uc1 D11(s) u1 G21(s) G11(s) y1
D21(s)
D12(s) u2
G12(s) y2
r2
Gc2(s)
uc2
D22(s)
G22(s)
问题：当两回路均为“自动”时，若u2 在运行过程中受 到了约束，两控制器有可能都驱使u1趋向约束。
调和过程解耦控制仿真（续）
模型：
1 y1 ( s ) 2s 1 5s K 21 e y2 (s) ( 2 s 1)( 10 s 1) u (s) 3s 1 1 5 s u (s) K 22 e 2 ( 3 s 1)( 10 s 1) 1
稳态工作点：Q0（ u10, u20, y10, y20）
y 10 y 20 100 50 , u 10 u 20 60 40 , C 1 70 C 20 2
u 10 y 10 u 20 y 10 u 20 y 10 u 10 y 10
（1）变量配对：用量大的操作 变量控总流量；用量小的操作变 量控浓度。 （2）若用量大的操作变量占总 流量75%以上，则只要用常规多 回路就可以；否则，若两种进料 量接近，则需要采用非常规方法， 例如解耦设计。
y2, sp
PID2
v2
u2
y1 f1 ( u 1 , u 2 ) y 2 f 2 (u1 , u 2 )
+
u 1 g 1 ( v1 , v 2 ) u 2 g 2 ( v1 , v 2 )
y 1 h1 ( v 1 ) y 2 h2 (v 2 )
调和过程的非线性静态解耦
调和过程解耦控制系统仿真
被控过程：
y1 F y C , 2 u 1 F1 u F 2 2
y1 u 1 u 2 y2 C 1u 1 C 2 u 2 u1 u 2
变量配对举例(书例7-2)
F1, C1 调和罐 C F2, C2
F
y1 u 1 u 2 y2 C 1u 1 C 2 u 2 u1 u 2