数字逻辑实验、知识点总结(精编文档).doc
数字逻辑知识点总结.doc

数字逻辑知识点总结ch1.1、三极管的截止条件是VVBEBE<<0.5V0.5V,截止的特点是IIbb=I=Icc≈≈00;饱和条件是IIbb≥(≥(EECC--VcesVces))//(β·(β·RRCC)),饱和的特点是VVBEBE≈≈0.7V0.7V,,VVCECE=V=VCESCES≤≤0.3V0.3V。
2、逻辑常量运算公式3、逻辑变量、常量运算公式4、逻辑代数的基本定律根据逻辑变量和逻辑运算的基本定义,可得出逻辑代数的基本定律。
①互非定律:A+A=l,A•A=0;1,;②重叠定律(同一定律):A•A=A,A+A=A;③反演定律(摩根定律):,;④还原定律、三种基本逻辑是与、或、非。
2、三态输出门的输出端可以出现高电平、底电平和高阻三种状态。
ch3.1、组合电路的特点:电路任意时刻输出状态只取决于该时刻的输入状态,而与该时刻前的电路状态无关。
2、编码器:实现编码的数字电路3、译码器:实现译码的逻辑电路4、数据分配器:在数据传输过程中,将某一路数据分配到不同的数据通道上。
5、数据选择器:逻辑功能是在地址选择信号的控制下,从多路数据中选择一路数据作为输出信号。
6、半加器:只考虑两个一位二进制数相加,而不考虑低位进位的运算电路。
7、全加器:实现两个一位二进制数相加的同时,再加上来自低位的进位信号。
8、在数字设备中,数据的传输是大量的,且传输的数据都是由若干位二进制代码0和1组合而成的。
9、奇偶校验电路:能自动检验数据信息传送过程中是否出现误传的逻辑电路。
10、竞争:逻辑门的两个输入信号从不同电平同时向相反电平跳变的现象。
11、公式简化时常用的的基本公式和常用公式有(要记住):1))德.摩根定律)3)))、逻辑代数的四种表示方法是真值表、函数表达式、卡诺图和逻辑图。
ch4.1、触发器:具有记忆功能的基本逻辑单元。
2、触发器能接收、保存和输出数码0,1。
各类触发器都可以由门电路组成。
数字逻辑知识点报告总结

数字逻辑知识点报告总结1. 数字逻辑的定义数字逻辑是一种以数字为基础的逻辑学科,它研究数字之间的关系和数字系统的运算规律。
在数字逻辑中,数字通常表示为0和1,这两个数字是数字逻辑中的基本元素。
数字逻辑研究的范围包括数制、逻辑运算、逻辑代数、逻辑函数、数字逻辑电路等。
2. 基本概念在数字逻辑中,有几个基本概念是必须要了解的,包括数制、位权、数字编码、二进制加法和减法、二进制码等。
其中,数制是指用来表示数字的一组符号和表示方法,位权是指数字中各个位上的数值和位置的关系,数字编码是把数字用一定的代码表示出来,二进制加法和减法是对二进制数字进行加减运算。
3. 逻辑门逻辑门是数字逻辑的基本构件,它用来实现逻辑运算功能。
常见的逻辑门包括与门、或门、非门、异或门和与非门等。
这些逻辑门可以根据输入信号的不同,输出不同的逻辑运算结果。
逻辑门是数字逻辑电路的核心部件,它可以实现各种逻辑功能。
4. 布尔代数布尔代数是逻辑代数的一种,它是一种用来表示逻辑运算的代数系统。
在布尔代数中,逻辑运算可以用加法、乘法和求反运算来表示,这些运算具有一些特定的性质,比如交换律、结合律、分配律等。
布尔代数是数字逻辑的数学基础,它可以用来描述和分析各种逻辑函数和逻辑运算。
5. 逻辑功能在数字逻辑中,逻辑功能是指逻辑门实现的具体功能。
常见的逻辑功能包括与运算、或运算、非运算、异或运算等。
这些逻辑功能可以根据实际需求进行组合和变换,从而实现复杂的逻辑运算。
6. 数字逻辑电路数字逻辑电路是数字逻辑的物理实现,它由逻辑门和其他逻辑功能部件组成。
数字逻辑电路可以用来实现各种逻辑运算、逻辑函数和逻辑功能,它是数字系统中的核心部件。
7. 存储器存储器是一种用来存储信息的设备,它可以用来保存数字信息、程序信息和数据信息等。
在数字逻辑中,存储器通常是由触发器组成的,它可以存储和传输数字信号。
8. 计数器和触发器计数器是一种用来计数和累加的设备,它可以用来实现各种计数功能和定时功能。
数字逻辑知识点总结

ch1.1、三极管的截止条件是V BE <,截止的特点是I b =I c ≈0;饱和条件是 I b ≥(E C -Vces )/(β·R C ),饱和的特点是V BE ≈,V CE =V CES ≤。
2、逻辑常量运算公式3、逻辑变量、常量运算公式4、 逻辑代数的基本定律根据逻辑变量和逻辑运算的基本定义,可得出逻辑代数的基本定律。
①互非定律: A+A = l ,A • A = 0 ;1=+A A ,0=•A A ; ②重叠定律(同一定律):A • A=A , A+A=A ;③反演定律(摩根定律):A • B=A+B 9 A+B=A • B B A B A •=+,B A B A +=•; ④还原定律: A A =ch2.1、三种基本逻辑是与、或、非。
2、三态输出门的输出端可以出现高电平、底电平和高阻三种状态。
ch3.1、组合电路的特点:电路任意时刻输出状态只取决于该时刻的输入状态,而与该时刻前的电路状态无关。
2、编码器:实现编码的数字电路3、译码器:实现译码的逻辑电路4、数据分配器:在数据传输过程中,将某一路数据分配到不同的数据通道上。
5、数据选择器:逻辑功能是在地址选择信号的控制下,从多路数据中选择一路数据作为输出信号。
6、半加器:只考虑两个一位二进制数相加,而不考虑低位进位的运算电路。
7、全加器:实现两个一位二进制数相加的同时,再加上来自低位的进位信号。
8、在数字设备中,数据的传输是大量的,且传输的数据都是由若干位二进制代码0和1组合而成的。
9、奇偶校验电路:能自动检验数据信息传送过程中是否出现误传的逻辑电路。
10、竞争:逻辑门的两个输入信号从不同电平同时向相反电平跳变的现象。
11、公式简化时常用的的基本公式和常用公式有(要记住): 1)()()C A B A BC A ++=+2)B A AB += B A B A +=+ (德.摩根定律) 3)B A B A A +=+4)B A AB BC B A AB +=++5)AB B A B A B A +=+ B A B A AB B A +=+12、逻辑代数的四种表示方法是真值表、函数表达式、卡诺图和逻辑图。
数字逻辑知识点
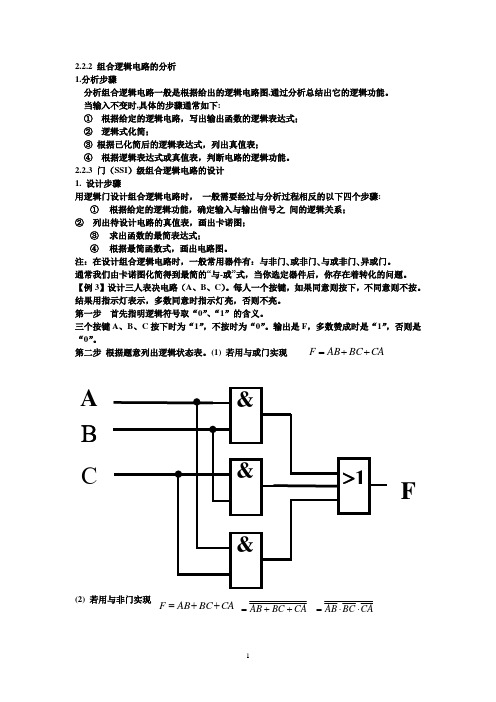
2.2.2 组合逻辑电路的分析1.分析步骤分析组合逻辑电路一般是根据给出的逻辑电路图,通过分析总结出它的逻辑功能。
当输入不变时,具体的步骤通常如下:① 根据给定的逻辑电路,写出输出函数的逻辑表达式;② 逻辑式化简;③ 根据已化简后的逻辑表达式,列出真值表;④ 根据逻辑表达式或真值表,判断电路的逻辑功能。
2.2.3 门(SSI )级组合逻辑电路的设计1. 设计步骤用逻辑门设计组合逻辑电路时, 一般需要经过与分析过程相反的以下四个步骤:① 根据给定的逻辑功能,确定输入与输出信号之 间的逻辑关系;② 列出待设计电路的真值表,画出卡诺图;③ 求出函数的最简表达式;④ 根据最简函数式,画出电路图。
注:在设计组合逻辑电路时,一般常用器件有:与非门、或非门、与或非门、异或门。
通常我们由卡诺图化简得到最简的“与-或”式,当你选定器件后,你存在着转化的问题。
【例3】设计三人表决电路(A 、B 、C )。
每人一个按键,如果同意则按下,不同意则不按。
结果用指示灯表示,多数同意时指示灯亮,否则不亮。
第一步 首先指明逻辑符号取“0”、“1”的含义。
三个按键A 、B 、C 按下时为“1”,不按时为“0”。
输出是F ,多数赞成时是“1”,否则是“0”。
第二步 根据题意列出逻辑状态表。
(1) 若用与或门实现(2) 若用与非门实现ABC FCA BC AB F ++=CA BC AB F ++=CA BC AB ++=CABC AB ⋅⋅=2.2.4 逻辑门多余输入端的处理当设计过程中逻辑门有多余输入端时,一般可按照以下方法进行处理:① 与门、与非门的多余输入端可接到逻辑1所对应的电平上, 或和使用的“与”输入端接到一起;② 或门、 或非门的多余输入端可接到逻辑0所对应的电平上, 或和使用的“或”输入端接到一起;③ 与或非门与项多余输入端的处理方法和与门、与非门相同, 但多余的与项至少应有一个输入端接到逻辑0所对应的电平上, 或完全和使用的与项并联;2.2.4 逻辑门多余输入端的处理当设计过程中逻辑门有多余输入端时,一般可按照以下方法进行处理:① 与门、与非门的多余输入端可接到逻辑1所对应的电平上, 或和使用的“与”输入端接到一起;② 或门、 或非门的多余输入端可接到逻辑0所对应的电平上, 或和使用的“或”输入端接到一起;③ 与或非门与项多余输入端的处理方法和与门、与非门相同, 但多余的与项至少应有一个输入端接到逻辑0所对应的电平上, 或完全和使用的与项并联;2.3.2 模块级电路分析1. 分析方法① 能写出给定逻辑电路的输出逻辑函数表达式时,尽量写出表达式,然后列出真值表,判断电路的逻辑功能;② 不能写出表达式、但能根据模块的功能及连接方法列出电路的真值表时,尽量列出真值表,从真值表判断电路的逻辑功能;③ 既不能写出逻辑表达式、也不能列出真值表时,可根据所使用模块的功能及连接方法,通过分析和推理,判断电路的逻辑功能。
数字逻辑知识点总结

数字逻辑知识点总结数字逻辑有着相当丰富的知识点,包括逻辑门的基本原理、布尔代数、数字信号的传输与处理、数字电路的设计原理等。
在这篇文章中,我将对数字逻辑的一些重要知识点进行总结,希望能够为初学者提供一些帮助。
1. 逻辑门逻辑门是数字电路中的基本单元,它可以完成各种逻辑运算,并将输入信号转换为输出信号。
常见的逻辑门包括与门、或门、非门、与非门、或非门、异或门等。
每种逻辑门都有其特定的逻辑功能,通过不同的组合可以完成各种逻辑运算。
在数字电路设计中,逻辑门是构建各种复杂逻辑电路的基础。
2. 布尔代数布尔代数是表示逻辑运算的一种代数系统,它将逻辑运算符号化,并进行了各项逻辑规则的代数化处理。
布尔代数是数字逻辑的基础,通过布尔代数可以很方便地表达和推导各种逻辑运算,对于理解数字电路的工作原理非常有帮助。
3. 二进制与十进制的转换在数字逻辑中,我们经常需要进行二进制与十进制的转换。
二进制是计算机中常用的数字表示方法,而十进制则是我们日常生活中常用的数字表示方法。
通过掌握二进制与十进制之间的转换规则,可以方便我们在数字逻辑中进行各种数字运算。
4. 组合逻辑与时序逻辑数字电路可以分为组合逻辑电路与时序逻辑电路。
组合逻辑电路的输出只取决于输入信号的瞬时状态,而时序逻辑电路的输出还受到时钟信号的控制。
理解组合逻辑与时序逻辑的差异对于理解数字电路的工作原理至关重要。
5. 有限状态机有限状态机是数字逻辑中一个重要的概念,它是一种认知和控制系统,具有有限的状态和能够在不同状态之间转移的能力。
有限状态机在数字系统中有着广泛的应用,可以用来设计各种具有状态转移行为的电路或系统。
6. 计数器与寄存器计数器与寄存器是数字逻辑中常用的两种逻辑电路。
计数器用于对计数进行处理,而寄存器则用于存储数据。
理解计数器与寄存器的工作原理和使用方法,对于数字系统的设计和应用具有非常重要的意义。
7. 逻辑电路的设计与分析数字逻辑的一大重点是逻辑电路的设计与分析。
数字逻辑实验、知识点总结

数字逻辑实验报告、总结专业班级:计算机科学与技术3班学号:41112115 姓名:华葱一、实验目的1.熟悉电子集成实验箱的基本结构和基本操作2.通过实验进一步熟悉各种常用SSI块和MSI块的结构、各管脚功能、工作原理连接方法3.通过实验进一步理解MSI块的各输入使能、输出使能的作用(存在的必要性)4.通过实验明确数字逻辑这门课程在计算机专业众多课程中所处的位置,进一步明确学习计算机软硬件学习的主线思路以及它们之间的关系学会正确学习硬件知识的方法。
二、实验器材1.集成电路实验箱2.导线若干3.14插脚、16插脚拓展板4.各种必要的SSI块和MSI块三、各次实验过程、内容简述(一)第一次实验:利用SSI块中的门电路设计一个二进制一位半加器1.实验原理:根据两个一位二进制数x、y相加的和与进位的真值表,可得:和sum=x异或y,进位C out=x×y。
相应电路:2. 实验内容:a) 按电路图连接事物,检查连接无误后开启电源b) 进行测试,令<x ,y>={<0,0>,<0,1>,<1,0>,<1,1>},看输出位sum 和C out 的变化情况。
c) 如果输出位的变化情况与真值表所述的真值相应,则达到实验目的。
(二) 第二次实验:全加器、74LS138译码器、74LS148编码器、74LS85比较器的测试、使用,思考各个输入、输出使能端的作用1. 实验原理:a) 全加器i. 实验原理:在半加器的基础上除了要考虑当前两个二进制为相加结果,还要考虑低位(前一位)对这一位的进位问题。
由于进位与当前位的运算关系仍然是和的关系,所以新引入的低位进位端C in 应当与当前和sum 再取异或,而得到真正的和Sum ;而进位位C out 的产生有三种情况:<x ,y ,C in >={<1,1,0>,<1,0,1>,<0,1,1>},也就是说当x 、y 、C in 中当且仅当其中的两个数为1,另一个数为0的SumCout时候C out =1,因此:C out =xy+xC in +yC in 得电路图(也可以列出关于C in 的真值表,利用卡诺图求解C in 的函数表达式):ii. 实验内容:进行测试,穷举<x ,y ,C in >的8中指派作为测试,重点测试<x ,y ,C in >={<1,1,0>,<1,0,1>,<0,1,1>}这三种情况。
数字逻辑复习知识点

数字逻辑课程知识点第一章数字逻辑概论1.计算机中常见的几种数制及其转换方法(十进制、二进制、十六进制)2.有符号数的补码表示方法(要求会求符号数的补码或从补码求实际的有符号数)3.掌握ASCII码概念。
知道常用字符(空格、数字0-9和字母A – Z,a- z等)的ASCII 码。
4.掌握8421BCD码的概念,会用BCD码表示十进制数5.掌握基本逻辑运算(“与”、“或”、“非”、“与非”、“或非”、“异或”以及“同或”等运算)及其逻辑符号。
6.掌握逻辑函数的5种表示方法(真值表表示法、逻辑表达式表示法、逻辑图表示法、波形图表示法、卡诺图表示法)第二章逻辑代数1.逻辑代数的基本定律和恒等式(摩根定理)2.逻辑代数的基本规则(代入规则、反演规则、对偶规则)3.把“与---或”表达式变换为“与非---与非”和“或非---或非”表达式的方法4.逻辑函数的代数化简方法:并项法(A+/A=1)吸收法(A+AB=A)消去法(A+/AB=A+B)配项法(A=A*(B+/B))5.卡诺图的特点:每个小方格都惟一对应于一个不同的变量组合(一个最小项),而且,上、下、左、右在几何上相邻的方格内只有一个因子有差别。
任何一个函数都等于其卡诺图中为1的方格所对应的最小项之和。
6.掌握用卡诺图化简逻辑函数的方法7.理解无关项的概念:即实际应用中,在真值表内对应于变量的某些取值,函数的值是可以任意的,或者这些变量的取值根本不会出现,这些变量取值对应的最小项即称为无关项或任意项,每个无关项的值既可以取0,也可以取1,具体的取值以得到最简的函数表达式为准。
第三章MOS逻辑门电路1.数字集成电路的分类:从集成度方面分:小规模(SSI)、中规模(MSI)、大规模(LSI)、超大规模(VLSI)和甚大规模(ULSI)。
从制造工艺方面分:CMOS、TTL、ECL以及BiCMOS等2.CMOS的特点:(功耗低、抗干扰能力强、电源范围宽)3.理解集成电路各种参数的意义:(1)V IL(max)、V IH(min)、V OH(min)、V OL(max)、I IH(max)、I IL(max)、I OH(max)、I OL(max)(2)高电平噪声容限期VNH = V OH(min) —V IH(min)(3)低电平噪声容限期VNL = V IL(max)—V OL(max)(4)传输延迟时间t PLH、t pHL以及tpd = (t PLH + t pHL)/2(5)功耗(动态功耗和静态功耗)。
数字逻辑 知识点总结大全

数字逻辑知识点总结大全数字逻辑是一门研究数字信号在计算机中传输和处理的学科,它涉及到数字电路和逻辑电路的设计、分析和应用。
数字逻辑在计算机科学、电子工程、通信工程等领域都有着广泛的应用。
下面将对数字逻辑的知识点进行详细的总结,包括数字系统、布尔代数、逻辑门、时序逻辑和组合逻辑等内容。
数字系统数字系统是由有限个数的符号和数字组成的一种系统。
在计算机中,使用的数字系统一般为二进制,即由0和1组成。
除了二进制,还有十进制、八进制和十六进制等其他进制系统。
其中,二进制是计算机内部使用的基本进制。
数字系统中的基本概念包括位、字节、字和字长。
位是数字系统中的最小单位,它只有两种状态:0和1。
字节是8位的二进制数,用来表示一个字符或一个字母。
字是由多个字节组成的一个固定长度的数据单元。
而字长是一个数字系统中的字的长度,它决定了一个数字系统中能够表示的最大的数值范围。
布尔代数布尔代数是一种逻辑代数,它用来描述逻辑语句的真假情况。
在布尔代数中,所有逻辑变量的取值只有两种情况:真和假。
布尔代数中的基本运算包括与运算、或运算和非运算。
与运算表示两个逻辑变量同时为真时结果为真,否则为假;或运算表示两个逻辑变量中任意一个为真时结果为真,否则为假;非运算表示逻辑变量的取值取反。
布尔代数中的定理包括分配律、结合律、德摩根定律、消去律等。
这些定理是布尔代数中的基本规则,用于简化布尔表达式,并帮助我们理解逻辑电路的设计和分析。
逻辑门逻辑门是数字电路中的基本组成部分,它用来实现布尔代数中的逻辑运算。
逻辑门一般包括与门、或门、非门、异或门、与非门、或非门等类型。
这些门都有着特定的逻辑功能和真值表。
与门表示与运算,或门表示或运算,非门表示非运算,异或门表示异或运算,与非门表示与非运算,或非门表示或非运算。
这些逻辑门可以组成各种复杂的逻辑电路,包括加法器、减法器、多路选择器、触发器、寄存器等。
时序逻辑时序逻辑是数字逻辑中的一个重要分支,它涉及到数字电路中的时序关系和时序控制。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
【最新整理,下载后即可编辑】数字逻辑实验报告、总结专业班级:计算机科学与技术3班 学号:41112115 姓名:华葱一、 实验目的1. 熟悉电子集成实验箱的基本结构和基本操作2. 通过实验进一步熟悉各种常用SSI 块和MSI 块的结构、各管脚功能、工作原理连接方法3. 通过实验进一步理解MSI 块的各输入使能、输出使能的作用(存在的必要性)4. 通过实验明确数字逻辑这门课程在计算机专业众多课程中所处的位置,进一步明确学习计算机软硬件学习的主线思路以及它们之间的关系学会正确学习硬件知识的方法。
二、 实验器材1. 集成电路实验箱2. 导线若干3. 14插脚、16插脚拓展板4. 各种必要的SSI 块和MSI 块三、 各次实验过程、内容简述(一) 第一次实验:利用SSI 块中的门电路设计一个二进制一位半加器1. 实验原理:根据两个一位二进制数x 、y 相加的和与进位的真值表,可得:和sum=x 异或y ,进位C out =x×y 。
相应电路:2. 实验内容:a) 按电路图连接事物,检查连接无误后开启电源b) 进行测试,令<x ,SumCouty>={<0,0>,<0,1>,<1,0>,<1,1>},看输出位sum和C out 的变化情况。
c) 如果输出位的变化情况与真值表所述的真值相应,则达到实验目的。
(二) 第二次实验:全加器、74LS138译码器、74LS148编码器、74LS85比较器的测试、使用,思考各个输入、输出使能端的作用1. 实验原理:a) 全加器i. 实验原理:在半加器的基础上除了要考虑当前两个二进制为相加结果,还要考虑低位(前一位)对这一位的进位问题。
由于进位与当前位的运算关系仍然是和的关系,所以新引入的低位进位端C in 应当与当前和sum再取异或,而得到真正的和Sum ;而进位位C out 的产生有三种情况:<x ,y ,C in >={<1,1,0>,<1,0,1>,<0,1,1>},也就是说当x 、y 、C in 中当且仅当其中的两个数为1,另一个数为0的时候C out =1,因此:C out =xy+xC in +yC in 得电路图(也可以列出关于C in 的真值表,利用卡诺图求解C in 的函数表达式):ii. >的8中指,y ,C inx y C in Sum C outiii. 如果输出位的变化情况与真值表所述的真值相应,则达到实验目的。
b) 74LS138译码器i. 实验原理:译码器是一个能够将一串序列号(我个人理解为地址)所对应的有序编号(按照某种认为约定)进行表达的电子逻辑器件,74LS138译码器是译码器的一种,它能够将一个与十进制整数值等值的二进制序列翻译为相应的十进制值,将信号输出在相应的数据线上。
原理:每一个一位(0~7)十进制值Y i 都对应一个三位二进制序列的表达,也就对应一个极小项m i ,即Y i =m i ,则可根据m i 对应的三个输入变量组合设计门电路(例如Y 5=m 5=ABC )。
将这8个十进制值都做这样的门电路设计,在进行相应的封装、集成,就形成了这种3-8译码器,其外部逻辑状态如图所示:ii. 实验内电路,将使能端按<G 1,G 2A ,G 个输入端按<A,B,C>={A,B,C 组成的极小项| m i0≤i ≤7}测试译码器,观察各个输出端Y i 是否正确输出,如果能,则达到实验目的。
iii. 思考:G 1,G 2A ,G 2B 作用。
1. G 1的作用:G 1在3-8译码器中起开启/封锁各与门的作用,它的存在决定了该3-8译码器芯片是否工作,因此如果需要拓展译码输入的位数由3位到多位,则需要利用该使能端。
__ 。
。
。
。
。
。
。
。
如:若需要设计一个4线-16线译码器,则可用最高位N 3控制G 1,因为如果N 3为0则表明输入实际上是3位二进制,译码只许一块3-8译码器,但如果N 3为1则表明输入为4位二进制,则需要开启第二块74LS138工作,因此可以通过N 3的值驱动第二块74LS138,所以N 3可以接到第二块74LS138的G 1端。
2. G 2A 的作用:如1所述,当N 3的值为1(N 3N 2N 1N 0所对应的十进制大于7了),则第二块74LS138需要启用,但由于Y i 的i > 7因此第一块74LS138不再有译码输出,因此第一块74LS138需要被封锁,这如果用第一块74LS138的G 1来控制,这将会破坏译码器器件使能输入的一致性(标准性)影响将来进一步的级联拓展(这将在3中具体说明)。
G 2A 的存在就解决了这个问题,N 3可以通过G 2A 来控制第一块74LS138的工作状态,而不影响整个4线-16线译码器的使能。
3. G 2B 的作用:考虑到整个4线-16线译码器的使能控制以及译码器器件输入使能的一致性,即人们希望设计出来的4线-16线译码器能够像74LS138一样具有三个使能端,第一个高有效,第二、三两个低有效,这样可以方便进一步的级联扩展,则有必要存在一个低有效使能端作为整个4-16译码器的第一个低有效使能端,而3-8译码器的G 1和G 2A 已被占用,不能承担此项工作,这就是G 2B 存在的意义。
4. 其实根据我个人的理解,G 1,G 2A ,G 2B 存在的意义并不是为方便级联拓展,因为级联的含义是前一个译码器的输出作为后一个译码器的输入,它解决的是n线-(8n-1)线(n为3的倍数)译码器设计,而4-16译码器(具体电路如图所示)的结构并不是两个74LS138级联,而是并联。
(注:由于我对译码器的级联比较熟悉,而对译码器的并联较为生疏,因此我在此只做译码器并联的复习,级联的问题省略)c) 74LS148编码器i.实验原理:当译码器的输出端数量小于输入端数量的时候,译码器就成为了编码器。
按照我的理解,我认为编码器的工作于译码器的工作互逆,如前所述,译码器是将一个十进制整数对应的二进制翻译到对应以这个十进制为下标的数据线上,而编码器的工作机制则相反,它能够通过判断哪根数据线上有数据信号,则将其还原为数据线下标十进制值对应的二进制代码,并将其结果输出。
如果将一个74LS138的8个输入端分别接到一个74LS148对应的8个输入端,构成一个组合电路,并让它正常工作,那么输入的三位二进制数将先被翻译成相应数据线上的内容,再输入到编码器里面又编码回对应的三位二进制数,即输入什么将输出什么,相当于什么都没有做,因此我认为编码器工作原理与译码器工作原理互逆。
其外部逻辑状态为:i i.实验内容:在每一个I i (0≤i ≤7)对应的管脚上先后分别输入信号,观察A 2A 1A 0的输出信号变化,如果输出对应的二进制值与i 相等则达到实验目的。
i ii.思考:编码器为什么要有优先权?两个输出使能GS 和EO 的存在有什么意义?经过测试,同时在编码器的多个输入管脚I i 上送入信号,输出信号的值总是与下标i 最大的I i 数据线对应的值相等,即其输入到其他下标较小的管脚中的信号没有被编码。
产生这个现象的原因就在于编码器的编码存在优先权。
反过来想,如果编码器没有优先权,那么当多个数据输入到编码器中,则编码器无法判断输入的数据究竟哪一个该编码,进而导致输出错误。
因此,编码需要考虑优先权。
应用:医院里的病房都分一般病房和重症监护室,由于重症监护室的病人更需要时时关注,那么当同时有两个求助信号从病房送到护士站的时候,如果其中一个信号来自一般病房,另一个来自重症监护室,在护士站受到的信号应是来自重症监护室的求助信号,而那个一般病房的信号将由于优先权低于重症监护室的信号而被“忽略”。
另外,编码器还可用作数据寻址,将一个数据信号翻译为其对应的地址,在计算机内部的数据总线上,挂有若干的外部设备,当外部设备需要进行某种工作时,都要向CPU 发送请求,这个请求将对应一个地址,使得CPU 在该地址取相应的指令来授权该外部设备工作,当同一时刻有多个外部设备向CPU 发送请求时,由于编码器具有优先权选择性,CPU 将选择对应编码优先权最高的外部设备做授权工作。
这样就不会由于若干的外部设备共享一根数据总线,发送求的时候产生混乱。
输出使能EO 的作用:与译码器类似,EO 用作级联扩展,当第一块74LS148的输入全部无效时,也就是需要编码的信号I i 中i 大于7,也就是在下一块74LS148的某个输入管脚,此时第一块74LS148的EO 为有效输出,而第二块需要开启工作,因此应把第一块74LS148的EO 接到第二块74LS148的EI 上,与74LS138类似,它能解决 (8n-1)线-n 线(n 为3的倍数)的编码器设计问题。
输出使能GS 的作用:此问题仍然与译码器类似,GS 不是供74LS148级联的而是供它并联,解决(8n-1)线-n 线(n 不是3的倍数)编码器的设计问题,比如设计一个16线-4线编码器。
下面就16线-4线编码器的设计谈一谈我的收获:16线输入的编码器与74LS148的区别在于它需要编码的信号不一定在I 0~I 7中,还有可能在I 8~I 15中。
就此需要分类讨论,当需要编码的信息落在I 0~I 7范围内,也就是编码后的四位二进制结果最高位A 3为0,那么第一块74LS148一定要使能,而74LS148没必要开启。
当需要编码的信息落在I 8~I 15也就是编码后的四位二进制结果最高位A 3为1,而编码结果的后三位由第一块74LS148的输出端A 2A 1A 0输出。
综上所述,编码结果的最高位为0时,也就是I i 的i 小于7时,第二块74LS148不工作,而编码结果的最高位A 3为1时,也就是I i 的i 大于7时,输入信号从第二块74LS148的相应管脚输入,第一块74LS148的所有输入均无效,其EO 有效输出,因此第二块74LS148必须要工作,而能够标志这种输入范围和是否工作关系的信号就是GS 信号,恰好可以让第一块74LS148的EO 使能第二块74LS148(接到其EI 上)因此GS 就正是我们要找的编码结果的最高位A 3。
具体电路如图所示:d).74LS85比较器的测试 i.实验原理:比较两个二进制数的方法是从最高位开始,依次比较每一位。
在比较到第i 位时,不仅要看两个二进制数第i 位的大小,还要看第i-1位的比较结果,由二者共同决定第i 位的比较结果。
74LS85的内部逻辑状态原理:在比较两个数A 、B 的第i 位A i 和B i 时,如果A i >B i ,则一定有A i =1,B i =0,将此情况记为PG i ,则PG i =A i B i ;同理,A i <B i 的情况PL i = A i B i ;对于A i =B i 的情况PE i ,则应该考虑两种:A i =1,B i =1和A i =0,B i =0,__ __因此PE i = A i ⊙B i (可用与或非门实现)。
