单样本比例假设检验
常见假设检验公式概览

常见假设检验公式概览假设检验是统计学中一种重要的推断方法,用于判断总体参数的真实情况。
在假设检验中,我们通常会提出一个原假设和一个备择假设,并通过采样数据来判断是否拒绝原假设。
在实际应用中,常见的假设检验方法有如下几种。
1. 单样本均值检验单样本均值检验用于判断一个样本的平均值是否等于一个已知的常数。
其中,我们常用的假设检验公式为:t = (x - μ) / (s / √n)其中,t表示t值,x为样本均值,μ为总体均值,s为样本标准差,n为样本容量。
通过比较t值与临界值,我们可以判断是否拒绝原假设。
2. 双独立样本均值检验双独立样本均值检验用于比较两个独立样本的平均值是否相等。
常用的假设检验公式如下:t = (x1 - x2) / √(s1²/n1 + s2²/n2)其中,t表示t值,x1和x2分别为两个样本的均值,s1和s2为两个样本的标准差,n1和n2为两个样本的容量。
通过比较t值和临界值,可以判断是否拒绝原假设。
3. 配对样本均值检验配对样本均值检验用于比较同一组样本的两个相关变量的平均值是否相等。
常用的假设检验公式如下:t = (x d - μd) / (sd / √n)其中,t表示t值,x d为配对差值的均值,μd为总体差值的均值,sd为配对差值的标准差,n为配对样本容量。
通过比较t值和临界值,可以得出是否拒绝原假设。
4. 单样本比例检验单样本比例检验用于判断一个样本比例是否等于一个已知的比例。
常用的假设检验公式如下:z = (p - π) / √(π(1-π)/n)其中,z表示z值,p为样本比例,π为总体比例,n为样本容量。
通过比较z值和临界值,可以判断是否拒绝原假设。
5. 独立样本比例检验独立样本比例检验用于比较两个独立样本的比例是否相等。
常用的假设检验公式如下:z = (p1 - p2) / √(p(1-p)(1/n1 + 1/n2))其中,z表示z值,p1和p2分别为两个样本的比例,n1和n2分别为两个样本的容量。
假设检验公式汇总单样本与双样本假设检验的计算方法

假设检验公式汇总单样本与双样本假设检验的计算方法假设检验公式汇总假设检验是统计学中常用的一种方法,用于判断统计推断的结果是否可以反映总体的特征。
在假设检验中,我们通常需要计算相关的统计量以判断样本数据是否能够支持我们的研究假设。
本文将详细介绍单样本与双样本假设检验的计算方法,以帮助读者更好地理解和应用假设检验。
一、单样本假设检验的计算方法单样本假设检验是用于检验一个总体参数的假设。
以下是单样本假设检验的计算方法:1. 设定假设在进行单样本假设检验前,我们首先需要明确研究问题并设定相应的假设。
通常,我们将待检验的总体参数表示为μ,构建如下假设:- 零假设(H0):总体参数μ等于某个特定值(通常为给定的数值);- 备择假设(H1):总体参数μ不等于某个特定值。
2. 选择显著性水平显著性水平(α)是用来衡量我们拒绝零假设的临界值。
通常,我们选择显著性水平为0.05或0.01,也可以根据具体研究需求来选择其他值。
3. 计算检验统计量在单样本假设检验中,我们需要计算检验统计量以判断样本数据是否对我们的假设提供足够的证据。
常见的检验统计量有t值、z值等。
具体计算方法如下:- t值的计算:当总体标准差未知时,使用t值进行假设检验。
计算公式为:t = (x - μ) / (s / √n),其中x为样本均值,μ为假设的总体均值,s为样本标准差,n为样本容量。
- z值的计算:当总体标准差已知或样本容量较大时,可以使用z值进行假设检验。
计算公式为:z = (x - μ) / (σ / √n),其中x为样本均值,μ为假设的总体均值,σ为总体标准差,n为样本容量。
4. 确定拒绝域和做出决策根据设定的显著性水平,我们可以确定拒绝域的临界值。
如果计算得到的检验统计量落入拒绝域,就可以拒绝零假设;否则,不能拒绝零假设。
根据具体情况,可以使用t分布表或标准正态分布表来查找相应的临界值。
5. 结论根据实际计算结果,我们可以根据拒绝与接受的原则,给出相应的结论。
假设检验基础:单一样本检验

5. 选择检验:
Z检验或 p值检验
6. 确定临界值 Critical Values
7. 收集数据
8. 计算检验统计量
9. 作出统计决策
10.
表述决策
已知的Z检验
Z-Test Statistic ( Known)
1. 将样本统计量(如, X )转换为标准正态分布Z
变量
Z
单一总体均值 (已知) One population mean 单侧和双侧检验 One & Two-Tailed Tests
什么是假设?
What’s a Hypothesis?
假设是对总体参数的 一种推断
我相信这个班级的平均 GPA为 3.5!
总体参数如:均值、 比率和方差
进行分析前必须先 识别参数
20
= 50
样本均值
H0
显著性水平 Level of Significance
1. 定义如果零假设成立样本统计量不可能 的取值区间
称为样本分布的拒绝域 Rejection region of sampling distribution
2. 用 表示
典型值为 0.01, 0.05, 0.10
P(Z -1.50 或 Z 1.50) = 0.1336
1/2 p=
.0668
1/2 p=
.0668
.4332
-1.50 0 1.50 Z
.5000
-.4332
.0668
乘2
从Z表中查到: 1.50
样本统计量的Z值
p 值解答
(p = .1336) ( = .05) 不拒绝零假设
1/2 p = .0668
0 1.50 Z
假设检验与样本数量分析④——单比率检验双比率检验(PPT精选课件)

此课件下载后可自行编辑修改 关注我 每天分享干货
预备知识 总体与样本
总体——研究的一类对象的全体组成的集合。 个体——总体中的每一个考察的对象。 样本——从总体中抽出的一部分个体的集合。 样本数量——样本中包含的个体的数量。
噢!这么多健身球, 应该全是合格的吧
X=
ห้องสมุดไป่ตู้
0
1
2
3
4
5
p= 0.59049 0.32805 0.0729 0.0081 0.00045 0.00001
Cnx
n(n
1) (n x!
x
1)
n = 总体中随机抽取样本个数
X = 出现不合格品数
Cn0 1
0.59049
p=0.1,n=5 概 率分布图
0.32805
0.0729
0.0081 0.00045 0.00001
断,这是单样本检验的问题。
H0:p =p0
H1: p ≠ p0
建立检验假设(如双侧检验)
H0:p =0.02 H1: p ≠ 0.02
不合格品率为2% 不合格品率不是2%
预备知识 总体与样本
双样本
统计推断是由2个样本的信息来推测2个总体 性能,推断特征相比是否有显著差异。
健身球1#
2种健身球生产过程 的不合格品率应该
精确检验
二项分布
Z检验的适用条件: 样本含量n足够大,nPˆ与 n(1均 大Pˆ )于5, 此时样本率的分布近似正态分布, 可利用正态分布的原理作Z检验。
Z检验
正态近似检验
精确检验
超几何分布
Z检验的适用条件:
当两样本含量n1及n2足够大,
概率统计实用公式整理专为研究者和实践者准备的指南

概率统计实用公式整理专为研究者和实践者准备的指南概率统计是数学中一门重要的学科,作为一种应用广泛的工具,被广泛应用于各个领域的研究和实践中。
在进行概率统计的计算和分析过程中,掌握一些实用的公式非常重要。
本文将整理一些常用的概率统计公式,旨在为广大研究者和实践者提供一个便捷的指南。
一、基本概率公式在概率统计的计算中,一些基本的概率公式是必不可少的。
下面是几个常用的基本概率公式:1. 乘法定理:P(A∩B) = P(A) × P(B|A)2. 加法定理:P(A∪B) = P(A) + P(B) − P(A∩B)3. 条件概率公式:P(A|B) = P(A∩B) / P(B)4. 全概率公式:P(B) = ∑[i=1, n] P(Ai) × P(B|Ai)二、离散分布公式在离散概率分布中,一些常见的分布公式可以用来描述随机变量的特征。
以下是几个常用的离散分布公式:1. 二项分布公式:P(X=k) = C(n,k) × p^k × (1-p)^(n-k)2. 泊松分布公式:P(X=k) = (e^(-λ) × λ^k) / k!3. 几何分布公式:P(X=k) = (1-p)^(k-1) × p三、连续分布公式连续概率分布描述的是在某一范围内随机变量取值的概率。
以下是几个常用的连续分布公式:1. 正态分布公式:f(x) = (1 / (σ * √(2π))) * e^(-(x-μ)^2 / (2σ^2))2. 指数分布公式:f(x) = λ * e^(-λx)3. 均匀分布公式:f(x) = 1 / (b-a),其中a ≤ x ≤ b四、描述统计公式描述统计是对数据进行整理和总结的过程,以下是一些常用的描述统计公式:1. 均值公式:μ = (x1 + x2 + ... + xn) / n2. 方差公式:σ^2 = [(x1-μ)^2 + (x2-μ)^2 + ... + (xn-μ)^2] / n3. 标准差公式:σ = √(σ^2)五、假设检验公式假设检验是概率统计中用来推断总体特征的方法。
假设检验-单样本检验
假设检验-单样本检验假设检验时数据分析必须学习的⽅法第⼀部分:误差思维和置信区间什么是误差思维?误差永远存在、不可避免随机⼲扰因素的影响⼀个量在测量、计算或观察过程中由于某些错误或通常由于某些不可控制的因素的影响⽽造成的变化偏离标准值或规定值的数量,误差是不可避免的。
只要有估计,就会有误差。
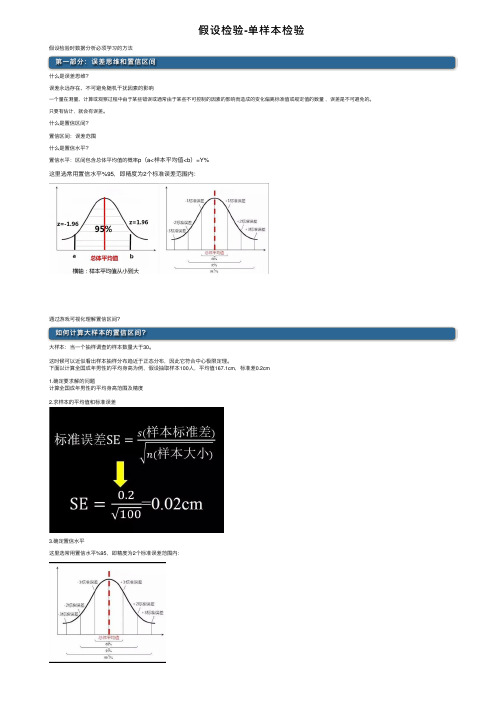
什么是置信区间?置信区间:误差范围什么是置信⽔平?置信⽔平:区间包含总体平均值的概率p(a<样本平均值<b)=Y%这⾥选常⽤置信⽔平%95,即精度为2个标准误差范围内:通过游戏可视化理解置信区间?如何计算⼤样本的置信区间?⼤样本:当⼀个抽样调查的样本数量⼤于30。
这时候可以近似看出样本抽样分布趋近于正态分布,因此它符合中⼼极限定理。
下⾯以计算全国成年男性的平均⾝⾼为例,假设抽取样本100⼈,平均值167.1cm,标准差0.2cm 1.确定要求解的问题计算全国成年男性的平均⾝⾼范围及精度2.求样本的平均值和标准误差3.确定置信⽔平这⾥选常⽤置信⽔平%95,即精度为2个标准误差范围内:4.求出置信区间上下限的值(1)由于选⽤的样本⼤⼩为100⼤于30符合正态分布,先求出如下图中两块红⾊区域⾯积(概率):(2)通过查z表格查出标准分Z=-1.96(3)求出a和b的值的⽅法:(4)根据中⼼极限定理,样本平均值约等于总体平均值,最终求出a和b的值:结论:当我们选⽤置信⽔平为%95时,求得置信区间为[167.0608,167.1392],即在两个标准误差范围内,全国成年男性的平均⾝⾼为167.0608cm到167.1392cm之间。
5.常⽤置信⽔平及其对应Z值(标准分)如何计算⼩样本的置信区间?⼩样本:当⼀个抽样调查的样本数量⼩于30。
这时候抽样分布符合t分布:在概率论和统计学中,t-分布(t-distribution)⽤于根据⼩样本来估计呈正态分布且⽅差未知的总体的均值。
如果总体⽅差已知(例如在样本数量⾜够多时),则应该⽤正态分布来估计总体均值。
假设检验的八种情况的公式

假设检验的八种情况的公式假设检验是统计学中常用的一种方法,用于判断样本数据与总体参数的关系是否具有显著性差异。
在进行假设检验时,我们需要根据实际问题和已知条件确定相应的假设检验公式。
以下是八种常见的假设检验情况及相应的公式。
1.单样本均值检验:在这种情况下,研究者想要判断一个样本的均值是否与一个已知的总体均值有显著性差异。
假设检验的公式为:其中,x̄为样本均值,μ为总体均值,s为样本标准差,n为样本容量,t为t分布的临界值。
2.双样本均值检验(方差已知):在这种情况下,研究者想要判断两个样本的均值是否有显著性差异,且已知两个样本的方差相等。
假设检验的公式为:其中,x̄1和x̄2分别为样本1和样本2的均值,μ1和μ2分别为总体1和总体2的均值,s为样本标准差,n1和n2分别为样本1和样本2的容量,z为标准正态分布的临界值。
3.双样本均值检验(方差未知):在这种情况下,研究者想要判断两个样本的均值是否有显著性差异,且两个样本的方差未知且不相等。
假设检验的公式为:其中,x̄1和x̄2分别为样本1和样本2的均值,μ1和μ2分别为总体1和总体2的均值,s1和s2分别为样本1和样本2的标准差,n1和n2分别为样本1和样本2的容量,t为t分布的临界值。
4.单样本比例检验:在这种情况下,研究者想要判断一个样本的比例是否与一个已知的总体比例有显著性差异。
假设检验的公式为:其中,p̄为样本比例,p为总体比例,n为样本容量,z为标准正态分布的临界值。
5.双样本比例检验:在这种情况下,研究者想要判断两个样本的比例是否有显著性差异。
假设检验的公式为:其中,p̄1和p̄2分别为样本1和样本2的比例,p1和p2分别为总体1和总体2的比例,n1和n2分别为样本1和样本2的容量,z为标准正态分布的临界值。
6.简单线性回归检验:在这种情况下,研究者想要判断自变量与因变量之间的线性关系是否显著。
假设检验的公式为:其中,β1为回归系数,se(β1)为标准误差,t为t分布的临界值。
假设检验与样本数量分析④——单比率检验、双比率检验.ppt

单比率检验
单比率检验
单比率检验用于根 据样本数据对总体 比率进行推断
单比率检验 1 Proportion-test
Z检验
正态近似检验
样本含量n足够大 nPˆ 5 n(1P ˆ) 5
单比率检验 双比率检验
检验假设 拒绝域 P值 决策
双侧检验
H0:p =p0 H1:p ≠ p0
左侧检验
H0:p p0 H1:p< p0
不合格品率有差异
样本与样本所代表的总体间存在显著差异
<3>
单比率检验 双比率检验
预备知识
二项分布的概念 二项分布(binominal distribution) 是一种重要的离散型分布。
数据属于只有两个可能结果的独立实验的结果,一个表示希望的“事件”,另一个表示“非 事件”(每一观察只具有相互独立的一种结果),如,通过与失败、合格与报废、有效或无效 、是或否、0 或 1等。
确定临界值
显著性水平α 与拒绝域
H1:p ≠ p0
临界值
拒绝零假设
2 =0.025
双侧检验
不拒绝H0范围
1-α=95%
临界值
α = 0.05
拒绝零假设
=0.025
2
Z a/2 Z 0.025= -1.96
Z1- a/2 Z 0.975 =1.96
单比率检验 双比率检验
H1:p< p0 左侧检验
临界值
1 建立检验假设
H0:p =0.02 H1:p ≠ 0.02
2 给定显著水平 α = 0.05
3 计算统计量
Z
pˆ p0
p0 (1 p0 )
n
0.018 0.02 0.02(1 0.02)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
单样本比例假设检验
在统计学中,假设检验是一种用来判断一个假设是否成立的方法。
单样本比例假设检验是一种用于检验一个总体比例是否等于某个特定
值的统计方法。
本文将介绍单样本比例假设检验的原理、步骤以及如
何进行。
一、原理
单样本比例假设检验的原理是基于二项分布的概率。
在假设检验中,我们假设一个总体的比例为p,然后通过对观察到的样本数据进行统计推断,判断p是否等于某个特定值。
假设检验的目的是帮助我们做出
关于总体的推断,从而对现象进行解释和预测。
二、步骤
进行单样本比例假设检验需要以下步骤:
1. 提出假设:首先,我们需要提出原假设(H0)和备择假设(Ha)。
原假设通常是我们想要证明的假设,备择假设则是对原假设
的互补或者相反的假设。
2. 设置显著性水平:显著性水平(α)是我们在假设检验中设置的
一个阈值,用来判断是否拒绝原假设。
通常情况下,显著性水平取
0.05或0.01。
3. 计算检验统计量:接下来,我们需要计算检验统计量。
对于单样
本比例假设检验,常用的检验统计量是Z值,计算公式为:
Z = (p - p0) / sqrt((p0 * (1 - p0)) / n)
其中,p是样本比例,p0是假设的比例值,n是样本容量。
4. 确定拒绝域:拒绝域是根据显著性水平和检验统计量的分布来确
定的。
如果检验统计量落在拒绝域内,就可以拒绝原假设。
5. 判断结果:根据拒绝域的判断,我们可以得出对原假设的结论。
如果检验统计量落在拒绝域内,我们可以拒绝原假设,认为样本提供
了足够的证据来支持备择假设。
如果检验统计量没有落在拒绝域,我
们无法拒绝原假设,即无法得出统计上的显著结果。
三、实例
为了更好地理解单样本比例假设检验的应用,我们来举一个实例。
假设某个公司宣称其产品的合格率达到了75%。
为了验证这个宣称
是否可信,我们从该公司生产的产品中随机抽取了100个样本,并统
计发现其中有65个样本合格。
现在我们需要进行单样本比例假设检验。
1. 提出假设:原假设H0:产品的合格率为75%;备择假设Ha:产
品的合格率不等于75%。
2. 设置显著性水平:假设我们设置显著性水平为0.05。
3. 计算检验统计量:根据样本数据,计算检验统计量的值为:
Z = (0.65 - 0.75) / sqrt((0.75 * 0.25) / 100) ≈ -2.53
4. 确定拒绝域:根据显著性水平和检验统计量的分布,我们可以查找Z表格或者使用统计软件来确定拒绝域。
在本例中,双侧拒绝域的临界值分别为-1.96和1.96。
5. 判断结果:由于检验统计量的值(-2.53)小于-1.96,落在拒绝域内,我们可以拒绝原假设。
因此,我们有足够的证据来认为该公司产品的合格率不等于75%。
结论
单样本比例假设检验是一种常用的统计方法,用于判断一个总体比例是否等于某个特定值。
通过对观察到的样本数据进行统计推断,我们可以得出对原假设的结论,并对现象进行解释和预测。
在应用单样本比例假设检验时,我们需要明确提出假设、设置显著性水平、计算检验统计量、确定拒绝域以及根据拒绝域的判断来得出结论。
以上是对单样本比例假设检验的一个简要介绍,希望能对您的学习和研究有所帮助。
