吉林省东北师范大学附属中学高中数学 1.8综合应用举例学案 理 新人教A版必修5
吉林省东北师范大学附属中学高中数学 1.6三角函数模型的简单应用学案 理 新人教A版必修4

吉林省东北师范大学附属中学高中数学 1.6三角函数模型的简单应用学案 理 新人教A 版必修4【学习目标】1.掌握三角函数模型应用基本步骤: (1)根据图象建立解析式; (2)根据解析式作出图象;(3)将实际问题抽象为与三角函数有关的简单函数模型.2.利用收集到的数据作出散点图,并根据散点图进行函数拟合,从而得到函数模型 【典型例题分析】.1.你能利用函数sin y x =的奇偶性画出图象吗?它与函数sin y x =的图象有什么联系?2.已知:1sin 2α=-,若(1),22ππα∈-⎛⎫⎪⎝⎭; (2)(0,2)απ∈;(3)α是第三象限角;(4)α∈R.分别求角α。
3.已知[]0,2θπ∈, sin ,cos θθ分别是方程210x kx k -++=的两个根,求角θ.4.设A 、B 、C 、D 是圆内接四边形ABCD 的四个内角,求证: (1)sin A =sin C ;(2)cos (A +B )=cos (C +D ); (3)tan (A +B +C )=-tan D .5.某商品一年内出厂价格在6元的基础上按月份随正弦曲线波动,已知3月份达到最高价格8元,7月份价格最低为4元,该商品在商店内的销售价格在8元基础上按月份随正弦曲线波动,5月份销售价格最高为10元,9月份销售价最低为6元,假设商店每月购进这种商品m 件,且当月销完,你估计哪个月份盈利最大?6.把一张纸卷到圆柱形的纸筒面上,卷上几圈.用剪刀斜着..将纸筒剪断,再把卷着的纸展开,你就会看到:纸的边缘线是一条波浪形的曲线,试一试动手操作一下.它是正弦曲线吗?7.如图,铁匠师傅在打制烟筒弯脖时,为确保对接成直角,在铁板上的下剪线正好是余弦曲线:cosx y a a的一个周期的图象,问弯脖的直径为12 cm 时,a 应是多少cm ?8.已知函数f (x )=x 2cos 12-,试作出该函数的图象,并讨论它的奇偶性、周期性以及区间[0,2π]上的单调性。
吉林省东北师范大学附属中学2021年春高中数学理科人教A版必修三教案:1.1.1算法的概念

一、教学目标:1、学问与技能:(1)了解算法的含义,体会算法的思想。
(2)能够用自然语言叙述算法。
(3)把握正确的算法应满足的要求。
(4)会写出解线性方程(组)的算法。
(5)会写出一个求有限整数序列中的最大值的算法。
(6)会应用Scilab求解方程组。
2、过程与方法:通过求解二元一次方程组,体会解方程的一般性步骤,从而得到一个解二元一次方程组的步骤,这些步骤就是算法,不同的问题有不同的算法。
由于思考问题的角度不同,同一个问题也可能有多个算法,能仿照求解二元一次方程组的步骤,写出一个求有限整数序列中的最大值的算法。
3、情感态度与价值观:通过本节的学习,使我们对计算机的算法语言有一个基本的了解,明确算法的要求,生疏到计算机是人类制服自然的一各有力工具,进一步提高探究、生疏世界的力量。
二、重点与难点:重点:算法的含义、解二元一次方程组和推断一个数为质数的算法设计。
难点:把自然语言转化为算法语言。
三、学法与教学用具:学法:1、写出的算法,必需能解决一类问题(如:推断一个整数n(n>1)是否为质数;求任意一个方程的近似解;……),并且能够重复使用。
2、要使算法尽量简洁、步骤尽量少。
3、要保证算法正确,且计算机能够执行,如:让计算机计算1×2×3×4×5是可以做到的,但让计算机去执行“倒一杯水”“替我理发”等则是做不到的。
教学用具:电脑,计算器,图形计算器四、教学设想:(1)创设情境:算法作为一个名词,在中学教科书中并没有消灭过,我们在基础训练阶段还没有接触算法概念。
但是我们却从学校就开头接触算法,生疏很多问题的算法。
如,做四则运算要先乘除后加减,从里往外脱括弧,竖式笔算等都是算法,至于乘法口诀、珠算口诀更是算法的具体体现。
我们知道解一元二次方程的算法,求解一元一次不等式、一元二次不等式的算法,解线性方程组的算法,求两个数的最大公因数的算法等。
因此,算法其实是重要的数学对象。
吉林省东北师范大学附属中学高中数学 1.8第24课时 导数及应用复习小结(3)教案 理 新人教A版选修22
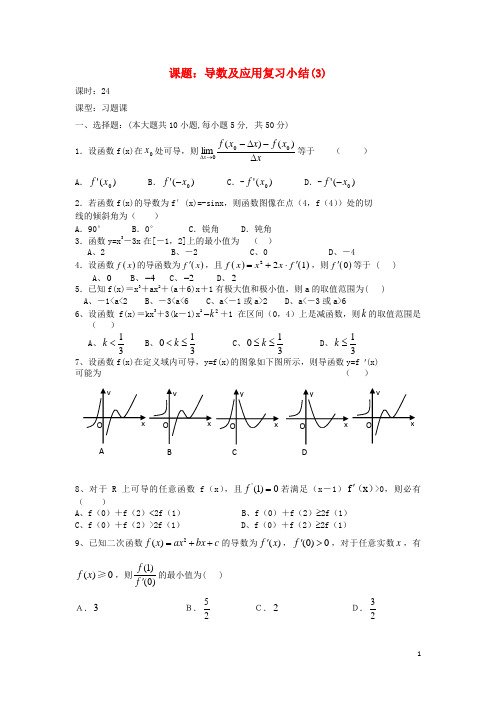
课题:导数及应用复习小结(3)课时:24 课型:习题课一、选择题:(本大题共10小题,每小题5分, 共50分) 1.设函数f(x)在0x 处可导,则xx f x x f x ∆-∆-→∆)()(lim000等于 ( )A .)('0x fB .)('0x f -C .-)('0x fD .-)('0x f -2.若函数f(x)的导数为f′(x)=-sinx ,则函数图像在点(4,f (4))处的切 线的倾斜角为( )A .90° B.0° C.锐角 D .钝角3.函数y=x 3-3x 在[-1,2]上的最小值为 ( ) A 、2 B 、-2 C 、0 D 、-44.设函数()f x 的导函数为()f x ',且()()221f x x x f '=+⋅,则()0f '等于 ( )A 、0B 、4-C 、2-D 、25.已知f(x)=x 3+ax 2+(a +6)x +1有极大值和极小值,则a 的取值范围为( ) A 、-1<a<2 B 、-3<a<6 C 、a<-1或a>2 D 、a<-3或a>66、设函数f(x)=kx 3+3(k -1)x 22k -+1在区间(0,4)上是减函数,则k 的取值范围是 ( ) A 、13k <B 、103k <≤C 、103k ≤≤D 、13k ≤7、设函数f(x)在定义域内可导,y=f(x)的图象如下图所示,则导函数y=f '(x) 可能为 ( )8、对于R 上可导的任意函数f (x ),且'(1)0f =若满足(x -1)f x '()>0,则必有 ( )A 、f (0)+f (2)<2f (1)B 、f (0)+f (2)≥2f (1)C 、f (0)+f (2)>2f (1)D 、f (0)+f (2)≥2f (1)9、已知二次函数2()f x ax bx c =++的导数为()f x ',(0)0f '>,对于任意实数x ,有()0f x ≥,则(1)(0)f f '的最小值为( ) A.3 B.52C.2D.32A B C D10、f (x )是定义在区间[-c,c]上的奇函数,其图象如图所示:令g (x )=af (x )+b ,则下 列关于函数g (x )的叙述正确的是( ) A .若a <0,则函数g (x )的图象关于原点对称.B .若a =-1,-2<b<0,则方程g (x )=0有大于2的实根.C .若a ≠0,b=2,则方程g (x )=0有两个实根.D .若a≥1,b<2,则方程g (x )=0有三个实根.二、填空题(共5小题,每小题5分,共25分) 11.求()31sin f x x=的导数 12.曲线S :y=3x-x 3的过点A (2,-2)的切线的方程是 。
吉林省东北师范大学附属中学高中数学1.2.3充分条件与

课题:充分条件与必要条件学时:003学习:新授课学习目标1.知识与技能:正确理解充分不必要条件、必要不充分条件的概念;会判断命题的充分条件、必要条件.2.过程与方法:培养学生分析、判断和归纳的逻辑思维能力.3.情感、态度与价值观:通过学生的举例,培养辨析能力以及培养良好的思维品质,在练习过程中进行辩证唯物主义思想教育.学习重点与难点重点:充分条件、必要条件的概念.难点:判断命题的充分条件、必要条件。
关键:分清命题的条件和结论,看是条件能推出结论还是结论能推出条件。
学生与教师共同探究过程:1.练习与思考写出下列两个命题的条件和结论,并判断是真命题还是假命题?(1)若x > a2 + b2,则x > 2ab, (2)若ab = 0,则a = 0.结论:置疑:对于命题“若p,则q”,有时是真命题,有时是假命题.如何判断其真假的?答:2.定义: 充分条件, 必要条件(1):充分条件(2):必要条件3.例题分析:例1:下列“若p,则q”形式的命题中,那些命题中的p是q的充分条件?(1)若x =1,则x2- 4x + 3 = 0;(2)若f(x)= x,则f(x)为增函数;(3)若x为无理数,则x2为无理数.例2:下列“若p,则q”形式的命题中,那些命题中的q是p的必要条件?(1)若x = y,则x2= y2;(2)若两个三角形全等,则这两个三角形的面积相等;(3)若a >b,则ac>bc.4、巩固练习:P12 习题1.2-- 1(1)(2),2(1)(2)题5.作业 P12:习题1.2A组--第3、4题6.学后反思:一般地,判断条件是结论的什么条件时,注意以下问题(1)条件是相互的;(2)p是q的什么条件,有四种回答方式:A. p是q的充分而不必要条件;B. p是q的必要而不充分条件;C.p是q的充要条件;D. p是q的既不充分也不必要条件.。
吉林省东北师范大学附属中学高中数学 1.3.8第一章 算法初步复习小结(3)学案 新人教A版必修3
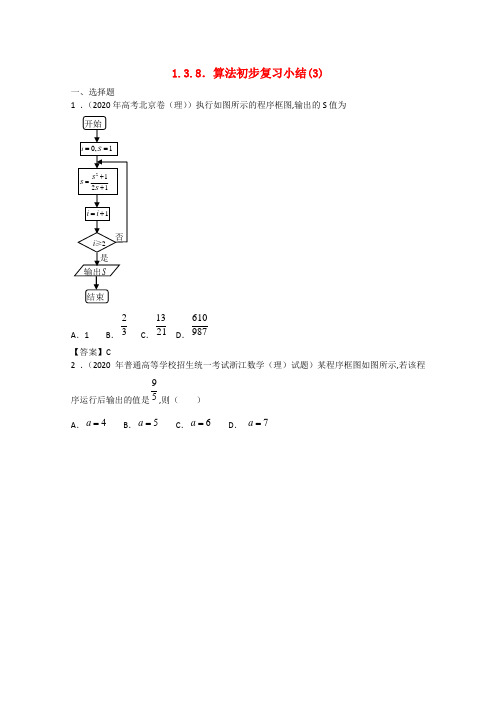
1.3.8.算法初步复习小结(3)一、选择题1 .(2020年高考北京卷(理))执行如图所示的程序框图,输出的S 值为A .1B .23C .1321D .610987【答案】C2 .(2020年普通高等学校招生统一考试浙江数学(理)试题)某程序框图如图所示,若该程序运行后输出的值是59,则( )A .4=aB .5=aC .6=aD . 7=a【答案】A3 .(2020年普通高等学校招生统一考试安徽数学(理)试题)如图所示,程序框图(算法流程图)的输出结果是A .16B .2524C .34D .1112【答案】D4 .(2020年普通高等学校招生统一考试重庆数学(理)执行如题(8)图所示的程序框图,如果输出3s =,那么判断框内应填入的条件是( )A .6k ≤B .7k ≤C .8k ≤D .9k ≤(第5题图)【答案】B5 .(2020年高考江西卷(理))阅读如下程序框图,如果输出5i =,那么在空白矩形框中应填入的语句为A .2*2S i =-B .2*1S i =-C .2*S i =D .2*4S i =+【答案】C6 .(2020年普通高等学校招生统一考试福建数学(理)试题)阅读如图所示的程序框图,若输入的10k =,则该算法的功能是( )A .计算数列{}12n -的前10项和B .计算数列{}12n -的前9项和 C .计算数列{}21n -的前10项和 D .计算数列{}21n -的前9项和【答案】A7 .(2020年普通高等学校招生统一考试新课标Ⅱ卷数学(理)执行右面的程序框图,如果输入的10N=,那么输出的S=A.1111+2310+++……B.1111+2310+++……!!!C.1111+2311+++……D.1111+2311+++……!!!【答案】B8 .(2020年普通高等学校招生统一考试辽宁数学(理)试题)执行如图所示的程序框图,若输入10,n S==则输出的()A.511B.1011C.3655D.7255【答案】A9 .(2020年高考新课标1(理))运行如下程序框图,如果输入的[1,3]t∈-,则输出s属于否是1,0,1===TSk开始N输入kTT=1+=kkTSS+=?Nk>S输出结束A .[3,4]-B .[5,2]-C .[4,3]-D .[2,5]-【答案】A10.(2020年高考陕西卷(理))根据下列算法语句, 当输入x 为60时, 输出y 的值为 ( )A .25B .30C .31D .61【答案】C11.(2020年普通高等学校招生统一考试天津数学(理)试题)阅读右边的程序框图, 运行相应的程序, 若输入x 的值为1, 则输出S 的值为( )A .64B .73C .512D .585【答案】B二、填空题12.( 2020年高考湖南卷(理))执行如图3所示的程序框图,如果输入1,2,a b a ==则输出的的值为_____9_____.输入xIf x ≤50 Theny =0.5 * xElsey =25+0.6*(x -50)End If输出y【答案】913.(2020年普通高等学校招生全国统一招生考试江苏卷)下图是一个算法的流程图,则输出的n的值是________.【答案】314.(2020年普通高等学校招生统一考试广东省数学(理)执行如图所示的程序框图,若输入n 的值为4,则输出s的值为______.【答案】715.(2020年高考湖北卷(理))阅读如图所示的程序框图,运行相应的程序,输出的结果i=【答案】 5。
吉林省东北师范大学附属中学高中数学 1.1.1任意角学案

吉林省东北师范大学附属中学高中数学 4-1.1.1任意角学案 理新人教A 版必修4一、复习: 角的概念:(1)在初中我们把有公共顶点的 组成的 叫做角,这个公共顶点叫做角的 ,这两条射线叫做角的 。
(2)角可以看成是一条射线绕着它的 从一个位置旋转到另一个位置所成的 。
二、自主学习:自学53P P ,回答: 1.正角、负角、零角:一条射线绕着它的端点旋转有两个相反方向:方向和 方向,习惯上规定:按照 方向旋转而成的角为正角;按照 方向旋转而成的角为负角,当射线没有 时为零角。
注意:(1)在画图时,常用带箭头的弧来表示旋转的 和旋转的 ,旋转生成的角,又常叫做 角。
(2)引入正角、负角的概念后,角的减法运算可以转化为角的加法运算,即α—β可以化为 ,这就是说,各角和的旋转量等于各角旋转量的。
2.终边相同的角:设α表示任意角,所有与α终边相同的角以及α本身组成一个集合,这个集合可记为S = 。
终边相同的角有 个,相等的角终边一定 ,但终边相同的角不一定 。
3.象限角:在直角坐标系中讨论角,是使角的顶点与 重合,角的始边与 重合,角的终边在第几象限,就把这个角叫做 ,如果终边在坐标轴上,就认为这个角 属于任何象限。
三、典型例题:1.自学4P 、5P 例1、例2、例4完成练习A2.自学5P 例3完成下面填空:终边落在x 轴正半轴上角的集合表示为 终边落在x 轴负半轴上角的集合表示为终边落在x 轴上角的集合表示为终边落在y 轴正半轴上角的集合表示为 终边落在y 轴负半轴上角的集合表示为 终边落在坐标轴上角的集合表示为第一象限角的集合表示为 第二象限角的集合表示为第三象限角的集合表示为 第四象限角的集合表示为3.补充例题:例5.已知α是第一象限的角,判断2α、α2分别是第几象限角?练习:7P 练习B2、3、5 4.小结: 5.作业:1.在“①160°②480°③-960°④-1600°”这四个角中属于第二象限角的是( )A.①B.①②C.①②③D.①②③④2.下列命题中正确的是( )A.终边相同的角都相等B.第一象限的角比第二象限的角小C.第一象限角都是锐角D.锐角都是第一象限角3.射线OA 绕端点O 逆时针旋转120°到达OB 位置,由OB 位置顺时针旋转270°到达OC 位置,则∠AOC =( )A.150°B.-150°C.390°D.-390°4.如果α的终边上有一个点P (0,-3),那么α是( )A.第三象限角B.第四象限角C.第三或四象限角D.不属于任何象限角 5.与405°角终边相同的角( )A. k ·360°-45° k ∈zB. k ·360°-405° k ∈zC. k ·360°+45° k ∈zD. k ·180°+45° k ∈z 6.(2005年全国卷Ⅲ)已知α是第三象限角,则2α所在象限是()A.第一或第二象限B.第二或第三象限C.第一或第三象限D.第二或第四象限7.把-1050°表示成k ·360°+θ(k ∈z )的形式,使θ最小的θ值是8.(2005年上海抽查)已知角α终边与120°终边关于y 轴对称, 则α的集合S =.9.已知β终边在图中阴影所表示的范围内(不包括边界), 那么β∈150°° xy。
吉林省东北师范大学附属高中数学人教A版必修一学案:1.3.2.2必修一第三章--函数应用小结(2)

1.3.2.2必修一第三章--函数应用小结(2)课时目标 1.进一步体会直线上升、指数爆炸、对数增长等不同增长的函数模型意义,理解它们的增长差异性.2.掌握几种初等函数的应用.3.理解用拟合函数的方法解决实际问题的方法. 一、基础过关1.汽车经过启动、加速行驶、减速行驶之后停车,若把这一过程中汽车的行驶路程s 看作时间t 的函数,其图象可能是________.2.根据统计,一名工人组装第x 件某产品所用的时间(单位:分钟)为f (x )=⎩⎨⎧cx,x <A ,cA,x ≥A (A ,c 为常数).已知工人组装第4件产品用时30分钟,组装第A 件产品用时15分钟,那么c 和A 的值分别是________.3.据报道,某淡水湖的湖水在50年内减少了10%,若按此规律,设2011年的湖水量为m ,从2011年起,经过x 年后湖水量y 与x 的函数关系为________.4.衣柜里的樟脑丸,随着时间会挥发而体积缩小,刚放进的新丸体积为a ,经过t天后体积V 与天数t 的关系式为:V =a ·e -kt .已知新丸经过50天后,体积变为49a .若一个新丸体积变为827a ,则需经过的天数为________.5.近几年由于北京房价的上涨,引起了二手房市场交易的火爆.房子几乎没有变化,但价格却上涨了,小张在2010年以80万元的价格购得一套新房子,假设这10年来价格年膨胀率不变,那么到2020年,这所房子的价格y (万元)与价格年膨胀率x 之间的函数关系式是________.6.某工厂生产某种产品固定成本为2 000万元,并且每生产一单位产品,成本增加10万元.又知总收入K是单位产品数Q的函数,K(Q)=40Q-120Q2,则总利润L(Q)的最大值是________万元.7.设某企业每月生产电机x台,根据企业月度报表知,每月总产值m(万元)与总支出n(万元)近似地满足下列关系:m=92x-14,n=-14x2+5x+74,当m-n≥0时,称不亏损企业;当m-n<0时,称亏损企业,且n-m为亏损额.(1)企业要成为不亏损企业,每月至少要生产多少台电机?(2)当月总产值为多少时,企业亏损最严重,最大亏损额为多少?二、能力提升8.若镭经过100年后剩留原来质量的95.76%,设质量为1的镭经过x年后剩留量为y,则x,y的函数关系是________________.9.某地区植被破坏、土地沙化越来越严重,最近三年测得沙漠增加值分别为0.2万公顷、0.4万公顷和0.76万公顷,则下列函数中与沙漠增加数y万公顷关于年数x的函数关系较为相似的是________.①y=0.2x;②y=110(x2+2x);③y=2x10;④y=0.2+log16x.10.如图所示,某池塘中浮萍蔓延的面积y(m2)与时间t(月)的关系y=a t,有以下几种说法:①这个指数函数的底数为2;②第5个月时,浮萍面积就会超过30 m2;③浮萍从4 m2蔓延到12 m2需要经过1.5个月;④浮萍每月增加的面积都相等.其中正确的命题序号是________.11.一片森林原来的面积为a,计划每年砍伐一些树,且每年砍伐面积的百分比相等,当砍伐到面积的一半时,所用时间是10年,为保护生态环境,森林面积至少要保留原面积的14,已知到今年为止,森林剩余面积为原来的22,t∈N ).求这种商品的日销售额(销售量与价格之积)的最大值. 三、探究与拓展 13.据预测,我国在“十二五”期间内某产品关税与市场供应量P 的关系近似地满足:P (x )=2(1-kt )(x -b )2(其中t 为关税的税率,且t ∈⎣⎡⎦⎤0,12,x 为市场价格,b ,k 为正常数),当t =18时的市场供应量曲线如图所示:(1)根据图象求k ,b 的值;(2)若市场需求量为Q ,它近似满足Q (x )=211-12x .当P =Q 时的市场价格称为均衡价格,为使均衡价格控制在不低于9元的范围内,求税率t 的最小值.解决实际问题的解题过程:(1)对实际问题进行抽象概括:研究实际问题中量与量之间的关系,确定变量之间的主、被动关系,并用x 、y 分别表示问题中的变量;(2)建立函数模型:将变量y 表示为x 的函数,在中学数学中,我们建立的函数模型一般都是基本初等函数;(3)求解函数模型:根据实际问题所需要解决的目标及函数式的结构特点,正确选择函数知识求得函数模型的解,并还原为实际问题的解.这些步骤用框图表示:3.答案 500.9x y m =解析 设某淡水湖的湖水原有量为b ,每年减少a %,所以y =b (1-a %)x ,由已知,x =50时,y =0.9b ,代入解析式,得a %=15010.9-.又∵2011年湖水量为m ,所以经过x 年后湖水量为y =m (1-a %)x=15050(110.9)0.9x x m m -+=⋅. 4.答案 75解析 由已知,得49a =a ·e -50k ,∴e -k =1504()9.设经过t 1天后,一个新丸体积变为827a ,则827a =a ·e -kt 1,∴827=(e -k)t 1=1504()9t, ∴t 150=32,t 1=75. 5.答案 y =80(1+x )10解析 一年后的价格为y =80+80·x =80(1+x ). 二年后的价格为y =80(1+x )+80(1+x )·x =80(1+x )(1+x )=80(1+x )2,由此可推得10年后的价格为y =80(1+x )10. 6.答案 2 500解析 L (Q )=40Q -120Q 2-10Q -2 000 =-120Q 2+30Q -2 000=-120(Q -300)2+2 500当Q =300时,L (Q )的最大值为2 500万元.7.解(1)由已知得,m-n=92x-14-(-14x2+5x+74)=14x2-12x-2.由m-n≥0,得x2-2x-8≥0,解得x≤-2或x≥4. 据题意,x>0,所以x≥4.故企业要成为不亏损企业,每月至少要生产4台电机.(2)若企业亏损最严重,则n-m取最大值.因为n-m=-14x2+5x+74-92x+14=-14[(x-1)2-9]=94-14(x-1)2.所以当x=1时,n-m取最大值9 4,此时m=92-14=174.故当月总产值为174万元时,企业亏损最严重,最大亏损额为94万元.10.答案①②解析由图象知,t=2时,y=4,∴a2=4,故a=2,①正确.当t =5时,y =25=32>30,②正确,当y =4时,由4=2t 1知t 1=2,当y =12时,由12=2t 2知t 2=log 212=2+log 23.t 2-t 1=log 23≠1.5,故③错误;浮萍每月增长的面积不相等,实际上增长速度越来越快,④错误. 11.解 (1)设每年砍伐面积的百分比为x (0<x <1),则a (1-x )10=12a ,即(1-x )10=12,解得11011()2x =-.(2)设经过m 年剩余面积为原来的22,则 a (1-x )m=22a ,即1102111()(),22102mm ==,解得m =5, 故到今年为止,已砍伐了5年. (3)设从今年开始,以后砍了n 年,则n 年后剩余面积为22a (1-x )n .令22a (1-x )n ≥14a ,即(1-x )n ≥24, 3102113()(),22102m n ≥≤,解得n ≤15. 故今后最多还能砍伐15年.12.解 据题意,商品的价格随时间t 变化,且在不同的区间0≤t <20与20≤t ≤40上,价格随时间t 的变化的关系式也不同,故应分类讨论.设日销售额为F (t ).①当0≤t <20,t ∈N 时,F (t )=(12t +11)(-13t +433)=-16(t -212)2+16(4414+946),故当t =10或11时,F (t )max =176.②当20≤t ≤40,t ∈N 时,F (t )=(-t +41)(-13t +433)=13(t -42)2-13,故当t =20时,F (t )max =161.综合①②知当t =10或11时,日销售额最大,最大值为176.13.解 (1)由图可知t =18时,有解得⎩⎪⎨⎪⎧k =6,b =5.。
吉林省东北师范大学附属中学高中数学人教A版必修一学案:1.3.4函数及基本性质小结(一).doc

一、课题:§134函数及基本性质小结(1)知识点记要1、函数的三要素:定义域、值域和对应法则.2、(一)求函数定义域的原则:(1)若/(X)为整式,则其定义域是心(2)若/(兀)为分式,则其定义域是使分母不为0的实数集合;(3)若/(无)是二次根式(偶次根式),则其定义域是使根号内的式子不小于0的实数集合;(4)若/(x) = x°,则其定义域是{x\x^O};(二)求窗数值域的方法以及分段两数求值(三)求函数的解析式3、函数的单调性:(1)增函数:设州,兀2丘I (/(兀)的定义域),当^<x2时,有/(x1)</(x2).(2)减函数:设X1, x2 G I (/(X)的定义域),当壬<兀2时,有/(坷)>/(兀2)・强调四点:①单调性是对定义域内某个区间而言的,离开了定义域和相应区间就谈不上单调性.②有的函数在整个定义域内单调(如一次函数),有的函数只在定义域内的某些区间单调(如二次函数),有的函数根本没有单调区间(如常函数).③函数在定义域内的两个区间上都是增(或减)函数,一般不能认为函数在AUB上是增(或减)函数.④定义的变形应用:如果证得对任意的州,匕G (a,b),且西*2有兀勺)一/3)>0或x2一尢I者(/(兀2)一/3))(兀2一兀1)>0,能断定函数/(兀)在区间(d,b)上是增函数;如果证得对任意的兀],兀2 e(d,b),且兀]工兀2有一<0或兀2_辛能断定函数/(兀)在区间⑺力)上是减函数。
几点说明:函数是增函数还是减函数,是对定义域内某个区间而言的.有的函数在一些区I'可 上是增函数,而在另一些区间上不是增函数;函数的单调区间是其定义域的子 集;该区间内任意的两个实数,忽略任意取值这个条件,就不能保证函数是增 函数(或减函数);讨论函数的单调性必须在定义域内进行,即函数的单调区间 是其定义域的子集,因此讨论函数的单调性,必须先确定函数的定义域。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
吉林省东北师范大学附属中学2015春高中数学 1.8综合应用举例学
案理新人教A版必修5
学习目标
1.能够运用正弦定理、余弦定理等知识和方法解决一些有关测量的实际问题;
2.三角形的面积及有关恒等式.
学习过程
一、课前准备
复习1:解三角形应用题的关键:将实际问题转化为解三角形问题来解决.
复习2:基本解题思路是:
①分析此题属于哪种类型(距离、高度、角度);
②依题意画出示意图,把已知量和未知量标在图中;
③确定用哪个定理转化,哪个定理求解;
④进行作答,并注意近似计算的要求.
二、新课导学
※典型例题
例1. 某观测站C在目标A的南偏西25o方向,从A出发有一条南偏东35o走向的公路,在C 处测得与C相距31km的公路上有一人正沿着此公路向A走去,走20km到达D,此时测得CD距离为21km,求此人在D处距A还有多远?
例2. 在某点B处测得建筑物AE的顶端A的仰角为θ,沿BE方向前进30m,至点C处测
得顶端A的仰角为2θ,再继续前进至D点,测得顶端A的仰角为4θ,求θ的大小和建筑物AE的高.
例 3. 如图,在四边形ABCD中,AC平分∠DAB,∠ABC=60°,AC=7,AD=6,S△
ADC=,
求AB 的长.
※ 动手试试
练1. 为测某塔AB 的高度,在一幢与塔AB 相距20m 的楼的楼顶处测得塔顶A 的仰角为30°,
测得塔基B 的俯角为45°,则塔AB 的高度为多少m ?
练2. 两灯塔A 、B 与海洋观察站C 的距离都等于a km ,灯塔A 在观察站C 的北偏东30°, 灯塔B 在观察站C 南偏东60°,则A 、B 之间的距离为多少?
三、总结提升
※ 学习小结
1. 解三角形应用题的基本思路,方法; 2.应用举例中测量问题的强化.
知识拓展
秦九韶“三斜求积”公式:
S =
学习评价
※ 自我评价 你完成本节导学案的情况为( ). A. 很好 B. 较好 C. 一般 D. 较差
※ 当堂检测(时量:5分钟 满分:10分)计分:
1. 某人向正东方向走x km 后,向右转150o ,然后朝新方向走3km
,结果他离出发点恰好
km ,
则x 等于( ). A
B
. C
D .3
2.在200米的山上顶,测得山下一塔顶与塔底的俯角分别为30,60o o ,则塔高为( )米.
A .2003
B .
C .400
3 D .
3. 在∆ABC 中,60A ∠=︒,16AC =,面积为,那么BC 的长度为( ).
A .25
B .51
C .
D .49
4. 从200米高的山顶A 处测得地面上某两个景点B 、C 的俯角分别是30º和45º,且∠BAC =45º,
则这两个景点B 、C 之间的距离 .
5. 一货轮航行到M 处,测得灯塔S 在货轮的北偏东15°相距20里处,随后货轮按北偏西30°的方向
航行,半小时后,又测得灯塔在货轮的北偏东45︒,则货轮的速度 .
课后作业
1. 3.5米长的棒斜靠在石堤旁,棒的一端在离堤足1.2米地面上,另一端在沿堤上
2.8米的地方,
求堤对地面的倾斜角.
2. 已知a ,b ,c 为△ABC 的三个内角A ,B ,C 的对边,向量m 1-),n =(cosA ,sinA ).
若m ⊥n ,且acosB+bcosA=csinC ,求角B.
3. 【2014江苏】(本小题满分14分) 已知),2(ππα∈,
55sin =α. (1)求
)4sin(απ+的值; (2)求
)265cos(απ-的值.。
