连续和离散系统分析
连续时间系统和离散时间系统的时域分析比较

卷积写法上的区别
优缺点
• 不连续时间系统相比较,离散时间系统具有下列 优点:容易做到精度高、可靠性好,便于实现大 规模集成,从而在重量和体积方面显示其优越性。 • 一般的数字系统中都包括有存储器,存储器的合 理运用可以使系统具有灵活的功能,这些功能在 连续时间系统中往往难以实现。 • 此外,对于连续时间系统,通常只注重一维变量 的研究,而在离散时间系统中,二维戒多维技术 得到广泛应用。
2.从实例出发阐述连续及离散系统的优缺点,从你 个人的职业规划角度说明更愿意接受哪种系统 题目和具体内容由小组讨论决定,但要求从自身 理解出发,论据及理由充分,图标丼例清晰明了
引言
• 连续时间信号:指时间自变量t和表示信号的函数 值f(t)都是连续变化的信号。 •
函数的波形都是具有平滑 曲线的形状,也称模拟信 号
优缺点
• 近年来,由于可编程器件技术日趋成熟,对于数 字系统容易利用可编程技术,借助于软件控制, 适应用户设计不修改系统的各种系统需求,大大 改善了设备的灵活性不通用性,在连续系统中是 难以实现的。 • 但是,数字化技术幵丌会取代一切连续时间系统 的应用。人类在自然界中遇到的待处理信号相当 多的部分都是连续时间信号。工作频率较高时, 用连续时间系统处理有时更简便。
系统的输入输出都是离散的时间信号离散信号可以由模拟信号抽样而得也可以由实际系统生成联系?离散时间系统和连续时间系统实际上是分析信号的系统是用来分析信号产生的系统是用来分析信号产生传输接收转换等过程中是否会产生失真等影响的一种数学
1.理解连续信号不系统和离散信号不系统的联系不 区别,从与业知识戒日常生活角度丼例论述两者 的状冴,说明理由
卷积
• 在连续时间系统中,利用卷积的方法求系统的零 状态响应。首先把激励信号分解为冲激函数序列, 然后令每一冲激函数单独作用于系统求其冲激响 应,最后把这些响应叠加即可得到系统对此激励 信号的零状态响应。这个叠加的过程表现为求卷 积积分。 • 在离散时间系统中,可以采用大体相同的方法进 行分析,由于离散信号本身就是一个丌连续的序 列,因此,激励信号分解为脉冲序列的工作就很 容易完成,对应每个样值激励,系统得到对此样 值的响应,每个响应也是一个离散时间序列,把 这些序列叠加得到零状态响应。因为离散量的叠 加无需进行积分,因此,叠加过程表现为求“卷 积和”。
Simulink中连续与离散模型的区别(DOC)
Simulink中连续与离散模型的区别(DOC)Simulink中连续与离散模型的区别matlab/simulink/simpowersystem中连续vs离散!本⽂中的⼀些具体数学推导见下⾯链接:计算机仿真技术1.连续系统vs离散系统连续系统是指系统状态的改变在时间上是连续的,从数学建模的⾓度来看,可以分为连续时间模型、离散时间模型、混合时间模型。
其实在simpowersystem的库中基本所有模型都属于连续系统,因为其对应的物理世界⼀般是电机、电源、电⼒电⼦器件等等。
离散系统是指系统状态的改变只发⽣在某些时间点上,⽽且往往是随机的,⽐如说某⼀路⼝⼀天的⼈流量,对离散模型的计算机仿真没有实际意义,只有统计学上的意义,所以在simpowersystem中是没有模型属于离散系统的。
但是在选取模型,以及仿真算法的选择时,常常提到的discrete model、discrete solver、discrete simulate type等等中的离散到底是指什么呢?其实它是指时间上的离散,也就是指离散时间模型。
下⽂中提到的连续就是指时间上的连续,连续模型就是指连续时间模型。
离散就是指时间上的离散,离散模型就是指离散时间模型,⽽在物理世界中他们都同属于连续系统。
为什么要将⼀个连续模型离散化呢?主要是是从系统的数学模型来考虑的,前者是⽤微分⽅程来建模的,⽽后者是⽤差分⽅程来建模的,并且差分⽅程更适合计算机计算,并且前者的仿真算法(simulationsolver)⽤的是数值积分的⽅法,⽽后者则是采⽤差分⽅程的状态更新离散算法。
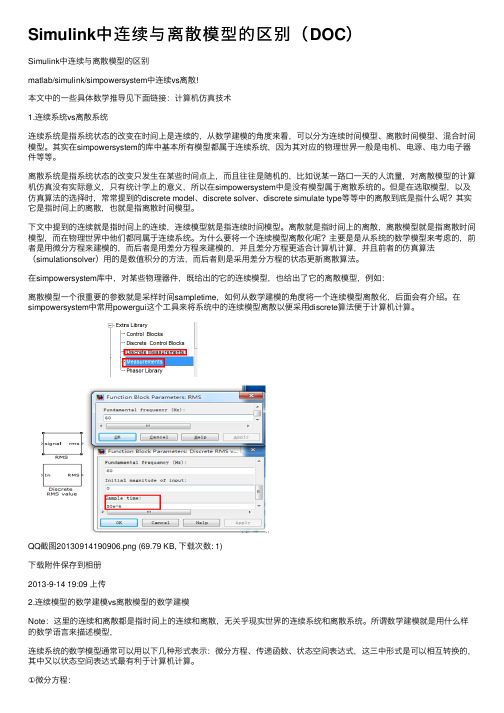
在simpowersystem库中,对某些物理器件,既给出的它的连续模型,也给出了它的离散模型,例如:离散模型⼀个很重要的参数就是采样时间sampletime,如何从数学建模的⾓度将⼀个连续模型离散化,后⾯会有介绍。
在simpowersystem中常⽤powergui这个⼯具来将系统中的连续模型离散以便采⽤discrete算法便于计算机计算。
信号与系统知识点归纳

周期信号的频谱是离散的,由一系列频率分量组成,每个 分量对应一个傅里叶系数。
幅度谱和相位谱
幅度谱表示各频率分量的幅度大小,相位谱表示各频率分 量的相位信息。
非周期信号频谱分析
傅里叶变换
将非周期信号表示为一系列复指数函数的积分,即 $F(omega) = int_{-infty}^{infty} f(t) e^{jomega t} dt$,其中 $F(omega)$ 是信号的频谱。
单位样值信号
在某一时刻取值为1,其余时 刻为0的信号。
正弦型信号
形如sin(ωn)或cos(ωn)的周期 性信号,其中ω为角频率。
复杂指数型信号
形如ean的形式,其中a和ω为 常数,n为离散时刻。
离散时间信号频谱分析
离散时间信号的频谱
通过傅里叶变换将离散时间信号从时域转换 到频域,得到信号的频谱。
信号分类
根据信号的性质和特征,信号可以分 为多种类型,如连续时间信号和离散 时间信号、周期信号和非周期信号、 能量信号和功率信号等。
系统定义及性质
系统定义
系统是一个由输入信号激励、内部含有某种变换关系、并能产生输出信号的物理装置或算法。在信号处理中,系 统通常表示为对输入信号进行某种变换或处理的过程。
周期信号的频谱
周期信号可以表示为无穷级数,其频谱由傅 里叶系数确定。
非周期信号的频谱
非周期信号的频谱是连续的,可以通过傅里 叶变换求得。
信号的能量和功率谱
能量信号和功率信号的频谱特性不同,分别 对应能量谱和功率谱。
离散时间系统响应
线性时不变系统的响应
线性时不变系统对输入信号的响应具有叠加性和时不变性。
卷积和运算
线性时不变系统的响应可以通过输入信号与系统单位样值响应的卷积 和求得。
离散控制与连续控制的比较与分析

离散控制与连续控制的比较与分析离散控制与连续控制是自动控制领域中两种不同的控制方法。
离散控制适用于那些以离散事件为基础的系统,而连续控制则适用于那些以连续参数为基础的系统。
本文将对离散控制与连续控制进行比较与分析。
一、基本概念离散控制:离散控制是一种以时间为基础的控制方法,它依靠离散事件的发生来触发控制动作。
在离散控制中,系统的状态在不同的时间点上以离散的方式进行变化。
连续控制:连续控制是一种以连续参数的变化为基础的控制方法,它依靠系统的连续性状态来实时调整控制器的输出值。
在连续控制中,系统的状态在任意时间点上以连续的方式进行变化。
二、控制器设计离散控制:离散控制通常使用离散控制算法,如PID控制算法。
这些算法将采样时间作为基准,通过对离散数据进行处理来确定控制器的输出值。
离散控制器的设计相对简单,容易实现。
连续控制:连续控制通常使用连续控制算法,如模糊控制、神经网络控制等。
这些算法通过对系统状态的连续监测,实时调整控制器的输出值。
连续控制器的设计复杂度高,需要考虑系统的动力学特性等因素。
三、响应速度离散控制:离散控制的响应速度相对较慢,因为其控制动作是通过离散事件的发生来触发的。
离散控制器在两个采样点之间的时间段内,无法对系统状态进行控制。
连续控制:连续控制的响应速度相对较快,因为其控制动作是实时调整的。
连续控制器可以在任意时间点上对系统状态进行控制,能够快速响应系统的变化。
四、系统稳定性离散控制:离散控制系统相对容易保持稳定,因为其控制动作是基于对离散数据的处理。
离散控制器可以通过调整采样周期来实现系统的稳定性。
连续控制:连续控制系统相对较难保持稳定,因为其控制动作是基于对连续参数的调整。
连续控制器需要考虑系统的动力学特性以及噪声等因素,以保证系统的稳定性。
五、应用领域离散控制:离散控制适用于那些以离散事件为基础的系统,如自动化生产线、数字电子设备等。
离散控制在许多工业领域中得到广泛应用。
连续控制:连续控制适用于那些以连续参数为基础的系统,如化工过程、机械控制系统等。
连续和离散系统分析

连续和离散系统分析连续系统分析:连续系统的数学描述通常使用微分方程。
对于一个线性时不变(LTI)系统,其数学模型可以表示为:y(t)=x(t)*h(t)其中,y(t)是系统的输出,x(t)是输入,h(t)是系统的冲激响应(即单位冲激函数对系统的响应)。
该式可以进一步表示为积分形式:y(t)=∫[x(τ)*h(t-τ)]dτ这是一种卷积形式的表达。
对连续系统进行频域分析时,通常使用拉普拉斯变换。
假设输入信号x(t)的拉普拉斯变换为X(s),输出信号y(t)的拉普拉斯变换为Y(s),系统的传递函数(频域特性)为H(s),则系统的频域响应可以表示为:Y(s)=X(s)*H(s)其中,*表示拉普拉斯变换中的乘法运算。
离散系统分析:离散系统的数学描述通常使用差分方程。
对于一个线性时不变系统,其数学模型可以表示为:y[n]=x[n]*h[n]其中,y[n]是系统的输出,x[n]是输入,h[n]是系统的冲激响应。
离散系统的频域分析通常使用傅里叶变换或者z变换。
在离散系统中,傅里叶变换将离散信号转换到周期连续频域上。
假设输入信号x[n]的傅里叶变换为X(e^jω),输出信号y[n]的傅里叶变换为Y(e^jω),系统的传递函数为H(e^jω),则系统的频域响应可以表示为:Y(e^jω)=X(e^jω)*H(e^jω)其中,*表示傅里叶变换中的卷积运算。
另一种广泛应用的离散系统分析方法是z变换。
z变换将离散信号转换到z平面上,相当于傅里叶变换的离散形式。
假设输入信号x[n]的z变换为X(z),输出信号y[n]的z变换为Y(z),系统的传递函数为H(z),则系统的频域响应可以表示为:Y(z)=X(z)*H(z)其中,*表示z变换中的乘法运算。
对于离散系统,还需要考虑采样定理以及采样频率对系统分析的影响。
采样定理指出,如果连续信号的最高频率成分小于采样频率的一半,那么可以通过离散信号获得连续信号的信息。
总之,连续和离散系统分析是信号与系统理论中的基础内容。
自动控制原理离散系统知识点总结

自动控制原理离散系统知识点总结自动控制原理中的离散系统是指在时间域和数值范围上都是离散的系统。
在离散系统中,信号是以离散时间点的形式传递和处理的。
本文将对自动控制原理离散系统的知识点进行总结,包括离散系统的概念、离散信号与离散系统的数学表示、离散系统的稳定性分析与设计等。
一、离散系统的概念与特点离散系统是指系统输入、输出和状态在时间上都是以离散的方式存在的系统。
与连续系统相比,离散系统具有以下特点:1. 离散时间:离散系统的输入、输出和状态是在离散时间点上采样得到的,而不是连续的时间信号。
2. 离散数值:离散系统的输入、输出和状态都是以离散数值的形式存在的,而不是连续的模拟数值。
二、离散信号与离散系统的数学表示离散信号是指在离散时间点上采样得到的信号。
离散系统可以通过离散信号的输入与输出之间的关系进行描述。
常见的离散系统数学表示方法有差分方程和离散时间传递函数。
1. 差分方程表示:差分方程是通过离散时间点上的输入信号和输出信号之间的关系来描述离散系统的。
差分方程可以是线性的或非线性的,可以是时不变的或时变的。
2. 离散时间传递函数表示:离散时间传递函数描述了离散系统输入与输出之间的关系,类似于连续时间传递函数。
离散时间传递函数可以通过Z变换得到。
三、离散系统的稳定性分析与设计离散系统的稳定性是指系统的输出在有限时间内收敛到有限范围内,而不是无限增长或震荡。
离散系统的稳定性分析与设计是自动控制原理中的重要内容。
1. 稳定性分析:离散系统的稳定性可以通过判断系统的极点位置来进行分析。
若系统的所有极点都位于单位圆内,则系统是稳定的;若存在至少一个极点位于单位圆外,则系统是不稳定的。
2. 稳定性设计:若离散系统不稳定,可以通过调整系统的参数或设计控制器来实现稳定性。
常见的稳定性设计方法包括PID控制器调整、根轨迹设计等。
四、离散系统的性能指标与优化离散系统的性能指标与优化是指通过调整控制器参数或控制策略,使离散系统的性能得到优化。
仿真建模中的离散事件仿真与连续系统模拟技术

仿真建模中的离散事件仿真与连续系统模拟技术在仿真建模领域中,离散事件仿真(Discrete Event Simulation, DES)与连续系统模拟技术是两种常用的方法。
离散事件仿真通过模拟系统组成部分之间的事件交互,以离散的时间步长进行模拟,适用于涉及离散事件和事件交互的系统。
而连续系统模拟技术则基于连续时间模型,将系统的状态从一个时间点演化到下一个时间点,适用于涉及连续变量和连续过程的系统。
本文将对离散事件仿真与连续系统模拟技术进行详细介绍和对比。
离散事件仿真是一种在离散事件驱动的基础上进行系统模拟的方法。
离散事件驱动指的是系统的状态变化是由离散事件的发生所触发的。
这些事件可以是任何可能影响系统行为的事物,如任务到达、资源请求和完成等。
离散事件仿真将系统中的所有活动建模为一系列事件,并通过事件的发生和处理来模拟系统的行为。
在仿真过程中,建模者需要明确定义系统中的各个事件及其发生的条件,以及事件发生后系统状态的变化规则。
离散事件仿真的优点是能够精确地模拟系统中的时间和事件交互,使得仿真结果具有较高的精确度。
它常用于模拟涉及排队、流程调度、供应链管理等问题的系统,如银行业务、交通系统和制造业生产线。
在离散事件仿真中,时间步长是指仿真模型中的事件触发机制。
不同的仿真模型可以选择不同的时间步长,以确保仿真结果的准确性和效率。
时间步长的选择应考虑系统中事件的发生频率和对结果的精确度要求。
当事件发生频率较高时,适合选择较小的时间步长,以提高仿真的精确度。
而当事件发生频率较低时,可以选择较大的时间步长以提高模拟效率。
常用的时间步长选择策略包括固定时间步长和自适应时间步长。
固定时间步长是指在整个仿真过程中使用相同的时间间隔,适用于事件发生频率稳定的仿真模型。
自适应时间步长则根据事件发生的频率动态调整时间间隔,以保持较高的仿真精确度和效率。
相比之下,连续系统模拟技术则更适用于描述连续变量和连续过程的系统。
在连续系统模拟中,系统的状态是以连续的时间点为基准进行演化的。
采样离散控制系统
上页
下页 末页
F (z) f (0) f (T )z1 f (2T )z2 ... f (nT )zn ...
结束
电气信息学院
电子笔
10
【例1】求单位阶跃函数的z变换
自 解:对单位阶跃函数有 f(nT)=1
动 控
故
制
理 论
Z[1(t)]
f (0)
f (T )z1
首页 上页 下页 末页 结束
电气信息学院
电子笔
12
(二)部分分式法
自 若函数f(t)的拉氏变换可以展开位部分分式的形式
动
控 制 理 论
n
F(s)
Ai
8.1 绪言
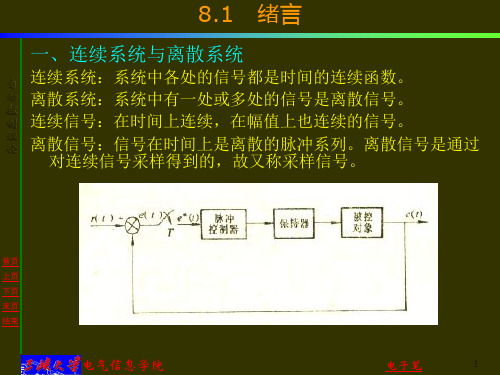
一、连续系统与离散系统
自 连续系统:系统中各处的信号都是时间的连续函数。
动 控
离散系统:系统中有一处或多处的信号是离散信号。
制 连续信号:在时间上连续,在幅值上也连续的信号。
理 论
离散信号:信号在时间上是离散的脉冲系列。离散信号是通过
对连续信号采样得到的,故又称采样信号。
ห้องสมุดไป่ตู้
首页 上页 下页 末页 结束
电气信息学院
电子笔
3
采样器的输出信号 e*(t) 为:
自 动 控 制
e*(t) e(t)T (t) e(t) (t nT ) n
理 在实际的控制系统中,通常当t<0时,e(t)=0,因
论 此,上式改写为:
e*(t) e(t) (t nT ) e(nT ) (t nT )
理
论 f *(t) f (nT ) (t nT )
n0
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验一 连续和离散系统分析
一、实验目的
学习连续系统和离散系统响应的matlab 求解方法; 二、实验主要仪器设备和材料
计算机
三、实验方法、步骤及结果测试
实验方法:编程,上机调试,分析实验结果; 步骤: 编程实现上述各实验内容 四、实验结果
1、某系统的传递函数为:)
2)(1(1
)(/)(++=
s s x X s Y
试求系统的冲激响应和阶跃响应。
2、编制程序求解下列两个系统的单位冲激响应和阶跃响应,并绘出其图形。
要求分别用filter、conv、impz三种函数完成。
给出理论计算结果和程序计算结果并讨论。
(I)
]1
[
]
[
]2
[
125
.0
]1
[
75
.0
]
[-
-
=
-
+
-
+n
x
n
x
n
y
n
y
n
y
理论计算结果:
程序计算结果:
A:单位冲激响应
(1)用Filter函数(2)用Conv函数(3)用impz函数
单位冲激响应:
n012345 h(n)1
单位阶跃响应:
n012345 y(n)1
B:单位阶跃响应
(1)用Filter函数
(2)用Conv函数
(3)用Impz函数
(II )]}4[]3[]2[]1[{25.0][-+-+-+-=n x n x n x n x n y
理论计算结果:
程序计算结果:
A :单位冲激响应 (1)用filter 函数
(2)用Conv 函数
(3)用Impz 函数
B :单位阶跃响应
单位冲激响应:
n 0 1 2 3 4 5 h(n) 0
单位阶跃响应:
N 0 1 2 3 4 5 y(n) 0
1
1
(1)用filter 函数
(2)用Conv 函数
(3)用Impz 函数
结论:
y=filter(p,d,x)用来实现差分方程,d 表示差分方程输出y 的系数,p 表示输入x 的系数,而x 表示输入序列。
输出结果长度数等于x 的长度; 而y=conv(x,h)是用来实现卷积的,对x 序列和h 序列进行卷积,输出的结果个数等于x 的长度与h 的长度之和减去1;
y=impz(p,d,N)是用来实现冲击响应的,d 和p 的定义同filter ,N 表示冲击响应输出的序列个数。
3 已知描述某连续系统的微分方程为
)(8)(2)(6)(5)(''''t x t x t y t y t y +=++
求该系统的单位冲激响应。
程序:
b=[2 8];a=[1 5 6];
sys=tf(b,a);
t=0::10;
y=impulse(sys,t);
plot(t,y);
xlabel(‘时间(t)’);ylabel(‘y(t)’);tltle(‘单位冲激响应’);
4 计算上述系统在输入为
)()(t u e t x t -=时的零状态响应。
5 已知系统函数2
11
12.04.0121)(----++=z
z z z H ,求 1)离散系统的单位冲激响应h(n);
2) 输入为)()(n u n x =,求系统的零状态响应。
程序:
num=[1 2];den=[1 ]; % system model y1=impz(num,den,20); subplot(121); stem(y1); title('impulse response'); n=0:20; x2=ones(1,21);
y1filter=filter(num,den,x2);
subplot(122);
stem(n,y1filter); title('filter_step'); xlabel('x');
ylabel('y');
程序:
ts=0;te=10;dt=;
sys=tf([2 8],[1 5 6]);
t=ts:dt:te;
f=exp(-t);
y=lsim(sys,f,t);
plot(t,y)
xlabel('time(sec)') ylabel('y(t)')
6 已知某离散因果系统的系统函数2
11
5.011)(---+-+=z
z z z H ,试分析该系统的幅频特性。
程序:
num=[1 1]; den=[1 -1 ];
sys=tf(num,den);
w=-10::10; H=freqs(num,den,w);
subplot(2,1,1);plot(w,abs(H));title('幅频特性'); subplot(2,1,2);plot(w,angle(H));title('相频特性');
五、思考题
1)连续系统响应的计算机求解可以分为哪些方法各是什么原理
答:①连续时间系统零状态响应的求解
(
y
sys
lsim
f
)t
,
,
t表示计算系统响应的抽样点向量,f是系统输入信号向量
sys是LTI系统模型,借助tf函数获得。
②连续系统冲激响应和阶跃响应的求解
连续时间系统冲激响应可用impulse函数直接求出,其调用形式为:
y=impulse(sys,t)
连续时间系统阶跃响应可用step函数直接求出,其调用形式为:
y=step(sys,t)
t表示计算系统响应的抽样点向量,sys是LTI系统模型.
2)matlab中用于离散系统求解的命令有哪些各基于什么求解方法
答:①y=filter(p,d,x)用来实现差分方程,d表示差分方程输出y的系数,p表示输入x的系数,而x表示输入序列。
输出结果长度数等于x的长度;
②y=conv(x,h)是用来实现卷积的,对x序列和h序列进行卷积,输出的结果个数等于x的长度与h的长度之和减去1;
③y=impz(p,d,N)是用来实现冲击响应的,d和p的定义同filter,N表示冲击响应输出的序列个数。
