山东省淄博市2020版高二下学期期中数学试卷(理科)(II)卷
山东省淄博市高二下学期数学期中考试试卷

山东省淄博市高二下学期数学期中考试试卷姓名:________ 班级:________ 成绩:________一、选择题:本大题共12小题,每小题5分,共60分. (共12题;共60分)1. (5分) (2020高二下·天津期中) 4名同学分别报名参加学校的手工、绘画、机器人设计三个校本课程,每人限报其中一个课程,不同报法的种数是()A . 81B . 64C . 24D . 162. (5分) (2017高二下·沈阳期末) 定义在R上的可导函数f(x),f ′(x)是其导函数.则下列结论中错误的是()A . 若f(x)是偶函数,则f ′(x)必是奇函数B . 若f(x)是奇函数,则f ′(x)必是偶函数C . 若f ′(x)是偶函数,则f(x)必是奇函数D . 若f ′(x)是奇函数,则f(x)必是偶函数3. (5分)离散型随机变量X的分布列为P(X=k)=pkq1﹣k(k=0,1,p+q=1),则EX与DX依次为()A . 0和1B . p和p2C . p和1﹣pD . p和p(1﹣p)4. (5分) (2019高二下·拉萨月考) 从5名男生和4名女生中选出4人参加比赛,如果4人中须既有男生又有女生,选法有()种A . 21B . 120C . 60D . 915. (5分)从6名男同学,3名女同学中任选3名参加体能测试,则选到的3名同学中既有男同学又有女同学的概率为()A .B .C .D .6. (5分)对于上可导的任意函数,若满足,则必有()A .B .C .D .7. (5分)在研究吸烟与患肺癌的关系中,通过收集数据、整理分析数据得“吸烟与患肺癌有关”的结论,并且有99%以上的把握认为这个结论是成立的,则下列说法中正确的是()A . 100个吸烟者中至少有99人患有肺癌B . 1个人吸烟,那么这人有99%的概率患有肺癌C . 在100个吸烟者中一定有患肺癌的人D . 在100个吸烟者中可能一个患肺癌的人也没有8. (5分) (2016高二下·吉林期中) 在10个球中有6个红球和4个白球(各不相同),不放回地依次摸出2个球,在第一次摸出红球的条件下,第2次也摸到红球的概率为()A .B .C .D .9. (5分)某班选派6人参加两项志愿者活动,每项活动最多安排4人,则不同的安排方法有()A . 50种B . 70种C . 35种D . 55种10. (5分)定义:如果函数在区间上存在,满足则称函数在区间上的一个双中值函数,已知函数是区间上的双中值函数,则实数的取值范围是()A .B .C .D .11. (5分) (2015高二下·张掖期中) 下列说法正确的是()A . 类比推理是由特殊到一般的推理B . 演绎推理是特殊到一般的推理C . 归纳推理是个别到一般的推理D . 合情推理可以作为证明的步骤12. (5分)函数的最大值为()A .B .C .D .二、填空题:本大题共4小题,每小题5分,共20分。
山东省淄博市淄川中学2020学年高二数学下学期期中试题

山东省淄博市淄川中学2020学年高二数学下学期期中试题时间150分钟分值150分第Ⅰ卷(共60分)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.设复数满足,则()A. B. C. D.2.某工厂生产的零件外直径(单位:)服从正态分布,今从该厂上、下午生产的零件中各随机取出一个,测得其外直径分别为和,则可认为()A.上午生产情况异常,下午生产情况正常B.上午生产情况正常,下午生产情况异常C.上、下午生产情况均正常D.上、下午生产情况均异常3.将一枚质地均匀的硬币抛掷四次,设为正面向上的次数,则等于()A. B. C. D.4.为了弘扬我国优秀传统文化,某中学广播站在春节、元宵节、清明节、端午节、中秋节五个中国传统节日中,随机选取两个节日来讲解其文化内涵,那么春节和端午节恰有一个被选中的概率是()A. B. C. D.5.在报名的名男生和名女生中,选取5人参加义务劳动,要求男生、女生都有,则不同的选取方式的种数为( ).A. 120 B. 126 C. 240 D.2526.已知随机变量服从正态分布,若,则()A. B. C. D.7.函数,则在点处的切线方程为()A. B. C. D.8.在二项式的展开式中,各项系数之和为,二项式系数之和为,若,则()A. B. C. D.9.一个盒子里装有大小、形状、质地相同的个球,其中黄球个,篮球个,绿球个.现从盒子中随机取出两个球,记事件为“取出的两个球颜色不同”,事件为“取出一个黄球,一个绿球”,则()A. B. C. D.10.已知是定义在上的可导函数,的图象如下图所示,则的单调减区间是()A. B. C. D.11.甲、乙、丙、丁、戊五名同学参加某种技术竞赛,决出了第一名到第五名的五个名次,甲、乙去询问成绩,组织者对甲说:“很遗憾,你和乙都未拿到冠军”;对乙说:“你当然不会是最差的”.从组织者的回答分析,这五个人的名次排列的不同情形种数共有()A. B. C. D.12.已知定义在上的函数的导函数为,满足,且,则不等式的解集为()A. B. C. D.第Ⅱ卷(共90分)二、填空题(每题5分,满分20分,将答案填在答题纸上)13.随机变量,变量,则.14.二项式展开式中含项的系数是.15.已知函数的导函数为,且满足,则.16.设,若随机变量的分布列是:则当变化时,的极大值是.三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17.已知的展开式中所有项的系数和为.(1)求的展开式中二项式系数最大的项;(2)求的展开式中的常数项.18. 已知函数,且当时,函数取得极值为.(1)求的解析式;(2)若关于的方程在上有两个不同的实数解,求实数的取值范围.19. 实力相等的甲、乙两队参加乒乓球团体比赛,规定5局3胜制(即5局内谁先赢3局就算胜出并停止比赛).⑴试求甲打完5局才能取胜的概率.⑵按比赛规则甲获胜的概率20.某校从学生会宣传部6名成员(其中男生4人,女生2人)中,任选3人参加某省举办的演讲比赛活动.(1)设所选3人中女生人数为ξ,求ξ的分布列;(2)求男生甲或女生乙被选中的概率;(3)设“男生甲被选中”为事件A,“女生乙被选中”为事件B,求P(B)和P(B|A).21.某公司计划购买2台机器,该种机器使用三年后即被淘汰.机器有一易损零件,在购进机器时,可以额外购买这种零件作为备件,每个200元.在机器使用期间,如果备件不足再购买,则每个500元.现需决策在购买机器时应同时购买几个易损零件,为此搜集并整理了100台这种机器在三年使用期内更换的易损零件数,得下面柱状图:以这100台机器更换的易损零件数的频率代替1台机器更换的易损零件数发生的概率,记表示2台机器三年内共需更换的易损零件数,表示购买2台机器的同时购买的易损零件数.(I)求的分布列;(II)若要求,确定的最小值;(III)以购买易损零件所需费用的期望值为决策依据,在与之中选其一,应选用哪个?22.已知函数=e x(e x﹣a)﹣a2x.(1)讨论的单调性;(2)若,求a的取值范围.高二数学试卷答案一、选择题本大题共12个小题,每小题5分,共60分1-5:DBCCA 6-10:CAADB 11、D 12、A二、填空题13. 14. 15. 16.三、解答题17.解:(1)由题意,令得,即,所以展开式中二项式系数最大的项是第项,即(2)展开式的第项为.由,得;由,得.所以的展开式中的常数项为18.解:(1),由题意得,即解得∴.(2)由有两个不同的实数解,得在上有两个不同的实数解,设,则,由,得或,当时,,则在上递增,当时,,则在上递减,由题意得即解得,所以,实数的取值范围是.19. 甲、乙两队实力相等,所以每局比赛甲获胜的概率为,乙获胜的概率为.⑴甲打完5局才能取胜,相当于进行5次独立重复试验,且甲第5局比赛取胜,前4局恰好2胜2负∴甲打完5局才能取胜的概率.(2) 记事件 “甲打完3局才能取胜”,记事件=“甲打完4局才能取胜”,记事件=“甲打完5局才能取胜”.事件=“按比赛规则甲获胜”,则,又因为事件、、彼此互斥,故.答:按比赛规则甲获胜的概率为20. (1)ξ的所有可能取值为0,1,2,依题意得P (ξ=0)=63=51,P (ξ=1)=63=53,P (ξ=2)=63=51.∴ξ的分布列为(2)设“甲、乙都不被选中”为事件C ,则P (C )=63=204=51.∴所求概率为P ()=1-P (C )=1-51=54.(3)P (B )=63=2010=21;P (B |A )=52=104=52.21.【答案】(I )见解析(II )19(III )22.【答案】(1)当,在单调递增;当,在单调递减,在单调递增;当,在单调递减,在单调递增;(2).【解析】试题分析:(1)分,,分别讨论函数的单调性;(2)分,,分别解,从而确定a 的取值范围. 试题解析:(1)函数的定义域为,,①若,则,在单调递增.②若,则由得.当时,;当时,,所以在单调递减,在单调递增.③若,则由得.当时,;当时,,故在单调递减,在单调递增.。
山东省淄博市淄博中学2023-2024学年高二下学期期中考试数学试题(含解析)

淄博中学2023-2024学年第二学期高二期中考试数学试题一、单选题(每小题5分,共40分,只有一个正确选项)1.已知函数,则( )A .B .1CD2.是等差数列a 的前项和,,,则首项( )A .1B .2C .3D .43.在数列中,若,则( )A .B .2C .1D .4.某同学是个数学迷,他在设置手机的数字密码时,打算将圆周率的前六个数字3、1、4、1、5、9进行某种排列得到密码,要求两个1必须相邻,那么可以设置的不同密码有( )A .120B .240C .60D .305.数学家杨辉在其专著《详解九章算术法》和《算法通变本末》中,提出了一些新的高阶等差数列,其中二阶等差数列是一个常见的等差数列,如数列2,4,7,11,16,从第二项起,每一项与前一项的差组成新数列2,3,4,5,新数列2,3,4,5为等差数列,则称数列2,4,7,11,16为二阶等差数列,现有二阶等差数列,其中前几项分别为2,5,10,17,26,37,记该数列的后一项与前一项之差组成新数列,则( )A .15B .17C .18D .196.设,函数的导函数是,若是奇函数,则曲线在处的切线方程为( )A .B .C .D .7.如图,用四种不同颜色给矩形A 、B 、C 、D 涂色,要求相邻的矩形涂不同的颜色,则不同的涂色方法共有()A .12种B .24种C .48种D .72种8.已知函数在区间上单调递减,则a 的值可能为()()cos f x x =066lim x f x f xππ∆→⎛⎫⎛⎫+∆- ⎪ ⎪⎝⎭⎝⎭=∆12-n S {}n a 3412a a +=749S =1a ={}n a 11a =-()1121n n a n a -=≥-2024a =1-12{}n a {}n b 8b =a R ∈()()4323f x x a x ax =-++()f x '()f x '()y f x =1x =31y x =-+2y x=-24y x =+24y x =-+()ln x f x ae x =-()1,2A .B .C .D .e二、多选题(每小题6分,共18分,选错得0分)9.下列求导运算正确的是()A .若,则B .若,则C .若,则D .若,则10.为弘扬我国古代的“六艺文化”,某夏令营主办单位计划利用暑假开设“礼”、“乐”、“射”、“御”、“书”、“数”六门体验课程,每周一门,连续开设六周,则下列说法正确的是( )A .某学生从中选2门课程学习,共有15种选法B .课程“乐”“射”排在相邻的两周,共有240种排法C .课程“御”“书”“数”排在不相邻的三周,共有72种排法D .课程“礼”不排在第一周,课程“数”不排在最后一周,共有504种排法11.已知数列的通项公式为,,记为数列的前n 项和,则下列说法正确的是( )A .B .C .若,则D .若,则三、填空题(每小题5分,共15分)12.函数在上的最大值为______.13.已知数列为等比数列,,公比,若是数列的前n 项积,则取最大值时,n 的值为______.14.已知函数有两个不同的零点,则实数a 的取值范围是______.四、解答题(本大题共77分)15.(13分)某医院有内科医生7名,外科医生5名,现选派4名参加赈灾医疗队,其中,(1)甲、乙有且仅有一人参加,有多少种选法?2e2e-3e-()()cos 21f x x =+()()2sin 21f x x '=+()23x f x e -+=()232x f x e -+'=-()x x f x e =()1x xf x e +'=()lg f x x x =()1lg ln10f x x '=+{}n a ()214n n a π-=tan n n b a =n S {}n a ()11n n b -=-()1123112n n b b b b -+-++++=n n n c a b =()12314nnn c c c c π-++++=n n n d b S =()2123224n d d d d n n π++++=-+ ()ln f x x x =-(]0,e {}n a 164a =12q =n T {}n a n T ()()ln 2f x x ax a =-+∈R(2)队中至少有一名内科医生和一名外科医生,有几种选法?16.(15分)设函数,曲线在点处的切线斜率为1.(1)求a 的值;(2)设函数,求的最小值;17.(15分)已知等比数列中,且是和的等差中项.(1)求数列的通项公式;(2)若函数,满足,求的前n 项和.18.(17分)已知数列的前n 项和为,满足.(1)求的通项公式;(2)删去数列的第3i 项(其中),将剩余的项按从小到大的顺序排成新数列,设的前n 项和为,请写出的前6项,并求出和.19.(17分)已知函数(,e 为自然对数的底数).(1)若在处的切线与直线垂直,求a 的值;(2)讨论函数的单调性;(3)当时,求证:.淄博中学2023-2024学年第二学期高二期中考试数学试题答案一、单选题(每小题5分,共40分,只有一个正确选项)1.【答案】,选A 2.【答案】得所以选A3.【答案】,,,所以周期为3,所以选D ()()()2ln 1f x x x ax =++-()y f x =()()0,0f ()()g x f x ='()g x {}n a 12a =22a 3a 14a {}n a {}n b ()22n n b n a n N *=+∈{}n b n S {}n a n S 22n n S a =-{}n a {}n a 1,2,3,i = {}n b {}n b n T {}n b 6T 2n T ()()21x f x axe x =-+a ∈R ()f x 0x =y ax =()f x 21a e≥()2ln 2f x x x x ≥---()sin f x x =-'()016limsin 662x f x f x f x πππ∆→⎛⎫+∆- ⎪⎛⎫⎝'⎭==-=- ⎪∆⎝⎭3471249a a S +=⎧⎨=⎩112a d =⎧⎨=⎩11a =-212a =32a =41a =-{}n a 2024212a a ==4.【答案】,选A5.【答案】前几项为3、5、7、9、11,所以,所以,所以选B 6.【答案】因为是奇函数所以所以所以切点为所以所以选B7.【答案】选C 8.【答案】因为,所以,因为在区间上单调递减,所以在上恒成立,即在上恒成立,当时,因为在上恒成立,故上式成立,满足题意;当时,则在上恒成立,令,,所以在上恒成立,所以在上单调递增,又,故,即,选C 二、多选题(每小题6分,共18分,选错得0分)9.【答案】A .B .55120A ={}n b 21n b n =+817b =()()324332f x x a x ax +'=-+()f x '3a =-()423f x x x =-()1,2-()12f '=-2y x =-432248⨯⨯⨯=()()ln 0x f x ae x x =->()1x f x ae x'=-()f x ()1,2()10xf x ae x =-≤'()1,21x a xe≤()1,20a ≤10xxe >()1,20a >1x xe a≥()1,2()x g x xe =()1,2x ∈()()10x g x x e =+>'()1,2()g x ()1,2()()222g x g e <=212e a ≥2102a e<≤()()2sin 21f x x =-+'()232x f x e -+'=-C .D . 选BD 10.【答案】A .B .C .D .选ABD11.【答案】由可知是以,的等差数列。
山东省2020版高二下学期期中数学试卷(理科)(II)卷(新版)

山东省2020版高二下学期期中数学试卷(理科)(II)卷姓名:________ 班级:________ 成绩:________一、选择题 (共12题;共24分)1. (2分)已知,其中m,n是实数,i是虚数单位,则m+n=()A . 1+2iB . 1﹣2iC . 2+iD . 2﹣i2. (2分)(2020·成都模拟) 已知,函数在区间上恰有个极值点,则正实数的取值范围为()A .B .C .D .3. (2分)设,则下列关系式成立的是()A .B .C .D .4. (2分) (2016高二下·咸阳期末) 设a=n(n﹣1)(n﹣2)…(n﹣50),则a可表示为()A .B .C .D .5. (2分)规定[x]表示不超过x的最大整数,例如:[3.1]=3,[-2.6]=-3,[-2]=-2;若f'(x)是函数f(x)=ln|x|导函数,设g(x)=f(x)f'(x),则函数y=[g(x)]+[g(-x)]的值域是()A . {偶数}B . {0,1}C . {0}D . {-1,0}6. (2分)欧拉(LeonhardEuler,国籍瑞士)是科学史上最多产的一位杰出的数学家,他发明的公式eix=cosx+isinx(i为虚数单位),将指数函数的定义域扩大到复数,建立了三角函数和指数函数的关系,这个公式在复变函数理论中占有非常重要的地位,被誉为“数学中的天桥”.根据此公式可知,表示的复数在复平面内位于()A . 第一象限B . 第二象限C . 第三象限D . 第四象限7. (2分)已知是虚数单位,若复数是纯虚数,则实数等于()A .B .C .D .8. (2分)(2014·辽宁理) 6把椅子排成一排,3人随机就座,任何两人不相邻的坐法种数为()A . 144B . 120C . 72D . 249. (2分) (2017高三下·河北开学考) 若,则a等于()A . ﹣1B . 1C . 2D . 410. (2分)若方程的根在区间上,则K的值为()A . -1B . 1C . -1或2D . -1或111. (2分)(2017·达州模拟) 的展开式的所有二项式系数之和为128,则n为()A . 5B . 6C . 7D . 812. (2分) (2016高二下·东莞期中) 函数函数f(x)=(x﹣3)ex的单调递增区间是()A . (﹣∞,2)B . (0,3)C . (1,4)D . (2,+∞)二、填空题 (共4题;共4分)13. (1分) (2016高二上·大庆期中) 设双曲线的一条渐近线与抛物线y=x2+1 只有一个公共点,则双曲线的离心率为________.14. (1分)(2016·中山模拟) 已知m=3 sinxdx,则二项式(a+2b﹣3c)m的展开式中ab2cm﹣3的系数为________.15. (1分) (2016高二下·黄冈期末) 某校开设9门课程供学生选修,其中A,B,C3门课由于上课时间相同,至多选1门,若学校规定每位学生选修4门,则不同选修方案共有________种.16. (1分)函数的单调增区间是________.三、解答题 (共6题;共55分)17. (10分)(2020·镇江模拟) 定义:若数列满足所有的项均由构成且其中-1有m个,1有p 个,则称为“ ﹣数列”.(1)为“ ﹣数列” 中的任意三项,则使得的取法有多少种?(2)为“ ﹣数列” 中的任意三项,则存在多少正整数对使得且的概率为 .18. (15分)(2013·福建理) 已知函数f(x)=sin(wx+φ)(w>0,0<φ<π)的周期为π,图象的一个对称中心为(,0),将函数f(x)图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再将得到的图象向右平移个单位长度后得到函数g(x)的图象.(1)求函数f(x)与g(x)的解析式(2)是否存在x0∈(),使得f(x0),g(x0),f(x0)g(x0)按照某种顺序成等差数列?若存在,请确定x0的个数,若不存在,说明理由;(3)求实数a与正整数n,使得F(x)=f(x)+ag(x)在(0,nπ)内恰有2013个零点.19. (10分) (2018高二上·宁夏期末) 已知函数(1)求这个函数的导数;(2)求这个函数的图像在处的切线方程.20. (10分) (2016高一上·佛山期中) 已知函数f(x)=ax﹣(a,b∈N*),f(1)= 且f(2)<2.(1)求a,b的值;(2)判断并证明函数y=f(x)在区间(﹣1,+∞)上的单调性.21. (5分)已知在的展开式中,第4项为常数项,(1)求f(x)的展开式中含x﹣3的项的系数;(2)求f(x)的展开式中系数最大的项.22. (5分) (2018高三上·汕头模拟) 设函数 .(Ⅰ)求证:;(Ⅱ)当时,函数恒成立,求实数的取值范围.参考答案一、选择题 (共12题;共24分)答案:1-1、考点:解析:答案:2-1、考点:解析:答案:3-1、考点:解析:答案:4-1、考点:解析:答案:5-1、考点:解析:答案:6-1、考点:解析:答案:7-1、考点:解析:答案:8-1、考点:解析:答案:9-1、考点:解析:答案:10-1、考点:解析:答案:11-1、考点:解析:答案:12-1、考点:解析:二、填空题 (共4题;共4分)答案:13-1、考点:解析:答案:14-1、考点:解析:答案:15-1、考点:解析:答案:16-1、考点:解析:三、解答题 (共6题;共55分)答案:17-1、考点:解析:答案:18-1、答案:18-2、答案:18-3、考点:解析:答案:19-1、答案:19-2、考点:解析:答案:20-1、答案:20-2、考点:解析:答案:21-1、考点:解析:答案:22-1、考点:解析:。
山东省2020版高二下学期期中数学试卷(理科)(II)卷
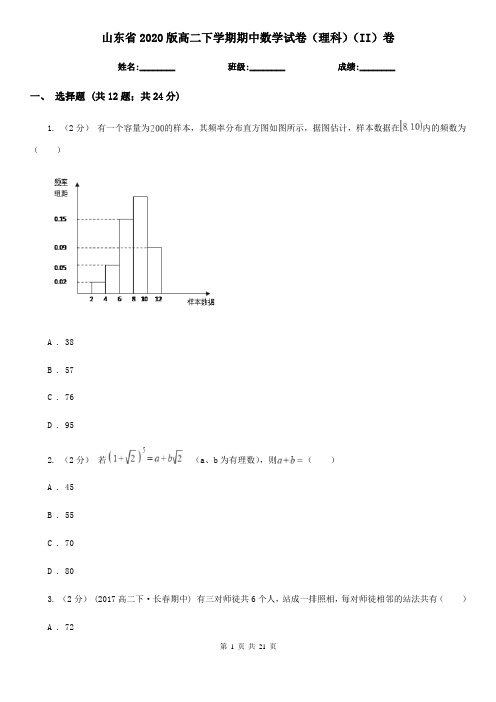
山东省2020版高二下学期期中数学试卷(理科)(II)卷姓名:________ 班级:________ 成绩:________一、选择题 (共12题;共24分)1. (2分)有一个容量为的样本,其频率分布直方图如图所示,据图估计,样本数据在内的频数为()A . 38B . 57C . 76D . 952. (2分)若(a、b为有理数),则()A . 45B . 55C . 70D . 803. (2分) (2017高二下·长春期中) 有三对师徒共6个人,站成一排照相,每对师徒相邻的站法共有()A . 72B . 54C . 48D . 84. (2分)如图是高尔顿板的改造装置,当小球从B自由下落时,进入槽口A处的概率为()A .B .C .D .5. (2分)利用随机模拟方法计算y=x2+1与y=5围成的面积时,先利用计算器产生两组0~1之间的均匀随机数a1=RAND,b1=RAND,然后进行平移与伸缩变换a=4a1﹣2,b=4b1+1,实验进行了1000次,前998次中落在所求面积区域内的样本点数为624,若最后两次实验产生的0~1之间的均匀随机数为(0.3,0.1),(0.9,0.7),则本次模拟得到的面积的估计值是()A . 10B .C .D .6. (2分)线性回归方程=bx+a必过()B . (, 0)点C . (0,)点D . (,)点7. (2分) (2018高三上·重庆月考) 下列说法中错误的是()A . 先把高二年级的2000名学生编号为1到2000,再从编号为1到50的50名学生中随机抽取1名学生,其编号为,然后抽取编号为,,的学生,这样的抽样方法是系统抽样法;B . 独立性检验中,越大,则越有把握说两个变量有关;C . 若两个随机变量的线性相关性越强,则相关系数的值越接近于1;D . 若一组数据1、a、3的平均数是2,则该组数据的方差是 .8. (2分)某班有50名学生,一次数学考试的成绩ξ服从正态分布N(105,102),已知P(95≤ξ≤105)=0.32,估计该班学生数学成绩在115分以上的人数为()A . 10B . 9C . 8D . 79. (2分) (2019高三上·吉安月考) 某种植基地将编号分别为1,2,3,4,5,6的六个不同品种的马铃薯种在如图所示的A B C D E F这六块实验田上进行对比试验,要求这六块实验田分别种植不同品种的马铃薯,若种植时要求编号1,3,5的三个品种的马铃薯中至少有两个相邻,且2号品种的马铃薯不能种植在A、F这两块实验田上,则不同的种植方法有()B . 432种C . 456种D . 480种10. (2分) (2018高二上·鹤岗月考) 设,则()A . -B .C . -D .11. (2分) (2015高二上·河北期末) 在高校自主招生中,某学校获得5个推荐名额,其中清华大学2名,北京大学2名,复旦大学1名.并且北京大学和清华大学都要求必须有男生参加.学校通过选拔定下3男2女共5个推荐对象,则不同的推荐方法共有()A . 20种B . 22种C . 24种D . 36种12. (2分)在[0,π]上随机取一个数x,则事件“2sin cos+cosx≥”发生的概率为()A .B .C .D .二、填空题 (共4题;共4分)13. (1分) (2017高二上·钦州港月考) 某校高中生共有900人,其中高一年级300人,高二年级200人,高三年级400人,现采用分层抽样法抽取一个容量为45的样本,那么从高一、高二、高三各年级抽取人数分别为________.14. (1分) (2018高二下·顺德期末) 位同学在一次聚会活动中进行纪念品的交换,任意两位同学之间最多交换一次,进行交换的两位同学互赠一份纪念品。
山东省淄博市高二数学下学期期中联考试题理(扫描版)

山东省淄博市2016-2017学年高二数学下学期期中联考试题理(扫描版)数学答案(科学倾向)一、选择题:DBDDB CBCCD BC 二、填空题:112++n n 2 -20 ),(323三、解答题:17.【解析】(1)∵21021010(3)33310i i i z i i i +--====-++,∴z =(2)∵2(3)(3)(3)(3)83i i ai i a a a i b --+=-+-=+-+,∴83(6)113a b a a b +==-⎧⎧⇒⎨⎨-+==-⎩⎩.18.(Ⅰ)当1a =时,32()1f x x x x =-+++,得(2)1f =- 1分 且2()321f x x x '=-++,(2)7f '=-. 3分所以,曲线32()21f x x x x =-+-+在点(2(2))f ,处的切线方程是17(2)y x +=--, 5分整理得7130x y +-=. 6分 (Ⅱ)解:322()1f x x ax a x =-+++,22()32(3)()f x x ax a x a x a '=-++=-+-.令()0f x '=,解得3ax =-或x a =. 8分 若0a >,当x 变化时,()f x '的正负如下表:因此,函数()f x 在3ax =-处取得极小值3a f ⎛⎫- ⎪⎝⎭,且351327a f a ⎛⎫-=- ⎪⎝⎭;函数()f x 在x a =处取得极大值()f a ,且3()1f a a =+. 12分19.【解析】证明:证法一(综合法):因为a>0,b>0()a b=+==-2=≥≥.证法二(分析法)≥,即证()0a b-≥,因为a>0,b>0,a-b所以()a b-≥≥20.【解析】设小正方形的边长为x cm,则盒子底面长为(82x-)cm,宽为(52x-)cm,32(82)(52)42640V x x x x x x=--=-+,()x<<52 4分210125240,0,1().3V x x V x x''=-+===令得或舍去(1)18V V==极大值,在定义域内仅有一个极大值,maxV∴=18 10分即小正方形边长为1cm时,盒子容积最大为cm318 12分21.试题解析:(ⅰ)当1=n时,左边=1112=,右边=3411214=+⨯⨯,左边<右边,即不等式成立;(ⅱ)假设)(*Nkkn∈=时,不等式成立,即222211114123421kk k++++⋅⋅⋅+<+则当1+=kn时,22222211111411234(1)21(1)kk k k k++++⋅⋅⋅++<++++问题可通过证明1)1(2)1(4)1(11242+++<+++kkkkk来实现要证:32441)1(2)1(4)1(11242++=+++<+++k k k k k k k 只需证:1243244)1(12+-++<+k k k k k ,只需证:)12)(32(4)1(12++<+k k k 只需证:2)1(4)32)(12(+<++k k k ,只需证:4124312422++<++k k k k ∵43<,∴1)1(2)1(4)1(11242+++<+++k k k k k 即当1+=k n 是不等式也成立.综上:由(ⅰ)(ⅱ)可得,对于一切的*∈N n 不等式恒成立.22. (1)解:求导函数,可得f′(x )= 221xax x +-(Ⅱ) 当a=2时,,的定义域是(0,+)∞,2221ln 21ln 211)('xx x x x x x x g --=⋅--= 令,,,递增,又时,,,递减,当时,,,递增,;(Ⅲ)证明:由(Ⅱ)得,时,,令,则,()()122ln )12)12(212)12(2122ln(2212111221+=++⋅⋅⋅++⋅+>+++-=∑n n n n nk k k。
山东省淄博市高二数学下学期期中联考试题 理(扫描版)

山东省淄博市2016-2017学年高二数学下学期期中联考试题理(扫描版)数学答案(科学倾向)一、选择题:DBDDB CBCCD BC 二、填空题:112++n n 2 -20 ),(323三、解答题:17.【解析】(1)∵21021010(3)33310i i i z i i i +--====-++,∴z =(2)∵2(3)(3)(3)(3)83ii ai i a a a i b--+=-+-=+-+,∴83(6)113a b a a b +==-⎧⎧⇒⎨⎨-+==-⎩⎩.18.(Ⅰ)当1a =时,32()1f x x x x =-+++,得(2)1f =- 1分 且2()321f x x x '=-++,(2)7f '=-. 3分所以,曲线32()21f x x x x =-+-+在点(2(2))f ,处的切线方程是17(2)y x +=--, 5分整理得7130x y +-=. 6分 (Ⅱ)解:322()1f x x ax a x =-+++,22()32(3)()f x x ax a x a x a '=-++=-+-.令()0f x '=,解得3ax =-或x a =. 8分 若0a >,当x 变化时,()f x '的正负如下表:因此,函数()f x 在3ax =-处取得极小值3a f ⎛⎫- ⎪⎝⎭,且351327a f a ⎛⎫-=- ⎪⎝⎭;函数()f x 在x a =处取得极大值()f a ,且3()1f a a =+. 12分19.【解析】证明:证法一(综合法):因为a>0,b>0+-()a b=+==-2=≥≥.证法二(分析法)≥≥即证()0a b-≥,因为a>0,b>0,a-b所以()a b-≥≥20.【解析】设小正方形的边长为x cm,则盒子底面长为(82x-)cm,宽为(52x-)cm,32(82)(52)42640V x x x x x x=--=-+,()x<<52 4分210125240,0,1().3V x x V x x''=-+===令得或舍去(1)18V V==极大值,在定义域内仅有一个极大值,maxV∴=18 10分即小正方形边长为1cm时,盒子容积最大为cm318 12分21.试题解析:(ⅰ)当1=n时,左边=1112=,右边=3411214=+⨯⨯,左边<右边,即不等式成立;(ⅱ)假设)(*Nkkn∈=时,不等式成立,即222211114123421kk k++++⋅⋅⋅+<+则当1+=kn时,22222211111411234(1)21(1)kk k k k++++⋅⋅⋅++<++++问题可通过证明1)1(2)1(4)1(11242+++<+++kkkkk来实现要证:32441)1(2)1(4)1(11242++=+++<+++k k k k k k k 只需证:1243244)1(12+-++<+k k k k k ,只需证:)12)(32(4)1(12++<+k k k 只需证:2)1(4)32)(12(+<++k k k ,只需证:4124312422++<++k k k k ∵43<,∴1)1(2)1(4)1(11242+++<+++k k k k k 即当1+=k n 是不等式也成立.综上:由(ⅰ)(ⅱ)可得,对于一切的*∈N n 不等式恒成立.22. (1)解:求导函数,可得f′(x )= 221xax x +-(Ⅱ) 当a=2时,,的定义域是(0,+)∞,2221ln 21ln 211)('xx x x x x x x g --=⋅--= 令,,,递增,又时,,,递减,当时,,,递增,;(Ⅲ)证明:由(Ⅱ)得,时,,令,则,()()122ln )12)12(212)12(2122ln(2212111221+=++⋅⋅⋅++⋅+>+++-=∑nn n n nk k k。
山东省淄博市2020年(春秋版)数学高二下学期理数期中考试试卷(II)卷

山东省淄博市2020年(春秋版)数学高二下学期理数期中考试试卷(II)卷姓名:________ 班级:________ 成绩:________一、单选题 (共10题;共20分)1. (2分)(2020·顺德模拟) 复数()A . 1B . -1C .D .2. (2分) (2020高二下·新余期末) 用反证法证明命题“三角形的内角中至少有一个角不大于”时,应假设()A . 三角形的三个内角都不大于B . 三角形的三个内角都大于C . 三角形的三个内角至多有一个大于D . 三角形的三个内角至少有两个大于3. (2分)已知复数是z的共轭复数,则=()A .B .C . 1D . 24. (2分)如下图为一串白黑相间排列的珠子,按这种规律往下排起来,那么第36颗珠子应是什么颜色的()A . 白色B . 黑色C . 白色可能性大D . 黑色可能性大5. (2分)已知为定义在上的可导函数,且对于任意恒成立,则()A .B .C .D .6. (2分)(2016·太原模拟) 某台小型晚会由6个节目组成,演出顺序有如下要求:节目甲必须排在前两位、节目乙不能排在第一位,节目丙必须排在最后一位,该台晚会节目演出顺序的编排方案共有()A . 36种B . 42种C . 48种D . 54种7. (2分)定积分的值为()A .B .D .8. (2分)设函数f (x)=x3-4x+a,0<a<2.若f (x)的三个零点为x1 , x2 , x3 ,且x1<x2<x3 ,则()A . x1>-1B . x2<0C . x2>0D . x3>29. (2分)把1,3,6,10,15,21,…这些数叫做三角形数,这是因为这些数目的点子可以排成一个正三角形,则第七个三角形数是()A . 21B . 28C . 32D . 3610. (2分)(2020·上饶模拟) 已知函数和函数,关于这两个函数图像的交点个数,下列四个结论:①当时,两个函数图像没有交点;②当时,两个函数图像恰有三个交点;③当时,两个函数图像恰有两个交点;④当时,两个函数图像恰有四个交点.正确结论的个数为()A . 1B . 2C . 3二、填空题 (共5题;共6分)11. (1分)函数f(x)=excosx的图象在点(0,f(0))处的切线的倾斜角为________12. (1分)(2020·淮北模拟) 展开式中项的系数是________.13. (1分)(2019·宁波模拟) 五一假期从5月1日至4日调休4天,某班6名同学准备五一期间去参加社会实践做志愿者,每人社会实践一天,且甲乙两人不在同一天的不同安排方案有________种(用数字作答).14. (1分) (2016高二下·民勤期中) 定义一种运算如下: =ad﹣bc,则复数的共轭复数是________.15. (2分)对于三次函数,定义:设是函数的导数的导数,若方程有实数解,则称点为函数的“拐点”.有同学发现“任何一个三次函数都有‘拐点’;任何一个三次函数都有对称中心;且‘拐点’就是对称中心.”请你将这一发现视为条件,若函数,则它的对称中心为________;并计算________.三、解答题 (共4题;共35分)16. (10分)综合题。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
山东省淄博市2020版高二下学期期中数学试卷(理科)(II)卷
姓名:________ 班级:________ 成绩:________
一、选择题 (共12题;共24分)
1. (2分) (2017高二上·长沙月考) 已知集合,则()
A .
B .
C .
D .
2. (2分) (2016高二下·黔南期末) i是虚数单位,若复数z满足zi=﹣1+i,则复数z的实部与虚部的和是()
A . 0
B . 1
C . 2
D . 3
3. (2分) (2018高二下·抚顺期末) 某班准备从甲、乙、丙等6人中选出4人参加某项活动,要求甲、乙、丙三人中至少有两人参加,那么不同的方法有()
A . 18种
B . 12种
C . 432种
D . 288种
4. (2分)设是三个不重合的平面,l是直线,给出下列命题:
①若,则;②若则
③若l上存在两点到的距离相等,则;④若l不在内,且,则
其中正确的命题是()
A . ①②
B . ②③
C . ②④
D . ③④
5. (2分) (2016高三上·清城期中) 下列说法正确的是()
A . 命题“若x2=1,则x=1”的否命题为:“x2=1,则x≠1”
B . 若命题p:∃x∈R,x2﹣x+1<0,则命题¬p:∀x∈R,x2﹣x+1>0
C . 命题“若x=y,则sinx=siny”的逆否命题为真命题
D . “x2﹣5x﹣6=0”必要不充分条件是“x=﹣1”
6. (2分) (2017高三下·平谷模拟) 已知实数、满足:,则的最大值为().
A .
B .
C .
D .
7. (2分) (2015高三上·太原期末) 执行如图的程序框图输出的T的值为()
A . 4
B . 6
C . 8
D . 10
8. (2分) (2017高一上·焦作期末) 如图为一个几何体的三视图,三视图中的两个不同的正方形的边长分别为1和2,则该几何体的体积为()
A . 6
B . 7
C . 8
D . 9
9. (2分)曲线y= 上点M处的切线与直线y=3﹣x垂直,则切线方程为()
A . 5x﹣5y﹣4=0
B . 5x+5y﹣4=0
C . 5x+5y﹣4=0或5x+5y+4=0
D . 5x﹣5y﹣4=0或5x﹣5y+4=0
10. (2分) (2017高二下·晋中期末) 已知椭圆E:,圆O:x2+y2=a2与y轴正半轴交于点B,过点B的直线与椭圆E相切,且与圆O交于另一点A,若∠AOB=60°,则椭圆E的离心率为()
A .
B .
C .
D .
11. (2分) (2019高一上·嘉善月考) 若函数为定义在R上的奇函数,且在内是增函数,又
,则不等式的解集为()
A .
B .
C .
D .
12. (2分) (2016高二上·黄骅期中) 如图,已知椭圆C的中心为原点O,F(﹣2 ,0)为C的左焦点,P为C上一点,满足|OP|=|OF|且|PF|=4,则椭圆C的方程为()
A . =1
B . =1
C . =1
D . =1
二、填空题 (共4题;共4分)
13. (1分) (2018高二下·牡丹江期末) 设命题,,则为________.
14. (1分)(2018·孝义模拟) 已知向量与的夹角是,且,则向量与的夹角是________.
15. (1分)(2017·南通模拟) 已知a,b∈R,a>b,若2a2﹣ab﹣b2﹣4=0,则2a﹣b的最小值为________.
16. (1分) (2016高一下·大丰期中) 若一个长方体的长、宽、高分别为,,1,则它的外接球的表面积是________.
三、解答题:解答应写出文字说明、证明过程或演算步骤. (共6题;共55分)
17. (10分)(2012·浙江理) 在△ABC中,内角A,B,C的对边分别为a,b,c.已知cosA= ,sinB=
C.
(1)求tanC的值;
(2)若a= ,求△ABC的面积.
18. (10分) (2016高二下·揭阳期中) 已知.
(1)求f(x)的周期及其图象的对称中心;
(2)△ABC中,角A、B、C所对的边分别是a、b、c,满足(2a﹣c)cosB=bcosC,求f(B)的值.
19. (10分) (2016高三上·黄冈期中) 在等比数列{an}中,an>0,(n∈N*),公比q∈(0,1),且a1a5+2a3a5+a2a8=25,a3与a5的等比中项为2.
(1)求数列{an}的通项公式;
(2)设bn=log2an,数列{bn}的前n项和为Sn,当最大时,求n的值.
20. (10分) (2019高二下·涟水月考) 如图,已知矩形所在平面垂直于直角梯形所在平面于直线,且,,,且 .
(1)求平面与平面所成的二面角的余弦值;
(2)线段上是否存在一点,使得直线与平面所成角的正弦值等于?若存在,试确定点的位置;若不存在,请说明理由.
21. (10分) (2018高二上·宁夏期末) 已知椭圆:的一个顶点为,离心率为,直线与椭圆交于不同的两点 .
(1)求椭圆的方程;
(2)当的面积为时,求的值.
22. (5分) (2016高二上·淮南期中) 已知函数g(x)= +lnx在[1,+∞)上为增函数,且θ∈(0,π),f(x)=mx﹣﹣lnx(m∈R).
(Ⅰ)求θ的值;
(Ⅱ)若f(x)﹣g(x)在[1,+∞)上为单调函数,求m的取值范围;
(Ⅲ)设h(x)= ,若在[1,e]上至少存在一个x0 ,使得f(x0)﹣g(x0)>h(x0)成立,求m的取值范围.
参考答案
一、选择题 (共12题;共24分)
1、答案:略
2-1、
3-1、
4-1、
5-1、
6-1、
7-1、
8-1、
9-1、
10-1、
11-1、
12-1、
二、填空题 (共4题;共4分)
13-1、
14-1、
15-1、
16-1、
三、解答题:解答应写出文字说明、证明过程或演算步骤. (共6题;共55分) 17-1、
17-2、
18-1、
18-2、
19-1、19-2、
20-1、
20-2、
21-1、
21-2、
22-1、。
