回归分析SPSS习题复习资料
《SPSS统计分析》第11章 回归分析

返回目录
多元逻辑斯谛回归
返回目录
多元逻辑斯谛回归的概念
回归模型
log( P(event) ) 1 P(event)
b0
b1 x1
b2 x2
bp xp
返回目录
多元逻辑斯谛回归过程
主对话框
返回目录
多元逻辑斯谛回归过程
参考类别对话框
保存对话框
返回目录
多元逻辑斯谛回归过程
收敛条件选择对话框
创建和选择模型对话框
返回目录
曲线估计
返回目录
曲线回归概述
1. 一般概念 线性回归不能解决所有的问题。尽管有可能通过一些函数
的转换,在一定范围内将因、自变量之间的关系转换为线性关 系,但这种转换有可能导致更为复杂的计算或失真。 SPSS提供了11种不同的曲线回归模型中。如果线性模型不能确 定哪一种为最佳模型,可以试试选择曲线拟合的方法建立一个 简单而又比较合适的模型。 2. 数据要求
线性回归分析实例1输出结果2
方差分析
返回目录
线性回归分析实例1输出结果3
逐步回归过程中不在方程中的变量
返回目录
线性回归分析实例1输出结果4
各步回归过程中的统计量
返回目录
线性回归分析实例1输出结果5
当前工资变量的异常值表
返回目录
线性回归分析实例1输出结果6
残差统计量
返回目录
线性回归分析实例1输出结果7
返回目录
习题2答案
使用线性回归中的逐步法,可得下面的预测商品流通费用率的回归系数表:
将1999年该商场商品零售额为36.33亿元代入回归方程可得1999年该商场 商品流通费用为:1574.117-7.89*1999+0.2*36.33=4.17亿元。
SPSS题目及答案汇总版

《SPSS原理与运用》练习题数据对应关系:06-均值检验;07-方差分析;08-相关分析;09-回归分析;10-非参数检验;17-作图1、以data06-03为例,分析身高大于等于155cm的与身高小于155cm的两组男生的体重和肺活量均值是否有显著性。
分析:一个因素有2个水平用独立样本t检验,此题即身高因素有155以上和以下2个水平,因此用独立样本t检验(analyze->compare means->independent-samples T test)。
报告:一、体重①m+s:>=155cm 时, m= 40.838kg; s= 5.117;<155cm 时, m= 34.133kg;s= 3.816;②方差齐性检验结果:P=0.198>0.05,说明方差齐性。
③t=4.056; p=0.001< 0.01,说明身高大于等于155cm 的与身高小于155cm的两组男生的体重有极显著性差异。
二、肺活量①m+s: >=155cm 时,m=2.404; s=0.402;<155cm 时, m=2.016;s=0.423;②方差齐性检验结果:P=0.961>0.05,说明方差齐性。
③t=2.512; p=0.018 < 0.05,说明说明身高大于等于155cm的与身高小于155cm的两组男生的体重有显著性差异。
2、以data06-04为例,判断体育疗法对降低血压是否有效。
分析:比较前后2种情况有无显著差异,用配对样本t检验,(analyze->compare means-> paired-samples T test).报告:①m+s 治疗前舒展压:m=119.50; s=10.069;治疗后舒展压:m=102.50; s=11.118;②相关系数correlation=0.599; p=0.067>0.05,说明体育疗法与降低血压相关。
spss复习题

spss复习题SPSS复习资料⼀、选择题1、SPSS数据⽂件的扩展名是()。
.sav2、SPSS软件的三种运⾏管理⽅式:()、()和()。
完全窗⼝菜单运⾏管理⽅式程序运⾏管理⽅式混合运⾏管理⽅式输出窗⼝的主要功能:()。
显⽰和管理SPSS统计分析结果、报表和图形。
3、统计学依据数据的度量尺度将数据划分为三⼤类,()、()和()。
定距型数据定类型数据定序型数据4、SPSS有两个基本窗⼝:()和()。
数据编辑窗⼝和结果输出窗⼝。
5、SPSS数据的组织⽅式有两种:()和()。
原始数据的组织⽅式和计数数据的组织⽅式5、常见的基本描述统计量有三⼤类:()、()和()。
刻画集中趋势的统计量刻画离中趋势的统计量刻画分布形态的统计量6、数据编辑窗⼝的主要功能:()、()和()。
定义SPSS数据的结构录⼊编辑管理待分析的数据。
7、填写下⾯的⽅差分析表ANOV A()1252 522 18 298、SPSS对不同类型的变量应采⽤不同的相关系数来度量,常⽤的相关系数主要有()、()和()。
Pearson简单相关系数、Spearman等级相关系数和Kendallτ相关系数等。
9、利⽤样本相关系数r进⾏变量间线性关系的分析,⼀般( ) 表⽰两变量有较强的线性关系; ( )表⽰两变量之间的线性关系较弱。
|r|>0.8表⽰两变量有较强的线性关系; |r|<0.3表⽰两变量之间的线性关系较弱10、利⽤样本相关系数r进⾏变量间线性关系的分析,r=( ) 表⽰两变量存在完全正相关;r=( ) 表⽰两变量存在完全负相关; r =()表⽰两变量不相关。
r=1表⽰两变量存在完全正相关;r=-1表⽰两变量存在完全负相关;r=0表⽰两变量不相关11、样本相关系数r的取值范围是()。
在-1~+1之间12、对回归⽅程的检验主要包括()、()、()和()。
回归⽅程的拟合优度检验回归⽅程的显著性检验回归系数的显著性检验残差分析13、层次聚类有两种类型,分别是()和()。
《SPSS数据分析与应用》第8章 逻辑回归分析

➢ TPR—在所有真实值为阳性的样本中,被正确地判断为阳性的样本所占的比例。
TPR=TP / TP FN
➢ FPR—在所有真实值为阴性的样本中,被正确地判断为阳性的样本所占的比例。
FPR=FP / FP TN
Part 8.2
逻辑回归分析模型 的实现与解读
定性变量 (3水平)
定量变量
定性变量
取值范围 1代表幸存 0代表死亡 1=男、2=女 [0.42,80]
1代表一等舱, 2代表二等舱, 3代表三等舱
[0, 512.3292]
C = 瑟堡港, Q =昆士敦,S = 南安普顿
定性变量
0代表无家庭成员,1代表成员为1~3人的中 型家庭,2代表成员为4人及以上的大型家庭
2.逻辑回归分析模型
逻辑回归分析模型
在经过Logit变换之后,就可以利用线性回归模型建立因 变量与自变量之间的分析模型,即
经过变换,有
Sigmoid函数 (S型生长曲线)
逻辑回归分析模型
Sigmoid函数
➢ Sigmoid函数,表示概率P和自变量之间 的非线性关系。通过这个函数,可以计 算出因变量取1或者取0的概率。
总计
混淆矩阵
预测值
Y=0(N)
Y=1(P)
TN
FP
FN
TP
总计 TN+FP FN+TP TP+FP+FN+TN
➢ TP:预测为1,预测正确,即实际1; ➢ FP:预测为1,预测错误,即实际0; ➢ FN:预测为0,预测错确,即实际1; ➢ TN:预测为0,预测正确即,实际0。
4.模型评价
➢ 准确率
SPSS多元回归分析-11页word资料
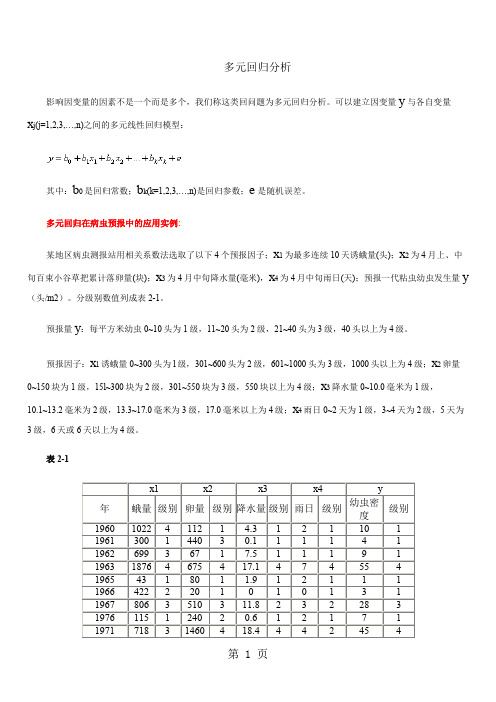
多元回归分析影响因变量的因素不是一个而是多个,我们称这类回问题为多元回归分析。
可以建立因变量y与各自变量x j(j=1,2,3,…,n)之间的多元线性回归模型:其中:b0是回归常数;b k(k=1,2,3,…,n)是回归参数;e是随机误差。
多元回归在病虫预报中的应用实例:某地区病虫测报站用相关系数法选取了以下4个预报因子;x1为最多连续10天诱蛾量(头);x2为4月上、中旬百束小谷草把累计落卵量(块);x3为4月中旬降水量(毫米),x4为4月中旬雨日(天);预报一代粘虫幼虫发生量y (头/m2)。
分级别数值列成表2-1。
预报量y:每平方米幼虫0~10头为1级,11~20头为2级,21~40头为3级,40头以上为4级。
预报因子:x1诱蛾量0~300头为l级,301~600头为2级,601~1000头为3级,1000头以上为4级;x2卵量0~150块为1级,15l~300块为2级,301~550块为3级,550块以上为4级;x3降水量0~10.0毫米为1级,10.1~13.2毫米为2级,13.3~17.0毫米为3级,17.0毫米以上为4级;x4雨日0~2天为1级,3~4天为2级,5天为3级,6天或6天以上为4级。
表2-1数据保存在“DATA6-5.SAV”文件中。
1)准备分析数据在SPSS数据编辑窗口中,创建“年份”、“蛾量”、“卵量”、“降水量”、“雨日”和“幼虫密度”变量,并输入数据。
再创建蛾量、卵量、降水量、雨日和幼虫密度的分级变量“x1”、“x2”、“x3”、“x4”和“y”,它们对应的分级数值可以在SPSS数据编辑窗口中通过计算产生。
编辑后的数据显示如图2-1。
图2-1或者打开已存在的数据文件“DATA6-5.SAV”。
2)启动线性回归过程单击SPSS主菜单的“Analyze”下的“Regression”中“Linear”项,将打开如图2-2所示的线性回归过程窗口。
图2-2 线性回归对话窗口3) 设置分析变量设置因变量:用鼠标选中左边变量列表中的“幼虫密度[y]”变量,然后点击“Dependent”栏左边的向右拉按钮,该变量就移到“Dependent”因变量显示栏里。
SPSS专题2 回归分析(线性回归、Logistic回归、对数线性模型)

19
Correlation s lif e_ expectanc y _ f emale(y ear) .503** .000 164 1.000 . 192 .676**
cleanwateraccess_rura... life_expectancy_femal... Die before 5 per 1000
Model 1 2
R .930
a
R Square .866 .879
Model 1
df 1 54 55 2 53 55
Regres sion Residual Total Regres sion Residual Total
Mean Square 54229.658 155.861 27534.985 142.946
2
回归分析 • 一旦建立了回归模型 • 可以对各种变量的关系有了进一步的定量理解 • 还可以利用该模型(函数)通过自变量对因变量做 预测。 • 这里所说的预测,是用已知的自变量的值通过模型 对未知的因变量值进行估计;它并不一定涉及时间 先后的概念。
3
例1 有50个从初中升到高中的学生.为了比较初三的成绩是否和高中的成绩 相关,得到了他们在初三和高一的各科平均成绩(数据:highschool.sav)
50名同学初三和高一成绩的散点图
100
90
80
70
60
高 一成 绩
50
40 40
从这张图可以看出什么呢?
50 60 70 80 90 100 110
4
初三成绩
还有定性变量 • 该数据中,除了初三和高一的成绩之外,还有 一个定性变量 • 它是学生在高一时的家庭收入状况;它有三个 水平:低、中、高,分别在数据中用1、2、3 表示。
研一spss复习资料 06_回归分析

2021/8/17
17
(2)回归方程的显著性检验(F检验)
回归方程的显著性检验是对因变量与所有 自变量之间的线性关系是否显著的一种假 设检验。
回归方程的显著性检验一般采用F检验,利 用方差分析的方法进行。
条件指标: 0<k<10 无多重共线性; 10<=k<=100 较强; k>=100 严重
2021/8/17
37
回归分析中的自变量筛选
多元回归分析引入多个自变量. 如果引入自变 量个数较少,则不能较好说明因变量的变化;
并非自变量引入越多越好.原因:
有些自变量可能对因变量的解释没有贡献 自变量间可能存在较强的线性关系,即:多重共线性.
绘制指定序列的散点图,检测残差的随机性、 异方差性
ZPRED:标准化预测值 ZRESID:标准化残差 SRESID:学生化残差
2021/8/17
32
线性回归方程的残差分析
残差序列的正态性检验
绘制标准化残差的直方图或累计概率图
残差序列的随机性检验
绘制残差和预测值的散点图,应随机分布在经 过零的一条直线上下
因而不能全部引入回归方程.
2021/8/17
38
自变量向前筛选法(forward)
即自变量不断进入回归方程的过程. 首先,选择与因变量具有最高相关系数的自变量进入方
程,并进行各种检验; 其次,在剩余的自变量中寻找偏相关系数最高的变量进
入回归方程,并进行检验; 默认:回归系数检验的概率值小于(0.05)才可以进入方
SSE
A dj.R 2 1 n p1 SST n 1
SPSS软件课程复习资料

SPSS软件课程考试题型:一、填空10分(每题1分,共10分)二、判断10分(每题1分,共10分)三、名词20分(每题2分,共20分)四、简答30分(每题5分,共6分,其中两个分析表格或图形)五、分析表格(每题15分,共30分)蓝色:为考点重要名词:1、5%修正均数剔除5%的最大与最小观测量后计算的均值。
2、四分位间距为了避免全距受两极端数值影响的缺点,按照一定顺序排列的一组数据中间部分50%的频数的差异作为反映数据的差异程度的指标,即四分位距,用QD表示。
3、三种T检验的分别得英文名称、One- Samples T Test Independent-Samples T Test Paired-Samples T Test4、交互作用当一个因素的主效应随另一个因素的变化而变化时,称两个因素间存在交互效应。
5、边际均值在多因素方差分析中,每种因素水平组合的因变量均值称为单元均值。
一个因素水平的因变量均值称为边际均值(Marginal Means)6、重复测量方差分析组内变异的主要的原因是实验对象之间的个体差异。
由于个体差异存在,即使实验对象受到相同的处理,他们的因变量值也可能相当不同。
重复测量设计的方差分析也是像协方差分析一样,是在研究中减少个体差异带来的误差方差的一种有效方法,而且由于对相同个体进行重复测量,在一定程度上降低了人力、物力、财力的消耗。
7、因素因素是影响因变量变化的客观条件8、处理、是影响因变量变化的人为条件。
也可通称为因素9、主效应因变量在一个因素各水平间的平均差异。
10、协方差分析利用线性回归方法消除混杂因素的影响过后进行的方差分析。
11、偏相关计算两个变量间在控制其他变量的影响下的相关系数。
12、距离相关对变量或观测量进行相似性或不相似性测度。
13、偏回归系数简称回归系数,表示其他自变量不变,xi每改变一个单位时,预测的y的平均变化量。
假设在其他所有自变量不变的情况下,某一个自变量变化引起因变量变化的比率。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
回归分析习题1通常用来评价商业中心经营好坏的一个综合指标是单位面积的营业额,它是单位时间内(通常为一年)的营业额与经营面积的比值。
对单位面积营业额的影响因素的指标有单位小时车流量、日人流量、居民年平均消费额、消费者对商场的环境、设施及商品的丰富程度的满意度评分。
这几个指标中车流量和人流量是通过同时对几个商业中心进行实地观测而得到的。
而居民年平均消费额、消费者对商场的环境、设施及商品的丰富程度的满意度评分是通过随机采访顾客而得到的平均值数据。
(数据集wyzl4_2中存放了从某市随机抽取的20个商业中心有关指标的数据,利用该数据完成下列工作(1)研究变量间的相关程度。
(其余6个变量与“单位面积年营业额”间的相关程度,其余6个变量之间的相关程度);(2)由(1)的结论建立“单位面积年营业额”与和其线性相关程度最高的变量的一元线性回归方程;(3)采用逐步回归方法建立“单位面积年营业额”的预测公式。
表20个商业中心有关指标的数据2.我国从1982~2001年间的20年的财政收入(Y)和国内生产总值(X)的数据存放在数据集wyz4_4_7.中。
试分别采用指数回归、对数回归、幂函数回归和多项式回归给出回归方程,并选择最佳回归方程。
1.解:(1)变量间的相关性分析利用SPSS软件构造所有变量的散点图矩阵和相关矩阵,结果见图1和表1从散点图矩阵直观可以看出Y “单位面积年营业额”与x2“日人流量(万人) ”和x3“居民年消费额(万元) ”线性关系较密切。
x2“日人流量 (万人) ”与x6 “对商场商品丰富程度满意度” 线性关系较密切从表1得)3,(x y ρ=0.795**,)2,(x y ρ=0.790**,)6,(x y ρ=.0 .697**,说明 Y “单位面积年营业额”与x3“居民年消费额(万元) ”,x2“日人流量 (万人) ”,x6 “对商场商品丰富程度满意度”及x5 “对商场设施满意度”在0 .01 水平(双侧)上显著相关线性关。
可以考虑采用多元线性回归模型来建立“单位面积年营业额”的预测公式。
图1散点图矩阵单位面积 年营业额 (万元/m2) 每小时机 动车流量 (万辆) 日人流量 (万人) 居民年 消费额 (万元) 对商场 环境 满意度 对商场 设施 满意度 对商场商品丰富程 度满意度单位面积 年营业额 (万元/m2)Pearson 相关性1 .413 .790** .795** .341 .450* .697** 显著性(双侧) .071 .000 .000 .141 .046 .001 N2020 20 20 202020 每小时机动车流量(万辆) Pearson 相关性.413 1 .751** -.129 .664** .424 .774** 显著性(双侧) .071 .000 .588 .001 .062 .000 N2020 20 20 202020 日人流量(万人) Pearson 相关性.790** .751**1.273.594** .279.983**(2)建立Y “单位面积年营业额”与“居民年消费额”的一元线性回归方程 设 ⎩⎨⎧++=),0(~2310σεεββN x y 利用SPSS 软件的线性回归分析的模块进行分析,结果见表2~表6和图2~图3由最小二乘估计得到一元线性回归方程(见表4)Y (单位面积年营业额)=0.928+0.877x3(居民年消费额)由回归方程的显著性检验的p 值Sig.= .000,知回归方程在α=0.01的水平上通过检验,即Y 与x3的线性关系是显著的(见表3方差分析表)由常量β0的t 检验的p 值Sig.=0.005<0.01知回归方程的常数项不为零。
拟合有常数 项的回归方程是合适的 (见表4 系数表)由方程的拟合优度(可决系数)R 2=0.631,知方程的拟合优度(可决系数)还不够高,即方程有改进的余地,还可以引入有关的变量 。
(见表1)对残差作Shapiro-Wilk 正态性检验,p 值Sig.=0.538>0.05(见表5)知随机误差项εi服从正态分布的假定满足。
作回归标准化残差的标准P-P 图(见图2),进一步验证了随机误差项εi服从正态分布的假定满足对残差序列作D-W 检验,检验统计量Durbin-Watson=2.125知εεεn ,,,21Λ之间存在 一定的负自相关:εεεn ,,,21Λ相互独立的假定不一定满足(见表2)以标准化的残差e t 为纵坐标,而以标准化的预测值y i ∧为横坐标做残差的散点图(见图3)。
图中显示散点随机地分布在–2到+2的带子里,可以认为线性回归模型的等方差假定成立 。
结论:(1)一元线性回归方程Y (单位面积年营业额)=0.928+0.877x3(居民年消费额)在α=0.01的水平上通过检验,拟合优度为0.631,方程有改进的余地,还可以引入有关的变量 。
(2)误差项正态分布的假设和和误差项的等方差假设均成立,但误差项的独立性假设不满足。
表3 方差分析表Anova b模型 平方和df均方 F Sig. 1回归 8.125 1 8.125 30.824.000a残差 4.745 18 .264总计12.87019a. 预测变量: (常量), 居民年消费额(万元)。
b. 因变量: 单位面积年营业额(万元/m2)表4系数a模型 非标准化系数标准系数 t Sig.B 标准 误差试用版1(常量).928.2883.220.005居民年消费额(万元).887 .160 .795 5.552 .000 a. 因变量: 单位面积年营业额(万元/m2)表5 残差的正态性检验Tests of NormalityKolmogorov-Smirnov a Shapiro-WilkStatistic df Sig. Statistic df Sig. Standardized Residual .090 20 .200*.960 20 .538 a. Lilliefors Significance Correction*. This is a lower bound of the true significance.图2 回归标准化残差的标准P-P图图3 标准化残差图 残差统计量a极小值 极大值 均值 标准 偏差N预测值 1.4244 4.0049 2.3950 .65393 20 残差 -.89496 .76957 .00000 .49972 20 标准 预测值 -1.484 2.462 .000 1.000 20 标准 残差-1.7431.499.000.97320a. 因变量: 单位面积年营业额(万元/m2)(3)采用逐步回归方法建立“单位面积年营业额”的预测公式。
解 设y 与x1,x2,…,x8满足⎩⎨⎧++++=),0(~288110σεβββN εx x y Λ 规定:进入方程的变量的显著性水平为0.05,从方程中剔出变量的显著性水平为0.10,(见表7)逐步回归的步骤:(见表10)第一步引入变量x3居民年消费额(万元)得到一元线性回归方程Y (单位面积年营业额)=0.928+0.877x3(居民年消费额),第二步引入变量x2日人流量(万人)得到线性回归方程Y (单位面积年营业额)=-0.117+0.698x3(居民年消费额) +0.317x2(日人流量(万人)), 第三步引入变量x4对商场环境满意度,所得线性回归方程为:Y (单位面积年营业额)=-.297+0.723x3(居民年消费额)+0.291 x2 (日人流量(万人))+0.037 x4(对商场环境满意度)以上3方程在显著性水平为0.05上均通过检验(见表9)。
第3个方程的回归系数(包括常数项)t 检验的p 值0.010,0.000,0.000,0.034,在显著性水平为0.05上均通过检验(见表10)。
三个方程的修正R 方值逐步增大0.611<0.985<.988,故第3个方程为最优的(见表8)对第3个方程的自变量作共线性诊断(见表10):回归方程第i 个回归系数的方差膨胀因子VIF 分别1.235、1.885、1.767,说明方程中的3个回归变量不存在共线性,对残差序列作D-W 检验,检验统计量Durbin-Watson=2.574> 2知εεεn ,,,21Λ之间存在一定的负自相关:εεεn ,,,21Λ相互独立的假定不一定满足(见表8)对残差作Shapiro-Wilk 正态性检验,p 值Sig.= =0 <0.01(见表15)知随机误差项εi不服从正态分布。
作回归标准化残差的标准P-P 图(见图3),进一步验证了随机误差项εi不服从正态分布。
以标准化的残差e t 为纵坐标,而以标准化的预测值y i ∧为横坐标做残差的散点图(见图5)。
图中显示散点随机地分布在–2到+2的带子里(除一个点),可以认为线性回归模型的等方差假定成立 。
结论:(1)“单位面积年营业额”的预测公式为:Y (单位面积年营业额)=-.297+0.723x3(居民年消费额)+0.291 x2 (日人流量(万人))+0.037 x4(对商场环境满意度)方程在显著性水平为0.05上通过检验,调整的R 方值=0.988,(2)模型的假定误差项的正态性和不相关性存在问题,估计方法有待改进。
系数a模型共线性统计量容差VIF1 居民年消费额(万元) 1.000 1.0002 居民年消费额(万元).926 1.080日人流量(万人).926 1.080 3 居民年消费额(万元).810 1.235日人流量(万人).530 1.885Tests of NormalityKolmogorov-Smirnov a Shapiro-WilkStatistic df Sig. Statistic df Sig. Standardized Residual .172 20 .121 .775 20 .000 a. Lilliefors Significance Correction图4 回归标准化残差的标准P-P图图5 标准化残差图2.我国从1982~2001年间的20年的财政收入(Y)和国内生产总值(X)的数据存放在数据集wyz4_4_7.中。
试分别采用指数回归、对数回归、幂函数回归和多项式回归给出回归方程,并选择最佳回归方程。
解:(1)利用SPSS软件作Y与X的散点图由散点图可以看出可以利用指数(Exponential )回归 y = a e x b 对数(Logarithmic )回归 y = a +b x ln 幂函数(Power )回归 y = a x b二次曲线(Quadratic ) y =x b x b b 2210++ 三次曲线(Cubic ) y =x b x b x b b 332210+++ 作曲线拟合(2)利用SPSS 软件拟合结果指数(Exponential )回归 y = e x 00002428.095.1562 对数(Logarithmic )回归 y = -34350.518 + 3913.184x ln 幂函数(Power )回归 y = 1.384x 785.0二次曲线(Quadratic ) y =x E x 2)6523.1(01.065.2040-+-三次曲线(Cubic ) y =x E x E x 32)11674.3()6886.3(202.0429.304-+--+三次曲线的R Square=0.998>二次曲线的R Square=0.979>指数回归的R Square=0.965>幂函数回归的R Square=0.962,以上四种曲线拟合都可以,三次曲线拟合最好。
