四面体网格上的Lagrange插值
研究生数值分析(14)拉格朗日(Lagrange)插值多项式 共22页PPT资料

事实上,
s5 i0 n 0 L 1 (5 ) 0 0 .01 ; s 05 i0 1 n 0 L ~ 1 ( 0 5 ) 0 0 .005
因此做线性内插时取 x00.2,x10.3 相应地 y01 .2 2 1 4 ,y11 .3 4 9 9
由线性插值公式,得
L 1 (x ) 0 x .2 0 0 .3 .3 1 .2 2 1 4 0 x .3 0 0 .2 .2 1 .3 4 9 9
所得近似值为
e 0 . 2 8 5 L 1 ( 0 . 2 8 5 ) 0 0 . 2 . 2 8 5 0 0 . 3 . 3 1 . 2 2 1 4 0 0 . 2 . 3 8 5 0 . 0 2 . 2 1 . 3 4 9 9 1 . 3 3 0 6
由线性插值余项公式
所以
s in 5 0 0 L 1 ( 5 0 ) 1 2 2 3 ( 1 8 0 )2 2 0 5 0 .0 1 3 1 9 0
同理,由
s5 i 0 n L ~ 0 1 ( 5 ) 1 2 0 ( s) i1 n ( ) 2 ( 8 5 4 0 0 ) 5 5 ( 6 0 )3 0 0 0 6 0
插值多项式⑤称为拉格朗日插值多项式,记作 L n ( x )
当n=2时,由⑤式可得三点插值公式
L 2 ( x ) y 0 ( ( x x 0 x x 1 1 ) ) ( ( x x 0 x x 2 2 ) ) y 1 ( ( x x 1 x x 0 0 ) ) ( ( x x 1 x x 2 2 ) ) y 2 ( ( x x 2 x x 0 0 ) ) ( ( x x 2 x x 1 ) 1 ) 这是一个二次函数。用二次函数 L 2 ( x ) 近似
lagrange插值

%拉格朗日插值方法%可以同时对多点插值%t可以为向量function s=lag(x,y,t)%采用符号推导,这样可以给出插值具体公式syms p;%读取x向量维数n=length(x);s=0;for(k=1:n)la=y(k);%构造基函数for(j=1:k-1)la=la*(p-x(j))/(x(k)-x(j));end;for(j=k+1:n)la=la*(p-x(j))/(x(k)-x(j));end;s=s+la;simplify(s);end%对输入参数个数做判断,如果只有两个参数%直接给出插值多项式%如果三个参数则给出插值点的插值结果%第三个参数可以为向量if(nargin==2)s=subs(s,'p','x');%展开多项式s=collect(s);%把系数取到6位精度表达s=vpa(s,4);else%读取t长度m=length(t);%分别对t的每一个分量插值for i=1:mtemp(i)=subs(s,'p',t(i));end%得到的是系列插值点的插值结果%既得到的是向量,赋值给ss=temp;end%lagrange方法主函数%同时计算多点插值%已有点x ,yx=[pi/4,pi/6,pi/3,pi/2];y=[cos(pi/4),cos(pi/6),cos(pi/3),cos(pi/2)];%需要插值点t=[-40*pi/180,47*pi/180,53*pi/180,79*pi/180,174*pi/180]; disp('角度')du=[-40 47 53 79 174]%插值计算结果disp('插值结果')yt=lag(x,y,t)%cos函数值disp('cos函数值')yreal=[cos(-40*pi/180)cos(47*pi/180)cos(53*pi/180)cos(79*pi/180)cos(174*pi/180)]'disp('插值与函数值误差')dy=yt-yreal%给出插值多项式,需要显示的话去掉下行的分号yt=lag(x,y)%画出插值多项式图形ezplot(yt,[-pi/4,pi])hold on%画出cos函数图形ezplot('cos(t)',[-pi/4,pi]);grid onhold off。
计算方法插值法-Lagrange插值

b
a
x2
用 的值作为f(x)的近似值,不仅希望 能较好地逼近f(x),而且还希望它计算简单 。
评论:
由于代数多项式具有数值计算和理论分析方便的优点。所以本章主要介绍利用代数多项式进行插值,即代数插值。
定义:若存在一个次数不超过n次的多项式
使得满足:
则称P(x)为f(x)的n次插值多项式。
因为 ,所以方程组有解唯一解:
系数矩阵
可用于求2次插值多项式
仿照线性插值,现在试图用基函数的方法确定2次插值多项式
显然 应该有以下的形式
由 确定系数
从而导出
求二次式 ,使满足条件:
01
02
类似地可以构造出插值多项式
于是确定了3个抛物插值的基函数:
x0
x2
x1
x
y
1
y=l0(x)
y=l1(x)
y=l2(x)
3个抛物插值的基函数
取已知数据 作为线性组合系数,将基函数 线性组合可得
容易看出,P(x)满足条件
即
一般形式的拉格朗日插值多项式
已知: 2个插值点可求出一次插值多项式,而 3个插值点可求出二次插值多项式。
…
…
插值点增加到n+1个时,可通过n+1个不同的已知点 来构造一个次数为n的代数多项式P(x)。先构造一个特殊n次多项式 的插值问题,使其在各节点 上满足
对于线性插值,误差公式:
01
对于抛物插值(2次插值),误差公式:
02
例2.8 已知x0 =100, x1 =121,用线性插值近似计算 的时候,估计在x=115时的截断误差.
解: 由插值余项公式知
得
Lagrange 插值
今天的上机作业1. Lagrange 插值给出()ln f x x 的数值表用Lagrange 插值计算ln 0.54的近似值。
2.Newton 插值用Newton 插值计算x=0.41的近似值。
3.插值法的全部内容把chap_2试验.doc 的全部内容作一边,粘在这个文件里(包括图形)答:grange 插值function f=lagrange_5(x) x0=[0.4,0.5,0.6,0.7,0.8];y0=[-0.916291,-0.693147,-0.510826,-0.356675,-0.223144]; L1=0;m=length(x0);n=length(y0);if m~=n, error('向量x 与y 的长度必须一致');end for i=1:nL=ones(1,length(x)); for j=1:n if j~=iL=L.*(x-x0(j))/(x0(i)-x0(j)); end endL1=L1+L*y0(i); end L1lagrange_5(0.54) L1 =-0.616142715200002.Newton插值function f=newton_li5(x) %x0为入的节点值,y0相应节点的函数值x0=[0.25 0.30 0.39 0.45 0.53];y0=[0.5000 0.5477 0.6245 0.6708 0.7280];n=length(x0)%syms xfor i=1:nf(i,1)=y0(i);endhx=f(1,1);xx=(1.0);for k=2:nfor i=k:nf(i,k)=(f(i,k-1)-f(i-1,k-1))/(x0(i)-x0(i-k+1)); %构造差商表endxx=xx*(x-x0(k-1));hx=hx+f(k,k)*xx; %计算函数的近似值end%f=expand(hx)Hxnewton(0.41)n =5hx =0.64030542443064ans =0.50000000000000 0 0 0 00.54770000000000 0.95400000000000 0 0 00.62450000000000 0.85333333333333 -0.71904761904761 0 00.67080000000000 0.77166666666666 -0.54444444444446 0.87301587301575 00.72800000000000 0.71500000000000 -0.40476190476189 0.60731538992422 -0.948930296755483.插值法的全部内容把chap_2试验.doc的全部内容作一边,粘在这个文件里(包括图形)P28 例22点插值function f=lagrange_2(x)x0=[0.32,0.34];y0=[0.314567,0.333487];L1=0;m=length(x0);n=length(y0);if m~=n, error('向量x与y的长度必须一致');endfor i=1:nL=ones(1,length(x));for j=1:nif j~=iL=L.*(x-x0(j))/(x0(i)-x0(j));endendL1=L1+L*y0(i);endL1lagrange_2(0.3367)L1 =0.330365200000003点插值function f=lagrange_3(x)x0=[0.32,0.34,0.36];y0=[0.314567,0.333487,0.352274];L1=0;m=length(x0);n=length(y0);if m~=n, error('向量x与y的长度必须一致');endfor i=1:nL=ones(1,length(x));for j=1:nif j~=iL=L.*(x-x0(j))/(x0(i)-x0(j));endendL1=L1+L*y0(i);endL1lagrange_3(0.3367)L1 =0.33037436203750Lagrange插值法%eg1_lagr.mclear;clf;xx=linspace(-5,5,50); y=sin(xx); %作被插函数的图象disp('n x=4.5处的插值绝对误差的绝对值')x1=linspace(-5,5,3); y1=sin(x1); yy1=lagr1(x1,y1,xx); %2次插值chazhi_y45_2=lagr1(x1,y1,4.5);gd_wucha_limit_y45_2=abs(chazhi_y45_2-sin(4.5));disp(sprintf('%d %15.4f %15.4f',2,chazhi_y45_2,gd_wucha_limit_y45_2))x2=linspace(-5,5,5); y2=sin(x2); yy2=lagr1(x2,y2,xx); %4次插值chazhi_y45_4=lagr1(x2,y2,4.5);gd_wucha_limit_y45_4=abs(chazhi_y45_4-sin(4.5));disp(sprintf('%d %15.4f %15.4f',4,chazhi_y45_4,gd_wucha_limit_y45_4))x3=linspace(-5,5,9); y3=sin(x3); yy3=lagr1(x3,y3,xx); %8次插值chazhi_y45_8=lagr1(x3,y3,4.5);gd_wucha_limit_y45_8=abs(chazhi_y45_8-sin(4.5));disp(sprintf('%d %15.4f %15.4f',8,chazhi_y45_8,gd_wucha_limit_y45_8))plot(xx,y,'m-');hold on,pause,plot(x1,y1,'rs',xx,yy1,'r-'); hold on,pause,plot(x2,y2,'b*',xx,yy2,'b-'); hold on,pause,plot(x3,y3,'ko',xx,yy3,'k-'); hold on计算函数值function f=newton_li4(x) %x0为入的节点值,y0相应节点的函数值x0=[0.40,0.55,0.65,0.80,0.90,1.05];y0=[0.41075,0.57815,0.69675,0.88811,1.02652,1.25382];n=length(x0)%syms xfor i=1:nf(i,1)=y0(i);endhx=f(1,1);xx=(1.0);for k=2:nfor i=k:nf(i,k)=(f(i,k-1)-f(i-1,k-1))/(x0(i)-x0(i-k+1)); %构造差商表endxx=xx*(x-x0(k-1));hx=hx+f(k,k)*xx; %计算函数的近似值end%f=expand(hx)hxnewton(0.596)n =5hx =0.77193768707246ans =0.50000000000000 0 0 0 00.54770000000000 0.95400000000000 0 0 00.62450000000000 0.85333333333333 -0.71904761904761 0 00.67080000000000 0.77166666666666 -0.54444444444446 0.87301587301575 00.72800000000000 0.71500000000000 -0.40476190476189 0.60731538992422 -0.94893029675548Newton插值法%eg1_newton.mclear;clf;xx=linspace(-5,5,50); y=sin(xx); %作被插函数的图象disp('n x=4.5处的插值绝对误差的绝对值')x1=linspace(-5,5,3); y1=sin(x1); yy1=newton1(x1,y1,xx,2); %2次插值chazhi_y45_2=newton1(x1,y1,4.5,2);gd_wucha_limit_y45_2=abs(chazhi_y45_2-sin(4.5));disp(sprintf('%d %15.4f %15.4f',2,chazhi_y45_2,gd_wucha_limit_y45_2))x2=linspace(-5,5,5); y2=sin(x2); yy2=newton1(x2,y2,xx,4); %4次插值chazhi_y45_4=newton1(x2,y2,4.5,4);gd_wucha_limit_y45_4=abs(chazhi_y45_4-sin(4.5));disp(sprintf('%d %15.4f %15.4f',4,chazhi_y45_4,gd_wucha_limit_y45_4))x3=linspace(-5,5,9); y3=sin(x3); yy3=newton1(x3,y3,xx,8); %8次插值chazhi_y45_8=newton1(x3,y3,4.5,8);gd_wucha_limit_y45_8=abs(chazhi_y45_8-sin(4.5));disp(sprintf('%d %15.4f %15.4f',8,chazhi_y45_8,gd_wucha_limit_y45_8))plot(xx,y,'m-');hold on,pause,plot(x1,y1,'rs',xx,yy1,'r-'); hold on,pause,plot(x2,y2,'b*',xx,yy2,'b-'); hold on,pause,plot(x3,y3,'ko',xx,yy3,'k-'); hold on。
插值法与Lagrange插值课件 共28页PPT资料
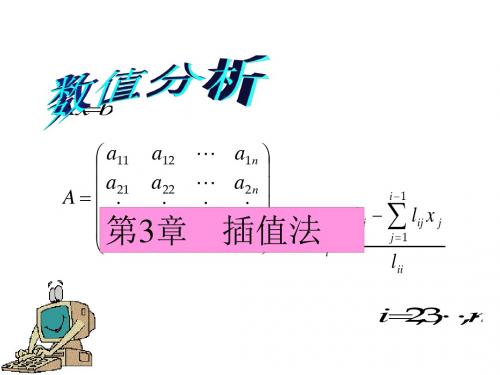
n ( x xi ) i0 ( x j xi )
j0,1,2, ,n -------(7)
i j
n+1次多项式
令n1(x)(x x 0 )x ( x 1 ) (x x n )
则n1(xj)
( x j x 0 ) x j ( x 1 ) ( x j x j 1 ) x j ( x j 1 ) ( x j x n )
上述方程组的系数行列式为n+1阶Vandermond行列式
1
x0
x
2 0
x0n
V 1
x1
x12
x1n
n1 n
xi x j
(xj xi ) 0
i0 jபைடு நூலகம்1
1
xn
xn2
x
n n
由Cramer法则,线性方程组(4)有唯一解
定理1. 若插值xi节 xj点 (ij),则满足插值条件 P n (x i) y i i 0 ,1 ,2 , ,n--------(3)
比 如 多 项 式 函 数 P (x )使
P (x i) y i i 0 ,1 ,2 , ,n------(1) 并且P用 (x)近似代 f(x替 ) 这就是插值问题, (1)式为插值条件,
称函P(数 x)为函f(数 x)的插值函数
如果 P(x)为多项式,函 则数 称之为插值多 称点 xi ,i0,1,2,,n为插值节点 称区间 [a,b]为插值区间
其中 xi ,i0,1,2, ,n为插值节
y if(x i) i 0 ,1 ,2 , ,n
如 果 a x 0 x 1 x 2 x n b 为 区 间 [a ,b ]上 的 一 组 节 点
拉格朗日(Lagrange)插值

18
x1 x2 利用 x0 = π , x1 = π L1 ( x ) = x π / 4 × 1 + x π / 6 × 1 6 4 π / 6 π / 4 2 π / 4 π / 6 2 π sin 50 0 ≈ L1 ( 5 ) ≈ 0.77614 这里 f ( x) = sin x , f (2) (ξ x ) = sinξ x , ξ x ∈(π , π ) 内插通常优于外插。 ) 18 内插通常优于外插。2选择 6 3 ( f (ξ x ) 而 1要计算的3x 所在的区间的x π )( x π ) , R1 ( x) = ( < sinξ x < 2 2 2! 6 4 端点,插值效果较好。 端点,插值效果较好。 sin 50° = 0.7660444… 0.01319 < R1 ( 5π ) < 0.00762 18
+1)
( n + 1) ! Nhomakorabeax
Rn ( x) =
(n + 1) !
∏( x x )
i i =0
注:
M n +1 n 作为误差估计上限。 将 ( n + 1)! ∏ | x x i | 作为误差估计上限。 i =0
通常不能确定 ξx , 而是估计
f ( n + 1 ) ( x ) ≤ M n + 1, x∈(a,b) ∈
这样求Lagrange插值多项式计算量大,不便于实际应用。 Lagrange插值多项式计算量大 注: 这样求Lagrange插值多项式计算量大,不便于实际应用。 过两点直线。 一次多项式插值 --- 过两点直线。 过三点抛物线。 二次多项式插值 --- 过三点抛物线。 则插值多项式不唯一 不唯一。 若不将多项式次数限制为 n ,则插值多项式不唯一。
《Lagrange插值》课件
更高效的插值算法介绍
简要介绍一些比Lagrange插 值更高效、更精确的插值算 法,并对其特点进行分析。
总结与展望
总结Lagrange插值的优点和应用前景,探讨该方法的未来发展方向和可能的扩展领域。
参考文献
相关文献推荐
介绍与Lagrange插值相关的优秀文献,供进一步学习和研究之用。
研究领域的进展
分享Lagrange插值在相关研究领域中的最新进展和重要成果。
相关专家学者的成果分享
介绍在Lagrange插值领域取得杰出成就的专家学者及其成果。
《Lagrange插值》PPT课 件
本PPT课件介绍Lagrange插值的概述、数学表达式、实例分析、算法优劣比 较、总结与展望。将深入剖析LaHale Waihona Puke range插值的基本思想和应用前景。
概述
什么是Lagrange插值?为什么使用Lagrange插值?Lagrange插值的基本思想 是什么?这一部分将首先解答这些问题。
数学表达式
Lagrange插值公式的推导、值多项式的计算、以及Lagrange插值多项式的刻 画在这一部分将一一介绍。
实例分析
一元实例
通过一个一元Lagrange插 值实例来深入理解这种方 法的应用和原理。
多元实例
探索多元Lagrange插值的 实例,揭示其在实际问题 中的应用和效果。
应用案例分析
通过具体案例分析,揭示 Lagrange插值方法解决实 际问题的能力和局限性。
算法优劣比较
与牛顿插值的比较
对比Lagrange插值与牛顿插 值方法的优劣,以及它们在 不同情景下的适用性。
Lagrange插值算法的优 缺点
评估Lagrange插值方法的优 点与缺点,探讨其在不同场 景下的性能和限制。
拉格朗日(Lagrange)插值
( n 1) !
i0
( ( 1 0 (x Rolle’s f ( x ) Ln (若)至少个有 n+1根 ( x 0 ) Rnx)x )K ( x),则 xi ) R n ( x ) Theorem: x ( x ) 充分光滑, i 0 n 存在 ( x 0 , x 1 ) 使得 ( ) 0 。 任意固定 x xi (i = 0, 求导 考察 ( t ) Rn ( t ) K ( x ) ( t x i ) 注意这里是对 t …, n), 0 ( x 0 , x 1 ), 1 i ( 0 1 , x 2 ) x 推广:若 ( x 0 ) ( x 1 ) ( x 2 ) 0 (x)有 n+2 个不同的根x0) …0xn x ( , ( n) 1 ) ( x ) 0(, ) ( a , b ) x 0 使得 ( 0 ) ( 1 0 1 使得
于是 : L 2 ( x )
再利用 l 0 ( x 0 ) 1 C
1 ( x 0 x 1 )( x 0 x 2 )
( x x0 )( x x1 ) l2 ( x ) ( x2 x0 )( x2 x1 )
l ( x) y
i i0
2
i
l 0 ( x ) y 0 l1 ( x ) y1 l 2 ( x ) y 2
i0 n
[证明]上式的左端为插值基函数的线性组合,其组合 系数均为1。显然,函数f(x) 1在这n +1个节点取值 为1,即yi=f (xi) 1 (i=0,1,…,n), 它的n次Lagrange插值多项式为:
Ln ( x ) l i ( x ) y i l i ( x )
第4章 Lagrange插值
x xi i 0 x j xi
i j
⑤
l j (x j ) 1 l j ( xi ) 0 i j
显然 l j ( x ) 满足{
Lagrange插值函数Ln(x)
定理 4.2 在[a、b]上有
2 n
span 1, x, x , , x span l0 ( x), l1 ( x), l2 ( x), , ln ( x)
这只是一张函数表;有的函数虽然有解析表达式,但由于计 算复杂,使用不方便,通常也构造一个函数表。如三角函数表、 对数表、平方根表、立方根表等等。
引言
科学实验得到数据: i , yi ) (x yi f ( xi ) (i 0,1,2,..., n), 它反映客观存在的函数y f ( x)在这些点的情况: (i 0,1,..., n) (i 0,1,2,..., n)。 但f ( x)时未知的。因此就想寻找函数 ( x ) f ( x ) 且保持 ( xi ) f ( xi ) yi 的插值函数。 称xi为节点, ( x)为f ( x)关于节点xi (i 0,1,2,..., n)
o i 0 i j n
2o v v l j y j ; 4) 输出 : u, v。
4.3 误差估计
定理 4.3 设函数 f ( x) C n [a, b] , f ( n1) ( x) 在开区间 (a,b)内存在,则 Lagrange 插值多项式 Ln( x) 的余式有如下估 计式
第4章 函数逼近的插值法 与曲线拟和法
引言
许多实际问题都用函数y f (x)来表示某种内在规律的数量
关系,其中相当一部分函数是通过实验或观测得到的.虽然 f (x)
在某个区间[a,b]上是存在的,有的还是连续的,但却只能 给出[a,b]上一系列点 xi的函数值yi f ( xi )
Lagrange插值
二、插值余项 /* Remainder */
定理1 若 f (n1) ( x) 在[a , b]内存在, 则在[a , b]上
的n+1个互异的点,对 f(x)所作的n次Lagrange插
值多项式Ln (x) 有误差估计
Rn (x)
f (x) Ln (x)
f (n1) ( )
(n 1) !
cos x
3!
(x
6
)( x
4
)( x
3
);
1 2
cos x
3 2
0.00044
R2
5
18
0.00077
sin 50 = 0.7660444…
2次插值的实际误差 0.00061
关于Langrange插值的几点说明
(1) Ln (x) 仅与已知数据 (xi , yi ) (i 0,1,,n) 有关, 与 f (x) 的原来形式无关,但余式与 f (x)密切
L1
(
x)
x /
/ 6
4 /
4
1 2
x /
/ 4
6 /6
1 2
sin 500
5
L1( 18
)
0.77614
R1(x)
f
(2) (x )
2!
(x
6
)( x
4
),
1 2
sin x
3 2
0.01319
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
On the basis of Lagrange interpolation on triangular mesh, this paper further studies Lagrange interpolation on tetrahedral mesh, gives the suitably fixed node group theorem in space composed of ternary polynomial, constructs the Lagrange interpolation formula on tetrahedral mesh, and verifies the given formula.
OAC,ABC,且四面体的方程分别为:
α0 ( x, y, z ) = A1x + B1 y + C1z + D1 = 0 , β0 ( x, y, z ) = A2 x + B2 y + C2 z + D2 = 0 ,
γ 0 ( x, y, z ) = A3x + B3 y + C3z + D3 = 0 ,
摘要
本文在三角形网点上的Lagrange插值的基础上,进一步的研究了四面体网格上的Lagrange插值,给出了 三元多项式构成的空间中的适定结点组定理,构造出了四面体网格上的Lagrange插值公式,并对所给公 式进行了验证。
关键词
四面体,多元Lagrange插值,适定结点组
文章引用: 姜文芳, 牟朝会, 崔利宏. 四面体网格上的 Lagrange 插值[J]. 应用数学进展, 2018, 7(12): 1486-1489. DOI: 10.12677/aam.2018.712172
多项式。 解:
Q000 (0, 0, 0) Q001 (0,1, 0) Q002 (0, 2, 0) Q010 (1, 0, 0) Q011 (1,1, 0) Q020 (2, 0, 0) 10 (1, 0,1) Q200 (0, 0, 2)
Copyright © 2018 by authors and Hans Publishers Inc. This work is licensed under the Creative Commons Attribution International License (CC BY). /licenses/by/4.0/
和 k 的三元实系数多项式。
定理
2:若
{ } Qi
k i =1
是
R3
上关于插值空间℘m,n,l
的适定结点组。若它的每个点都不在水平面
x
+
y
=a 上,
则在该水平面上任取
n
+
1
个互不相同的点与
{Qi
}k i =1
一起必定构成℘m+1,n,l
的适定结点组。同样
α0 ( x, y, z) =
A1x + B1 y + C1z + D1 =
经验证: P ( x, y, z) = f ( x, y, z)
例 2:利用四面体网格上的 Lagrange 插值公式,构造如下多项式:四面体 O-ABC 为 OAB,OAC,
OBC 三个面分别是直角三角形的四面体,被插值函数为 f ( x, y, z ) = x2 + y2 + z2 +1 ,构造出三元二次插值
f1= ( x, y, z) q ( x, y, z) ⋅ r1 ( x, y, z) , f2= ( x, y, z) q ( x, y, z) ⋅ r2 ( x, y, z) ,
f3= ( x, y, z) q ( x, y, z) ⋅ r3 ( x, y, z) ,式中, r1 ( x, y, z) , r2 ( x, y, z) 和 r3 ( x, y, z) 分别是次数不小于 m,n
L000 ( x, y, z ) =−x − y − z +1 L001 ( x, y, z ) = y L010 ( x, y, z ) = x L100 ( x, y, z ) = z f (Q000 ) = 1 f (Q001 ) = 4 f (Q010 ) = 3 f (Q100 ) = 2
将该四面体作等距剖分。我们用 Qijk 表 αi ( x, y, z ) = 0 示, β j ( x, y, z) = 0 与 γ k ( x, y, z ) = 0 的交点则有
{ } = ℑn Q= ijk | i 0,1, = , n, j 0,1, 2, , n −= i, k 0,1, , n − i − j 构成℘n 的适定结点组。
Open Access
姜文芳 等
1. 引言
多元函数插值是一元函数插值理论的进一步发展,是在插值工具和被插值对象的多元推广,多元函数 插值是计算数学研究领域的一个重要方面。(见文献[1])近年来,人们发现二元插值(见文献[2])已经远远不 能满足科学发展的需要。在解决某些科学计算问题时,常常涉及到多元函数插值问题。(见文献[3])经过很 多学者在多元插值和逼近的研究,(见文献[4] [5] [6] [7] [8])我发现在许多实际问题中,常常会遇到与四面体 网格有关的插值,而怎样将四面体网格划分和插值就成了难题。本文就将介绍如何在四面体上进行网格划 分,如何选取适定结点组和如何在四面体上进行 Lagrange 插值进行研究,并给出了相应的研究成果。四面 体是生活中最常见的立体图形之一,在很多机械模型中都会出现。例如:对机械零件进行四面体网格划分 确定精度,对不规则的零部件进行四面体网格划分和插值计算,所得结果比其他算法更精准。
A0 ≡ 1 A=1 α=0 z A2 =α1 ⋅α0 = z2 − z B0 ≡ 1 B=1 β=0 x B2 = β1 ⋅ β0 = x2 − x C0 ≡ 1 C=1 γ=0 y C2 = γ1 ⋅γ 0 = y2 − y
DOI: 10.12677/aam.2018.712172
1488
应用数学进展
i, j,k =1
Lagrange 基本多项式。
定理 1:若 m 次代数曲面 f1 ( x, y, z) ,n 次代数曲面 f2 ( x, y, z) 和 k 次代数曲面 f3 ( x, y, z) 交点个数多 于 mnk ,则一定有次数不超过 m 也不超过 n 和 k 的非零多项式 q ( x, y, z) 存在,使得
令
i −1
j −1
= Ai ( x, y, z) ∏αl ( x, y, z), A0 (= x, y, z) ≡ 1, Bj ( x, y, z) ∏ βl ( x, y, z), B0 ( x, y, z) ≡ 1 ,
l=0
l=0
k −1
h −1
= Ck ( x, y, z) ∏γ l ( x, y, z),C0 ( x= , y, z) ≡ 1 , Dh ( x, y, z) ∏τl ( x, y, z), D0 ( x, y, z) ≡ 1
D Q n−i− j −k ijk
( ) 从而得到 ℑn 上的 Lagrange 插值公式如下: P ( x, y, z ) = ∑ f Qijk Lijk ( x, y, z ) 。
0≤i+ j+k≤n
例 1:利用四面体网格上的 Lagrange 插值公式,构造如下多项式:四面体 O-ABC 为 OAB,OAC,OBC
0
地,若
{ } Q k i i=1
的每个点都不在
x
+
z
=b (
y
+
z
=c )上,则在该平面上任
{ } 取 m +1( l +1 )个互不相同的点与
Qi
k i =1
一起必定构成℘m,n+1,l
(℘m,n,l +1
)的适定结点组。
特殊的 Lagrange 插值:四面体网格上的 Lagrange 插值,设四面体 O-ABC 的四面体分别为 OAB,OBC,
Lj
( x,
y,
z) ∈℘ ,
j
= 1, 2,
,l
( ) Lk ( x, y, z ) ∈℘ , k = 1, 2, ,l 使得满足 Lijk (Qi ) = ∂ijk ,i = j = k = 1, 2, ,l ,则对 f ( x, y, z ) ∈ D R3 可求得它
( ) l
的插值多项式如下: p ( x, y, z ) = ∑ f Qijk Lijk ( x, y, z ) ,这种方法称为 Lagrange 方法, Lijk ( x, y, z ) 称为
三个面分别是直角三角形的四面体,被插值函数为 f ( x, y, z) = 2x + 3y + z +1 构造出三元一次插值多项式。
解:
Q000 (0, 0, 0) Q001 (0,1, 0) Q010 (1, 0, 0) Q100 (0, 0,1)
A0 ≡ 1 A=1 α=0 z B0 ≡ 1 B=1 β=0 x C0 ≡ 1 C=1 γ=0 y D0 ≡ 1 D1 = τ 0 = x + y + z −1
2. 基本定义和基本定理
本文主要研究在四面体网格上进行多元 Lagrange 插值的问题.
首先引入若干基本概念:
基本引理:
{Qi
}l i
=1
是℘
的适定结点组的充分必要条件是
{Qi
}l i
=1
不落在℘
中的任何一个曲面上。
{ } Lagrange 方法:设
Qijk
l i, j,k =1
是多项式空间℘ 的适定结点组。设法求得
λ0 ( x, y, z ) = A4 x + B4 y + C4 z + D4 = 0 ,
