计算例题
经济基础必须掌握的计算题例题

一、关于边际产量。
边际产量=总产量1—总产量2。
例题:当企业投入劳动的数量为3个单位时,其总产量和平均产量分别为3500、1167;当投入劳动数量为4个单位时,其总产量和平均产量分别为3800、950。
则该企业的边际产量为——3800减去3500,等于300。
二、关于平均产量。
平均产量=总产量÷单位个数例如:当企业投入劳动的数量为2个单位时,其总产量和平均产量分别为3000、1000;当投入劳动数量为3个单位时,其总产量和平均产量分别为3500、500。
则该企业的投入劳动数量为3个单位时的平均产量是——3500÷5等于1167。
三、关于边际成本。
边际成本=总成本1—总成本2。
例题:当某企业的产量为2个单位时,其总成本、总固定成本、总可变成本、平均成本分别为2000、1200、800、1000元。
当产量为3个单位时,其总成本、总固定成本、总可变成本、平均成本分别为2100、1300、900、700元。
则该企业的边际成本为——2100减去2000等于100。
三、关于全要素生产率。
全要素生产率=经济增长率—(劳动份额乘以劳动增加率)—(资本份额乘以资本增长率)例题:如果一国在一定时期内经济增长率为7%,劳动增长率为2%,资本增长率为3%。
劳动产出弹性和资本产出弹性分别为0.65和0.35。
根据索洛余值法,在7%的经济增长率中,全要素生产率对经济的贡献约为——百分之7减去 (0.65乘以2%)减去(0.35乘以3%)=4.65%约等于4.7%。
四、关于货币量。
记住两个例题。
第一个例题:已知全社会现有货币供应量为24亿元。
中央银行又重新放出基础货币2亿元。
当时的货币乘数为4.5,则全社会将形成的最高货币供应量为——24+2乘以4.5=33亿元。
第二个例题:当存款准备金率为6%,货币供给比例为14%时,中央银行放出1000万元信用,最终形成的货币供应量为——1000乘以(6%加上14%之和的倒数)=5000万元。
工程量计算例题
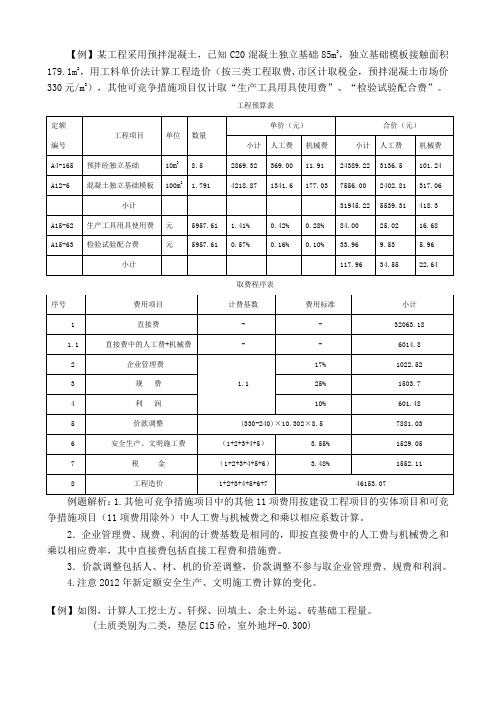
【例】某工程采用预拌混凝土,已知C20混凝土独立基础85m3,独立基础模板接触面积179.1m2,用工料单价法计算工程造价(按三类工程取费,市区计取税金,预拌混凝土市场价330元/m3),其他可竞争措施项目仅计取“生产工具用具使用费”、“检验试验配合费”。
工程预算表取费程序表例题解析:1.其他可竞争措施项目中的其他11项费用按建设工程项目的实体项目和可竞争措施项目(11项费用除外)中人工费与机械费之和乘以相应系数计算。
2.企业管理费、规费、利润的计费基数是相同的,即按直接费中的人工费与机械费之和乘以相应费率,其中直接费包括直接工程费和措施费。
3.价款调整包括人、材、机的价差调整,价款调整不参与取企业管理费、规费和利润。
4.注意2012年新定额安全生产、文明施工费计算的变化。
【例】如图,计算人工挖土方、钎探、回填土、余土外运、砖基础工程量。
(土质类别为二类,垫层C15砼,室外地坪-0.300)【例】如下图所示尺寸,求混凝土带型基础模板和混凝土的工程造价。
备注:按三类工程取费,企业管理费费率为17%,利润费率为10%,规费费率为25%,税金税率为3.48%,安全生产、文明施工费为4.25%。
解:(1)带型基础外侧模板 S1=[(4.5×2+0.5×2)×2+(4.8+0.5×2)×2]×0.3=9.48 m2(2) 带型基础内侧模板 S2=[(4.5-0.5×2)×2+(4.8-0.5×2)×2]×0.3×2=8.76 m2带型基础模板工程量 S= S1+ S2=18.24 m2(模板工程量3分)(3)带形基础混凝土外墙 V=1×0.3×(4.5+4.5+4.8)×2=8.28 m3 (混凝土工程量2分)内墙 V=1×0.3×(4.8-1)=1.14 m3 (混凝土工程量2分)合计:9.42 m3预算表取费:1. 直接费 3329.7元2.其中人+机 1021.36元3.企业管理费 1021.36×17%=173.63元4.规费 1021.36×25%=255.34元5.利润 1021.36×10%=102.14元6安全生产、文明施工费 3860.81×4.25%=164.08元7.税金 4024.89×3.48%=140.07元【例】如图所示内外墙毛石基础、砖基础平面图和剖面图,毛石基础每级高度为350mm,试计算砌体基础工程量。
微观经济学计算题例题

1、假设某产品的市场需求、供给曲线分别如下:Qd=1000-100P,Qs=10+200P求:(1)均衡产量和价格;(2)若政府对每单位产品征税3元,求征税后短期内的均衡产量、供给价格和需求价格。
答:(1)令1000-100P =10+200P 得P=3.3,Q=670(2)征税后,供给曲线向左上方移动,新的供给曲线为垂直向上移动3,Qs=10+200P 200P= Qs-10P= Qs/200-1/20+3 Qs=200P-590令供给等与需求200P-590=1000-100P解此式,得Q=470,Ps=2.3,Pd=5.32、某甲有26元钱,X商品的价格6元,边际效用12个单位;Y商品价格4元,边际效用10个单位;多消费一个单位商品,该商品的边际效用降低0.5个单位;每1元钱的边际效用不变为1.5个单位。
问:某甲的钱应该如何分配才能实现他的效用最大化。
解:因为两种商品的边际效用之比为12/6=2<10/4=2.5 应该既买X,又买Y,但Y要多买一个,它们的边际效用才能相等。
尽可能不持有货币,因为货币的边际效用最小。
如果不考虑边际效用递减,应该买6个Y,持有2元钱,可得63单位的总效用(6×10+2×1.5)。
因为一元钱用在不同商品上的边际效用递减,多消费一个X和Y,其边际效用下降为2和3个单位。
所以应该买2个X,3个Y,保留2元钱,它们的边际效用相等,总效用最大化。
12/6=2 2个X的总效用:6×2+6×1.510/4=2.5 3个Y的总效用:4×2.5+4×2.0+4×1.52元钱的总效用:2×1.5总效用:12+9+10+8+6+2×1.5=48总预算:2×6+3×4+2=263.完全竞争行业的成本函数是C(q)=10+5q+5q^3求:1、A VC、AFC 、AC 、MC;2、停产价格和图像;3、供给函数和图像;4、行业的均衡价格;5、如果行业的需求函数是D(p)=100-p求其长期的均衡产量。
计算题例题及公式 doc

计算题例题及公式 doc计算题1.>某板坯连铸机拉坯速度为2.0m/min,出结晶器的安全坯壳厚度为12mm,结晶器冷凝系数为20mm/min,求该铸机的结晶器长度。
答案:解:l=V([δ]/K)2+100=(15/20)2×2000+100=820mm 答:该铸机的结晶器长度为820mm。
2.>已知铸坯断面尺寸是250mm×1500mm,拉速是1.3m/min,比水量是11/kg,取凝固系数k=28,计算液芯深度?(结果保留二位小数) 答案:解:根据公式:L=(D/K)2×V=(125/28)2×1.3=25.91m 答:液芯深度为25.91m。
3.>一台断面200mm×1250mm单流铸机,平均拉速为0.9m/min,铸坯理论比重7.8t/m3,铸机平均作业率为85%,求该铸机的年产量多少?(保留一位小数) 答案:解:G =0.2×1.25×0.9×60×24×85%×7.8×365=784063.8t 答:该铸机的年产量为784063.8t。
4.>已知铸坯的断面为150mm×150mm,拉速为1.4m/min,二冷却水的耗水量为270L/min,求该铸机二冷区的冷却强度。
(已知铸坯的比重为7.6t/m3) 答案:解:G=Q/(FVγ)=270/(0.15×0.15×1.4×7.6×103)=1.13kg/t5.>已知铸坯的名义宽度为1000mm,结晶器下口宽度为1005mm,上口宽度为1015mm,求宽度方向的锥度值是多少?(计算结果保留三位小数点) 答案:解:锥度值=(上口宽度-下口宽度)/下口宽度×100%=0.995%6.>某厂二月份产坯20418t,浇钢98次,中间包浇注时间累计为496小时45分钟,若每次浇注的生产准备时间平均为:开浇前,中间包在中间包车就位装定径水口、吊包盖,中间包在线对中,共计30分钟,最后一流浇毕,至最后一根铸坯离线计15分钟,求该机二月份的作业率。
计算题典型例题汇总

计算题典型例题汇总:1 消费者均衡条件。
1. 已知张先生每月收入收入1600元,全部花费于X 和Y 两种产品,他的效用函数为U XY =,X 的价格是10元,Y 的价格20元。
求:为获得最大效用,他购买的X 和Y 各为多少?2 APL MPL 的极大值的计算。
假定某厂商只有一种可变要素劳动L ,产出一种产品Q ,固定成本为既定,短期生产函数L L L Q 1261.023++-=,求解:(1)劳动的平均产量L AP 为极大时雇佣的劳动人数。
(2)劳动的边际产量L MP 为极大时雇佣的劳动人数3 成本一定,产量最大化;产量一定,成本最小化条件。
3588=Q L K 已知某厂商的生产函数为,劳动价格为3美元,资本价格为5美元,求产量为10时的最低成本,求总成本为160美元时的产量。
4 完全竞争厂商长期生产中利润最大化条件。
322+1510Q Q -+完全竞争厂商的短期成本函数为STC=0.1Q ,试求厂商的短期供给函数。
5 完全垄断厂商短期均衡。
2=32Q ++已知某垄断厂商的成本函数为TC 0.6Q ,反需求函数为P=8-0.4Q.求厂商实现利润最大化时的产量、价格、收益和利润。
6 GDP 核算假定某国某年发生了一下活动:(a )一银矿公司支付7.5万美元给矿工开采了50千克银卖给一银器制造商,售价10万美元;(b )银器制造商支付5万美元工资给工人造了一批项链卖给消费者,售价40万美元。
(1)用最终产品生产法计算GDP(2)每个生产阶段生产多少价值?用增值法计算GDP(3)在生产活动中赚得的工资和利润各为多少?7均衡收入的决定。
假定某经济社会的消费函数为C =100+0.8YD (YD 为可支配收入),投资支出为I=50, 政府购买为G =200,政府转移支付为TR=62.5,税收为T =250 求:(1)均衡的国民收入(2)投资乘数,政府购买乘数,税收乘数,转移支付乘数。
8 IS —LM 模型产品市场货币市场同时均衡时的利率和收入。
统计学计算题例题
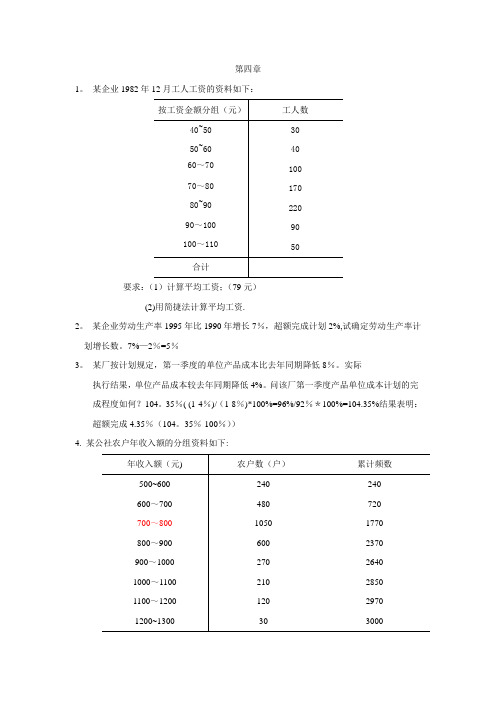
第四章1。
某企业1982年12月工人工资的资料如下:要求:(1)计算平均工资;(79元)(2)用简捷法计算平均工资.2。
某企业劳动生产率1995年比1990年增长7%,超额完成计划2%,试确定劳动生产率计划增长数。
7%—2%=5%3。
某厂按计划规定,第一季度的单位产品成本比去年同期降低8%。
实际执行结果,单位产品成本较去年同期降低4%。
问该厂第一季度产品单位成本计划的完成程度如何?104。
35%( (1-4%)/(1-8%)*100%=96%/92%*100%=104.35%结果表明:超额完成4.35%(104。
35%-100%))4. 某公社农户年收入额的分组资料如下:要求:试确定其中位数及众数。
中位数为774.3(元)众数为755。
9(元)求中位数:先求比例: (1500—720)/(1770-720)=0。
74286分割中位数组的组距:(800-700)*0。
74286=74.286加下限700+74。
286=774。
286求众数:D1=1050—480=570D2=1050-600=450求比例:d1/(d1+d2)=570/(570+450)=0。
55882分割众数组的组距:0。
55882*(800-700)=55。
882加下限:700+55.882=755。
8825.1996年某月份某企业按工人劳动生产率高底分组的生产班组数和产量资料如下:.64。
43(件/*140+85*60)/)6。
根据表中资料计算中位数和众数。
中位数为733.33(元)众数为711。
11(元)求中位数:先求比例:(50-20)/(65-20)=0。
6667分割中位数组的组距:(800—600)*0。
6667=66。
67 加下限:600+66.67=666。
677。
某企业产值计划完成103%,比去年增长5%.试问计划规定比去年增长 多少?1。
94%(上年实际完成1。
03/1.05=0。
981 本年实际计划比上年增长(1-0。
算术题大全

算术题大全1. 加法1.1 两位数相加例题:计算以下两位数相加的结果:34 + 58 = ?答案:921.2 三位数相加例题:计算以下三位数相加的结果:247 + 359 = ?答案:6061.3 带进位的相加例题:计算以下带进位的相加的结果:35 + 68 = ?答案:1032. 减法2.1 两位数相减例题:计算以下两位数相减的结果:75 - 23 = ?答案:522.2 三位数相减例题:计算以下三位数相减的结果:387 - 125 = ?答案:2622.3 减法中的借位例题:计算以下减法中的借位后的结果:54 - 78 = ?答案:-243. 乘法3.1 乘数为个位数例题:计算以下乘数为个位数的乘法结果:7 × 6 = ?答案:423.2 乘数为两位数例题:计算以下乘数为两位数的乘法结果:15 × 24 = ?答案:3603.3 乘法竖式计算例题:计算以下乘法竖式的结果:23× 14-----答案:3224. 除法4.1 除数为个位数例题:计算以下除数为个位数的除法结果:12 ÷ 3 = ?答案:44.2 除数为两位数例题:计算以下除数为两位数的除法结果:120 ÷ 8 = ?答案:154.3 除法中的余数例题:计算以下除法中的余数:24 ÷ 7 = ?答案:35. 混合运算5.1 加法与减法混合例题:计算以下加法与减法混合运算的结果:27 + 10 - 8 = ?答案:295.2 加法、减法与乘法混合例题:计算以下加法、减法与乘法混合运算的结果:12 + 3 × 5 = ?答案:275.3 多项式运算例题:计算以下多项式运算的结果:(8 + 3) × (5 - 2) = ?答案:33以上是一些常见的算术题,通过练习可以提升计算能力。
希望这些例题能对您有所帮助!。
六种折扣计算的例题

六种折扣计算的例题折扣是消费者在购买商品时可以享受到的一种优惠方式,通过降低商品价格来吸引消费者。
在日常生活中,我们经常会遇到各种不同形式的折扣计算问题。
本文将介绍六种常见的折扣计算例题,帮助读者更好地理解和应用折扣计算。
1. 固定折扣计算例题:某商店正在举行清仓活动,一款原价为100元的衣服打6折,求该衣服的最终价格。
解答:打6折表示打九折,即打1-0.4=0.6折。
最终价格 = 原价 ×折扣 = 100元 × 0.6 = 60元。
2. 百分数折扣计算例题:一本书原价是80元,半价出售,请问这本书的折扣是多少?解答:折扣 = (原价 - 出售价格)/ 原价 × 100% = (80元 - 40元)/ 80元 × 100% = 50%。
3. 多项折扣计算例题:某品牌手机原价为5000元,商场正在进行活动,先打8折,然后再打95折,最终价格是多少?解答:先打8折,最终价格 = 原价 ×折扣1 = 5000元 × 0.8 = 4000元;再打95折,最终价格 = 上一步的价格 ×折扣2 = 4000元 × 0.95 = 3800元。
4. 连续折扣计算例题:某品牌服装店举行促销活动,一件原价200元的外套先打6折,然后再打8折,最终价格是多少?解答:先打6折,最终价格 = 原价 ×折扣1 = 200元 × 0.6 = 120元;再打8折,最终价格 = 上一步的价格 ×折扣2 = 120元 × 0.8 = 96元。
5. 满额减免折扣计算例题:某超市举行满300元减50元的活动,小明购买了价值400元的商品,他需要支付多少钱?解答:满300元减50元,小明购买了400元的商品,根据减免规则,需要支付的金额 = 购买总额 - 减免金额 = 400元 - 50元 = 350元。
6. 满额赠品折扣计算例题:某化妆品品牌进行满100元赠送礼品的活动,小红购买了该品牌的商品,共计120元,她将获得什么样的礼品?解答:满100元赠送礼品,小红购买了120元的商品,根据满赠规则,小红将获得对应的礼品,具体礼品可以根据活动具体规定而定。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.大小主应力法
1 f
o o 3 tan 45 2c tan 45 450 .8kPa 2 2
2
计算结果表明:1f大于该单元土体实际大主应力 1,实际应力圆半径小于极限应力圆半径,所以, 该单元土体处于弹性平衡状态
5
3 f 1 tan 2 45o
4
例 地基中某一单元土体上的大主应力为430kPa,小主应力 为200kPa。通过试验测得土的抗剪强度指标c=15 kPa, =20o。试问①该单元土体处于何种状态?②单元土体最大剪 应力出现在哪个面上,是否会沿剪应力最大的面发生剪破?
【解答】
已知1=430kPa,3=200kPa,c=15kPa, =20o
114.5 0.970 0.937 0.0618 115.2 0.960 0.936 0.0122 104.5 0.954 0.940 0.0072 97.0 0.948 0.942 0.0031 98.8 0.944 0.940 0.0021
7.2
89.0
12.3
按分层总和法求得基础最终沉降量为s=Σsi =54.7mm
9
a 0 1 zK a 1 17 0 0.31 0
a 1 1 zK a 1 17 2 0.31 10.5kPa
a 1 4.4 kPa
a 2 36.9kpa
10
(4)计算主动土压力
1 1 E a 10 .5 2 4.4 3 36 .9 4.4 3 2 2 10 .5 13 .2 48 .75 72 .5kN / m
(2)、计算其余的各个物理指标: ①、e=Vv/ VS=0.65 ②、n= Vv /V=39.4% ③、Sr= Vw / Vv =46.2% ④、ρ sat =( ms+ Vvρ w)/v=2.21 g/cm3 ⑤、γ sat=ρ sat×g=22.1KN/m3
⑥、ρ d = ms / v=1.82 g/cm3
例
题
某厂房柱下单独方形基础,已知基础底面积尺寸为 4m×4m,埋深d=1.0m,地基为粉质粘土,地下水位距 天然地面3.4m。上部荷重传至基础顶面F=1440kN,土的 天然重度=16.0kN/m³ ,饱和重度 sat=17.2kN/m³ ,有关 计算资料如下图。试用分层总和法计算基础最终沉降。
2 3 3 13.2 48.75 1.5 m 3 2 3
Ea的作用方向水平,作用点距墙基为z,则
1 z 10.5 3 72.5
11
例题 用水土分算法计算图所示的挡土墙上的 主动土压力、水压力及其合力。
12
解(1)计算主动土压力系数
底面 a 2 1 h1 2 z K a 2 18 6 9 4 0.333 48.0kPa
水压力:顶面 w 1 w z 9.8 0 0 底面 w 2 w z 9.8 4 39.2kPa
13
a0 0
ห้องสมุดไป่ตู้a 1 36.0kPa
w1 0
a 1 36.0kPa
a 2 48.0kPa
w 2 39.2kPa
14
(4)计算总主动土压力和总水压力 1 1 E a 36 6 36 4 48 36 4 108 144 24 276kN / m
22
23
24
25
7.2
6.确定沉降计算深度zn 根据σz = 0.2σc的确定原则,由计算结果,取zn=7.2m 7.最终沉降计算 根据e-σ曲线,计算各层的沉降量
3
z( m ) 0 1.2 2.4 4.0 5.6
h σc σz σz+ σc (kPa) (kPa) (mm) (kPa) (kPa) (kPa)
σc
(5)挡土墙上主动土压力及水压力如图所示。
16
17
例题 某工程地质柱状图及土的物理性质指标如图所示。试求 各土层界面处自重应力,并画出自重应力分布图:
18
解:由土的自重应力得:
(1)、填土层底: σcz1=γt× h1 =15 KN/ M2 (2)、黏土层底: σcz2=σcz1+γ2'× h2 =15+(18-10)×2=31KN/ M2 (3)、淤泥层底: σcz3=σcz2+γ3'× h3 =31+(17-10)×3=52 KN/ M2
(2)计算第一层的土压力 顶面 a 0 1 zK a 1 17 0 0.31 0
a1 1 a1 底面 (3)计算第二层的土压力
K a 2 0.75
zK
17 2 0.31 10.5kPa
顶面
a 1 1 h1 2 z K a 2 2C K a 2
库仑定律
f tan c 129.7kPa
最大剪应力面上τ<τf ,所以,不会沿剪应力最大的面发生破 7 坏
例题 挡土墙高5m,墙背直立,光滑,墙后填 土水平,共分两层,各土层的物理力学指标如图 所示,试求主动土压力并绘出土压力分布图。
8
解:(1)计算主动土压力系数
32 K a 1 tan2 45 0.31 2 16 K a 2 tan2 45 0.57 2
K a1 K a 2
(2)计算地下水位以上的主动土压力 顶面 a 0 1 zK a 1 18 0 0.333 0
30 tan 45 0.333 2
2
底面 a 1 1 zK a 2 18 6 0.333 36.0kPa (3)计算地下水位以下土层的主动土压力及水压力 因水下土为砂土,采用水土分算法 主动土压力: 顶面 a 1 1 h1 2 z K a 2 18 6 9 0 0.333 36.0kPa
2 2
Ea作用方向水平,作用点距墙基为z,则
1 6 4 4 z 108 4 144 24 3.51m 276 3 2 3
15
水压力
1 Pw 39.2 4 78.4kN / m 2
Pw作用方向水平,作用点距墙基4/3=1.33m。
(4)、不透水层层顶:
σcz3'=σcz3+γw× (h3+h2) =52+10×(2+3)=102KN/ M2 (5)、不透水层底: σcz4=σcz3'+γ4× h4 =102+20×4=182 KN/ M
19
例题 某工程地基勘察中测得原状土的天然密度 ρ =2.0g/cm3,含水量ω =10%,相对密度ds=3.0,要求 绘制该地基土的三相草图,求出三相草图中的各相的 物理指标,并求出孔隙比e,孔隙率n,饱和度Sr,饱和 密度ρ sat,饱和容重γ sat,干密度ρ d,干容重γ d, 浮密度ρ ',浮容重γ '等物理指标。
F=1440kN
e 0.96
d=1m
0.94
3.4m
b=4m
0.92
0.90 50 100 200
1 σ 300
【解答】
分层总和法计算
3.4m d=1m
F=1440kN
1.确定分层厚度 每层厚度hi <0.4b=1.6m,地下 水位以上分两层,各1.2m,地下 水位以下按1.6m分层 2.计算地基土的自重应力 自重应力从天然地面起算,z 的取值从基底面起算
底面 a 2 1 h1 2 z K a 2 2C K a 2
17 2 19 0 0.57 2 10 0.75 4.4kPa
17 2 19 3 0.57 2 10 0.75 36.9 kPa
20
解:(1)、绘制三相草图,计算三相草图中的各相的物理指标:
质量M(g)
ma
体积V(cm3)
气相 液相
Va Vw Vv
mw
V m
ms
固相
Vs
①、设VS=1.0cm3 ②、由ds=ms/VS×ρw=3.0,则ms=3.0g ③、由ω= mw/ ms=10%,则mw =0.3g,ma=0,Vw=0.3 cm3 21 总上:m= ma +ms +mw=3.3. ④、由V= m/ρ=1.65 cm3,则Vv=0.65 cm3
3.图解法
实际应力圆 τmax
极限应力圆
c
3f
1 1f
最大剪应力与主应力作用面成45o 1 max 1 3 sin 90 115kPa 2 最大剪应力面上的法向应力
1 1 3 1 1 3 cos 90 315kPa 2 2
16
σz
e1
e2
e1i- e2i 1+ e1i
si (mm) 20.2 14.6 11.5 5.0 3.4
94.0 83.8 57.0 31.6 18.9
35.2 54.4 65.9 77.4
1200 25.6 88.9 1200 44.8 70.4 1600 60.2 44.3 1600 71.7 25.3 1600 83.2 15.6
用角点法计算,过基底中点将荷载面四等分,计算边长l=b=2m, σz=4Kcp0,Kc由表确定
z(m) 0 1.2 2.4 4.0 5.6 7.2 z/b 0 0.6 1.2 2.0 2.8 3.6 Kc σz(kPa) σcz(kPa) σz /σc 0.2500 94.0 16 0.2229 83.8 35.2 0.1516 57.0 54.4 0.0840 31.6 65.9 0.0502 18.9 77.4 0.24 0.0326 12.3 89.0 0.14 zn (m)
