北师大版九年级数学下册第一章三角函数知识点总结及典型习题(超级详细)
北师大版数学九年级下册知识点总结及例题不错.docx

北师大版数学九年级下册知识点总结及例题第一章 直角三角形的边角关系1.正切:在 Rt △ABC 中,锐角∠ A 的对边与邻边的比叫做∠ A 的正切,记作 tanA ,即A的对边;tanAA的邻边 ;① tanA 是一个完整的符号,它表示 ∠A 的正切,常省去角的符号 “∠”; ② tanA 没有单位,它表示一个比值,即直角三角形中 ∠ A 的对边与邻边的比; ③ tanA 不表示 “tan 乘”以 “A ”;④ tanA 的值越大,梯子越陡, ∠A 越大; ∠ A 越大,梯子越陡, tanA 的值越大。
例 在 Rt △ABC 中,如果各边长度都扩大为原来的 2 倍,那么锐角 A 的正弦值( )A.扩大 2倍B.缩小 2 倍 C. 扩大 4 倍 D. 没有变化2. 正.弦.:A 的对边 sin A斜边3. 余弦:A 的邻边 cosA斜边C .2D . 2 24. 一个锐角的正弦、余弦分别等于它的余角的余弦、正弦。
在 Rt △ ABC 中, 锐角 ∠A 的对边与斜边的比叫做 ∠A 的正弦,记作 sinA ,即例 在 ABC 中,若 C90,sin A 1, AB 2, 2则 ABC 的周长为在 Rt △ABC 中,锐角 ∠A 的邻边与斜边的比叫做 ∠ A 的余弦,记作 cosA ,即例 等腰三角形的底角为 30° ,底边长为 2 3 ,则腰长为( )A .4例 △ ABCsin α中,∠ A ,∠ B 均为锐角,且有cos α|tanB 3 | (2sin A 3)2 0,则△ABC 是 tan α1()A .直角(不等腰)三角形 B .等腰直角三角形C .等腰(不等边)三角形D.等边三角形5. 当从低处观测高处的目标时,视线与水平线所成的锐角称为仰角当从高处观测低处的目标时,视线与水平线所成的锐角称为俯角6. 在直角三角形中,除直角外,一共有五个元素,即三条边和二个锐角。
由直角三角 形中除直角外的已知元素,求出所有未知元素的过程,叫做解直角三角形。
北师大版九年级数学下册第一章三角函数知识点总结(超级详细)
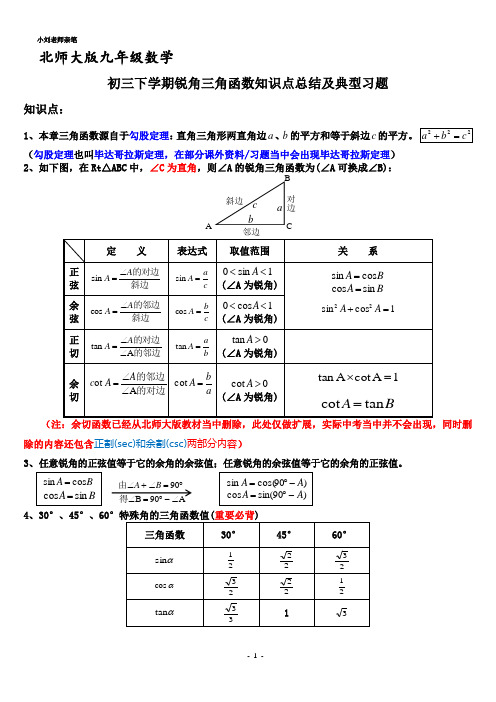
北师大版九年级数学初三下学期锐角三角函数知识点总结及典型习题知识点:1、本章三角函数源自于勾股定理:直角三角形两直角边a 、b 的平方和等于斜边c(勾股定理也叫毕达哥拉斯定理,在部分课外资料/习题当中会出现毕达哥拉斯定理) 2、如下图,在Rt △ABC 中,∠C 为直角,则∠A 的锐角三角函数为(∠A 可换成∠B):除的内容还包含正割(sec)和余割(csc)两部分内容)3、任意锐角的正弦值等于它的余角的余弦值;任意锐角的余弦值等于它的余角的正弦值。
4、30°、45°、60A 90B 90∠-︒=∠︒=∠+∠得由B A对边邻边 C6、正弦、余弦的增减性:当0°≤α≤90°时,sin α随α的增大而增大,cos α随α的增大而减小。
7、正切、的增减性:当0°<α<90°时,tan α随α的增大而增大,解直角三角形的定义1、:已知边和角(两个,其中必有一边)→所有未知的边和角。
依据:①边的关系:222c b a =+;②角的关系:A+B=90°;③边角关系:三角函数的定义。
(注意:尽量避免使用中间数据和除法)2、应用举例:(1)仰角:视线在水平线上方的角;俯角:视线在水平线下方的角。
仰角水平线视线视线俯角(2)坡面的铅直高度h 和水平宽度l 的比叫做坡度(坡比)。
用字母i 表示,即h i l=。
坡度一般写成1:m 的形式,如1:5i =等。
把坡面与水平面的夹角记作α(叫做坡角),那么tan hi lα==。
3、从某点的指北方向按顺时针转到目标方向的水平角,叫做方位角。
如图 ,OA 、OB 、OC 、OD 的方向角分别是:45°、135°、225°。
指北或指南方向线与目标方向 线所成的小于90°的水平角,叫做方向角。
所以,OA 、OB 、OC 、OD 的方向角分别是:北偏东30°(东北方向) , 南偏东45°(东南方向), 南偏西60°(西南方向), 北偏西60°(西北方向)。
(完整版)新北师大九年级数学下册知识点总结

新北师大版九年级数学下册知识点总结第一章直角三角形边的关系一•锐角三角函数 1.正切:定义:在Rt △ ABC 中,锐角/A 的对边与邻边的比叫做/A的正切,记作tanA ,① tanA 是一个完整的符号,它表示/A的正切,记号里习惯省去角的符号“/”;② tanA 没有单位,它表示一个比值,即直角三角形中/A 的对边与邻边的比;③ tanA 不表示"tan ”乘以"A ”;④ 初中阶段,我们只学习直角三角形中,/A是锐角的正切;⑤ tanA 的值越大,梯子越陡,ZA 越大;ZA 越大,梯子越陡,tanA 的值越大。
2. 正弦:定义:在Rt △ ABC 中,锐角/A 的对边与斜边的比叫做/A 的正弦,记作sinA ,即sin AA的对边................................... """■ 斜边3. 余弦:定义:在Rt △ ABC 中,锐角/A 的邻边与斜边的比叫做/A 的余弦,记作cosA ,即cosA A的邻边 .............................. ■■■■■斜边之变化三•三角函数的计算1. 仰角:当从低处观测高处的目标时,视线与水平线所成的锐角称为 仰角2. 俯角:当从高处观测低处的目标时,视线与水平线所成的锐角称为 俯角值随着角度的增大(或减小)而增大(或减小);余弦值随着角度的增大 < sin a< 1, 0< cos a< 1。
4. 坡度:如图2,坡面与水平面的夹角叫做坡角坡角的正切称为坡度i tan Al5. 方位角:从某点的指北方向按顺时针转到目标方向的水平角,叫做方位角...。
如图3,OA OB OC 的方位角分别为 45 °、135 °、225 °。
6. 方向角:指北或指南方向线与目标方向线所成的小于90°的水平角,叫做方向角.。
北师大版九年级(下)数学知识点归纳总结

第一章直角三角形的边角关系九年级下册第1节锐角三角函数一、锐角三角函数锐角A的正弦、余弦、正切都叫做∠A的锐角三角函数。
如图所示,在Rt△ABC中,∠C=90°【说明】①三角函数表示的是两边的比值,所以它只是一个数值,没有单位。
②当用一个大写字母表示角时,其三角函数中角的符号省略,如sin A,cos B,tan C;当用一个希腊字母表示角时,其三角函数中角的符号省略,如sinα,cosβ,tanθ;当用三个大写字母表示角时,其三角函数中角的符号不能省略,如sin∠ABC,cos∠DEF,tan∠GHI;当用一个阿拉伯数字表示角时,其三角函数中角的符号不能省略,如sin∠1,cos∠2,tan∠3。
③如果要表示三角函数的倍数与乘方,应分别表示为2 sin A,3cos B,4tan C,sin2A,cos3B,tan4C;2 sin30°,3cos30°,4tan30°,sin230°,cos330°,tan430°。
二、坡度1、坡度的概念如图所示,我们把坡面的铅直高度h和水平宽度l的比值叫做坡度(或坡比),通常用字母i表示。
【说明】坡面的坡度实际上就是坡角的正切值,即i=tanα=hl2、三角函数与坡面的陡峭程度(1)tan A的值越大,坡面越陡。
(2)sin A的值越大,坡面越陡。
(3)cos A的值越小,坡面越陡。
三、锐角三角函数的增减性(0°~90°)1、正弦值随着角度的增大(或减小)而增大(或减小);2、余弦值随着角度的增大(或减小)而减小(或增大);3、正切值随着角度的增大(或减小)而增大(或减小)。
四、同角三角函数的关系1、互余关系:sinA =cos(90°-A) cosA =sin(90°-A)2、平方关系:s in 2A +cos 2A =13、弦切关系:tan A =sin cos AA4、倒数关系:tan A ·tan(90°-A)=1第2节 30°,45°,60°角的三角函数值一、探索30°,45°,60°角的三角函数值求30°角的三角函数值,关键根据“直角三角形中30°的锐角所对的直角边等于斜边的一半”,可设30°的锐角的对边为a ,则斜边为2a ,由勾股定理可求得30°3a ,因此可以求出30°的锐角的各个三角函数值:sin30°=2a a =12 cos30°3a3 tan30°3a 33也可以求出60°的锐角的各个三角函数值:sin60°3a =3 cos60°=2a a =12tan60°3a 3求45°角的三角函数值,关键根据“有一个角是45°的直角三角形是等腰直角三角形”,可设一条直角边为a ,则另一条直角边也为a 2a ,因此可以求出45°的锐角的各个三角函数值:sin45°2a 22 cos45°2a 2 tan45°=aa =1二、熟记特殊角的三角函数值第3节三角函数的计算一、用计算器求任意锐角的三角函数值1、求整数度数的锐角的三角函数值首先使计算器的面板上出现DEG,然后再按sin cos tan这三个键之一,再从高位向低位按出表示度数的整数,再按键=,就可以在显示屏上得到答案。
北师大版九年级数学下册第一章30°,45°,60°角的三角函数值课件

如图,一段长1500m的水渠,它的横截面为梯形 ABCD,其中AB∥CD,BC=AD,渠深AE=0.8m,底AB=1.2m, 坡角为450,那么该段水渠最多能蓄水多少立方米?
2400m3.
某阶梯的形状如图所示,其中线段AB=BC,AB部分 的坡角为450,BC部分的坡角为300,AD=1.5m.如果 每个台阶的高不超过20cm,那么这一阶梯至少有多 少个台阶?(最后一个台阶的高不足20cm时,按 一个台阶计算)
角α 30°
45°
60°
1
3
2
2
2
2
2
2
3
1
2
2
tanα
3 3
1
3
三角函 三角
数值
函数
sinα
cosα tanα
角α
30°
1
3
3
2
2
3
45°
2
2
1
2
2
60°
3
1
2
2
3
要能记住有多好!
这张表还可以看出哪些知识之间的内在联系?
例1 计算: (1)sin300+cos450;(2) sin2600+cos2600-tan450.
至少有13个台阶。
提示:BD AD 1.5m,
CE 1 BC 1 AB 3 2 m,
2
2
4
BD CE 13. 0.2
已知∠A为锐角,且cosA= 3 ,你能求出∠A的
度数吗。
2
已知a为锐角,tan(90°-a)= 3,求a.
在Rt△ABC中, ∠C=90°,若cosB= 2 ,求sinA
sin 300 BC a 1 ; AB 2a 2
北师大数学九年级下册第一章-三角函数的应用(含解析)

第02讲_三角函数的应用知识图谱解直角三角形知识精讲一.解直角三角形的定义在直角三角形中,由已知元素求未知元素的过程,就是解直角三角形.二.解直角三角形要用到的关系1.三边之间的关系222a b c +=2.两锐角之间关系90A B ∠+∠=︒ 3.边角之间的关系sin =A a A c ∠=的对边斜边, sin =B bB c ∠=的对边斜边;cos =A b A c ∠=的邻边斜边, cos =B aB c ∠=的邻边斜边;tan =A a A b ∠=的对边邻边, tan =B bB a∠=的对边邻边.三.圆中的相关计算1.利用勾股定理和锐角三角函数求解圆中有关直角三角形的边长问题; 2.利用直径所对圆周角为90︒,构造直角三角形; 3.利用切线的性质求解线段长度.三点剖析一.考点:解直角三角形,与圆结合求解线段长度.二.重难点:1.特殊三角函数值的记忆以及应用;2.圆中直径与所对圆周角的构造以及直角三角形选取的问题; 3.射影定理与锐角三角函数结合.三.易错点:特殊三角函数值的三边比例对应关系.解直角三角形例题1、 在Rt△ABC 中,△C=90°,sinA=,AC=6cm ,则BC 的长度为( )A.6cmB.7cmC.8cmD.9cm【答案】 C【解析】 △sinA==,△设BC=4x ,AB=5x , 又△AC 2+BC 2=AB 2, △62+(4x )2=(5x )2, 解得:x=2或x=﹣2(舍), 则BC=4x=8cm ,例题2、 在Rt △ABC 中,∠C=90°,如果AC=2,cosA=23,那么AB 的长是( ) A.3 B.43C.5D.13【答案】 A 【解析】 ∵cosA=23AC AB =, ∴AB=232233AC ==. 例题3、 如图,在四边形ABCD 中,90B D ∠=∠=︒,3AB =,2BC =,4tan 3A =,则CD =__________.【答案】65【解析】 解:延长AD 和BC 交于点E .Rt ABE ∆在中,4tan 3A =,3AB =,4BE ∴=,422EC BE BC ∴=-=-=,ABE ∆和CDE ∆中,90B EDC ∠=∠=︒,E E ∠=∠, DCE A ∴∠=∠,Rt CDE ∴∆中,4tan tan 3DE DCE A DC ∠===,∴ 设4DE x =,则3DC x =,在Rt CDE ∆中,222EC DE DC =+,224169x x ∴=+,解得:25x =,则65CD =.例题4、如图,在△ABC中,AD是BC边上的高,tanC=,AC=3,AB=4,求△ABC的周长.【答案】10+3+.【解析】在Rt△ADC中,tanC==,设AD=k,CD=2k,AC==k,△AC=3,△k=3,解得k=3,△AD=3,CD=6,在Rt△ABD中,BD===,△△ABC的周长=AB+AC+BD+CD=4+3++6=10+3+.例题5、如图,在△ABC中,sinB=45,点F在BC上,AB=AF=5,过点F作EF⊥CB交AC于点E,且AE:EC=3:5,求BF的长与sinC的值.【答案】6;5 5【解析】过点A作AD⊥CB,垂足为点D,∵4 sin5B=,∴3 cos5B=,在Rt△ABD中,3cos535BD AB B=⋅=⨯=,∵AB=AFAD⊥CB,∴BF=2BD=6,∵EF⊥CBAD ⊥CB , ∴EF ∥AD , ∴DF AE CF EC=, ∵AE :EC =3:5 DF =BD =3, ∴CF =5, ∴CD =8,在Rt △ABD 中,4sin 545AD AB B =⋅=⨯=, 在Rt △ACD 中,2245AC AD CD =+=,∴5sin 5AD C AC ==. 例题6、 如图,在菱形ABCD 中,对角线AC 与BD 相交于点O ,过点D 作DE ⊥BD 交BC 的延长线于点E . (1)求证:四边形ACED 是平行四边形; (2)若BD =4,AC =3,求cos ∠CDE 的值.【答案】 (1)见解析 (2)35【解析】 (1)∵四边形ABCD 是菱形∴AD ∥BC ,∠BOC =90°,∵DE ⊥BD ,∴∠BDE =90°,∴∠BDE =∠BOC ,∴AC ∥DE ,∴四边形ACED 是平行四边形;(2)解:∵四边形ACED 是平行四边形,∴AD =CE ,∵AD =BC ,∴BC =CE ,∵∠BDE =90°,∴DC =CE ,∴∠CDE =∠E ∴cos ∠CDE =cos ∠E ,∵BD =4,AC =3,∠BDE =90°,∴BE =5,∴3cos 5DE E BE ∠==,∴3cos cos 5CDE E ∠=∠=.随练1、 在Rt ABC △中,90C ∠=︒,若1BC =,2AC =,则sin A 的值为( ) A.55B.255C.12D.2【答案】 A【解析】 该题考查的是解直角三角形.在Rt △ABC ,sin BC A AB=,根据勾股定理,2222125AB AC BC =+=+=,则15sin 55BC A AB ===随练2、 如图所示,菱形ABCD 的周长为20cm ,DE⊥AB ,垂足为E ,sinA=35,则下列结论正确的个数有( )⊥DE=3cm ;⊥BE=1cm ;⊥菱形的面积为15cm 2;⊥BD=210cm . A.1个 B.2个 C.3个 D.4个【答案】 C【解析】 此题主要考查学生对菱形的性质的运用能力. ⊥菱形ABCD 的周长为20cm ⊥AD=5cm ⊥sinA=DE AD =35⊥DE=3cm (⊥正确) ⊥AE=4cm ⊥AB=5cm⊥BE=5-4=1cm (⊥正确)⊥菱形的面积=AB×DE=5×3=15cm 2(⊥正确) ⊥DE=3cm ,BE=1cm⊥BD=10cm (⊥不正确) 所以正确的有三个,故选C .随练3、 已知:如图,线段AB 、DE 表示一个斜靠在墙上的梯子的两个不同的位置,若CB =3m ,∠ABC =45°,要使∠EDC =60°,则需BD =__________m .【答案】 3322-【解析】 该题考查的是特殊直角三角形.△ABC 是等腰直角三角形;△EDC 是含30°的直角三角形, ∵3CB =,∴22223332AB ED CB AC ==+=+=,113332222CD ED ==⨯=,∴3332BD BC CD =-=-.随练4、 如图,将Rt △ABC 沿斜边AC 所在直线翻折后点B 落到点D ,过点D 作DE ⊥AB ,垂足为E ,如果AE=3EB ,EB=7,那么BC=_____________.【答案】 47【解析】 ∵DE ⊥AB ,∠B=90°,∴DE ∥BC , ∴∠1=∠3, ∵∠1=∠2, ∴∠2=∠3, ∴DH=DC , ∵DE ∥BC ,∴△AEH ∽△ABC , ∴34AE EH AB BC ==, 设EH=3x ,BC=DC=DH=4x , ∴DE=7x ,∵AE=3EB ,EB=7, ∴AE=21,∵AD=AB=AE+BE=7+21=28,在Rt △ADE 中,DE=2222282177AD AE -=-=, ∴7x=77, ∴x=7, ∴BC=47.随练5、 Rt △ABC 中,∠C =90°,如果AC =9,cosA =13,那么AB =________.【答案】 27 【解析】 如图.∵在Rt △ABC 中,∠C =90°,AC =9,cosA =13AC AB =,∴913AB =, ∴AB =27.随练6、 如图,四边形ABCD 、CDEF 、EFGH 都是正方形,则tan ∠CAF =________.【答案】13【解析】 连接AG ,设正方形的边长为a ,222AC a a a =+=,∵22==AC aCF a ,222CG a AC a==, ∴AC CG CF AC=, ∵∠ACF =∠ACF , ∴△ACF ∽△GCA , ∴∠AGB =∠CAF ,∴1tan tan 33AB a CAF AGB BG a ∠=∠===.随练7、 在Rt △ABC 中,∠C =90°,AB =8,3cos 4A =.求BC 的长. 【答案】 27 【解析】 ∵3cos 4AC A AB ==,AB =8, ∴AC =6,根据勾股定理得,22228627BC AB AC =-=-=.随练8、 如图,在Rt⊥ABC 中,⊥C=90°,⊥A 的平分线交BC 于点E ,EF⊥AB 于点F ,点F 恰好是AB 的一个三(1)求证:⊥ACE⊥⊥AFE ; (2)求tan⊥CAE 的值.【答案】 (1)见解析(2)55【解析】 本题考查了直角三角形的判定、性质和利用三角函数解直角三角形,根据已知条件表示出线段的值是解本题的关键.(1)根据角的平分线的性质可求得CE=EF ,然后根据直角三角形的判定定理求得三角形全等.(2)由⊥ACE⊥⊥AFE ,得出AC=AF ,CE=EF ,设BF=m ,则AC=2m ,AF=2m ,AB=3m ,根据勾股定理可求得,tan⊥B=AC BC =25,CE=EF=2m 5,在RT⊥ACE 中,tan⊥CAE=CEAC =2m52m =55;(1)证明:⊥AE 是⊥BAC 的平分线,EC⊥AC ,EF⊥AF ,⊥CE=EF ,在Rt⊥ACE 与Rt⊥AFE 中, CE EFAE AE=⎧⎨=⎩, ⊥Rt⊥ACE⊥Rt⊥AFE (HL );(2)由(1)可知⊥ACE⊥⊥AFE , ⊥AC=AF ,CE=EF ,设BF=m ,则AC=2m ,AF=2m ,AB=3m , ⊥BC=22AB AC -=229m 4m -=5m , 解法一:⊥⊥C=⊥EFB=90°, ⊥⊥EFB⊥⊥ACB , ⊥EF AC =FB BC,⊥CE=EF ,⊥CEAC =m 5m =55; 解法二:⊥在RT⊥ABC 中,tan⊥B=AC BC =2m5m=25, 在RT⊥EFB 中,EF=BF•tan⊥B=2m 5,⊥CE=EF=2m 5,在RT⊥ACE 中,tan⊥CAE=CEAC =2m52m=55;⊥tan⊥CAE=55.锐角三角函数的实际应用知识精讲一.仰角和俯角在视线与水平线所成的角中,视线在水平线的上方是仰角;视线在水平线的下方是俯角,如图一所示.(上仰下俯)二.坡度与坡角坡度(坡比):坡面的铅直高度h 和水平宽度l 的比叫做坡度.用字母i 表示,tan hi lα== 坡角:坡面与水平面的夹角叫坡角.用字母α表示.三.方位角指南或指北方向线与目标方向线所成的小于90︒的角叫做方位角.四.用解直角三角形的知识解决实际问题的基本方法是:说明:解直角三角形的方法:有斜则弦,无斜则切,宁乘毋除,取原避中.五.用解直角三角形的知识解决实际问题的一般步骤:俯角仰角水平线视线视线铅垂线αlh实际问题实际问题的解数学问题(解直角三角形)数学问题的解抽象 (转化)解释求解 得到 得到1. 审题;通过图形,弄清已知和未知.2. 找出相关的直角三角形(或通过辅助线作出);把问题转化为解直角三角形问题.3. 根据直角三角形边、角关系解直角三角形.三点剖析一.考点:解直角三角形的应用二.重难点:把实际问题转化为解直角三角形三.易错点:1. 仰角和俯角理解错误;2. 检验答案是否符合实际情况.锐角三角函数的实际应用例题1、 河堤横断面如图所示,堤高BC=6米,迎水坡AB 的坡比为1:3,则AB 的长为( )A.12米B.43米C.53米D.63米【答案】 A【解析】 ∵BC=6米,迎水坡AB 的坡比为1:3, ∴AC=63(米), ∴AB=()22663+=12(米).故选A .例题2、 如图,在某监测点B 处望见一艘正在作业的渔船在南偏西15°方向的A 出,若渔船沿北偏西75°方向以60海里/小时的速度航行,航行半小时后到达C 处,在C 处观测到B 在C 的北偏东60°方向上,则B 、C 之间的距离为__________.【答案】 302海里【解析】 由题意得,AC=60×0.5=30海里, ∵CD ∥BF ,∴∠CBF=∠DCB=60°,又∠ABF=15°, ∴∠ABC=45°, ∵AE ∥BF ,∴∠EAB=∠FBA=15°,又∠EAC=75°, ∴∠CAB=90°,∴BC=2AC=302海里,例题3、 有一轮船在A 处测得南偏东30°方向上有一小岛P ,轮船沿正南方向航行至B 处,测得小岛P 在南偏东45°方向上,按原方向再航行10海里至C 处,测得小岛P 在正东方向上,则A ,B 之间的距离是( )海里.A.103B.102﹣10C.10D.103﹣10【答案】 D【解析】 由题意得:∠CAP=30°,∠CBP=45°,BC=10海里, 在Rt △BCP 中, ∵∠CBP=45°,∴CP=BC=10海里, 在Rt △APC 中,AC=10tan 33PC CAP =∠=103海里, ∴AB=AC ﹣BC=(103﹣10)海里,例题4、 某数学兴趣小组同学进行测量大树CD 高度的综合实践活动,如图,在点A 处测得直立于地面的大树顶端C 的仰角为36°,然后沿在同一剖面的斜坡AB 行走13米至坡顶B 处,然后再沿水平方向行走6米至大树脚底点D 处,斜面AB 的坡度(或坡比)i=1:2.4,那么大树CD 的高度约为(参考数据:sin36°≈0.59,cos36°≈0.81,tan36°≈0.73)( )A.8.1米B.17.2米C.19.7米D.25.5米【答案】 A【解析】 作BF ⊥AE 于F ,如图所示: 则FE=BD=6米,DE=BF , ∵斜面AB 的坡度i=1:2.4, ∴AF=2.4BF ,设BF=x 米,则AF=2.4x 米,在Rt △ABF 中,由勾股定理得:x 2+(2.4x )2=132, 解得:x=5,∴DE=BF=5米,AF=12米, ∴AE=AF+FE=18米,在Rt△ACE中,CE=AE•tan36°=18×0.73=13.14米,∴CD=CE﹣DE=13.14米﹣5米≈8.1米;例题5、如图,在一条笔直的东西向海岸线l上有一长为1.5km的码头MN和灯塔C,灯塔C距码头的东端N有20km.以轮船以36km/h的速度航行,上午10:00在A处测得灯塔C位于轮船的北偏西30°方向,上午10:40在B处测得灯塔C位于轮船的北偏东60°方向,且与灯塔C相距12km.(1)若轮船照此速度与航向航向,何时到达海岸线?(2)若轮船不改变航向,该轮船能否停靠在码头?请说明理由.(参考数据:≈1.4,≈1.7)【答案】(1)轮船照此速度与航向航向,上午11::00到达海岸线;(2)轮船不改变航向,轮船可以停靠在码头.【解析】(1)延长AB交海岸线l于点D,过点B作BE△海岸线l于点E,过点A作AF△l于F,如图所示.△△BEC=△AFC=90°,△EBC=60°,△CAF=30°,△△ECB=30°,△ACF=60°,△△BCA=90°,△BC=12,AB=36×=24,△AB=2BC,△△BAC=30°,△ABC=60°,△△ABC=△BDC+△BCD=60°,△△BDC=△BCD=30°,△BD=BC=12,△时间t==小时=20分钟,△轮船照此速度与航向航向,上午11::00到达海岸线.(2)△BD=BC,BE△CD,△DE=EC,在RT△BEC中,△BC=12,△BCE=30°,△BE=6,EC=6≈10.2,△CD=20.4,△20<20.4<21.5,△轮船不改变航向,轮船可以停靠在码头.随练1、如图,已知楼高AB为50m,铁塔基与楼房房基间的水平距离BD为50m,塔高DC为1505033m,下列结论中,正确的是()A.由楼顶望塔顶仰角为60︒B.由楼顶望塔基俯角为60︒C.由楼顶望塔顶仰角为30︒D.由楼顶望塔基俯角为30︒【答案】C【解析】过点A作水平线AE,则EAD∠为楼顶望塔基俯角,CAE∠为由楼顶望塔顶仰角.50AB=,∴50DE=.∴1505035035033CE CD ED+=-=-=∴3tan::3CAE CE AE CE BD∠===.∴30CAE∠=︒.tan:50:1EAD DE AE BD∠===∴45EAD∠=.随练2、如图,小明在大楼30米高(即PH=30米)的窗口P处进行观测,测得山坡上A处的俯角为15°,山脚B 处的俯角为60°,巳知该山坡的坡度i(即tan△ABC)为1:,点P,H,B,C,A在同一个平面上,点H、B、C在同一条直线上,且PH丄HC.(1)山坡坡角(即△ABC)的度数等于度;(2)求A、B两点间的距离(结果精确到0.1米,参考数据:≈1.732).【答案】(1)30;(2)34.6米【解析】(1)30;(2)由题意得:△PBH=60°,△△ABC=30°,△△ABP=90°,又△APB=45°,△△PAB为等腰直角三角形,在直角△PHB中,PB===20.在直角△PBA中,AB=PB=20≈34.6米.答:A,B两点间的距离是34.6米.随练3、为测量操场上旗杆的高度,小丽同学想到了物理学中平面镜成像的原理,她拿出随身携带的镜子和卷尺,先将镜子放在脚下的地面上,然后后退,直到她站直身子刚好能从镜子里看到旗杆的顶端E,标记好脚掌中心位置为B,测得脚掌中心位置B到镜面中心C的距离是50cm,镜面中心C距离旗杆底部D的距离为4m,如图所示.已知小丽同学的身高是1.54m,眼睛位置A距离小丽头顶的距离是4cm,则旗杆DE的高度等于()DCBAA.10mB.12mC.12.4mD.12.32m【答案】 B 【解析】 由题意可得:AB=1.5m ,BC=0.4m ,DC=4m ,△ABC ∽△EDC , 则=AB BC ED DC, 即1.50.54=DE , 解得:DE=12,随练4、 如图,活动课上,小王想要利用所学的数学知识测量某个建筑地所在山坡AE 的高度,她先在山脚下的点E 处测得山顶A 的仰角是30°,然后,她沿着坡度i=1:1的斜坡步行15分钟到达C 处,此时,测得点A 的俯角是15°.已知小王的步行速度是20米/分,图中点A 、B 、E 、D 、C 在同一平面内,且点D 、E 、B 在同一水平直线上,求出建筑地所在山坡AE 的高度AB .(精确到0.1米,参考数据:≈1.41).【答案】 105.8(米).【解析】 作EF △AC 于点F ,根据题意,CE=20×15=300米,△i=1:1,△tan △CED=1,△△CED=△DCE=45°,△△ECF=90°﹣45°﹣15°=30°,△EF=CE=150米,△△CEF=60°,△AEB=30°,△△AEF=180°﹣45°﹣60°﹣30°=45°,△AF=EF=150米,△AE===150(米),△AB=×150≈105.8(米). 答:建筑地所在山坡AE 的高度AB 约为105.8米随练5、 南海是我国的南大门,如图所示,某天我国一艘海监执法船在南海海域正在进行常态化巡航,在A 处测得北偏东30°方向上,距离为20海里的B 处有一艘不明身份的船只正在向正东方向航行,便迅速沿北偏东75°的方向前往监视巡查,经过一段时间后,在C 处成功拦截不明船只,问我海监执法船在前往监视巡查的过程中行驶了多少海里(最后结果保留整数)?(参考数据:cos75°=0.2588,sin75°=0.9659,tan75°=3.732,=1.732,=1.414)【答案】 67海里【解析】 过B 作BD △AC ,△△BAC=75°﹣30°=45°,△在Rt △ABD 中,△BAD=△ABD=45°,△ADB=90°,由勾股定理得:BD=AD=×20=10(海里),在Rt △BCD 中,△C=15°,△CBD=75°,△tan △CBD=,即CD=10×3.732=52.77048,则AC=AD+DC=10+10×3.732=66.91048≈67(海里),即我海监执法船在前往监视巡查的过程中行驶了67海里.拓展1、 在Rt △ABC 中,∠C =90°,AB =4,AC =1,那么∠B 的余弦值为( )A.154B.14C.1515D.41717【答案】 A【解析】 解;由勾股定理得22224115BC AB AC =-=-=,15cos 4BC B AB ∠==.2、 如图,在等腰直角三角形ABC 中,∠C=90°,D 为BC 的中点,将△ABC 折叠,使点A 与点D 重合,EF 为折痕,则sin ∠BED 的值是( )A.35B.34C.23D.57 【答案】 A【解析】 ∵△DEF 是△AEF 翻折而成,∴△DEF ≌△AEF ,∠A=∠EDF ,∵△ABC 是等腰直角三角形,∴∠EDF=45°,由三角形外角性质得∠CDF+45°=∠BED+45°,∴∠BED=∠CDF ,设CD=1,CF=x ,则CA=CB=2,∴DF=FA=2﹣x ,∴在Rt △CDF 中,由勾股定理得,CF 2+CD 2=DF 2,即x 2+1=(2﹣x )2,解得x=34,∴sin ∠BED=sin ∠CDF=35CFDF =.3、 如图,由四个全等的直角三角形围成的大正方形的面积是169,小正方形的面积为49,则sinα-cosα=()A.513B.513-C.713 D.713-【答案】 D【解析】 ∵小正方形面积为49,大正方形面积为169,∴小正方形的边长是7,大正方形的边长是13,在Rt △ABC 中,AC 2+BC 2=AB 2,即AC 2+(7+AC )2=132,整理得,AC 2+7AC -60=0,解得AC =5,AC =-12(舍去),∴2212BC AB AC =-=,∴5sin 13AC AB α==,12cos 13BC AB α==,∴5127sin cos 131313αα-=-=-.4、 如图,将一副三角板按图中方式叠放,4BC =,那么BD =__________【答案】 26【解析】 该题考查的是三角形的性质.根据题得,90CAB ABD ∠=∠=︒,45C ABC ∠=∠=︒,30D ∠=︒,∵4BC =,∴2222AB BC ==, ∴326BD AB ==. 5、 在△ABC 中,∠C=90°,cosA=35,则tanA 等于_________.【答案】 43【解析】 ∵cosA=35知,设b=3x ,则c=5x ,根据a 2+b 2=c 2得a=4x .∴tanA=a b =4x 3x =43. 6、 在Rt △ABC 中,∠ACB =90°,点D 在边AC 上,DE ⊥AB 于点E ,连CE .(1)如图1,已知AC =BC ,AD =2CD ,①△ADE 与△ABC 面积之比;②求tan ∠ECB 的值;(2)如图2,已知BC AD k AC DC==,求tan ∠ECB 的值(用含k 的代数式表示). 【答案】 (1)①29;②2 (2)3221tan k k ECB k++∠= 【解析】 (1)①作EH ⊥AD 于H ,如图1,设CD =x ,则AD =2x ,AC =BC =3x ,∵AC =BC ,∠ACB =90°,∴△ACB 为等腰直角三角形,∴∠A =45°,而DE ⊥AB ,∴△ADE 为等腰直角三角形,∴AH =HD =HE =x ,∴2122ADE S x x x ==△, ∵2193322ACB S x x x ==△, ∴222992ADE ACB S x S x ==△△; ②在Rt △CHE 中,2tan 2CH x HEC HE x∠===, ∵HE ∥BC ,∴∠BCE =∠HEC ,∴tan ∠ECB =2;(2)作EH ⊥AD 于H ,如图2,设CD =a ,∵BC AD k AC DC==, ∴AD =ak ,BC =kAC ,∴AC =(k +1)a ,∴BC =(k 2+k )a , ∴222222(1)()(1)1AB k a k k a k k a =+++=++,∵DE ⊥AE ,∴∠AED =90°,∵∠DAE =∠BAC ,∴△ADE ∽△ABC ,∴AD AE AB AC =,即2(1)(1)1ak AE k a k k a =+++,解得21ak AE k =+, ∵HE ∥BC ,∴△AHE ∽△ACB ,∴AH HE AE AC BC AB==,即2221(1)()(1)1akAH HE k k a k k a k k a +==++++, ∴21ak AH k =+,221k a HE k =+, ∴32221(1)11ak k k CH AC AH k a a k k ++=-=+-=++, ∴32322222111tan 1k k a CH k k k HEC k a HE k k +++++∠===+, ∵HE ∥BC ,∴∠BCE =∠HEC ,∴3221tan k k ECB k ++∠=.7、 如图,某无人机于空中A 处探测到目标B ,D ,从无人机A 上看目标B ,D 的俯角分别为30°,60°,此时无人机的飞行高度AC 为60m ,随后无人机从A 处继续飞行30m 到达A′处,(1)求A ,B 之间的距离;(2)求从无人机A′上看目标D 的俯角的正切值.【答案】 (1)120(m );(2) .【解析】 (1)由题意得:△ABD=30°,△ADC=60°,在Rt△ABC 中,AC=60m ,△AB===120(m );(2)过A′作A′E△BC交BC的延长线于E,连接A′D,则A′E=AC=60,CE=AA′=30,在Rt△ABC中,AC=60m,△ADC=60°,△DC=AC=20,△DE=50,△tan△AA′D=tan△A′DC===.答:从无人机A′上看目标D的俯角的正切值是.8、如图所示,某办公大楼正前方有一根高度是15米的旗杆ED,从办公楼顶端A测得旗杆顶端E的俯角α是45°,旗杆底端D到大楼前梯坎底边的距离DC是20米,梯坎坡长BC是12米,梯坎坡度i=1:,则大楼AB的高度约为()(精确到0.1米,参考数据:≈1.41,≈1.73,≈2.45)A.30.6B.32.1C.37.9D.39.4【答案】D【解析】延长AB交DC于H,作EG⊥AB于G,如图所示:则GH=DE=15米,EG=DH,∵梯坎坡度i=1:,∴BH:CH=1:,设BH=x米,则CH=x米,在Rt△BCH中,BC=12米,由勾股定理得:x2+(x)2=122,解得:x=6,∴BH=6米,CH=6米,∴BG=GH﹣BH=15﹣6=9(米),EG=DH=CH+CD=6+20(米),∵∠α=45°,∴∠EAG=90°﹣45°=45°,∴△AEG是等腰直角三角形,∴AG=EG=6+20(米),∴AB=AG+BG=6+20+9≈39.4(米);9、在某飞机场东西方向的地面l上有一长为1km的飞机跑道MN(如图),在跑道MN的正西端14.5千米处有一观察站A.某时刻测得一架匀速直线降落的飞机位于点A的北偏西30°,且与点A相距15千米的B处;经过1分钟,又测得该飞机位于点A 的北偏东60°,且与点A 相距53千米的C 处. (1)该飞机航行的速度是多少千米/小时?(结果保留根号)(2)如果该飞机不改变航向继续航行,那么飞机能否降落在跑道MN 之间?请说明理由.【答案】 (1)6003(2)可以落在跑道MN 之间,理由见解析【解析】 (1)由题意,得∠BAC=90°,∴BC=()221553+=103,∴飞机航行的速度为:103×60=6003(km/h );(2)能;作CE ⊥l 于点E ,设直线BC 交l 于点F .在Rt △ABC 中,AC=53,BC=103,∴∠ABC=30°,即∠BCA=60°,又∵∠CAE=30°,∠ACE=∠FCE=60°,∴CE=AC•sin ∠CAE=532,AE=AC•cos ∠CAE=152.则AF=2AE=15(km ),∴AN=AM+MN=14.5+1=15.5km ,∵AM <AF <AN ,∴飞机不改变航向继续航行,可以落在跑道MN 之间.。
北师大版数学九年级下册:第一章《直角三角形的边角关系》知识点整理复习

直角三角形的边角关系知识点复习考点一、锐角三角函数的概念如图,在△ABC 中,∠C=90°正弦:_____sin =∠=斜边的对边A A 余弦:____cos =∠=斜边的邻边A A 正切:_____tan =∠∠=的邻边的对边A A A三角函数 30°45°60°sin α cos α tan α考点三、各锐角三角函数之间的关系(1)互余关系:sinA=cos(90°—A),cosA=sin(90°—A) ; (2)平方关系:1cos sin 22=+A A (3)倒数关系:tanA •tan(90°—A)=1 (4)商的关系:tanA=AAcos sin 考点四、锐角三角函数的增减性当角度在0°~90°之间变化时,(1) 正弦值随着角度的增大而_______;(2) 余弦值随着角度的增大而_______;(3) 正切值随着角度的增大而___________; 考点五、解直角三角形 1、解直角三角形的概念在直角三角形中,除直角外,一共有五个元素,即三条边和两个锐角,由直角三角形中除直角外的已知元素求出所有未知元素的过程叫做解直角三角形。
2、解直角三角形的理论依据在Rt △ABC 中,∠C=90°,∠A ,∠B ,∠C 所对的边分别为a ,b ,c (1)三边之间的关系:______________________(勾股定理) (2)锐角之间的关系:______________________(3)边角之间的关系:正弦sinA=___________,余弦cosA=____________,正切tanA=______________ (4) 面积公式:c ch ab s 2121==(h c 为c 边上的高) 考点六、解直角三角形应用1、将实际问题转化到直角三角形中,用锐角三角函数、代数和几何知识综合求解2、仰角、俯角、坡面 知识点及应用举例:(1)仰角:视线在水平线上方的角;俯角:视线在水平线下方的角。
北师大九年级数学下册知识点总结

图 1图 3图4新北师大版九年级数学下册知识点总结第一章 直角三角形边的关系一.锐角三角函数 1.正切:叫做∠A 的正切..,记作tanA ,定义:在Rt△ABC 中,锐角∠A 的对边与邻边的比即的邻边的对边A A A ∠∠=tan ;①tanA 是一个完整的符号,它表示∠A 的正切,记号里习惯省去角的符号“∠”; ②tanA 没有单位,它表示一个比值,即直角三角形中∠A 的对边与邻边的比; ③tanA 不表示“tan”乘以“A”;④初中阶段,我们只学习直角三角形中,∠A 是锐角的正切;⑤tanA 的值越大,梯子越陡,∠A 越大;∠A 越大,梯子越陡,tanA 的值越大。
2.正弦..: 定义:在Rt△ABC 中,锐角∠A 的对边与斜边的比叫做∠A 的正弦,记作sinA ,即斜边的对边A A ∠=sin ;3.余弦:定义:在Rt△ABC 中,锐角∠A 的邻边与斜边的比叫做∠A 的余弦,记作cosA ,即斜边的邻边A A ∠=cos ;锐角A 的正弦、余弦和正切都是∠A 的三角函数当锐角A 变化时,相应的正弦、余弦和正切之也随之变化。
二.特殊角的三角函数值 三.三角函数的计算1. 仰角:当从低处观测高处的目标时,视线与水平线所成的锐角称为仰角..2. 俯角:当从高处观测低处的目标时,视线与水平线所成的锐角称为俯角..3.规律:利用特殊角的三角函数值表,可以看出,(1)当角度在0°~90°间变化时,正弦值、正切值随着角度的增大(或减小)而增大(或减小);余弦值随着角度的增大(或减小)而减小(或增大)。
(2)0≤sin α≤1,0≤cos α≤1。
4.坡度:如图2,坡面与水平面的夹角叫做坡角坡角的正切称为坡度........... (或坡比..)。
用字母i 表示,即A lhi tan == 5.方位角:从某点的指北方向按顺时针转到目标方向的水平角,叫做方位角...。
如图3,OA 、OB 、OC 的方位角分别为45°、135°、225°。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
北师大版九年级数学
初三下学期锐角三角函数知识点总结及典型习题
知识点:
1、本章三角函数源自于勾股定理:直角三角形两直角边a 、b 的平方和等于斜边c
(勾股定理也叫毕达哥拉斯定理,在部分课外资料/习题当中会出现毕达哥拉斯定理) 2、如下图,在Rt △ABC 中,∠C 为直角,则∠A 的锐角三角函数为(∠A 可换成∠B):
34
6、正弦、余弦的增减性:
当0°≤α≤90°时,sin α随α的增大而增大,cos α随α的增大而减小。
7、正切、的增减性:
当0°<α<90°时,tan α随α的增大而增大,
解直角三角形的定义
1、:已知边和角(两个,其中必有一边)→所有未知的边和角。
依据:①边的关系:222c b a =+;②角的关系:A+B=90°;③边角关系:三角函数的定义。
(注意:尽量避免使用中间数据和除法)
2、应用举例:
(1)仰角:视线在水平线上方的角;俯角:视线在水平线下方的角。
仰角水平线
视线
视线俯角
(2)坡面的铅直高度h 和水平宽度l 的比叫做坡度(坡比)。
用字母i 表示,即h i l
=。
坡度一般写成1:m 的形式,如1:5i =等。
把坡面与水平面的夹角记作α(叫做坡角),那么tan h
i l
α=
=。
3、从某点的指北方向按顺时针转到目标方向的水平角,叫做方位角。
如图 ,OA 、OB 、OC 、OD 的方向角分别是:45°、135°、225°。
指北或指南方向线与目标方向 线所成的小于90°的水平角,叫做方向角。
所以,OA 、OB 、OC 、OD 的方向角分别是:
北偏东30°(东北方向) , 南偏东45°(东南方向), 南偏西60°(西南方向), 北偏西60°(西北方向)。
例1:已知在Rt ABC △中,3
90sin 5
C A ∠==°,,则tan B 的值为( )
A .43
B .45
C .54
D .
34
【解析】本题考查三角函数的定义和勾股定理,在RT ΔABC 中,∠C=90°,则sin a A c =
,tan b
B a
=和222a b c +=;由3sin 5A =知,如果设3a x =,则5c x =,结合222a b c +=得4b x =;∴44
tan 33
b x B a x ===,
所以选A .
:i h l =h
l
α
例2
:104cos30sin 60(2)2008)-︒︒+--=______.
【解析】本题考查特殊角的三角函数值.零指数幂.负整数指数幂的有关运算,
104cos30sin 60(2)2008)-︒︒+--
=13412222
⎛⎫⨯
⨯+--= ⎪⎝⎭, 故填3
2.
1.
A .8米
2. 一架5A .5sin 40°
3. 线,∠ABC 是( ) A C .
4. 铅直高度BC A . 米C .15米 D .
5.如图,在矩形ABCD 中,DE ⊥AC 于E ,∠EDC ∶∠EDA=1∶3,且AC=10,则DE 的长度是( ) A .3 B .5 C .25 D .2
2
5
6. 如图所示,小明在家里楼顶上的点A 处,测量建在与小明家楼房同一水平线上相邻的电梯楼的高,在点A 处看电梯楼顶部点B 处的仰角为60°,在点A 处看这栋电梯楼底部点C 处的俯角为45°,两栋楼之间的距离为30m ,则电梯楼的高BC 为 米(精确到0.1). (参考数据:2 1.414≈ 3 1.732≈)
7. 如图,热气球的探测器显示,从热气球A 看一栋大楼顶部B 的俯角为30°,看这栋大楼底部C 的俯角为60°,热气球A 的高度为240米,求这栋大楼的高度.
解:过点A 作直线BC 的垂线,垂足为点D .
则90CDA ∠=°,60CAD ∠=°,30BAD ∠=°,CD =240米.
在Rt ACD △中,tan CD
CAD AD
∠=, 240
80 3.tan 603
CD AD ∴=
==°
在Rt ABD △中,tan BD
BAD AD
∠=
, 3
tan 30803803
BD AD ∴==⨯
=·°. ∴BC CD BD =-=240-80=160. 答:这栋大楼的高为160米.
B
C
8. 如图所示,城关幼儿园为加强安全管理,决定将园内的滑滑板的倾斜角由45°降为30°,已知原滑滑板AB 的长为4米,点D 、B 、C 在同一水平面上.
(1)改善后滑滑板会加长多少米?
(2)若滑滑板的正前方能有3米长的空地就能保证安全,原滑滑板的前方有6米长的空地,像这样改造是否可行?请说明理由.
(参考数据:141.12=,732.13=,449.26=,以上结果均保留到小数点后两位.)
解:(1)在Rt △ABC 中,∠ABC=45°
∴AC=BC=AB ·sin45°=222
2
4=⨯
在Rt △ADC 中,∠ADC=30°
∴AD= 2421
2230sin =÷=o
AC
∴AD-AB=66.1424≈-
∴改善后滑滑板会加长约1.66米.
(2)这样改造能行,理由如下: ∵989.46233
2230
tan ≈=÷==
o
AC CD ∴07.22262≈-=-=BC CD BD ∴6-2.07≈3.93>3
∴这样改造能行.
练一练
9.求值1
01|32|20093tan 303-⎛⎫
-+--+ ⎪⎝⎭°
2009
12sin 603tan 30(1)3⎛⎫
-++- ⎪⎝⎭°°
原式=. 解:原式=。
