2020年对口高职高考数学模拟试卷
2020年职业教育对口数学模拟试题(带答案)

机密★启用前山东省高等职业教育对口招生数学模拟试题注意事项:1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.满分100分,考试时间90分钟.考试结束后,将本试卷和答题卡一并交回.2.本次考试允许使用函数型计算器,凡使用计算器的题目,最后结果精确到0.01.第Ⅰ卷(选择题,共60分)一、选择题(本大题共30小题,每小题2分,共60分.在每小题列出的四个选项中,只有一项符合题目要求,请将符合题目要求的选项选出)1.已知集合A={ x 1≤x≤4},B={ x x- a>0}, 若A ⊆ B,则实数a的取值范围为()(A) (1,+∞) (B) (-∞,1)(C) [1,+∞) (D) (-∞,1]2.已知方程x2 +a x+ (a+3)=0有实根,则a的取值范围()(A) {a|a>6或a<- 2} (B) {a| -2≤a ≤6}(C) {a|a≥6或a≤- 2} (D) {a| -2< a < 6}3. 已知圆的方程为22-+-=,则点(1,2)(3)(5)16x y-().(A)在圆内(B)在圆上(C)在圆外(D)与圆心重合4.函数y=f (x) 的图象与直线x=k (k 是常数)的交点的个数()(A) 有且只有一个(B) 至少有一个(C) 至多有一个(D) 有一个或两个5.若x > y > 0, 0 < a < 1, 则下列各式成立的是()(A) a x≤a y(B) log a x < log a y(C) a x ≥a y(D) log a x > log a y6. 设a , b是实数,则a2+b2 ≠ 0的充要条件是()(A) a ≠ 0 (B) b ≠ 0 (C) a ≠ 0且b ≠ 0 (D) a ≠ 0或b ≠ 0 7.二次函数 y =x 2+px +q 的顶点在第二象限, 则p 和q 的符号是( )(A) p > 0, q >0 (B) p > 0, q < 0 (C) p < 0, q < (D) p < 0, q > 0 8.在数列3,4,7,12,x ,28, … 中,x 的值是( ).(A ) 18 (B ) 19 (C ) 20 (D ) 21 9. 过点()1,0且平行于y 轴的直线方程是( ).(A )1y = (B ) 1y =- (C )1x = (D ) 1x =-10.在四边形ABCD 中,若→A B = 2→a ,→C D = - 3 →a , ∣→A D ∣=∣→B C ∣ , 则 四边形ABCD 是( ) (A) 平行四边形 (B)菱形 (C) 等腰梯形 (D) 矩形 11.函数y =3 sin (ω x + π3 )(ω > 0)的最小正周期为π3, 则ω等于( )(A) 3 (B) 6 (C) 52(D) 912. 若平面α∥平面β,P 是平面α、β外一点,过P 的两条直线AB 、CD 交平面α于A 、C ,交平面β于B 、D ,且P A =6,AB =2,BD =12,则AC 的长是( ). (A ) 10 (B ) 9 (C ) 8 (D ) 713. 若双曲线的焦点在x 轴上,并且6a =、2b =,则双曲线的标准方程为( ). (A) 221364x y -= (B ) 221436x y -= (C ) 22162x y -= (D ) 22126x y -=14. 某数学兴趣小组成员的数学中考成绩如下:116 99 108 93 100 111 98 95 106 113 若102分以上(包括102)为优秀, 则优秀率为( ).(A ) 0.30 (B ) 0.40 (C ) 0.50 (D ) 0.60 15.0.3()log (2)f x x =,若()0f a =,则实数a 的值是( ).(A )16 (B ) 1 (C ) 0 (D ) 1216. 抛甲、乙两粒骰子,甲骰子点数不小于乙骰子点数的概率是( ). (A )512 (B ) 12 (C ) 712 (D ) 2317. 若椭圆的方程为224312x y +=,则它的焦点坐标为( ). (A ) ()()1,01,0-、 (B ) ()()0,10,1-、(C ) ((0,、 (D ))()、18.有四条线段,长度分别是2cm ,3cm ,4cm ,5cm ,从中任取两条, 长度之和不小于8cm 的概率是( ).(A) 14(B) 12(C) 13(D) 119.不等式 | 3- 2x | ≥ 5 的解集是( )(A) [-1, 4 ] (B) (- ∞, - 1]∪[ 4,+∞) (C) (- ∞, - 4)∪[ 1,+∞) (D) [- 4, 1]20.已知f (x )是奇函数,且x ≥ 0时,f (x )= 2x -x 2,则当x < 0时,f (x ) 的解析式为( )(A) f (x ) = x 2+2x (B) f (x ) = - x 2- 2x (C) f (x ) = x 2- 2x (D) f (x ) = - x 2+2x 21.设函数log ()4a x f x =,且1(16)2f =,则a 的值为( ). (A ) 4 (B ) 8 (C )18(D ) 1422.已知∣→a ∣= 4,→b 在 →a 方向上的射影的数量为- 3,则 →a ·→b =( ) (A) - 12 (B) - 7 (C) - 34 (D) 3423. 若抛物线的焦点在x 轴正半轴上,焦点到准线的距离是12,则它的 标准方程是( ).(A ) 2y x =- (B ) 2y x = (C ) 2x y =- (D ) 2x y = 24.5人参加4项比赛,每人限报一项,报名方法有( )(A) 45 (B) 54 (C) 20 (D) 25 25.函数y = 2sin 2x +4sin x +2 的最大值和最小值分别为( )(A) 6, 0 (B) 6, - 1 (C) 8, 0 (D) 8, - 1 26.等差数列前10项和1060S =,则110a a +等于( ).(A )10 (B ) 11 (C ) 12 (D ) 13 27. 函数()f x 在()5,5-上是增函数,下列选项错误的是( ).(A ) (2)(0)f f ->(B ) (1)(1)f f -< (C ) (2)(3)f f < (D ) (0)(4)f f < 28.△ABC 中:AB =10,S △= 160, 则边AC 的最小值为( )(A) 32 (B) 16 (C) 8 (D) 16 3 29.函数22y x x =+与22y x x =-的图像( ).(A ) 关于x 轴对称 (B ) 关于y 轴对称(C ) 关于原点对称 (D ) 关于x 轴和y 轴都不对称 30.在等比数列{a n }中,a 1+ a 2=30,a 3+ a 4=120,那么a 5+ a 6 =( ) (A) 210 (B) 240 (C) 480 (D) 700第Ⅱ卷(非选择题,共40分)二、填空题(本大题共4小题,每小题3分,共12分)31. 某超市大米3.5元/千克,现设x表示购买大米的重量(千克),y表示应付款数(元),将,x y 的函数关系用列表法表示为:32.若正四棱锥的体积为12,底面对角线的长为_____.33. 若圆的方程222230x y by b+--=,则圆心坐标为_______,半径为_______.34.已知t anα是方程x2-2x-3=0的一个根,且α是第一象限的角,则cosα·tanα= . 三、解答题(本大题共4小题,共28分)35. (7分)设二次函数的图象的顶点是(-2, 32)与x轴的两个交点之间的距离是6,求这个二次函数的解析式.36. (7分) 角α.37.(7分) 如图,正三棱柱ABC —A 1B 1C 1的底面边长为a ,在侧棱BB 1上取BD =2a,在侧棱CC 1上截取CE =a ,过A 、D 、E 作棱柱的截面,试证明截面ADE 与侧面ACC 1A 1垂直。
2020对口高职数学试卷
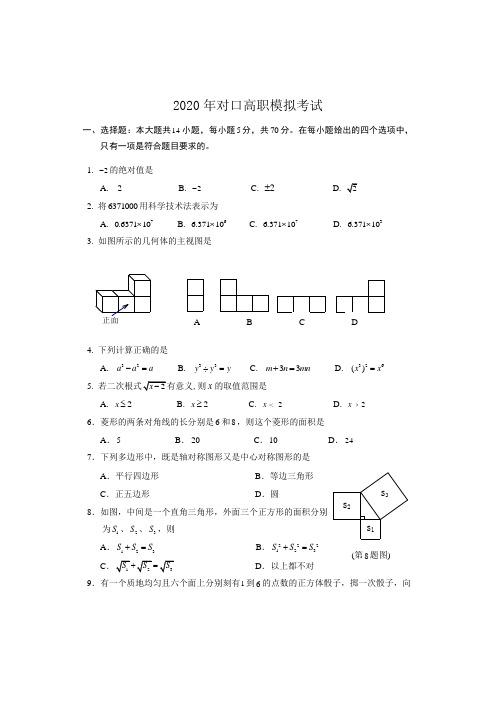
2020年对口高职模拟考试一、选择题:本大题共14小题,每小题5分,共70分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1. 2-的绝对值是A. 2B. 2-C. 2±D.2.将6371000用科学技术法表示为A. 70.637110⨯ B.66.37110⨯ C. 76.37110⨯ D. 36.37110⨯3.如图所示的几何体的主视图是4. 下列计算正确的是A.32a a a-=B.33y y y÷=C.33m n mn+=D.326()x x=5. ,则x的取值范围是A. 2x≤ B. 2x≥ C. x<2 D. x﹥26.菱形的两条对角线的长分别是6和8,则这个菱形的面积是A.5B.20C.10D.247.下列多边形中,既是轴对称图形又是中心对称图形的是A.平行四边形B.等边三角形C.正五边形D.圆8.如图,中间是一个直角三角形,外面三个正方形的面积分别为1S、2S、3S,则A.123S S S+=B.222123S S S+=C=D.以上都不对9.有一个质地均匀且六个面上分别刻有1到6的点数的正方体骰子,掷一次骰子,向正面S2S3S1上一面的点数为1的概率是A .0 B.C.D .110.母线长为5,底面半径长为3的圆锥的侧面积为A .12πB .15πC .24πD .30π 11.不等式1x -<0的解集在数轴上表示为A .B .C .D . 12.抛物线28y x =-+的顶点坐标是A .(0, 8)B .(8, 0)C .(0, 8)-D .(1-, 8) 13. 已知集合{}2,3,5,6A =,集合{}1,3,4,6,7B =,则集合AB =A . {}2,5B . {}3,6C . {}2,5,6D . {}1,2,3,4,5,6,7 14. 数据1,2-,3,4-,3的中位数和众数分别是A . 1, 3B . 2-, 3C . 3, 1D . 4-, 3 二、填空题:本大题共6小题,每小题5分,共30分。
2020年对口高职高考数学模拟试卷

2020年口高职高考数学模拟试卷一、 选择题1.集合P={1、2、3、4},Q={x ||x |≤2,x ∈R }则P ∩Q 等于( )A 、{1、2}B 、{3、4}C 、{1}D 、{-1、-2、0、1、2}2.数f(x)=√1+x 的定义域为( )A.[0,+∞) B (-1, +∞) C.(-∞,-1) D.R3.数y = 3 sinx + 4 cosx 的最小正周期为( )A. πB. 2πC. 2π D. 5π 4.数y = ㏒2(6-x-x 2)的单调递增区间是( )A.(-∞,- 21]B.( -3,-21)C. [-21,+∞)D. [-21,2) 5.等比数列{a n }中,a n >0,a 2a 4+2a 3a 5+a 4a 5=36那么a 3+a 5的值等于( )A.6B.12C.18D.246.函数y =log 3( x +x1) (x>1)的最大值是( ) A.-2 B.2 C.-3 D.37.直线L:4x+3y-12=0与两坐村轴围成三角形的面积是( )A.24B.12C.6D.188.函数f (x)=3cos 2x+21sin2x 的最大值为( ) A.1-23 B. 23+1 C. 23-1 D.1 9.在等差数列中,已知S 4=1 ,S 8=4则a 17 + a 18 + a 19+ a 20( )A.8B.9C.10D.1110.|a |=|b |是a 2=b 2的( )A 、充分条件而悲必要条件,B 、必要条件而非充分条件,C 、充要条件,D 、非充分条件也非必要条件11.在⊿ABC 中内角A,B 满足t anAtanB=1则⊿ABC 是( )A 、等边三角形,B 、钝角三角形,C 、非等边三角形,D 、直角三角形12.函数y=sin(43x +4π )的图象平移向量(- 3π,0)后,新图象对应的函数为y=( ) A.Sin 43x B.- Sin 43x c. Cos 43x D.-Cos 43x 13.顶点在原点,对换称轴是x 轴,焦点在直线3x-4y-12=0上的抛物线方程是( )A.y 2=16xB. y 2=12xC. y 2=-16xD. y 2=-12x第二部分 非选择题(共75分)二、 填空题(每小题5分,共25分)14.x 2-32y =1的两条渐近线的夹角是 . 15.若直线(m-2)x+2y-m+3=0的斜率等于2,则直线在轴上的截距2是 .16.等比数列{a n }中,前n 项和S n = 2 n + a 则a = .17.函数f(x)=log 24x+203,则f(1)= .18.函数y=2x-3+√13−4x 的值域 .三、解答题(21、22两小题各10分,23、24两小题各15分)21、解不等式:log 3( 3 +2x-x 2)> log 3( 3 x+1)22、设等差数列{a n }的公差是正数,且a 2a 6 = -12, a 3+a 5 = -4求前项20的和.23、如图所示若过点M (4,0)且斜率为-1的直线L 与抛物线C :y 2=2px(p>0),交于A 、B 两点,若OA ⊥OB求(1)直线L 的方程,(2)抛物线C 的方程,(3)⊿ABC 的面积24、B 船位于A 船正东26公里处,现A 、B 两船同时出发,A 船以每小时12公里的速度朝正北方向行驶,B 船以每小时5公里的速度朝正西方向行驶,那么何时两船相距最近,最近距离是多少。
2020年职业教育对口数学模拟试题3(带答案)

机密★启用前山东省高等职业教育对口招生数学模拟试题注意事项:1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.满分100分,考试时间90分钟.考试结束后,将本试卷和答题卡一并交回.2.本次考试允许使用函数型计算器,凡使用计算器的题目,最后结果精确到0.01.第Ⅰ卷(选择题,共60分)一、选择题(本大题共30小题,每小题2分,共60分.在每小题列出的四个选项中,只有一项符合题目要求,请将符合题目要求的选项选出)1.满足关系式M ⊆{1,2,3}的集合M的个数为()(A) 5个(B) 6个(C) 7个(D) 8个2.x= - 3且y = 2是(x+3)2 + (y-2)2 = 0的()(A) 充分不必要条件(B)必要不充分条件(C) 充要条件(D)既不充分也不必要条件3.设函数f (x) = 3x + 4 , g (x) = x+3 , 求f [g(x) ]=( )(A) 3x +13(B) 3x +9(C) 4x +7(D) 3x +74. 如果直线210Ax y--=和直线640x y C-+=平行,那么A、C应当().(A)3,2A C==-(B)3,2A C=≠-(C)3,2A C≠=-(D)3,2A C≠≠-5.若∣→A B∣= 8 ,∣→A C∣= 5 ,则∣→B C∣的取值范围是()(A) [ 3, 8 ] (B) ( 3, 8 )(C) [ 3, 13 ] (D) ( 3, 13 )6.已知α = - 2,则角α是第()象限角(A)一(B)二(C)三(D)四7. 若平面α∥平面β,直线l⊂α,,点B∈β,则在β内过点B的所有直线中(). (A)不一定存在与l平行的直线(B)只有两条与l平行的直线(C)存在无数多条与l平行的直线(D)存在唯一一条与l平行的直线8.已知0 < a < 1, log a m < log a n < 0 ,则下列式子正确的是( )(A) m > n > 1 (B) n > m > 1 (C) m < n < 1 (D) n < m < 19. 若椭圆标准方程为22154x y +=,则该椭圆的焦点坐标为( ). (A ) ()()3,03,0-、 (B ). ()()0,30,3-、 (C ) ()()1,01,0-、 (D )()()0,10,1-、10.三个数成等差数列,三个数之和为9,积为15,则这三个数为( ) (A) 1, 3, 5(B) 5,3,1(C) 1,3,5或5,3,1(D) -1,3,-511.据统计,某企业自1994年到2003年10年间年产值的增长率相同,若95年年产值为a 万元,98年年产值为b 万元,则2001年的年产值为( ) (A) a +b2 万元 (B) ab 万元(C) (2a – b )万元 (D) b 2a万元12.已知∣→a ∣= 1 ,∣→b ∣= 2,且(→a - →b )与 →a 垂直 ,则 →a 与 →b 的夹角 ( ) (A) 30° (B) 45° (C) 60° (D)135° 13.化简1+2cos 2θ- cos2θ 的结果为( ) (A) 1(B) 2 (C) 3 (D) 414. 求以(1,2)-的圆的方程为( ).(A )22(1)(2)x y -++= (B ) 22(1)(2)5x y -++=(C )22(1)(2)x y ++-= (D ) 22(1)(2)5x y ++-= 15.下列叙述错误的是( )(A) 若两个变量之间没有确定的函数关系,则这两个变量相关 (B) 正相关是两个变量相关关系中的一种(C) “庄家一枝花,全靠粪当家”说明农作物产量与施肥量之间具有相关关系 (D) 根据散点图可判断两个变量之间有无相关关系16.已知a > b , 且a , b 均不为零,则下列正确的是( )(A) 1a > 1b (B) 1a < 1b(C) 1a = 1b (D) 1a 和 1b 的大小不确定17.函数 y =log (x-1)(3 -x )的定义域是 ( )(A) (1, 3) (B) (1, 3] (C) (1, 2) ∪ (2, 3] (D) (1, 2) ∪ (2, 3)18.已知函数f (x ) 是偶函数,g (x )是奇函数,且在区间 [0, a ] (a>0) 上f (x ) 和g (x )都是增函数,则在[- a , 0 ] 上( )(A) f (x ) 和g (x )都是减函数 (B) f (x ) 是减函数, g (x ) 是增函数 (C) f (x ) 是增函数, g (x ) 是减函数 (D) f (x ) 和g (x )都是增函数19.若log 2 3 = a , log 2 5= b , 则log 2 95= ( )(A) a 2 - b (B) 2a - b(C) a 2b (D) 2a b20.某单位职工的工资经过5年翻了一番,按照相同的增长率,多少年后可以翻两番( ). (A ) 8 (B ) 9 (C ) 10 (D ) 12 21.数列{}n a 中,13a =,且1n a +与1na 是方程2320x x -+= 的根,则3S 为( ). (A ) 9 (B ) 9- (C ) 21- (D ) 21 22.在△ABC 中,a = 3,b = 4, 且a 2+b 2 =c 2+ a b , 则△ABC 的面积是( ) (A) 3 (B) 6 (C) 3 3 (D) 6 323. 若方程22111x y m m-=+-表示双曲线,则实数m 的取值范围是( )(A ) 1<<1m - (B ) >0m (C )m <0 (D) >1m 或<1m -24. 为了研究某班45名学生上学期数学期末考试成绩,特抽查了15名学生的成绩,下列说法错误的个数是( ). ① 全班学生是总体② 每名学生的数学期末考试成绩是个体 ③ 抽查的15名学生的数学成绩是样本 ④ 样本容量是45(A ) 1个 (B ) 2个 (C ) 3个 (D ) 4个 25.不等式 1 ≤ | 3x +4 | < 6 的解集为( )(A) {x | -1 ≤ x < 23 }(B) {x | - 103 < x ≤ - 53 或-1 ≤ x < 23 } (C) {x | - 103 < x ≤ - 53 } (D) {x |-103 ≤ x ≤ - 53 或-1 ≤ x ≤ 23} 26. 函数()g x 在(),-∞+∞上是增函数,且(0)25g =,下列选项正确的是( ) (A ) ()428g = (B ) ()225g ->(C ) ()1225g < (D ) 1()252g >27.若双曲线2212516x y -=上一点P 到双曲线一个焦点的距离是12,则P 点到另一个焦点的距离为( ).(A ) 2 (B ) 22 (C ) 5 (D ) 22或228. 有5件新产品,其中A 型产品3件,B 型产品2件,现从中任抽2件,它们都是A 型产品的概率是( ). (A )35(B ) 25 (C ) 310 (D ) 32029.工人月工资y (元)与劳动生产率x (千元)的回归直线方程为y =50+80x , 则下列判断不正确的是( )(A) 劳动生产率为1000元时,月工资为130元(B) 劳动生产率提高1000元时,则月工资平均提高80元 (C) 劳动生产率提高1000元,则月工资平均提高130元 (D) 当月工资为210元时,劳动生产率为2000元 30. 二次函数f (x )= x 2- 2x +4,x ∈[2,3]的最小值是( ) (A) 1 (B) 3(C) 4 (D) -6第Ⅱ卷(非选择题,共40分)二、填空题(本大题共4小题,每小题3分,共12分)31.函数()f x 用图像法表示为:则它的单调增区间是 .32.若正三棱锥底面边长为4,体积为1,则侧面和底面所成二面角的正切值为___________. 33.函数y =4 sin (2x - π3 )单调递减区间是 .34. 若直线230x y ++=与直线()22150x k y +--=()1k ≠±平行,则k 是 .三、解答题(本大题共4小题,共28分)35.(7分) 已知函数f (x )=x 2+2ax +3 求:(1)如果函数图象恒在x 轴上方,求a 的取值范围. (2) 如果f (a ) - f (a +1) = - 9 ,求a 的值.36.(7分) 某房地产公司在2010年对某户型推出两种售房方案:第一种是一次性付款方案,购房的优惠价为28.5万元;第二种是分期付款方案,要求购房时缴纳首付款10万元,然后从第二年起连续十年,在每年的购房日向银行付款2.25万元.假设在此期间银行存款的年利率为3%,若不考虑其他因素,试问:对于购房者来说,采用哪种方案省钱?请计算说明.37.(7分) 如图,三棱锥P—ABC中,△ABC是正三角形,∠PCA 90°,D为P A的中点,二面角P—AC—B为120°,判断AC与BD是否垂直,并说明理由.38.(7分)一条直线与抛物线y2=2px(p>0)交于A,B两点,O为坐标原点,若OA OB,并且OD⊥AB,垂足是D(2, -1).求抛物线的标准方程.答案一、选择题1.D 2.C 3.A 4.B 5.D 6.C 7.D 8.A 9.C 10.C 11.D 12.C 13.B 14.D 15.A 16.D 17.D 18.B 19.B 20.C 21.D 22.C 23.A24.B25.B26.D27.D28.C29.C30.C二、填空题31.(-2 , O] ∪[2,+∞) 32. 38 33.[5π12+k π, 11π12+k π] k ∈Z34.± 5三.解答35.解:(1) ƒ(x)=x 2+2ax +3的图象恒在x 轴上方∴△=4a 2-12<0∴a 2<3∴- 3 < a < 3 ∴a 的取值范围(- 3 , 3 )(2) 2849]3)1(22)1[(32229)1()(=∴-=-∴-=++++-++∴-=+-a a a a a a a a f a f36解:第一种方案,十年后付款的本息之和为:28.5×(1+0.03)10≈38.30(万元).第二种方案,还款结束时实际付款的本息之和为:10×(1+0.03)10+2.25×(1+0.03)9+2.25×(1+0.03)8+…+2.25 =10×1.0310+2.25×(1.0310-1)1.03-1≈39.23(万元). 因此对于购房者来说,采用第一种方案省钱. 37.解:过C 作CE ⊥AC 交AB 的延长线于E , 连结PE .则∠BCE = 30º ∠CBE =120º ∴∠BEC = 30º ∴BC =BE B 为AE 的中点。
中职对口升学资料-2020年高考数学模拟试卷-6份- 24

第二部分 数学(模拟题1)一、单项选择题.(每题5分,共8小题,共40分)1、设A ={a },则下列写法正确的是( )。
A .a =A B.a ∈A C. a ⊆A D.a ∉A2.函数f (x )=lg (1-x )的定义域为( )A .x ≠1B .{x |x ≠1 }C .(1,+∞)D .[1,+∞)3.如果函数f (x )=g (x )+2 ,已知g (2)=-2,那么f (2)=( )A .2B . 5C .4D .04.已知→a =(0,-2),→b =(-1,1),则→a ∙→b =( ) A .-2 B .0 C .-3 D .25.与角-450终边相同的角是 ( )A 、π45B 、-405ºC 、π47- D 、765º 6.已知直线l : 2x -y -1=0,那么这条直线的斜率和截距分别为( )A .2,1B .1,2C .2,-1D .-2,-17.下列命题中,正确的是( )A 、平面就是平行四边形 。
B 、过直线外一点有且只有一条直线与这条直线平行 。
C 、空间内不相交的两条直线一定是平行直线。
D 、垂直于同条直线的两条直线平行。
8. 书架上有语文、英语、数学、物理、化学共5本不同的书,现从中任抽一本,则没有抽到物理书的概率是( ).A .51B . 52C .53D .54 二、填空题(本大题共5小题,每题6分,共30分)9. 已知集合A ={小于4的自然数},B ={0,1},则A ∩B = ;10.函数y =1+3sin (2x +1)的最小正周期是 ;11.已知两直线l 1: x -y+2=0与l 2: x -y -1=0,则这两条直线的距离为 ;12.假设某人从甲地到乙地有8种不同的方法,从乙地到丙地有5种不同的方法,则从甲地到丙地一共有种方法;13.已知圆柱体的模具的底面半径为10cm,高15cm,现在在模具中间挖空一个半径为4cm,高为15cm的小圆柱体,问剩下的这个模具的体积为;三、解答题(本大题共2小题,共30分)14.已知数列为:1,2,4,7,11...,求这个数列的第12项。
2020年职业教育对口数学模拟试题5(带答案)

机密★启用前山东省高等职业教育对口招生数学模拟试题注意事项:1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.满分100分,考试时间90分钟.考试结束后,将本试卷和答题卡一并交回.2.本次考试允许使用函数型计算器,凡使用计算器的题目,最后结果精确到0.01.第Ⅰ卷(选择题,共60分)一、选择题(本大题共30小题,每小题2分,共60分.在每小题列出的四个选项中,只有一项符合题目要求,请将符合题目要求的选项选出) 1.设集合M ={a ,-1}, N ={0,1},且M ∩N ={1},则M ∪N =( )(A){a ,-1,0,1} (B){1,-1,0,1} (C) {-1,0,1} (D)不确定 2.已知m = a 2 + a -2, n = 2a 2 – a -1,其中a ∈ R ,则下列不等式成立的是( )(A) m > n (B) n > m (C) m ≥ n (D) n ≥ m3.已知:f (x ) = {-2x +1 (x >0)-x -3 (x <0),则f ( f (f (3) ) )等于 ( )(A) - 3 (B) 3 (C) - 9 (D) 94. 飞机着陆后滑行的距离S (米)与滑行的时间t (秒)之间的函数关系式为260 1.5S t t =-,则飞机着陆后滑行( )米才能停下来.(A ) 200 (B ) 300 (C ) 400 (D ) 600 5.函数y = ⎪ a - 1⎪ x 在(-∞,+∞)上单调递减,则a 的取值范围为( )(A) 0 < a < 2 (B) 0< a < 1 (C) 0 < a < 2 且a ≠1(D) 1 < a < 26. 等差数列{}n a 中,71-=a ,2=d ,则前8项的和为( ).(A ) 2- (B ) 0 (C ) 2 (D ) 7- 7.已知:→a = (5,2),→b = ( 6 ,y ), 且 →a ∥→b ,则y 的值等于( ) (A) 3 (B) 125(C)512 (D) - 1258.已知角α的终边经过点P(2, m ), 若sin α = - 45, 则m 的值为( )(A )- 83 (B ) 83 (C )± 83 (D )- 389.下列条件中,能判定平面α与平面β互相平行的是( ). (A ) α内有不在同一条直线上的三点与β的距离相等 (B ) α、β与同一条直线所成的角相等 (C ) α内有两条不平行的直线都与β平行 (D ) α、β与同一条直线的距离相等10.已知方程22ax ay b -=,且,a b 异号,则方程表示( ). (A ) 焦点在x 轴上的椭圆 (B ) 焦点在y 轴上的椭圆 (C ) 焦点在x 轴上的双曲线 (D ) 焦点在y 轴上的双曲线 11. 下列说法中错误的是( ).(A ) 2000年2月2日晚7:00中央电视台播放新闻联播节目时,电视台有关部门对全国100个城市2222个家庭进行调查,结果有1992户正在收看此节目,占89%,那么我们就可以说,全国所有的城市家庭中,此时收看新闻联播的收视率为89% (B ) 进行产品检验时,应采用随机抽样的方法(C ) 在统计中,要了解一块玉米地里所有单株玉米的产量情况,则这块地里各单株玉米产量的全体是总体(D ) 对产品进行检验时,应该对产品进行一一检验 12. 若“p ∧ q ”是假命题,则下列结论正确的是( )(A) p ∨ q 是真命题 (B) p 和q 都是真命题 (C) ⌝ p 和⌝q 都是真命题 (D) ⌝ p ∨⌝q 是真命题 13.关于x 的不等式ax 2 + 5 x + b > 0的解集是(13 , 12),则a +b 等于( )(A) - 7 (B) 7 (C) -5 (D) 5 14.函数 y =log 2(4x 2 - 4x +1)的定义域是 ( )(A) (-∞, - 1) ∪ (- 1, +∞) (B) (0, +∞) (C) (-∞, 12 ) ∪ (12 , +∞) (D) (-∞, +∞)15.某厂1995年的产值为a 万元,预计产值每年以5%递增,则该厂 到2007年的产值(万元)是( ).(A ) 13(15%)a + (B ) 13(15%)a - (C ) 12(15%)a + (D ) 12(15%)a - 16.在小于100的正自然数中,7的倍数共有( )个,它们的和是( ) (A) 14,735 (B) 15,707 (C) 13,630 (D)13,73517.已知∣→a ∣= 6 ,∣→b ∣= 5,<→a , →b > = 12 0°,则 ∣→a - →b ∣= ( ) (A) 31 (B) 91 (C) 91 (D) 31 18.如果sin α - 3 cos α = 2 a – 3 ,则实数a 的取值范围是( ) (A) (12 ,52 ) (B) [12 ,52 ] (C) [12 , 32 ] (D) (12 , 32 )19.在△ABC 中,AB =4, AC = 6, ,且2cos(B +C )- 1=0 , 那么BC 的长度是( ) (A) 8 (B) 210 (C) 219 (D) 2720. 若双曲线的焦点在y 轴上,且6a =、10c =,则双曲线的标准方程为( ). (A ) 2213664x y -= (B ) 2213664y x -=(C ) 2216436x y -= (D ) 2216436y x -=21.从4名男教工,3名女教工中任选3人参加教工代表大会,则至少选中2名男教工的概率为( ). (A )2235 (B ) 13(C ) 14 (D ) 1835 22.同时抛掷两枚大小相同的骰子,用(x , y )表示结果,记A 为“所的点数之和小于5”,则事件A 包含的基本事件总数是( )(A) 3 (B) 4 (C) 5 (D) 623.已知 y =f (x ) 是奇函数,在区间 (-∞,-1] 上是减函数且有最小值3,则 y =f (x ) 在区间 [1,+∞) 上( )(A) 是增函数且有最小值3 (B) 是增函数且有最小值-3(C) 是减函数且有最大值3 (D) 是减函数且有最大值-324.在等差数列{a n }中,a 1= 20 , a n =54, S n = 999,则n 等于( ) (A) 24 (B) 36 (C) 27 (D) 3725. 已知点1(4,9)P 、2(6,3)P ,⊙o 是以线段12P P 为直径的圆,下列各点中在⊙o 上的点是( ). (A ) (6,9) (B ) (3,3) (C ) (5,3) (D ) (2,4)26.某企业共有职工150人,其中高级职称15人,中级职称45人,一般职员90人. 现在用分层抽样法抽取30人,则样本中各职称人数分别为( )(A) 5,10,15 (B) 3,9,18 (C) 3,10,17 (D)5,9,1627. 若2log 13a<,则a 的取值范围是( ). (A ) 20,(1,)3⎛⎫+∞ ⎪⎝⎭(B ) 2,3⎛⎫+∞ ⎪⎝⎭(C ) 2,13⎛⎫⎪⎝⎭(D )220,(,)33⎛⎫+∞ ⎪⎝⎭28. 抛物线23y x =的焦点坐标和准线方程分别是( ).(A )3(,0)4F -,34x = (B ) 3(,0)4F ,34x =-(C )3(,0)2F -,32x = (D ) 3(,0)2F ,32x =-29. 若函数f (x ) = 3x 2 + b x + c ,对任意的t 都有f (2+t ) = f (2- t ), 则( )(A) f (2) < f (1) < f (4) (B) f (1) < f (2) < f (4) (C) f (2) < f (4) < f (1) (D) f (4) < f (2) < f (1) 30. 如图直线1l 、2l 、3l 的斜率分别是1k 、2k 、3k ,则有( ).(A ) 123<<k k k (B ) 312<<k k k (C )321<<k k k (D ) 132<<k k k第Ⅱ卷(非选择题,共40分)二、填空题(本大题共4小题,每小题3分,共12分)31. 农村常需搭建截面为半圆形的全封闭蔬菜塑料棚,已知菜棚长度为40米,则需塑料膜y平方米与截面半径r米的函数关系式是___________(不考虑塑料膜埋在土里的部分).32.函数y = 2sin 2x+4sin x+2 的最大值和最小值分别为。
中职对口升学资料-2020年高考数学模拟试卷-8份-新

第二部分 数学(模拟题1)一、单项选择题.(每题5分,共8小题,共40分)1.设集合M ={-1,0,1}, N ={0,1}, 则 ( )A .M ∩N =ØB .N ∈MC .N ⊆MD .-1∈N2.函数12y -+=x x 的定义域为是( ) A .(-2,1) B .(-∞,-2)∪(1,+∞) C .(-∞,1]∪(2,+∞) D .[-2,1)∪(1,+∞)3.函数y=| x|-2的值域是( )A .(0,+∞)B .(2,+∞)C .[2,+∞)D .R4.函数y =sin α 的图像关于( )A .原点对称B .x 轴对称C .直线y =1对称D .y 轴对称5.若α=-450,则下列终边相同的角是( )A .-3150B .2πC .6750D .-3π6.已知点A (1,-2)到直线3x - 4y -1=0的距离为( )A .0B .1C .2D .37.空间中两平面同时垂直于另一个平面,则两个平面的位置关系是( )A .相交B .平行C .相交或平行D .无法确定8. 随机抽查工厂生产的一批灯泡100个,一等品和二等品为合格产品,其余为残次品,抽到一等品为60件,抽到二等品为36件,则该灯泡的合格率为( )A .60%B .36%C .96%D .4%二、填空题(本大题共5小题,每小题6分,共30分)9.已知集合A ={(x,y )|x+y -1=0},B ={(x,y )|2x -y +4=0},则A ∩B= .10.已知若→a =(-2,n ),→b =(2,-3),且b a ρρ⊥,则n 的值为 . 11.经过点P(-3,4) ,且圆心在(1,0)的圆的标准方程是 .12.有20个学生,8个老师,要分别派一个学生和一个老师组合参加会议,共有种不同派法;13.圆锥的底面半径为5cm,母线长为8cm,则这个圆锥的侧面积为.三、解答题(本大题共2小题,共30分)14. 已知数列{a n}中,a1=2且a n+1-a n=n,求a8 . (10分)15.为了鼓励节约用水,某地方水费按这样的形式:每户每月用水不超过10立方时,按1.8元每立方收费,超过15立方时,超出部分按2元每立方收费,设某户用水量为x立方,应每月缴费为y元.(1)列出的函数解析式.(10分)(2)若该户某月用了18立方水,应交多少钱?如交了40元钱,可用多少立方水?(10分)第二部分 数学(模拟题2)一、单项选择:(每小题5分,共40分)1.下列关系式中不正确的是( ).A.-2∈ZB. 4∉{3,6}C.1∈{(1,-1)}D.3∈{ x |x ≤3}2.不等式2log )(2-=x x f 定义域是( ). A.{x | x ≥4} B.{ x |x ≥1} C.{ x |x ≥2} D. {x |x ≥0}3.下列函数中f (x )=a x -5,若f (2)=1,则f (1)=( ).A.5B.3C.2D. -2 4. =56sinπ( ). A. 21- B. 23- C. 21 D. 23 5.下列各组向量互相平行的是( ).A.a =(0,2),b =(-1,4)B. a =(1,-2),b =(-2,4)C.a =(3,0),b =(-1,8)D. a =(2,-3),b =(-3,2)6.半径为2,且与x 轴相切于原点的原方程可能为( ).A.(x -2)2+y 2=2B.(x -2)2+y 2=4C. x 2+(y -2)2=2D. x 2+(y -2)2=47.下列命题正确的是( ).A.平面内两条直线平行于另一个平面内的两条直线,则这个平面互相平行。
2020年对口高职高考数学预测模拟试卷

2020年对口高职高考数学模拟试卷一、 选择题1. 设集合M={ x |X 2>16},N={ x |log 3x >1},则M ∩N=( ).A. {x |x >3}B. {x |x >4}C. {x |x <−4}D. {x |x >4或x <4}2.下列函数既是奇函数又是增函数的是()A.y =x −1B. y =x 3C. y =log 2xD.y=2x 3.直线(√3−√2)x+y=3和x+(√2−√3)y=2的位置关系是( )A.相交不垂直B. 垂直C. 平行D.重合4.等差数列{a n }中, a 1+a 4+a 7=39, a 3+a 6+a 9=27,则数列{a n }的前9项和S n =( )A.66B. 99C. 144D.2975.若抛物线y 2=2px(p>0)过点M(4,4),则点M 到准线的距离d=( ).A.5B. 4C. 3D.26.设全集U={ x |4≤X ≤10,X ≥∈N },A={4,6,8,10},则C U A=( ).A.{5}B.{5,7}C. {5,7,9}D.{7,9} 7. “a>0且b>0”是“ab>0”的( )条件。
A. 充分不必要B.充分且必要C.必要不充分D. 以上答案都不对8.如果f(X)=a x 2+bx+c(a ≠0)是偶函数,那么g(X)=a x 3+b x 2−cx 是( ). A.偶函数 B.奇函数C.非奇非偶函数D. 既是奇函数又是偶函数9.设函数f(X)= log a x(a>0且a ≠1),f(4)=2,则f(8)=( ). A.2 B.3 C.3 D.13 10.sin 800-√3cos 800−2 sin 200的值为( )。
A.0 B.1 C.−sin200 D.4sin200 11.等比数列的前4项和是203,公比q=−13,则a 1=( ). A.-9 B.3 C.9 D.13 12.已知(23) y =(32) x2+1,则y 的最大值是( )。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2020年口高职高考数学模拟试卷
一、 选择题
1.集合P={1、2、3、4},Q={x ||x |≤2,x ∈R }则P ∩Q 等于( )
A 、{1、2}
B 、{3、4}
C 、{1}
D 、{-1、-2、0、1、2}
2.数f(x)=√1+x 的定义域为( )
A.[0,+∞) B (-1, +∞) C.(-∞,-1) D.R
3.数y = 3 sinx + 4 cosx 的最小正周期为( )
A. π
B. 2π
C. 2
π D. 5π 4.数y = ㏒2(6-x-x 2)的单调递增区间是( )
A.(-∞,- 21]
B.( -3,-21)
C. [-21,+∞)
D. [-2
1,2) 5.等比数列{a n }中,a n >0,a 2a 4+2a 3a 5+a 4a 5=36那么a 3+a 5的值等于( )
A.6
B.12
C.18
D.24
6.函数y =log 3( x +x
1) (x>1)的最大值是( ) A.-2 B.2 C.-3 D.3
7.直线L:4x+3y-12=0与两坐村轴围成三角形的面积是( )
A.24
B.12
C.6
D.18
8.函数f (x)=3cos 2x+2
1sin2x 的最大值为( ) A.1-23 B. 23+1 C. 2
3-1 D.1 9.在等差数列中,已知S 4=1 ,S 8=4则a 17 + a 18 + a 19+ a 20( )
A.8
B.9
C.10
D.11
10.|a |=|b |是a 2=b 2的( )
A 、充分条件而悲必要条件,
B 、必要条件而非充分条件,
C 、充要条件,
D 、非充分条件也非必要条件
11.在⊿ABC 中内角A,B 满足t anAtanB=1则⊿ABC 是( )
A 、等边三角形,
B 、钝角三角形,
C 、非等边三角形,
D 、直角三角形
12.函数y=sin(43x +4
π )的图象平移向量(- 3π,0)后,新图象对应的函数为y=( ) A.Sin 43x B.- Sin 43x c. Cos 43x D.-Cos 4
3x 13.顶点在原点,对换称轴是x 轴,焦点在直线3x-4y-12=0上的抛物线方程是( )
A.y 2=16x
B. y 2=12x
C. y 2=-16x
D. y 2=-12x
第二部分 非选择题(共75分)
二、 填空题(每小题5分,共25分)
14.x 2-3
2y =1的两条渐近线的夹角是 . 15.若直线(m-2)x+2y-m+3=0的斜率等于2,则直线在轴上的截距2是 .
16.等比数列{a n }中,前n 项和S n = 2 n + a 则a = .
17.函数f(x)=log 24x+203,则f(1)= .
18.函数y=2x-3+√13−4x 的值域 .
三、解答题(21、22两小题各10分,23、24两小题各15分)
21、解不等式:log 3( 3 +2x-x 2)> log 3
( 3 x+1)
22、设等差数列{a n }的公差是正数,且a 2a 6 = -12, a 3+a 5 = -4求前项20的和.
23、如图所示若过点M (4,0)且斜率为-1的直线L 与抛物线C :y 2=2px(p>0),交于A 、B 两点,若OA ⊥OB
求(1)直线L 的方程,(2)抛物线C 的方程,(3)⊿ABC 的面积
24、B 船位于A 船正东26公里处,现A 、B 两船同时出发,A 船以每小时12公里的速度朝正北方向行驶,B 船以每小时5公里的速度朝正西方向行驶,那么何时两船相距最近,最近距离是多少。
