极化恒等式(学生版)
平面向量中的极化恒等式及有关最值(范围)问题(1)

2(a·b-a·c-b·c+1)=48+2(a+b)·c=48+2|a+b|cos θ(其中θ为 a+b
与 c 的夹角),因为|a-b|=|a+b|,所以|a-b|2=48+2|a-b|cos θ,则由
cos θ∈[-1,1],得 48-2|a-b|≤|a-b|2≤48+2|a-b|,解得 6≤|a-
1x 2
2-1x2=1.
4
4
(2)如图,由已知|OF|=1,取 FO 中点 E,连接 PE,由极化恒等式得
O→P·F→P=|PE|2-1|OF|2=|PE|2-1,
4
4
∵|PE|2max=245,∴O→P·F→P的最大值为 6.
答案 (1)1 (2)C
题型二 平面向量中的最值(范围)问题
类型 1 利用函数型
则A→P·B→P的取值范围是________;若向量A→C=λD→E+μA→P,则λ+μ的最
小值为________.
解析 (1)由题意,不妨设 b=(2,0),a=(cos θ,sin θ)(θ∈[0,2π)),
则 a+b=(2+cos θ,sin θ),a-b=(cos θ-2,sin θ).
令 y=|a+b|+|a-b|
= (2+cos θ)2+sin2θ+ (cos θ-2)2+sin2θ
= 5+4cos θ+ 5-4cos θ,
则 y2=10+2 25-16cos2θ∈[16,20].
由此可得(|a+b|+|a-b|)max= 20=2 5,
(|a+b|+|a-b|)min= 16=4,
即|a+b|+|a-b|的最小值是 4,最大值是 2 5.
4a2
4a2
θ)2=1,化简得
b2(1-cos2θ)=
向量复习专题二极化恒等式
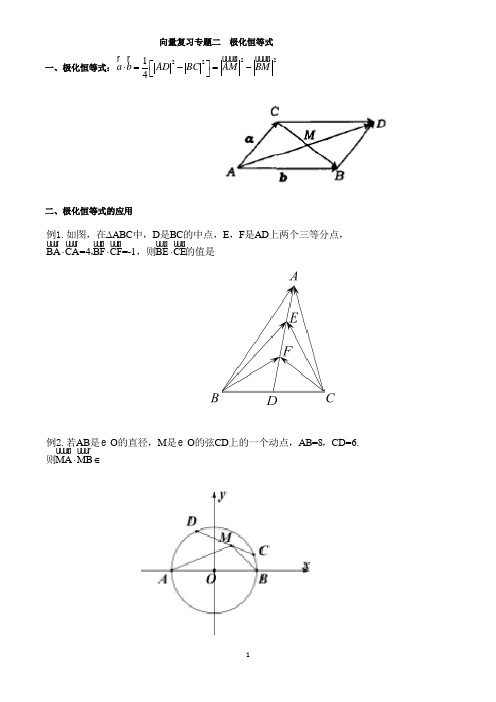
向量复习专题二 极化恒等式 一、极化恒等式:222214
a b AD BC AM BM ⎡⎤⋅=-=-⎣⎦
二、极化恒等式的应用
ABC D BC E F AD BA CA=4BF CF=-1BE CE ∆⋅⋅⋅ 例1.如图,在中,是的中点,,是上两个三等分点,,,则的值是
AB O M O CD AB=8CD=6.MA MB ⋅∈
例2.若是的直径,是的弦上的一个动点,,则
例 4.在中,,,已知点是内一点,则 的最
小值是_______.
()
ABCD OB OC ⋅ 例5.如图放置的边长为1的正方形顶点分别在x 轴,y 轴正半轴含原点滑动,则的最大值为
.3,2,()P ABO OA OB P AB OP OA OB ∆==⋅- 例3为所在平面内一点,线段在线段的垂直平分线上,则
的值为
例6.(2013浙江理7)在ABC ∆中,0P 是边AB 上一定点,满足AB B P 410=,且对于边AB 上任一点P ,恒有C P B P PC PB 00∙≥∙,则
A. 2π=
∠ABC B. 2π=∠BAC C. AC AB = D. BC AC =
例7.已知圆的半径为,是圆上的两点,且,是圆的任意一条直径,
若点满足,则的最小值为
O 1,A B 3AOB π
∠=MN O C 1(1)()2
OC OA OB R λλλ=+-∈ CM CN ⋅。
极化恒等式课件-2025届高三数学一轮复习

磨尖点一 求向量数量积的定值
磨尖点二 求向量数量积的最值(范围)
磨尖点三 求参数及其他问题
磨尖课04 极化恒等式
1
4
1. 极化恒等式: ⋅ = [ +
2
2
− − 2 ].
(1)公式推导:
+
2
+ ሻ2 −
=
2
+ 2 ⋅ +
2 ,
−
2
=
2
− 2 ⋅
(3)记忆规律:向量的数量积等于第三边的中线长与第三边边长的一半的平方差.
磨尖课04 极化恒等式
4
磨尖点一 求向量数量积的定值
磨尖课04 极化恒等式
6
典例1 (2023 ·全国乙卷)正方形的边长是2,是的中点,则 ⋅ =
( B ) .
A. 5
B.3
C.2 5
解析 设的中点为,由极化恒等式可得 ⋅ =
为△ 所在平面内的动点,且 = 1,则 ⋅ 的取值范围是( D ) .
A.[−5,3]
B.[−3,5]
C.[−6,4]
D.[−4,6]
磨尖课04 极化恒等式
11
解析 (法一)依题意建立如图所示的平面直角坐标系,则 0,0 , 3,0 , 0,4 ,
磨尖课04 极化恒等式
4sin +
sin2
= 1 − 3cos − 4sin = 1 − 5sin + ,其中tan =
因为−1 ≤ sin + ≤ 1,所以−4 ≤ 1 − 5sin + ≤ 6,
3
,
4
磨尖课04 极化恒等式
13
十二、极化恒等式

十二、极化恒等式.两倍等于两条邻边平方和的平方和平行四边形的对角线的你能用向量方法证明:何模型。
示向量加法和减法的几引例:平行四边形是表,,b AD a AB ==证明:不妨设 ,,则b a DB b a A -=+=C ()222222C C b b a a b a A A +⋅+=+== (1)()222222b b a a b a DB DB +⋅-=-== (2)(1)(2)两式相加得:⎪⎭⎫ ⎝⎛+=⎪⎭⎫ ⎝⎛+=+22222222C AD AB b a DB A 结论:平行四边形对角线的平方和等于两条邻边平方和的两倍.如果将上面(1)(2)两式相减,能得到什么结论呢?b a ⋅=()()⎥⎦⎤⎢⎣⎡--+2241b a b a ————极化恒等式 几何意义:向量的数量积可以表示为以这组向量为邻边的平行四边形的“和对角线”与“差对角线”平方差的41. 即:[]2241DB AC b a -=⋅(平行四边形模式) 思考:在图1的三角形ABD 中(M 为BD 的中点),此恒等式如何表示呢?因为AM AC 2=,所以2241DB AM b a -=⋅(三角形模式) 1. 在ABC ∆中,M 是BC 的中点,3,10AM BC ==,则AB AC ⋅=____ ..______1.2的值为则边上的动点,是,点的边长为已知正方形DA DE AB E ABCD ⋅ .________O O 2.3的取值范围是一个动点,则上的是圆,点的圆内接于半径为已知正三角形PB PA P ABC ⋅ 22.2.2.1.)(,0)()(2,.4D C B A c c b c a c b a 的最大值是则满足,若向量个互相垂直的单位向量是平面内已知=-⋅-M图1 AB CM5.在ABC ∆中,0P 是边AB 上一定点,满足014P B AB =,且对于边AB 上任一点P ,恒有00PB PC P B PC ⋅≥⋅。
极化恒等式学生版

极化恒等式(学生版) 极化恒等式是线性代数中的一个重要恒等式,它反映了矩阵和向量之间的内在关系。
这个恒等式可以表示为:A⋅(β+γ)=Aβ+Aγ,其中A是一个矩阵,β和γ是向量,A⋅表示矩阵A和向量的乘积。
在证明极化恒等式之前,我们需要先了解一下矩阵和向量的乘法。
矩阵和向量的乘法是通过将矩阵的每一行与向量相乘,然后将这些乘积相加得到的。
例如,如果A是一个3×2的矩阵,β是一个2×1的向量,那么A⋅β可以通过以下步骤计算:1.将第一行a11a12与向量β相乘得到第一个乘积a11β1+a12β2,将第二行a21a22与向量β相乘得到第二个乘积a21β1+a22β2,将第三行a31a32与向量β相乘得到第三个乘积a31β1+a32β2。
2.将上述三个乘积相加得到A⋅β=(a11β1+a12β2)+(a21β1+a22β2)+(a31β1+a32β2)=a11β1+a12β2 +a21β1+a22β2+a31β1+a32β2=∑i=13∑j=12Aijβj。
现在我们可以证明极化恒等式。
首先,我们需要将矩阵A拆分成两个部分,即A=A−+A+,其中A−=(A−1)ij=−∑k=1nAkij(i=1,m;j=1,n)是一个(m×n)矩阵,A+=εijk(i=1,m;j=1,n;k=−m−(+j)=i)也是一个(m×n)矩阵。
其中εijk是一个排列符号,当i、j、k三个指标循环排列时,其值为1或−1。
根据矩阵拆分的定义,我们可以将极化恒等式表示为:(A−+A+)⋅(β+γ)=A−⋅β+A−⋅γ+A+⋅β+A+⋅γ对于右侧第一项A−⋅β,根据矩阵和向量的乘法计算规则可得:A−⋅β=(−∑k=1nAkij)⋅β=(−Akij)⋅βk=(−∑k=1n(Aiuj)⋅Bvkaj)⋅ɛvka)=(−∑k= 1n(Aui)⋅Bk)(ɛik⋅ɛivk)=(−∑k=1n(Aui⋅Bk))⋅ɛik=(−Aui⋅B)⋅eivi=(−Aui⋅B)⋅βi= tika⋅Mk耿 ltiZMn耿 wnow瓣towZMn耿 +yla"owe看来及。
微专题6 极化恒等式、投影向量

微专题6 极化恒等式、投影向量极化恒等式:a ·b =14[(a +b )2-(a -b )2].(1)几何意义:向量的数量积可以表示为以这组向量为邻边的平行四边形的“和对角线”与“差对角线”平方差的14.(2)在平行四边形PMQN 中,O 是对角线交点,则: ①PM→·PN →=14[|PQ →|2-|NM →|2](平行四边形模式); ②PM→·PN →=|PO →|2-14|NM →|2(三角形模式).类型一 投影向量的应用由投影与投影所在的向量共线,问题转化为求向量间的投影数量与投影所在向量方向上单位向量的积.例1 已知|a |=4,e 为单位向量,它们的夹角为2π3,则向量a 在向量e 上的投影向量是________;向量e 在向量a 上的投影向量是________. 答案 -2e -18a解析 由|a |=4,e 为单位向量,它们的夹角为2π3, 向量a 在向量e 上的投影数量:|a |cos 23π=-2, 向量e 在向量a 上的投影数量:|e |cos 23π=-12, 故向量a 在向量e 上的投影向量:-2e , 向量e 在向量a 上的投影向量:-12×a |a |=-18a .训练1 (1)已知向量a 与b 的夹角为34π,且|a |=2,|b |=3,则a 在b 方向上的投影向量与投影向量的长度分别是( ) A.23b ,2 B.23b ,-2 C.-23b , 2D.-23b ,-2(2)已知向量a =(1,2),A (6,4),B (4,3),b 为向量AB →在向量a 上的投影向量,则|b |=________. 答案 (1)D (2)455解析 (1)设a 在b 方向上的投影向量为λb (λ∈R ), 则a ·b =λb ·b , 故λ=a ·b b 2=|a |cos 34π|b |=-23.故a 在b 方向上的投影向量为-23b ,a 在b 方向上的投影向量的长度为|a | cos 34π=- 2. (2)AB→=(-2,-1), 由投影公式可知|b |=|AB→·a ||a |=|-2×1+(-1)×2|5=455.类型二 利用极化恒等式求向量的数量积利用极化恒等式求平面向量数量积的步骤: (1)取第三边的中点,连接向量的起点与中点;(2)利用极化恒等式将数量积转化为中线长与第三边长的一半的平方差; (3)求中线及第三边的长度,从而求出数量积的值.注:对于不共起点或不共终点的向量需通过平移转化为共起点(终点)的向量,再利用极化恒等式.例2 (1)如图,在△ABC 中,D 是BC 的中点,E ,F 是AD 上的两个三等分点.BA →·CA →=4,BF→·CF →=-1,则BE →·CE →的值为________.(2)如图,在平行四边形ABCD 中,AB =1,AD =2,点E ,F ,G ,H 分别是AB ,BC ,CD ,AD 边上的中点,则EF →·FG →+GH →·HE →=________.答案 (1)78 (2)32解析 (1)设BD =DC =m , AE =EF =FD =n , 则AD =3n .根据向量的极化恒等式,有AB →·AC →=AD →2-DB →2=9n 2-m 2=4,FB →·FC →=FD →2-DB →2=n 2-m 2=-1, 联立解得n 2=58,m 2=138.因此EB →·EC →=ED →2-DB →2=4n 2-m 2=78. 即BE→·CE →=78. (2)连接EG ,FH 交于点O (图略), 则EF→·FG →=EO →2-OH →2=1-⎝ ⎛⎭⎪⎫122=34,GH→·HE →=GO →2-OH →2=1-⎝ ⎛⎭⎪⎫122=34, 因此EF→·FG →+GH →·HE →=32. 训练2 (1)在△ABC 中,M 是BC 的中点,AM =3,BC =10,则AB→·AC →=________.(2)如图,在△ABC 中,已知AB =4,AC =6,∠BAC =60°,点D ,E 分别在边AB ,AC 上,且AB →=2AD →,AC →=3AE →,若F 为DE 的中点,则BF →·DE →的值为________.答案 (1)-16 (2)4解析 (1)因为M 是BC 的中点, 由极化恒等式得AB→·AC → =|AM →|2-14|BC →|2=9-14×100=-16. (2)取BD 的中点N ,连接NF ,EB ,因AB =4,AE =2,∠BAC =60°,故BE ⊥AE ,所以BE =2 3.在△DEB 中,FN 綊12BE , 所以FN =3, 故BF→·DE →=2FB →·FD →=2⎝ ⎛⎭⎪⎫FN →2-14DB →2=2(3-1)=4. 类型三 利用极化恒等式求数量积的最值(范围)(1)利用极化恒等式求数量积的最值(范围)时,关键在于取第三边的中点,找到三角形的中线,再写出极化恒等式.(2)难点在于求中线长的最值(范围),可通过观察图形或用点到直线的距离等求解.例3 (1)如图,在同一平面内,点A 位于两平行直线m ,n 的同侧,且A 到m ,n 的距离分别为1,3,点B ,C 分别在m ,n 上,|AB →+AC →|=5,则AB →·AC →的最大值是________.(2)(2022·济南调研)在△ABC 中,点E ,F 分别是线段AB ,AC 的中点,点P 在直线EF 上,若△ABC 的面积为2,则PB →·PC →+BC →2的最小值为________. 答案 (1)214 (2)23 解析 (1)法一(极化恒等式法)连接BC ,取BC 的中点D ,AB →·AC →=AD →2-BD →2,又AD =12|AB →+AC →|=52,故AB→·AC →=254-BD →2=254-14BC →2, 又因为BC min =3-1=2,所以(AB →·AC →)max =214. 法二(坐标法)以直线n 为x 轴,过点A 且垂直于n 的直线为y 轴,建立如图所示的平面直角坐标系xOy ,如图,则A (0,3),C (c ,0),B (b ,2), 则AB→=(b ,-1),AC →=(c ,-3) 从而(b +c )2+(-4)2=52, 即(b +c )2=9,又AC →·AB →=bc +3≤(b +c )24+3=214,当且仅当b =c 时,等号成立. (2)取BC 中点O ,PB→·PC →=PO →2-14BC →2⇒PB →·PC →+BC →2=PO →2+34BC →2≥2PO→2·34BC →2=3|PO→||BC →|,当且仅当PO =32BC 时等号成立. ∵PO ≥12h ,∴3|PO →||BC →|≥32h |BC →|=3S △ABC =23,∴PB →·PC →+BC →2的最小值为2 3.训练3 (1)如图所示,正方体ABCD -A 1B 1C 1D 1的棱长为2,MN 是它的内切球的一条弦(我们把球面上任意两点之间的线段称为球的弦),P 为正方体表面上的动点,当弦MN 的长度最大时,PM→·PN →的取值范围是________.(2)如图所示,正方形ABCD 的边长为1,A ,D 分别在x 轴,y 轴的正半轴(含原点)上滑动,则OC→·OB →的最大值是________.答案 (1)[0,2] (2)2解析 (1)由正方体的棱长为2, 得内切球的半径为1, 正方体的体对角线长为2 3.当弦MN 的长度最大时,MN 为球的直径. 设内切球的球心为O ,则PM→·PN →=PO →2-ON →2=|PO →2|-1. 由于P 为正方体表面上的动点, 故|OP |∈[1,3], 所以PM→·PN →∈[0,2]. (2)如图,取BC 的中点M ,AD 的中点N ,连接MN ,ON ,则OC→·OB →=OM →2-14=|OM →|2-14. 因为OM ≤ON +NM =12AD +AB =32, 当且仅当O ,N ,M 三点共线时取等号. 所以OC→·OB →的最大值为2.一、基本技能练1.设向量a ,b 满足|a +b |=10,|a -b |=6,则a ·b 等于( ) A.1 B.2 C.3 D.4答案 A解析 由极化恒等式得a ·b =14[(a +b )2-(a -b )2]=14×(10-6)=1.2.如图,在平面四边形ABCD 中,O 为BD 的中点,且OA =3,OC =5,若AB →·AD →=-7,则BC→·DC →=( )A.-9B.21C.-21D.9答案 D解析 AB→·AD →=|AO →|2-14|BD →|2=-7,∴14|BD →|2=16,BC →·DC →=|CO →|2-14|BD →|2=25-16=9.3.如图,BC ,DE 是半径为1的圆O 的两条直径,BF→=2FO →,则FD →·FE →=( )A.-34B.-89C.-14D.-49答案 B解析 ∵BF →=2FO →,圆O 的半径为1,∴|FO→|=13. 法一 FD →·FE →=(FO →+OD →)·(FO →+OE →)=FO →2+FO →·(OE →+OD →)+OD →·OE →=⎝ ⎛⎭⎪⎫132+0-1=-89.法二 由极化恒等式得FD→·FE →=FO →2-14DE →2=19-1=-89. 4.已知正方形ABCD 的面积为2,点P 在边AB 上,则PD →·PC →的最大值是( )A.92B.2C.32D.34答案 B解析 如图所示,取CD 的中点E ,连接PE ,由极化恒等式可得PD →·PC →=PE →2-EC →2=|PE →|2-12, 所以当P 与A (B )重合时,|PE→|=52最大,从而(PD →·PC →)max =2. 5.已知a ,b 是平面内两个互相垂直的单位向量,若c 满足(a -c )·(b -c )=0,则|c |的最大值是( ) A.1 B.2 C.2 D.22答案 C解析 由极化恒等式(a -c )·(b -c ) =14[(a +b -2c )2-(a -b )2], ∵(a -c )·(b -c )=0, 所以(a +b -2c )2=(a -b )2, 故c 2=(a +b )·c , 又因为|a |=|b |=1,a ⊥b , ∴|a +b |=2,于是|c |2≤|a +b ||c |=2|c |, ∴|c |≤ 2.6.已知AB 为圆x 2+y 2=1的一条直径,点P 为直线x -y +2=0上任意一点,则P A →·PB →的最小值为( ) A.1 B.2 C.2 D.22 答案 A解析 如图所示,由极化恒等式易知,当OP 与直线x -y +2=0垂直时,P A →·PB →有最小值,即P A →·PB →=PO →2-OB →2=(2)2-12=1. 故选A.7.已知AB 是圆O 的直径,AB 长为2,C 是圆O 上异于A ,B 的一点,P 是圆O 所在平面上任意一点,则(P A →+PB →)·PC →的最小值为( ) A.-14 B.-13 C.-12 D.-1答案 C解析 ∵P A →+PB →=2PO →,∴(P A →+PB→)·PC →=2PO →·PC →, 取OC 中点D (图略),由极化恒等式得,PO→·PC →=|PD →|2-14|OC →|2=|PD →|2-14, 又|PD →|2min=0,∴(P A →+PB→)·PC →的最小值为-12. 8.已知△ABC 是边长为2的等边三角形,P 为平面ABC 内一点,则P A →·(PB →+PC →)的最小值为( ) A.-2 B.-32 C.-43 D.-1 答案 B解析 取BC 的中点D ,连接AD ,PD ,取AD 的中点E ,连接PE .由△ABC 是边长为2的等边三角形,E 为中线AD 的中点得AE =12AD =32, 则P A →·(PB→+PC →) =2P A →·PD →=2(|PE →|2-|EA →|2) =2⎣⎢⎡⎦⎥⎤|PE →|2-⎝ ⎛⎭⎪⎫322≥2×⎝ ⎛⎭⎪⎫0-34=-32,当且仅当|PE→|=0时,取等号,∴P A →·(PB→+PC →)的最小值为-32. 9.已知正方形ABCD 的边长为1,点E 是AB 边上的动点,则DE →·DA →的值为________.答案 1解析 取AE 中点O ,设AE =x (0≤x ≤1),则AO =12x ,∴DE→·DA →=|DO →|2-14|AE |2=12+⎝ ⎛⎭⎪⎫12x 2-14x 2=1.10.在△ABC 中,AB =6,AC =5,A =120°,动点P 在以C 为圆心,2为半径的圆上,则P A →·PB →的最小值为________.答案 16解析 设AB 的中点为M ,则P A →·PB →=PM →2-MA →2=|PM →|2-9, 所以要求P A →·PB→的最小值,只需求|PM →|的最小值, 显然当点P 为线段MC 与圆的交点时,|PM→|取得最小值,最小值为|MC |-2. 在△AMC 中,由余弦定理得|MC |2=32+52-2×3×5×cos 120°=49, 所以|MC |=7,所以|PM →|的最小值为5, 则P A →·PB→的最小值为16. 11.在Rt △ABC 中,CA =CB =2,M ,N 是斜边AB 上的两个动点,且MN =2,则CM →·CN →的取值范围是________. 答案 ⎣⎢⎡⎦⎥⎤32,2解析 取MN 的中点为P ,由极化恒等式得CM→·CN →=|CP →|2-14|MN |2=|CP →|2-12. 当P 为AB 的中点时,|CP →|取最小值为2,则CM→·CN →的最小值为32; 当M 与A (或N 与B )重合时,|CP→|取最大值为102,则CM →·CN →的最大值为2,所以CM→·CN →的取值范围是⎣⎢⎡⎦⎥⎤32,2. 12.已知AB 为圆O 的直径,M 为圆O 的弦CD 上一动点,AB =8,CD =6,则MA →·MB →的取值范围是________. 答案 [-9,0]解析 如图,取CD 的中点G ,连接OG ,MO ,CO ,得OG ⊥CD ,MA→·MB →=|MO →|2-14|BA →|2=|MO →|2-16, ∵|OC→|≥|OM →|≥|OG →|, ∴7≤|OM→|≤4,∴MA→·MB →∈[-9,0]. 二、创新拓展练13.若点O 和点F 分别为椭圆x 24+y 23=1的中心和左焦点,点P 为椭圆上的任意一点,则OP →·FP →的最大值为( )A.2B.3C.6D.8答案 C解析 如图,由已知OF =1,取FO 中点E ,连接PE ,由极化恒等式得:OP →·FP →=|PE→|2-14|OF →|2=|PE →|2-14,∵当P 在椭圆右顶点时,|PE →|2有最大值,|PE →|2max=254, ∴OP→·FP →的最大值为6. 14.(多选)已知在△ABC 中,P 0是边AB 上一定点,满足P 0B =14AB ,且对于边AB 上任一点P ,恒有PB →·PC →≥P 0B →·P 0C →,则( ) A.PB→·PC →=PD →2-DB →2 B.存在点P ,使|PD →|<|P 0D →| C.P 0C →·AB →=0 D.AC =BC 答案 AD解析 如图所示,取BC 的中点D ,连接PD ,根据向量的极化恒等式,有PB →·PC →=PD →2-DB →2,P 0B →·P 0C →=P 0D →2-DB →2. 又PB →·PC →≥P 0B →·P 0C →,所以|PD →|≥|P 0D →|,A 正确;B 错误;故由点P 为边AB 上任意一点知:点D 到边AB 上点的距离的最小值为|DP 0→|,从而DP 0⊥AB ,∴P 0C →·AB →≠0,C 错误;取AB 的中点E ,则由P 0B =14AB 知,CE ∥DP 0,故CE ⊥AB ,于是AC =BC ,D 正确.15.在半径为1的扇形中,∠AOB =60°,C 为弧上的动点,AB 与OC 交于P ,则OP →·BP →的最小值为________. 答案 -116解析 取OB 的中点D ,作DE ⊥AB 于点E ,连接PD ,则OP→·BP →=|PD →|2-|OD →|2=|PD →|2-14,易知|PD →|∈⎣⎡⎦⎤|DE →|,|AD →|=⎣⎢⎡⎦⎥⎤34,32, 则OP→·BP →=PD →2-14∈⎣⎢⎡⎦⎥⎤-116,12,故所求最小值为-116. 16.如图,在平面四边形ABCD 中,AC =AD =2,∠DAC =120°,∠ABC =90°,则BD→·BC →的最大值为________.答案1解析取CD的中点E,连接EA,EB,∵AC=AD=2,∠DAC=120°,∴AE⊥CD,DE=AD sin 60°=3,由∠ABC=∠AEC=90°,∴A,B,C,E四点共圆,且AC为直径,则BD→·BC→=|BE→|2-|ED→|2=|BE→|2-(3)2≤|AC→|2-3=22-3=1,所以BD→·BC→的最大值为1.。
高中数学极化恒等式

高中数学极化恒等式(初中物理公式及其变形式)
极化恒等式?
极化恒等式是联系内积与范数的一个重要的等式,是用范数表示内积的公式。
极化恒等式设H是内积空间,‖·‖是由内积(·,·)导出的范数。
范数是具有“长度”概念的函数。
范数在线性代数、泛函分析及相关的数学领域,是一个函数,其为向量空间内的所有向量赋予非零的正长度或大小。
半范数反而可以为非零的向量赋予零长度。
极化恒等式公式是什么?
设H是内积空间,‖·‖是由内积(·,·)导出的范数,下列等式常被称为极化恒等式:
1、当H是实空间时,(x,y)=(1/4)(‖x+y‖2-‖x-y‖2);当h是复空间时,(x,y)=(1/4)(‖x+y‖2-‖x-y‖2+i‖x+iy‖2-i‖x-iy‖2)。
对于实内积空间上的双线性Hermitian函数和复内积空间上的双线性φ(x,y)函数,有类似的恒等式。
2、当H是实内积空间时
3、当H是复内积空间时
著名恒等式
1、欧拉恒等式:
eiπ+1=0,e是自然对数的底,π是圆周率,i是虚数单位。
它来源于eix=cosx+isinx(复数的三角表示),令x=π就得。
2、牛顿恒等式:
设F(X)=0的n个根X1,X2,……,Xn.对于k∈N,记Sk=X1k+X2k +……+Xnk.则有
C0Sk+C1Sk-1+……+CnSk-n=0,当k>0(N1)
C0Sk+C1Sk-1+……+Ck-1S1+kCk=0,当1≤k≤n(N2)。
第2讲 极化恒等式

第2讲极化恒等式结论:设a b、是两个平面向量,则有恒等式()()2214a b a b a b ⎡⎤=+--⎢⎥⎣⎦ ,在三角形中,也可以用三角形的中线来表示,22AB AC AM MB =- 。
极化恒等式的作用主要在于,它可以将两个向量的数量积转化为这两个向量之和或之差,因此,当两个向量之和或之差为定值时,常常可以考虑利用极化恒等式进行转化求解。
典型例题1.(2012浙江15)在ABC ∆中,M 是BC 的中点,3AM =,10BC =,则AB AC =.法1解:设AMB θ∠=,则AMC πθ∠=-.又AB MB MA =- ,AC MC MA =- ,∴(AB AC = )(MB MA - 2)MC MA MB MC MB MA MA MC MA -=--+,2553cos 35cos()916θπθ=--⨯-⨯-+=-,故答案为16-.法2:极化恒等式22223516AB AC AM MB =-=-=-2.如图,在ABC ∆中,D 是BC 的中点,E ,F 是AD 上的两个三等分点,4BA CA =,1BF CF =- ,则BE CE的值是.法1解:D 是BC 的中点,E ,F 是AD 上的两个三等分点,∴BF BD DF =+ ,CF BD DF =-+ ,3BA BD DF =+ ,3CA BD DF =-+ ,∴221BF CF DF BD =-=- ,2294BA CA DF BD =-= ,∴258DF = ,2138BD = ,又 2BE BD DF =+ ,2CE BD DF =-+,∴22748BE CE DF BD =-= ,故答案为:78法2:极化恒等式FDAD BD FD CF BF BD AD CA BA 3142222=-=-=∙=-=∙分别解出FD ²和BD ²的值,即可求解CMDG O3.已知AB 为圆O 的直径,M 为圆O 的弦CD 上一动点,8AB =,6CD =,则MA MB的取值范围是.法1解:以AB 所在的直线为x 轴,以线段AB 的垂直平分线为y 轴建立平面直角坐标系,如图所示;且圆O 的直径为AB ,设(,)M x y ,则(4,0)A ,(4,0)B -,(4,)MA x y =-- ,(4,)MB x y =--- ,222(4)(4)()16MA MB x x y x y =---+-=+-,又M 是圆O 的弦CD 上一动点,且6CD =,所以2216916x y -+ ,即22716x y + ,其中最小值在CD 的中点时取得,所以MA MB的取值范围是[9-,0].故答案为:[9-,0].法2直接使用极化恒等式22MA MB MO OA=-4MO ≤≤ ,4OA =[]9,0MA MB ∴∈-一课一练1.(2013•浙江二模)如图放置的边长为1的正方形ABCD 的顶点A 、D 分别在x 轴、y 轴正半轴上(含原点)上滑动,则OB OC的最大值是.2.(2018•天津)如图,在平面四边形ABCD 中,AB BC ⊥,AD CD ⊥,120BAD ∠=︒,1AB AD ==.若点E 为边CD 上的动点,则AE BE的最小值为()A .2116B .32C .2516D .33、(2017•新课标Ⅱ)已知ABC ∆是边长为2的等边三角形,P 为平面ABC 内一点,则()PA PB PC +的最小值是()A .2-B .32-C .43-D .1-参考答案1)法1解:如图令OAD θ∠=,由于1AD =故0cos A θ=,sin OD θ=,如图2BAX πθ∠=-,1AB =,故cos cos()cos sin 2Bx πθθθθ=+-=+,sin()cos 2B y πθθ=-=故(cos sin ,cos )OB θθθ=+同理可求得(sin ,cos sin )C θθθ+,即(sin ,cos sin )OC θθθ=+,∴(cos sin OB OC θθ=+,cos )(sin θθ ,cos sin )1sin 2θθθ+=+,OB OC的最大值是2故答案是2法2:极化恒等式如图,取BC ,AD 中点E ,F ,22214OB OC OE EB OE =-=-根据极化恒等式13122OE OF EF ≤+=+=所以有最大值22)法1解:如图所示,以D 为原点,以DA 所在的直线为x 轴,以DC 所在的直线为y 轴,过点B 做BN x ⊥轴,过点B 做BM y ⊥轴,AB BC ⊥ ,AD CD ⊥,120BAD ∠=︒,1AB AD ==,1cos602AN AB ∴=︒=,3sin 602BN AB =︒=,13122DN ∴=+=,32BM ∴=,3tan 302CM MB ∴=︒=,3DC DM MC ∴=+=,(1,0)A ∴,3(2B ,32,C ,设(0,)E m ,∴(1,)AE m =- ,3(2BE =- ,32m -,0m ,∴22233321(()224216416AE BE m m m =+-=-+-=-+ ,当m =2116.故选:A .法2:极化恒等式22214EA EB EF FA EF =-=-当EF CD ⊥时,15144EF EK KF =+=+=251214416EA EB ⎛⎫=-=⎪⎝⎭最小3)法1解:建立如图所示的坐标系,以BC 中点为坐标原点,则A ,(1,0)B -,(1,0)C ,设(,)P x y ,则()PA x y =-- ,(1,)PB x y =--- ,(1,)PC x y =--,则22223()222[(]4PA PB PC x y x y +=-+=+--∴当0x =,y =时,取得最小值332(42⨯-=-,故选:B .法2:极化恒等式222222()()()2PA PB PC PE EA PF FA PE PF +=-+-=+- 当P 位于EF 中点时,有最小值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
课题:极化恒等式在向量问题中的应用
学
习
目
标
目标1:通过自主学习掌握极化恒等式两种模式,理解其几何意义; 目标2-1:通过对例1的自主学习掌握用极化恒等式求数量积的值; 目标2-2:通过对例2的自主学习掌握用极化恒等式求数量积的最值、范围; 目标2-3:通过小组合作学习掌握极化恒等式解决与数量积有关的综合问题。
重点
掌握极化恒等式,利用它解决一类与数量积有关的向量问题 难点 根据具体的问题情境,灵活运用极化恒等式
目标达成途径
学习自我评价
阅读以下材料: .
两倍等于两条邻边平方和的平方和
平行四边形的对角线的你能用向量方法证明:何模型。
示向量加法和减法的几引例:平行四边形是表,,b AD a AB ==证明:不妨设
,,则b a DB b a A -=+=C ()222222C C b b a a b a A A +⋅+=+== (1)
()222222b b a a b a DB DB +⋅-=-== (2)
(1)(2)两式相加得:⎪⎭
⎫ ⎝⎛+=⎪⎭⎫ ⎝⎛+=+22222222C AD AB b a DB A 结论:平行四边形对角线的平方和等于两条邻边平方和的两倍.
思考1:如果将上面(1)(2)两式相减,能得到什么结论呢
b a ⋅=()()
⎥⎦⎤⎢⎣⎡--+2241b a b a ————极化恒等式 对于上述恒等式,用向量运算显然容易证明。
那么基于上面的引例,你觉得
极化恒等式的几何意义是什么
几何意义:向量的数量积可以表示为以这组向量为邻边的平行四边形的“和对
角线”与“差对角线”平方差的4
1. 即:[]
2241DB AC b a -=
⋅(平行四边形模式) 目标1:阅读材料,了解极化恒等式的由来过程,掌握极化恒等式 的两种模式,并理解其几何意义 M
图1
思考:在图1的三角形ABD 中(M 为BD 的中点),此恒等式如何表示呢
因为AM AC 2=,所以2241DB AM
b a -=⋅(三角形模式) 例1.(2012年浙江文15)在ABC ∆中,M 是BC 的中点,3,10AM BC ==,
则AB AC ⋅=____ .
解:因为M 是BC 的中点,由极化恒等式得: 2241BC AM AC AB -=⋅=9-1004
1⨯= -16 【小结】在运用极化恒等式的三角形模式时,关键在于取第三边的中点,找到三
角形的中线,再写出极化恒等式。
目标检测
.______1)132012(的值为边上的动点,则是点,
的边长为已知正方形改编北京文DA DE AB E ABCD ⋅
.
________O O 2.2的取值范围是则上的一个动点,
是圆,点的圆内接于半径为(自编)已知正三角形例PB PA P ABC ⋅解:取AB 的中点D ,连结CD ,因为三角形ABC 为
正三角形,所以O 为三角形ABC 的重心,O 在CD 上,
且22==OD OC ,所以3=CD ,32=AB
(也可用正弦定理求AB )
又由极化恒等式得:
34
1222-=-=⋅PD AB PD PB PA 因为P 在圆O 上,所以当P 在点C 处时,3||max =PD
当P 在CO 的延长线与圆O 的交点处时,1||min =PD
所以]6,2[-∈⋅PB PA
【小结】涉及数量积的范围或最值时,可以利用极化恒等式将多变量转变为单变
量,再用数形结合等方法求出单变量的范围、最值即可。
目标检测
8
.6.3.2.)
(13
4)112010(2
2D C B A FP OP P y x F O 的最大值为则为椭圆上的任意一点,的中心和左焦点,点分别为椭圆和点若点福建文⋅=+
目标2-1:掌握用极化恒等式求数量积的值
A
B C
M 目标2-2:掌握用极化恒等式求数量积的最值、范围
问题、疑惑、错解汇集
能力提升
例3.(2013浙江理7)在ABC ∆中,0P 是边AB 上一定点,满足014
P B AB =
,且对于边AB 上任一点P ,恒有00
PB PC P B PC ⋅≥⋅。
则( ) A. 90ABC ∠= B. 90BAC ∠=
C. AB AC =
D. AC BC =
目标检测 2
2.
2.2.1.)
(,0)()(2,)92008(D C B A c c b c a c b a 的最大值是则满足
,若向量个互相垂直的单位向量是平面内已知浙江理=-⋅-
问题、疑惑汇集
知识、方法总结
本课的主要学习内容是什么
极化恒等式:
平行四边形模型:
三角形模型:
极化恒等式在处理与_________________有关问题时,显得较有优越性。
目标2-3:会用极化恒等式解决与数量积有关的综合问题
∆中,AB=
在ABC
.
AC。
