小波变换详解
(完整版)小波变换去噪基础知识整理

1.小波变换的概念小波(Wavelet)这一术语,顾名思义,“小波”就是小的波形。
所谓“小”是指它具有衰减性;而称之为“波”则是指它的波动性,其振幅正负相间的震荡形式。
与Fourier变换相比,小波变换是时间(空间)频率的局部化分析,它通过伸缩平移运算对信号(函数)逐步进行多尺度细化,最终达到高频处时间细分,低频处频率细分,能自动适应时频信号分析的要求,从而可聚焦到信号的任意细节,解决了Fourier变换的困难问题,成为继Fourier变换以来在科学方法上的重大突破。
有人把小波变换称为“数学显微镜”。
2.小波有哪几种形式?常用的有哪几种?具体用哪种,为什么?有几种定义小波(或者小波族)的方法:缩放滤波器:小波完全通过缩放滤波器g——一个低通有限脉冲响应(FIR)长度为2N和为1的滤波器——来定义。
在双正交小波的情况,分解和重建的滤波器分别定义。
高通滤波器的分析作为低通的QMF来计算,而重建滤波器为分解的时间反转。
例如Daubechies和Symlet 小波。
缩放函数:小波由时域中的小波函数(即母小波)和缩放函数(也称为父小波)来定义。
小波函数实际上是带通滤波器,每一级缩放将带宽减半。
这产生了一个问题,如果要覆盖整个谱需要无穷多的级。
缩放函数滤掉变换的最低级并保证整个谱被覆盖到。
对于有紧支撑的小波,可以视为有限长,并等价于缩放滤波器g。
例如Meyer小波。
小波函数:小波只有时域表示,作为小波函数。
例如墨西哥帽小波。
3.小波变换分类小波变换分成两个大类:离散小波变换(DWT) 和连续小波转换(CWT)。
两者的主要区别在于,连续变换在所有可能的缩放和平移上操作,而离散变换采用所有缩放和平移值的特定子集。
DWT用于信号编码而CWT用于信号分析。
所以,DWT通常用于工程和计算机科学而CWT经常用于科学研究。
4.小波变换的优点从图像处理的角度看,小波变换存在以下几个优点:(1)小波分解可以覆盖整个频域(提供了一个数学上完备的描述)(2)小波变换通过选取合适的滤波器,可以极大的减小或去除所提取得不同特征之间的相关性(3)小波变换具有“变焦”特性,在低频段可用高频率分辨率和低时间分辨率(宽分析窗口),在高频段,可用低频率分辨率和高时间分辨率(窄分析窗口)(4)小波变换实现上有快速算法(Mallat小波分解算法)另:1) 低熵性变化后的熵很低;2) 多分辨率特性边缘、尖峰、断点等;方法, 所以可以很好地刻画信号的非平稳特性3) 去相关性域更利于去噪;4) 选基灵活性: 由于小波变换可以灵活选择基底, 也可以根据信号特性和去噪要求选择多带小波、小波包、平移不变小波等。
小波变换

小波变换一、 小波变换原理:()f t 是平方可积函数,()t ψ是基本小波,则称1(,)()(),()f a t WT a f t dt a f t t τττψψ∞*-∞-⎧⎫=⎨⎬⎩⎭=⎰ 为 ()f t 的连续小波变换,简写为(,)f CWT a τ。
这里小波采用墨西哥帽小波:220.5()(1)t t t e ψ-=-。
二、实验仿真: (一)、当0τ=时,()a t τψ当0.5,1,2a =时,对应的()a t τψ如图1所示:-8-6-4-202468t/s图1 墨西哥帽小波簇()a t τψ由图1可以得到结论:随着a 越大,小波持续的时间越宽。
(二)、对a 取不同值的墨西哥帽小波做傅里叶变换,得到它们对应的频谱图如图2所示:012345678910w/radω图2 墨西哥帽小波频谱图从图2可以得到结论:随着a 成倍增大,中心频率与频率带宽都成倍减小。
从图2中可以看出2a =时,对应的中心频率约为00.7rad ω=;1a =时,对应的中心频率约为02 1.4rad ω=;12a =时,对应的中心频率约为04 2.8rad ω=。
(三)、假设基波频率00.7rad ω=,构造信号()f t ,其中1,020cos(0.7),2040()cos(1.4),4060cos(2.8),6080t t t f t t t t t ≤<⎧⎪≤<⎪=⎨≤<⎪⎪≤≤⎩如图3所示:1020304050607080t/s图3 ()f t 信号时域图(四)、根据公式(,)()f t WT a f t dta ττψ∞*-∞-⎧⎫=⎨⎬⎩⎭⎰,求出当10,30,50,70s τ=即位于不同频率中心时刻点时,对应小波变换的结果。
(1)在直流中心时刻10s τ=时,当a 取不同的值时,()f t 和,10()a t t a τψ*-⎧⎫=⎨⎬⎩⎭如图4所示:1020304050607080-202t/s a=0.51020304050607080-202t/s a=11020304050607080-202t/sa=2图4根据公式10(,10)()f t WT a f t dt a ψ∞*-∞-⎧⎫=⎨⎬⎩⎭⎰,可以得到随着a 的变化小波变换结果的幅度如图5所示:a图5 10s τ=时小波变换图从图5可以看出,在10s τ=时,小波变换结果随着a 的增大而单调递增,这是由于a 越大,其中心频率越小,越接近直流信号,所以a 越大,小波变换结果的值越大。
第3章小波变换简介

j t
d
da W f (a, b)a,b (t )db a 2 0
1 t b a ,b (t ) ( ) a a
小波系数的意义
Wf (a,b)表示信号与尺度为a小波的相关程 度。小波系数越大,二者越相似。
F ( )
f (t )e
j t
傅立叶变换
F ( )
f (t )e
j t
dt
将信号分解为不同频率的正弦波的叠加
傅立叶变换
架起了时域和频域的桥梁
只有频率分辨率而没有时间分辨率。 可确定信号中包含哪些频率的信号,但不能确 定具有这些频率的信号出现在什么时候。
傅立叶变换
如果想要研究函数在区间(a,b)上的性质, 一个很自然的想法就是利用函数 乘f(t)
小波变换简介
傅立叶变换
信号分析是为了获得时间和频率之间的相互关系。 1807年,Joseph Fourier 傅立叶变换以在两个方向上都无限伸展的正弦曲 线波作为正交基函数, 提供了有关频率域的信息, 但有关时间的局部化信息却基本丢失。 原因是对于瞬态信号或高度局部化的信号(如边 缘),由于这些成分并不类似于任何一个傅立叶 基函数,它们的变换系数(频谱)不紧凑的,频 谱上呈现出一幅相当混乱的构成 。
1980:Morlet 1970s,在法国石油公司工作的年轻地球物理 学家Jean Morlet提出小波变换 (wavelet transform,WT)的概念。 1980s,连续小波变换 (continuous wavelet transform, CWT)。 1986:Y. Meyer 法国科学家Y.Meyer与其同事创造性地构造出 具有一定衰减性的光滑函数,用于分析函数; 用缩放(dilations)与平移(translations)均为2 j(j≥0 的整数)的倍数构造了L2(R)空间的规范正交基, 使小波分析得到发展。
数字信号处理中的小波变换

数字信号处理中的小波变换数字信号处理是一种数字化处理技术,主要用于对连续信号进行采样和转换,以便在数值计算设备上进行处理。
在数字信号处理中,小波变换是一种重要的技术,可以用来分析和处理信号。
一、小波变换的定义和基本原理小波变换(Wavelet Transform)是一种数学变换方法,它将原始信号分解为不同尺度和频率的小波成分。
与傅里叶变换相比,小波变换具有更好的时域和频域分辨率,并且能够捕捉信号的瞬态特性。
小波变换的数学定义如下:∫f(t)ψ*(t-k)dt其中,f(t)表示原始信号,ψ(t)是小波函数,*表示复共轭,k表示平移参数。
小波变换通过在时域内对小波函数进行平移和缩放来分析信号的不同频率成分。
二、小波变换的应用领域小波变换在数字信号处理中有广泛的应用,下面是一些常见领域:1. 信号处理:小波变换可以用于信号去噪、信号压缩和谱分析等方面。
通过对信号进行小波分解和重构,可以提取信号的主要特征信息,去除噪声干扰,实现信号的有效处理和分析。
2. 图像处理:小波变换可以应用于图像压缩、图像去噪和图像分析等方面。
通过对图像进行小波分解和重构,可以实现图像的压缩存储、去除图像中的噪声,并提取图像的局部特征。
3. 视频处理:小波变换可以用于视频压缩、视频去噪和视频分析等方面。
通过对视频信号进行小波分解和重构,可以实现视频的高效压缩和去除视频中的噪声,提取视频的运动特征。
4. 生物医学工程:小波变换可以应用于生物信号处理和医学图像分析等方面。
通过对生物信号和医学图像进行小波分解和重构,可以实现生物信号的识别和分类,以及医学图像的分割和特征提取。
三、小波变换与傅里叶变换的比较小波变换和傅里叶变换都是信号分析的重要工具,它们之间存在一些区别和联系。
1. 分辨率:小波变换具有局部分辨率,可以捕捉信号的瞬态特性,而傅里叶变换具有全局分辨率,适用于分析信号的频率成分。
2. 多尺度性:小波变换可以分解信号为不同尺度的小波成分,可以提取信号的多尺度信息,而傅里叶变换只能提取信号在不同频率上的分量。
小波变换课件

小波变换的基本思想是将信号分 解成一系列的小波函数,每个小 波函数都有自己的频率和时间尺
度。
小波变换通过平移和缩放小波函 数,能够适应不同的频率和时间 尺度,从而实现对信号的精细分
析。
小波变换的特点
01
02
03
多尺度分析
小波变换能够同时分析信 号在不同频率和时间尺度 上的特性,提供更全面的 信号信息。
图像去噪
利用小波变换去除图像中的噪声,提高图像的清晰度和质 量。
在小波变换中,噪声通常表现为高频系数较大的值,通过 设置阈值去除这些高频系数,可以达到去噪的效果。去噪 后的图像能够更好地反映原始图像的特征和细节。
图像增强
ቤተ መጻሕፍቲ ባይዱ
利用小波变换增强图像的某些特征,突出显示或改善图像的某些部分。
通过调整小波变换后的系数,可以增强图像的边缘、纹理等特定特征。这种增强 方式能够突出显示图像中的重要信息,提高图像的可读性和识别效果。
在信号处理、图像处理、语音识别等 领域有广泛应用。
特点
能够同时分析信号的时域和频域特性 ,具有灵活的时频窗口和多分辨率分 析能力。
离散小波变换
定义
离散小波变换是对连续小波变换 的离散化,通过对小波函数的离 散化处理,实现对信号的近似和
细节分析。
特点
计算效率高,适合于数字信号处理 和计算机实现。
应用
在信号处理、图像处理、数据压缩等领域有广泛应用,如语音压缩、图像压缩 、数据挖掘等。
CHAPTER 04
小波变换在图像处理中的应用
图像压缩
利用小波变换对图像进行压缩,减少存储空间和传输带宽的 需求。
通过小波变换将图像分解为不同频率的子带,去除高频细节 ,保留低频信息,从而实现图像压缩。压缩后的图像可以通 过逆小波变换重新构造,保持图像质量的同时减小数据量。
小波变换的基本概念和原理

小波变换的基本概念和原理小波变换是一种数学工具,用于分析信号的频谱特性和时域特征。
它在信号处理、图像处理、数据压缩等领域有着广泛的应用。
本文将介绍小波变换的基本概念和原理。
一、什么是小波变换?小波变换是一种将信号分解为不同频率的成分的数学工具。
它类似于傅里叶变换,但不同之处在于小波变换不仅能提供频域信息,还能提供时域信息。
小波变换使用一组称为小波基函数的函数族,通过对信号进行连续或离散的变换,将信号分解为不同尺度和频率的成分。
二、小波基函数小波基函数是小波变换的基础。
它是一个用于描述信号特征的函数,具有局部性和可调节的频率特性。
常用的小波基函数有Morlet小波、Haar小波、Daubechies 小波等。
这些小波基函数具有不同的性质和应用场景,选择适当的小波基函数可以更好地适应信号的特征。
三、小波分解小波分解是将信号分解为不同尺度和频率的过程。
通过对信号进行连续或离散的小波变换,可以得到小波系数和小波尺度。
小波系数表示信号在不同尺度和频率下的能量分布,而小波尺度表示不同尺度下的信号特征。
小波分解可以将信号的局部特征和全局特征分离开来,为信号分析提供更多的信息。
四、小波重构小波重构是将信号从小波域恢复到时域的过程。
通过对小波系数进行逆变换,可以得到原始信号的近似重构。
小波重构可以根据需要选择保留部分小波系数,从而实现信号的压缩和去噪。
五、小波变换的应用小波变换在信号处理、图像处理、数据压缩等领域有着广泛的应用。
在信号处理中,小波变换可以用于信号去噪、特征提取、模式识别等任务。
在图像处理中,小波变换可以用于图像压缩、边缘检测、纹理分析等任务。
在数据压缩中,小波变换可以将信号的冗余信息去除,实现高效的数据压缩和存储。
六、小波变换的优势和局限性小波变换相比于傅里叶变换具有一些优势。
首先,小波变换可以提供更多的时域信息,对于非平稳信号和瞬态信号具有更好的分析能力。
其次,小波变换可以实现信号的局部分析,对于局部特征的提取和分析更为有效。
小波变换定义公式

小波变换定义公式1. 什么是小波变换?小波变换是一种数学方法,可以将任意复杂的信号分解成一系列基本的波形组成的信号组。
这些基本的波形组成的信号组称为小波基,而小波变换则是将信号转换到小波基上的过程。
小波变换通过将不同频率的信号分解成频率范围更窄的信号,从而提供了一种能够描述信号局部特征的方法。
2. 小波变换的定义公式设 x(t) 是一个连续时间信号,小波变换将信号转换到小波基上,得到小波系数 C(a,b):C(a,b)=∫x(t)ψ*ab(t) dt其中,ψ*ab(t) 是小波基函数,表示尺度为a,时移为b的小波基的共轭,a 和 b 分别表示尺度和位置参数,T 表示时间域上的范围。
3. 小波变换的特点和优势与傅里叶变换和短时傅里叶变换相比,小波变换具有以下特点和优势:(1)小波变换能够对非平稳信号进行分析,具有较好的时频局部性,能够提取信号短时的局部特征。
(2)小波变换能够对信号的高频部分和低频部分进行分离,具有较好的分辨率性。
(3)小波基函数无需是正交的,因此可选择适合不同信号处理需求的小波基函数。
(4)小波变换具有数据压缩和降噪的功能,可以有效地去除信号中的噪声和冗余信息。
4. 小波变换在实际应用中的应用小波变换在信号处理、图像处理和语音处理等方面具有广泛的应用。
例如,在信号处理中,小波变换可用于地震信号处理、生物信号处理和语音信号处理等方面;在图像处理中,小波变换可用于图像压缩、图像增强和边缘检测等方面;在语音处理中,小波变换可用于语音压缩、语音识别和语音增强等方面。
总之,小波变换作为一种有效的信号分析方法,在实际应用中发挥着重要的作用,对于提高信号处理的效率和精度都具有重要的意义。
小波变换
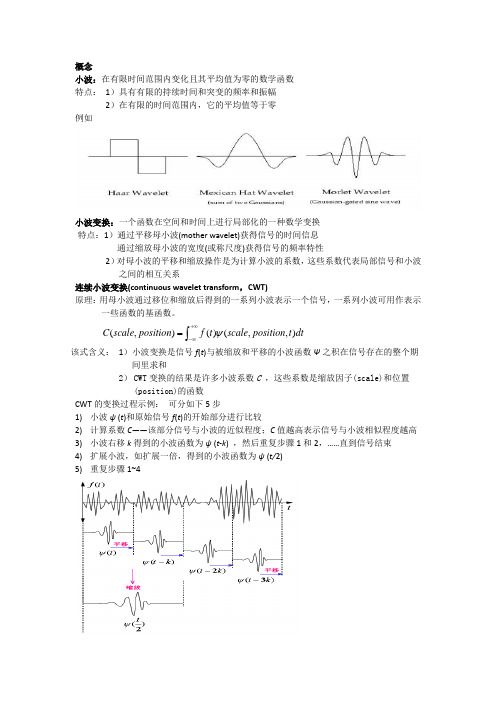
概念小波:在有限时间范围内变化且其平均值为零的数学函数特点: 1)具有有限的持续时间和突变的频率和振幅2)在有限的时间范围内,它的平均值等于零例如小波变换:一个函数在空间和时间上进行局部化的一种数学变换特点:1)通过平移母小波(mother wavelet)获得信号的时间信息通过缩放母小波的宽度(或称尺度)获得信号的频率特性2)对母小波的平移和缩放操作是为计算小波的系数,这些系数代表局部信号和小波 之间的相互关系连续小波变换(continuous wavelet transform ,CWT)原理:用母小波通过移位和缩放后得到的一系列小波表示一个信号,一系列小波可用作表示一些函数的基函数。
(,)()(,,)C scale position f t scale position t dt ψ+∞-∞=⎰该式含义: 1)小波变换是信号f (t )与被缩放和平移的小波函数Ψ之积在信号存在的整个期间里求和2) CWT 变换的结果是许多小波系数C ,这些系数是缩放因子(scale)和位置(position)的函数CWT 的变换过程示例: 可分如下5步1) 小波ψ (t )和原始信号f (t )的开始部分进行比较2) 计算系数C ——该部分信号与小波的近似程度;C 值越高表示信号与小波相似程度越高3) 小波右移k 得到的小波函数为ψ (t-k ) ,然后重复步骤1和2,……直到信号结束4) 扩展小波,如扩展一倍,得到的小波函数为ψ (t/2)5) 重复步骤1~4离散小波变换(discrete wavelet transform ,DWT)原理1)波的基函数序列或称子小波(baby wavelets)函数是由单个小波或称为母小波函数通过缩放和平移得到的2)缩放因子和平移参数都选择2j (j >0的整数)的倍数,这种变换称为双尺度小波变换 (dyadic wavelet transform)DWT 的变换过程示例:A 表示信号的近似值(approximations),大的缩放因子产生的系数,表示信号的低频分量D 表示信号的细节值(detail),小的缩放因子产生的系数,表示信号的高频分量小波分解树(wavelet decomposition tree)小波分解方式小波包分解树(wavelet packet decomposition tree)IDWT小波重构方法:一个最简单的小波变换:哈尔小波变换哈尔基:101()0x x φ≤<⎧=⎨⎩其他 哈尔基尺度函数:()(2),0,1,,(21)j j j i x x i i φφ=-=⋅⋅⋅-生成矢量空间V 0的常值函数:生成矢量空间V 1的常值函数:生成矢量空间V 2的常值函数:哈尔小波:101/2()11/210x x x ψ≤<⎧⎪=-≤<⎨⎪⎩当当其他生成矢量空间W 0的哈尔小波:生成矢量空间W1的哈尔小波:生成矢量空间W 2的哈尔小波:例、计算图像[9 7 3 5]的哈尔小波变换系数步骤1:求均值;步骤2:求差值;步骤3:重复步骤1和2;得[8 4 1-1] [6 2 1 -1] 22220123()9()7()3()5()I x x x x x φφφφ=+++11110101()8()4()1()1()I x x x x x φφψψ=++-00110001()6()2()1()1()I x x x x x φψψψ=++-。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
基于小波变换的人脸识别近年来,小波变换在科技界备受重视,不仅形成了一个新的数学分支,而且被广泛地应用于模式识别、信号处理、语音识别与合成、图像处理、计算机视觉等工程技术领域。
小波变换具有良好的时频域局部化特性,且其可通过对高频成分采取逐步精细的时域取样步长,从而达到聚焦对象任意细节的目的,这一特性被称为小波变换的“变聚焦”特性,小波变换也因此被人们冠以“数学显微镜”的美誉。
具体到人脸识别方面,小波变换能够将人脸图像分解成具有不同分辨率、频率特征以及不同方向特性的一系列子带信号,从而更好地实现不同分辨率的人脸图像特征提取。
4.1 小波变换的研究背景法国数学家傅立叶于1807年提出了著名的傅立叶变换,第一次引入“频率”的概念。
傅立叶变换用信号的频谱特性来研究和表示信号的时频特性,通过将复杂的时间信号转换到频率域中,使很多在时域中模糊不清的问题,在频域中一目了然。
在早期的信号处理领域,傅立叶变换具有重要的影响和地位。
定义信号(t)f 为在(-∞,+∞)内绝对可积的一个连续函数,则(t)f 的傅立叶变换定义如下:()()dt e t f F t j ωω-⎰∞-∞+= (4-1) 傅立叶变换的逆变换为:()()ωωπωd e F t f t j ⎰+∞∞-=21 (4-2)从上面两个式子可以看出,式(4-1)通过无限的时间量来实现对单个频率的频谱计算,该式表明()F ω这一频域过程的任一频率的值都是由整个时间域上的量所决定的。
可见,式(4-1)和(4-2)只是同一能量信号的两种不同表现形式。
尽管傅立叶变换可以关联信号的时频特征,从而分别从时域和频域对信号进行分析,但却无法将两者有效地结合起来,因此傅立叶变换在信号的局部化分析方面存在严重不足。
但在许多实际应用中,如地震信号分析、核医学图像信号分析等,研究者们往往需要了解某个局部时段上出现了哪个频率,或是某个频率出现在哪个时段上,即信号的时频局部化特征,傅立叶变换对于此类分析无能为力。
因此需要一种如下的数学工具:可以将信号的时域和频域结合起来构成信号的时频谱,描述和分析其时频联合特征,这就是所谓的时频局部化分析方法,即时频分析法。
1964年,Gabor 等人在傅立叶变换的基础上引入了一个时间局部化“窗函数”g(t),改进了傅立叶变换的不足,形成窗口化傅立叶变换,又称“Gabor 变换”。
定义“窗函数”(t)g 在有限的区间外恒等于零或很快地趋于零,用函数(t )g -τ乘以(t)f ,其效果等同于在t =τ附近打开一个窗口,即:()()()dt e t g t f G t j f ωττω-+∞∞--=⎰, (4-3)式(4-3)即为函数f(t)关于g(t)的Gabor 变换。
由定义可知,信号(t)f 的Gabor 变换可以反映该信号在t =τ附近的频谱特性。
其逆变换公式为:()()()ττωτωπωd G t g e d t f f t j ,21⎰⎰+∞∞---= (4-4)可见()τω,f G 的确包含了信号(t)f 的全部信息,且Gabor 窗口位置可以随着τ的变化而平移,符合信号时频局部化分析的要求。
虽然Gabor 变换一定程度上克服了傅立叶变换缺乏时频局部分析能力的不足,且兼顾信号的时频分辨率,但其本身仍存在不可克服的局限性,即Gabor 窗口不具有自适应性,其大小是固定不变的,因此Gabor 变换只能进行单一分辨率的分析。
而在实际研究中,我们常常希望窗口的大小会随着频率的高低而改变,比如在研究高频信号时,希望窗口开得小一点;反之,在研究低频信号时,则希望窗口开得大一点,这样才更符合实际研究中低频信号分辨率比高频信号分辨率低的特点,因此需要研究更好的解决办法来改善Gabor 变换的不足。
为了克服前面所描述的傅立叶变换和Gabor 变换存在的不足,学者们提出了小波变换(Wavelet Transform)。
4.2 小波变换与逆变换4.2.1 连续小波变换和离散小波变换小波变换是一种窗El 面积(即窗口大小)固定但窗口形状可变的时频局部化分析方法,其高频部分的时间分辨率较高而频率分辨率较低,而低频部分的频率分辨率较高而时间分辨率较低,因此对信号具有良好的自适应性,被冠以“数学显微镜”的美誉。
小波变换又可分为连续小波变换和离散小波变换两种。
连续小波变换的概念是由Morlet 等人提出[1]。
设()x ψ为小波变换的核函数,若核函数()()R L x 2∈ψ若满足容许性条件 :()()+∞<=⎰ωωωψψd F C R2(4-5)则称该函数)(x ϕ为基小波。
一维信号f(t))(2R L ∈的连续小波变换可定义为:()()()dx a b t x f ab a f W R⎪⎭⎫⎝⎛-=⎰ψψ1, (4-6)根据上述对基小波定义,可知:()∞<⎰dx x R ϕ,且()x ϕ在无穷远处趋近于零。
一般的,记:()⎪⎭⎫⎝⎛-=a b x x b a ϕϕ, R b a ∈,,a<0 (4-7) 函数()x b a ,ϕ是由基小波函数()x ϕ经过尺度a 的伸缩和b 的平移之后所得。
常用的连续小波包括:Morlet 小波、Daubechies 小波、三次样条小波、Meyer 小波和Simoncelli 小波等。
与连续小波变换相对应的是离散小波变换,其一般形式为:()()>==<n m f n m f W ,,,ϕϕ()dx a nb x x f a m Rm⎪⎪⎭⎫⎝⎛-⎰-002ϕ (4-8)其中()⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧∈⎪⎪⎭⎫⎝⎛-=-Z n m a nb x a x m m n m ,0020,ϕϕ为小波基,0a 、0b 为两个常量且0a >0。
离散小波最具代表性的为二进小波,即0a 为2的幂次J 2,0b 取整。
由于小波变换在时域和频域同时兼有局部化能力,且能逐步聚焦到对象的任何细节进行分析,因此在人脸识别方面得到众多研究者的关注。
4.2.2 几种常见的小波同傅立叶分析不同,小波分析的基(小波函数)不是唯一存在的,所有满足小波条件的函数都可以作为小波函数,那么小波函数的选取就成了十分重要的问题[8]。
(1) Haar 小波A.Haar 于1990年提出一种正交函数系,定义如下:⎪⎩⎪⎨⎧-=011)(x H ψ 其它12/12/10<≤≤≤x x (4-9)这是一种最简单的正交小波,即)()(=-⎰∞∞-dx n x t ψψ ,2,1±±=n (4-10)(2) Daubechies(dbN)小波系该小波是Daubechies 从两尺度方程系数{}k h 出发设计出来的离散正交小波。
一般简写为dbN ,N 是小波的阶数。
小波ψ和尺度函数阈中的支撑区为2N-1。
ϕ的消失矩为N 。
除N =1外(Haar 小波),dbN 不具对称性〔即非线性相位〕;dbN 没有显式表达式(除N =1外)。
但{}k h 的传递函数的模的平方有显式表达式。
假设∑-=+-=11)(N k kk N k y C y P ,其中,kN k C +-1为二项式的系数,则有)2(sin )2(cos )(2220ωωωP m N = (4-11)其中∑-=-=120021)(N k ik k e h m ωω(3) Biorthogonal(biorNr.Nd)小波系Biorthogonal 函数系的主要特征体现在具有线性相位性,它主要应用在信号与图像的重构中。
通常的用法是采用一个函数进行分解,用另外一个小波函数进行重构。
Biorthogonal 函数系通常表示为biorNr.Nd 的形式:Nr=1 Nd=1,3,5 Nr=2 Nd=2,4,6,8 Nr=3 Nd=1,3,5,7,9 Nr=4 Nd=4 Nr=5 Nd=5 Nr=6 Nd=8其中,r 表示重构,d 表示分解。
(4) Coiflet(coifN)小波系coiflet 也是函数由Daubechies 构造的一个小波函数,它具有coifN(N=1,2,3,4,5)这一系列,coiflet 具有比dbN 更好的对称性。
从支撑长度的角度看,coifN 具有和db3N 及sym3N 相同的支撑长度;从消失矩的数目来看,coifN 具有和db2N 及sym2N 相同的消失矩数目。
(5) SymletsA(symN)小波系Symlets 函数系是由Daubechies 提出的近似对称的小波函数,它是对db 函数的一种改进。
Symlets 函数系通常表示为symN(N=2,3,…,8)的形式。
(6) Morlet(morl)小波Morlet 函数定义为x Ce x x5cos )(2/2-=ψ,它的尺度函数不存在,且不具有正交性。
(7) Mexican Hat(mexh)小波 Mexican Hat 函数为2/24/12)1(32)(x e x x ---=ψπ (4-12)它是Gauss 函数的二阶导数,因为它像墨西哥帽的截面,所以有时称这个函数为墨西哥帽函数。
墨西哥帽函数在时间域与频率域都有很好的局部化,并且满足)(=⎰∞∞-dx x ψ (4-13)由于它的尺度函数不存在,所以不具有正交性。
(8) Meyer 函数Meyer 小波函数ψ和尺度函数ϕ都是在频率域中进行定义的,是具有紧支撑的正交小波。
⎪⎪⎪⎩⎪⎪⎪⎨⎧--=ψ--0))123(2cos()2())123(2sin()2()(ˆ2/2/12/2/1ωπυππωπυππωωωj j e e ]38,32[38343432ππωπωππωπ∉≤≤≤≤ (4-14) 其中,)(a υ为构造Meyer 小波的辅助函数,且有⎪⎪⎩⎪⎪⎨⎧-=--0))123(2cos()2()2()(ˆ2/12/1ωπυπππωφ 34343232πωπωππω>≤≤≤(4-15) 4.2.3 二维小波变换与逆变换把对一维的表示推广到二维,考虑二维尺度函数是可分离的情况,可有3个二维小波]9[,则二维尺度函数和小波函数可表示为:()()()y x y x ϕϕϕ=,()()()y x y x hψϕψ=, (4-16) ()()()y x y x v ϕψψ=,()()()y x y x d ψψψ=, (4-17) 设(){}21,k k c j表示一幅离散图像,用低通滤波器h 和高通滤波器g 分别对jc的每一行作滤波,并作隔点抽样,然后再用它们分别对jc 的每一列滤波并作隔点抽样,得到图像低频概貌1+j c 和图像高频细节h j d 1+,v j d 1+,dj d 1+,则有如下小波正变换(分解算法):()()()()∑∑--=+21212211211,22,k k k j k k c k n h k nh n n c()()()()∑∑--=+21212211211,22,k k k h j k k c k n g k nh n n d ()()()()∑∑--=+21212211211,22,k k k v j k k c k n h k ng n n d()()()()∑∑--=+21212211211,22,k k k d j k k c k n g k ng n n d (4-18)其小波逆变换(重构算法)如下式:()()()()()()()()()()()()()211221121122112112211211221121,2~2~,2~2~,2~2~,2~2~,11111111n n d n k g n kgn n d n k h n k g n n d n k g n k h n n c n k h n k h k k c d j n n v j n n h j n n k j n n j ++++--+--=--+--=∑∑∑∑∑∑∑∑(4-19)对于N×N像素的图像,小波变换能分解J 层,整数n J 2log ≤ 。
