9.3 裂缝计算方法
裂缝计算

8.2 裂缝宽度计算——荷载引起的裂缝宽度 在工程遇到裂缝原因很多 (1)荷载引起的裂缝
(2)温度、收缩裂缝
(3)构造裂缝
(4)施工裂缝
裂缝控制等级分为 (1)一级
(2)二级
(3)三级
ä Ç Í ú Á Ñ · ì ô Ç ¼ Ð Á Ñ · ì ô Ç ¼ Ð Á Ñ · ì
(a) Ê ú Ï ò º É Ô Ø Ï Â µ Ä Á Ñ · ì
荷载引起的裂缝
N
轴心受拉构件
P
P
P
P
受弯构件
一、裂缝的出现、分布与开展
ª Á ¿ Ñ Î » Ö Ã
¹ À ¿ Ç ¿ ¶ È · Ö ² ¼ ft,min (a) Ö á Ï ò ¿ ¹ À Ç ¿ ¶ È · Ö ² ¼
ª Á ¿ Ñ Ç °Ë ² ¼ ä Ó ¦ ± ä ª Á ¿ Ñ Ç °Ó ¦ ± ä · Ö ² ¼ ¯ Ð µ Ô Ê Ü À Ó ¦ ± ä · Ö ² ¼
deq——钢筋等效直径(mm)。
三、平均裂缝宽度
c wm s lcr clcr s (1 )lcr s
c c (1 ) s
采用rte 后,裂缝间距可统一表示为,
工字形截面有效受拉面积
lcr k2ck 1
d
r te
根据试验资料统计分析,并考虑受力特征的影响,对于常用的 带肋钢筋,《规范》给出的平均裂缝间距lm的计算公式为,
d eq l ( 1 . 9 c 0 . 08 ) cr
r te
c——最外层纵向受拉钢筋外边缘到受拉区底边的距离(mm;
★如果两条裂缝的间距小于2 l,则由于粘结应力传递长度不够,混 凝土拉应力不可能达到ft,因此将不会出现新的裂缝,裂缝的间距最 终将稳定在(l ~ 2 l)之间,平均间距可取1.5 l。 ★从第一条(批)裂缝出现到裂缝全部出齐为裂缝出现阶段,该阶 段的荷载增量并不大,主要取决于混凝土强度的离散程度。 ★裂缝间距的计算公式即是以该阶段的受力分析建立的。 ★裂缝出齐后,随着荷载的继续增加,裂缝宽度不断开展。裂缝的 开展是由于混凝土的回缩,钢筋不断伸长,导致钢筋与混凝土之间 产生变形差,这是裂缝宽度计算的依据。 ★由于混凝土材料的不均匀性,裂缝的出现、分布和开展具有很大 的离散性,因此裂缝间距和宽度也是不均匀的。但大量的试验统计 资料分析表明,裂缝间距和宽度的平均值具有一定规律性,是钢筋 与混凝土之间粘结受力机理的反映。
裂缝深度计算公式

裂缝深度计算公式
裂缝深度的计算公式通常取决于裂缝的类型和具体情况。
一般来说,裂缝深度可以通过以下公式进行估算:
裂缝深度 = 裂缝长度× 裂缝宽度 / 裂缝的平均角度。
裂缝深度也可以通过地质勘探和测量来准确测量。
在实际工程中,一般会根据具体情况采用不同的测量方法和公式来计算裂缝深度,以确保准确性和可靠性。
同时,裂缝深度的计算还可能受到地质构造、岩石性质、地下水位等因素的影响,因此在实际工程中需要综合考虑各种因素来确定裂缝深度的计算公式。
裂缝计算
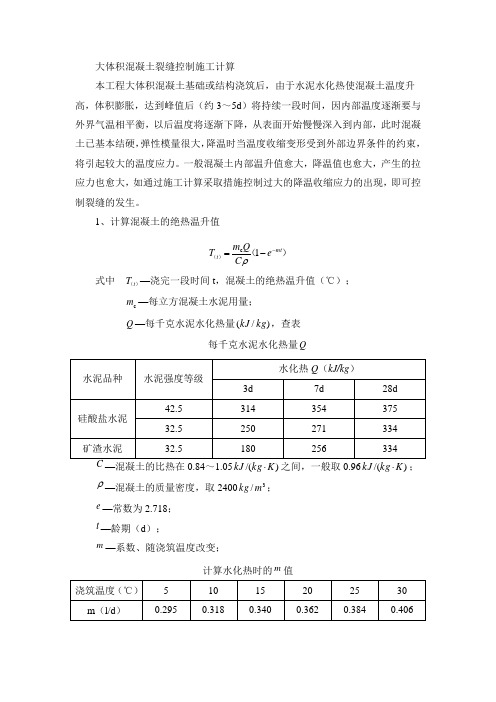
大体积混凝土裂缝控制施工计算本工程大体积混凝土基础或结构浇筑后,由于水泥水化热使混凝土温度升高,体积膨胀,达到峰值后(约3~5d )将持续一段时间,因内部温度逐渐要与外界气温相平衡,以后温度将逐渐下降,从表面开始慢慢深入到内部,此时混凝土已基本结硬,弹性模量很大,降温时当温度收缩变形受到外部边界条件的约束,将引起较大的温度应力。
一般混凝土内部温升值愈大,降温值也愈大,产生的拉应力也愈大,如通过施工计算采取措施控制过大的降温收缩应力的出现,即可控制裂缝的发生。
1、计算混凝土的绝热温升值)()(mt t e C Qm T --=1c ρ式中 )(t T —浇完一段时间t ,混凝土的绝热温升值(℃); c m —每立方混凝土水泥用量;Q —每千克水泥水化热量)/(kg kJ ,查表每千克水泥水化热量Q水泥品种水泥强度等级水化热Q (kJ/kg )3d 7d 28d 硅酸盐水泥 42.5 314 354 375 32.5 250 271 334 矿渣水泥32.5180256334C —混凝土的比热在0.84~1.05)/(K kg kJ ⋅之间,一般取0.96)/(K kg kJ ⋅;ρ—混凝土的质量密度,取24003/m kg ;e —常数为2.718;t —龄期(d );m —系数、随浇筑温度改变;计算水化热时的m 值浇筑温度(℃) 5 10 15 20 25 30 m (l/d )0.2950.3180.3400.3620.3840.406实际大体积混凝土基础或结构外表是散热的,混凝土的实际温升低于绝热温升,计算值偏于安全。
℃)()(00718.2-1240096.0375m T 284.0-c 28=⨯⨯=⨯2、计算各龄期混凝土收缩变形值n bt y t y M M M M e ⨯⋯⨯⨯⨯-=-3210)()1(εε式中 0y ε—标准状态下的最终收缩值(即极限收缩值),取41024.3-⨯;)(t y ε—非标准状态下混凝土任意龄期(d )的收缩变形值;e —常数为2.718; b —经验系数,取0.01;t —混凝土浇筑后至计算时的天数(d );n M M M M ⋯321、、—考虑各种非标准条件,与水泥品种细度、骨料品种、水灰比、水泥浆量、养护条件、环境相对湿度、构件尺寸、混凝土捣实方法、配筋率等有关的修正系数,按表取用。
第9章裂缝和挠度计算 PPT

e0
e0
1 荷载产生的裂缝
Ns Ns
(a)
Ns
Ts
Ns
(b)
Ns
Ns
(c)
(d)
T (e)
2 非荷载裂缝
非荷载裂缝一般通过构造措施控制。
为防止温度应力过大引起的开裂,规范规定了最大伸缩缝之间
非 荷
间距。
载
裂
缝 为防止由于钢筋周围砼过快的碳化失去对钢筋的保护作用,出现
控 制
锈胀引起的沿钢筋纵向的裂缝,规定了钢筋的混凝土保护层的最
标准组合并考虑 长期作用的影响
9.2 裂缝宽度验算
裂
半理论半经
分析裂缝形成开展机理,建立力学模
缝
验方法
宽
型,推导计算公式,试验资料确定计 算参数。
度
计
算
方
法
数理统计
分析试验资料,确定影响参数和主要
方法
因素,数理统计方法确定计算公式。
注:我国规范采用半理论半经验方法计算裂缝宽度。
9.2.1 裂缝出现与开展规律
小厚度。
通常,裂缝宽度和挠度一般可分别用控制最大钢筋直径和最大跨 高比来控制,只有在构件截面尺寸小,钢筋应力高时进行验算。
钢筋混凝土结构伸缩缝最大间距(m)
纵向受力钢筋的混凝土最小保护层厚度(mm)
注:混凝土保护层厚度不应小于钢筋的公称直径。基础中纵向受力钢 筋保护层厚度不应小于40mm,当无垫层时不应小于70mm。 有防火要求建筑,其混凝土保护层厚度应符合有关规定。
结构构件的裂缝控制公式
m ax lim
结构构件的裂缝控制及最大裂缝宽度限值
混凝土结构的环境类别
严寒:最冷月平均温度≤-10度,日平均温度不高于5度的天数≥145天; 寒冷:最冷月平均温度0~-10度,日平均温度不高于5度天数90~145天。
裂缝和挠度计算

材料强度
材料强度原则值
按荷载效应 旳原则组组合
原则组合并考虑 长久作用旳影响
裂缝计算
裂缝宽度计算措施
m
lcr 0
( s
c )dl
( sm
cm )lcr
1
cm sm
sm
lcr
c
sm
Es
lcr
式中: c
1
cm sm
,考虑裂缝间砼本身伸长对裂缝宽度旳影响系数;
与配筋率、截面形式、砼保护层厚度等原因有关,但在一般情况下变化
裂缝计算
9.2.2 平均裂缝间距
无粘结滑移理论以为钢筋与混凝土之间旳粘结滑移很小,裂缝宽度在
钢筋处为0,在混凝土表面最大,裂缝宽度距离钢筋越远越大,裂缝
宽度是因为钢筋外围混凝土弹性收缩引起,混凝土保护层是影响裂缝
宽度旳主要原因。综合粘结滑移理论和无粘结滑移理论,根据试验资
料分析得到平均裂缝间距计算公式为:
cq 准永久荷载作用下抗裂验算边沿混凝土旳预压应力。
裂缝计算
9.1.1 裂缝控制旳三个等级
3 三级:构件上允许出现拉应力,但对裂缝宽度需要进行控制。 要求:在荷载效应原则组合并考虑长久作用影响旳最大裂缝宽度不超出 要求旳限值(详细计算见后)。
注意 (1)一级、二级为抗裂验算,一般属于预应力混凝土构件;三级为裂 缝宽度验算,一般属于一般混凝土构件; (2)一般混凝土构件在使用中一般会存在裂缝,但是过大旳裂缝宽度 会影响构造外观并影响正常使用。 (3)裂缝控制等级和裂缝宽度限值根据环境类别和构造类别拟定(附 表1-13)。
裂缝计算

4,持久状况正常使用极限状态下裂缝宽度验算按《公预规》的规定,最大裂缝宽度按下式计算:12330()0.2810ss fK S d W C C C E σρ+=+ 0()s f fA bh b b h ρ=- 式中:1C :钢筋表面形状系数,取1C =1.0;2C :作用长期效应影响系数,长期荷载作用时,2C =1+0.5l sN N ,l N 和s N 分别按作用长期效应组合和短期组合效应计算的内力值; 3C —与构件受力有关的系数,取3C =1.0;d —受拉钢筋的直径,若直径不同可用换算直径代替;ρ—纵向受拉钢筋的配筋率;S E —钢筋的弹性模量;f b —构件的翼缘宽度f h —构件的受拉翼缘厚度ss σ—受拉钢筋在使用荷载下的应力,按《公预规》公式计算:0.87S s S M A h σ= 式中:S M —按构件长期效应组合计算的弯矩值;S A —受拉钢筋纵向受拉钢筋截面面积; 由0()s f fA bh b b h ρ=-得到: 56800.1641801057(1600180)110ρ==⨯+-⨯ 根据前文计算,取1号梁的跨中弯矩效应进行组合212110.7 1.0(587.10.7579.8/1.31)896.9m n s GiK j QjK G Q K Q K i j M S S M M M kN mφ===+=++=+⨯=⋅∑∑长期效应组合:212110.40.4587.1(0.4579.8/1.31)765.5m n s GiK j QjK G Q K Q K i j M S S M M M kN mψ===+=++=+⨯=⋅∑∑受拉钢筋在短期效应组合作用下的应力为:60896.910171.70.87568010570.87S s S MPa M A h σ⨯==⨯⨯= 20.50.5765.511 1.43896.3s t N C N ⨯=+=+= 钢筋为HRB335,52.010s MPa E =⨯,代入12330()0.2810ss fK S d W C C C E σρ+=+后得: 5171.730311.0 1.43 1.0()0.20.28100.1642.010LK mm W +=⨯⨯⨯⨯<+⨯⨯ 满足《公预规》“在一般正常大气作用下,钢筋混凝土受弯构件不超过最大裂缝宽度”要求,还满足《公预规》规定“在梁腹高的两侧设置直径为φ6-φ8的纵向防裂钢筋,以防止裂缝的产生”本例中采用6φ8,则:'''301.8301.8,0.00141801200s S s A mm bh A μ====⨯,介于0.0012-0.002之间,可行。
第九章_钢筋混凝土构件_抗裂度和裂缝计算(第二课)
Ns Ncr 1
N
ct=ftk
(a)
1 ftk (b)
Ncr
Ns
s
(c) (d)
ss
max
第九章 变形和裂缝宽度的计算
2 裂缝的开展
★当荷载达到0.5Mu0~ 0.7Mu0时,裂缝基本“出齐”。 两条裂缝 的间距小于2 l,由于粘结应力传递长度不够,砼拉应力不可能 达到ft,因此将不会出现新的裂缝,裂缝的间距最终将稳定在 (l ~ 2 l)之间,平均间距可取1.5 l。
f
b hf bh
•• • •
第九章 变形和裂缝宽度的计算
9.2.2 轴心受拉构件抗裂度的计算
由力的平衡条件可得开裂轴向拉力:
Ncr Ac ftk As 2 E ftk ftk Ac 2 E As
As/2
Asσs/2 Ncr
Asσs/2
As/2 ftk
第九章 变形和裂缝宽度的计算
或
tu 2 ftk Ec
第九章 变形和裂缝宽度的计算
截面各纤维应变: 受拉钢筋应变:
2 ftk s tu Ec
X cr a X cr a s s 2 f tk s tu h X cr h X cr Ec
X cr X cr 2f tu tk h X cr h X cr Ec
第二讲主要内容 • 钢筋混凝土受弯构件最大裂缝宽度的计算方法及验算要求; • 改善裂缝宽度的措施; • 截面弯曲刚度的概念及短、长期刚度的计算方法; • 最小刚度原则及挠度的计算方法。 第二讲重点内容
• 钢筋混凝土受弯构件最大裂缝宽度的计算方法及验算要求;
• 截面弯曲刚度的概念及短、长期刚度的计算方法; • 最小刚度原则及挠度的计算方法。
混凝土裂缝计算
混凝土裂缝计算混凝土是建筑工程中广泛使用的材料之一,但在使用过程中,混凝土裂缝是一个常见的问题。
混凝土裂缝的出现不仅会影响建筑物的外观,还可能降低其结构的安全性和耐久性。
因此,准确地计算混凝土裂缝对于工程设计和施工至关重要。
混凝土裂缝产生的原因是多种多样的。
首先,混凝土在硬化过程中会发生收缩,如果这种收缩受到约束,就容易产生裂缝。
其次,荷载作用也是导致混凝土裂缝的重要原因,例如建筑物承受的静荷载、动荷载等超过了混凝土的承载能力。
此外,温度变化、基础不均匀沉降、钢筋锈蚀等因素也可能引发混凝土裂缝。
为了计算混凝土裂缝,需要考虑多个因素。
其中,混凝土的抗拉强度是一个关键参数。
抗拉强度越低,混凝土越容易开裂。
在计算时,通常会参考相关的规范和标准中给出的混凝土抗拉强度值。
另一个重要因素是混凝土所承受的应力。
应力的计算需要综合考虑荷载、温度变化、收缩等多种因素的影响。
例如,在计算由于荷载引起的应力时,需要根据结构的受力情况,运用力学原理进行分析。
而对于温度变化和收缩产生的应力,计算方法则有所不同。
在实际工程中,常用的混凝土裂缝计算方法有多种。
其中,比较常见的是基于线弹性理论的计算方法。
这种方法假设混凝土材料在受力时的变形是线性的,通过计算应力和抗拉强度的比值来评估裂缝的开展情况。
然而,需要注意的是,混凝土实际上是一种非线性材料,在较大应力作用下会表现出明显的非线性特性。
因此,线弹性理论的计算结果可能存在一定的误差。
为了更准确地计算混凝土裂缝,一些非线性计算方法也逐渐得到应用。
例如,有限元法可以考虑混凝土材料的非线性特性,通过建立复杂的数值模型来模拟混凝土结构在各种工况下的受力和变形情况,从而更精确地计算裂缝的开展和分布。
在计算混凝土裂缝时,还需要考虑钢筋对混凝土裂缝的约束作用。
钢筋可以承担一部分拉力,从而减小混凝土中的应力,限制裂缝的开展宽度。
因此,在计算中需要合理考虑钢筋的配筋率、直径、间距等参数对裂缝的影响。
裂缝宽度计算
正截面裂缝宽度计算
梁横向裂缝
正截面裂缝宽度计算
正截面裂缝宽度计算
正截面裂缝宽度计算
剪力墙X形 剪力墙 形裂缝
正截面裂缝宽度计算
2.变形因素引起的裂缝 变形因素引起的裂缝——温度变化引起的裂缝 变形因素引起的裂缝
δT
气温升高时
温度区段
正截面裂缝宽度计算
变形因素引起的裂缝——钢筋锈蚀引起的裂缝 变形因素引起的裂缝
受弯、偏拉、偏压构件 受弯、偏拉、 轴拉构件
Ate = 0.5bh + ( bf −b) hf
Ate取全截面
平均裂缝宽度
正截面裂缝宽度计算
平均裂缝间距 lm 对于常用的带肋钢筋, 规范》 对于常用的带肋钢筋,《规范》给出的平均裂缝间 距 lm 的计算公式为
轴心受拉构件
lm =1.1(1.9c + 0.08
正截面裂缝宽度计算
我国《规范》 裂缝控制等级分为三级 我国《规范》将裂缝控制等级分为三级 分为
一级:严格要求不出现裂缝的构件。 一级:严格要求不出现裂缝的构件。 二级:一般要求不出现裂缝的构件。 二级:一般要求不出现裂缝的构件。 三级:允许出现裂缝的构件。 普通钢筋混凝土构件 三级:允许出现裂缝的构件。—普通钢筋混凝土构件 按荷载效应标准组合并考虑荷载长期作用影响验算时,构 按荷载效应标准组合并考虑荷载长期作用影响验算时, 件的最大裂缝宽度ωmax不应超过最大裂缝宽度限值ωlim, 即:
正截面裂缝宽度计算
最大裂缝宽度计算公式
wmax = ττ l wm
式中, ωm—平均裂缝宽度; 平均裂缝宽度; 式中, τ——荷载短期效应裂缝扩大系数 ; ——荷载短期效应裂缝扩大系数 对受弯构件,取τ =1.66 。 受弯构件, 对于轴心受拉和偏心受拉构件 对于轴心受拉和偏心受拉构件,取τ =1.9 。 轴心受拉和偏心受拉构件,
裂缝计算
4,持久状况正常使用极限状态下裂缝宽度验算按《公预规》的规定,最大裂缝宽度按下式计算:12330()0.2810ss fK S d W C C C E σρ+=+ 0()s f fA bh b b h ρ=- 式中:1C :钢筋表面形状系数,取1C =1.0;2C :作用长期效应影响系数,长期荷载作用时,2C =1+0.5l sN N ,l N 和s N 分别按作用长期效应组合和短期组合效应计算的内力值; 3C —与构件受力有关的系数,取3C =1.0;d —受拉钢筋的直径,若直径不同可用换算直径代替;ρ—纵向受拉钢筋的配筋率;S E —钢筋的弹性模量;f b —构件的翼缘宽度f h —构件的受拉翼缘厚度ss σ—受拉钢筋在使用荷载下的应力,按《公预规》公式计算:0.87S s S M A h σ= 式中:S M —按构件长期效应组合计算的弯矩值;S A —受拉钢筋纵向受拉钢筋截面面积; 由0()s f fA bh b b h ρ=-得到: 56800.1641801057(1600180)110ρ==⨯+-⨯ 根据前文计算,取1号梁的跨中弯矩效应进行组合212110.7 1.0(587.10.7579.8/1.31)896.9m n s GiK j QjK G Q K Q K i j M S S M M M kN mφ===+=++=+⨯=⋅∑∑长期效应组合:212110.40.4587.1(0.4579.8/1.31)765.5m n s GiK j QjK G Q K Q K i j M S S M M M kN mψ===+=++=+⨯=⋅∑∑受拉钢筋在短期效应组合作用下的应力为:60896.910171.70.87568010570.87S s S MPa M A h σ⨯==⨯⨯= 20.50.5765.511 1.43896.3s t N C N ⨯=+=+= 钢筋为HRB335,52.010s MPa E =⨯,代入12330()0.2810ss fK S d W C C C E σρ+=+后得: 5171.730311.0 1.43 1.0()0.20.28100.1642.010LK mm W +=⨯⨯⨯⨯<+⨯⨯ 满足《公预规》“在一般正常大气作用下,钢筋混凝土受弯构件不超过最大裂缝宽度”要求,还满足《公预规》规定“在梁腹高的两侧设置直径为φ6-φ8的纵向防裂钢筋,以防止裂缝的产生”本例中采用6φ8,则:'''301.8301.8,0.00141801200s S s A mm bh A μ====⨯,介于0.0012-0.002之间,可行。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
sk
(1 . 9 c 0 . 08
Es
r te
)
受弯构件 cr =1.5×1.66×0.85=2.1 构件受力特征系数
类 型
轴心受拉构件 cr =1.5×1.9×0.85×1.1=2.7
钢筋砼构件
预应力砼构件
受弯、偏心受压
偏心受拉
2.1
2.4
1.7
--
轴心受拉
2.7
t m d
4 tm
r te
9.3 裂缝宽度的计算
第九章 变形和裂缝宽度的计算
l
f t Ac
t mu
1
4 tm
ft
d
r
lm K 1
d
r te
◆ 上式表明,当配筋率r 相同时,钢筋直径越细,裂缝间距越小,裂缝宽度 也越小,也即裂缝的分布和开展会密而细,这是控制裂缝宽度的一个重要原 则。
★对直接承受重复荷载作用的构件,取 =1.0。
9.3 裂缝宽度的计算
第九章 变形和裂缝宽度的计算
M
c
0 . 8 [ 0 . 5 bh ( b f b ) h f ] f tk c h
M
k
s
sk
A s h 0
近似取c/ =0.67,h/h0=1.1, r te
As 0 . 5 bh ( b f b ) h f
对于受弯构件,可将受拉区近似作为一 轴心受拉构件,根据粘结力的有效影响 范围,取有效受拉面积Ate=0.5bh+(bfb)hf,因此将式中配筋率r 的用以下受 拉区有效配筋率替换后,即可用于受弯 构件
lm K 2 c K 1
d eq
r te
r te
As 0 . 5 bh ( b f b ) h f
取超越概率为5%的最大裂缝宽度可由下式求得:
w max w m (1 1 . 645 )
式中 为裂缝宽度变异系数,
对受弯构件,试验统计得 =0.4,故取裂缝扩大系数t =1.66。
对于轴心受拉和偏心受拉构件,由试验结果统计得最大裂缝宽 度的扩大系数为t =1.9。
9.3 裂缝宽度的计算
第九章 变形和裂缝宽度的计算
长期荷载的影响:由于混凝土的滑移徐变和拉应力的松弛,
会导致裂缝间混凝土不断退出受拉工作,钢筋平均应变增大, 使裂缝随时间推移逐渐增大。 混凝土的收缩也使裂缝间混凝土的长度缩短,也引起裂缝随时 间推移不断增大。 荷载的变动,环境温度的变化,都会使钢筋与混凝土之间的粘 结受到削弱,也将导致裂缝宽度不断增大。 根据长期观测结果,长期荷载下裂缝的扩大系数为t l =1.5。
' f
偏心受弯构件
s
sk
N k (e h0 )
h0 As
)(
h0 e
)
2
偏心受拉构件
s
sk
Nke
' '
As (h0 a s )
9.3 裂缝宽度的计算
9.3 裂缝宽度的计算
第九章 变形和裂缝宽度的计算
二、裂缝间距
s
s1 A s
s
s2
A s f t Ate
s s1 A s s s 2 A s t m u l
t m u l f t Ate
l f t A te f t A te
1 ft d
t mu
r te
d )
轴心受拉构件
l m 1 . 1(1 . 9 c 0 . 08
r te
c——最外层纵向受拉钢筋外边缘到受拉区底边的距离(mm), 当c<20mm时,取c=20mm; d——钢筋直径(mm),当用不同直径的钢筋时,d改用换算直 径4As/u,u为纵向钢筋的总周长。
9.3 裂缝宽度的计算
采用rte 后,裂缝间距可统一表示为:
lm K 2 c K 1
d eq
r te
9.3 裂缝宽度的计算
第九章 变形和裂缝宽度的计算
根据试验资料统计分析,并考虑受力特征的影响,对于常用的 带肋钢筋,《规范》给出的平均裂缝间距lm的计算公式为: 受弯构件
l m 1 . 9 c 0 . 08 d
1
s sm s
增 量 Ds 成 正 比 , Ds 则 取 决 于 开 裂 时截面受拉区混凝土退出拉力的大 小,也即与开裂时截面混凝土部分 所承担的弯矩 Mc 成正 比。所以, ( s s ) / s 与 M c / M 成 正 比 。 因 此, 可表示为 M 与M
2.2
9.3 裂缝宽度的计算
第九章 变形和裂缝宽度的计算
六、裂缝截面处钢筋应力
受弯构件
s
sk
w max cr
M
k
s
sk
(1 . 9 c 0 . 08 87 A s h 0
轴心受拉构件
s
sk
Nk As
h 0 0 . 87
0 . 87 0 . 12 (1
f tk
Mc 1 . 1 1 M
1 . 1 0 . 65
s
sk
r te
9.3 裂缝宽度的计算
第九章 变形和裂缝宽度的计算
四、最大裂缝宽度
实测表明,裂缝宽度具有很大的离散性。 取实测裂缝宽度wt与上述计算的平均裂缝宽度wm的比值为t 。
大量裂缝量测结果统计表明,t 的概率密度分布基本为正态。
钢筋应力不均匀系数 sm s
由于钢筋与混凝土间存在粘结应力,随着距裂缝截面距离的增 加,裂缝间混凝土逐渐参与受拉工作,钢筋应力逐渐减小,因此 钢筋应力沿纵向的分布是不均匀的。 裂缝截面处钢筋应力最大,裂缝中间钢筋应力最小,其差值反映 了混凝土参与受拉工作的大小。
钢筋应力不均匀系数 是反映 裂缝间混凝土参加受拉工作程 度的影响系数
◆ 但上式中,当d/r te趋于零时,裂缝间距趋于零,这并不符合实际情况。
◆ 试验表明,当d/r 很大时,裂缝间距趋近于某个常数。该数值与保护层c 和钢筋净间距有关,根据试验分析,对上式修正如下:
lm K 2 c K 1
d eq
r te
9.3 裂缝宽度的计算
第九章 变形和裂缝宽度的计算
9.3 裂缝宽度的计算
第九章 变形和裂缝宽度的计算
★如果两条裂缝的间距小于2 l,则由于粘结应力传递长度不够,混凝土拉应 力不可能达到ft,因此将不会出现新的裂缝,裂缝的间距最终将稳定在(l ~ 2 l)之间,平均间距可取1.5 l。 ★从第一条(批)裂缝出现到裂缝全部出齐为裂缝出现阶段,该阶段的荷载 增量并不大,主要取决于混凝土强度的离散程度。 ★裂缝间距的计算公式即是以该阶段的受力分析建立的。 ★裂缝出齐后,随着荷载的继续增加,裂缝宽度不断开展。裂缝的开展是由 于混凝土的回缩,钢筋不断伸长,导致钢筋与混凝土之间产生变形差,这是 裂缝宽度计算的依据。 ★由于混凝土材料的不均匀性,裂缝的出现、分布和开展具有很大的离散性, 因此裂缝间距和宽度也是不均匀的。但大量的试验统计资料分析表明,裂缝 间距和宽度的平均值具有一定规律性,是钢筋与混凝土之间粘结受力机理的 反映。
c c
M My
s
s
½ ù ¦ ä Æ ¾ Ó ± s Ñ ì Ø æ Á ·½ Ã
/ M 的函数。
/ M 关系的试验结果为 :
Mcr
s s
Ds
Mc 1 . 1 1 M
9.3 裂缝宽度的计算
第九章 变形和裂缝宽度的计算
★当 <0.2时,取 =0.2;当 >1.0时,取 =1.0;
★裂缝出现瞬间,裂缝截面位置的混凝土退出受拉工作,应力为零,而钢筋 拉应力应力产生突增Dss= ft /r,配筋率越小,Dss就越大。
★由于钢筋与混凝土之间存在粘结,随着距裂缝截面距离的增加,混凝土中 又重新建立起拉应力sc,而钢筋的拉应力则随距裂缝截面距离的增加而减小。 ★当距裂缝截面有足够的长度 l 时,混凝土拉应力sc增大到ft,此时将出现新 的裂缝。
w max t t l w m 0 . 85 t t l
w max cr
s
sk
Es
lm
s
sk
(1 . 9 c 0 . 08
d eq
Es
r te
)
9.3 裂缝宽度的计算
第九章 变形和裂缝宽度的计算
最大裂缝宽度验算
s
w max w lim
d eq
Wlim——《混凝土结构设计规范》规定的允许最大裂缝宽度
第九章 变形和裂缝宽度的计算
9.3 裂缝宽度计算——荷载引起的裂缝宽度
一、裂缝的出现、分布与开展
9.3 裂缝宽度的计算
第九章 变形和裂缝宽度的计算
★在裂缝出现前,混凝土和钢筋的应变沿构件的长度基本上是均匀分布的。 ★当混凝土的拉应力达到抗拉强度时,首先会在构件最薄弱截面位置出现第 一条(批)裂缝。
第九章 变形和裂缝宽度的计算
三、裂缝宽度
w m sm l m ctml m sm (1
ctm sm
ctm sm
s
)lm
(1
) 0 . 85
sm
s
sk
Es
◆平均裂缝宽度
w m 0 . 85
s
sk
Es
lm
9.3 裂缝宽度的计算
第九章 变形和裂缝宽度的计算
sm s
1
s sm s
9.3 裂缝宽度的计算
第九章 变形和裂缝宽度的计算
式 中 , 裂 缝 截 面 的 钢 筋 应 变 s 与 作 用 弯 矩 M 成 正 比 ; 而 应 变 差
